Capítulo 2 Variación y equilibrio de Hardy-Weinberg

Una de las características evidentes de la vida en nuestro planeta es la heterogeneidad de los organismos, aún dentro del nivel taxonómico más bajo que se nos ocurra para clasificarlos razonablemente (por ejemplo, especie o sub-especie). Es decir, aún a simple vista podemos usualmente distinguir esa “falta de uniformidad” como una de las características aparentemente distintivas de los seres vivos. Pensemos esto en contraposición con el resultado de los productos industriales, como autos, lámparas LED, televisores, etcétera. Existe en estos objetos artificiales muchísima homogeneidad, más allá de que el uso de todas estas cosas las transforma de alguna manera en únicas (en general luego de un tiempo y más allá de la matrícula o el número de chasis, todos somos capaces de reconocer nuestro propio vehículo, especialmente si en el mismo viajan 4 niñas pequeñas). Como veremos y analizaremos más adelante, el fenotipo, aquello que podemos observar (usualmente a simple vista en los organismos macroscópicos, luego veremos definiciones más precisas) es el producto de la información contenida en el genotipo (la información genética, aunque veremos que esto no es muy preciso dicho así) y de su interacción con el ambiente, que a los efectos operacionales termina siendo todo lo no-genético.

La importancia de “lo genético” en el fenotipo no deja lugar a dudas: por un lado, los individuos “similares” se aparean entre ellos y no con los “distintos” (tanto sea a nivel de especie, o sub-especie, por ejemplo). Por otro lado, en un mismo ambiente co-existen individuos muy distintos (i.e., individuos pertenecientes a especies diferentes), por lo que el ambiente per se no estaría determinando una gran parte de los fenotipos. Pese a esta importancia de lo genético, entender los mecanismos que están por detrás de este fenómeno fue un proceso largo y complejo que recién pasada la mitad del siglo XX permitió elaborar una teoría relativamente completa a los distintos niveles involucrados (desde el nivel macro de los organismos, al nivel molecular del ADN, pasando por los niveles de organización intermedia de la información y sus formas de transferencia). Más aún, gran parte de la teoría en genética fue desarrollada sin conocer los mecanismos explícitos subyacentes, lo que llevó a interesantes confrontaciones académicas entre teorías que explicaban mejor o peor una parte de los datos (el debate del inicio del siglo XX entre mendelianos y biométricos, por ejemplo). Esto viene a colación porque el concepto de gen ha ido cambiando con el paso del siglo, así como la interpretación del concepto de alelo, pensada originalmente como una de pocas formas alternativas posibles (estados) de un gen. Desde hace muchos años, la comprensión de las bases moleculares de la herencia (o de algunas, al menos) nos ha permitido entender que la variabilidad subyacente es enorme. La misma comprende la existencia de SNPs (que pueden rondar el orden de 1/1000 bases en diferentes especies de mamíferos, por ejemplo), o la existencia de “indels”, variantes en el número de copias -CNVs-, etc. Esto implica que el número de formas alternativas de un gen en la población también puede ser enorme, y solemos recurrir a un concepto más operacional del término alelo: una forma alternativa del gen que tiene consecuencias para nuestro fenotipo.

En un sentido importante la realidad de la genética ha experimentado un cambio trascendental en los últimos decenios: hasta hace relativamente poco (aunque parezca increíble para los lectores más jóvenes) el genotipo real de los individuos era en general desconocido y muchas veces imposible de determinar, excepto a través de experimentos o del análisis de un gran número de descendientes. Sin embargo, con la aparición de las tecnologías de genotipado y de secuenciado masivo (NGS, Next Generation Sequencing, por ejemplo) esto ha cambiado definitivamente y hoy en día esto no solo es posible, sino que constituye una alternativa real en mejoramiento genético (por ejemplo genotipado de reproductores en varios programas de mejoramiento genético). Más allá de la definición que usemos para el concepto de alelo y en qué nivel de variación estemos pensando, es posible analizar la relación esperada entre la frecuencia de los distintos alelos y los genotipos que se forman por su combinación al azar. En este capítulo introduciremos un modelo matemático básico para esto (conocido como equilibrio de Hardy-Weinberg), el cual nos será de utilidad en varios capítulos posteriores. El uso de modelado matemático (y el contraste entre las predicciones de estos modelos y los datos observados en las poblaciones naturales) constituye una de las bases de la genética de poblaciones como disciplina.

OBJETIVOS DEL CAPÍTULO

\(\square\) Introducir el modelo de Hardy-Weinberg. Este es un modelo matemático sencillo que, basado en una serie de premisas claras, nos permite estimar las frecuencias genotípicas esperadas en una población a partir de sus frecuencias alélicas.

\(\square\) Adaptar el modelo básico planteado para modelar y realizar predicciones en distintos escenarios de relevancia biológica, como lo son la existencia de dos sexos distinguibles en la población, el comportamiento de alelos ligados a cromosomas sexuales, la existencia de más de dos alelos en el locus estudiado o la existencia de poliploidías en la especie estudiada.

\(\square\) Discutir aspectos prácticos de la aplicación de este modelo, tales como la repercusión del tamaño muestral al momento de estimar frecuencias alélicas, o la derivación de modelos para la estimación de frecuencias basándose en el conteo de individuos.

2.1 El equilibrio de Hardy-Weinberg

La “ley de Hardy-Weinberg”, a veces conocida también como de Hardy-Weinberg-Castle por los trabajos de Castle (1903), Hardy (1908) y Weinberg (1908),²¹ es posiblemente uno de los resultados mejor conocidos de la genética de poblaciones. La misma permite predecir la composición de genotipos en un locus determinado, una vez alcanzado el equilibrio, a partir de la frecuencia de los alelos cuando se cumplen una serie de condiciones (básicamente, el apareamiento aleatorio entre los individuos de la población). La base de la misma es conceptualmente sencilla: en un individuo diploide, la probabilidad de observar un genotipo en particular en un locus autosómico determinado (es decir, no se encuentra en los cromosomas “sexuales”) es el producto de la frecuencia de los gametos que lo formaron. Pongamos un ejemplo sencillo para mostrarlo; supongamos un locus autosómico con dos alelos, \(A_1\) y \(A_2\), con frecuencias \(p\) y \(q\). Tenemos \(q=1-p\), ya que la suma de las frecuencias de los dos alelos debe ser 1 (ya que asumimos que este locus solo tiene 2 alelos). Más aún, supongamos que se trata de una especie diploide hermafrodita, es decir, todos los individuos producen gametos masculinos y femeninos. Para simplificar aún más, asumamos que estos gametos se colocan en dos “pools”: uno de gametos masculinos y otro de gametos femeninos, todos los individuos produciendo exactamente la misma cantidad de gametos. Para simplificar el efecto del tamaño poblacional, asumimos también que dos gametos provenientes del mismo individuo, uno masculino y otro femenino, se pueden combinar. Finalmente, aseguremos que los apareamientos sean completamente al azar, una condición que se conoce como panmixia. Para “crear” los individuos de la nueva generación extraemos un gameto de cada “pool”. Por lo tanto, la probabilidad de cada genotipo estará dada por la probabilidad de extraer esa combinación, que al tratarse de eventos independientes (el gameto masculino del femenino) es el producto de ambas probabilidades. Es decir:

\[\begin{equation} \begin{split} P(A_1A_1)=P(A_1)\cdot P(A_1)=p\cdot p=p^2 \\ P(A_1A_2)=2\cdot P(A_1)\cdot P(A_2)=2\cdot p\cdot q=2pq \\ P(A_2A_2)=P(A_2)\cdot P(A_2)=q\cdot q=q^2\\ \end{split} \tag{2.1} \end{equation}\]

que es la expresión más sencilla de la ley de Hardy-Weinberg. Es de notar que el factor 2 que aparece multiplicando la frecuencia de los genotipos heterocigotos (\(A_1A_2\)) se debe a que existen dos formas de obtener estos individuos: a) sacando un alelo \(A_1\) del “pool” masculino y un \(A_2\) del “pool” femenino y b) sacando un alelo \(A_2\) del “pool” masculino y un \(A_1\) del “pool” femenino, ambas con la misma probabilidad (\(pq\)).

Lo primero que debemos verificar es que estas frecuencias sumen a 1, ya que no existen otros genotipos posibles (recordemos que \(q=1-p\)):

\[\begin{equation} p^2+2pq+q^2=p^2+2p(1-p)+(1-p)^2=p^2+2p-2p^2+1-2p+p^2=\\ =(2p^2-2p^2)+(2p-2p)+1=0+0+1=1 \end{equation}\]

Una vez verificado esto, el siguiente paso será determinar las nuevas frecuencias de los alelos \(A_1\) y \(A_2\), llamémosles \(p'\) y \(q'\). Lo podemos hacer sumando los aportes de alelos de cada genotipo. Los heterocigotos aportan la mitad de su frecuencia para cada tipo de alelo (\(A_1\) y \(A_2\)), mientras que los homocigotos aportan toda su frecuencia del respectivo alelo:

\[\begin{equation} p'=p^2+\frac{1}{2} 2pq=p^2+pq=p(p+q)=p(1)=p\\ q'=q^2+\frac{1}{2} 2pq=q^2+pq=q(q+p)=q(1)=q \end{equation}\]

Por lo tanto, después de una generación bajo este apareamiento al azar en nuestra especie hermafrodita, las frecuencias alélicas permanecen inalteradas (\(p=p'\) y \(q=q'\)). Obviamente ocurrirá lo mismo para las siguientes generaciones, tanto a nivel de la frecuencia de los genotipos como de los alelos (las frecuencias de los genotipos solo dependen de las frecuencias de los alelos, como vimos en la ecuaciones (2.1) y siguientes), por lo que luego de una generación hemos alcanzado el equilibrio: esta condición se conoce como equilibrio de Hardy-Weinberg.

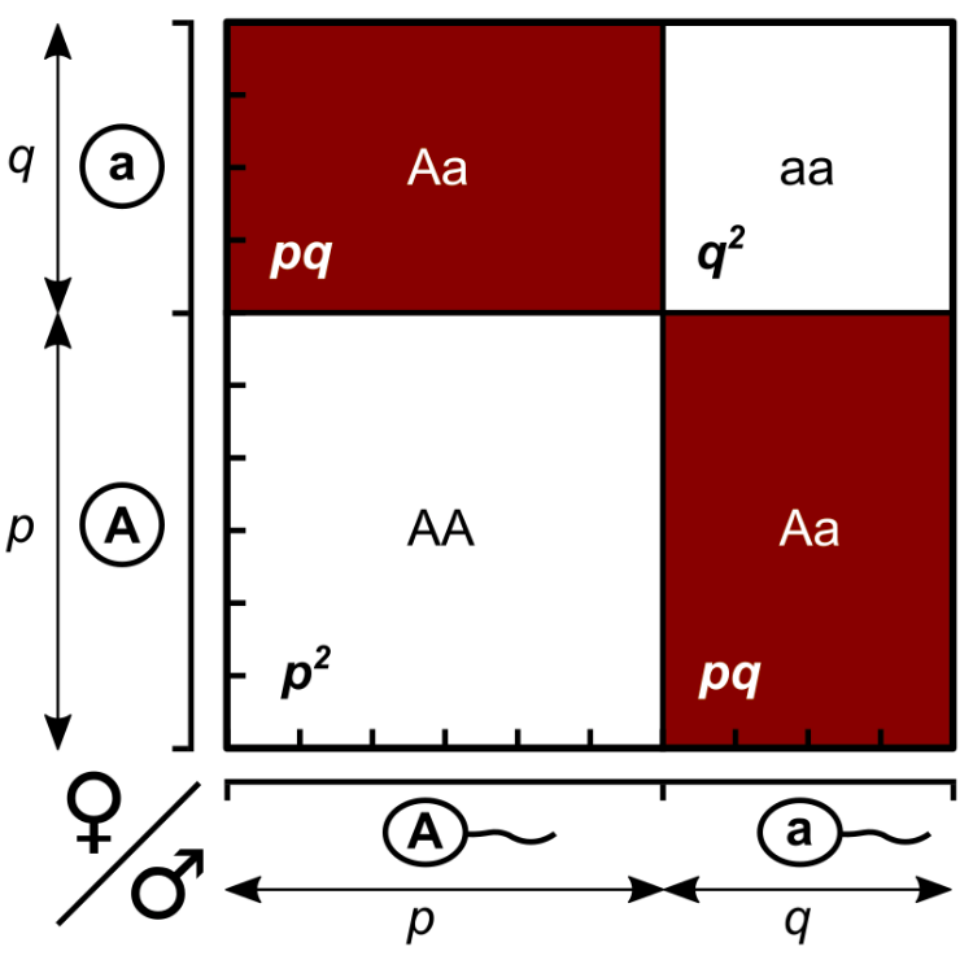
Figura 2.1: Cuadrado de Punnett con frecuencias \(p=0,6\) y \(q=0,4\). Las áreas de los rectángulos/cuadrados representan las frecuencias de los genotipos. Figura tomada de Wikipedia (CC0), modificada a partir de Rosenberg and Kang (2015)

Una forma gráfica de ver estos resultados son los llamados “cuadrados de Punnett”²², como el que se aprecia en la Figura 2.1. En la misma, en el eje horizontal tenemos la frecuencia con la que aparecen los gametos masculinos, mientras que en el vertical aparecen las frecuencias de los gametos femeninos; por lo tanto, el producto de estas frecuencias será el área de los rectángulos y cuadrados correspondientes (de geometría elemental, el área de cuadrados y rectángulos es el producto de dos lados contiguos). Se observa además claramente el origen del factor 2 en los heterocigotos (la suma de las 2 áreas coloreadas en rojo, cada una con valor \(pq\)).

PARA RECORDAR

Hardy-Weinberg en un locus con dos alelos, considerando una especie hermafrodita diploide

• En el equilibrio, las frecuencias de los genotipos \(A_1A_1\), \(A_1A_2\) y \(A_2A_2\) serán \(p^2\), \(2pq\) y \(q^2\), respectivamente.

• Las frecuencias de los alelos (\(p\) y \(q\)) no cambian luego de una generación de apareamiento y por lo tanto, como este razonamiento se puede extender a la próxima generación también, no cambiará nunca (mientras no intervengan otras fuerzas evolutivas como la selección o la deriva y el apareamiento sea al azar).

• Las frecuencias de los genotipos quedan completamente determinados por la frecuencia de los alelos en la generación previa (porque son las frecuencias de los gametos, haploides) y en el caso particular de nuestro modelo de un locus con dos alelos, todo queda determinado por la frecuencia de uno de los dos alelos (\(p\), por ejemplo).

• Además, en el caso particular de nuestro modelo, población hermafrodita, el equilibrio definitivo de las frecuencias de los genotipos se alcanza en una sola generación de apareamientos.

Supuestos que asumimos se cumplen para H-W

1. Todos los genotipos poseen el mismo “fitness”²³ (es decir, ningún genotipo posee una ventaja respecto al número de descendientes que deja).

2. La población debe estar formada por un número infinitamente grande de individuos.

3. El apareamiento al azar debe producirse en toda la población.

4. No debe existir migración que altere las frecuencias.

5. Debe existir un equilibrio mutacional (es decir, las frecuencias de los alelos no varían pese a existir mutaciones).

2.2 Hardy-Weinberg en especies dioicas (dos sexos)

Nuestro modelo previo fue extremadamente sencillo, pero su aplicación se ve reducida a aquellas especies que son hermafroditas. Veamos entonces qué ocurre en especies dioicas (i.e., con dos sexos separados). Supongamos, para mayor generalidad que las frecuencias iniciales en los dos sexos son diferentes, por lo que en la generación inicial tenemos \(p_{M}\) y \(p_{H}\) (y por lo tanto \(q_{M}=1-p_{M}\) y \(q_{H}=1-p_{H}\)). Ahora, los diferentes genotipos serán el producto de combinar estos estos alelos con diferentes frecuencias en machos y hembras:

\[\begin{equation} \begin{split} P(A_1A_1)=P(A_{1M})\cdot P(A_{1H})=p_{M}\cdot p_{H}\\ P(A_1A_2)=P(A_{1M})\cdot P(A_{2H})+P(A_{2M})\cdot P(A_{1H})=\\=p_{M}\cdot q_{H}+q_{M}\cdot p_{H}\\ P(A_2A_2)=P(A_{2M})\cdot P(A_{2H})=q_{M}\cdot q_{H}\\ \end{split} \tag{2.2} \end{equation}\]

Como de estos apareamientos no esperamos diferencias en el número de machos y hembras en cada una de las clases, a partir de ahora tanto machos como hembras tendrán la misma frecuencia de los alelos \(A_1\) y \(A_2\). ¿Pero cuál es esa frecuencia? Para encontrarla, simplemente volveremos a sumar los alelos que aporta cada una de las clases, ponderados por su frecuencia. Es decir, para el alelo \(A_1\), tendremos que la nueva frecuencia \(p'\) se puede obtener sumando las contribuciones de \(P(A_1A_1)\) y \(P(A_1A_2)\):

\[\begin{equation} \begin{split} p'=P(A_1A_1)+\frac{1}{2} P(A_1A_2)=p_{M}\cdot p_{H}+\frac{1}{2}(p_{M}\cdot q_{H}+q_{M}\cdot p_{H}) \end{split} \tag{2.3} \end{equation}\]

Multiplicando por 2 ambos lados de la ecuación y separando términos obtenemos:

\[\begin{equation} \begin{split} 2p'=2p_{M}\cdot p_{H}+p_{M}\cdot q_{H}+q_{M}\cdot p_{H} \\ 2p'=p_{M}\cdot p_{H}+p_{M}\cdot p_{H}+p_{M}\cdot q_{H}+q_{M}\cdot p_{H} \end{split} \tag{2.4} \end{equation}\]

Reordenando y sacando factor común, tenemos:

\[\begin{equation} \begin{split} 2p'=(p_{M}\cdot p_{H}+p_{M}\cdot q_{H})+(p_{M}\cdot p_{H}+q_{M}\cdot p_{H})\\ 2p'=p_{M} (p_{H}+q_{H}) + p_{H} (p_{M}+q_{M})= p_{M} (1) + p_{H} (1) \\ 2p'= p_{M}+ p_{H} \Leftrightarrow p'=\frac{p_{M}+ p_{H}}{2} \end{split} \end{equation}\]

\[\begin{equation} p'=\frac{p_{M}+ p_{H}}{2} \tag{2.5} \end{equation}\]

Es decir, luego de la primer generación de apareamiento entre machos y hembras con diferentes frecuencias de los alelos \(A_1\) y\(A_2\), la frecuencia de ambos alelos será igual en machos y en hembras y su valor será \(p'=\frac{p_{M}+ p_{H}}{2}\) para el alelo \(A_1\) y \(q'=\frac{q_{M}+ q_{H}}{2}\) para el alelo \(A_2\). A este último resultado se puede llegar razonando por simetría (¿hubiera cambiado llamar al revés a los alelos?) o haciendo las cuentas:

\[\begin{equation} \begin{split} p'=\frac{p_{M}+ p_{H}}{2}=\frac{(1-q_{M})+(1-q_{H})}{2}=\\ =\frac{2-q_{M}-q_{H}}{2}=1-\frac{(q_{M}+q_{H})}{2} \therefore\\ \frac{(q_{M}+q_{H})}{2}=1-p'=q' \end{split} \tag{2.6} \end{equation}\]

El último resultado está justificado, además, porque la suma de los alelos siempre debe dar una frecuencia relativa de 1. Más allá de todas las cuentas que nos han llevado a estos resultados en forma analítica, una alternativa primera sería utilizar el argumento de que el aporte de material genético para formar la siguiente generación debe ser igual en machos que en hembras: es decir, cada sexo aporta la mitad del material genético (autosómico) de la nueva generación. Por lo tanto, la frecuencia de los alelos en la generación de hijos debe ser el promedio de las frecuencias en sus padres, que es el resultado que hemos visto.

Ejemplo 2.1

El genotipado molecular (“chips”) nos permite conocer las bases (A, C, G, T) particulares que presenta un animal en diferentes posiciones del genoma, desde unas pocas posiciones a centenas de miles (e.g., alrededor de 700 mil, en algunos “chips”). Estos marcadores se conocen como SNPs (“Single Nucleotide Polymorphisms”, en inglés) y si bien son relativamente poco informativos como marcadores (se suelen escoger marcadores bi-alélicos en el diseño), su elevado número los transforma en una herramienta sumamente poderosa. Usando un “chip” comercial para bovinos en 1000 animales no emparentados de la raza “Guernsey” se encontró que el SNP rs43375517, en la región 5’UTR del gen ARL4A y asociado a la producción de leche a 305 días en varios estudios, presentaba las siguientes frecuencias de genotipos: CC 372, CG 476, GG 152. Calcular la frecuencia relativa de ambos alelos, así como la esperanza del número observado de cada genotipo si la población se encontrase en equilibrio de Hardy-Weinberg para este marcador.

Figura 2.2: Chip “BovineSNP50 v3” de genotipado Bovino, de la empresa Illumina, con capacidad para analizar simultaneamente en 24 muestras 53218 SNPs altamente informativos (fotografía e información de la página de Illumina).

Dado que tenemos 1000 individuos genotipados (372+476+152=1000), el número total de alelos en genotipados es 2000 (son individuos diploides). La frecuencia relativa del alelo ‘C’, llamémosle \(p\), es:

\[\begin{equation} p=\frac{2\times 372+1\times 476}{2000}=\frac{744+476}{2000}=\frac{1220}{2000}=0,61, \end{equation}\]

por lo que, la frecuencia relativa del alelo ‘G’ es \(q=1-p=0,39\). Si la población se encontrase en equilibrio de Hardy-Weinberg, con 1000 individuos genotipados esperaríamos obtener las siguientes frecuencias:

\[\begin{equation} \begin{split} CC=p^2\times 1000=0,61^2\times 1000=0,3721\times 1000=372,1\\ CG=2pq\times 1000=2\times 0,61\times 0,39=0,4758\times 1000=475,8\\ GG=q^2\times 1000=0,39^2\times 1000=0,1521\times 1000=152,1, \end{split} \end{equation}\]

lo que más allá de las diferencias atribuibles al redondeo (es imposible genotipar fracciones de individuo, pero incrementando el tamaño de la muestra estos errores pueden reducirse más), tenemos un ajuste casi perfecto a las expectativas del equilibrio Hardy-Weinberg.

2.3 H-W: la frecuencia de heterocigotas en función de la frecuencia alélica

En un locus con dos alelos, ¿a qué frecuencia del alelo \(p\) podemos observar la mayor frecuencia de heterocigotas, asumiendo que la población se encuentra en equilibrio de Hardy-Weinberg? La alternativa más sencilla para tener una idea aproximada del comportamiento del número de heterocigotas bajo estos supuestos es graficar la misma como función de \(p\). Tenemos que \(2pq=2p(1-p)\), y podemos graficar esta relación en cualquier software que permita graficar funciones, calculadora, o aún en una planilla electrónica (por ejemplo generando una serie en el intervalo 0-1). La Figura 2.3 es el resultado de graficar esta función, donde se ve que la máxima frecuencia de heterocigotas se encuentra en el entorno de \(p=0,5\), o sea en frecuencias intermedias de los dos alelos; la máxima proporción de heterocigotas esperable para una población en equilibrio de HW es \(0,5\).

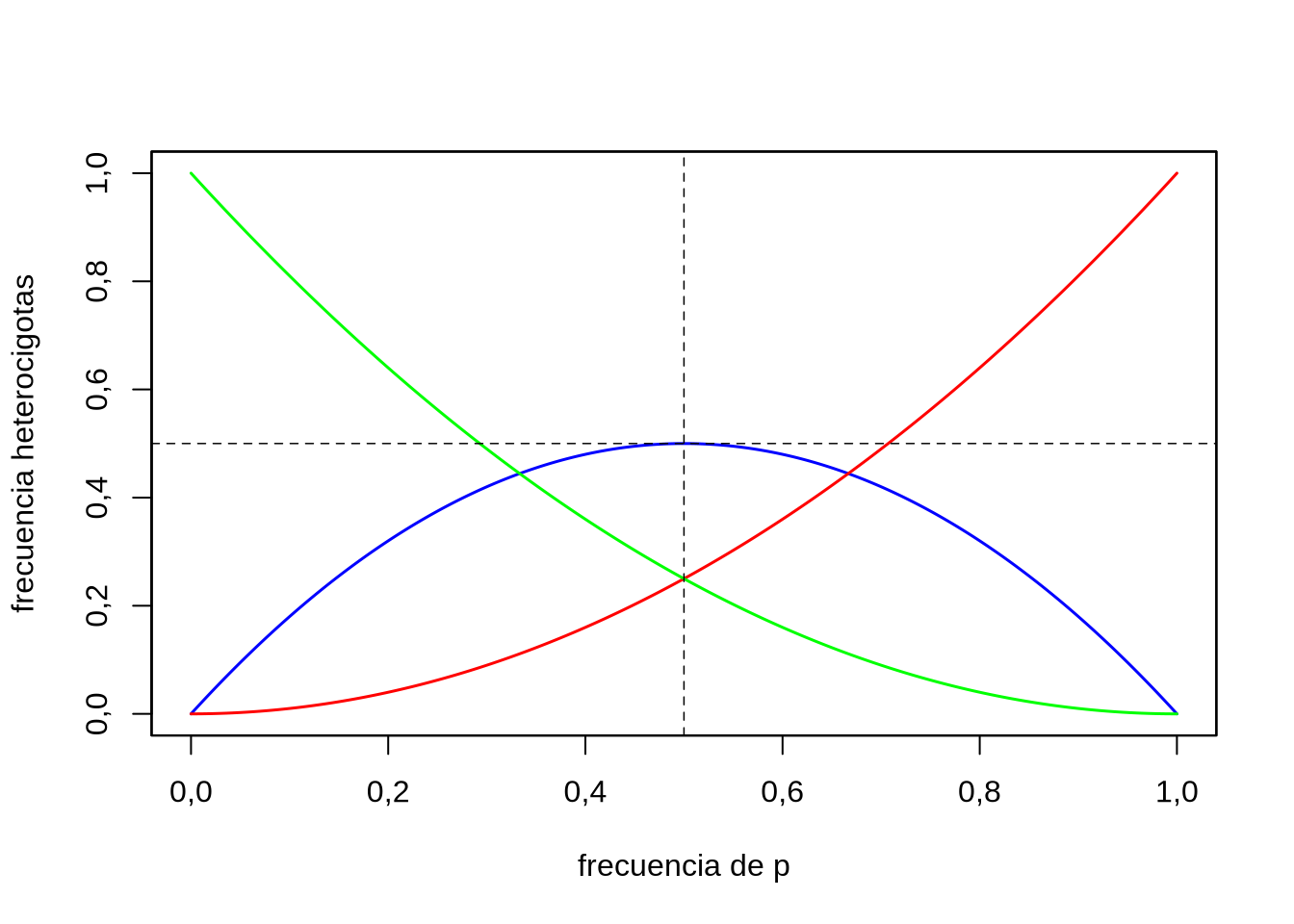
Figura 2.3: Frecuencia de heterocigotas en función de la frecuencia del alelo \(p\) en un modelo de un locus con dos alelos, bajo equilibrio Hardy-Weinberg. En azul la frecuencia de los heterocigotas, rojo y verde los homocigotas.

Una forma más precisa, complementaria con la anterior, es el estudio analítico de esta función. Es decir, dada la función \(f_{Het}(p)=2pq=2p(1-p)=2p-2p^2\), podemos reconocer los extremos relativos (máximos y mínimos) de la misma como los lugares donde la pendiente de la recta tangente es igual a cero. Lo que es equivalente, estos son los puntos donde la derivada primera de la función se hace cero. Por lo tanto, derivando la función obtenemos:

\[\begin{equation} \begin{split} f_{Het}(p)=2pq=2p(1-p)=2p-2p^2\\ \frac{d f_{Het}}{dp}=2-4p\\ 2-4p=0 \Leftrightarrow p=\frac{1}{2} \end{split} \end{equation}\]

Es decir, la función tiene un solo máximo o mínimo en \(p=\frac{1}{2}=0,5\). Para reconocer de cuál de los dos se trata es necesario ver el signo de la derivada segunda (lo que hacemos volviendo a derivar la derivada primera):

\[\begin{equation} \frac{d^2 f_{Het}(p)}{dp^2}=-4 \end{equation}\]

Como el signo es negativo, se trata de un máximo. Más aún, la forma de función original (\(f_{Het}=2p-2p^2\)) es claramente reconocible como la de una parábola con forma de “U” invertida y cuyas intersecciones con el eje de las abcsisas (raíces) son 0 y 1, por lo que por simetría el vértice debe estar en el punto medio (es decir, \(\frac{1}{2}\)). Sustituyendo, tenemos:

\[\begin{equation} \begin{split} f_{Het_{max}}(p=\frac{1}{2})=2p-2p^2=2 \frac{1}{2}-2\left(\frac{1}{2}\right)^2=\\ 2 \frac{1}{2} -2 \frac{1}{4} =1- \frac{1}{2}=\frac{1}{2} \end{split} \end{equation}\]

2.4 El equilibrio de Hardy-Weinberg en cromosomas ligados al sexo

En los razonamientos previos hemos asumido que el locus de interés era autosómico, es decir que no estaba en uno de los cromosomas sexuales ¿Qué ocurriría si este locus se encuentra en el cromosoma X del sistema XY de determinación del sexo?²⁴
A diferencia de antes, los machos poseen ahora solo un cromosoma X (son hemicigotas), que es donde está nuestro locus de interés y que por lo tanto tienen el alelo \(A_1\) con probabilidad \(p_{M}\) y el alelo \(A_2\) con probabilidad \(q_{M}=1-p_{M}\). En las hembras tenemos los dos cromosomas X y en ambos los alelos \(A_1\) y \(A_2\) tendrán probabilidad \(p_{H}\) y \(q_{H}\) respectivamente (con \(q_{H}=1-p_{H}\)). Las hembras descendientes de este cruzamiento tendrán dos cromosomas X, uno del padre y otro de la madre, y las frecuencias de los genotipos serán equivalentes a los de las ecuaciones (2.2) y siguientes. En cambio, los machos tienen un solo cromosoma X, aportado por la madre (el padre aporta el cromosoma Y), y por lo tanto las frecuencias de los alelos \(A_1\) y \(A_2\) en esta nueva generación de machos serán iguales a las frecuencias del respectivo alelo en las hembras de la generación anterior.

En resumen, en la nueva generación de machos y hembras (la distinguimos de la anterior con ’) tendremos ahora las siguientes frecuencias:

\[\begin{equation} \begin{split} p'_{H}=\frac{p_{M}+ p_{H}}{2} \\ q'_{H}=\frac{q_{M}+ q_{H}}{2} \\ p'_{M}=p_{H} \\ q'_{M}=q_{H} \end{split} \end{equation}\]

El mismo razonamiento lo podemos extender para la próxima generación (la distinguimos de la anterior con “), por lo que ahora tendremos:

\[\begin{equation} \begin{split} p''_{H}=\frac{p'_{M}+ p'_{H}}{2}=\frac{p_{H}+\frac{p_{M}+ p_{H}}{2}}{2} \\ q''_{H}=\frac{q'_{M}+ q'_{H}}{2}=\frac{q_{H}+\frac{q_{M}+ q_{H}}{2}}{2} \\ p''_{M}=p'_{H}= \frac{p_{M}+ p_{H}}{2} \\ q''_{M}=q'_{H}=\frac{q_{M}+ q_{H}}{2} \end{split} \end{equation}\]

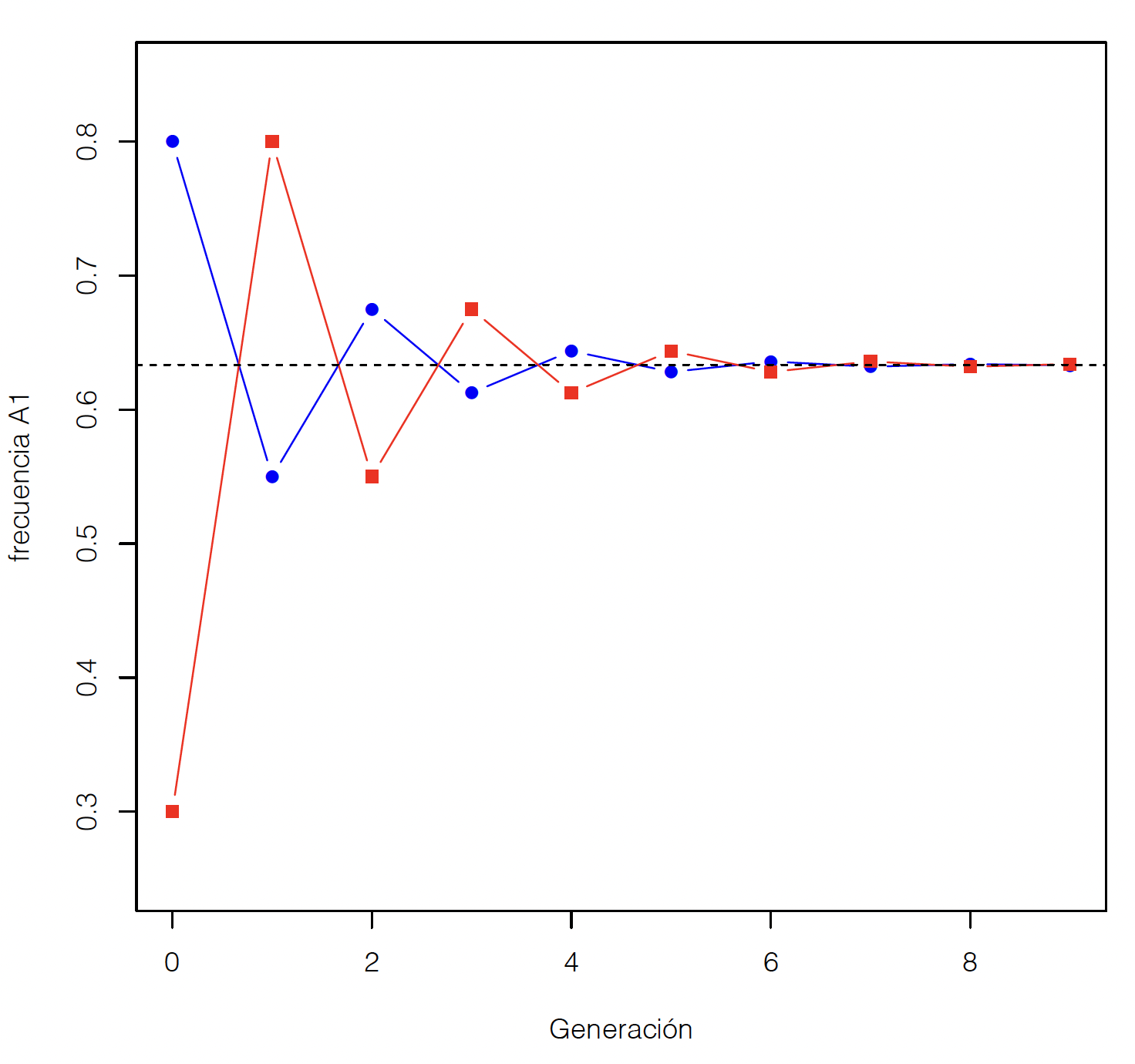
Figura 2.4: Evolución de las frecuencias alélicas en machos (cuadrados rojos) y hembras (círculos azules) en un locus perteneciente al cromosoma X en especies en que el Y determina el sexo. La línea a trazos negros representa la media de la población. Las frecuencias de partida (generación 0) son \(p_{M}=0,3\) y \(p_{H}=0,8\).

O sea, hemos establecido una regla de recurrencia para calcular las frecuencias de \(p\) y \(q\) a partir de la generación anterior (se puede llegar hasta la generación inicial), pero aún no hemos estudiado el comportamiento a largo plazo de este proceso. Para entenderlo mejor podemos resumir la información, como aparece en el siguiente cuadro, donde además de las frecuencias del alelo \(A_1\) para hembras y machos en las 3 primeras generaciones también calculamos la frecuencia del alelo en toda la población (media) y la diferencia de frecuencias entre hembras y machos.

\(\textbf{Generación}\)	\(A_{1H}\)	\(A_{1M}\)	\(\text{Media}\)	\(\text{Diferencia}\)
0	\(p_{H}\)	\(p_{M}\)	\(\frac{2 p_{H}+p_{M}}{3}\)	\(p_{H}-p_{M}\)
1	\(\frac{p_{M}+ p_{H}}{2}\)	\(p_{H}\)	\(\frac{2 p_{H}+p_{M}}{3}\)	\(\frac{p_{M}-p_{H}}{2}=-\frac{(p_{H}-p_{M})}{2}\)
2	\(\frac{p_{H}+\frac{p_{M}+ p_{H}}{2}}{2}\)	\(\frac{p_{M}+ p_{H}}{2}\)	\(\frac{2 p_{H}+p_{M}}{3}\)	\(\frac{p_{H}-p_{M}}{4}\)

Es de notar que para calcular la frecuencia del alelo en la población, debemos ponderar la frecuencia en hembras por 2/3 y la de machos por 1/3, ya que esas son las proporciones de cromosomas X que aportan cada uno de los sexos a la población.

Si nos fijamos en la columna de la media en el cuadro anterior, lo primero que observamos es que la misma no cambia con el tiempo. Es decir, la frecuencia general en la población de los alelos \(A_1\) y \(A_2\) está determinada desde el principio, y su valor es

\[\begin{equation} p=(2 p_{H}+p_{M})/3. \end{equation}\]

Lo segundo que podemos apreciar, si observamos la columna que muestra la diferencia entre los dos sexos, es que el valor absoluto de esta diferencia se va reduciendo a la mitad en cada generación, mientras que el signo de la misma alterna de generación en generación. Con estas observaciones en mano es fácil entender que el proceso tiende igualar las frecuencias entre los dos sexos (asumiendo que parten de valores diferentes en machos y hembras). Si bien teóricamente estas frecuencias nunca llegan a ser iguales, desde el punto de vista práctico la diferencia es despreciable luego de unas pocas generaciones, y en general los procesos estocásticos (e.g., la deriva, que veremos más adelante) tendrán un impacto mucho mayor que estas diferencias.
El comportamiento de estas frecuencias puede observarse gráficamente también, como lo muestra por ejemplo la Figura 2.4, partiendo en este caso de \(p_{M}=0,3\) y \(p_{H}=0,8\). Se aprecia claramente en esta figura que a) la frecuencia en machos es igual a la frecuencia en las hembras de la generación anterior, b) la frecuencia en hembras es el promedio de las frecuencias de machos y hembras en la generación anterior, c) la media de la población permanece estable (línea a trazos negros), y d) la diferencia entre machos y hembras se reduce a la mitad en cada generación.

PARA RECORDAR

Para el equilibrio de Hardy-Weinberg en cromosomas ligados al sexo, asumiendo que el macho es el sexo heterogamético (al revés si la hembra lo es), tenemos:

• La frecuencia del alelo \(\bf{A_1}\) en machos (\(p_M\)) de la generación \(t\) es igual a \(p_H\) en la generación \(t-1\).

• La frecuencia del alelo \(\bf{A_1}\) en hembras (\(p_H\)) de la generación \(t\) es igual a \(\frac{p_H+p_M}{2}\) en la generación \(t-1\).

• Este proceso converge relativamente rápido al valor \(p=\frac{(2p_H+p_M)}{3}\), que es la frecuencia inicial de alelos \(p\) en el pool de gametos.

2.5 Tres o más alelos

Hasta ahora hemos manejado los diferentes problemas asumiendo que se trataba de un locus con únicamente dos alelos, lo que en principio permite simplificar algunas cuentas ya que la frecuencia de \(q\) queda determinada por la frecuencia de \(p\) (i.e., \(q=1-p\)). Sin embargo, la extensión a tres o más alelos es relativamente sencilla y no requiere de cosas nuevas, por más que aprovecharemos la oportunidad para presentar el resultado central del equilibrio de Hardy-Weinberg de una forma diferente.

Si recordamos nuestro modelo de dos alelos, podíamos representar el conjunto de los alelos en la población como la suma de \(p\) y \(q\), es decir \((p+q)\). Cuando hacemos el apareamiento en condiciones de panmixia, estamos cruzando este \((p+q)\) con otro similar (porque los alelos salen de la misma población), o lo que es equivalente:

\[\begin{equation} (p+q)(p+q)=(p+q)^2=p^2+2pq+q^2 \end{equation}\]

De lo anterior surge claro que podemos representar las frecuencias genotípicas esperadas en el equilibrio Hardy-Weinberg como el cuadrado del binomio formado por las frecuencias alélicas en la generación previa (frecuencias gaméticas). Con esto en mano, resulta tentador extender este resultado a más de 2 alelos. Supongamos entonces que tenemos un locus con 3 alelos, \(A_1\), \(A_2\) y \(A_3\), con frecuencias respectivas \(p\), \(q\) y \(r\). Nuestro “todo” estará ahora conformado por la suma de \(p\), \(q\) y \(r\), es decir \((p+q+r)\), y el cruzamiento resultará en:

\[\begin{equation} (p+q+r)(p+q+r)=(p+q+r)^2=p^2+q^2+r^2+2pq+2pr+2qr \end{equation}\]

Es decir, si llamamos \(A_i\) a los \(i=1,2,...,k\) alelos diferentes, y \(p_i\) a las frecuencias correspondientes, la frecuencia de los genotipos homocigotas estará determinada por \(p_{i}p_{i}=p_{i}^2\) y la de los heterocigotas por \(2p_{i}p_{j}, i \neq j\). Obviamente, el razonamiento del binomio y del trinomio se puede extender a un número mayor de alelos.

En general, para \(k\) alelos diferentes, el número de genotipos heterocigotas es igual a \(k(k-1)/2\). Para ver de dónde se desprende esto, es fácil imaginar un “cuadrado de Punnett”, ahora con 3 o más alelos. El total de celdas del cuadrado es \(k*k=k^2\), de las cuales, los homocigotas serán las celdas que se encuentren en la diagonal, o sea \(k\) celdas. Esto nos deja \(k^2-k=k(k-1)\). Sin embargo, las celdas simétricas respecto a la diagonal representan el mismo genotipo (i.e., \(p_{ij} \equiv p_{ji}, \forall i \neq j\); de ahí el factor 2 para los heterocigotas), por lo que al total de celdas que nos quedaban debemos dividirlo entre 2 para tener el número de genotipos heterocigotos y de ahí que este sea igual a \(k(k-1)/2\). Finalmente, el número total de genotipos es la suma de homocigotos (\(k\)) y heterocigotos (\(k(k-1)/2\)). Es decir, el número de genotipos corresponde a \(k+k(k-1)/2=(2k/2)+k(k-1)/2=k(k+1)/2\).
De acuerdo a lo anterior, la frecuencia total de homocigotos será:

\[\begin{equation} G=\sum_{i=1}^{k} p_{i}^2, \end{equation}\]

lo que nos deja la posibilidad de definir la heterocigosis del locus como lo que falta para completar la totalidad, o sea:

\[\begin{equation} H=1-G=1-\sum_{i=1}^{k} p_{i}^2 \end{equation}\]

Es importante entender que la fórmula anterior no es función de la proporción real de heterocigotos que existen en una población determinada para un locus dado, sino que se trata de la esperanza en función de las frecuencias alélicas, si se cumpliera el equilibrio de Hardy-Weinberg.

PARA RECORDAR

• Para 3 alelos el equilibrio de Hardy-Weinberg es la expansión del cuadrado del trinomio, es decir para los alelos \(\bf{A_1}\), \(\bf{A_2}\), \(\bf{A_3}\), con frecuencias respectivas \(p\), \(q\) y \(r\), \(p+q+r=1\),

\[\begin{equation} (p+q+r)^2=p^2+q^2+r^2+2pq+2pr+2qr \end{equation}\]

los 3 primeros términos de la derecha correspondientes a los homocigotos \(\bf{A_1A_1}\), \(\bf{A_2A_2}\), \(\bf{A_3A_3}\) y el resto a los heterocigotos \(\bf{A_1A_2}\), \(\bf{A_1A_3}\) y \(\bf{A_2A_3}\).

• La ecuación anterior es generalizable a un número \(k\) de alelos, \(\bf{A_1}, \bf{A_2}, ..., \bf{A_k}\) de acuerdo a

\[\begin{equation} (p_1+p_2+p_3...+p_k)^2 \end{equation}\]

• Bajo equilibrio de Hardy-Weinberg, la proporción esperada de homocigotas será

\[\begin{equation} G=\sum_{i=1}^{k} p_{i}^2, \end{equation}\]

por lo que la heterocigosis del locus quedará como lo que falta para completar la totalidad, o sea:

\[\begin{equation} H=1-G=1-\sum_{i=1}^{k} p_{i}^2 \end{equation}\]

2.6 La estimación de frecuencias y el equilibrio (o no)

En una población con un gran número de individuos, tendiendo a infinito, si la población se encuentra en equilibrio de Hardy-Weinberg el número de individuos de los distintos genotipos coincidirá estrechamente con las esperanzas de los mismos a partir las frecuencias de los alelos. Es decir, la variación estocástica en cada uno de los apareamientos (o en la unión de los gametos) tiende a cancelarse cuando consideramos el gran número de individuos en la población. Sin embargo, aún en esas grandes poblaciones no solemos tener acceso a la información de todos los individuos y sí, solamente, a la información de una muestra aleatoria de la misma. El concepto de muestra aleatoria es fundamental ya que será el que nos permitirá extender nuestras conclusiones de la muestra hacia la población, que en última instancia suele ser lo que nos interesa. Al trabajar con una muestra aleatoria relativamente reducida de la población, los números ahora serán mucho menores, y por lo tanto los efectos del azar se verán incrementados.
Supongamos, para ver el impacto del tamaño de la muestra, que tenemos interés en estimar las frecuencias de los dos alelos en un locus autosomal de una especie diploide en una población determinada. Como se trata de una especie salvaje, difícil de capturar para muestrear, nos contentamos con los 5 individuos que pudimos genotipar para este locus; sin duda es mucho mejor que no tener nada. Como se trata de una especie diploide, si tenemos \(n\) individuos vamos a tener \(2n\) alelos genotipados (i.e., 10 alelos genotipados). Supongamos ahora que de esos 10 alelos genotipados, 3 fueron del alelo \(A_1\) y 7 del alelo \(A_2\). Es decir, la proporción de \(A_1\) es igual a \(p=3/10=0,3\), mientras que la del alelo \(A_2\) es de \(q=7/10=0,7\) (hubiésemos llegado también a este resultado como \(q=1-p\)). Parece razonable usar este valor de \(p\) como un estimador del “verdadero valor”²⁵ del parámetro en la población, en este caso la frecuencia del alelo \(A_1\), tanto que coincide con el estimador por máxima verosimilitud (es decir, escogemos como valor estimado aquel que tiene mayor probabilidad de ocurrir de acuerdo a lo que hemos observado).

Ahora, ¿que certeza tenemos que este valor que estimamos esté cerca del “verdadero valor”? En principio, como solo tenemos 10 alelos genotipados, nuestras estimaciones irán de 10% en 10% (los saltos en la cuenta de alelos son de a 1, pero en 10 total, así que tenemos \(\frac{1}{10}=0,1=10\%\)). O sea, la precisión de nuestra estimación es realmente baja.

Otra forma de ver este problema es pensar en cuál sería la probabilidad de observar este conteo de alelos \(A_1\), por ejemplo, dado que conocemos el verdadero valor del parámetro. Si suponemos que los individuos representan un muestreo al azar de los gametos en la población y que los individuos de la muestra fueron seleccionados al azar, entonces la probabilidad de observar un conteo \(x\) en particular, dado el número total de alelos genotipados \(n\), se puede describir por la distribución binomial (en nuestro caso de dos alelos):

\[\begin{equation} \begin{split} f(x)={n\choose x} p^x (1-p)^{n-x} \end{split} \tag{2.7} \end{equation}\]

con las combinaciones de \(n\) elementos tomados de a \(x\) elementos iguales a:

\[\begin{equation} \begin{split} {n\choose x}=\frac{n!}{x!(n-x)!} \end{split} \end{equation}\]

Por ejemplo, si la frecuencia “real” en la población entera para el alelo \(A_1\) es de \(p=0,5\), ¿cuál sería la probabilidad de observar este conteo en 3 alelos de los 10 que genotipamos? De acuerdo a la ecuación (2.7), la probabilidad de obtener 3 conteos en una muestra de 10, con una probabilidad \(p=0,5\) en la población, es de:

\[\begin{equation} f(3)={10\choose 3} (0,5)^3 (1-0,5)^{10-3}=\frac{10!}{7! 3!} (0,5)^3 (0,5)^{7}= \end{equation}\] \[ \frac{10*9*8}{6} (0,5)^{10}=0,1171875 \sim 11,7\%. \]

Es decir, aún cuando la frecuencia real en la población es de \(p=0,5\), en más de 1 de cada 10 muestras que tomemos, solo por azar, observaremos un conteo de 3 alelos. En estos casos, estimaríamos erróneamente \(p \approx 0,33\). Esto puede parecer poco, pero si nos fijamos en la Figura 2.5(a), donde graficamos la probabilidad de observar cada uno de los 11 conteos posibles (de 0 a 10 alelos \(A_1\)), resulta claro que la probabilidad de no acertar en el único número correcto (5 alelos), es realmente alta.

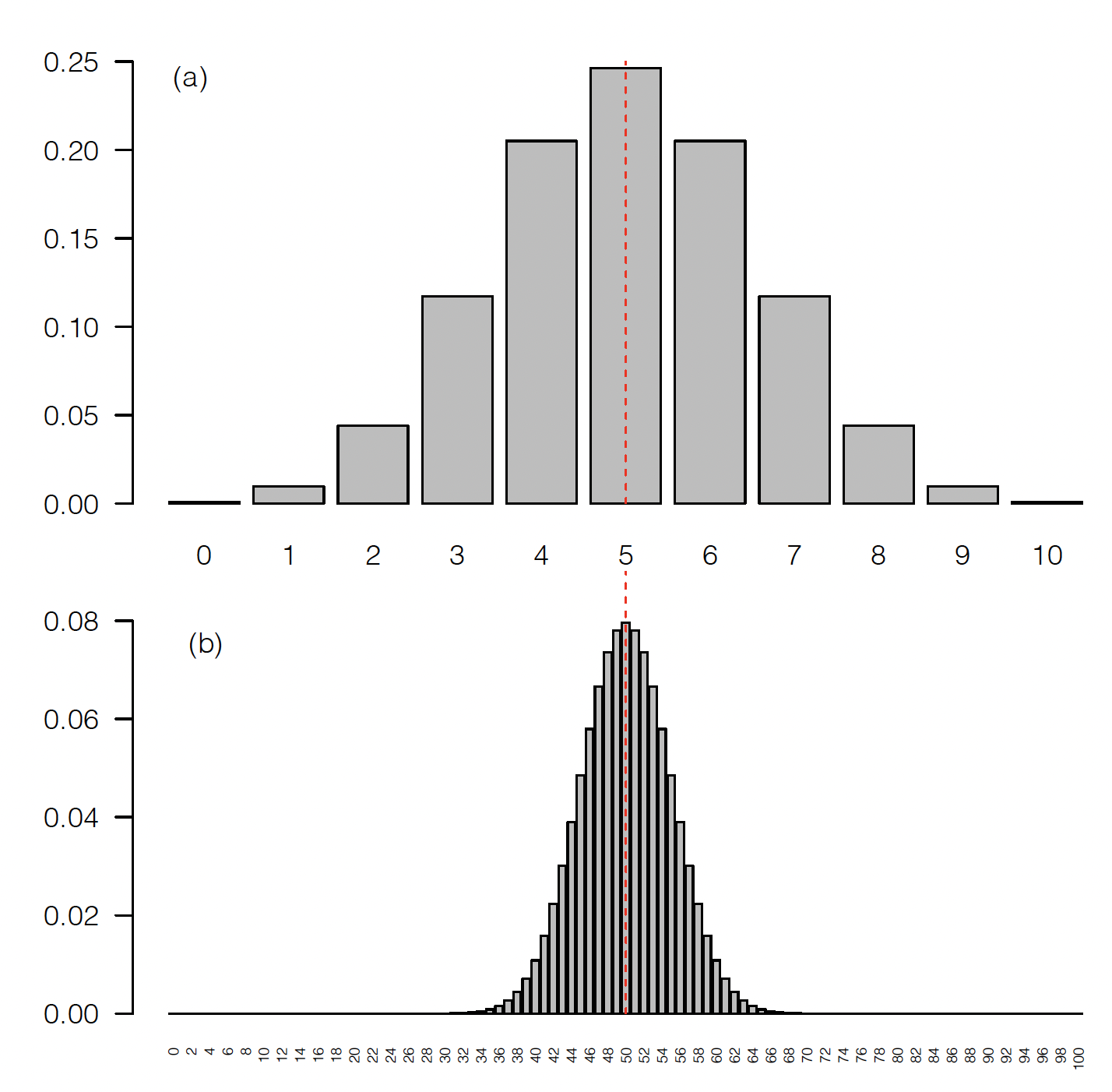
Figura 2.5: Probabilidad de observar un conteo de alelos determinado en una muestra de 5 individuos (a) y en una muestra de 50 individuos (b), dado que la frecuencia del mismo en la población es de 0,5.

De hecho, si calculamos la probabilidad de observar exactamente 5 alelos en 10, dada la frecuencia real de \(p=0,5\), esta probabilidad es igual a \(0,2460938\), por lo que la probabilidad de NO obtener el “verdadero” valor de \(p\) en una muestra de este tamaño es igual a \(1-0,2460938=0,7539062 \sim 75,4\%\). Por otro lado, la probabilidad de tener un estimado de \(p \leq 0,3\) es la suma de las probabilidades de obtener 0, 1, 2 o 3 conteos, y esto es igual a \(0,171875 \sim 17,2\%\) (el lector lo puede verificar fácilmente).
Claramente, de lo anterior surge que este tamaño muestral de 5 individuos no nos conducirá a nada muy razonable. ¿Qué ocurriría si conseguimos aumentar el tamaño muestral a 50 individuos? Las probabilidades esperadas de los distintos conteos en la muestra aleatoria se grafican en la Figura 2.5(b). Ahora resulta claro que, por un lado, la “granularidad” de las barras es mucho más fina (i.e., la “precisión” de nuestros estimados podría ser mucho mayor) y por el otro, que las estimaciones muy alejadas del “verdadero valor” son bastante improbables. Por ejemplo, ¿cuál sería la probabilidad de tener un estimado de \(p \leq 0,3\)? En este caso se trata de la suma de las probabilidades de todos los conteos, de 0 a 30 (\(30/100=0,3\)). En decir, se trata de la función de distribución (a veces conocida como probabilidad acumulada, o también CDF en inglés). En este caso, para la distribución binomial, tenemos para un valor \(k\) (30 en nuestro caso)

\[\begin{equation} \begin{split} Pr(X \leq k)=\sum_{x=0}^{k} {n\choose x} p^x (1-p)^{n-x} \end{split} \tag{2.8} \end{equation}\]

Sería algo tedioso calcularlo a mano, pero una primer idea del valor se puede tener observando la Figura 2.5(b), donde resulta claro que las probabilidades para conteos de hasta 30 son despreciables. De hecho, utilizando la función de distribución en cualquier software que la tenga implementada, la probabilidad de observar un conteo de 30 o menos alelos en 100 genotipados es de 3,92507x10^-5 (\(\sim 0,004\%\)) si la frecuencia del alelo \(A_1\) en la población es \(p=0,5\); o sea, prácticamente improbable.

Ahora también bajó la probabilidad de acertar exactamente en la estimación de \(p=0,5\). ¿Pero qué sucede con la probabilidad de obtener observaciones en un intervalo que nos lleve a una estimación razonablemente cercana a \(p = 0,5\)? Comparemos con nuestra muestra de 5 individuos, donde la probabilidad de observar exactamente 5 alelos era de \(\sim 24,6\%\). El interalo de frecuencias equivalente en nuestra muestra de 50 individuos corresponde al que contempla observar entre 45 y 54 alelos (probabilidades entre \(0,45\) y \(0,54\))²⁶; este intervalo concentra ahora \(\sim 63\%\) de la probabilidad. Dicho de otra manera, ahora los resultados se concentrarán (aproximadamente) entre 49 y 51 con una probabilidad similar a la que observabamos en nuestra muestra de 5 individuos. Claramente, nuestras estimaciones se vuelven mucho más precisas y útiles.

Hasta el momento hicimos nuestras estimaciones de las frecuencias alélicas poblacionales (y, por lo tanto, la posibilidad de conocer nuestras expectativas para el equilibrio de Hardy-Weinberg) de una manera bastante sencilla: asumimos que -genómica mediante- podemos acceder al verdadero estado alélico (e.g., ADN) de cada una de las muestras. Sin embargo, en muchos casos esto no es posible. Por ejemplo, puede desconocerse la base molecular de la diferencias fenotípicas observadas. En otros casos, obtener esta información no es práctico, y la única información disponible es la fenotípica. Por lo tanto, en estos casos solo contamos con el conteo de los distintos fenotipos. Esto introduce un nuevo factor en el problema: es necesario conocer el modelo de herencia (mendeliana, codominancia, etc.) para poder pasar de los fenotipos a los genotipos, y de allí a las frecuencias de los alelos.

Supongamos, para comenzar, que el modelo de herencia es de codominancia en un locus autosomal con dos alelos (\(A_1\) y \(A_2\)) en una especie diploide. Bajo este modelo, ambos alelos se expresan en el fenotipo y hay una correspondencia biunívoca entre fenotipo y genotipo. En este caso tenemos tres genotipos que son identificables directamente, por lo que podemos estimar las frecuencias relativas a partir del conteo de individuos. PAra ello, tendremos en cuenta: a) que los homocigotas presentan 2 alelos \(A_1\) y los heterocigotas 1, y b) que para \(n\) individuos tenemos \(2n\) alelos. Así, en una muestra de \(n\) individuos la frecuencia relativa (muestral) del alelo \(A_1\) será igual a la suma de 2 veces el número de homocigotas \(A_1\) más el número de heterocigotas, todo dividido entre 2 veces el número de individuos:

\[\begin{equation} \begin{split} p=\frac{2n_{A_1A_1}+n_{A_1A_2}}{2n}, q=\frac{2n_{A_2A_2}+n_{A_1A_2}}{2n}\\ n=n_{A_1A_1}+n_{A_1A_2}+n_{A_2A_2} \end{split} \end{equation}\]

En todo caso, si conocemos los genotipos a nivel molecular (ver Ejemplo 2.1), la forma de estimar es análoga al caso donde los genotipos corresponden en forma biunívoca con los fenotipos²⁷. Tanto si se trata de un modelo de codominancia como de dominancia parcial, lo relevante aquí es la posibilidad de distinguir los heterocigotas de ambos homocigotas. Esto nos permite simplemente hacer el “conteo” de alelos, ya que la base genética es clara: en diploides, los homocigotas poseen dos alelos del mismo tipo y los heterocigotas poseen uno de cada tipo.

Las cosas empiezan a complicarse un poco más cuando aparece el efecto de dominancia. Supongamos, por ejemplo, que en el locus anterior (autosomal en especie diploide, con dos alelos), el alelo \(A_1\) domina completamente al \(A_2\). En este caso, tanto el genotipo \(A_1A_1\) como el \(A_1A_2\) tendrán idéntico fenotipo, mientras que el \(A_2A_2\) tendrá un fenotipo diferente. Estom implica que el conteo de fenotipos ya no permite determinar las frecuencias de los ambos alelos, ya que los conteos del fenotipo \(A_1\) corresponde al de dos genotipos en simultáneo (\(G_{11}=A_1A_1\) y \(G_{12}=A_1A_2\)), ambos con diferente número de alelos \(A_1\) y \(A_2\) (2 y 0 para el homocigota, 1 y 1 para el heterocigota). Dicho de otra forma, sabemos calcular las frecuencias alélicas a partir de los 3 genotipos, pero solo contamos con dos fenotipos: el del alelo dominante y el del alelo recesivo. De hecho, con solo esta información se trata de un problema indeterminado. Para poder salir de esta situación debemos agregar algún tipo de información adicional. Una alternativa sencilla (suponiendo que no podemos conocer los genotipos, lo que resolvería el problema) es asumir que la población se encuentra en equilibrio de Hardy-Weinberg. Esta asunción establece una relación explícita entre frecuencias alélicas (lo desconocido) y genotipos. Notemos que el la clase genotípica \(A_2A_2\) (homocigota) es la única que corresponde con un único fenotipo. Si la población se encuentra en equilibrio de Hardy-Weinberg, sabemos que la esperanza del número de individuos para este genotipo es igual a \(nq^2\), donde \(n\) es el número total de individuos (\(n=G_{1}.+G_{22}\)). Sabemos además que el número de individuos con el fenotipo dominante está dado por \(G_{1}.=G_{11}+G_{12}\). Esto nos permite estimar \(q\) (i.e. la frecuencia del alelo \(A_2\)),

\[\begin{equation} \begin{split} G_{22}=nq^2 \therefore q=\pm \sqrt{\frac{G_{22}}{n}}=\pm \sqrt{\frac{G_{22}}{G_1.+G_{22}}} \end{split} \tag{2.9} \end{equation}\]

De las dos raíces que tiene esta ecuación (una positiva y otra negativa), solo una posee sentido biológico: no existen frecuencias álelicas negativas, y por lo tanto dicha raíz no es una solución válida. Es importante recalcar en este punto que la validez de nuestra estimación depende de que la población se encuentre en equilibrio de Hardy-Weinberg, pues de lo contrario no será una estimación que tenga una base teórica.

Ejemplo 2.2

La fenilcetonuria (PKU) es un error innato del metabolismo que resulta en una disminución del metabolismo del aminoácido fenilalanina. La enfermedad es resultado de una deficiencia en la enzima fenilalanina hidroxilasa, codificada por el gen PAH. El resultado de esto es la acumulación de fenilalanina a niveles potencialmente tóxicos. Desde el punto de vista del modelo de herencia se comporta como autosómica recesiva, por lo que es necesario heredar dos copias “defectuosas” del gen PAH (a decir verdad, que tengan actividad seriamente disminuída) para que la enfermedad se manifieste. La incidencia es muy variable de población en población, pero dos casos extremos podrían ser el de la población de Finlandia (1 afectado en 200 mil nacimientos) y el de la población de Turquía (1 afectado en 2600 nacimientos). Calcular para ambas poblaciones la frecuencia de “el” ²⁸ alelo defectuoso, así como la proporción de portadores (que no manifiestan la enfermedad), asumiendo que las poblaciones se encuentran en equilibrio de Hardy-Weinberg.
Utilizando la ecuación (2.9), tenemos para los dos casos

\[\begin{equation} \begin{split} q_{Fin}=\sqrt{\frac{1}{200000}}=0,002236068 \sim 0,22\% \\ q_{Tur}=\sqrt{\frac{1}{2600}}=0,01961161 \sim 1,96\% \end{split} \end{equation}\]

Los portadores serán los heterocigotas, por lo que, si asumimos que las poblaciones se encuentran en equilibrio de Hardy-Weinberg, entonces tendremos

\[\begin{equation} \begin{split} Het_{Fin}=2p_{Fin}q_{Fin}=2*(1-0,002236068)*0,002236068=0,004462136\sim 0,45\% \\ Het_{Tur}=2p_{Tur}q_{Tur}=2*(1-0,01961161)*0,01961161=0,038454 \sim 3,85\% \end{split} \end{equation}\]

2.7 El sistema ABO

Hasta el momento nos hemos centrado en el caso de un locus con dos alelos. En general, la relación entre los distintos alelos de un locus suele ser más compleja. En principio, esto se debe a que existen más de dos alelos cuyo impacto en el fenotipo es distinguible. A su vez, las relaciones entre dichos alelos puede ser variable, implicando muchas veces diferentes modos de herencia (e.g., dominancia y codominancia en el mismo locus). Un ejemplo de esto es el sistema de grupos sanguíneos ABO, el más importante en humanos,²⁹ cuya herencia (en forma simplificada) puede apreciarse en la Figura 2.6.

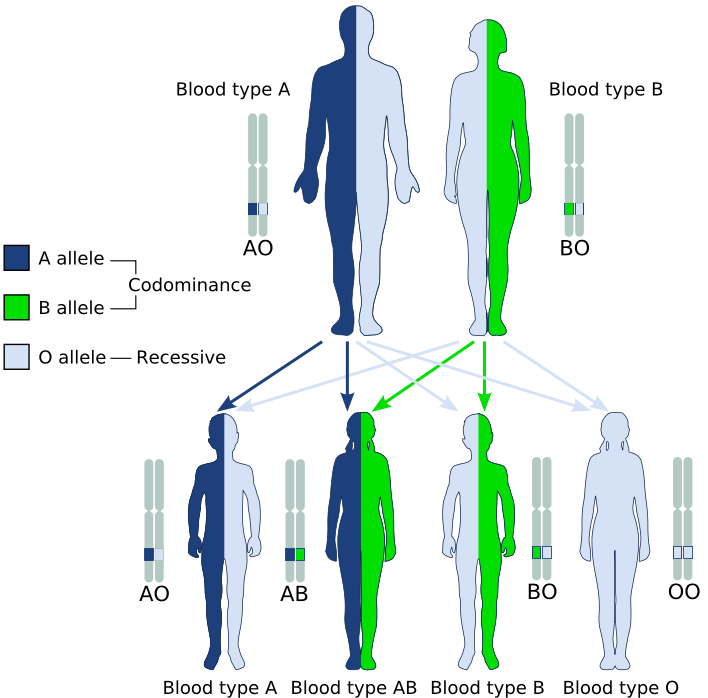
Figura 2.6: Sistema de determinación sanguínea ABO. Los alelos A y B muestran codominancia entre sí, mientras que ambos son dominantes respecto al O. Figura de Dominio Público tomada de Wikipedia (“ABO system codominance.svg”).

El locus codifica para antígenos de superficie en los eritrocitos (glóbulos rojos de la sangre), existiendo tres alelos para el mismo. Básicamente, tanto el alelo \(I^A\) como el \(I^B\) (codificantes para los antígenos A y B, respectivamente) dominan al alelo \(i\), que no produce antígenos de superficie (O). La relación entre el \(I^A\) y el \(I^B\) es de codominancia, expresándose ambos antígenos en la superficie de los eritrocitos si estos alelos se encuentran presentes al mismo tiempo. En función de las combinaciones alélicas posibles, existirán cuatro fenotipos diferentes detectables por los tests inmunológicos de rutina (i.e., test de aglutinación).

Si denominamos a las frecuencias de los alelos \(I^A\), \(I^B\) e \(i\) como \(p\), \(q\) y \(r\), respectivamente, estos cuatro fenotipos son definidos como

• Fenotipo A, formado por los homocigotas del alelo \(I^A\) , más los heterocigotos del alelo \(I^A\) y el alelo \(i\). La frecuencia esperada bajo equilibrio de Hardy-Weinberg es de \(p^2+2pr\).

• Fenotipo B, formado por los homocigotas del alelo \(I^B\) , más los heterocigotos del alelo \(I^B\) y el alelo \(i\). La frecuencia esperada bajo equilibrio de Hardy-Weinberg es de \(q^2+2qr\).

• Fenotipo AB, formado por los heterocigotas del alelo \(I^A\) y el alelo \(I^B\). La frecuencia esperada bajo equilibrio de Hardy-Weinberg es de \(2pq\).

• Fenotipo O, formado por los homocigotas del alelo \(i\). La frecuencia esperada bajo equilibrio de Hardy-Weinberg es de \(r^2\).

Notemos que la estimación de las tres frecuencias a partir del conteo de individuos ya no es tan sencilla como en los sistemas previamente analizados. Por un lado, existen en el sistema ABO 3 alelos en lugar de dos. Por el otro, lo que realmente complejiza el panorama es la relación de dominancia-codominancia entre alelos. De hecho, en casi todos los casos resulta imposible inferir el genotipo de un inviduo observando su fenotipo; en efecto, esto es solo posible para el fenotipo O (homocigotas del alelo \(i\)). En la Sección La estimación de frecuencias en el locus ABO se desarrolla un método para inferir las frecuencias alélicas a partir del conteo de los cuatro fenotipos detectables por el test de aglutinación.

2.8 ¿Dónde se “esconden” los alelos recesivos?

Muchas mutaciones tienen consecuencias deletéreas o muy graves cuando están presentes en homocigosis, pero no tienen mayores consecuencias para el individuo heterocigota. A modo de ejemplo, se puede pensar en un sistema que requiera de una única copia funcional de una enzima para mantener una actividad metabólica necesaria. Resulta claro que una mutación en homocigosis puede afectar la actividad enzimática (e.g., alterando la capacidad de unión a ligando), alterando así a este sistema metabólico. No obstante, la misma mutación en heterocigosis no afectará la eficiencia del sistema, en tanto seguirá existiendo una copia funcional codificante para la enzima en cuestión.

La diferencia entre el efecto fenotípico de algunos alelos en homocigosis respecto a heterocigosis puede apreciarse también en casos donde una característica evolutivamente favorable se ha transformado con el paso del tiempo en algo negativo (e.g., debido a las implicancias para la domesticación). Este es el caso de los cuernos en el bovino. En las razas bovinas “británicas”, la ausencia de cuernos (mochos, o “polled” en inglés) se trata de una característica que muestra un evidente modo de herencia dominante. Aún habiéndose podido “mapear” la ubicación de la característica en el genoma bovino, resulta bastante elusivo el mecanismo que genera esta ausencia (Allais-Bonnet et al. (2013); Medugorac et al. (2012)). Pese a esto, dado que los individuos con ambos alelos astados (recesivos) presentan un fenotipo astado, resulta bastante tentador evitar que se reproduzcan: intuitivamente se puede presumir que esto permitiría avanzar rápidamente en la eliminación de este alelo de la población, erradicandose así la existencia del fenotipo astado. Sin embargo, si se sigue esta premisa se observa un fenómeno interesante. Luego de una rápida caída en la proporción de individuos astados, el ritmo de la erradicación comienza a detenerse. Nuestra percepción inicial era apenas una ilusión, y la erradicación del fenotipo comienza a parecer una meta cada vez más lejana. ¿Por qué sucede esto? El principal problema con esta idea es que, al tratarse de un alelo recesivo el que queremos eliminar, resulta imposible distinguir fenotípicamente a los individuos heterocigotas de los homocigotas para el alelo dominante. Para entenderlo, veamos qué ocurre con la relación entre los heterocigotas y los homocigotas cuando nos acercamos a la eliminación del alelo. Sin pérdida de generalidad, llamaremos \(A_1\) al alelo dominante y \(A_2\) al alelo recisivo (con frecuencias \(p\) y \(q\), respectivamente). En la situación planteada, tenemos que \(q \rightarrow 0\), y por lo tanto \(p \rightarrow 1\), por lo que la proporción de heterocigotas respecto a homocigotas estará dada por

\[\begin{equation} \frac{2pq}{q^2}=\frac{2p}{q}=\frac{2(1-q)}{q}\approx \frac{2}{q} \therefore \lim_{q \to 0} \frac{2pq}{q^2}=+\infty \end{equation}\]

Es decir que, a medida que \(q\) tiende a cero, la relación tenderá a infinito. Dicho de otra forma, la enorme mayoría de los alelos recesivos estarán presentes en los individuos heterocigotas, los cuales son fenotípicamente indistinguibles de los homocigotas para el alelo dominante. La Figura 2.7 muestra gráficamente esta relación. A medida que nos acercamos hacia la frecuencia de cero para el alelo \(A_2\) (\(q\)), la pendiente de la relación se incrementa en valor absoluto (notemos que la derivada primera es igual a \(-2/q^2\)) y rápidamente la función aparece como vertical.

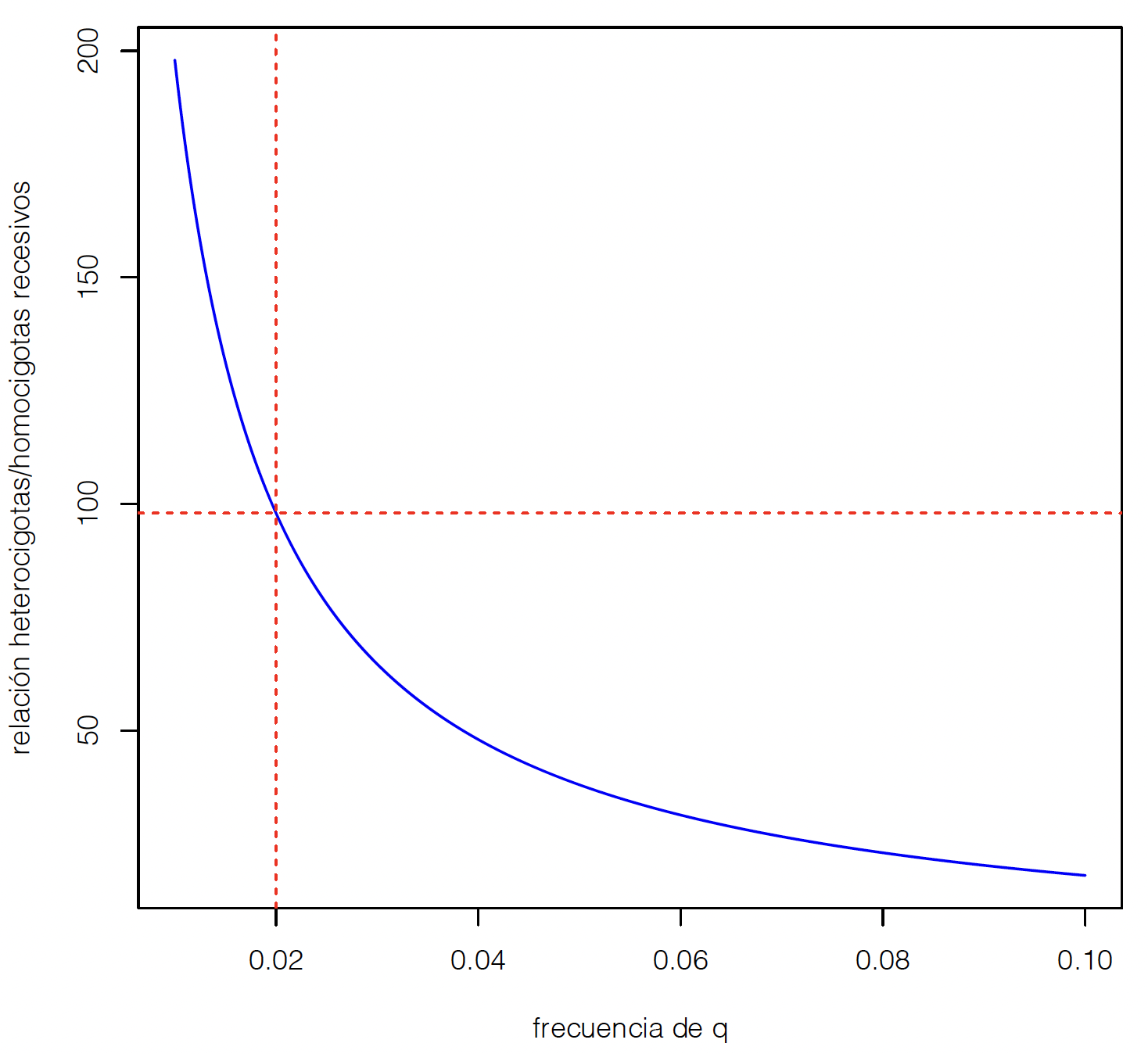
Figura 2.7: Relación del número de heterocigotas a homocigotas recesivos en función de la frecuencia del alelo \(q\) en un modelo de un locus con dos alelos, bajo equilibrio Hardy-Weinberg.

Como ya se había planteado, observamos que casi todos los alelos provienen de los individuos heterocigotas. A una frecuencia \(q=0,02\) (i.e., el 2% de los alelos son \(A_2\)), hay 98 veces más individuos heterocigotas que homocigotas recesivos. Pese a esto, si bien es imposible eliminar los alelos de la población por este mecanismo, sí es posible reducir sustancialmente su incidencia si mantener el criterio de “refugo” no tuviese otras implicancias asociadas.

Ejemplo 2.3

Con los datos del Ejemplo 2.2, calcular la relación entre el número de portadores y el número de individuos que padecerán la enfermedad, asumiendo que las poblaciones se encuentran en equilibrio de Hardy-Weinberg.

\[\begin{equation} \begin{split} q_{Fin}=\sqrt{\frac{1}{200000}}=0,002236068 \sim 0,22\% \\ q_{Tur}=\sqrt{\frac{1}{2600}}=0,01961161 \sim 1,96\% \end{split} \end{equation}\]

Los portadores serán los heterocigotas, por lo que, si asumimos que las poblaciones se encuentran en equilibrio de Hardy-Weinberg, entonces tendremos

\[\begin{equation} \begin{split} \frac{Het_{Fin}}{HomR_{Fin}}=\frac{2p_{Fin}}{q_{Fin}}=2*(1-0,002236068)/0,002236068=892,43 \\ \frac{Het_{Tur}}{HomR_{Tur}}=\frac{2p_{Tur}}{q_{Tur}}=2*(1-0,01961161)/0,01961161=99,98 \end{split} \end{equation}\]

Es decir, en la población de Turquía tenemos casi 100 portadores por cada enfermo, mientras que en la de Finlandia la relación es de aproximadamente 892 portadores por cada enfermo.

PARA RECORDAR

• La relación entre los heterocigotas y los homocigotas con el alelo recesivo (que sin pérdida de generalidad supondremos es el \(A_2\), con frecuencia \(q\)) cuando nos acercamos a la eliminación del alelo \(A_2\) y por lo tanto la frecuencia del \(A_1\) (\(p\)) se aproxima a 1 será:

\[\begin{equation} \frac{2pq}{q^2}=\frac{2p}{q}=\frac{2(1-q)}{q}\approx \frac{2}{q} \therefore \lim_{q \to 0} \frac{2pq}{q^2}=+\infty \end{equation}\]

• Es decir, a medida que \(q\) tiende a cero, la relación tenderá a infinito. Dicho de otra forma, casi todos los alelos recesivos estarán en los individuos heterocigotas, los que son fenotípicamente imposibles de distinguir de los homocigotas con el alelo dominante.

2.9 Hardy-Weinberg en especies poliploides

El fenómeno de la poliploidía (varias copias del genoma) representa un importante factor evolutivo que lleva a la especiación y es bastante usual en diferentes especies de todos los dominios de la vida, como se observa en la Figura 2.8. En particular, la poliploidía es frecuente en muchas de las especies vegetales, y algunas animales, de interés productivo. Ejemplo de esto son las bananas y sandías sin semillas (triploides), el maní y las moras (tetraploides), o el trigo y el boniato (hexaploides). En algunos casos, como el de la frutilla, el número básico de cromosomas (7) es repetido diferente número de veces en las más de 20 especies, existiendo individuos diploides, tetraploides, hexaploides, octaploides y hasta decaploides.

Las frecuencias alélicas esperadas en equilibrio Hardy-Weinberg se pueden calcular a partir de la generalización fórmula que describe el equilibrio para especies diploides. Recordemos del diagrama de Punnett que las frecuencias genotípicas que obtenemos para el caso diploide son el resultado de multiplicar las frecuencias de las combinaciones de alelos correspondientes. Podemos describir este resultado como

\[\begin{equation} (f_{\bf{A}}+f_{\bf{a}})(f_{\bf{A}}+f_{\bf{a}})=(p+q)(p+q)=(p+q)^2 \end{equation}\]

Figura 2.8: Eventos de paleopoliploidías (poliploidías que datan de millones de años) en la evolución, con evidencia fuerte (puntos rojos) y eventos putativos (puntos amarillos). Figura extraída de Wikipedia, creada por Peter Zhang, (CC BY-SA 3.0)

En el caso diploide, el producto de dos paréntesis \((p+q)\) representa el producto de dos eventos independientes: la generación de gametos. En el caso de los organismos poliploides (pongamos por caso un tetraploide), existe en primer lugar el proceso de sorteo aleatorio de qué par de alelos terminarán en el mismo gameto, y luego la combinación de gametos para producir el cigoto. Es decir, en el caso del tetraploide hay 4 multiplicaciones de las frecuencias de los alelos A y a, por lo que ahora la distribución de las frecuencias de los distintos genotipos estará dada por

\[\begin{equation} (f_{\bf{A}}+f_{\bf{a}})(f_{\bf{A}}+f_{\bf{a}})(f_{\bf{A}}+f_{\bf{a}})(f_{\bf{A}}+f_{\bf{a}})=(p+q)(p+q)(p+q)(p+q)=(p+q)^4 \end{equation}\]

Para el caso de un locus con dos alelos en una especie tetraploide, el desarrollo de la fórmula anterior nos lleva a la distribución de las frecuencias que se puede observar en el siguiente cuadro:

Genotipo	Frecuencia
\(\textbf{AAAA}\)	\(p^4\)
\(\textbf{AAAa}\)	\(4p^3q\)
\(\textbf{AAaa}\)	\(6p^2q^2\)
\(\textbf{Aaaa}\)	\(4pq^3\)
\(\textbf{aaaa}\)	\(q^4\)

Claramente esto es generalizable a otras ploidias, al menos a las pares (recordar que las ploidias impares suelen tener problemas de segregación), de acuerdo a

\[\begin{equation} (f_{\bf{A}}+f_{\bf{a}})*...*(f_{\bf{A}}+f_{\bf{a}})=(p+q)*...*(p+q)=(p+q)^n \end{equation}\]

donde \(n\) corresponde a la ploidía (\(n=2\) para diploides, \(n=4\) para tetraploides, \(n=6\) para hexaploides, etc.). Obviamente, al tratarse de un locus con dos alelos, los coeficientes que aparecen en el cuadro de más arriba, y que surgen de la generalización, son los coeficientes del “binomio de Newton”, o lo que es equivalente del “triángulo de Pascal” (o de Tartaglia, pese a que el desarrollo del mismo claramente antecede a ambos).

PARA RECORDAR

Al estimar frecuencias en un sistema de un locus con dos alelos:

• Si suponemos que los individuos representan un muestreo al azar de los gametos en la población y que los individuos de la muestra fueron seleccionados al azar, entonces la probabilidad de observar un conteo \(x\) en particular, dado el número total de alelos genotipados \(n\), se puede describir por la distribución binomial: \(f(x)={n\choose x} p^x (1-p)^{n-x}\), con las combinaciones de \(n\) elementos tomados de a \(x\) elementos dados por \({n\choose x}=\frac{n!}{x!(n-x)!}\)

Equilibrio de Hardy-Weinberg en especies poliploides:

• A modo de ejemplo, en el caso de organismos tetraploides hay 4 multiplicaciones de las frecuencias de los alelos A y a, por lo que ahora la distribución de las frecuencias de los distintos genotipos será dada por \((p+q)^4\).

• Esto es generalizable a otras ploidias, al menos a las pares de acuerdo a \((f_{\bf{A}}+f_{\bf{a}})*...*(f_{\bf{A}}+f_{\bf{a}})=(p+q)*...*(p+q)=(p+q)^n\)

2.10 Geometría y Genética: los diagramas de de Finetti

Aunque nos pueda parecer algo extraño, existe una fuerte conexión entre genética y geometría. De hecho, como veremos más adelante, Sewall Wright ³⁰ imaginó la evolución como un paisaje adaptativo, con picos y valles por los que se movían las poblaciones (S. Wright 1932), lo que conecta mentalmente de inmediato a un mundo de formas geométricas. Sin embargo, ya antes de esa fecha, Bruno de Finetti (Finetti 1926) había establecido que gran parte de los mecanismos y resultados de la genética mendeliana se podían obtener de consideraciones geométricas. Uno de los aportes más relevantes en este sentido es la idea de que para un locus con dos alelos en una especie diploide es posible representar todas las combinaciones posibles de las frecuencias genotípicas como los puntos interiores de un triángulo equilátero. Para ello, de Finetti hace uso del resultado del teorema de Viviani, por lo que primero veremos en primer lugar qué establece dicho teorema.
El teorema de Viviani ³¹ establece que, para triángulos equiláteros, la suma de las distancias desde cualquier punto interno del mismo a los tres lados es igual a la altura del triángulo. Para demostrarlo nos basaremos en el esquema de la Figura 2.9, donde dentro del triángulo de vértices A, B y C, con altura \(h\) y lado \(a\), tenemos al punto P.

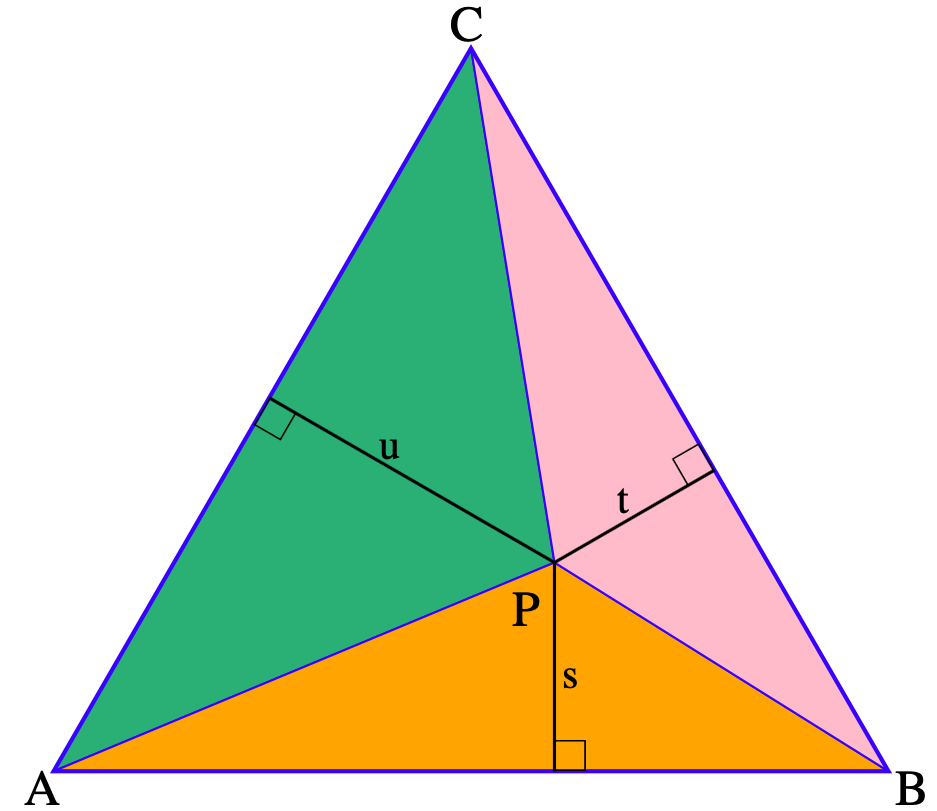
Figura 2.9: Triángulo usado para demostrar el teorema de Viviani. Figura tomada de Wikipedia, CC0 (Archivo:Viviani Theorem.svg).

Llamemos s, t y u a las distancias de P a los lados \(\overline{\rm AB}\), \(\overline{\rm BC}\) y \(\overline{\rm CA}\), respectivamente, que son las alturas (por definición) de los tres triángulos internos de vértices APB, BPC y CPA. Estos triángulos, a su vez completan toda el área del triángulo de vértices ABC. Como el área de un triángulo es igual a \(\frac{\text{base} \cdot \text{altura}}{2}\), tenemos entonces que

\[\begin{equation} \frac{a.s}{2}+\frac{a.t}{2}+\frac{a.u}{2}=\frac{a.h}{2} \Leftrightarrow \frac{a}{2}(s+t+u)=\frac{a}{2} h \Leftrightarrow s+t+u=h \end{equation}\]

por lo que queda demostrado este teorema. Dicho de otra manera, la significación de este teorema es que para cualquier punto interno a un triángulo equilátero, la suma de distancias a los lados es constante e igual a la altura del triángulo.

Veamos ahora cómo se relaciona este teorema con la genética. Supongamos que tenemos un locus con dos alelos. Asignamos los tres genotipos posibles a los vértices de un triángulo equilátero de altura igual a 1. Sin pérdida de generalidad, pongamos por ejemplo los homocigotas en la base (es un triángulo equilátero, por lo que todos sus lados son iguales) como muestra la Figura 2.10.

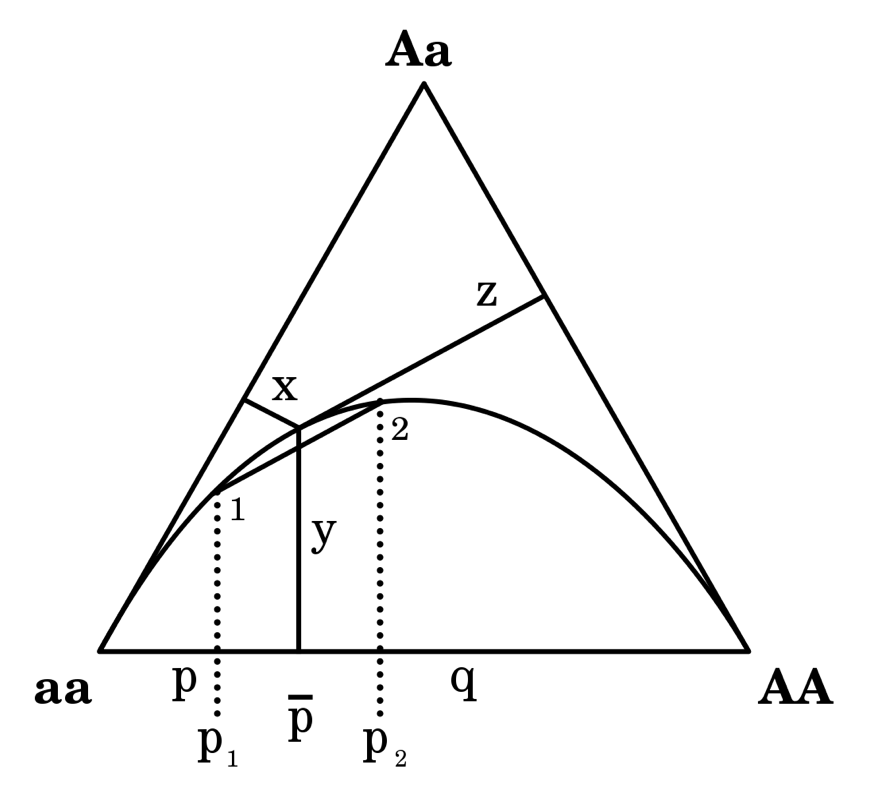
Figura 2.10: Diagrama de de Finetti.Figura tomada de Wikipedia, CC BY-SA 2.5 (Archivo:De Finetti diagram.svg).

Denotamos \(p\) a la frecuencia del alelo \(A\) y \(q=1-p\) la frecuencia del alelo \(a\). Ahora, de acuerdo al teorema de Viviani, sabemos que para cualquier punto interno del tríangulo la suma de distancias a los lados es igual a 1 (la altura del triángulo). Pero, ¿qué representan estas distancias? Para entender este punto, imaginemos primero que estamos en el vértice AA (abajo a la derecha): ahora la distancia de este punto hasta el lado opuesto es igual a 1; lo mismo ocurrirá con los otros dos vértices. Es decir que cuando estamos en algún vértice, la distancia al lado opuesto es igual a 1, o lo que es lo mismo, la frecuencia del correspondiente genotipo es de 1 (todos los individuos son de ese genotipo). Tenemos entonces que cada distancia a un lado del triángulo representa la frecuencia del genotipo en el vértice opuesto. A medida de que nos apartamos de los vértices comienzan a aparecer distancias no nulas a los dos otros lados, además de al lado opuesto al vértice. Esto se ve gráficamente en la Figura 2.10, donde las distancias x, y y z representan las frecuencias de los genotipos AA, Aa y aa, respectivamente. Que la suma de las frecuencias de los genotipos sea igual a 1 está garantizado por el teorema de Viviani.

Más aún, el punto de intersección de la distancia y con el eje formado por los vértices AA y aa separa a este lado en dos segmentos; el de la izquierda es proporcional a la frecuencia del alelo A (\(p\)), mientras que el de la derecha es proporcional a la frecuencia del alelo a (\(p=1-q\)). La distancia y representa la frecuencia de los heterocigotas (Aa) y, como ya vimos previamente (Sección H-W: la frecuencia de heterocigotas en función de la frecuencia alélica), bajo equilibrio de Hardy-Weinberg la misma describe una parábola en función de la frecuencia del alelo A (\(p\), o en forma alternativa del otro alelo). Por lo tanto, el equilibrio de Hardy-Weinberg se encuentra representado en la Figura 2.10 por la curva que va desde el vértice aa al vértice AA. Es decir, solo los puntos que se encuentran en esta curva (y por lo tanto las distancias asociadas a los lados) representan configuraciones de genotipos que se encuentran en equilibrio de Hardy-Weinberg.

Un ejemplo de la utilidad de lo anterior es la demostración visual de un efecto que veremos más adelante: la unión de (los individuos de) dos poblaciones en equilibrio de Hardy-Weinberg usualmente no produce una población conjunta en equilibrio H-W (antes de la reproducción). Esto suele resultar en la deficiencia en el número de heterocigotos respecto a la frecuencia esperada del promedio de las frecuencias alélicas en las dos poblaciones. Para ver esto en la Figura 2.10, supongamos que tenemos dos poblaciones 1 y 2 (del mismo tamaño) que se encuentran en equilibrio H-W, y por lo tanto son puntos sobre la curva. La frecuencias del alelo A en cada una de esta poblaciones será el segmento de recta izquierdo en el eje entre los vértices AA y aa, \(p_1\) y \(p_2\), cuyo promedio es \(\bar p\). Si ahora subimos \(\bar p\) hasta la curva de equilibrio, vemos que la intersección con el segmento de recta que une los puntos 1 y 2 (el promedio de las frecuencias genotípicas entre estas poblaciones) ocurre antes que con la curva. Lo que es equivalente, la distancia que representa la frecuencia promedio de los heterocigotas es menor a la que representa el valor esperado bajo equilibrio de Hardy-Weinberg.

Un análisis más exhaustivo sobre las posibilidades del diagrama de Finetti se encuentra en Cannings and Edwards (1968), donde por ejemplo los autores muestran que la endocría (“inbreeding”, concepto que veremos también más adelante) produce una parábola por debajo de la que corresponde al equilibrio de H-W, mientras que los procesos de selección producen una serie de “cónicas” (curvas resultantes de cortar un cono variando el ángulo del plano de corte) que también pasan por los vértices AA y aa.

2.11 La estimación de frecuencias en el locus ABO

Los métodos elaborados para la estimación de las frecuencias hacen uso del concepto de máxima verosimilitud, pero (Yasuda 1984) propuso un método sencillo basado en conteo. Supongamos que \(T=A+B+AB+O\), es decir el total de individuos de los distintos fenotipos. Trabajaremos con la determinación de \(p\), la frecuencia del alelo \(I^A\), pero para \(q\) (la frecuencia del \(I^B\)) la situación es idéntica por simetría y basta con sustituir A por B e \(I^A\) por \(I^B\). La frecuencia del alelo \(I^A\) será igual a la cantidad total de alelos \(I^A\) en los fenotipos que tienen este alelo, es decir A (\(I^AI^A\)) y AO (\(I^Ai\)) que solo expresan el A, más el AB (\(I^AI^B\)) que expresa los dos alelos, todo dividido entre \(2T\) que es el número total de alelos en los individuos. En el primer caso hay dos alelos \(I^A\) por cada individuo, mientras que en los otros dos hay solo un alelo por individuo. Sin embargo, nosotros no podemos distinguir los 3 fenotipos, ya que tanto el A como el AO solo expresan el alelo \(I^A\), por lo que debemos buscar una forma de separar el aporte de cada uno de estos genotipos al conteo. Mientras que el \(I^Ai\) aporta un alelo \(I^A\), el \(I^AI^A\) aporta dos alelos, por lo que todos los fenotipos A aportarán un alelo, mientras que una cierta fracción (los homocigotos) aportará un segundo alelo también. ¿Cuál es la fracción del fenotipo A que corresponde a los homocigotas \(I^AI^A\)? De acuerdo a lo predicho por el equilibrio de Hardy-Weinberg, los homocigotas \(I^AI^A\) serán \(p^2\), mientras que los heterocigotas \(I^Ai\) serán \(2pr\), por lo que la fracción de homocigotas \(h_A\) será

\[\begin{equation} h_A=\frac{p^2}{p^2+2pr}=\frac{p^2}{p(p+2r)}=\frac{p}{p+2r} \tag{2.10} \end{equation}\]

Es decir, si sumamos las contribuciones de AB, todos los A y el resto de los A homocigotos, tenemos

\[\begin{equation} p=\frac{[AB+A+Ah_A]}{2T} \tag{2.11} \end{equation}\]

Si definimos a partir de los fenotipos observables A y O, \(k_A=O/(A+O)\), entonces podemos expresar \(k_A\) en términos de lo esperable bajo equilibrio Hardy-Weinberg como

\[\begin{equation} \begin{split} k_A=\frac{Tr^2}{T(p^2+2pr)+Tr^2}= \frac{r^2}{p^2+2pr+r^2}=\frac{r^2}{(p+r)^2}=[r/(p+r)]^2\\ \therefore \sqrt{k_A}=\frac{r}{(p+r)} \end{split} \tag{2.12} \end{equation}\]

¿Cuál es la relación entre \(h_A\) y \(k_A\)? Usando las definiciones de \(h_A\) (ecuación (2.10)) y \(k_A\) (ecuación (2.12)), tenemos que

\[\begin{equation} \begin{split} h_A=\frac{p}{p+2r}=\frac{p+r-r}{p+r+r}=\frac{\frac{p+r-r}{p+r}}{\frac{p+r+r}{p+r}}=\frac{\frac{p+r}{p+r}-\frac{r}{p+r}}{\frac{p+r}{p+r}+\frac{r}{p+r}}=\\ =\frac{1-\frac{r}{p+r}}{1+\frac{r}{p+r}}=\frac{1-\sqrt{k_A}}{1+\sqrt{k_A}}\\ h_A=\frac{1-\sqrt{k_A}}{1+\sqrt{k_A}}=\frac{(1-\sqrt{k_A})}{(1+\sqrt{k_A})} \frac{(1-\sqrt{k_A})}{(1-\sqrt{k_A})}=\\ =\frac{(1-\sqrt{k_A})^2}{1-k_A} \end{split} \tag{2.13} \end{equation}\]

¡Excelente! Tenemos la relación entre \(h_A\) y \(k_A\) (expresada de dos formas), pero aún nos falta llegar a una forma de \(h_A\) que sea una función de cantidades observables, es decir los fenotipos. Si recordamos la definición de \(k_A\) a partir de los fenotipos observables (\(k_A=O/(A+O)\)) y sustituimos en la ecuación (2.13), tenemos

\[\begin{equation} \begin{split} h_A=\frac{(1-\sqrt{k_A})^2}{1-k_A} \Leftrightarrow h_A (1-k_A)=(1-\sqrt{k_A})^2 \Leftrightarrow h_A (1-\frac{O}{A+O})=1-2\sqrt{k_A}+k_A \end{split} \end{equation}\]

Llevando todo a denominador \(A+O\), tenemos

\[\begin{equation} \begin{split} h_A (\frac{A+O}{A+O} - \frac{O}{A+O}) = h_A (\frac{A+O-O}{A+O})=1-2 \cdot \sqrt{\frac{O}{A+O}}+\frac{O}{A+O} \Leftrightarrow \\ h_A (\frac{A}{A+O})=\\=\frac{A+O}{A+O} - \frac{\sqrt{A+O}}{\sqrt{A+O}} \cdot 2 \cdot \frac{\sqrt{O}}{\sqrt{A+O}}+\frac{O}{A+O}\\h_A (\frac{A}{A+O})=\frac{(A+O)-2\sqrt{O(A+O)}+O}{A+O} \Leftrightarrow \\ Ah_A (\frac{O}{A+O})\cdot (A+O) = A+O-2\sqrt{O(A+O)}+O \\Ah_A=A+O-2\sqrt{O(A+O)}+OAh_A \therefore \\Ah_A = A+2O-2\sqrt{O(A+O)} \end{split} \end{equation}\]

Finalmente, si volvemos al principio con este resultado y sustituimos en (2.11), tenemos el estimador basado en conteo

\[\begin{equation} \begin{split} \hat{p}=\frac{[AB+A+Ah_A]}{2T}=\frac{[AB+A+(A+2O-2\sqrt{O(A+O)})]}{2T} \therefore \\ \hat{p}=\frac{[(1/2)AB+A+O-\sqrt{O(A+O)}]}{T} \end{split} \end{equation}\]

Analogamente, por simetría, para la estimación de \(q\) tenemos

\[\begin{equation} \hat{q}=\frac{[(1/2)AB+B+O-\sqrt{O(B+O)}]}{T} \end{equation}\]

y por lo tanto, \(\hat{r}=1-\hat{p}-\hat{q}\). Sencillo, ¿no?

Ejemplo 2.4

Entre donantes de sangre de la ciudad de Ankara (Turquía) se determinó que de 1500 donantes sanos se observaron 669 del grupo A, 484 del grupo O, 232 del grupo B y 115 del grupo AB. Utilizando los estimadores que propuso (Yasuda 1984) estimar las frecuencias de los alelos \(I^A\), \(I^B\) e \(i\), así como el número esperado de los distintos fenotipos si la población estuviese en equilibrio de Hardy-Weinberg.

\[\begin{equation*} \begin{split} \hat{p}=\frac{[(1/2)AB+A+O-\sqrt{O(A+O)}]}{T}=\frac{((115/2)+669+484-\sqrt{(484(669+484))})}{1500}=0,3089808 \\ \hat{q}=\frac{[(1/2)AB+B+O-\sqrt{O(B+O)}]}{T}=\frac{((115/2)+232+484-\sqrt{(484(232+484))})}{1500}=0,1232134 \\ \hat{r}=1-\hat{p}-\hat{q}=1-0,3089808-0,1232134=0,5678058 \end{split} \end{equation*}\]

De acuerdo a las frecuencias estimadas previamente, el número esperado de cada fenotipo sería

\[E(A)=(p^2+2pr)T=(0,3089808^2+2\cdot 0,3089808\cdot 0,5678058)\cdot 1500=\] \[669,527 \sim 670\] \[E(B)=(q^2+2qr)T=(0,1232134^2+2\cdot 0,1232134\cdot 0,5678058)\cdot 1500=\] \[232,6562 \sim 233\] \[E(AB)=2pqT=2\cdot 0,3089808\cdot 0,1232134\cdot 1500=\] \[114,2117 \sim 114 \] \[E(O)=r^2T=0,5678058^2\cdot 1500=483,6051=484\]

lo que coincide estrechamente con los números observados, por lo que no podemos descartar que la población se encuentre en equilibrio Hardy-Weinberg (en general no podemos resolver a favor de una hipótesis alternativa basados en la estadística, a lo sumo podemos afirmar que la misma es completamente improbable dados los supuestos del test que aplicamos).

2.12 Conclusión

En este capítulo planteamos un modelo matemático básico, el equilibrio de Hardy-Weinberg, para realizar predicciones sobre las frecuencias genotípicas observadas en una población partiendo de las frecuencias alélicas existentes en la misma. A su vez observamos cómo el modelo es fácilmente ajustable a distintas situaciones de interés biológico. Las asunciones del modelo pueden resultar muy poco realistas (¿qué población natural tiene tamaño infinito?, ¿dónde se vió que los individuos se apareen al azar?). Si bien esto puede parecer una debilidad del modelo, en capítulos posteriores veremos cómo el equilibrio de Hardy-Weinberg puede utilizarse como una hipótesis nula para contrastar si es viable plantear que una población natural se comporta o no bajo alguna de las premisas del modelo. Gracias a su simpleza, el modelo resulta una excelente puerta de entrada al uso de la matemática para el estudio de la genética de poblaciones, aproximación de la que nos seguiremos nutriendo en lo que resta de este libro.

2.13 Actividades

2.13.1 Control de lectura

1. Varias de las asunciones necesarias para que se cumpla el modelo de equilibrio de Hardy-Weinberg no parecen ser realistas. ¿Cuál es la utilidad del modelo, si esto es así? Plantee al menos un ejemplo donde se viole alguna de las asunciones del modelo, y discuta la utilidad del modelo en dicho caso.
2. Describa qué sucede con las frecuencias alélicas esperadas en una población cuando existen diferentes proporciones de individuos machos y hembras.
3. A medida que aumenta el número de alelos presentes en una población en equilibrio de Hardy-Weinberg, aumenta necesariamente el número de genotipos heterocigotas en la misma. En estos casos, ¿cómo se puede calcular de forma sencilla la heterocigosidad esperada en la población, sin necesidad de sumar todas las frecuencias de genotipos heterocigotas?
4. Si un locus se ve asociado a un cromosoma sexual, ¿se comporta igual que un locus autosómico? Describa qué dinámica espera para las frecuencias alélicas en machos y hembras, así como el valor esperado para la frecuencia alélica a largo plazo en la población.
5. Las frecuencias alélicas deben ser estimadas a través de muestreos cuando se realiza un estudio poblacional. a. ¿En qué medida afectan los tamaños muestrales en este contexto? b. Nombre al menos un método que permita la determinación de los alelos presentes en un individuo muestreado.

2.13.2 ¿Verdadero o falso?

1. Si se cambian las frecuencias alélicas \(p\) y \(q\) de una población que se encuentra en equilibrio Hardy-Weinberg, las mismas se ajustarán en la próxima generación y volverán a su valor inicial (lo cual implica que las frecuencias genotípicas permanecerán invariables). A esta propiedad es que alude la palabra “equilibrio”.
2. El modelo de equilibrio de Hardy-Weinberg predice que un alelo que sea letal en homocigosis no será eliminado de una población si el fenotipo heterocigota es indistinguible del resto de los fenotipos homocigotas.
3. La suma de las frecuencias genotípicas en una población que segrega un locus bi-alélico (con frecuencias \(p\) y \(q\)) siempre cumple con la ecuación \(p^2 + 2pq + q^2 = 1\).
4. Para un locus bi-alélico, la máxima heterocigosidad esperada corresponde al caso donde ambas frecuencias alélicas son iguales.
5. Si dos poblaciones se encuentran bajo equilibrio de Hardy-Weinberg, una población constituída por ambas también lo hará.

Solución

1. Falso. Un cambio en las frecuencias alélicas llevará a un cambio de las frecuencias genotípicas esperadas bajo equilibrio de Hardy-Weinberg. La palabra “equilibrio” refiere al hecho de que, una vez establecidas estas frecuencias genotípicas, las mismas permenecerán iguales si las condiciones no cambian.

2. Verdadero. A medida que la frecuencia del alelo disminuye, el modelo prevé una prevalencia del alelo en los individuos heterocigotas (los cuales no son eliminados, ya que su fenotipo no sufre los efectos de cargar con el alelo). El alelo por tanto no es erradicado de la población.

3. Falso. Es correcto que la suma de las frecuencias genotípicas en una población debe equivaler a 1, ya que la suma de todas las frecuencias equivale al total de los casos posibles. No obstante, la ecuación \(p^2 + 2pq + q^2 = 1\) sólo será correcta si la población se encuentra bajo equilibrio de Hardy-Weinberg, ya que en dicho caso las frecuencias de genotipos homocigotas y heterocigotas se encuentran reflejadas en la ecuación.

4. Verdadero. En efecto, este caso implica que las frecuencias alélicas sean \(p=q=0,5\), con una hetercigosidad esperada de \(2 \cdot 0,5 \cdot 0,5 =0,5\). Ver sección de Ejercicios, donde se propone demostrar esta propiedad mencionada en el texto del capítulo.

5. Falso. La población total no se encontrará bajo equilibrio de Hardy-Weinberg. La causa de fondo es que los individuos de cada una de las poblaciones no se aparean con los de la otra (i.e., no existe panmixia en la población total). Un calculo sencillo muestra que existirá un déficit de heterocigotas (lo cual es observable en los diagramas de de Finetti). Ahondaremos en este fenómeno en el capítulo Apareamientos no-aleatorios.

Ejercicios

Ejercicio 2.1

Un locus A posee dos alelos conocidos (\(A_1\) y \(A_2\)), los cuales segregan en dos poblaciones independientes de organismos diploides. Las poblaciones tienen tamaños \(N_1 = N\) y \(N_2 = 2N\), respectivamente. Las frecuencias genotípicas en las poblaciones son

\[ \begin{cases} f_1(A_1A_1) = 0,36;\ f_1(A_1A_2) = 0,48;\ f_1(A_2A_2) = 0,16 \\ f_2(A_1A_1) = 0,09;\ f_2(A_1A_2) = 0,42;\ f_2(A_2A_2) = 0,49 \end{cases} \]

Se asume que en ambos casos el locus segrega acorde a lo esperado bajo equilibrio de Hardy-Weinberg. Calcule las frecuencias genotípicas esperadas si se unen las poblaciones.

Solución

Para poder calcular las frecuencias genotípicas esperadas bajo equilibrio de Hardy-Weinberg, debemos calcular las nuevas frecuencias alélicas en la población resultante de la unión de ambas poblaciones, las cuales llamaremos \(f_T(A_1)\) y \(f_T(A_2)\). Una vez obtenidos estos valores, podemos proceder a calcular las frecuencias genotípicas esperadas.

La frecuencia alélica \(f_T(A_1)\) corresponde a \[f_T(A_1) = \frac{\text{Núm. alelos }A_1}{\text{Núm. total de alelos}} = \frac{(2N_1 \cdot f_1(A_1)) + (2N_2 \cdot f_2(A_1))}{2N_1 + 2N_2}\]

donde \(f_1(A_1) = f_1(A_1A_1) + \frac{1}{2}\cdot f_1(A_1A_2)\) y \(f_2(A_1) = f_2(A_1A_1) + \frac{1}{2}\cdot f_2(A_1A_2)\).

Sustituyendo, tenemos

\[ f_T(A_1) = \frac{(2N_1 \cdot [f_1(A_1A_1) + \frac{1}{2}\cdot f_1(A_1A_2)]) + (2N_2 \cdot [f_2(A_1A_1) + \frac{1}{2}\cdot f_2(A_1A_2)])}{2N_1 + 2N_2}\] \[f_T(A_1) = \frac{(2N \cdot [f_1(A_1A_1) + \frac{1}{2}\cdot f_1(A_1A_2)]) + (2(2N) \cdot [f_2(A_1A_1) + \frac{1}{2}\cdot f_2(A_1A_2)])}{2N + 2(2N)} \]

\[\begin{equation} f_T(A_1) = \frac{(2 N \cdot [0,36 + \frac{1}{2}\cdot 0,48]) + (2(2 N) \cdot [0,09 + \frac{1}{2}\cdot 0,42])}{2N + 2(2 N)} \end{equation}\]

\[f_T(A_1) = 0,4\]

Por analogía, se puede calcular \(f_T(A_2)\). A su vez, se puede considerar que \(f_T(A_1) + f_T(A_2) = 1 \Rightarrow f_T(A_2) = 1 - f_T(A_1) = 1 - 0,4 = 0,6\)

De esto se desprende que

\[ \begin{cases} f_T(A_1A_1) = 0,4^2 = 0,16 \\ f_T(A_1A_2) = 2 \cdot 0,4 \cdot 0,6 = 0,48 \\ f_T(A_2A_2) = 0,6^2 = 0,36 \end{cases} \]

Ejercicio 2.2

Dos poblaciones independientes de igual tamaño (\(N\)) se encuentran divididas por una barrera geográfica que impide la reproducción entre organismos de ambos lugares. Las poblaciones segregan un locus \(A\) con tres alelos conocidos (\(A_1\), \(A_2\) y \(A_3\)), acorde a lo esperado en equilibrio de Hardy-Weinberg. Las poblaciones presentan las siguientes frecuencias genotípicas:

\[ \begin{cases} f_1(A1) = 0,6; f_1(A_2) = 0,4; f_1(A_3) = 0 \\ f_2(A1) = 0; f_2(A_2) = 0,3; f_2(A_3) = 0,7 \end{cases} \]

En un momento dado se desaparece la barrera geográfica que dividen a las poblaciones, pasándose a un régimen de panmixia para la población resultante.

a. Calcule el promedio de la heterocigosidad de las poblaciones, previa a la ruptura de las barrera geográficas.

b. Calcule la heterocigosidad en la población resultante de la unión de las poblaciones, asumiendo que esta cumple con las asunciones del equilibrio Hardy-Weinberg.

c. ¿Son iguales los valores obtenidos en a y b? Vincule su respuesta a las asunciones del equilibrio Hardy-Weinberg.

Solución

a. Calculamos la heterocigosidad esperada en cada caso: \[H_1 = 2 \cdot 0,6 \cdot 0,4 = 0,48\] \[H_2 = 2 \cdot 0,7 \cdot 0,3 = 0,42\]

de esto se desprende \[\overline{H} = \frac{H_1 + H_2}{2} = \frac{0,48 + 0,42}{2} = 0,45\]

b. Primero debemos recalcular las frecuencias alélicas (\(f_T(A_i)\), para cada alelo \(i\)), a efectos de poder estimar frecuencias genotípicas bajo equilibrio de Hardy-Weinberg en la población total.

Tenemos que

\[\begin{equation} \begin{cases} f_T(A_1) = \frac{2 N \cdot 0,6 + 2 N \cdot 0}{2 N + 2 N} = \frac{0,6}{2} \\ f_T(A_2) = \frac{2 N \cdot 0,4 + 2 N \cdot 0,3}{2 N + 2 N} = \frac{0,4 + 0,3}{2} = \frac{0,7}{2} \\ f_T(A_3) = \frac{2 N \cdot 0,7 + 2 N \cdot 0}{2 N + 2 N} = \frac{0,7}{2} \end{cases} \end{equation}\]

Notemos que las frecuencias alélicas suman 1.

La heterocigosidad esperada se puede calcular a partir de la homocigosidad, notando que \[H = 1 - \sum_{i=1}^{i=3} A_i^2\]

por lo que

\[H_T = 1 - (0,3^2 + 0,35^2 + 0,35^2)\] \[H_T = 0,665\]

c. La heterocigosidad esperada bajo equilibrio Hardy-Weinberg para la población en conjunto es mayor al promedio de heterocigosidad entre ambas. Esto es de esperar (el lector puede referirse a la subsección 2.10 Geometría y Genética: los diagramas de de Finetti para una demostración visual del fenómeno). ¿A qué se debe esto? Una forma de aproximarse al problema es pensar desde el inicio en la población en su totalidad: bajo equilibrio de Hardy-Weinberg se asume panmixia, y los heterocigotas son producto del apareamiento al azar en la población. Cuando la población se estructura en dos o más grupos que sólo se reproducen entre sí (en nuestro caso, las poblaciones iniciales) se rompe este régimen de panmixia general, disminuyendo el número de heterocigotas producidos. Una forma clara de ver esto en el ejemplo planteado es que, cuando se consideran dos poblaciones, no se generan individuos heterocigotas \(A_1A_3\).

Ejercicio 2.3

Un locus \(A\) presenta seis alelos que segregan acorde a lo esperado por el equilibrio Hardy-Weinberg. Las proporciones alélicas son las siguientes:

\[ \begin{cases} f(A_1) = 0,15 \\ f(A_2) = 0,25 \\ f(A_3) = 0,3 \\ f(A_4) = 0,09 \\ f(A_5) = 0,2 \\ f(A_6) = 0,01 \end{cases} \]

a. Calcular la heterocigosidad esperada para el locus.

b. Durante un período las condiciones ambientales cambian, y se pierden todos los individuos con alelos \(A_4\), \(A_5\) y \(A_6\). Una vez reestablecido el equilibrio de Hardy-Weinberg, las proporciones alélicas son ahora

\[ \begin{cases} f(A_1) = 0,1 \\ f(A_2) = 0,7 \\ f(A_3) = 0,2 \\ \end{cases} \]

¿La heterocigosidad aumentó o disminuyó en la población? ¿Qué tanto respecto a lo obtenido en la primera parte del ejercicio?

Solución

a. Recordemos que la frecuencia total de heterocigotas (heterocigosidad) se puede calcular a partir de la frecuencia total de homocigotas, en tanto la suma de ambas frecuencias debe sumar uno (ya que un organismo es o bien homocigota, o bien heterocigota).

Tenemos por tanto que

\[H = 1 - \sum_{i=1}^{i=6} A_i^2\]

por lo que

\[H = 1 - (0,15^2 + 0,25^2 + 0,3^2 + 0,09^2 + 0,2^2 + 0,01^2)\] \[H = 0,7768\]

b. Aplicando la misma lógica, tenemos que en el nuevo escenario \[H = 1 - (0,1^2 + 0,7^2 + 0,2^2) = 0,46\]

La heterocigosidad disminuyó. Aplicando un cociente, podemos expresar qué fracción del primer valor representa este nuevo valor de heterocigosidad. Llamaremos a estas heterocigosidades \(H_1\) y \(H_2\). Tenemos que

\[\frac{H_2}{H_1} = \frac{0,46}{0,7768} \approx 0,59\]

Vemos que la heterocigosidad disminuyó en el segundo escenario a casi el 60% del valor planteado en primera instancia.

Ejercicio 2.4

Dos loci bi-alélicos, \(A\) y \(B\), se encuentran segregando de forma independiente en una población de organismos diploides. Las frecuencias alélicas en la población son

\[ \begin{cases} f(A_1) = 0,2 \\ f(A_2) = 0,8 \\ f(B_1) = 0,4 \\ f(B_2) = 0,6 \\ \end{cases} \]

a. Realice un diagrama de Punnett mostrando los posibles genotipos en la población.

b. Calcule las frecuencias genotípicas esperadas bajo equilibrio de Hardy-Weinberg.

Solución

a. Se muestran el cuadro de 16 combinaciones posibles, correspondientes a .

b. Los loci segregan de forma independiente, por lo que la presencia de un alelo de \(A\) no altera la probabilidad de encontrar un determinado alelo de \(B\). Se calculan las frecuencias genotípicas para cada locus, y la multiplicación de los mismos equivale a la frecuencia de organismos que los portarán los genotipos correspondientes en simultáneo

\[ \begin{cases} f(A_1A_1) = 0,2^2; f(A_1A_2) = 2 \cdot 0,2 \cdot0,8; f(A_2A_2) = 0,8^2 \\ f(B_1B_1) = 0,4^2; f(B_1B_2) = 2\cdot0,4\cdot0,6; f(B_2B_2) = 0,6^2 \end{cases} \]

por lo que

\[ \begin{cases} f(A_1A_1; B_1B_1) = 0,2^2 \cdot 0,4^2 = 0,0064 \\ f(A_1A_1; B_1B_2) = 0,2^2 \cdot (2 \cdot 0,4 \cdot 0,6) = 0,0192 \\ f(A_1A_1; B_2B_2) = 0,2^2 \cdot 0,6^2 = 0,0144 \\ f(A_1A_2; B_1B_1) = (2 \cdot 0,2 \cdot 0,8) \cdot 0,4^2 = 0,0512 \\ f(A_1A_2; B_1B_2) = (2 \cdot 0,2 \cdot 0,8) \cdot (2 \cdot 0,4 \cdot 0,6) = 0,1536 \\ f(A_1A_2; B_2B_2) = (2 \cdot 0,2 \cdot 0,8) \cdot 0,6^2 = 0,1152 \\ f(A_2A_2; B_1B_1) = 0,8^2 \cdot 0,4^2 = 0,1024 \\ f(A_2A_2; B_1B_2) = 0,8^2 \cdot (2 \cdot 0,4 \cdot 0,6) = 0,3072 \\ f(A_2A_2; B_2B_2) = 0,8^2 \cdot 0,6^2 = 0,2304 \end{cases} \]

Ejercicio 2.5

Un factor de transcripción (denotado por \(F\)) regula la expresión de un gen codificante para una enzima (denotada \(E\)) vinculada a la coloración en una especie diploide. Se asume que ambos loci segregan de forma independiente.

Los siguientes alelos son conocidos para estos loci - Alelo \(F_a\): alelo codificante para una copia funcional del factor de transcripción. - Alelo \(F_b\): alelo codificante para una copia disfuncional del factor de transcripción. - Alelo \(E_a\): alelo codificante para una copia funcional de la enzima. - Alelo \(E_b\): alelo codificante para una copia disfuncional de la enzima.

La presencia de una copia funcional para el factor de transcripción basta que el sistema sea funcional. En cambio, la coloración de los organismos depende del número de copias funcionales para la enzima \(E\): dos copias funcionales resultan en coloración roja, una copia funcional resulta en coloración rosada y la ausencia de copias funcionales resulta en ausencia de color.

a. Considere una población de tamaño \(N\), donde se tienen las siguientes frecuencias alélicas: \(f(F_a) = 0,5;\ f(E_a) = 1\). Describa la proporción de individuos que presentan coloración roja, rosada y nula en la población si se asume esta se encuentra en equilibrio de Hardy-Weinberg.

b. Considere una población de tamaño \(N\), donde se tienen las siguientes frecuencias alélicas: \(f(F_a) = 1;\ f(E_a) = 0,5\). Describa la proporción de individuos que presentan coloración roja, rosada y nula en la población si se asume esta se encuentra en equilibrio de Hardy-Weinberg.

c. Considere la población resultante de unificar las poblaciones anteriormente mencionadas. Describa la proporción de individuos que presentan coloración roja, rosada y nula en la población si se asume esta se encuentra en equilibrio de Hardy-Weinberg.

Solución

a. La proporción de individuos que mostraran algún tipo de coloración corresponde a aquellos que preentan alguna copia funcional para el factor de transcripción \(F\). La proporción de individuos homocigotas \(F_bF_b\) para el alelo disfuncional está dada por \(f(F_b)^2 = 0,5^2 = 0,25\). Por lo tanto, la proporción de individuos que presentan coloración equivale a \(1-0,25 = 0,75\). De estos, la totalidad portarán dos alelos \(E_a\), lo que resulta en coloración roja. Por lo tanto, se esperan las siguientes proporciones de coloración: \(f(\text{Rojo}) = 0,75, f(\text{Rosado}) = 0; f(\text{Albino}) = 0,25\).

b. La totalidad de los organismos serán homocigotas \(F_aF_a\) para el locus \(F\), por lo cual la coloración dependerá exclusivamente de las frecuencias esperadas de individuos \(E_aE_a\), \(E_aE_b\) y \(E_bE_b\) para el locus \(E\). Tenemos que

\[ \begin{cases} f(\text{Rojo}) = f(E_aE_a) = f(E_a)^2 = 0,5^2 = 0,25 \\ f(\text{Rosado}) = f(E_aE_b) + f(E_bE_a) = 2 \cdot f(E_a) \cdot f(E_b) = 2 \cdot 0,5 \cdot 0,5 = 0,5 \\ f(\text{Albino}) = f(E_bE_b) = f(E_b)^2 = 0,5^2 = 0,25 \end{cases} \]

c) El fenotipo de coloración dependerá tanto de los alelos presentes en el locus \(E\) como en el locus \(F\). Al combinar las poblaciones, las frecuencias alélicas (y genotípicas) cambiarán, y por lo tanto cambiará la proporción esperada para cada fenotipo. Los loci segregan de forma independiente, por lo cual podemos obtener las frecuencias genotípicas esperadas para cada locus por separado, y luego multiplicar las frecuencias resultantes para obtener las frecuencias esperadas en conjunto, las cuales correlacionan con los fenotipos esperados. Para ello, primero necesitamos establecer las nuevas frecuencias alélicas \(f(F_a);\ f(F_b);\ f(E_a);\ f(E_b)\) para la población resultante.

Observemos qué pasa para un caso particular, el alelo \(F_a\):

\[\begin{equation} f(F_a) = \frac{\text{núm. alelos }F_a}{2N + 2N} = \frac{(2 N \cdot f_1(F_a) + 2(N \cdot f_2(F_a)))}{4 N} = \frac{2 \cdot 0,5 + 2 \cdot 1}{4} = 0,75 \end{equation}\]

Por analogía, se calculan las nuevas frecuencias alélicas en la población en el resto de los casos

\[ \begin{cases} f(F_b) = 0,25 \\ f(E_a) = 0,75 \\ f(E_b) = 0,25 \end{cases} \]

Por lo tanto, las frecuencias genotípicas esperadas en equilibrio Hardy-Weinberg para cada locus, son:

\[ \begin{cases} f(F_aF_a) = 0,75^2; f(F_aF_b) = 2 \cdot 0,75 \cdot 0,25; f(F_bF_b) = 0,25^2 \\ f(E_aE_a) = 0,75^2; f(E_aE_b) = 2 \cdot 0,75 \cdot 0,25; f(E_bE_b) = 0,25^2 \end{cases} \]

Considerando los dos genotipos al mismo tiempo, podemos dar las frecuencias fenotípicas esperadas para coloración.

\[ \begin{cases} f(\text{Rojo}) = f(F_aF_a) \cdot f(E_aE_a) = 0,75^2 \cdot 0,75^2 \\ f(\text{Albino}) = f(F_bF_b;\ E_\text{.}E_\text{.}) + f(F_\text{.}F_\text{.}; E_bE_b) - f(F_bF_b;\ E_bE_b) = \\ 0,25^2 + 0,25^2 - (0,25^2 \cdot 0,25^2) \end{cases} \]

en donde en el último caso restamos \(f(F_bF_b;\ E_bE_b)\) para no contar este genotipo dos veces.

Para facilitar los cálculos, notemos que los individuos que no sean rojos o albinos deberán ser necesariamente rosados, por la configuración del sistema. Esto nos da

\[f(\text{Rosado}) = 1 - (0,75^2 \cdot 0,75^2) - (0,25^2 + 0,25^2 - (0,25^2 \cdot 0,25^2)) \] \[f(\text{Rosado}) = 0,5625 \]

Se puede verificar que esta frecuencia es equivalente a sumar las frecuencias de los genotipos que expresan este color.

Ejercicio 2.6

Demostrar (a) que para un locus con dos alelos en una especie diploide en equilibrio Hardy-Weinberg, la diferencia de frecuencias alélicas es igual a la diferencia de frecuencia entre los homocigotos respectivos y (b) que esta diferencia es igual a \(2p -1\).

Solución

Supongamos que llamamos \(p\) y \(q=1-p\) a las frecuencias de los dos alelos. Para la parte (a) debemos demostrar que su diferencia es igual a la diferencia entre los genotipos homocigotos, es decir, \(p-q=p^2-q^2\). Para ellos utilizaremos el hecho de que multiplicar por 1 ambos lados de la ecuación y el hecho de que \(p+q=1\).

\[\begin{equation} (p-q)=1(p-q)=(p+q)(p-q)=p^2+pq-pq-q^2=p^2-q^2 \end{equation}\]

En tanto, para la parte (b) utilizaremos que \(q=1-p\), por lo que

\[\begin{equation} p-q=p-(1-p)=p-1+p=2p-1 \end{equation}\]

Ejercicio 2.7

En general, si bien en muchas enfermedades humanas y animales que se clasifican como de herencia mendeliana se considera que se trata de un solo alelo recesivo, a nivel molecular suelen co-existir varios alelos deletéreos que producen similar fenotipo. Demostrar que si en un locus existen dos alelos deletéreos recesivos respecto al alelo normal, bajo equilibrio de Hardy-Weinberg los resultados respecto al número de portadores y de enfermos son equivalentes a considerarlos como un solo alelo defectuoso.

Solución Supongamos que llamamos \(A_1\) al alelo normal y \(A_2\) y \(A_3\) a los alelos defectuosos, con frecuencias respectivas \(p\), \(q\) y \(r\), \(p+q+r=1\). Llamemos \(u=q+r\) a la frecuencia de los dos alelos defectuosos sumados, o lo que es lo mismo, a la frecuencia de alelos defectuosos (como si fuera uno solo). De acuerdo a lo visto para más de un alelo, las frecuencias esperadas bajo equilibrio Hardy-Weinberg serán

\[\begin{equation} (p+q+r)^2=p^2+q^2+r^2+2pq+2pr+2qr \end{equation}\]

De estos genotipos, los enfermos serán aquellos que tengan 2 alelos defectuosos, sean cuales sean, o sea \(A_2A_2\), \(A_3A_3\) y \(A_2A3\), es decir

\[\begin{equation} q^2+r^2+2qr=(q+r)^2=u^2 \end{equation}\]

Es decir, demostramos que el número de enfermos esperados es equivalente a considerarlo como un solo alelo. Ahora, el número de portadores será la suma de los genotipos que tienen un solo alelo defectuoso y el otro normal, o sea \(A_1A_2\) y \(A_1A_3\), es decir

\[\begin{equation} 2pq+2pr=2p(q+r)=2pu \end{equation}\]

con lo que queda demostrado que también la frecuencia de portadores es equivalente a considerarlo un solo alelo defectuoso.

Ejercicio 2.8

En muchos casos las ecuaciones que derivamos se simplifican enormemente debido a la restricción \(p+q=1\). Demostrar que las siguientes relaciones son válidas (adaptado de Hartl and Clark (2007))

\[\begin{equation} \begin{split} p^2-q^2=p-q \\ p^2+pq=p \\ p-q=1-2q \\ p^2+q^2=1-2pq \\ (p-q)^2=1-4pq \end{split} \end{equation}\]

Solución

Haciendo uso de que \(p+q=1\), por lo que también \((p+q)^2=p^2+2pq+q^2=1\) (ya que lo que está dentro del paréntesis vale \(1\) y \(1^2=1\)), tenemos que

\[\begin{equation} \begin{split} p^2-q^2=(p+q)(p-q)=(1)(p-q)=p-q \\ p^2+pq=p(p+q)=p(1)=p \\ p-q=(1-q)-q=1-q-q=1-2q \\ p^2+q^2=1-2pq \Leftrightarrow p^2+q^2+2pq=1 \Leftrightarrow (p+q)^2=1 \Leftrightarrow 1^2=1\\ (p-q)^2=p^2-2pq+q^2=p^2-2pq+q^2+2pq-2pq=p^2+2pq+q^2-2pq-2pq=(p+q)^2-4pq=1-4pq \end{split} \end{equation}\]

---

Bibliografía

Allais-Bonnet, A., C. Grohs, I. Medugorac, S. Krebs, A. Djari, A. Graf, S. Fritz, et al. 2013. “Novel insights into the bovine polled phenotype and horn ontogenesis in Bovidae.” PLoS ONE 8 (5): e63512.

Cannings, C., and A. W. Edwards. 1968. “Natural selection and the de Finetti diagram.” Ann. Hum. Genet. 31 (4): 421–28.

Castle, W. E. 1903. “The laws of Galton and Mendel and some laws governing race improvement.” Proceedings of the American Academy of Arts and Sciences 35 (8): 233–42.

Finetti, B. de. 1926. “Considerazioni matematiche sull’ereditarietà mendeliana.” Metron 6 (1): 3–41.

Hardy, G. H. 1908. “MENDELIAN PROPORTIONS IN A MIXED POPULATION.” Science 28 (706): 49–50.

Hartl, Daniel L, and Andrew G Clark. 2007. Principles of Population Genetics. 4th. ed. Sinauer.

Medugorac, I., D. Seichter, A. Graf, I. Russ, H. Blum, K. H. Göpel, S. Rothammer, M. Förster, and S. Krebs. 2012. “Bovine polledness–an autosomal dominant trait with allelic heterogeneity.” PLoS ONE 7 (6): e39477.

Rosenberg, N. A., and J. T. Kang. 2015. “Genetic Diversity and Societally Important Disparities.” Genetics 201 (1): 1–12.

Vries, H. de. 1900. “Sur la loi de disjonction des Hybrides.” Comptes Rendus de l‘Académie Des Sciences 130 (-): 845–47.

Weinberg, W. 1908. “Über den Nachweis der Vererbung beim Menschen.” Jahreshefte Des Vereins für Vaterländische Naturkunde in Württemberg. 64: 369–82.

———. 1932. “The roles of mutation, inbreeding, cross- breeding and selection in evolution.” Proceedings of the Sixth Annual Congress of Genetics 1 (-): 356–66.

Yasuda, N. 1984. “A note on gene frequency estimation in the ABO and ABO-like system.” Jinrui Idengaku Zasshi 29 (3): 371–80.

---

21. Aunque la misma ya había sido claramente establecida por Vries (1900) durante el re-descubrimiento de las leyes de Mendel↩︎

22. Reginald Crundall Punnett, genetista británico que fue quien los desarrolló. Además, Punnett se relaciona directamente con el equilibrio de Hardy-Weinberg, ya que al no poder contrarrestar los argumentos de George Udny Yule acerca del crecimiento sostenido de los alelos dominantes, llevó el problema al matemático Godfrey Harold Hardy, con quien jugaba al cricket; el resto es historia conocida.↩︎

23. Esta condición involucra a todos los aspectos que pudieran llevar a diferencias en el éxito reproductivo. Por ejemplo, implica que no existan diferencias ni en la viabilidad de los diferentes genotipos hasta llegar a su etapa reproductiva, ni en la fecundidad de los mismos.↩︎

24. En el sistema XY, presente en los mamíferos, el gen Y es el que determina el sexo (masculino), siendo los machos heterogaméticos (XY) y las hembras homogaméticas (XX). Es otras especies, como las aves, existen otros sistemas como el ZW, en el que son las hembras las que son heterogaméticas (ZW), mientras que los machos son homogaméticos (ZZ)↩︎

25. Ya veremos en otras partes que el concepto de “verdadero valor” de un parámetro está ligado a una corriente estadística llamada “frecuentista” y que se contrapone en cierta manera a una visión más subjetiva de la probabilidad, representada en la escuela “bayesiana”.↩︎

26. Si observamos \(45/100\) alelos en nuestro muestreo, nuestra estimación será \(p = 0,45\) (\(p = 0,5\), si redondeamos a una cifra significativa). Lo mismo sucedería si observamos cualquier valor entre 45 y 54 alelos.↩︎

27. En estos casos observar el fenotipo aporta la misma información que determinar el genotipo↩︎

28. Asumiremos que se trata de un solo tipo de alelo defectuoso. Si bien a nivel molecular los alelos defectuosos pueden ser de varios tipos diferentes, con efectos deletéreos, a nivel fenotípico se comportan como si se tratase de un mismo alelo (ver [Ejercicio 2.6]).↩︎

29. Descubierto por el médico e inmunólogo austríaco Karl Landsteiner en 1901, lo que le valió el premio Nobel de Medicina y Fisiología en 1931.↩︎

30. Sewall Green Wright (21 de diciembre, 1889 - 3 marzo, 1988), fue un genetista que realizó notables aportes sobre los efectos de la selección y la deriva, así como el análisis de pequeñas poblaciones y el efecto de la consanguinidad . Junto a Ronald A. Fisher y JBS Haldane establecieron la fundación matemática de la genética de poblaciones y de la teoría evolutiva.↩︎

31. Vincenzo Viviani (5 de abril,1622 - 22 de setiembre, 1703), matemático y científico italiano, pupilo de Torricelli y discípulo de Galileo.↩︎