Capítulo 4 Selección natural

En los capítulos anteriores vimos cómo la frecuencias alélicas de las poblaciones evolucionan, simplemente por las “leyes de la herencia”, es decir el modelado matemático de los mecanismos moleculares y de los efectos estocásticos asociados al muestreo de los gametos en poblaciones de tamaño finito. En otras palabras, hasta ahora no hemos incorporado en nuestros modelos el efecto que la ventaja de algún alelo o genotipo pudiese tener sobre los otros. Como veremos en este capítulo, esto último constituye la base de la selección, el tema de nuestro capítulo actual. En particular, en este capítulo sentaremos las bases de la selección natural, aquella que opera en las poblaciones naturales y dejaremos para otros capítulos en la (PART*) Parte III: Genética Cuantitativa el tema de la selección artificial, que si bien se funda en las mismas bases, su análisis tendrá otros componentes en cuenta que aún no hemos visto.

Bajo cualquier tipo de selección los genotipos ya no tendrán la misma oportunidad de pasar sus gametos a la siguiente generación y como las frecuencias de los alelos están vinculadas a las de los genotipos, por lo tanto ya no podremos seguir asumiendo que estas frecuencias simplemente siguen en promedio a las de la generación anterior. Central a este capítulo, por tanto, es el concepto de fitness, con el cual nos introduciremos a la temática.

OBJETIVOS DEL CAPÍTULO

\(\square\) Presentar y analizar el concepto de selección natural, proceso que genera cambios sistemáticos en las frecuencias alélicas de las poblaciones naturales.

\(\square\) Distinguir entre distintos regímenes de selección natural y sus posibles consecuencias biológicas.

\(\square\) Plantear un modelo matemático explícito que permita plantear de forma precisa la dinámica de las frecuencias alélicas bajo estos distintos regímenes de selección natural.

\(\square\) Analizar y modelar la interacción entre la selección natural y otras fuerzas relevantes en la evolución, tales como la mutación y la deriva genética.

\(\square\) Discutir en qué influye (y en qué no) la magnitud de la intensidad de la selección natural en la evolución de las poblaciones.

4.1 El concepto de “fitness”

En cualquier población natural, los individuos no dejan el mismo número de descendientes que alcanzan la edad reproductiva con éxito y menos aún que son capaces de generar a su vez el mismo número de crías que sus padres. Es decir, existe una variabilidad importante en el número de descendientes que dejan los individuos. Una parte de esta variabilidad es puramente estocástica, es decir, producto del azar. Por ejemplo, individuos que mueren antes de la edad reproductiva por eventos dependientes del azar (semillas que caen en terrenos completamente infértiles, animales o plantas con “mala suerte”, etc.). Otra parte de la variabilidad en el éxito reproductivo es en cambio sistemática: si los animales con un genotipo particular en un locus determinado son más exitosos en promedio en el número de descendientes que alcanzan la edad reproductiva, entonces dejarán más descendientes que el resto y en función de que esto haga crecer la frecuencia de su genotipo en relación a los otros entonces tenemos una base genética para la variabilidad. Claramente, la ventaja de unos genotipos sobre otros suele estar asociada al ambiente, considerando el término ambiente como algo genérico, tiempo y espacio dónde y cuándo viven nuestros individuos, por lo que usualmente vamos a restringir nuestros desarrollos a lo que consideramos como un ambiente estable (a los efectos de evitar que cambien las presiones selectivas durante nuestro análisis).

Por un tema de conveniencia general nosotros vamos a utilizar el término inglés fitness, ya que su traducción más usual al castellano como aptitud deja a nuestro entender bastante que desear. Para ser más claros en nuestros conceptos veamos unas definiciones que nos ayudarán a entender la relación entre las diferentes formas del fitness, conceptos que desarrollaremos en la siguiente sección. El fitness absoluto es la tasa de aumento o crecimiento que predice el número absoluto de individuos de un genotipo determinado en una población a lo largo del tiempo. En otras palabras, se trata del número medio de descendientes de un tipo determinado, por cada progenitor del mismo tipo (por ejemplo, el tipo podría ser el genotipo o el alelo, en otros casos).

Por otro lado, para el fitness relativo existen dos definiciones diferentes, cada una con sus ventajas, con diferencias en el denominador, es decir en el relativo a qué. En las secciones que siguen usaremos preferencialmente la siguiente: es la tasa de crecimiento de los genotipos (cuando consideramos genotipos, por ejemplo) en relación con un genotipo elegido como estándar de comparación (a menudo el genotipo con la mayor aptitud absoluta). Normalmente se simboliza con la letra \(w\) en los modelos en los que el tiempo se representa en generaciones discretas (conocida a veces como selección darwiniana) y como \(m\) en los modelos en los que el tiempo es continuo (a veces llamada selección malthusiana, por Thomas Malthus⁴⁶). Otra definición de relativo es la que divide los fitness absolutos entre el fitness medio (\(\bar{w}\)), que ocasionalmente usaremos con ventaja sobre la primer definición.

Por último, el fitness medio es simplemente el promedio de los fitness relativos, es decir la suma de los valores de fitness relativos ponderados por la frecuencia de cada genotipo de la población, es decir que para \(k\) genotipos, \(\bar{w}=\sum_{i=1}^k w_i p_i\).

4.2 Selección natural en el modelo de un locus con dos alelos

Las causas de del éxito relativo entre los genotipos pueden ser varias. Por ejemplo, los distintos genotipos pueden estar asociados a distintas viabilidades de los cigotos. Luego de esto, durante el crecimiento las viabilidades pueden también ser diferentes, ya sea por la habilidad para crecer más rápido que la de otros genotipos, por ser más resistentes a condiciones ambientales prevalentes, por ser más aversos al riego o por ser menos llamativos como presas, por ejemplo. Ya crecidos los individuos y en plena etapa reproductiva, el éxito puede estar condicionado a varias cosas, de acuerdo a la forma de reproducción, física y etológica de la especie. Por ejemplo, en algunas especies los machos más llamativos (y a menudo más expuestos como presas) son los preferidos por las hembras. En otros casos, los machos disputan su posición privilegiada como reproductores mediante combates, asegurándose el apareamiento con tantas hembras como les sea posible, aunque los machos perdedores suelen encontrar también oportunidades para aparearse. Finalmente, la fertilidad es otro parámetro fundamental para la diferencia en el éxito reproductivo de algunos genotipos, en parte determinado por la acción de genotipos y en otro caso por el éxito o viabilidad de los alelos (e.g., en gametos).

Para estudiar la influencia de la selección en la evolución de las frecuencias de los alelos vamos a asumir que nos encontramos en un locus autosomal con dos alelos, en un organismo diploide y vamos a asumir que no hay diferencias en la viabilidad de los gametos (que en principio está directamente asociado a un fitness de alelos). El modelo fundamental que utilizaremos de acá en adelante es el que aparece en la Figura 4.1. Los individuos recién nacidos tendrán una viabilidad diferencial (probabilidad de supervivencia hasta la edad adulta-reproductiva) que será la base de nuestra selección. En efecto, todo el proceso en una generación se puede resumir en el cuadro azul de la Figura 4.1. Los recién nacidos serán el producto (de la frecuencia) de los gametos en la generación anterior. Luego, durante todo el período hasta llegar a la etapa reproductiva estarán sujetos a la selección, con diferentes viabilidades asociadas a los genotipos en nuestro locus de interés. Esto provocará que los individuos por genotipo que contribuyen al pool de gametos no sean en idénticas proporciones a los recién nacidos. Dicho de otra forma, es como si aplicásemos un filtro diferente a cada uno de los genotipos, entre los recién nacidos y los adultos, que cambiarán nuestras frecuencias de genotipos y posiblemente de los alelos (ya que están asociados a los fenotipos).

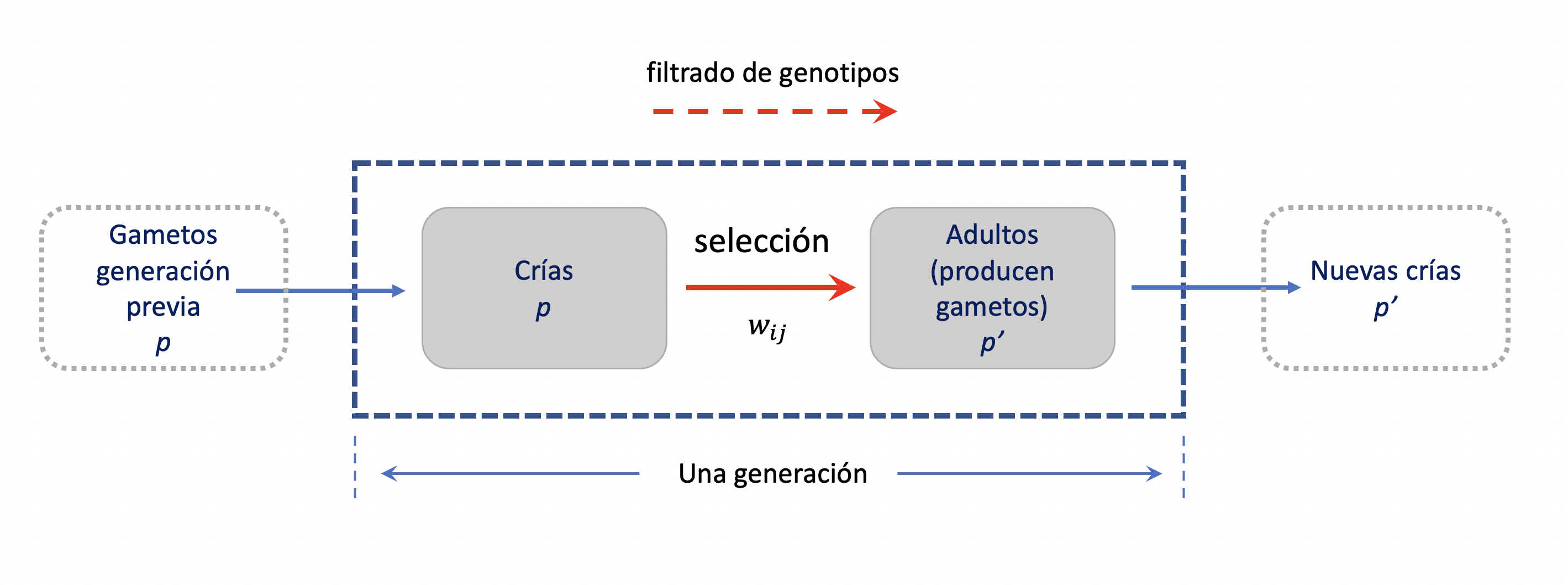
Figura 4.1: Modelo fundamental utilizado para estudiar la selección en un locus con dos alelos. Los gametos de la generación anterior (frecuencia \(p\)) producirán las crías de la generación presente, que luego del proceso de selección determinarán que adultos participarán del nuevo pool gamético (con frecuencia \(p'\)). Elaboración propia sobre idea de John H. Gillespie (2004).

Podemos llamar a cada uno de los filtros anteriores la viabilidad de cada genotipo. Obviamente, las nuevas frecuencias de los genotipos antes y después de la selección deberán sumar a uno, ya que se trata de proporciones de un total y no aparecen nuevos genotipos. Si, siguiendo la notación de John H. Gillespie (2004), llamamos \(w_{ij}\) a la viabilidad del genotipo con alelos \(i\) y \(j\) (pudiendo ser \(i \ne j\) o \(i=j\)), entonces la frecuencia del genotipo \(A_iA_j\) después de la selección estará dada por el producto de su frecuencia antes de la selección (por ejemplo, \(p_ip_j\) si los genotipos se encontraban en equilibrio Hardy-Weinberg), multiplicada por el filtro \(w_{ij}\) y divido por el fitness medio, de forma que el fitness relativo de cada genotipo, ponderado por su frecuencia, sume a uno. Poniendo en un cuadro la situación antes y después de la selección, tenemos

Genotipo	\(A_1A_1\)	\(A_1A_2\)	\(A_2A_2\)
\(\text{Frecuencia}\)	\(p^2\)	\(2pq\)	\(q^2\)
\(\text{Viabilidad}\)	\(w_{11}\)	\(w_{12}\)	\(w_{22}\)
\(\text{Frecuencia post-selección}\)	\(p^2w_{11}\)	\(2pqw_{12}\)	\(q^2w_{22}\)
\(\text{Frecuencia relativa post-selección}\)	\(\frac{p^2w_{11}}{\bar{w}}\)	\(\frac{2pqw_{12}}{\bar{w}}\)	\(\frac{q^2w_{22}}{\bar{w}}\)

En el cuadro anterior \(\bar{w}\) representa el *fitness promedio** de la población y es igual a

\[\begin{equation} \bar{w}=p^2w_{11}+2pqw_{12}+q^2w_{22} \tag{4.1} \end{equation}\]

que no es más que el promedio de los fitness de cada genotipo⁴⁷. Además, se cumple \(\frac{p^2w_{11}}{\bar{w}}+\frac{2pqw_{12}}{\bar{w}}+\frac{q^2w_{22}}{\bar{w}}=\frac{p^2w_{11}+2pqw_{12}+q^2w_{22}}{\bar{w}}=1\), como era esperado.

Después del proceso de selección la frecuencias de los gametos serán las correspondientes a los genotipos de la última línea del cuadro anterior, y por lo tanto la nueva generación tendrá esas frecuencias alélicas ya que no suponemos ningún proceso de filtrado adicional (por ejemplo, selección cigótica o supervivencia fetal diferencial). Los genotipos con alelos \(A_1\) son \(A_1A_1\) y \(A_1A_2\), de los cuales el primero todos son alelos \(A_1\) y la mitad del segundo también son \(A_1\), por lo que sumando las frecuencias de esta forma obtenemos la frecuencia de \(A_1\) en la siguiente generación:

\[\begin{equation} p'=\frac{p^2w_{11}}{\bar{w}}+\frac{1}{2}\frac{2pqw_{12}}{\bar{w}}=\frac{p^2w_{11}+pqw_{12}}{\bar{w}} \end{equation}\]

El cambio ocurrido entre generaciones, que siguiendo la notación de John H. Gillespie (2004) llamaremos \(\Delta_s p\) para reforzar la idea de que el cambio se debe a la selección, será la frecuencia actual del alelo \(A_1\), es decir \(p'\) (notar el \('\) para la nueva generación), menos la frecuencia en la generación anterior (o sea, \(p\)).

\[\begin{equation} \Delta_s p=p'-p=\frac{p^2w_{11}+pqw_{12}}{\bar{w}}-p=\frac{p^2w_{11}+pqw_{12}-p\bar{w}}{\bar{w}} \tag{4.2} \end{equation}\]

Si trabajamos un poco el numerador, teniendo en cuenta además que \(pq=p(1-p)=p-p^2\) y que \(1-2p=(1-p)-p=q-p\), tenemos para el numerador de la ecuación (4.2)

\[p^2w_{11}+pqw_{12}-p\bar{w}=p[pw_{11}+qw_{12}-p^2w_{11}-2pqw_{12}-q^2w_{22}]\] \[=p[(p-p^2)w_{11}+q(1-2p)w_{12}-q^2w_{22}]=pq[pw_{11}+(q-p)w_{12}-qw_{22}]\] \[=p[pqw_{11}+q(1-2p)w_{12}-q^2w_{22}]=pq[pw_{11}+(q-p)w_{12}-qw_{22}]\] \[\begin{equation} =pq[p(w_{11}-w_{12})+q(w_{12}-w_{22})] \tag{4.3} \end{equation}\]

Si ahora llevamos este resultado de nuevo a la ecuación (4.2), tenemos una forma simplificada de la misma

\[\begin{equation} \Delta_s p=\frac{pq[p(w_{11}-w_{12})+q(w_{12}-w_{22})]}{p^2w_{11}+2pqw_{12}+q^2w_{22}} \tag{4.4} \end{equation}\]

Ejemplo 4.1

Una población de Thrips tabaci (trips de la cebolla) se encuentra reproduciéndose en un cultivo de cebolla . El locus \(A\) codifica para una enzima, la cual es blanco de acción de un plaguicida. En la población se encuentran segregando dos alelos para el locus, el alelo \(A_1\) y el alelo \(A_2\). El primero de estos codifica para una variante sobre la cual el plaguicida es altamente efectivo; el alelo \(A_2\), en cambio, codifica para una variante sobre la cual el plaguicida no tiene efecto. Se asume que la población se encuentra cumpliendo los supuestos del equilibrio de Hardy-Weinberg.

Bajo el régimen del plaguicida, los individuos dejan según su genotipo 5, 8 o 15 descendientes por cada 10 individuos.

a. ¿Cuál es el fitness relativo de cada genotipo?

b. Si en la generación inmediatamente anterior a que se comience a utilizar el plaguicida las frecuencias alélicas son \(f(A_1) = 0.8\) y \(f(A_2) = 0.2\), ¿qué frecuencias alélicas se esperan en la siguiente generación?

a. Notemos que el promedio de descendencia es de \(0.5\), \(0.8\) y \(1.5\) para los individuos de genotipo \(A_1A_1\), \(A_1A_2\) y \(A_2A_2\), respectivamente. Estos consitituyen los valores de fitness absoluto de cada genotipo.

Como se mencionó anteriormente, tenemos al menos dos definiciones de fitness relativo, las cuales varían respecto a qué se toma como referencia. La más usual define al fitness relativo normalizando respecto al genotipo de mayor fitness (en este caso, el genotipo \(A_2A_2\)).

Siguiendo esta definición, tenemos los siguientes fitness relativos:

\[ \begin{cases} w_{A_1A_1} = \frac{0,5}{1,5} \\ w_{A_1A_1} = \frac{0,8}{1,5} \\ w_{A_2A_2} = \frac{1,5}{1,5} = 1 \end{cases} \]

También podemos definir el fitness relativo en base al fitness promedio de la población. Este es \(\bar{w} = \sum_{i=1}^{i=k}w_ip_i\), donde \(p_i\) es la frecuencia de cada genotipo. Bajo equilibrio de Hardy-Weinberg estas frecuencias son \(f(A_1A_1) = 0,8^2;\ f(A_1A_2) = 2 \cdot 0,8 \cdot 0,2;\ f(A_2A_2) = 0,2^2\). Tenemos entonces

\(\bar{w} = 0,5 \cdot 0,8^2 + 2 \cdot 0,8 \cdot 0,2 \cdot 0,8 + 0,2^2 \cdot 1,5\). Tenemos entonces los fitness relativos

\[ \begin{cases} w_{A_1A_1} = \frac{0,5}{0,5 \cdot 0,8^2 + 2 \cdot 0,8 \cdot 0.2 \cdot 0,8 + 0,2^2 \cdot 1,5} \\ w_{A_1A_1} = \frac{0,8}{0,5 \cdot 0,8^2 + 2 \cdot 0,8 \cdot 0.2 \cdot 0,8 + 0,2^2 \cdot 1,5} \\ w_{A_2A_2} = \frac{1,5}{0,5 \cdot 0,8^2 + 2 \cdot 0,8 \cdot 0.2 \cdot 0,8 + 0,2^2 \cdot 1,5} \end{cases} \]

b. El cambio en la frecuencia del alelo \(A_1\) está dado por\[ \Delta_sf(A_1) = \frac{f(A_1)f(A_2)\cdot[f(A_1) \cdot(w_{A_1A_1} - w_{A_1A_2}) + f(A_2) \cdot(w_{A_1A_2}-w_{A_2A_2}) )]}{\bar{w}} \]

En este caso, tenemos

\[ \Delta_sf(A_1) = \frac{0,8 \cdot 0,2 \cdot[0,2 \cdot(0,5 - 0,2) + 0,2 \cdot(0,8-1,5) )]}{0,5 \cdot 0,8^2 + 2 \cdot 0,8 \cdot 0,2 \cdot 0,8 + 0,2^2 \cdot 1,5} \]

Recordando que \(\Delta_s f(A_1) = f'(A_1) - f(A_1) \Rightarrow f'(A_1) = f(A_1)+ \Delta_sf(A_1)\), por lo que

\[ f'(A_1) = 0,8 + \frac{0,8 \cdot 0,2 \cdot[0,2 \cdot(0,5 - 0,2) + 0,2 \cdot(0,8-1,5) )]}{0,5 \cdot 0,8^2 + 2 \cdot 0,8 \cdot 0,2 \cdot 0,8 + 0,2^2 \cdot 1,5} \approx \]

Esto a su vez implica \(f'(A_2) = 1-f(A_1)\). Vemos que, como era de esperar, bajo el régimen del plaguicida se da un aumento de la frecuencia del alelo \(A_2\) (que confiere fenotipo de resistencia).

---

Ya veremos que es posible hacer una transformación de la escala que simplifique aún más la ecuación (4.4), pero el numerador de la misma parece bastante informativo desde ya. El término \(pq\), que es igual a \(p(1-p)=p-p^2\) y que aparece multiplicando todo, y ya vimos que alcanza su máximo cuando \(p=q=\frac{1}{2}\)⁴⁸. También vimos en el capítulo anterior que \(pq\) era el numerador de la varianza en frecuencias por deriva. El otro término, entre paréntesis rectos, es el promedio, ponderado por las frecuencias de \(p\) y \(q\), respectivamente, de las diferencias en fitness entre homocigotos \(A_1A_1\) y heterocigotos y entre estos últimos y los homocigotos \(A_2A_2\)⁴⁹.

Veamos si podemos avanzar en la simplificación de todo esto. Como nuestro interés hasta ahora (en este capítulo) es ver cómo el proceso de selección afecta los genotipos y las frecuencias alélicas dentro de una población, podemos transformar todos los fitness de su escala absoluta a una escala relativa. Por ejemplo, podemos dividir todos los valores entre el mayor valor de fitness (asumamos para el ejemplo que se trata de\(w_{11}\)). Ahora los fitness relativos para los tres genotipos serán \(\frac{w_{11}}{w_{11}}=1\), \(\frac{w_{12}}{w_{11}}\) y \(\frac{w_{22}}{w_{11}}\). Más aún, si llamamos \(s\) al coeficiente de selección (la intensidad de la misma) contra el genotipo \(A_2A_2\) (sin pérdida de generalidad, ya que la designación de los alelos \(A_1\) y \(A_2\) es completamente arbitraria y podemos elegir a nuestro gusto cuál es uno y cuál el otro) y definimos un parámetro \(h\) de tal forma de poder acomodar libremente los valores de fitness de los heterocigotos, tenemos que los nuevos fitness relativos estarán dados ahora por

Genotipo	\(A_1A_1\)	\(A_1A_2\)	\(A_2A_2\)
\(\text{Frecuencia}\)	\(p^2\)	\(2pq\)	\(q^2\)
\(\text{Viabilidad}\)	\(w_{11}\)	\(w_{12}\)	\(w_{22}\)
\(\text{Viabilidad relativa}\)	\(\frac{w_{11}}{w_{11}}=1\)	\(\frac{w_{12}}{w_{11}}\)	\(\frac{w_{22}}{w_{11}}\)
\(\text{Fitness relativo (forma } h \text{ y } s)\)	\(1\)	\(1-hs\)	\(1-s\)

En nuestro caso, vamos a permitir que \(0 \leqslant s \leqslant 1\), donde \(s=0\) corresponde al caso en que no hay ninguna fuerza detrimental contra los genotipos que no son \(A_1A_1\) y \(s=1\) corresponde al caso de inviabilidad total del genotipo \(A_2A_2\). El parámetro \(h\), llamado usualmente efecto del heterocigoto, es un parámetro que permite ubicar libremente a los heterocigotos entre (y aún por fuera) de los valores de fitness relativo de los homocigotos. En efecto, jugando con el parámetro \(h\) podemos entrar en los modos de acción génica más relevantes, como se aprecia en el cuadro siguiente

\(\textbf{Modo de acción}\)	\(\textbf{Valores de } h\)
\(A_1\text{ dominante, } A_2 \text{ recesivo}\)	\(h=0\)
\(A_2\text{ dominante, } A_1 \text{ recesivo}\)	\(h=1\)
\(\text{Dominancia incompleta}\)	\(0 < h < 1\)
\(\text{Sobredominancia}\)	\(h < 0\)
\(\text{Subdominancia}\)	\(h > 1\)

Veamos cómo funciona lo anterior. Si \(h=0\), entonces los fitness relativos serán \(1\) para el genotipo \(A_1A_1\), \(1-hs=1-0 \cdot s=1\) para el genotipo \(A_1A_2\) y \(1-s\) para el genotipo \(A_2A_2\), por lo que el genotipo heterocigoto tendrá el mismo valor de fitness que el genotipo \(A_1A_1\). Esto es equivalente a un modo de acción con el alelo \(A_1\) dominante sobre el alelo \(A_2\). De la misma manera, si \(h=1\), entonces los fitness relativos serán \(1\) para el genotipo \(A_1A_1\), \(1-hs=1-1 \cdot s=1-s\) para el genotipo \(A_1A_2\) y \(1-s\) para el genotipo \(A_2A_2\), por lo que el genotipo heterocigoto tendrá el mismo valor de fitness que el genotipo \(A_2A_2\). Esto es equivalente a su vez a un modo de acción con \(A_2\) dominante sobre \(A_1\). Un caso menos extremo, pero paradigmático también, es el caso en que \(h=\frac{1}{2}\); en ese caso, los fitness relativos serán \(1\), \(1-\frac{1}{2}s\) y \(1-s\), con lo que el genotipo heterocigoto estará exactamente en el punto medio de los genotipos homocigotos (\(\frac{1+(1-s)}{2}=1-\frac{1}{2}s\)). En este caso el modo de acción es completamente aditivo (algo sobre lo que abundaremos en el capítulo El Modelo Genético Básico). Una representación gráfica de los modos de acción génica descritos anteriormente se puede ver en la Figura 4.2, donde las alturas de las barras representan los fitness relativos de cada genotipo en las 5 configuraciones del cuadro anterior.

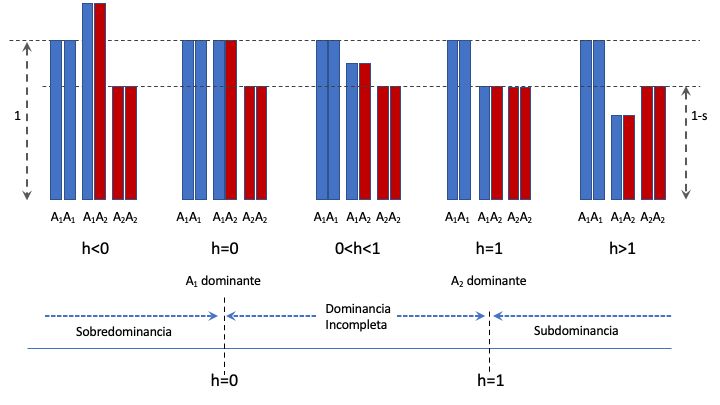
Figura 4.2: Representación gráfica de los modos de acción génica (o alélica) de acuerdo al parámetro \(h\). En cada caso se representan los 3 genotipos (\(A_1A_1\), \(A_1A_2\) y \(A_2A_2\)) y las alturas de las barras representan el \textbf{fitness relativo} de cada genotipo. Las barras en azul corresponden al alelo \(A_1\), mientras que las barras rojas corresponden al alelo \(A_2\).

Veamos ahora si logramos llegar al cambio de frecuencia esperada en \(p\) (es decir, \(\Delta_s p\)) con la re-parametrización de nuestro modelo fundamental. Para ello basta con sustituir en la ecuación (4.4) \(w_{11}\), \(w_{12}\) y \(w_{22}\) por sus valores relativos (i.e., \(1\), \(1-hs\) y \(1-s\)), lo que nos da

\[\Delta_s p=\frac{pq[p(w_{11}-w_{12})+q(w_{12}-w_{22})]}{\bar{w}}=\frac{pq[p(1-(1-hs))+q((1-hs)-(1-s)]}{\bar{w}}\] \[=\frac{pq[p(1-1+hs))+q(1-hs-1+s]}{\bar{w}}\ \therefore\]

\[\begin{equation} \Delta_s p=\frac{pqs[ph+q(1-h)]}{\bar{w}} \tag{4.5} \end{equation}\]

A su vez, el fitness medio vendrá ahora dado por sustituir los valores \(w_{11}\), \(w_{12}\) y \(w_{22}\) en la ecuación (4.1) por \(1\), \(1-hs\) y \(1-s\):

\[\bar{w}=p^2w_{11}+2pqw_{12}+q^2w_{22}=p^2 \cdot 1 + 2pq (1-hs) + q^2 (1-s) =(p^2+2pq+q^2)-2pqhs-q^2s\ \therefore\] \[\begin{equation} \bar{w}=1-2pqhs-q^2s \tag{4.6} \end{equation}\]

Volvamos a la ecuación (4.5) y veamos si podemos comprender en forma intuitiva su significado. El denominador de la misma es \(\bar{w}\) y es en general positivo, ya que \(p^2+2pq+q^2=1\) y generalmente \(2pqhs < 2pq\), lo mismo que \(sq^2 < q^2\) (recordar que \(0 \leqslant s \leqslant 1\) y usualmente \(s \ll 1\)). Además, \(pqs\) siempre es positivo por definición ya que \(0 \leqslant p \leqslant 1\), \(0 \leqslant q \leqslant 1\) y \(0 \leqslant s \leqslant 1\), por lo tanto \(pqs \geqslant 0\). Es decir, \(\frac{pqs}{\bar{w}} \geqslant 0\) y por lo tanto el signo de \(\Delta_s p\) está dado por el signo de \(ph+q(1-h)\). Dicho de otra forma, la frecuencia de \(p\) crecerá (\(\Delta_s p\) positivo) cuando \(ph+q(1-h)>0\) y decrecerá cuando \(ph+q(1-h)<0\). Una primera conclusión importante de lo anterior es que el sentido del cambio en la frecuencia de \(p\) entre generaciones no depende de \(s\).

La ilustración de la superficie de \(\Delta_s p\) en función de de la frecuencia del alelo \(A_1\) (\(p\)) y del valor del parámetro \(h\) pueden verse en la Figura 4.3. Claramente existen regiones donde \(\Delta_s p\) toma valores negativos y la forma de esta función de \(p\) cambia también en función del valor de \(h\), por lo que estudiaremos los distintos casos en forma separada.

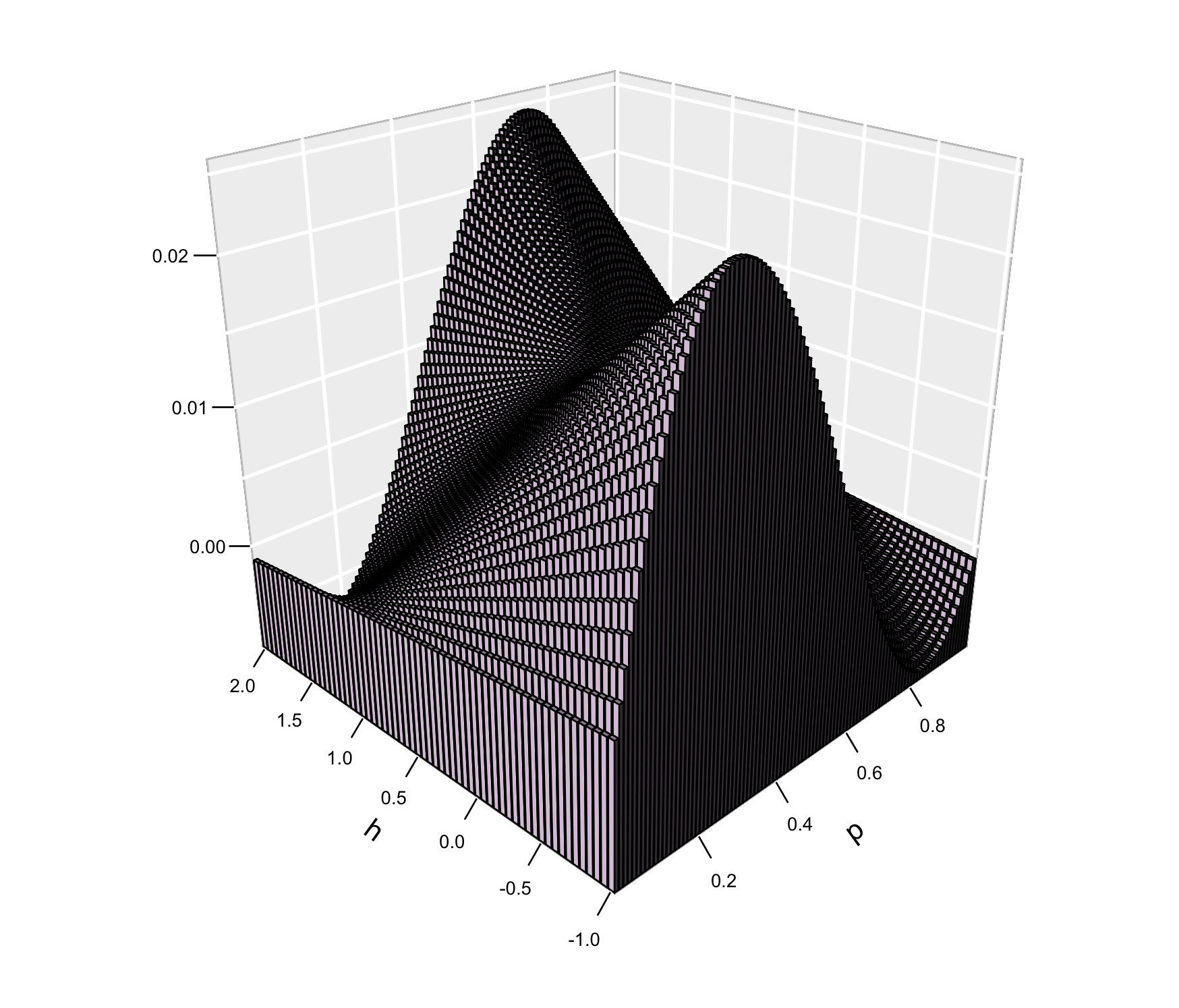
Figura 4.3: Valores de la función \(\Delta_s p\) en función de la frecuencia del alelo \(A_1\) (\(p\)) y del valor del parámetro \(h\), en el rango completo de \(h\), es decir \(-1<h<2\). A diferencia del comportamiento en la región restringida \(0<h<1\), se aprecian regiones del gráfico donde \(\Delta_s p\) es negativo, lo que lleva a que la evolución de la frecuencia de \(p\) no necesariamente seaen una sola dirección.

PARA RECORDAR

• El fitness medio de una población esta dado por \(\bar{w}=p^2w_{11}+2pqw_{12}+q^2w_{22}\).

• El cambio en la frecuencia del alelo \(A_1\) debido a la selección en un locus con dos alelos, luego de una generación es igual a \(\Delta_s p=\frac{pq[p(w_{11}-w_{12})+q(w_{12}-w_{22})]}{\bar{w}}\).

• Otra forma de describir el cambio en la frecuencia del alelo \(A_1\), en una parametrización que depende del efecto de los heterocigotos \(h\) y del coeficiente de selección s es \(\Delta_s p=\frac{pqs[ph+q(1-h)]}{\bar{w}}\)

4.3 Diferentes formas de selección

La forma en que parametrizamos el cambio en la frecuencia del alelo \(A_1\), o sea \(\Delta_s p\), en función de un parámetro \(h\) (efecto del heterocigoto) y de la frecuencia misma del alelo (\(p\)), nos va a permitir estudiar diferentes formas de selección que producirán distintos resultados en la distribución de genotipos en la población, de acuerdo al modo de acción y la frecuencia de partida. En la Figura 4.4 vemos los tres tipos de selección que trataremos, a partir de nuestro modelo fundamental de un locus con dos alelos. Arriba, la selección direccional, en la que la población se desplazará hacia la fijación del alelo favorecido. En el medio, la selección estabilizadora, en la que existe un óptimo en frecuencia intermedia de \(p\) y que además es un equilibrio estable. Abajo, la selección disruptiva, en la que el equilibrio de frecuencia intermedia es inestable y cualquier perturbación llevará a la población hacia la fijación o pérdida de uno de los alelos.

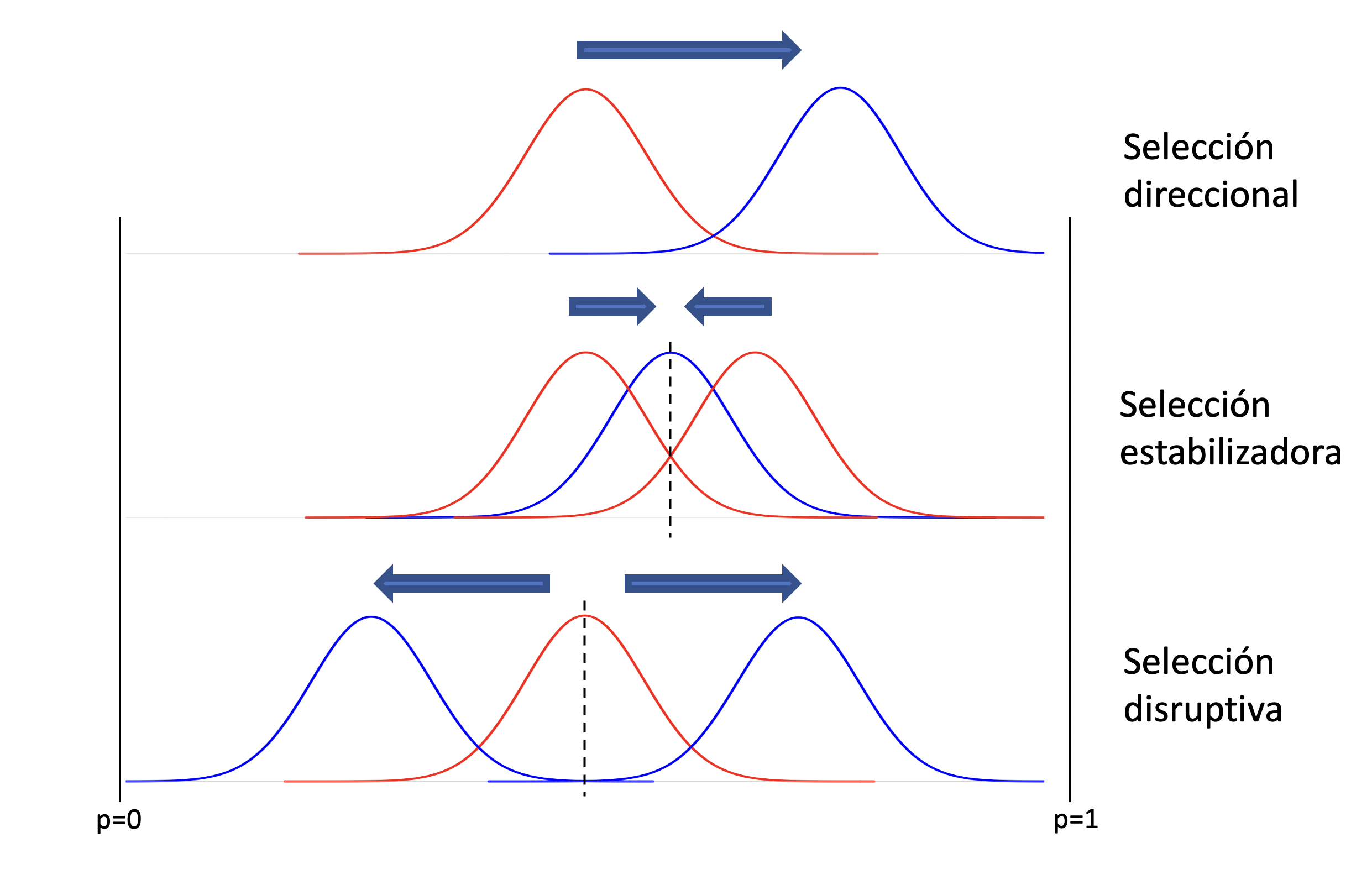
Figura 4.4: Tipos de selección que trataremos, a partir de nuestro modelo fundamental. En rojo las poblaciones antes de la acción de la selección, en azul después de la selección. Arriba, selección direccional, en la que la población se desplaza en una dirección, sin otro equilibrio que la fijación del alelo favorecido. En el medio, selección estabilizadora, en el que existe un punto óptimo en una frecuencia intermedia y el equilibrio es estable. Abajo, selección disruptiva, en la que existe un óptimo inestable en una frecuencia intermedia pero que cualquier pequeña perturbación lleva a la población a irse a la fijación o pérdida.

4.3.1 Selección direccional

Cuando existe dominancia incompleta, es decir cuando \(0<h<1\), o dicho de otra forma el heterocigoto tiene un fitness intermedio al de los homocigotas, entonces la expresión \(ph+(1-p)(1-h)\) es siempre mayor a cero ya que para que existan dos alelos \(0<p<1\) (idem para \(q=1-p\), notar que \(p=0\) o \(p=1\) no tienen sentido). Teniendo en cuenta lo que discutimos antes respecto a que el signo de \(\Delta_s p\) está determinado y es igual al signo de \(ph+(1-p)(1-h)\), como este último en el caso de dominancia incompleta es siempre positivo, entonces \(\Delta_s p\) también será siempre positivo. Al ser siempre positivo esto quiere decir que independientemente del punto de partida en la frecuencia del alelo \(A_1\), la misma siempre aumentará. La conclusión lógica de esto es que se irá aproximando a la frecuencia máxima del alelo \(A_1\), a la que nunca alcanzará en tiempo finito (claro que en determinado momento esta cercanía entra dentro del alcance típico de los efectos de la deriva, que podrán terminar de fijar el alelo \(A_1\)).

La representación gráfica de la superficie definida por \(\Delta_s p\) en función del parámetro \(h\), en la región \(0<h<1\) y de la frecuencia del alelo \(A_1\) se aprecia en la Figura 4.5. Se aprecia con claridad que todos los valores de \(\Delta_s p\) son positivos en la región considerada para \(h\), sin depender además del punto en que consideremos la frecuencia de \(A_1\) (es decir, \(p\)).

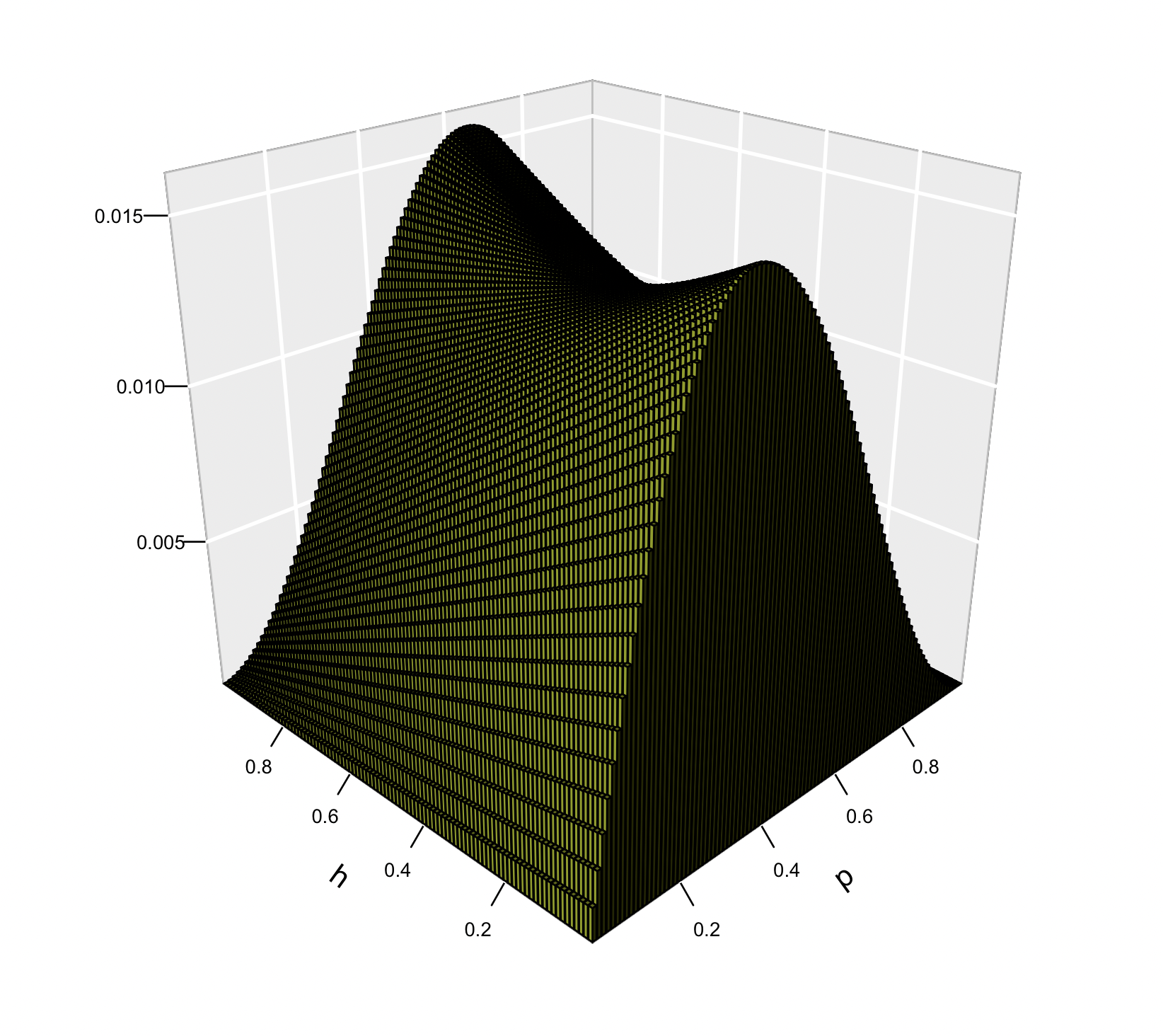
Figura 4.5: Valores de la función \(\Delta_s p\) en función del valor del parámetro \(h\) y de la frecuencia del alelo \(A_1\) (\(p\)). Claramente se aprecia que en el rango \(0<h<1\) (que es el que está graficado) \(\Delta_s p\) es siempre positivo, indicando un crecimiento de \(p\). A su vez, se aprecia que como función de la frecuencia \(p\), \(\Delta_s p\) es una parábola con un máximo en \(p=q=\frac{1}{2}\), mientras que como función de \(h\) la misma tiene un mínimo en \(h=\frac{1}{2}\).

Más aún, para un valor de \(h\) determinado, cualquiera en la región \(0<h<1\), \(\Delta p\) pasa a ser una función exclusivamente en \(p\). Si observamos con cuidado la figura, un valor fijo de \(h\), pongamos \(x\) es como hacer un corte con un plano \(h=x\), paralelo al borde derecho de la figura (\(h \to 1\)) y en lugar de fijarnos en la superficie vamos a atender a la curva que forma \(\Delta_s p\). Veamos que ocurre a distintos valores del parámetro \(h\), siempre dentro del intervalo \(0<h<1\).

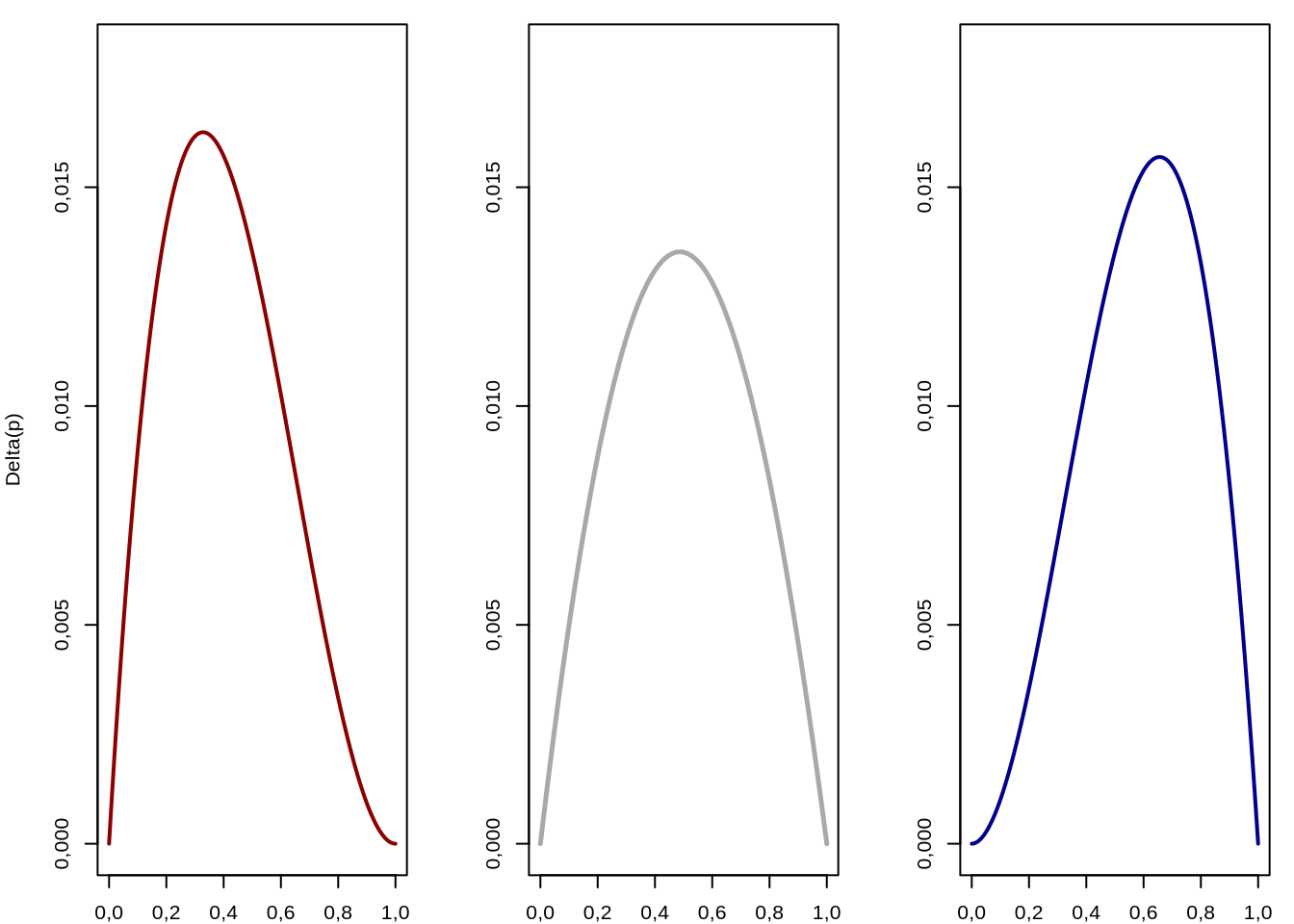
Figura 4.6: Funciones de \(\Delta_s p\) para valores fijos del parámetro \(h\). A la izquierda \(h=0,001\) (rojo), en el centro \(h=\frac{1}{2}=0,5\) (gris) y a la derecha \(h=0,999\) (azul). Se aprecia que el máximo de esta función de cambio en la frecuencia del alelo \(A_1\) se desplaza de izquierda a derecha también.

Los ejemplos de selección direccional son abundantes, tanto a nivel de selección natural (que es el foco de este capítulo) como lo que trabajaremos más adelante en los capítulos referidos a la selección artificial. Uno de los ejemplos más usados es el de la mariposa de los abedules, Biston betularia. La misma existe en al menos dos coloraciones contrastantes, como se aprecia en la Figura 4.7. Antes de la revolución industrial la mariposa de color claro era la predominante ya que esta coloración le permite un mimetismo mayor cuando se posa sobre la corteza de los abedules (género Betula) que además le sirven de alimento. La revolución industrial marcó un hito en las historia de nuestro planeta en lo que hace a contaminación, ya que gran parte de las fuentes de energía usadas (como el carbón) produjeron enorme cantidades de hollín, particularmente en las grandes ciudades y ciudades industriales. La consecuencia de esto fue que gran parte de los árboles donde se posaban las mariposas fueron cambiando de coloración hacia una mucho más oscura, lo que sin duda en lugar de permitir el mimetismo de la forma clara las transformaba en objetivo claro de los predadores. En gran parte por esta razón, en poco tiempo el tipo oscuro desplazó al tipo claro en los alrededores de las ciudades industriales, aunque la forma clara siguió predominando en zonas no contaminadas.

Figura 4.7: Biston betularia clara (arriba) y oscura (abajo). El tipo claro predominaba antes de la revolución industrial, aún cerca de las grandes ciudades, mientras que el tipo oscuro pasó a predominar durante los primeros tiempos de la revolución industrial en las grandes ciudades. Imágenes de wikipedia (autor Chiswick Chap, CC BY-SA 3.0).

Otro ejemplo famoso es el de los pinzones de Darwin. Cuando Charles Darwin visitó las islas Galápagos durante el segundo viaje del Beagle, recolectó varios pájaros, específicos de cada isla, que creyó en principio eran diferentes especies. Al retornar a Inglaterra, el ornitólogo John Gould logró determinar que se trataba de 12 especies de pinzones estrechamente emparentadas, pese a las importantes diferencias en las morfologías de los picos. En la Figura 4.8 se aprecian las diferencias entre 4 de ellas. Más allá de la especulación sobre la selección direccional por el tipo de alimento que persistió durante décadas, los biólogos evolutivos Peter y Rosemary Grant que dedicaron alrededor de 30 años al estudio de los pinzones de Darwin pudieron demostrar la existencia de diversas formas de alimentación de acuerdo a la morfología y tamaño de los picos. Más aún, recientemente se identificaron algunos genes relacionados a la forma y tamaño de los picos, en particular los genes bone morphogenetic protein 4 (BMP4) (Abzhanov et al. (2004)) y la calmodulina (CaM) (Abzhanov et al. (2006)), lo que aporta una base mecanística a un fenómeno observado a otra escala (la de poblaciones).

Figura 4.8: Pinzones de Darwin: 4 de las 18 especies. En sentido horario, de izquierda arriba, Geospiza magnirostris, Geospiza fortis, Certhidea fusca y Camarhynchus parvulus. Imagen de wikipedia, collage de Kiwi Rex (CC BY-SA 4.0).

En ambos ejemplos podemos observar algo muy importante: la selección natural tiene una relación directa con la evolución de los ambientes. Es decir, en general gran parte de las ventajas o desventajas que proporcionan determinados alelos en determinados locus son apenas temporales o dependientes del ambiente, por ejemplo de la geografía. En el ejemplo de Biston betularia vimos que un cambio temporal en el ambiente en un período de tiempo evolutivo muy corto, del orden de decenas de años (considera que la evolución de la vida en la tierra tiene más de 3 mil millones de años) provocó una ventaja selectiva para los alelos del fenotipo oscuro, solamente en los entornos con fuerte contaminación atmosférica. Es decir, la ventaja es geográfica y también temporal (en el entendido de que es esperable y deseable reducir la contaminación en las grandes ciudades). Esto nos lleva directamente a otro punto relevante que ya hemos discutido: para que la selección pueda actuar es necesario contar con variabilidad genética y si la selección direccional es muy fuerte y rápida como para que aparezcan nuevas variantes relevantes, el éxito adaptativo en un ambiente y tiempo puede transformarse en una catástrofe si las condiciones cambian rápidamente.

En el segundo ejemplo vimos un fenómeno muy importante, del que ya hablamos algo en el capítulo previo: la especiación. Las islas con cierta distancia geógrafica entre ellas (la escala depende de la capacidad de moverse de cada especie) suelen constituir un típico ejemplo y modelo para la aparición de nuevas especies, es decir la especiación. En el capítulo anterior vimos que los eventos estocásticos producto de tamaños poblacionales finitos (y usualmente pequeños), en ausencia de migración (y de otras fuerzas evolutivas) podían llevar a la fijación de alelos distintos en las poblaciones del ensemble. Más aún, vimos que el efecto fundador podía ser responsable de fuertes variaciones en los puntos de partida de las distintas poblaciones ([El rol de la subdivisión poblacional en la evolución de las frecuencias alélicas]). Por ejemplo, si la distancia entre islas de un archipiélago es suficiente como para hacer el evento de arribo de una determinada nueva especie algo infrecuente, entonces una vez arribada la primera pareja reproductiva, si las condiciones son favorables, tendrá un espacio de varias generaciones para que se desarrolle la población. Esto provocará que cuando ocurran nuevos arribos la población ya contará con muchos individuos (descendientes de la primera pareja) y hasta posiblemente un nicho saturado. Durante todo este tiempo la población fue además posiblemente evolucionando en forma adaptativa a las condiciones específicas de esta isla, lo que podría llegar a crear barreras reproductivas con los nuevos arribos (tanto físicas cómo genéticas o etológicas). El reforzamiento del aislamiento por las razones anteriores es un mecanismo clásico postulado para la especiación, que se conoce como especiación alopátrica (algo más veremos en otro capítulo, en la sección Mecanismos de especiación).

Ejemplo 4.2

Determinar el efecto de heterocigotos (\(h\)) y el coeficiente de selección (\(s\)) para el caso planteado en el Ejemplo 4.1. ¿De qué tipo de acción génica (alélica) se trata? Si la situación continúa invariante, ¿qué se espera respecto a las frecuencias de los alelos \(A_1\) y \(A_2\)?

Notemos que el fitness relativo de los organismos homocigotas \(A_1A_1\) está dado por \(w_{A_1A_1} = 1 - s = \frac{0.5}{1.5} \Rightarrow s = 1 - \frac{0.5}{1.5} = \frac{2}{3}\). A su vez, el fitness relativo de los organismos heterocigotas \(A_1A_2\) está dado por \(w_{A_1A_2} = 1 -hs \Rightarrow 1-hs = \frac{0.8}{1.5}\), por lo que \(hs = f \cdot \frac{2}{3} = 1-\frac{0.8}{1.5} \Rightarrow h = (1-\frac{0.8}{1.5} ) \cdot \frac{3}{2} = 0.7\).

Dado que \(0 < h < 1\) nos encontramos frente a un caso de dominancia incompleta. De hecho, ya contabamos con esta información, en tanto el fitness relativo de los organismos heterocigotas se encontraba en un punto intermedio entre los de los organismos homocigotas. De mantenerse inalteradas las presiones selectivas (i.e., la aplicación del plaguicida), es de esperar un aumento progresivo de la frecuencia del alelo \(A_2\). En un tiempo finito el efecto exclusivo de la selección direccional no será capaz de fijar el alelo. No obstante, la acción de la deriva genética puede llevar a esto, eliminándose de la población el alelo \(A_2\).

PARA RECORDAR

• Bajo dominancia incompleta, el efecto de los heterocigotos cumple \(0<h<1\) y para coeficientes de selección no nulos, \(s>0\) (es decir, \(w_{11}>w_{22}\)), entonces \(\Delta_s p>0\) para todo el intervalo \(0<p<1\), por lo que \(p \to 1\).

• La frecuencia de \(A_1\) crecerá hacia la fijación, pero no alcanzará la misma en tiempo finito si solo depende de la selección. Sin embargo, en la vecindad de \(p=1\), el efecto de la deriva puede terminar fijando el alelo \(A_1\).

• Bajo dominancia incompleta no existe un punto de equilibrio intermedio entre \(p=0\) y \(p=1\), tendiendo la frecuencia del alelo \(A_1\) a crecer indefinidamente (o sea, en la misma dirección), por lo que a este tipo de selección se le conoce como selección direccional.

4.3.2 Selección estabilizadora

El segundo tipo de selección que vamos a analizar ocurre cuando la sobredominancia es el modo de acción génica. Si recuerdás de la Figura 4.2, sobredominancia era cuando \(h<0\), lo que llevaba a que el fitness relativo del heterocigoto fuese mayor que el de ambos homocigotos y por tanto mayor que \(1\) (el fitness del homocigoto con mayor fitness). En términos matemáticos, como el fitness relativo del heterocigoto era \(1-hs\) y \(s>0\), \(h<0\), entonces \(-hs>0\) y \(1-hs>1\).

Razonemos primero basado en nuestra intuición, antes de pasar al desarrollo matemático. Si el fitness relativo de los heterocigotos es mayor que el de ambos homocigotos, entonces esperamos que haya mayor cantidad de estos, ¿cierto?. Pero los heterocigotos por definición tienen un alelo de cada tipo (e.g., un \(A_1\) y un \(A_2\)), entonces en principio no esperamos que desaparezca de la población ninguno de los dos. Ahora, ¿cuál será el punto de equilibrio, si es que existe? Por un lado, los heterocigotos aportan cada uno un alelo distinto, pero los homocigotos seguirán apareciendo generación tras generación ya que bajo apareamiento al azar los heterocigotos también producen homocigotos. ¿En que proporción?

Para estudiar el comportamiento de la frecuencia del alelo \(A_1\) bajo estas condiciones, veamos qué ocurre con la ecuación (4.5) en el equilibrio, es decir cuando ya no haya más cambios en la frecuencia (i.e., \(\Delta_s p=0\)). Si ponemos esta restricción en la ecuación (4.5), el numerador de la misma debe ser \(0\), por lo que (descartando el caso particular de \(s=0\) o cuando \(p=0\) o \(q=0\))

\[ \begin{split} \Delta_s p=0=\hat{p}\hat{q}s[\hat{p}h+\hat{q}(1-h)] \Leftrightarrow \hat{p}h+\hat{q}(1-h)=0 \\ \hat{p}h+(1-\hat{p})(1-h)=0\ \therefore \hat{p}h+1-\hat{p}-h+\hat{p}h \end{split} \]

\[ \begin{split} =0 \Leftrightarrow 2\hat{p}h -h + 1 \\ \hat{p} (2h-1)-(h-1)=0\ \therefore \end{split} \]

\[\begin{equation} \hat{p}=\frac{h-1}{2h-1} \tag{4.7} \end{equation}\]

Es decir, la frecuencia \(\hat{p}\) de equilibrio para el alelo \(A_1\) (y para el \(A_2\) su complemento a \(1\)), estará dada por la ecuación (4.7). Por esta razón, llamamos a la selección que ocurre a través de la ventaja de los heterocigotas selección estabilizadora (porque la frecuencia de los alelos se estabiliza en un valor intermedio manteniendo la variabilidad). De todas formas, es importante mencionar que en realidad la selección estabilizadora también se da bajo otros mecanismos como la selección dependiente de la frecuencia (que no vamos a analizar en esta sección). Un hecho primero a notar sobre la selección estabilizadora es que la frecuencia de equilibrio NO depende del coeficiente de selección \(s\) y que solo depende del efecto de los heterocigotos \(h\).

En la Figura 4.9 podemos ver (a la izquierda) el comportamiento de la frecuencia de equilibrio \(\bar{p}\) en función del valor de \(-1<h<0\). Claramente, a medida de que \(h \to 0\) por la izquierda (es decir, desde los valores negativos) la frecuencia de equilibrio \(\hat{p} \to 1\) (recordar que cuando \(h=0\) los heterocigotos valen \(1\), igual que los homocigotos \(A_1A_1\), es decir \(A_1\) dominante sobre \(A_2\)). En el resto del rango de valores de \(h\) considerados la frecuencia de equilibrio estará en algún lugar intermedio, pero siempre con frecuencia \(\hat{p}<1\).

El comportamiento anterior se puede ver claramente en la Figura 4.9 (centro), donde graficamos \(\Delta_s p\) en función de \(p\). Ahora, a diferencia de cuando tratamos Selección direccional, tenemos valores positivos y negativos, es decir que harán que la frecuencia de \(A_1\) aumente o descienda respectivamente. Si nos fijamos en la figura central de 4.9, la línea azul vertical representa el valor de equilibrio para \(h=-0,99\) que será \(\hat{p}=(h-1)/(2h-1) \approx 0,679\). Si nos ubicamos a la izquierda de ese valor, los \(\Delta_s p\) son todos positivos, por lo que la frecuencia \(p\) ser irá incrementando, pero a la izquierda del valor de equilibrio son todos negativos,por lo que \(p\) tenderá a bajar. La única solución a esto es que \(\hat{p}\) es el punto de equilibrio, como habíamos predicho y que en particular se trata de un punto de equilibrio estable: si nos apartamos un poquito para cualquiera de los dos lados del punto de equilibrio, las fuerzas actuantes (representadas en \(\Delta_s p\)) nos volverán a traer al punto \(\hat{p}\).

Finalmente, en la Figura 4.9 (izquierda) podemos ver la evolución en el tiempo (medido en generaciones) de la frecuencia \(p\) bajo selección estabilizadora, partiendo desde diferentes valores de \(p\) inicial. Claramente, independiente del punto de partida todas las poblaciones convergen hacia la frecuencia \(\hat{p} \approx 0,679\) (ya que \(h=-0,99\)). Cuanto más apartado el punto inicial de la frecuencia de equilibrio más esperaríamos que tarde en acercarse a este valor, pero si observas con cuidado la figura del centro verás la enorme diferencia en los valores absolutos de \(\Delta_s p\) a la derecha e izquierda. Por lo tanto, si bien la diferencia de frecuencias entre el punto de equilibrio \(\hat{p}\) y los puntos de partida son mucho mayores para los que arrancan por debajo de \(\hat{p}\), la velocidad de avance hacia la convergencia será mucho mayor que para los que arrancan por encima de \(\hat{p}\).

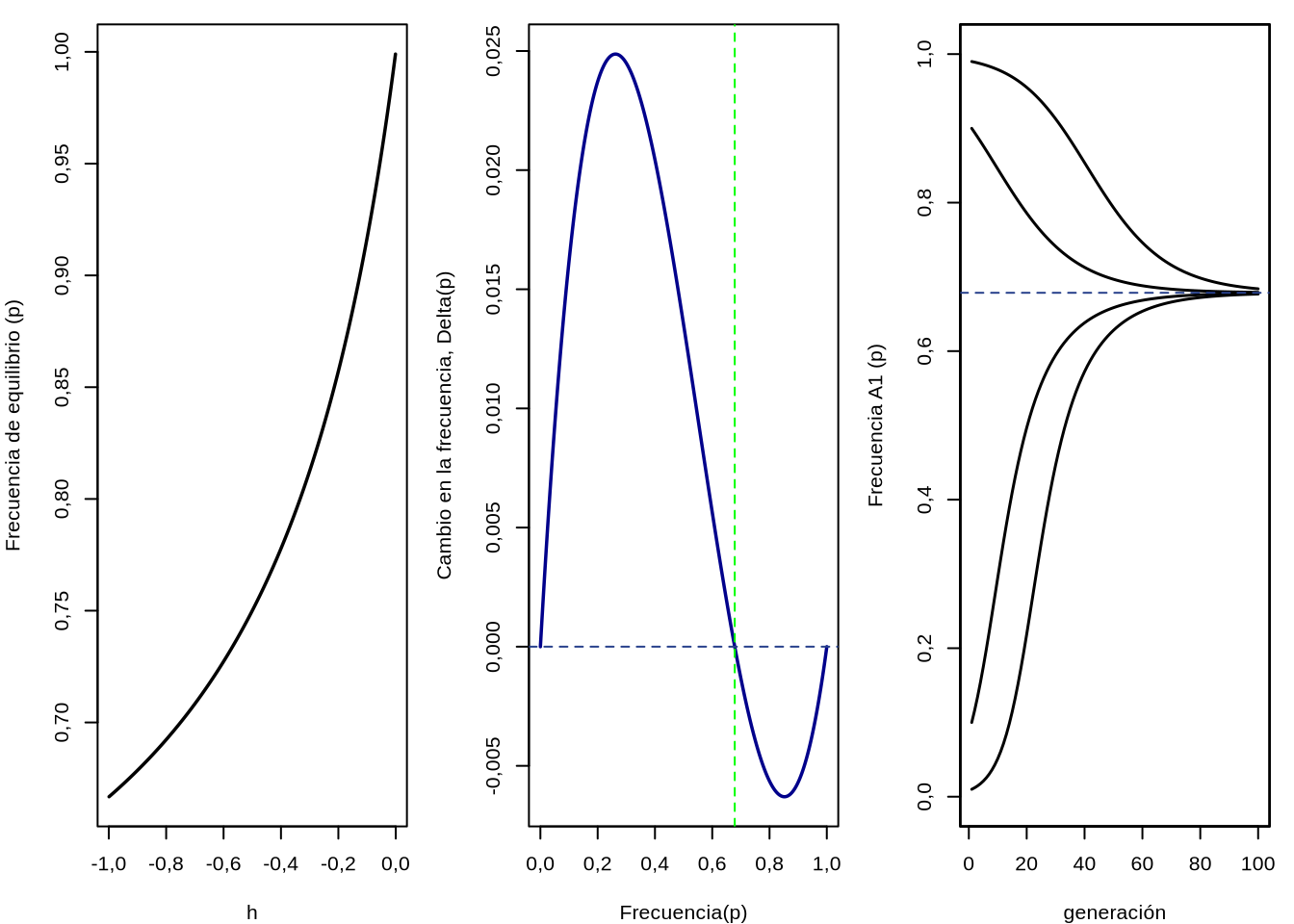
Figura 4.9: Frecuencia de equilibrio para el alelo \(A_1\) (\(\hat{p}\)) bajo selección estabilizadora (izquierda), cambio entre generaciones de la frecuencia (\(\Delta_s p\)) dependiendo de la frecuencia \(p\) (centro) y evolución de la frecuencia \(p\) en sucesivas generaciones a partir de diferentes puntos de partida en la frecuencia inicial \(p\) (izquierda). En los gráficos del centro e izquierda \(s=0,1\) y \(h=-0,99\) (por lo que \(\hat{p}=(h-1)/(2h-1) \approx 0,679\)).

Posiblemente, el ejemplo más conocido de selección estabilizadora sea el de la anemia falciforme o anemia de células falciformes. La anemia de células falciformes es una enfermedad de base genética que afecta los glóbulos rojos. En efecto, existe un alelo para el gen de la hemoglobina (Hgb) que se conoce como S (o como HgbS), que produce glóbulos rojos deformes, con forma de hoz⁵⁰ y extremadamente sensibles a la reducción en la tensión de oxígeno. Este alelo es el producto una sustitución nucleotídica en el gen codificante para globina \(\beta\), que a su vez lleva a sustituir el aminoácido ácido glutámico que se encuentra en la posición 6 de la cadena polipeptídica por una valina. Las personas que heredan dos alelos HgbS, de madre y padre, padecen la enfermedad que los lleva a una expectativa de vida reducida. En cambio, los individuos que reciben una sola copia de este, los heterocigotos, en principio no se ven afectados o sufren muy poco efecto detrimental (i.e., son portadores de la enfemedad). Hasta acá estamos en una situación conocida, con el alelo normal A dominando al alelo S. Sin embargo, frente a la presencia de malaria (una enfermedad causada por el parásito Plasmodium falciparum), aparece un efecto inesperado: los heterocigotos aparecen como relativamente resistentes a la infeción y por lo tanto, en regiones donde la malaria es endémica tienen una ventaja considerable frente al homocigoto para el alelo normal. Esto configura un esquema de ventaja para el heterocigoto, o de sobredominancia. En la Figura 4.10 se puede apreciar un mapa con las regiones de África donde la malaria es endémica (a la izquierda), así como un mapa de densidad con las frecuencias del alelo HgbS. En la misma se aprecia claramente una superposición de las regiones, efecto claro del modo de acción de este alelo bajo la presión selectiva de la malaria. Obviamente, sin esta presión selectiva (los lugares donde la malaria ha sido erradicada) la situación vuelve a la relación donde el fitness relativo de los heterocigotos es casi idéntico al de los homocigotos para el alelo normal A. Esto equivale a decir que \(h \approx 0\) y por lo tanto la selección se comportará como direccional contra el recesivo. Se tenderá a la eliminación de alelo S, aunque como ya vimos antes en la sección ¿Dónde se “esconden” los alelos recesivos?, esta selección es altamente ineficiente.

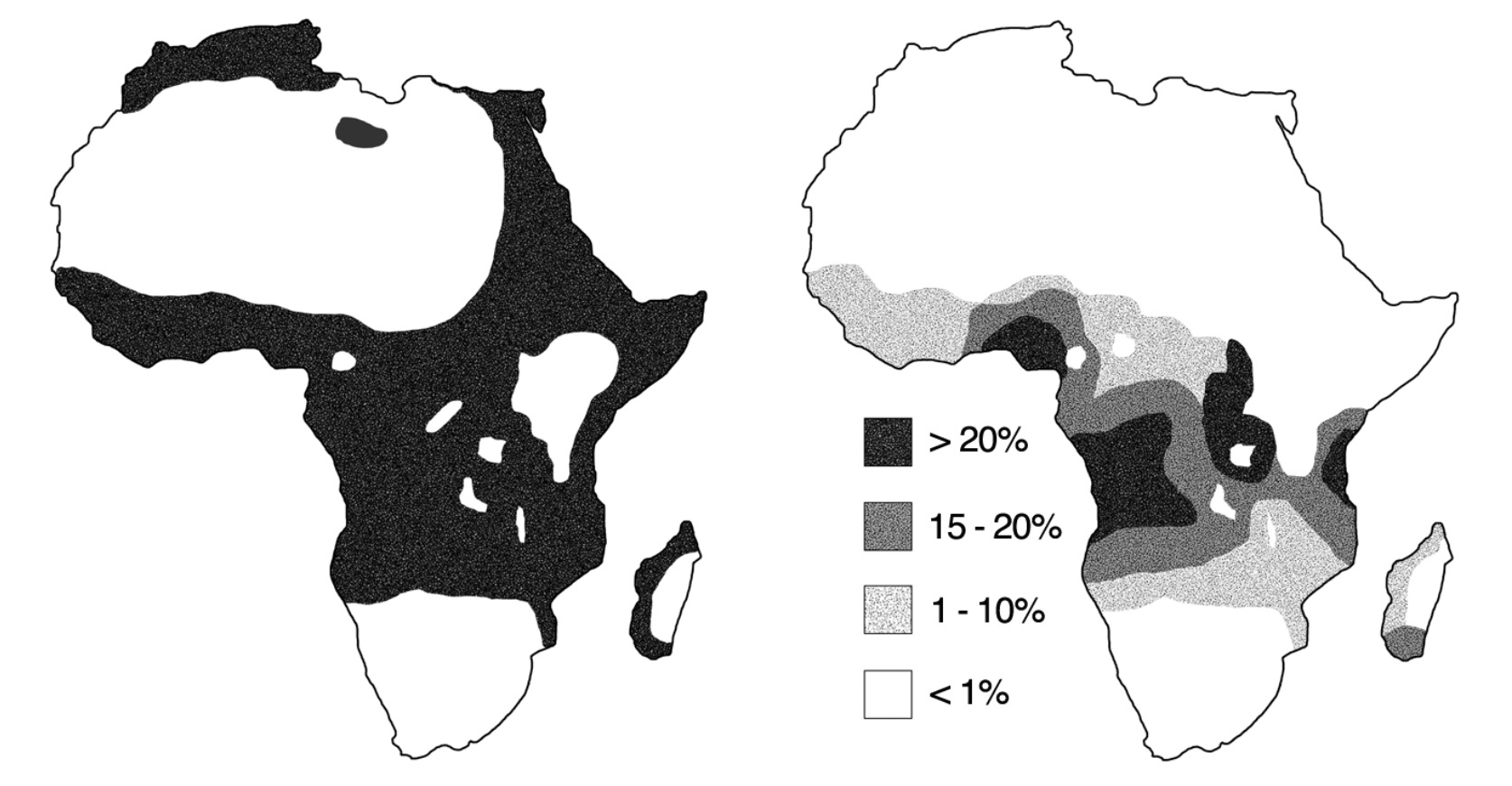
Figura 4.10: Distribución geográfica de la malaria (a la izquierda) y de la frecuencia del alelo S (a la derecha). Se observa la importante superposición de rangos geográficos entre la incidencia de malaria y la frecuencia del alelo que incrementa la resistencia a la misma. Figura de dominio público (Original work by Anthony Allison, CC0, https://commons.wikimedia.org/w/index.php?curid=8714486).

Ejemplo 4.3

Se ha postulado que la coloración de los pétalos de la flor de Gymnadenia rhellicani (una orquídea que crece en los Alpes) se enuentra bajo selección estabilizadora (Kellenberger et al. 2019).

La coloración de los pétalos se debe a la cantidad de pigmento (moléculas de la familia de las antocianinas). Esta se ve controlada por el locus GrMYB, codificante para un factor de transcripción que regula la síntesis de estos compuestos. Organismos homocigotas para el alelo \(\text{GrMYB}_1\) portan coloración negra, mientras que los homocigotas para \(\text{GrMYB}_2\) portan coloración blanca. Los heterocigotas \(\text{GrMYB}_1/\text{GrMYB}_2\) presentan coloración roja.

Supongamos que los polinizadores presentan una preferencias según la coloración, siendo los fitness relativos \(w_{11} = 1;\ w_{12} = 1.5;\ w_{22} = 0.7\) ¿Cuál es la frecuencia de equilibrio esperada para los alelos \(\text{GrMYB}_1\) y \(\text{GrMYB}_2\)?

El genotipo homocigota \(\text{GrMYB}_2\) es el que posee menor fitness relativo. Considerando \(w_{22} = 1-s = 0.7 \Rightarrow s = 1 - 0.7 = 0.3\). Por otro lado, tenemos que existe sobredominancia, con el fitness de los heterocigotas rojos \(w_{12} = 1 -hs = 1.5 \Rightarrow hs = 1 - 1.5 = -0.5\), lo cual implica \(h \cdot 0.3 = -0.5 \Rightarrow h = \frac{-0.5}{0.3}\). La frecuencia de equilibrio para el alelo \(\text{GrMYB}_1\) se puede calcular entonces considerando

\[ \hat{f(\text{GrMYB}_1)} = \frac{h-1}{2h-1} = \frac{(\frac{-0.5}{0.3}) - 1}{2 \cdot (\frac{-0.5}{0.3}) -1} \approx 0.62 \]

La frecuencia de equilibrio esperada para el alelo \(\text{GrMYB}_2\) es el complementario (\(\approx 0.38\)).

4.3.2.1 Otra parametrización**

En algunos libros se puede encontrar una parametrización diferente para el caso de sobredominancia y para la frecuencia de equilibrio. En esta parametrización diferente se asume que el heterocigoto tiene el fitness máximo e igual a 1. Por lo tanto, el homocigoto \(A_1A_1\) tendrá un fitness de \(1-t\) y el homocigoto \(A_2A_2\) tendrá un fitness de \(1-s\), como se aprecia en la Figura 4.11.

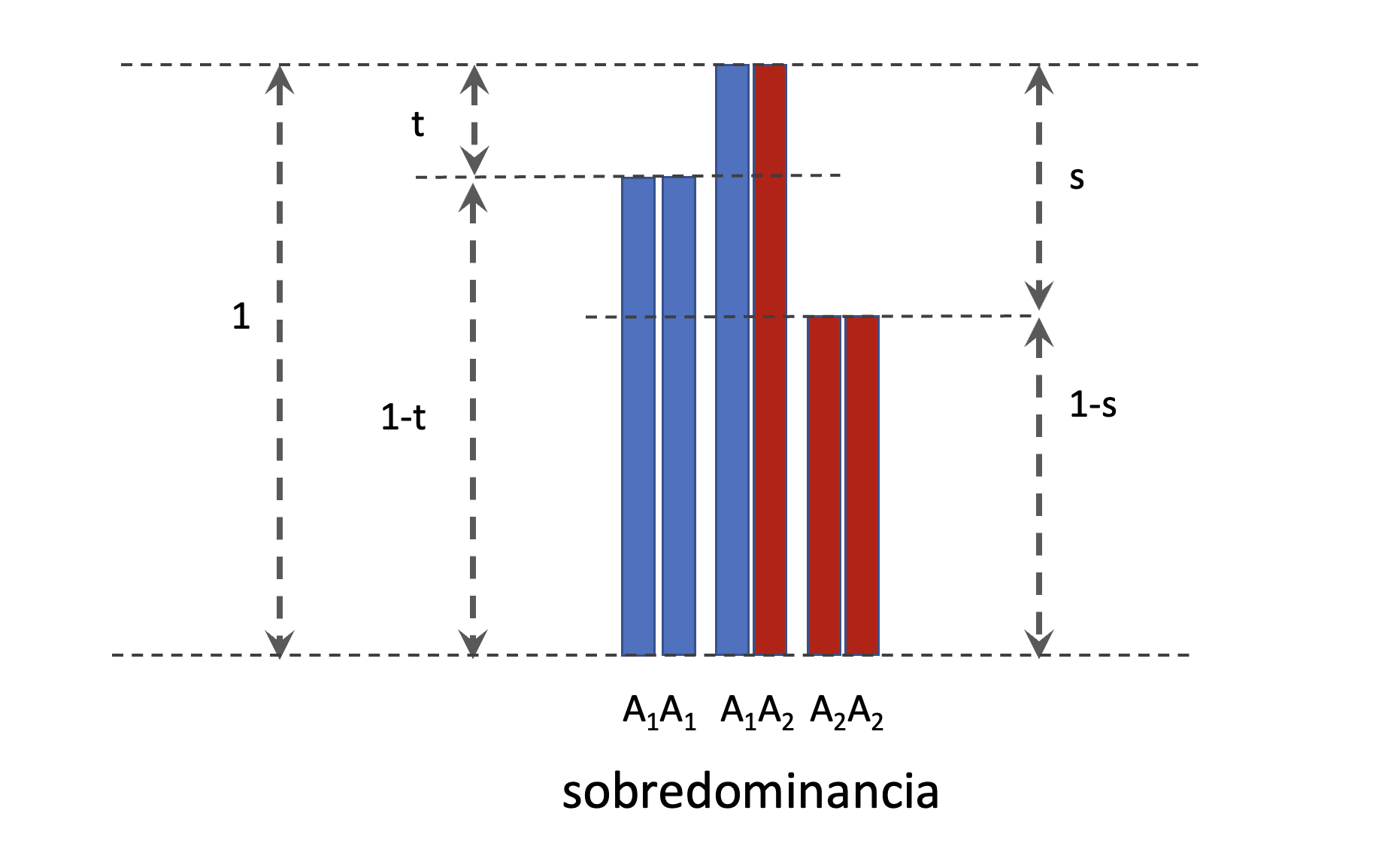
Figura 4.11: Representación gráfica de los fitness relativos para los distintos genotipos cuando el modo de acción génica es de sobredominancia. Ahora, en lugar de una parametrización en \(h\) y \(s\), con el homocigoto \(A_1A_1\) como valor igual a uno, en lugar de eso el heterocigoto será el máximo, con valor de uno y ambos homocigotos con valores de \(1-t\) y \(1-s\) respectivamente.

Si recordamos de más arriba, el cambio en frecuencia de \(p\), o sea \(\Delta_s p\) lo podíamos escribir como

\[\begin{equation} \Delta_s p=\frac{pq[p(w_{11}-w_{12})+q(w_{12}-w_{22})]}{\bar{w}} \tag{4.8} \end{equation}\]

Sustituyendo en (4.8) los valores de fitness definidos más arriba para esta parametrización, tenemos

\[\begin{equation} \Delta_s p=\frac{pq[p((1-t)-1)+q(1-(1-s))]}{\bar{w}} \tag{4.9} \end{equation}\]

Operando en (4.9), tenemos ahora que el cambio es

\[\begin{equation} \Delta_s p=\frac{pq[p(-t)+q(s)]}{\bar{w}}=\frac{pq[-pt+qs]}{\bar{w}} \end{equation}\]

y si sustituimos ahora \(q=(1-p)\) para quedarnos con un solo parámetro de frecuencia, tenemos ahora

\[\begin{equation} \Delta_s p=\frac{pq[-pt+(1-p)s]}{\bar{w}}=\frac{pq[-pt+s-ps]}{\bar{w}}=\frac{pq[s-p(s+t)]}{\bar{w}} \tag{4.10} \end{equation}\]

En el equilibrio, el cambio de frecuencia es cero, es decir \(\Delta_s p=0\). Obviando \(p=0\) y \(q=0\) que quedan fuera de nuestro espacio permitido para sobredominancia, tenemos que la única solución a \(\Delta_s p=0\) es

\[\begin{equation} \Delta_s \hat{p}=\frac{\hat{p}\hat{q}[s-\hat{p}(s+t)]}{\bar{w}}=0 \Leftrightarrow s-\hat{p}(s+t)=0 \Leftrightarrow s=\hat{p}(s+t) \end{equation}\]

por lo que

\[\begin{equation} \hat{p}=\frac{s}{s+t} \end{equation}\]

Por lo tanto, la frecuencia de equilibrio con estos parámetros será \(\hat{p}=\frac{s}{s+t}\). Esto es bien fácil de entender en forma intuitiva. Como los heterocigotas tienen un alelo \(A_1\) y un alelo \(A_2\) (y por tanto, no pueden distinguirlos) solo constituyen el fiel de la balanza entre ambos alelos. Donde se juega el partido entonces es en el balance entre los homocigotas. Los parámetros \(t\) y \(s\) representan el detrimento en los genotipos \(A_1A_1\) y \(A_2A_2\). Entonces, cuanto más importante es \(s\) en el total de detrimento \(s+t\), mayor será la ventaja de \(A_1\) sobre \(A_2\). Por lo tanto, la proporción de detrimento de \(A_2\) (i.e., \(\frac{s}{s+t}\)) será a su vez la ventaja del \(A_1\). El equilibrio esperado ocurre cuando la frecuencia de \(A_1\) es igual a la proporción de su ventaja: \(\hat{p}=\frac{s}{s+t}\).

PARA RECORDAR

• Bajo el efecto de la sobredominancia, es decir con el efecto de los heterocigotos \(h<0\) y para coeficientes de selección no nulos, \(s>0\) (es decir, \(w_{11}>w_{22}\)), entonces existirá un punto de equilibrio estable en el intervalo de frecuencias \(0<p<1\).

• Este punto de equilibrio solo depende del valor de \(h\) y no de \(s\) y se encontrará en \(\hat{p}=\frac{h-1}{2h-1}\).

• El anterior se trata de un punto de equilibrio estable ya que la selección a ambos lados es hacia ese punto y cualquier perturbación aleatoria de la frecuencia a los lados no hará más que activar la selección nuevamente hacia el punto de equilibrio (\(\Delta_s p\) lleva siempre \(p \to \hat{p}\)).

• Por lo anterior, a la selección bajo el modo de acción génica de sobredominancia se le conoce como selección estabilizadora.

• En el caso de usar la parametrización alternativa, con \(1-t\) y \(1-s\) como fitness relativo para los homocigotos \(A_1A_1\) y \(A_2A_2\) respectivamente, el punto de equilibrio en la frecuencia del alelo \(A_1\), \(\hat{p}\), estará dado por \(\hat{p}=\frac{s}{s+t}\).

4.3.3 Selección disruptiva

El tercer tipo de selección que vamos a abordar es cuando el modo de acción génica es la subdominancia (\(h>1\)). En ese caso, siendo que \(s>0\), entonces el heterocigoto se encuentra por debajo de ambos homocigotos, ya que \(1<1-s<1-hs\) (lo último porque \(hs>s\) ya que \(h>1\)). Esta situación es la representada más a la derecha en la Figura 4.2. Para estudiar el comportamiento de la selección bajo este régimen podemos comenzar por razonar nuevamente como lo hicimos en el caso de la Selección estabilizadora. Si el heterocigota es ahora el genotipo menos favorecido por la selección, entonces a la inversa del caso anterior los heterocigotos tenderán a desaparecer, aumentando la frecuencia de los homocigotos a sus expensas. Está claro que hay que escapar de la región que maximiza los heterocigotos (que era \(p=q=\frac{1}{2}\)), pero ahora no existe un sentido o punto hacia donde deba dirigirse \(\Delta_s p\) ya que las alternativas son dos: dirigirse hacia donde \(p\) es menor (hacia \(p=0\)) o dirigirse en el otro sentido (hacia \(p=1\)). Esta disyuntiva aparece más clara si graficamos \(\Delta_s p\) en función de \(p\) para distintos valores de \(h>1\). En la Figura 4.12 se puede visualizar lo que ocurre con \(\Delta_s p\) para \(h=1,1\) (izquierda), \(h=1,5\) (centro) y \(h=1,9\) (derecha). En principio, de forma inocente, podemos creer que estos gráficos son iguales a los de la Figura 4.9 (centro y derecha). En ambas figuras \(\Delta_s p\) tiene valores positivos y negativos a ambos lados de los puntos de equilibrio, los que parecen determinados por la ecuación \(\hat{p}=\frac{h-1}{2h-1}\). Sin embargo, las gráficas de la Figura 4.12 parecen ser en espejo de las de la Figura 4.9. ¿Tendrá esto alguna relevancia?

Veamos qué ocurre, por ejemplo con la gráfica del centro de la Figura 4.12. De acuerdo al valor de \(h\) el punto de equilibrio estaría en una frecuencia de \(\bar{p} = 0,25\), lo que aparece marcado por la línea azul vertical. Si partimos a la izquierda del punto de equilibrio, el signo de \(\Delta_s p\) es negativo, por lo que a cada generación \(p\) irá disminuyendo y a medida de que pasen las generaciones \(p \to 0\). Si arrancamos a la derecha del punto de equilibrio, el signo de \(\Delta_s p\) es positivo, por lo que a cada generación \(p\) irá aumentando y a medida de que pasen las generaciones \(p \to 1\).

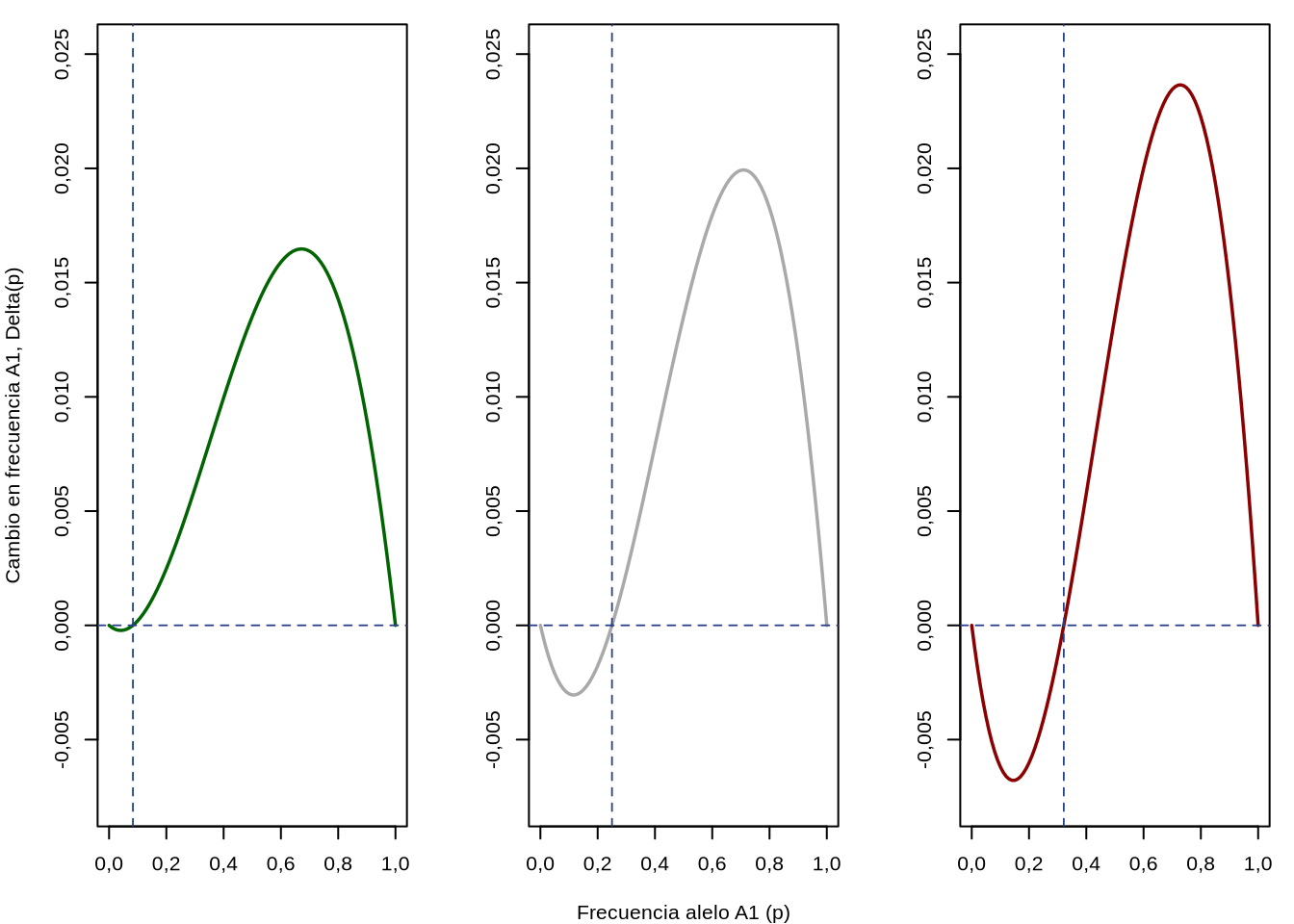
Figura 4.12: Evolución del cambio en frecuencia \(\Delta_s p\) en función del punto de partida \(p\) y del parámetro \(h\), en el modo de acción geníca subdominancia. A la izquierda \(h=1,1\), en el centro \(h=1,5\) y a la derecha \(h=1,9\). En todos los casos \(s=0,1\).

¿Entonces por qué decimos que es un punto de equilibrio si en ninguno de los dos casos terminamos en ese valor de \(\hat{p}\)? Veamos que ocurre si arrancamos exactamente de ese punto \(\hat{p}\) en la generación inicial. Por definición, \(\hat{p}\) se corresponde con el punto donde \(\Delta_s p=0\), por lo que no cambiará para la siguiente generación, que seguirá estando en \(\hat{p}\) y así sucesivamente. Sin embargo, aún la menor perturbación del punto de equilibrio (por deriva, por ejemplo) hará que \(p\) se desplace a derecha o izquierda, donde los \(\Delta_s p \ne 0\), lo que sellará definitivamente la suerte del alelo \(A_1\): si el desplazamiento inicial es a la izquierda del punto de equilibrio el destino será la desaparición de este alelo, mientras que si el desplazamiento es hacia la derecha el destino será la fijación. La evolución a lo largo del tiempo dependiendo del punto de partida se puede ver en la Figura 4.13 para 4 puntos de partida diferentes, por arriba y por abajo del punto de equilibrio.

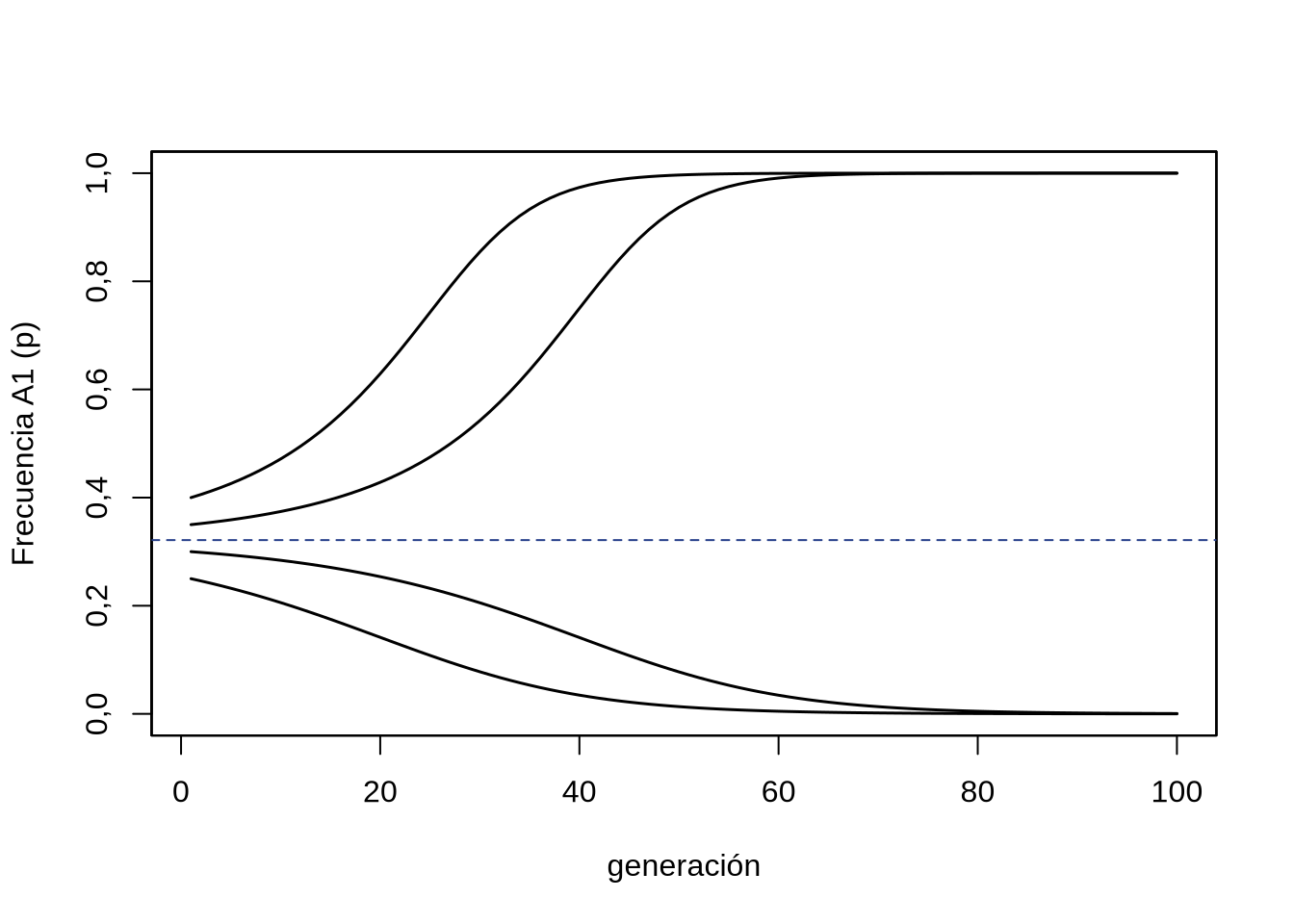
Figura 4.13: Evolución de la frecuencia \(p\) en sucesivas generaciones a partir de diferentes puntos de partida en la frecuencia inicial \(p\) bajo selección disruptiva. \(h=1,9\), \(p=0,25;0,30;0,35;0,40\).

Por esta razón, se dice que el punto \(\hat{p}\) en este tipo de acción génica corresponde a un equilibrio inestable. Es como tener tener equilibrado un lápiz en la punta de otro lápiz: el menor movimiento llevará al lápiz en equilibrio a caer por uno de los dos lados.

Desde el punto de vista biológico, la existencia de subdominancia se encuentra asociada a la selección disruptiva. Imaginemos dos poblaciones de la misma especie que solapan sus rangos geográficos (pero que por distintas razones se reproducen cada una dentro de su grupo) y que arrancan desde la misma frecuencia inicial en el punto de equilibrio inestable. Si por el efecto de la deriva genética (por ejemplo, porque ambas poblaciones son pequeñas en tamaño) una se desplaza hacia \(p>\hat{p}\), mientras que la otra en el sentido contrario (\(p<\hat{p}\)), al cabo de unas cuantas generaciones tendremos dos poblaciones diferenciadas en nuestro locus de referencia. Nuevamente, un ejemplo de este tipo de selección parece ser el de los pinzones de Darwin, esta vez los de la isla de Santa Cruz. La diferencia en el tamaño de semillas disponibles para la alimentación de las aves es grande, lo que ha llevado a especializarse en un tipo, desapareciendo las formas intermedias (que tendrían un mayor rango de alimentación pero son menos eficientes en ambos tipos). Otro lugar donde la selección disruptiva parece haber jugado un lugar importante es en lo eventos

PARA RECORDAR

• Bajo el efecto de la subdominancia, es decir con el efecto de los heterocigotos \(h>1\) y para coeficientes de selección no nulos, \(s>0\) (es decir, \(w_{11}>w_{22}\)), entonces existirá un punto de equilibrio inestable en el intervalo de frecuencias \(0<p<1\).

• Este punto de equilibrio solo depende del valor de \(h\) y no de \(s\) y se encontrará en \(\hat{p}=\frac{h-1}{2h-1}\).

• El anterior se trata de un punto de equilibrio inestable ya que cualquier perturbación aleatoria de la frecuencia a los lados del equilibrio no hará más que disparar la selección hacia alguno de los extremos, \(p \to 1\) si \(p>\hat{p}\) (es decir a la fijación) o \(p \to 0\) si \(p<\hat{p}\) (es decir a la pérdida del alelo).

• Por lo anterior, a la selección bajo el modo de acción génica de subdominancia se le conoce como selección disruptiva.

4.4 El teorema fundamental de la selección natural

Si sustituimos \(q\) por \((1-p)\) en la ecuación (4.6), luego de un poquito de trabajo llegamos a que expresado solo en función de \(p\), el fitness medio (en nuestra escala relativa) es

\[\begin{equation} \bar{w}=(1-s)-2ps(h-1)+p^2s(2h-1) \end{equation}\]

Ahora, si queremos estudiar el comportamiento del fitness medio en función de la frecuencia del alelo \(A_1\) (\(p\)), debemos hacer la derivada de esta función, que es simplemente (recordar que aquellos términos que no sean función de \(p\) son tratados como constantes)

\[\begin{equation} \frac{d\bar{w}}{dp}=-2s(h-1)+2sp(2h-1) \tag{4.11} \end{equation}\]

En los máximos o mínimos de \(\bar{w}\) la derivada respecto a la frecuencia \(p\) se hace cero, por lo que

\[\begin{equation} \frac{d\bar{w}}{dp}=-2s(h-1)+2sp(2h-1)=0 \Leftrightarrow (h-1)=p(2h-1) \Leftrightarrow p=\frac{h-1}{2h-1} \end{equation}\]

Notemos que, cuando \(2h-1=0 \Leftrightarrow h=\frac{1}{2}\) la derivada primera no existirá. Para saber si se trata de máximos o mínimos debemos estudiar el signo de la derivada segunda (recordar que si el signo de la derivada segunda es positivo en la región del cero de la derivada primera, entonces se trata de un mínimo, mientras que si el signo es negativo se trata de un máximo). La derivada segunda de \(\bar{w}\) respecto a \(p\) es

\[\begin{equation} \frac{d^2\bar{w}}{dp^2}=2s(2h-1) \end{equation}\]

y ya que \(2s\) es positivo, el signo de la derivada segunda dependerá de \((2h-1)\). Es decir, si \(h>\frac{1}{2}\) entonces la derivada segunda será positiva y se tratará de un mínimo; si \(h<\frac{1}{2}\) la derivada segunda será negativa y por lo tanto se tratará de un máximo. Si recordamos nuestra categorización anterior de los casos de acuerdo a los valores de \(h\), en el rango \(0<h<1\) no existía un punto de equilibrio. Esto se ve reforzado si estudiamos el rango de valores que tomará \(\hat{p}\) en \(\hat{p}=\frac{h-1}{2h-1}\), para el rango de \(0<h<1\) (caso de dominancia incompleta que resulta en selección direccional). Una forma sencilla es graficar esta función de \(h\) en ese intervalo. Como se muestra en la Figura 4.14 izquierda la función \(\hat{p}\) no toma valores admisibles (\(0 \leqslant p \leqslant 1\)) en el rango \(0<h<1\). En cambio, fuera de este rango (Figura 4.14, derecha) la función \(\hat{p}\) si toma valores admisibles, tanto en los casos de sobredominancia (\(h<0\)), subdominancia (\(h>1\)) o dominancia completa de uno de los dos alelos (\(h=0\) \(A_1\) dominante o \(h=1\) \(A_2\) dominante). Más aún, volviendo a nuestra derivada segunda, para valores de \(h<\frac{1}{2}\) era negativa y por lo tanto en la región de \(h<0<\frac{1}{2}\) (la región de sobredominancia) también será negativa y los puntos de equilibrio \(\hat{p}\) serán máximos del fitness, que coincide con lo que ya vimos en Selección estabilizadora. De la misma manera, para valores de \(h>\frac{1}{2}\) la derivada segunda era positiva y por lo tanto en la región de \(h>1>\frac{1}{2}\) (la región de subdominancia) también será positiva y los puntos de equilibrio \(\hat{p}\) serán mínimos del fitness, lo que coincide ahora con lo que ya vimos en Selección disruptiva.

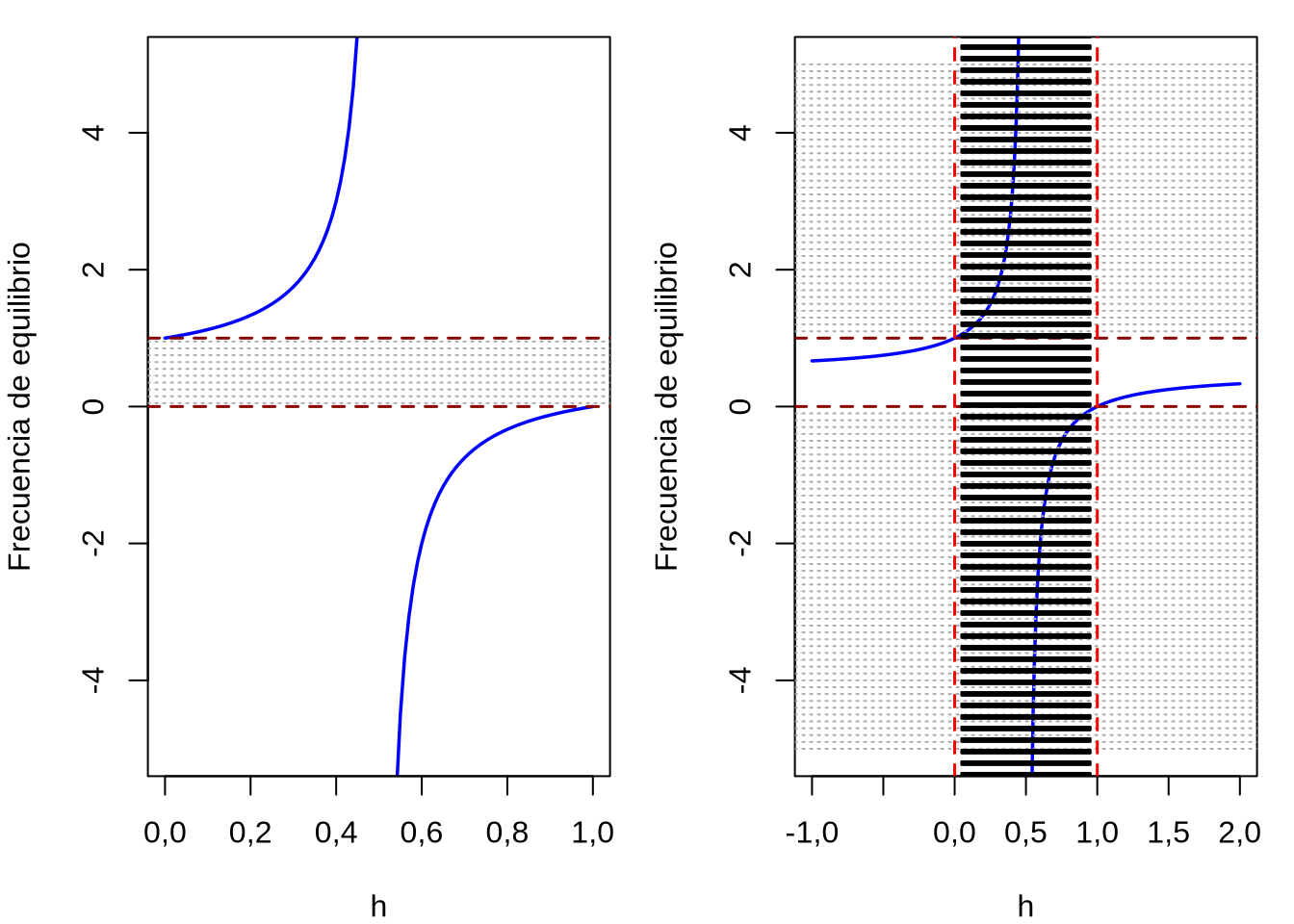
Figura 4.14: Inexistencia de puntos de equilibrio en el intervalo \(0<h<1\) (gráfica a la izquierda). Para valores de \(h\) en el rango de dominancia incompleta, la función que representa el punto de equilibrio en la frecuencia del alelo \(A_1\) (i.e., \(\hat{p}=\frac{h-1}{2h-1}\)) toma valores fuera del rango posible de \(p\), es decir \(0 \leqslant p \leqslant 1\) (el rango de valores posibles se representa por las líneas grises entre las dos líneas rojas). Fuera del rango \(0<h<1\) (gráfica a la derecha) las soluciones de \(\hat{p}=\frac{h-1}{2h-1}\) entran dentro de los rangos admisibles para \(p\), sobredominancia (\(h<0\)), subdominancia (\(h>1\)) o dominancia completa de uno de los dos alelos (\(h=0\) correspondiente a alelo \(A_1\) dominante, o \(h=1\) correspondiente a alelo \(A_2\) dominante).

Siguiendo el planteo de John H. Gillespie (John H. Gillespie 2004), en cierta forma esta división de los modos de selección reclama por una ecuación conceptualmente unificadora. Sewall Wright, en su artículo de 1937 (S. Wright 1937) muestra que es posible escribir el cambio en frecuencia \(\Delta_s p\) en una forma en principio muy diferente

\[\begin{equation} \Delta_s p=\frac{pq}{2\bar{w}}\frac{d\bar{w}}{dp} \tag{4.12} \end{equation}\]

Antes de analizar esta formulación de \(\Delta_s p\) veamos si podemos arribar a ella. Tomando en cuenta la forma que tiene \(\frac{d\hat{w}}{dp}\) en la ecuación (4.11) y sustituyendo en (4.12), tenemos

\[\Delta_s p=\frac{pq}{2\bar{w}} [-2s(h-1)+2sp(2h-1)]=\frac{pq}{2} \frac{2s(1-h)+2sp(2h-1)}{\bar{w}}\] \[= \frac{pqs[(1-h)+p(2h-1)]}{\bar{w}}=\frac{pqs[1-h+2ph-p]}{\bar{w}}=\frac{pqs[1-h+ph-p+ph]}{\bar{w}}\] \[\begin{equation} =\frac{pqs[(1-p)(1-h)+ph]}{\bar{w}}=\frac{pqs[ph+q(1-h)]}{\bar{w}}=\Delta_s p \tag{4.13} \end{equation}\]

por lo que claramente llegamos a la misma formulación que en nuestra ecuación (4.5).

Lo interesante de la formulación de Wright es el cambio en la frecuencia, \(\Delta_s p\) que es ahora mucho más conceptual: se trata del producto de un término que nos da idea de la varianza en frecuencias (el término \(\frac{pq}{2\hat{w}}\)) y de un término que habla del cambio en el fitness medio en función de la frecuencia de \(p\). El primer término es siempre positivo y lo lo tanto el sentido del cambio estará dado por el signo de \(\frac{d\hat{w}}{dp}\). El aspecto interesante de esta relación es que si la derivada tiene signo positivo, también \(\Delta_s p\) y por lo tanto aumentará la frecuencia de \(p\). Como \(\frac{d\hat{w}}{dp}>0\), entonces el fitness \(\hat{w}\) también lo aumentará. Por otro lado, si la derivada tiene signo negativo, entonces ambién \(\Delta_s p\) y por lo tanto disminuirá la frecuencia de \(p\). Como \(\frac{d\hat{w}}{dp}<0\), entonces (al ir \(p\) hacia menores valores) el fitness \(\hat{w}\) también aumentará. Es decir, en nuestro modelo de un locus con dos alelos, con el fitness independiente de la frecuencia, este siempre aumentará en la medida de que haya varianza genética.

Relacionado con este concepto de evolución de la población hacia un máximo en el fitness se encuentra otra aproximación que motiva el nombre de esta sección. En su libro de 1930 “The Genetical Theory of Natural Selection” (Fisher 1930), Ronald Fisher dedica un capítulo entero a lo que (algo pomposamente) llama El Teorema Fundamental de la Selección Natural. La formulación original del mismo (traducción nuestra) luce:

“La tasa de aumento de la aptitud de cualquier organismo en cualquier momento es igual a su varianza genética de aptitud en ese momento.”

En lo anterior, usamos aptitud en lugar de fitness. Este concepto fue reformulado con el paso del tiempo y una versión más moderna del mismo, con términos más usuales hoy en día, debida a Edwards (Edwards 1994) (de nuevo, traducción nuestra) sería:

“La tasa de aumento de la aptitud media de cualquier organismo, en cualquier momento, que es atribuible a la selección natural que actúa a través de los cambios en las frecuencias de los genes, es exactamente igual a su varianza genética en la aptitud en ese momento”

El “teorema” ha sido objeto de una profunda controversia durante todo el siglo XX cuyo origen probablemente esté en la disputa general entre Wright y Fisher, que continuó con abudantes mal interpretaciones del mismo y con dudas importantes acerca de su significancia. De hecho alcanza con ver la conclusión aportada por John H. Gillespie (John H. Gillespie 2004) (“Thus, it is neither fundamental nor a theorem.”⁵¹) para comprender que el alcance del mismo es algo limitado y su importancia difícil de decidir. En principio es totalmente cierto (y matemáticamente correcto) para poblaciones “teóricas”, en un modelo de un locus con selección simple.

El tratamiento completo de este teorema requiere de los conceptos de la descomposición de la varianza, en particular de la varianza genética y los efectos aditivos, algo que veremos en el capítulo El Modelo Genético Básico. Sin embargo, una aproximación simplificada y bastante intuitiva se encuentra en el libro de Hamilton (Hamilton 2009), que nosotros seguiremos acá.

Supongamos una población de un organismos haploide con reproducción asexual o clonal⁵². En este caso, el fitness medio de la población será la suma del fitness de cada haplotipo (recordar que asumimos que el organismo es haploide, entonces el genotipo es igual al haplotipo) multiplicado por la frecuencia del mismo. Es decir, para los \(k\) haplotipos en la población,

\[\begin{equation} \bar{w}=\sum_{i=1}^{i=k}(p_iw_i) \tag{4.14} \end{equation}\]

Para cada haplotipo la nueva frecuencia en la siguiente generación, luego de la selección natural, estará dada por

\[\begin{equation} p'_i=p_i\frac{w_i}{\bar{w}}=\frac{p_iw_i}{\bar{w}} \tag{4.15} \end{equation}\]

y por lo tanto, el nuevo fitness medio será igual a

\[\begin{equation} \bar{w}'=\sum_{i=1}^k(p'_iw_i) \tag{4.16} \end{equation}\]

Ahora, si sustituimos el valor de \(p'_i\) que obtuvimos en la ecuación (4.15) en la ecuación (4.16), tenemos

\[\begin{equation} \bar{w}'=\frac{1}{\bar{w}}\sum_{i=1}^k (p'_iw_i) w_i =\frac{1}{\bar{w}}\sum_{i=1}^k p'_iw_i^2 \tag{4.17} \end{equation}\]

El cambio relativo (al fitness en la generación previa) estará dado por:

\[\begin{equation} \Delta \bar{w}=\frac{\bar{w}'-\bar{w}}{\bar{w}} \tag{4.18} \end{equation}\]

y sustituyendo el resultado de la ecuación (4.17) en la ecuación (4.18), tenemos ahora que el cambio relativo lo podemos expresar como

\[\begin{equation} \Delta \bar{w}=\frac{\frac{1}{\bar{w}}\sum_{i=1}^k p'_iw_i^2-\bar{w}}{\bar{w}} \tag{4.19} \end{equation}\]

Si ahora multiplicamos y dividimos el término \(\bar{w}\) por si mismo, es decir \(\bar{w}=\frac{\bar{w}^2}{\bar{w}}\) tenemos que el cambio se puede escribir como

\[\begin{equation} \Delta \bar{w}=\frac{\frac{1}{\bar{w}}\sum_{i=1}^k p'_iw_i^2-\frac{\bar{w}^2}{\bar{w}}}{\bar{w}} \tag{4.20} \end{equation}\]

y luego de reordenar esta ecuación (recordar que dividir entre \(\bar{w}\) es lo mismo que multiplicar por su inverso, es decir \(\frac{1}{\bar{w}^2}\)), llegamos a que

\[\begin{equation} \Delta \bar{w}=\frac{1}{\bar{w}^2} \sum_{i=1}^k p'_iw_i^2-\bar{w}^2 \tag{4.21} \end{equation}\]

Pero si miramos con atención esta última ecuación, el término \(\sum_{i=1}^k p'_iw_i^2-\bar{w}^2\) es la varianza en el fitness (recuerda que \(\mathbb{V}(x)=\mathbb{E}(x^2)-\mathbb{E}^2(x)\)), por lo que \(\Delta_s p \propto \mathbb{V}(w)\). Como el escalado del fitness relativo es arbitrario, podemos elegirlo de tal forma que \(\bar{w}=1\) y entonces nos queda la definición del teorema fundamental de la selección natural:

\[\begin{equation} \Delta_s p = \mathbb{V}(w) \end{equation}\]

PARA RECORDAR

• Otra forma de escribir el fitness medio, ahora solo dependiendo de \(p\) (y no de \(q\)) es

\[\begin{equation} \bar{w}=(1-s)-2ps(h-1)+p^2s(2h-1) \end{equation}\]

• La tasa de cambio del fitness medio en función de la frecuencia se encuentra dado por la derivada primera del mismo, es decir

\[\begin{equation} \frac{d\bar{w}}{dp}=-2s(h-1)+2sp(2h-1) \end{equation}\]

• Esta derivada tendrá puntos extremos en \(\hat{p}=\frac{h-1}{2h-1}\), tanto para \(h<0\) o \(h>1\). De acuerdo a la derivada segunda, al ser negativa para \(h<\frac{1}{2}\), para \(h<0<\frac{1}{2}\) (sobredominancia), \(\hat{p}=\frac{h-1}{2h-1}\) corresponderá a un máximo, mientras que para \(h>1>\frac{1}{2}\) (sobredominancia), \(\hat{p}=\frac{h-1}{2h-1}\) corresponderá a un mínimo del fitness medio.

• Otra forma de escribir el cambio esperado en las frecuencias del alelo \(A_1\) que brinda mayor información evolutiva es

\[\begin{equation} \Delta_s p=\frac{pq}{2\hat{w}}\frac{d\bar{w}}{dp} \end{equation}\] es decir, \(\Delta_s p\) es el producto de un término referido a la varianza genética por un término que es la tasa de cambio del fitness medio relativo.

• El teorema fundamental de la selección natural, debido a Fisher (1930), establece que “La tasa de aumento de la aptitud media de cualquier organismo, en cualquier momento, que es atribuible a la selección natural que actúa a través de los cambios en las frecuencias de los genes, es exactamente igual a su varianza genética en la aptitud en ese momento” (Edwards (1994))

4.5 Equilibrio selección-mutación

Supongamos que ahora nuestro modelo no solo incluye el efecto de la selección favoreciendo al alelo \(A_1\), sino que además tenemos el efecto recurrente de la re-introducción del alelo \(A_2\). Este efecto, si es suficientemente significativo, impedirá la fijación del alelo \(A_1\) y por lo tanto ahora existirá un equilibrio entre los dos alelos, cosa que no ocurría en el caso de dominancia incompleta si solo consideramos la selección, como vimos en Selección direccional. Supongamos que el alelo \(A_1\) muta hacia el alelo \(A_2\) con una tasa \(u\), es decir \(A_1 \overset{u}{\rightarrow} A_2\). Suponemos además, por ahora dominancia incompleta (\(0<h<1\)).

Asumiendo que \(s\) es suficientemente fuerte para mantener la frecuencia de \(A_2\) muy baja y que por lo tanto la incidencia de la mutación reversa (\(A_2 \overset{v}{\rightarrow} A_1\)) es despreciable (porque es el producto de una tasa muy pequeña \(v\) por una frecuencia también muy pequeña \(q\)) entonces la frecuencia de \(A_1\) en la siguiente generación será

\[\begin{equation} p'=p(1-u) \end{equation}\]

y el cambio debido a la mutación será (notar la notación \(\Delta_u p\) ahora, con el subscrito \(_u\) para indicar mutación)

\[\begin{equation} \Delta_u p=p'-p=p(1-u)-p=-up=-u(1-q)=-u+uq \tag{4.22} \end{equation}\]

La tasa de mutación \(u\) es usualmente extremadamente pequeña, del orden de \(1\)x\(10^{-10}\) por base por replicación para muchos genomas de eucariotas multicelulares (aunque no del mismo orden en plantas). En grandes números esta tasa podría ser del orden de \(1\)x\(10^{-5}\) expresada en términos de mutaciones por locus por replicación (con una varianza muy importante entre organismos). Por lo tanto, como \(q \approx 0\), entonces

\[\begin{equation} \Delta_u p=-u+uq \approx -u \tag{4.23} \end{equation}\]

Veamos ahora cómo es el balance entre el cambio de frecuencias que produce la mutación (ecuación (4.23)), decreciendo la frecuencia de \(A_1\) y la selección que favorece a \(A_1\). Si recuerdas de la ecuación (4.5), el cambio esperado en la frecuencia de \(A_1\) por selección era

\[\begin{equation} \Delta_s p=\frac{pqs[ph+q(1-h)]}{\bar{w}} \end{equation}\]

Pero si \(q \approx 0\), entonces \(p \approx 1\) y \(\bar{w} \approx 1\) (ya que tanto \(2pqhs \approx 0\) como \(q^2s \approx 0\)). Además \(pqs \cdot ph \approx qs \cdot h \approx qhs\) y \(pqs \cdot q(1-h) = pq^2s (1-h) \approx 0\) (porque \(q^2 \ll q \approx 0\)). Entonces, con esta condición de que la frecuencia del alelos \(A_2\) se mantenga muy baja (\(q \approx 0\)), la ecuación anterior se transforma en

\[\begin{equation} \Delta_s p \approx qhs \end{equation}\]

El juego entre la fuerza de cambio hacia \(A_2\) (\(\Delta_u p\)) debida a la mutación y hacia \(A_1\) (\(\Delta_s p\)) debida a la selección se puede ver en la Figura 4.15. Para que las dos fuerzas se equilibren el balance debe ser cero (\(\Delta_u p + \Delta_s p=0\)), por lo que, usando \(\hat{q}\) para la frecuencia del alelo \(A_2\) en el equilibrio, tenemos que

\[\begin{equation} -u+\hat{q}hs \approx 0 \therefore \hat{q}hs \approx u \end{equation}\]

y finalmente

\[\begin{equation} \hat{q} \approx \frac{u}{hs} \tag{4.24} \end{equation}\]

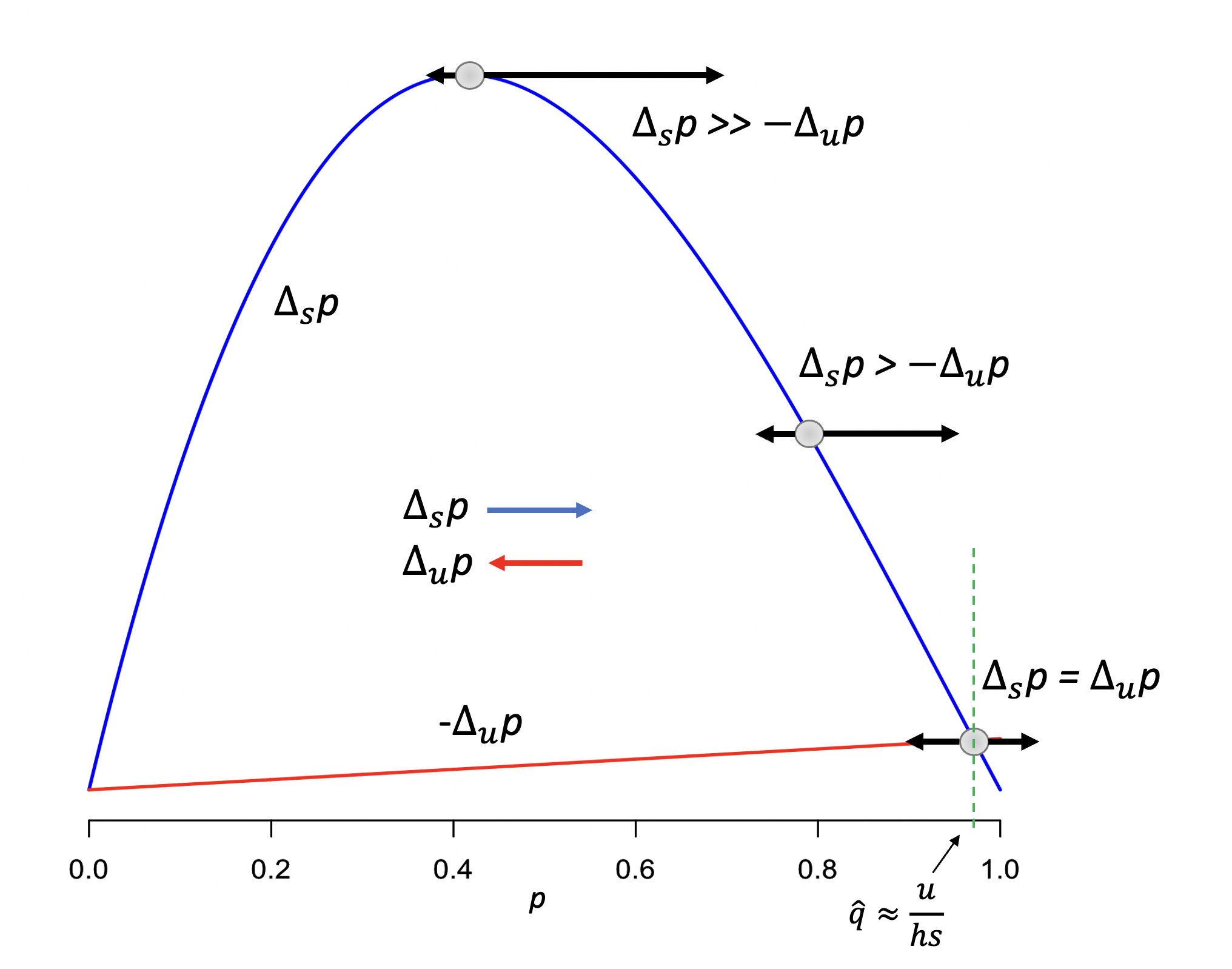
Figura 4.15: Ilustración del equilibrio selección-mutación. La selección tenderá a aumentar la frecuencia del alelo \(A_1\) (\(\Delta_s p\), línea azul), mientras que la mutación tenderá a reducirla (\(\Delta_u p\), línea roja). Cuando ambas fuerzas son de igual magnitud (abajo a la derecha) se establecerá un equilibrio en una frecuencia \(\hat{q}=\frac{u}{hs}\). Los valores usados para generar la figura son \(h=\frac{1}{3}\), \(s=0.1\) y \(u=1\)x\(10^{-3}\). En la figura aparece graficado \(-\Delta_u p\) para poder ubicar el punto de corte de ambas fuerzas.

En palabras, la frecuencia de equilibrio para el alelo \(A_2\), es el cociente entre la tasa de mutación con la que es introducido (\(u\)) y el producto del coeficiente de selección \(s\) (en su contra) y efecto de los heterocigotos \(h\). Recordando que se trata de una aproximación que depende de que \(q \approx 0\) y que además, como vimos en la sección ¿Dónde se “esconden” los alelos recesivos?, los alelos raros se encuentran en su mayoría en los individuos heterocigotos (porque \(2pq \gg q^2\)), entonces resulta más claro el por qué de que el denominador de la ecuación (4.24) incluya el efecto de la selección contra los individuos heterocigotos.

Un caso diferente es cuando \(h=0\). Esto sucede cuando \(A_1\) domina completamente a \(A_2\) (es decir, el alelo perjudicial es completamente recesivo). En ese caso, el cambio de frecuencia debido a la selección es

\[\begin{equation} \Delta_s p=\frac{pqs[p \cdot 0+q(1-0)]}{1-2pqs \cdot 0 -q^2s}=\frac{pq^2s}{1-q^2s} \end{equation}\]

En el equilibrio, tenemos que el cambio introducido por la mutación más el producido por la selección deben ser cero. Es decir, usando el resultado de la ecuación (4.22), tenemos

\[\Delta_s p + \Delta_u p=0=\frac{\hat{p}\hat{q}^2s}{1-\hat{q}^2s}-u+u\hat{q}=\frac{\hat{p}\hat{q}^2s}{1-\hat{q}^2s}-u(1-\hat{q}) \Leftrightarrow \] \[u(1-\hat{q}) = \frac{\hat{p}\hat{q}^2s}{1-\hat{q}^2s}\] \[u = \frac{\hat{p}\hat{q}^2s}{(1-\hat{q}^2s)(1-\hat{q})}\] \[u = \frac{\hat{q}^2(1-\hat{q})s}{(1-\hat{q}^2s)(1-\hat{q})}\] \[u = \frac{\hat{q}^2 s}{(1-\hat{q}^2s)} \Leftrightarrow\] \[\frac{u}{s}=\frac{\hat{q}^2}{(1-\hat{q}^2s)}\]

En el caso de que nuevamente la frecuencia de equilibrio de \(A_2\) sea muy baja (\(\hat{q} \approx 0\)) tenemos que \(1-\hat{q}^2s \approx 1\), lo que nos deja una excelente aproximación en

\[\begin{equation} \hat{q} \approx \sqrt{\frac{u}{s}} \tag{4.25} \end{equation}\]

4.5.1 El principio de Haldane-Muller

El principio de Haldane⁵³-Muller⁵⁴ se relaciona con la reducción en el fitness medio de una población como balance entre selección y mutación. En el caso de selección direccional e ignorando el efecto de las mutaciones recurrentes, en algún momento el alelo favorecido (\(A_1\)) se fijará y entonces \(\bar{w}=1-2pqhs-q^2s=1\), ya que \(q=0\). Sin embargo, cuando existe mutación recurrente, el alelo desfavorecido volverá a aparecer en forma recurrente y por lo tanto la frecuencia de equilibrio será tal que \(\hat{q}>0\). En el caso particular que \(h=0\) (cuando \(A_1\) domina completamente a \(A_2\)), entonces el fitness medio de la población será \(\bar{w}=1-q^2s\) ya que \(2pqhs=0\). Si sustituimos el resultado de la ecuación (4.25) en la expresión anterior, tenemos que

\[\begin{equation} \bar{w}=1-q^2s \approx 1-\left(\sqrt{\frac{u}{s}}\right)^2s=1-u \end{equation}\]

El cambio en el fitness medio (que llamaremos \(L\)⁵⁵) correspondiente a esta carga mutacional será la diferencia entre el fitness máximo (igual a \(1\)) y el producto del equilibrio mutación selección, es decir

\[\begin{equation} L=w_{max}-\bar{w}=1-(1-u)=u \end{equation}\]

es decir, \(L=w_{max}-\bar{w}\) es igual a la tasa mutacional \(u\).

En el caso de dominancia incompleta (\(0 < h < 1\)), usando la aproximación de la ecuación (4.24) el fitness medio será

\[\begin{equation} \bar{w}=1-2\hat{p}\hat{q}hs-\hat{q}^2s = 1-2phs\frac{u}{hs}-\left(\frac{u}{hs}\right)^2s=1-2pu-\frac{u^2}{h^2s} \tag{4.26} \end{equation}\]

Teniendo en cuenta que \(p \approx 1\) y despreciando el término \(\frac{u^2}{h^2s}\) por ser extremadamente pequeño para las tasas mutacionales habituales (ver por ejemplo (Drake et al. 1998), o tener en cuenta que \(u^2 \approx 0\)), tenemos entonces que en este caso

\[\begin{equation} \bar{w} \approx 1-2u \end{equation}\]

por lo que el cambio de fitness medio será ahora

\[\begin{equation} L=w_{max}-\bar{w}=1-(1-2u)=2u \end{equation}\]

En ambos casos la reducción en el fitness medio es independiente del efecto del coeficiente de selección. En otras palabras, más allá de lo fuerte o débil que sea el efecto de la selección contra un alelo perjudicial, la carga mutacional (i.e., la pérdida en fitness de la población) es solo proporcional a la tasa de mutación. Esta pérdida es equivalente a \(u\) en el caso de dominancia completa, y a \(2u\) en el caso de dominancia incompleta. Visto de otra manera, cuando el efecto de la mutación es fuerte, la frecuencia de equilibrio de la misma será mucho más baja que cuando el efecto de ésta es más suave; este balance es la razón de la independencia del coeficiente de selección. A este efecto se le conoce como principio de Haldane-Muller.

Ejemplo 4.4

El ejemplo más conocido del uso del principio (a veces conocido como “teorema”) de Haldane-Muller es la estimación de la tasa de mutación a partir de genotipos deletéreos. En particular, el ejemplo más conocido es la enfermedad de Huntington (a veces conocida como “corea de Huntington”) una enfermedad neurodegenerativa llamada así en honor de George Huntington, médico norteamericano que la describió en 1832. Se trata de una enfermedad producto de alelos deletéreos en el gen de la “Huntingtina”, una proteína vinculada al transporte celular y a factores de transcripción, que interacciona con cerca de otras 100 proteínas. En la secuencia, esta proteína tiene repetidos de la secuencia “CAG” que codifica para la Glutamina (por lo que se trata de una región PoliQ). El largo “normal” del número de repetidos es menor a 27, de 27 a 35 es una situación intermedia con cierto riesgo en la descendencia, de 36 a 39 se clasifica como de penetrancia incompleta y con más de 40 repetidos se trata de penetrancia total. El modo de acción génica es de dominancia completa del alelo perjudicial. Hartl and Clark (2007) dan un ejemplo del cálculo de la tasa mutacional a partir de los datos de afectados por este gen, ejemplo que adaptaremos aquí. El objetivo será entonces tener un rango de estimaciones de la tasa mutacional \(u\).

Si bien se trata de un gen con alelo completamente dominante, la disminución en fitness de los heterocigotos se estima en \(w_{12}=0,81\) en relación al normal \(w_{11}=1\) ya que el desarrollo de la enfermedad es en la edad adulta, usualmente después de comenzado la etapa reproductiva. Los homocigotos \(A_2A_2\) no se consideran ya que la frecuencia de ellos es totalmente despreciable (tendrían que tener dos padres con la enfermedad, que ya es rara de por sí). Con estos datos, \(1-hs=0,81 \Leftrightarrow hs=1-0,81=0,19\). En algunas poblaciones europeas, las cifras conocidas indican entre 4 y 15 individuos afectados por cada 100 mil habitantes, es decir una frecuencia de entre \(\mathbb{P}(\text{Af})=4\)x\(10^{-5}\) y \(\mathbb{P}(\text{Af})=1,5\)x\(10^{-4}\). Si los afectados son los heterocigotos (las cifras anteriores), es decir \(2pq=\text{ afectados}\), asumiendo que \(p \approx 1\) (en la cifra mayor de afectados \(p=0,99985\)), entonces una buena aproximación de la frecuencia de \(A_2\) es

\[\begin{equation} 2\hat{q} \approx 2pq = \mathbb{P}(\text{Af}) \Rightarrow \hat{q} \approx \frac{\mathbb{P}(\text{Af})}{2} \end{equation}\]

Como \(h \ne 0\) (porque \(hs \ne 0\)) la ecuación a utilizar es \(\hat{q}=\frac{u}{hs}\), que da lugar a \(\hat{u}=\hat{q}hs\) (el \(\hat{u}\) lo usamos para indicar que se trata de una “estimación” que hacemos del “verdadero valor”). Sustituyendo los valores correspondientes tenemos que la tasa mutacional varía entre \(\hat{u}=qhs=0,19 \cdot (4\)x\(10^{-5})/2=3,86\)x\(10^{-6}\) y \(\hat{u}=qhs=0,19 \cdot (1,5\)x\(10^{-4})/2=1,425\)x\(10^{-5}\).

PARA RECORDAR

• En nuestro modelo de un locus con dos alelos, con dominancia incompleta, asumiendo que la fuerza de selección contra el alelo \(A_2\) consigue mantener la frecuencia del mismo muy baja (y por lo tanto \(q \approx 0\)), si los alelos \(A_2\) se reintroducen con una tasa \(u\), entonces el balance entre la mutación y la selección está dado aproximadamente por \(\hat{q} \approx \frac{u}{hs}\).

• En el caso de que \(h=0\), es decir cuando \(A_1\) es dominante sobre \(A_2\), entonces una aproximación razonable a la frecuencia de equilibrio está dada por \(\hat{q} \approx \sqrt{\frac{u}{hs}}\).

• Principio de Haldane-Muller: cuando \(0 \le h<1\), la reducción en el fitness medio es independiente del efecto del coeficiente de selección. La carga mutacional, es decir la pérdida en fitness de la población, es solo proporcional a la tasa de mutación (\(L=w_{max}-\bar{w}=u\) en el caso de dominancia completa, \(L=w_{max}-\bar{w}=2u\) en el caso de dominancia incompleta).

4.6 La fuerza de la selección natural

Hasta ahora en el presente capítulo no le habíamos dedicado una atención especial al coeficiente de selección. Más aún, algunos resultados importantes de este capítulo son completamente independientes del coeficiente de selección: recordemos por ejemplo el punto de equilibrio en sobredominancia o subdominancia (\(\hat{p}=\frac{h-1}{2h-1}\)). Sin embargo, es este coeficiente de selección el centro de las diferencias de viabilidad entre los genotipos, y por lo tanto representa aquello que permite que la frecuencia de los alelos vaya cambiando de generación en generación. ¿Es que el valor del coeficiente de selección no tiene importancia en las consecuencias de la selección?

En realidad, como es de esperar, este coeficiente sí tiene gran relevancia. Intuitivamente, un coeficiente de selección muy pequeño no hará grandes diferencias entre la viabilidad de los distintos genotipos, y por lo tanto su impacto será menor en comparación con las otras fuerzas evolutivas como la deriva, la mutación y la migración. Pese a su importancia, hay dos hechos a destacar. En primer lugar, fijado el modelo de acción génica no hay un cambio importante en la forma que adquiere la evolución de las frecuencias alélicas en función del valor de \(s\): como veremos en breve, la forma de esta gráfica permanece relativamente similar. En segundo lugar, pese a su importancia, no es trivial cómo medir el coeficiente de selección, y solo a partir de la evolución de las tecnologías de secuenciación y otras ómicas que ocurrieron a finales del siglo XX y principios del XXI es posible identificar mejor el efecto de variantes específicas que tienen impacto en el fitness de los organismos.

En un estudio reciente, Thurman y Barret (Thurman and Barrett 2016) revisaron la literatura en busca de estimaciones publicadas sobre la selección natural que actúa a nivel genético y encontraron más de 3.000 estimaciones de coeficientes de selección, la mayoría en plantas (ya que son bastante más fáciles de estudiar), procedentes de 79 estudios distintos. Este tipo de estudio, que combina la información de otros muchos, se conoce como meta-análisis y se trata de estudios importantes para conocer la distribución de valores, así como la coherencia entre los resultados de diferentes estudios. En dicho estudio, los coeficientes de selección se distribuyeron de forma aproximadamente exponencial (negativa), lo que sugiere que el impacto de la selección a nivel genético es generalmente débil, pero en ocasiones puede ser bastante fuerte. Utilizando un modelo mixto lineal generalizado, los autores llegaron a estimar un coeficiente de selección medio de \(s=0,095\) (moda a posteriori, con un intervalo del \(95\%\) HPD de \(0,066-0,124\)). Hay que recordar que en la distribución exponencial la media es mayor que la mediana (\(\mu=\frac{1}{\lambda}\) y mediana \(\frac{\ln 2}{\lambda}\)). Por otro lado, estos autores observaron que la selección fue más fuerte cuando se midió en escalas de tiempo más cortas, siendo la magnitud media de \(s\) mayor para los estudios que midieron la selección en una sola generación. Finalmente, los autores destacan las dificultades inherentes a esta medición, la diferencia entre los modelos y parametrizaciones usados, y la dificultad de incorporar la estimación del efecto de los heterocigotos \(h\).

En la Figura 4.16 se puede apreciar la evolución de la frecuencia del alelo \(A_1\) bajo dominancia incompleta en diferentes configuraciones. La gráfica de la izquierda corresponde a un efecto de los heterocigotos de \(h=\frac{1}{4}\), la del medio a \(h=\frac{1}{2}\) y la de la derecha a \(h=\frac{3}{4}\) representando un conjunto de situaciones intermedias para dicho efecto (\(h=\frac{1}{2}\) se corresponde a un modelo completamente aditivo). En cada gráfica, las distintas curvas se corresponden con diferentes coeficientes de selección, entre \(s=0,05\) (rojo) y \(s=0,25\) (negro). Lo primero que observamos es que, como decíamos más arriba, no parece existir gran diferencia en las formas de las curvas, las que lucen como una S (i.e., aproximadamente sigmoidales). Una segunda observación en las gráficas de la Figura 4.16 es que, excepto la curva roja (que corresponde al menor \(s\)) donde no tenemos una visión completa, el comportamiento es bastante similar: un breve comienzo de evolución lenta que rápidamente se acelera, llevando las curvas a una evolución casi vertical, para finalmente aplanarse y comenzar a acercarse en forma asintótica a la “frecuencia de equilibrio”, que en este caso se corresponde con la fijación (\(p=1\)) del alelo \(A_1\). Otra vez, excepto para el coeficiente de selección más bajo (curva roja), en el resto de las configuraciones de \(h\) y \(s\) que mostramos las poblaciones se acercan a la fijación del alelo \(A_1\) en menos de 200 generaciones y la mitad del camino hacia la fijación (\(p=0,5\)) generalmente en menos de 100 generaciones. Más aún, parece haber una interacción entre coeficientes de selección bajos y \(h \to 1\) que potencia el efecto del primero (la curva roja en la gráfica de la derecha se encuentra muy “aplanada”).

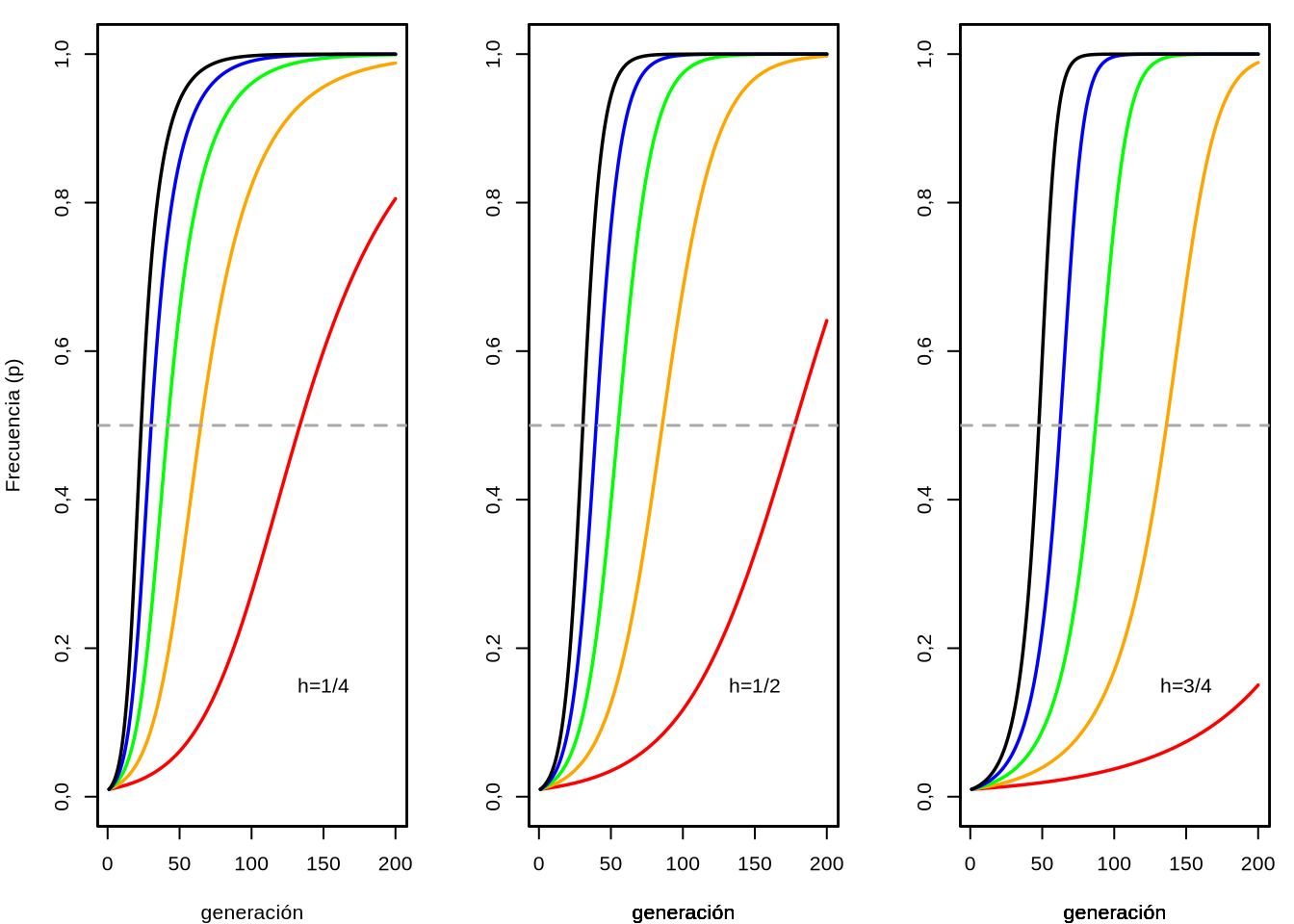
Figura 4.16: Evolución de las frecuencias bajo dominancia incompleta, de acuerdo a diferentes niveles del coeficiente de selección y del efecto de los heterocigotos. Coeficientes de selección \(s=0,05\) a \(s=0,25\), colores rojo, anaranjado, verde, azul y negro. Izquierda \(h=\frac{1}{4}\), centro \(h=\frac{1}{2}\) y derecha \(h=\frac{3}{4}\).

Veamos ahora qué ocurre cuando el modo de acción génica es la sobredominancia. En la Figura 4.17 se muestran diferentes configuraciones del efecto de los heterocigotos y del coeficiente de selección para dicho modo. Ahora el punto de equilibrio será a una frecuencia intermedia, como vimos en la sección Selección estabilizadora (\(\hat{p}=\frac{h-1}{2h-1}\)). Sin embargo, el comportamiento de las curvas sigue siendo aproximadamente sigmoidal, como en el caso de dominancia incompleta (selección direccional). Con sobredominancia, el punto de equilibrio se va haciendo menor a medida de que \(h\) se hace más negativo (\(h \to -1\)). Eso implica que la “carrera” por alcanzarlo disminuya de izquierda a derecha en las gráficas de la Figura 4.17, lo que hace que no sean directamente comparables. De todas formas se aprecia claramente que menores coeficientes de selección implican tiempos mayores para alcanzar el punto de equilibrio.

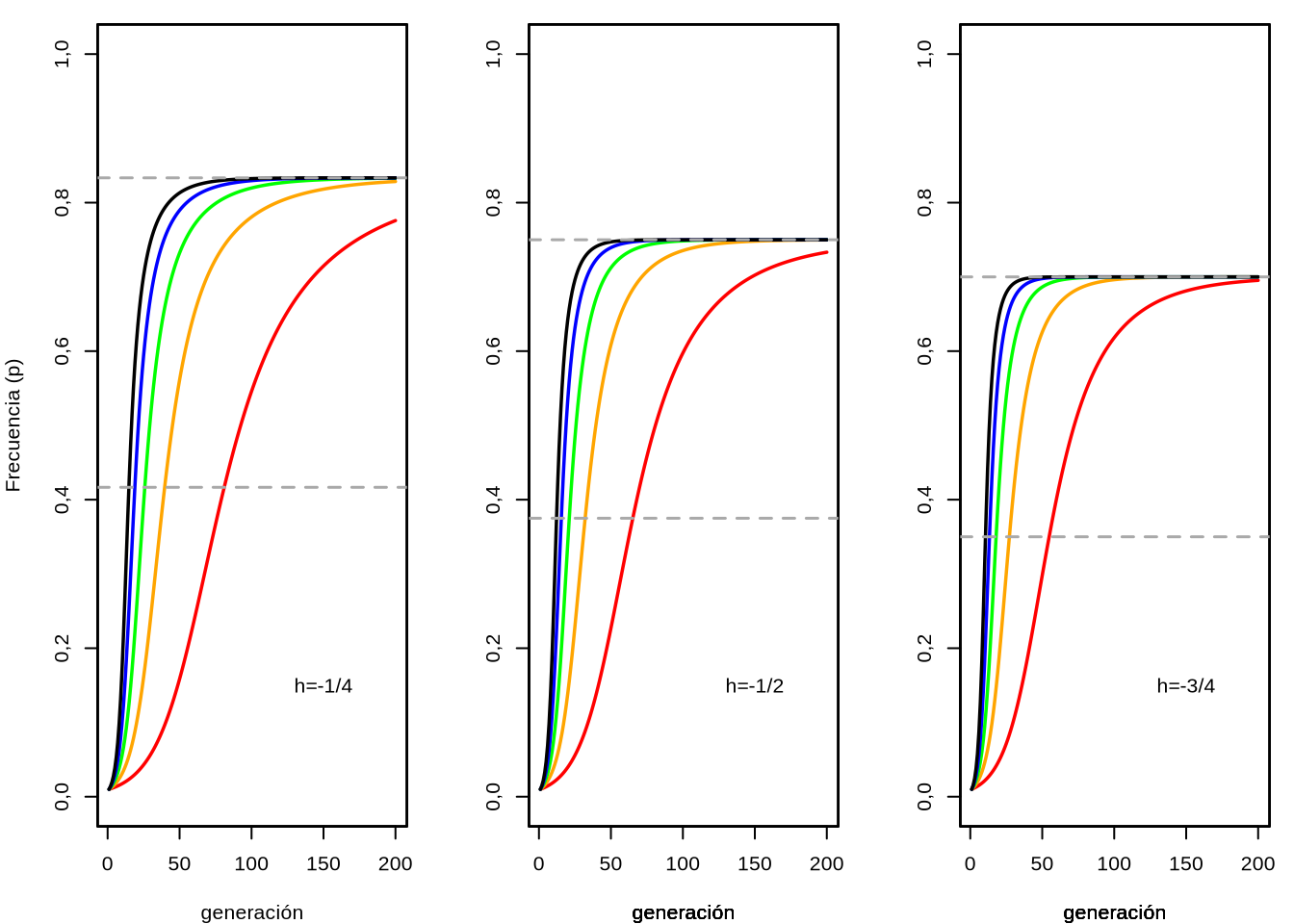
Figura 4.17: Evolución de las frecuencias bajo sobredominancia, de acuerdo a diferentes niveles del coeficiente de selección y del efecto de los heterocigotos. Coeficientes de selección \(s=0,05\) a \(s=0,25\) (en pasos de \(0,05\)), colores rojo, anaranjado, verde, azul y negro. Izquierda \(h=-\frac{1}{4}\), centro \(h=-\frac{1}{2}\) y derecha \(h=-\frac{3}{4}\).

Veamos ahora qué impacto tienen los coeficientes de selección en el tiempo hasta alcanzar la cercanía del punto de equilibrio correspondiente. En la Figura 4.18 se ve cuantas generaciones son necesarias para quedar a menos de \(1\%\) del punto de equilibrio (o fijación) de la frecuencia del alelo \(A_1\), dependiendo del coeficiente de selección, para dos modos de acción diferentes.

Claramente, las curvas no son lineales y a medida de que vamos reduciendo el coeficiente de selección (o sea, si nos movemos por la curva de derecha a izquierda), la misma se vuelve cada vez más empinada. Dicho de otra forma, coeficientes de selección muy pequeños requerirán un número desproporcionadamente alto de generaciones para acercarse a una situación de equilibrio (o de fijación, en el caso de dominancia incompleta).

Para terminar con esta sección hagamos una reflexión sobre los tiempos implicados para que la selección natural pueda actuar. En especies de mamíferos de gran tamaño, como los bovinos por ejemplo, el intervalo generacional es del orden de los 5 años. Con coeficientes de selección débiles (del orden de \(s \approx 0,01\)) y dominancia incompleta, como vimos en la Figura 4.18, entre 500 y 1000 generaciones son necesarias para llegar al entorno de la fijación de un alelo. Esto significa entre 2500 a 5000 años. Con fuerzas selectivas del orden de \(s \approx 0,05\) son necesarias unas 175 generaciones, es decir unos 875 años. Coeficientes de selección mayores no son frecuentes para la mayoría de las características, pero con coeficientes de selección del orden de \(s \approx 0,10\) tardaremos unas 85 generaciones, es decir unos 425 años. Con especies anuales, frecuentes en plantas, los tiempos son claramente inferiores (e iguales al número de generaciones) y en casos de especies que se reproducen más de una vez por año, estos tiempos son aún mucho menores. Si recordamos de la sección Probabilidad de fijación y tiempos de fijación que por efecto de la deriva el tiempo (en generaciones) a la fijación de un alelo que parte de una frecuencia de \(p=0,01\) (como en la Figura 4.18) es de \(\approx 4N\) (ya que \(p \approx 0\)), aún con coeficientes de selección tan bajos como \(s=0,01\) el efecto sistemático de la misma prevalecerá sobre la deriva.

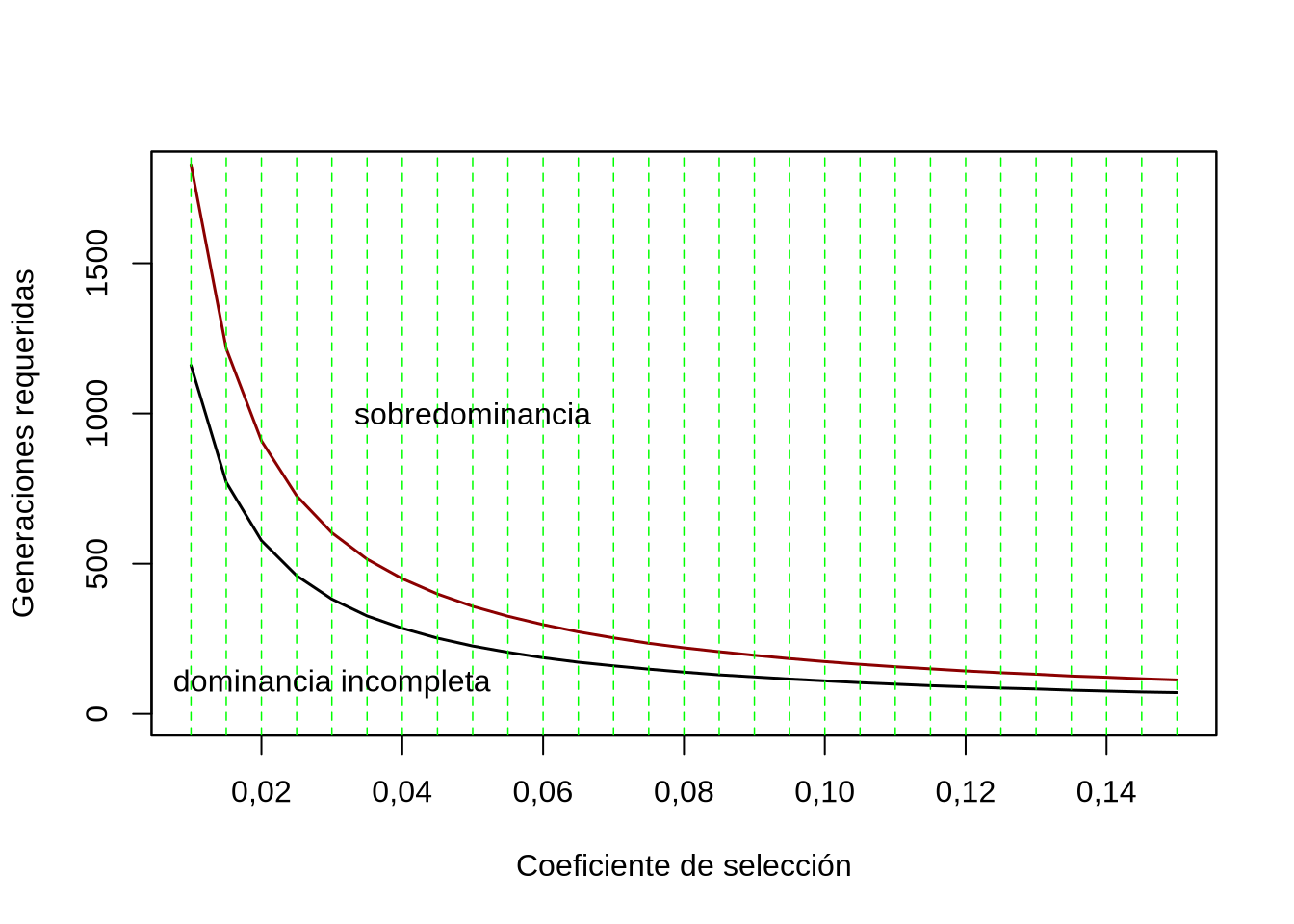
Figura 4.18: Número de generaciones requeridas para quedar a menos de \(1\%\) del punto de equilibrio bajo diferentes coeficientes de selección (entre \(s=0,01\) y \(s=0,15\), de a \(0,005\)) y en dos modos de acción génica (negro dominancia incompleta \(h=\frac{1}{2}\), rojo sobredominancia \(h=-\frac{1}{2}\)), partiendo de una frecuencia inicial \(p=0,01\). Claramente el comportamiento no es lineal y a medida de que el coeficiente de selección disminuye el número de generaciones se hace mucho mayor.

Además, como ya vimos en la sección Equilibrio selección-mutación, el valor del mismo es fundamental también a la hora de fijar el punto de equilibrio de la frecuencias alélicas. Un valor alto de \(s\) contribuirá a un valor de equilibrio \(\hat{q}\) muy cercano a cero, dentro del alcance de lo efectos de la deriva y por lo tanto de su pérdida.

PARA RECORDAR

• El valor del coeficiente de selección es fundamental para conocer el tiempo a la fijación de un alelo bajo dominancia incompleta o de alcanzar el equilibrio en sobredominancia.

• Los coeficientes de selección son difíciles de determinar bajo selección natural, pero diversos estudios confirman que en su mayoría tienen un valor pequeño, con una distribución del tipo exponencial.

• La forma de la evolución de las frecuencias alélicas bajo dominancia incompleta y sobredominancia es aproximadamente sigmoidal, con una aceleración en frecuencias más intermedias y una posterior meseta cerca de la fijación o del punto de equilibrio.

4.7 Equilibrio selección-deriva

En el presente capítulo, hasta ahora solo hemos mencionado el efecto de la deriva como usualmente pequeño y por lo tanto afectando el resultado de la selección solo en el entorno de los puntos críticos del proceso, es decir en torno a los puntos de equilibrio, fijación o pérdida, de acuerdo al tipo de selección, pero sin explicitar en forma matemática dicha relación. Es tiempo entonces de presentar esta relación en una forma tal que nos permita evaluar el impacto de cada una de las dos fuerzas en este entorno. La matemática implicada es bastante más compleja que la usada en este capítulo, ya que la matemática de los procesos estocásticos lo es, pero por suerte no deberemos hacer un gran esfuerzo ya que las herramientas las pusimos a punto en el capítulo Deriva Genética, en particular en la sección Aproximación de difusión (si antes decidiste no prestarle mucha atención a dicha sección, es probable que sea tiempo de ir de nuevo a ella).

Supongamos que tenemos un locus autosomal con dos alelos en un organismo diploide, con un modo de acción completamente aditivo, es decir \(h=\frac{1}{2}\) y con coeficiente de selección \(s\). Como recordarás de más arriba, el cambio de frecuencia por generación esperado era

\[\begin{equation} \Delta_s p=\frac{pqs[ph+q(1-h)]}{\bar{w}} \end{equation}\]

que sustituyendo los valores con \(h=\frac{1}{2}\) nos da

\[ \begin{split} \Delta_s p=\frac{pqs[\frac{1}{2}p+q(1-\frac{1}{2})]}{\bar{w}}=\frac{pqs[\frac{1}{2}(p+q)]}{\bar{w}}\ \therefore\ \\ \Delta_s p=\frac{pqs}{2}\frac{1}{\bar{w}} \end{split} \tag{4.27} \]

Esto era el cambio por generación en la frecuencia de \(p\) debido a la selección. Veamos cómo entra este resultado en el equilibrio entre selección y deriva. Para ello vamos a recurrir a nuestra Aproximación de difusión. Si recuerdas la idea, vamos a pasar de un tiempo discreto en generaciones (y con cambios discretos en frecuencias) a una aproximación suficientemente buena en tiempo y frecuencias continuas. En esta aproximación considerábamos dos fuerzas, una sistemática con dirección determinística, que notamos como \(M(x)\) (pero que técnicamente se conoce como “coeficiente de deriva”, lo que es algo confuso ya que a veces usamos el témino “deriva” para referirnos al azar) y una segunda fuerza aleatoria que notamos como \(V(x)\) (y que técnicamente se conoce como “coeficiente de difusión”). En el capítulo anterior, como todavía no habíamos hablado de la selección pusimos la restricción de que \(M(x)=0\), es decir que solo analizamos el efecto del movimiento al azar de la frecuencias. Ahora es tiempo de usar \(M(x)\) a nuestra conveniencia, en particular para modelar el efecto de la selección (que como ya vimos, es una fuerza determinística).

Si consideramos que en un intervalo de tiempo infinitesimal el cambio en el fitness medio será despreciable, sustituyendo \(p\) por \(x\) en la ecuación (4.27) para no confundirnos con el punto particular \(p\), nos permite aproximar

\[\begin{equation} \lim_{\delta t \to 0} \frac{\Delta_s x}{\delta t} \approx \frac{sx(1-x)}{2}=M(x) \end{equation}\]

Por otro lado, recordarás de la sección Solución de las ecuaciones que

\[\begin{equation} V(x)=\frac{x(1-x)}{2N_e} \end{equation}\]

Tenemos entonces todo para estimar la probabilidad de fijación de un alelo \(A_1\) con la ventaja selectiva que definimos más arriba. Para el cálculo de esta probabilidad, si recuerdas de la sección Solución de las ecuaciones, tenemos primero que calcular la función de escala \(G(x)\), como fue definida en la ecuación (3.40), es decir

\[\begin{equation} G(x)=\text{exp}[-2 \int^x \frac{M(y)}{V(y)}dy] \end{equation}\]

Sustituyendo los valores específicos de \(M(x)\) y \(V(x)\) obtenidos más arriba (con el cambio de notación de \(y\) en lugar de \(x\) en el integrando), tenemos que

\[\begin{equation} G(x)=\text{exp}\left[-2N_es \int^x \frac{y(1-y)}{y(1-y)}dy\right]=e^{-2N_esx} \tag{4.28} \end{equation}\]

Por lo tanto, de acuerdo a la ecuación (3.43), sustituyendo la notación \(u(p)\) anterior por la notación \(\pi_1(p)\) para la probabilidad de fijación del alelo con frecuencia \(p\) (a fin de no confundirnos con la tasa de mutación que también usamos \(u\))

\[\begin{equation} \pi_1(p)=\frac{\int_0^p G(x) dx}{\int_0^1 G(x) dx} \tag{4.29} \end{equation}\]

sustituyendo los valores de (4.28) en (4.29) tenemos

\[\begin{equation} \pi_1(p)=\frac{\int_0^p e^{-2N_esx} dx}{\int_0^1 e^{-2N_esx} dx}=\frac{1-e^{-2N_esp}}{1-e^{-2N_es}} \tag{4.30} \end{equation}\]

Es decir, arribamos a la probabilidad de fijación para este alelo \(A_1\) con ventaja selectiva \(s\) del genotipo \(A_1A_1\) respecto al homocigoto \(A_2A_2\), en un locus aditivo que se comporta como completamente aditivo, a partir de una frecuencia determinada \(p\) en la que se encuentre dicho alelo. Esto es muy importante: ahora la probabilidad de fijación no será como bajo la acción exclusiva de la deriva, que habíamos visto era \(\pi_1(p)=p\), ni tampoco estará determinada por \(h\) y \(s\), sino por la combinación de estos efectos.

Veamos qué ocurre con un alelo que recién arriba a la población y que tiene las condiciones definidas más arriba, es decir \(h=\frac{1}{2}\) básicamente. Una nueva mutación que arriba a una población de \(N\) individuos diploides tiene frecuencia \(p=\frac{1}{2N_e}\) (asumiendo que \(N=N_e\)). Sustituyendo en la ecuación (4.30), tenemos

\[\begin{equation} \pi_1(\frac{1}{2N_e})=\frac{1-e^{-2N_esp}}{1-e^{-2N_es}}=\frac{1-e^{-2N_es\frac{1}{2N_e}}}{1-e^{-2N_es}} \therefore \end{equation}\]

\[\begin{equation} \pi_1(\frac{1}{2N_e})=\frac{1-e^{-s}}{1-e^{-2N_es}} \tag{4.31} \end{equation}\]

Si \(s\) es muy pequeño (como usualmente lo es, para la mayor parte de las mutaciones que arriban), entonces \(e^{-s} \approx 1-s\) y si además \(2N_es\) es suficientemente grande (es decir \(N_e\) es muy grande) para que \(e^{-2N_es} \approx 0\), entonces la ecuación (4.31) se reduce a

\[\begin{equation} \pi_1(p)=\frac{1-e^{-s}}{1-e^{-2N_es}} \approx \frac{1-(1-s)}{1-0}\ \therefore \end{equation}\]

\[\begin{equation} \pi_1(p) \approx s \tag{4.32} \end{equation}\]

El resultado anterior es un caso particular de un resultado más general que permite una aproximación a la probabilidad de fijación de un alelo, que sería

\[\begin{equation} \pi_1(p) \approx 2(1-h)s \tag{4.33} \end{equation}\]

El sentido intuitivo de la aproximación anterior ya lo hemos discutido en otras instancias. Para los alelos “raros”, por ejemplo las nuevas mutaciones que arriban a la población, la mayoría se van a encontrar en los heterocigotos y por ello no es de extrañar esta dependencia de la probabilidad de fijación de los nuevos alelos en el fitness relativo de los heterocigotos. Si sustituimos \(h=\frac{1}{2}\) en (4.33) nos da, obviamente, \(\pi_1(p) \approx s\).

Nota de precaución

En algunos textos (e.g. Walsh & Lynch, Rice o incluso algunos trabajos de Kimura) se opta por una parametrización distinta de los fitness relativos, donde \(w_{11} = 1 + 2s;\ w_{12} = 1 + s;\ w_{22} = 1.\)

Empleando esta parametrización, utilizando el mismo abordaje a la aproximación por difusión que el planteado en este libro, se llega a la siguiente probabilidad de fijación para un alelo bajo modelo completamente aditivo:

\[\pi_1(p)=\frac{1-e^{-4N_esp}}{1-e^{-4N_es}}\]

Esto puede llevar a una aparente incongruencia. ¿Cómo se establece una equivalencia entre los dos resultados?

Notemos que la parametrización empleada, si se hace con referencia al homocigota \(A_1A_1\) es equivalente a \(w_{11} = 1;\ w_{12} = 1 -s;\ w_{22} = 1 - 2s\)

donde restamos en cada caso \(2s\), la diferencia entre el máximo w_{11} y el mínimo w_{22}. Pero bajo la parametrización empleada en este libro, con \(h = \frac{1}{2}\), tenemos \(w_{11} = 1;\ w_{12} = 1 - \frac{1}{2} \cdot s;\ w_{22} = 1 - s\).

Al comparar ambos planteos queda claro que el valor de \(s\) empleado en la parametrización de este libro equivale al \(2s\) empleado en la otra parametrización. Por lo tanto, el resultado al que arribamos en el desarrollo de este libro es, bajo la otra parametrización

\[\pi_1(p)=\frac{1-e^{-2N_e(2s)p}}{1-e^{-2N_e(2s)}} = \frac{1-e^{-4N_esp}}{1-e^{-4N_es}}\]

quedando clara la equivalencia de ambos resultados. Este caso muestra la importancia que posee analizar bajo qué modelos y parámetros se llega a un resultado: claramente, no es lo mismo emplear una ecuación que otra si no se tiene en cuenta qué parametrización se está empleando.

Para poner los resultados anteriores en perspectiva pongamos algunos números. Si la ventaja selectiva del nuevo alelo es, por ejemplo \(s=0,05\), para una población de \(N_e=500\), entonces en el modelo aditivo, utilizando la ecuación (4.31) la probabilidad de fijación es de \(\pi_1(\frac{1}{2N_e})=0,0488 \approx 0,05=s\), que es equivalente a la aproximación por la ecuación (4.32). En palabras, pese a que la ventaja selectiva de esta mutación es relativamente importante, la probabilidad de perderla es del \(95\%\). Si en cambio la población es ahora de 10 veces el tamaño de la anterior, podríamos intuir que el efecto de la deriva genética será mucho menor y por lo tanto la probabilidad de fijación aumentará. Desafortunadamente nuestra intuición es incorrecta y el resultado es casi idéntico. Si bien la deriva genética disminuye con el tamaño poblacional, también lo hace la frecuencia inicial de la nueva mutación, lo que en última instancia se ve reflejado en la aproximación de la ecuación (4.32), donde \(\pi_1(\frac{1}{2N_e}) \approx s\) la probabilidad de fijación no depende del tamaño poblacional. Una forma interesante de interpretar este resultado se encuentra en John H. Gillespie (2004): si un nuevo alelo arriba a una población, el mismo se encontrará en un heterocigoto; la continuidad del mismo en la población va a depender del muestreo en el número de descendientes que tiene ese heterocigoto y no en el tamaño de la población.

PARA RECORDAR

• En nuestro modelo de un locus autosómico en un organismo diploide, asumiendo que el efecto de los alelos es aditivo, la probabilidad de fijación de un alelo \(A_1A_1\) que se encuentra en frecuencia \(p\) y que en homocigosis tiene ventaja \(s\) sobre el genotipo \(A_2A_2\) es

\[\pi_1(p)=\frac{1-e^{-2N_esp}}{1-e^{-2N_es}}\]

• En el caso particular de que además de todo lo anterior (locus autosómico en un organismo diploide, efecto de los alelos es aditivo), la probabilidad de fijación de un nuevo alelo \(A_1A_1\) que en homocigosis tiene ventaja \(s\) sobre el genotipo \(A_2A_2\) es

\[\pi_1(\frac{1}{2N_e})=\frac{1-e^{-s}}{1-e^{-2N_es}}\]

Esto es debido a que al tratarse de un alelo nuevo su frecuencia inicial es \(p=\frac{1}{2N}\) y asumiendo \(N=N_e\), sustituyendo \(p\) por ese valor queda la expresión reducida anterior.

• En el caso en que \(s\) es muy pequeño, entonces \(e^{-s} \approx 1-s\) y si además \(2N_es\) es suficientemente grande para que \(e^{-2N_es} \approx 0\), entonces la probabilidad de fijación se aproxima razonablemente a \(\pi_1(p) \approx s\).

• En general, bajo los supuestos anteriores, la aproximación se generaliza a \(\pi_1(p) \approx 2(1-h)s\).

4.8 Otros tipos de selección y complejidades

En todo este capítulo nos hemos enfocado en entender las principales formas de selección natural, así como de la interacción entre algunas fuerzas evolutivas (mutación, deriva genética y selección). Pese a la aparente complejidad de algunos de los temas tratados, nuestro enfoque ha sido muy restringido para adecuarlo al nivel del presente curso. Esto deja por fuera una gran cantidad de formas de selección o de tópicos directamente relacionados. Pese a que no trataremos estos temas, resulta importante conocer las limitaciones de nuestras aproximaciones y como se distancian de la complejidad biológica, por lo que a continuación vamos a mencionar varios de estos tópicos.

Selección gamética

En ciertas plantas el ciclo de vida implica una fase haploide y otra diploide. En estos organismos las viabilidades asociadas a los alelos suelen ser diferentes en las dos fases, una con genotipos diploides y la otra con haplotipos (es decir, los alelos en estado haploide). A la selección en esta última se le conoce como selección gamética. Esto implica una alternancia en las formas de selección y los fitness de cada una de las fases. Si los fitness de \(A_1\) y \(A_2\) en esta fase son \(v_1\) y \(v_2\), entonces (como se muestra en Hartl and Clark (2007)) luego de una fase de selección en los haplotipos la frecuencias serán \(p^*=pv_1/\bar{v}\) y \(p^*=qv_2/\bar{v}\), con \(\bar{v}=pv_1+qv_2\). Por lo tanto, bajo equilibrio de Hardy-Weinberg estas serán la frecuencias con la que aparecerán los genotipos en la fase diploide, que luego serán seleccionados con viabilidad \(w_{11}\), \(w_{12}\) y \(w_{22}\). Por lo tanto, después de esta selección en la fase diploide, la frecuencia de \(A_1\) será

\[\begin{equation} p'=\frac{p^2w_{11}v_1^2+pqw_{12}v_1v_2}{p^2w_{11}v_1^2+2pqw_{12}v_1v_2+q^2w_{22}v_2^2} \end{equation}\]

y la forma de selección será determinada por la combinación de parámetros \(v\) y \(w\).

Selección por fecundidad

Cuando el fitness reproductivo no depende exclusivamente de cada genotipo sino de las combinaciones de parejas reproductivas, entonces la complejidad de los modelos se complica enormemente. Imaginemos, por ejemplo que machos de un genotipo son atraídos por hembras de otros genotipos con diferente probabilidad, que son diferentes de las probabilidades recíprocas. Ahora, para un locus con dos alelos ya no tenemos 3 fitness diferentes sino 9, ya que las combinaciones recíprocas pueden ser diferentes (macho de un genotipo y hembra de otro y el cruzamiento recíproco son diferentes). En general esas combinaciones implican muchos parámetros y eso complica las determinaciones, más aún que los modelos más realistas no suelen a reducirse a sumas o productos de pares de genotipos.

El efecto de la estructura de edades

Salvo en los casos de especies donde no hay solapamiento en la estructura de edades al momento de la reproducción, nuestro modelo es en general una simplificación considerable de lo que ocurre en la vida real. ¿Cómo afecta esto nuestros modelos? En principio es difícil de tratar en forma analítica, ya que al solaparse las generaciones, si la estructura de edades impacta por ejemplo en las viabilidades debemos incorporar este efecto en los modelos. Claramente estas complejidades exceden el alcance de nuestro curso.

Selección dependiente de la frecuencia

Hasta ahora hemos mencionado varias veces que nuestras conclusiones se referían exclusivamente a modelos en los que los que el fitness es independiente de la frecuencia de los genotipos. ¿Por qué es tan importante esa condición? En principio, si bien no vamos a trabajar los aspectos matemáticos del problema, si de alguna manera el fitness de los organismos depende de la frecuencia de los genotipos, entonces podríamos imaginarnos que se trata de una carrera donde la línea de meta se va corriendo como una función de la posición de los distintos corredores. Aún con reglas relativamente sencillas, excepto en ejemplos altamente estilizados, el tratamiento matemático suele ser más complejo de lo que pretendemos para este capítulo. Mencionaremos, sin embargo un caso interesante: con determinada dependencia del fitness en las frecuencias de los genotipos, aún en presencia de dominancia incompleta (que usualmente fijaría uno de los dos alelos mediante selección direccional) pueden existir puntos de equilibrio estable intermedios. Si recuerdas lo que vimos en los distintos tipos de selección discutidos, en principio esta selección estabilizadora solo se producía con sobredominancia. Es decir, ahora entendemos mejor por qué no podemos igualar sobredominancia a la causa de la selección estabilizadora. Un ejemplo típico de una configuración de este tipo aparece en Hartl and Clark (2007). Si el fitness de los genotipos disminuye en forma proporcional a su frecuencia, con una constante \(c\), entonces tenemos \(AA: w_{11}=1-cp^2 \text{ } Aa: w_{12}=1-2cpq \text{ } aa: w_{2}=1-cq^2\).
Haciendo las cuentas, \(\Delta p=cpq(q-p)(p^2-pq+q^2)/\bar{w}\) y por lo tanto (asumiendo que \(c>0\)) los puntos de equilibrio serán las frecuencias de \(p\) que hagan igual a cero el numerador. Estos puntos son \(p=0\), \(p=1\) (porque \(cpq\) multiplica todo y \(p=1 \Leftrightarrow q=0\)) y \(p=\frac{1}{2}\) (cuando \(p=q=\frac{1}{2} \Rightarrow p-q=0\)); la expresión \((p^2-pq+q^2)\) es igual a \(1-3pq=3p^2-3p+1=0 \Leftrightarrow p(1-p)=\frac{1}{3}\), pero esto nunca ocurre porque esa expresión es una parábola cuyo máximo es en \(p=\frac{1}{2}\) y es \(\frac{1}{4}=0,25\), por lo que no tiene ceros. O sea, despreciando los puntos \(p=\) y \(p=1\) que ya hemos discutido en otras oportunidades, en el punto de equilibrio intermedio (\(p=\frac{1}{2}\)) los nuevos fitness de cada genotipo serán \(AA: w_{11}=1-\frac{c}{4} \text{ } Aa: w_{12}=1-\frac{c}{2} \text{ } aa: w_{2}=1-\frac{c}{4}\), y por lo tanto el heterocigoto tendrá menos fitness que los homocigotos, es decir que en ese punto aparece como la acción de un efecto de subdominancia.

Ambientes heterogéneos y clinas

Como ya vimos en el caso de la mariposa Biston betularia, el fitness de los distintos genotipos puede variar en el tiempo y en el espacio. Las variaciones en el tiempo desplazarán las frecuencias en una forma relativamente permanente mientras los fitness sean estables, aunque les tome cierto tiempo esa aproximación. En cambio, las diferencias de fitness en el espacio, es decir con la geografía, pueden mantener mantener un nivel importante de polimorfismos a pesar de que los heterocigotos no sean el genotipo más ventajoso en ninguno de los ambientes.

Un caso especial de variación espacial de las frecuencias son las clinas. Una clina es un gradiente en una característica de una especie a lo largo de su rango geográfico. Dicho de otra forma, es la variación gradual de una característica biológica de una especie con la distancia geográfica. En nuestro caso, una clina en las frecuencias alélicas, es decir una variación continua en las frecuencias alélicas con la posición geográfica puede estar relacionada con una presión selectiva determinda, aunque también puede ser producida por otras razones (por ejemplo, dos poblaciones a cierta distancia con frecuencias extremas y migración entre ellas). Más aún, en pequeñas distancias geográficas es teóricamente posible que la clina sea producida por deriva solamente. En este caso, suelen durar poco tiempo y por lo tanto se conocen como “clinas transitorias”. Un ejemplo claro de clina por selección fue el presentado antes para la malaria y los alelos de la anemia de células falciformes. Otro ejemplo de clina se da en los grupo sanguíneos del locus ABO, por ejemplo entre Europa (frecuencia alta de A) y Asia (frecuencia alta del B), aunque en este caso parece más producto de la migración que de ventajas selectivas. Por lo tanto, más allá del comportamiento “clinal” de una característica, suele ser dificultoso entender si su base es genética, en particular selectiva y en ese caso cuál es el agente de esa presión selectiva.

Selección diferencial en los sexos y en genes ligados al X

La selección diferencial en los dos sexos implica que en ambos hay diferencias en los fitness relativos de los genotipos y por lo tanto, como usamos dos parámetros para cada unos (\(h\) y \(s\)), ahora necesitaremos 4 parámetros. Más aún, las frecuencias alélicas en los gametos pueden ser diferentes en ambos sexos y esto duplica los parámetros también. Finalmente, con este tipo de selección puede existir más de un punto de equilibrio interno, o aún un punto de equilibrio estable polimórfico si la dirección de selección es opuesta en ambos sexos.

En los genes ligados al sexo hay varios problemas similares a la selección diferencial en sexos, aunque ahora para el fitness de los genotipos necesitamos 3 parámetros: número de genotipos menos uno para cada sexo, pero en machos hay solo dos genotipos posibles porque hay un solo cromosoma X (en mamíferos, en aves es al revés). Las frecuencias alélicas también pueden ser diferentes en los gametos de ambos sexos, aunque como ya vimos antes la frecuencia de gametos en machos será igual a la de hembras en la generación anterior y la de hembras el promedio de machos y hembras en la anterior.

PARA RECORDAR

• Los modelos que hemos tratado in extenso en este capítulo son modelos extremadamente simplificados de cómo opera la selección en la realidad.

• En particular, para un tratamiento matemático razonable hemos considerado un locus autosomal de un organismo diploide con solo dos alelos. Normalmente los genes tienen gran cantidad de alelos y las categorías de fitness suelen ser difíciles de determinar.

• Uno de los supuestos fundamentales durante todo el capítulo fue que el fitness relativo de los genotipos no dependía de la frecuencia de los mismos. Cuando esto ocurre es necesario introducir esas funciones de dependencia en todas las ecuaciones de cambio de frecuencias. Esto las vuelve más complejas y suelen aparecer otros fenómenos novedosos, como la existencia de puntos de equilibrio interno aún en dominancia incompleta.

• La selección diferencial en los sexos, así como los genes ligados al cromosoma homogamético (X en mamíferos, en aves el Z, etc.) presenta problemas adicionales por el número de parámetros de fitness requeridos, así como la diferencia de frecuencias en los alelos en los dos sexos.

• Los ambientes heterogéneos pueden contribuir a desarrollar clinas en las frecuencias alélicas, aunque también esto puede ser producto de la deriva genética (por corto tiempo) o de procesos fundacionales y migración.

• En especies que tienen dos fases de vida libre alternando, una como diploide y la otra como haploide, se produce el fenómeno de la selección gamética y es necesario adaptar las ecuaciones de cambio de frecuencia para acomodar los parámetros adicionales que corresponden a la fase haploide.

• En la selección por fecundidad es necesario contemplar las combinaciones de fenotipos de los dos sexos, por lo que el número de parámetros a estimar es usualmente mucho mayor que en el modelo fundamental.

4.9 Conclusión

Las poblaciones naturales experimentan cambios en las frecuencias alélicas de los loci que segregan en ellas. Estos cambios no son sólo estocásticos: debido al éxito reproductivo diferencial que poseen los diversos genotipos en un ambiente estable (concepto de fitness) se producirán cambios sistemáticos en las frecuencias alélicas de la población, de modo tal que el fitness promedio de la población aumenta con el tiempo. A este proceso de cambio sistemático se le conoce como selección natural. Las características de este proceso estarán dictaminadas por varios factores, tales como el fitness relativo de cada genotipo, el efecto de heterocigotas y, naturalmente, la fuerza del régimen selectivo. En las poblaciones naturales existirá una interacción entre distintas fuerzas que generan cambios en las frecuencias alélicas (deriva genética, selección natural, mutación). El planteo de modelos matemáticos explícitos basados en asunciones claras, como el modelo para locus autosómico con dos alelos planteado en este capítulo o la aproximación por difusión, permite realizar estimaciones que tengan en cuenta estos procesos en simultáneo. Por último es importante remarcar que la selección natural puede operar a distintos niveles en los sistemas biológicos, acorde a la complejidad de los mismos.

4.10 Actividades

4.10.1 Control de lectura

1. Describa los diferentes modos de acción génica y los regímenes selectivos asociados a cada caso. Discuta qué dinámica se espera para las frecuencias alélicas de una población en cada caso.
2. Considere dos poblaciones que se enfrentan a un mismo régimen selectivo. Ambas se encuentran en igualdad de condiciones, salvo por el hecho de que una posee menor varianza genética que la otra. ¿Cómo afectará esto al cambio en el fitness de la población?
3. Describa cómo afecta la magnitud del coeficiente de selección \(s\) a las dinámicas de las frecuencias alélicas para los regímenes de selección direccional, estabilizadora y disruptiva.
4. Por efecto de la mutación un alelo perjudicial puede reaparecer recurrentemente en una población, disminuyendo el fitness medio de la misma en el equilibrio selección-mutación. Esta disminución, ¿depende de la magnitud de la selección contra el alelo?
5. Las poblaciones naturales tienen tamaño finito, y es de esperar que tanto la selección natural como la deriva génetica influyan en los cambios de las frecuencias alélicas. ¿Cómo nos podemos

4.10.2 ¿Verdadero o falso?

1. Bajo modo de acción génica de dominancia incompleta se espera un régimen de selección direccional, esperándose a largo plazo la fijación de uno de los alelos de la población.
2. El parámetro \(h\) (efecto del heterocigota) es un parámetro fijo, característico de cada locus.
3. Bajo equilibrio de selección-mutación y modo de acción génica de dominancia completa, la carga mutacional \(L\) depende únicamente del coeficiente de mutación \(u\) y del efecto heterocigota \(h\).
4. La frecuencia de equilibrio esperada para regímenes de selección estabilizadora y disruptiva es la misma, y equivale a \(\hat{p} = \frac{h-1}{2h-1}\).
5. En una población de tamaño finito el efecto de la deriva genética siempre prevalecerá por sobre el de la selección natural.

Solución

1. Verdadero. Bajo el modo de acción génica de dominancia incompleta, los alelos heterocigotos tienen un fenotipo intermedio entre los alelos homocigotos dominantes y recesivos. En este caso, se espera un régimen de selección direccional en el que uno de los alelos tiende a aumentar su frecuencia en la población a largo plazo, hasta eventualmente fijarse.

2. Falso. El parámetro \(h\) (efecto del heterocigoto) sí sera característico para cada combinación de alelos en un locus, pero representará el valor adaptativo de los individuos heterocigotas en una condición dada. Por lo tanto, el parámetro no es estrictamente fijo.

3. Falso. En la situaciónplanteada la carga mutacional \(L\) depende únicamente del coeficiente de mutación \(u\) (tasa de mutación), representando la reducción en la aptitud de la población debido a la acumulación de mutaciones perjudiciales.

4. Verdadero. Para selección estabilizadora, la frecuencia de equilibrio es \(\hat{p} = \frac{h-1}{2h-1}\), lo cual es independiente del ambiente.

5. Falso. El efecto relativo de la deriva genética y la selección natural depende del tamaño de la población. En poblaciones pequeñas, la deriva genética puede tener un efecto significativo sobre el cambio de las frecuencias alélicas, incluso en presencia de selección natural. A medida que el tamaño poblacional considerado aumenta, es de esperar que los efectos de la selección se impongan por sobre el efecto de la deriva genética.

Ejercicios

Ejercicio 4.1

En D. melanogaster la hormona juvenil es un regulador clave de procesos como la metamorfosis y la reproducción. La enzima 3-hidroxi-3-metilglutaril-CoA sintasa (HMG-S) es parte de la vía que regula la síntesis de esta hormona. Una población de D. melanogaster se encuentra segregando dos alelos codificantes para la enzima: el alelo \(A_1\) codifica para una enzima plenamente funcional, mientras que el alelo \(A_2\) codifica para una enzima menos eficiente. Los individuos homocigotas \(A_2A_2\) ven afectado su desarrollo, dejando en promedio la mitad de descendencia que los individuos que poseen una copia \(A_1\).

a. Modele la situación planteada, estableciendo el fitness relativos \(w_{11}\), \(w_{12}\) y \(w_{22}\) de los genotipos, así como el coeficiente de selección \(s\) y el coeficiente de efecto heterocigota \(h\).

b. En un momento dado se genotipan individuos de la población, estableciéndose las siguientes frecuencias genotípicas

\[ \begin{cases} f(A_1A_1) = 0,40 \\ f(A_1A_2) = 0,35 \\ f(A_2A_2) = 0,25 \end{cases} \]

Establezca las frecuencias genotípicas esperadas en la siguiente generación.

Solución

a. De la letra se deduce que el fenotipo \(A_1A_1\) y el fenotipo \(A_1A_2\) tienen igual fitness, lo cual implica que el alelo \(A_1\) es dominante; por lo tanto, el efecto heterocigota \(h = 0\). Ambos genotipos son los que presentan mayor ventaja selectiva, y por lo tanto tenemos fitness relativos \(w_{11} = w_{12} = 1\). Por último, el hecho de que los organismos \(A_2A_2\) dejen en promedio la mitad de descendencia implica que el fitness relativo \(w_{22} = \frac{1}{2} w_{11} \Rightarrow w_{22} = 0,5\), lo cual implica un coeficiente de selección \(s = 0,5\).

b. Luego del proceso selectivo se esperan las siguientes frecuencias genotípicas:

\[ \begin{cases} f'(A_1A_1) = f(A_1A_1) \cdot \frac{w_{11}}{\bar{w}} \\ f'(A_1A_2) = f(A_1A_2) \cdot \frac{w_{12}}{\bar{w}} \\ f'(A_2A_2) = f(A_2A_2) \cdot \frac{w_{22}}{\bar{w}} \end{cases} \]donde el fitness medio de la población \(\bar{w}\) está dado por

\[ \bar{w} = f(A_1)^2 w_{11} + 2f(A_1)f(A_2)w_{12} + f(A_2)^2 w_{22} \]

\[ \bar{w} = 0,4 + 0,35 + 0,25 \cdot 0,5 \]

Tenemos entonces en la siguiente generación

\[ \begin{cases} f'(A_1A_1) = 0,4 \cdot \frac{1}{0,4 + 0,35 + 0,25 \cdot 0,5} \approx 0,457 \\ f'(A_1A_2) = 0,35 \cdot \frac{1}{0,4 + 0,35 + 0,25 \cdot 0,5} \approx 0,400 \\ f'(A_2A_2) = 0,25 \cdot \frac{0,5}{0,4 + 0,35 + 0,25 \cdot 0,5} \approx 0,143 \end{cases} \]

El lector puede corroborar que dichas frecuencias suman 1.

Coherente con lo esperado, se observa un aumento de las frecuencias de los genotipos portadores de \(A_1\) y una disminución de la frecuencia de homocigotas \(A_2A_2\).

Ejercicio 4.2

El hongo Fusarium oxysporum es un patógeno del tomate (Solanum lycopersicum). Se ha postulado que variantes alélicas del locus XSP10 (a partir de ahora, locus \(X\) para simplificar) se encuentran asociadas a la susceptibilidad al patógeno. Considere una población que segrega dos alelos, \(X_A\) (no susceptible a F. oxysporum) y \(X_B\) (susceptible), donde los fitness relativos de los genotipos \(X_AX_A\), \(X_AX_B\) y \(X_BX_B\) son \(w_{AA} = 1;\ w_{AB} = 0,44;\ w_{BB} = 0,3\). En la población se encuentra presente el patógeno antes mencionado.

a. Si la tasa de mutación \(X_A \rightarrow X_B\) es \(u = 10^{-8}\) y la tasa de mutación \(X_B \rightarrow X_A\) es despreciable, ¿qué espera que suceda con las frecuencias alélicas \(f(X_A)\) y \(f(X_B)\)?

b. En un momento dado se comienza a emplear tiabendazol para disminuir la presencia del hongo en la población. Bajo esta nueva situación los fitness relativos de los genotipos son \(w_{AA} = 1;\ w_{AB} = 0.8;\ w_{BB} = 0,7\). ¿Qué espera que ocurra con las frecuencias alélicas bajo este nuevo régimen selectivo?

Solución

a. Los fitness relativos presentados corresponden a un modo de acción génica de dominancia incompleta. Esto implica un régimen de selección direccional, esperándose a largo plazo un aumento progresivo de la frecuencia del alelo \(X_A\). No obstante, dado que la tasa de mutación \(X_A \rightarrow X_B\) no es despreciable, se espera un aumento de esta frecuencia alélica hasta alcanzarse un equilibrio entre selección y mutación. La frecuencia de equilibrio para el alelo \(X_B\) se aproxima en el equilibrio a

\[ f(\hat{X_B}) \approx \frac{u}{hs} \]

Dado que \(w_{AB} = 0,44 = 1 - hs \Rightarrow hs = 1-0,44 = 0,56\), por lo que

\[ f(\hat{X_B}) \approx \frac{10^{-8}}{0,56} \]

punto en el cual se establece un equilibrio entre mutación y selección bajo el régimen selectivo. La frecuencia del alelo \(f(X_A)\) en este punto de equilibrio será por lo tanto de \(f(X_A) \approx 1 - (\frac{10^{-8}}{0,56})\).

b. El nuevo régimen selectivo continúa siendo de selección direccional, ya que el modo de acción génica es también en este caso la dominancia incompleta. No obstante, observemos que la disminución en la presencia de F. oxysporum relaja la presión selectiva sobre los organismos heterocigotas \(X_AX_B\) y \(X_BX_B\) (notemos que su fitness relativo aumentó). Es de esperar por lo tanto que la frecuencia de equilibrio (que llamaremos \(f'(\hat{X_B})\)). Notemos que en el nuevo régimen selectivo \(w_{BB} = 1 - hs = 0,8 \rightarrow hs = 1- 0,8 = 0,2\), por lo que la frecuencia de equilibrio para el alelo \(X_B\) es ahora

\[ f'(\hat{X_B}) \approx \frac{10^{-8}}{0,2} \]

Notemos que si bien esta frecuencia de equilibrio es baja, es

\[ \frac{f'(\hat{X_B})}{f(\hat{X_B})} = \frac{(10^{-8}/0,2)}{(10^{-8}/0,56)} = \frac{0,56}{0,2} = 2,8 \]

casi tres veces mayor que en el primer escenario planteado.

Ejercicio 4.3

Una población de tamaño \(N_e = 200\) se encuentra segregando un locus bi-alélico (alelos \(A_1\) y \(A_2\)). En promedio cada individuo deja aproximadamente un descendiente. En un momento dado las frecuencias genotípicas son

\[ \begin{cases} f(A_1A_1) = 0,2 \\ f(A_1A_2) = 0,3 \\ f(A_2A_2) = 0,5 \end{cases} \]

a. ¿Cuál es la probabilidad de fijación de cada alelo?

b. Considere ahora que en el momento planteado las condiciones ambientales cambian, alterando el régimen selectivo. En esta nueva situación los fitness relativos de cada genotipo son

\[ \begin{cases} w_{11} = 1 \\ w_{12} = 0,995 \\ w_{22} = 0,99 \end{cases} \]

Estime la probabilidad de fijación para cada alelo bajo el nuevo régimen selectivo.

Solución

a. El escenario planteado corresponde con un escenario selectivamente neutro (no existen diferencias en el fitness de los individuos) y con tamaño poblacional constante. En estas condiciones se asume que la única fuerza evolutiva es la deriva genética. Bajo el modelo de Wright-Fisher se puede plantear que la probabilidad de fijación de un alelo está dada por su frecuencia en el momento considerado.

Tenemos entonces para el alelo \(A_1\) una frecuencia alélica de \(f(A_1) = f(A_1A_1) + \frac{1}{2} \cdot f(A_1A_2) = 0,2 + 0,5 \cdot 0,3 = 0,35\). Dado que \(f(A_1) + f(A_2) = 1\), \(f(A_2) = 1 - 0,35 = 0,65\). Ambas frecuencias son equivalentes a la probabilidad de fijación de cada alelo.

b. El nuevo régimen selectivo plantea un modo de acción génica de dominancia incompleta, con ventaja selectiva (aparentemente pequeña) para los organismos portadores del alelo \(A_1\). Por lo tanto, la deriva génica no será la única fuerza evolutiva actuando, existiendo también una influencia de la selección natural. Notemos que

\[ w_{22} = 1 -s = 0,99 \Rightarrow s = 1-0,99 = 0,01 \]

A su vez

\[ w_12 = 1 - hs = 0,995 \Rightarrow hs = 1 - 0,995 = 0,005 \]

\[ h \cdot 0,01 = 0,005 \]

\[ h = \frac{0,005}{0,01} = 0,5 \]

El modelo de acción génica es por lo tanto completamente aditivo. Bajo este escenario la solución de las ecuaciones de la aproximación por difusión nos plantea que la probabilidad de fijación del alelo \(A_1\), con frecuencia \(A_1\), está dada por

\[ \pi_{A_1}(f(A_1)) = \frac{1 - e^{-2N_esf(A_1)}}{1-e^{-2N_e s}} \]

donde tenemos \(f(A_1) = 0,35\), \(N_e = 200\), y \(s = 0,01\), por lo que

\[ \pi_{A_1}(0,35) = \frac{1 - e^{-2 \cdot 200 \cdot 0,01 \cdot 0,35}}{1- e^{-2 \cdot 200 \cdot 0,01}} \]

\[ \pi_{A_1}(0.35) \approx 0,767 \]

de lo que se deduce que la probabilidad de fijación del alelo \(A_2\) será \(1 - (\frac{1 - e^{-2 \cdot 200 \cdot 0,01 \cdot 0,35}}{1- e^{-2 \cdot 200 \cdot 0,01}}) \approx 0,233\).

Es decir, el modelo planteado sugiere que aún una aparentemente pequeña ventaja selectiva para los organismos portadores del alelo \(A_1\) es suficiente para hacer que se revierta la situación planteada cuando se considera sólo el efecto de la deriva genética, siendo más probable que se fije este alelo que el alelo \(A_2\).

Ejercicio 4.4

Todas las personas saben que en las remotas Hébridas exteriores surgió un alelo de pigmentación que hace que la lana de las ovejas Scottish Blackface se vuelva verde bajo la luz crepuscular. Lo que pocas personas saben es otro alelo surgió, que confiere una tonalidad amarillenta. La probabilidad de dejar descendencia no es igual para todos los individuos, debido a la presencia de zorros que detectan y cazan diferencialmente los diferentes tipos de pigmentación. El fitness relativo de las ovejas según la presencia de alelos \(F_V\) y \(F_A\) (causantes de pigmentación verde y amarilla, respectivamente) es

\[ \begin{cases} w_{VV} = 1 \\ w_{VA} = 0,87 \\ w_{AA} = 0,9 \end{cases} \]

Discuta qué sucederá con las frecuencias alélicas de la población según se consideren diferentes frecuencias alélicas \(f(F_V)\) y \(f(F_A)\) de partida.

Solución Notemos que las ovejas heterocigotas \(F_VF_A\) parecen irradiar la luz que más fácilmente detectan los zorros, teniendo el menor fitness relativo. Esto implica que la subdominancia es el modo de acción génica, esperándose un régimen de selección disruptiva. Bajo este régimen existe un equilibrio inestable dependiente del efecto heterocigota \(h\), dado por

\[ f(\hat{F_V}) = \frac{h-1}{2h-1} \]

Tenemos

\[ w_{AA} = 1 - s = 0,9 \Rightarrow s = 1- 0,9 = 0,1 \]

y

\[ w_{VA} = 1 -hs = 0,87 \Rightarrow h\cdot 0,1 = 0,13 \]

\[ h = \frac{0,13}{0,1} = 1,3 \]

Esto es coherente con el modo de acción génica planteado (donde \(h > 1\)).

La frecuencia de equilibrio se encuentra por lo tanto en

\[ f(\hat{F_V}) = \frac{1,3 -1}{2 \cdot 1,3 -1} = \frac{0,3}{1,6} \]

\[ f(\hat{F_V}) = 0,1875 \Rightarrow f(F_A) = 1 - 0,1875 = 0,8125 \]

El valor de \(\Delta_s F_V\) dependerá de este punto de equilibrio: si en la población se parte de \(f(F_V) > 0,1875 \Rightarrow \Delta_s F_V > 0\), y por lo tanto la frecuencia de este alelo tenderá a aumentar hasta fijarse eventualmente por efecto combinado de la selección natural y la deriva genética. Si en cambio se parte de una frecuencia \(f(F_V) < 0,1875 \Rightarrow \Delta_s F_V < 0\), por lo que la frecuencia alélica tenderá a disminuir hasta perderse el alelo (fijándose el alelo \(F_A\)). Si la población considerada parte de \(f(F_V) = 0,1875 \Rightarrow \Delta_s F_V = 0\), y las frecuencias alélicas se mantendrán inalteradas.

Ejercicio 4.5

Una población se encuentra segregando los alelos \(A_1\) y \(A_2\) de un locus bi-alélico. El fitness relativo de los organismos homocigotas \(A_1A_1\), \(A_1A_2\) y \(A_2A_2\) está dado por

\[ \begin{cases} w_{11} = 1 \\ w_{12} = 1,5 \\ w_{22} = 0,6 \end{cases} \]

En un momento dado se miden las frecuencias alélicas en la población, estimándose \(f(A_1) = 0,73\) y \(f(A_2) = 0,27\).

a. ¿Qué modo de acción génica sugiere el modelo planteado para este locus? Teniendo esto en cuenta, ¿qué espera que suceda con las frecuencias de los alelos \(A_1\) y \(A_2\)?.

b. Un tiempo considerable pasa y las condiciones ambientales se modifican, cambiando así el régimen selectivo. Bajo el nuevo régimen selectivo el fitness relativo de cada genotipo es

\[ \begin{cases} w_{11} = 0,55 \\ w_{12} = 0,6 \\ w_{22} = 1 \end{cases} \]

¿Qué tipo de régimen selectivo está planteado en esta nueva situación? ¿Qué espera que suceda ahora con las frecuencias alélicas \(f(A_1)\) y \(f(A_2)\)?

c. Considere la misma situación planteada en b., pero considerando un coeficiente de selección \(s = 0,3\). ¿Cómo afecta esto a la situación planteada?

Solución

a. Los organismos con mayor fitness relativo son los heterocigotas \(A_1A_2\), lo cual se espera cuando la sobredominancia es el modo de acción génica. El régimen selectivo es de selección estabilizadora, y espera entonces que se alcance una frecuencia de equilibrio \(0 < \hat{f(A_1)} < 1\) (ídem para \(f(A_2)\)). Esta frecuencia de equilibrio es dependiente del efecto de heterocigotas \(h\), siendo \[ \hat{f(A_1)} = \frac{h-1}{2h-1} \]

por lo que es necesario determinar \(h\) para estimarla y predecir qué sucederá con las frecuencias alélicas \(f(A_1)\) y \(f(A_2)\).

Recordemos que \(w_{22} = 1-s\) y que \(w_{12} = 1-hs\). Tenemos entonces

\(w_{22} = 0,6 = 1 - s \Rightarrow s = 1 - 0,6 = 0,4\), por lo que

\[ w_{12} = 1,5 = 1 - 0,4 \cdot h \]

\[ 0,4 \cdot h = 1 - 1,5 = -0,5 \]

\[ h = -\frac{0,5}{0,4} \]

Esta estimación es coherente con un modo de acción de sobredominancia (donde \(h < 0\)). La frecuencia de equilibrio es entonces

\[ \hat{f(A_1)} = \frac{ (-0,5/0,4) -1}{2 \cdot (-0,5/0,4) -1} \]

\[ \hat{f(A_1)} \approx 0,643 \]

Por lo tanto, en el largo plazo se espera que la frecuencia alélica \(f(A_1)\) disminuya progresivamente, hasta alcanzarse el punto de equilibrio.

b. Notemos que bajo el nuevo régimen selectivo los individuos hetercogitas tienen valores de fitness intermedios. Esto corresponde a un modo de acción génica de dominancia incompleta, configurándose un régimen de selección direccional. Siendo el genotipo de mayor fitness el homocigota \(A_2A_2\), es de esperar un aumento progresivo de la frecuencia del alelo \(A_2\) hasta alcanzarse su eventual fijación (si consideramos los efectos de la deriva genética aún en poblaciones de tamaño considerable).

c. La fuerza de la selección natural jugará un papel en el tiempo necesario para alcanzarse la fijación del alelo \(A_2\). A igual efecto de heterocigotas \(h\), coeficientes de selección \(s\) menores resultarán en un mayor tiempo esperado para la fijacion del alelo (lo contrario ocurre para coeficientes mayores). En la situación planteada en b. tenemos \(w_{11} =0,55 = 1 -s \Rightarrow s = 1- 0,55 = 0,45\), por lo que si el coeficiente de selección fuera \(s = 0.3\) se esperaría la misma dinámica, requiriéndose un mayor tiempo generacional para la fijación del alelo \(A_2\).

---

Bibliografía

Abzhanov, A., W. P. Kuo, C. Hartmann, B. R. Grant, P. R. Grant, and C. J. Tabin. 2006. “The calmodulin pathway and evolution of elongated beak morphology in Darwin’s finches.” Nature 442 (7102): 563–67.

Abzhanov, A., M. Protas, B. R. Grant, P. R. Grant, and C. J. Tabin. 2004. “Bmp4 and morphological variation of beaks in Darwin’s finches.” Science 305 (5689): 1462–65.

Drake, J. W., B. Charlesworth, D. Charlesworth, and J. F. Crow. 1998. “Rates of spontaneous mutation.” Genetics 148 (4): 1667–86.

Edwards, A. W. 1994. “The fundamental theorem of natural selection.” Biol Rev Camb Philos Soc 69 (4): 443–74.

Fisher, Ronald Aylmer. 1930. The Genetical Theory of Natural Selection. OXFORD UNIV PRESS.

Gillespie, John H. 2004. Population Genetics. A Concise Guide. The Johns Hopkins University Press.

Hamilton, Matthew B. 2009. Population Genetics. Wiley-Blackwell.

Hartl, Daniel L, and Andrew G Clark. 2007. Principles of Population Genetics. 4th. ed. Sinauer.

Kellenberger, Roman T., Kelsey J. R. P. Byers, Rita M. De Brito Francisco, Yannick M. Staedler, Amy M. LaFountain, Jürg Schönenberger, Florian P. Schiestl, and Philipp M. Schlüter. 2019. “Emergence of a Floral Colour Polymorphism by Pollinator-Mediated Overdominance.” Nature Communications 10 (1). https://doi.org/10.1038/s41467-018-07936-x.

Thurman, T. J., and R. D. Barrett. 2016. “The genetic consequences of selection in natural populations.” Mol Ecol 25 (7): 1429–48.

———. 1937. “The Distribution of Gene Frequencies in Populations.” Proc Natl Acad Sci U S A 23 (6): 307–20.

---

46. Thomas Robert Malthus (13 de febrero de 1766 - 29 de diciembre de 1834) fue un clérigo y erudito británico cuyo ensayo “An Essay on the Principle of Population” fue fundamental para el desarrollo de la demografía. En lo que hace a nuestro curso su aporte fundamental es el modelo que plantea un crecimiento geométrico de las poblaciones, aproximado por un crecimiento exponencial.↩︎

47. Recuerda que el promedio de una variable es la suma de los valores, \(w_{11},w_{12},w_{22}\) multiplicados por sus frecuencias relativas respectivas, \(p^2\), \(2pq\) y \(q^2\) en nuestro caso.↩︎

48. Recuerda que si hacíamos la derivada y la igualábamos a cero, teníamos los máximos/mínimos de la función. En este caso, \(\frac{d(p-p^2)}{dp}=1-2p=0 \therefore p=\frac{1}{2}\)).↩︎

49. Recuerda que \(w_{11}\), \(w_{12}\) y \(w_{22}\) están todos divididos entre \(\bar{w}\), lo que los hace “relativos”)↩︎

50. Sickle, en inglés. De ahí el uso de la letra S para denotar al alelo.↩︎

51. Que podría traducirse como “Por lo tanto, ni es un teorema ni es fundamental”.↩︎

52. En realidad esto no es un requerimiento en la formulación del teorema, pero sí para nuestro tratamiento simplificado.↩︎

53. John Burdon Sanderson Haldane FRS (5 de noviembre de 1892 - 1 de diciembre de 1964), fue un científico británico conocido por sus trabajos en fisiología, genética, biología evolutiva y matemáticas. Junto con Ronald Fisher y Sewall Wright fue uno de los fundadores del neo-darwinismo, síntesis de la teoría evolutiva. Haldane profesaba abiertamente sus convicciones socialistas, marxistas y humanistas, siendo un ateo confeso, lo que lo llevó a emigrar a la India en 1956. Entre sus contribuciones notables se encuentran las relacionadas al ligamiento genético, cinética enzimática, el origen de la vida y numerosas contribuciones en genética de poblaciones, entre ellas la propuesta del mecanismo poblacional relacionado al equilibrio alélico en la anemia de células falciformes.↩︎

54. Hermann Joseph Muller (21 de diciembre de 1890 - 5 de abril de 1967) fue un genetista y educador estadounidense, más conocido por sus trabajos sobre los efectos fisiológicos y genéticos de la radiación (mutagénesis). Fue galardonado con el Premio Nobel de Medicina y Fisiología en 1946 por sus descubrimientos acerca del efecto de mutagénesis inducidos por los rayos-X. Durante su vida trabajó inicialmente en EEUU, se mudó a Alemania en 1932 para realizar una estadía de sabático pero este fue interrumpido por ascensión del régimen nazi. Se mudó a la Unión Soviética donde fundó un laboratorio muy productivo en el estudio de la “mosca de la fruta” Drosophila melanogaster pero la hegemonía de la visión de Lysenko en la genética y las persecusiones del Stalinismo lo llevaron a volver a EEUU (con un breve pasaje por Edimburgo) donde culminó su carrera en la Universidad de Indiana.↩︎

55. Esta denominación viene del inglés, ya que el término “carga mutacional” corresponde a “mutational load” en dicho idioma.↩︎