Capítulo 9 Parentesco y semejanza entre parientes

En nuestro modelo genético básico identificamos factores genéticos y ambientales (así como sus interacciones) que son, de acuerdo al modelo, los causantes de la variación fenotípica que observamos. Desafortunadamente, en una gran parte de los casos estamos limitados a observar solamente el fenotipo de los individuos y pese a esto debemos poder estimar los diferentes componentes de la varianza del modelo, tanto para su utilización directa como para calibrar las relaciones entre las distintas fuentes de variación. Afortunadamente, la genética de la mayor parte de las especies de interés económico posee unas reglas de transmisión de la información que son bastante sencillas (al menos a grandes rasgos), lo cual nos ha ido permitiendo construir modelos para representar la expresión de las características en los fenotipos. Son, por lo tanto, estas mismas reglas las que gobiernan las similitudes que observamos entre los organismos que comparten una parte de su información genética, algo que todos reconocemos como parentesco.

En el presente capítulo se discutirá el concepto de parentesco en términos generales, antes de presentar el concepto de parentesco aditivo, estrechamente relacionado a conceptos que vimos previamente en el capítulo [Apareamiento no-aleatorios]. Veremos cómo el parentesco aditivo se relaciona con nuestro modelo genético básico, así como diferentes formas de calcularlo y de representar las relaciones entre individuos. Discutiremos al mismo tiempo el concepto de consanguinidad y su relación con el parentesco aditivo. Más adelante pasaremos a discutir otro concepto relacionado con nuestro modelo genético básico que es el de parentesco de dominancia y veremos en qué relaciones de parentesco el mismo es distinto de cero.

Durante la construcción del modelo genético básico en el capítulo anterior vimos que la descomposición de la varianza fenotípica en sus distintas fuentes (tanto genéticas como ambientales, y su relativa importancia) se constituían en un elemento clave para entender las posibilidades de trabajar sobre la genética de una característica. Sin embargo, dado que la única varianza observable es la fenotípica, hasta ahora no hemos visto ni soslayado ninguna manera razonable de estimar los distintos componentes. El elemento clave para poder estimar los distintos componentes genéticos de la varianza es la semejanza que existe entre parientes, semejanza que se debe a la genética y las condiciones que comparten. Por lo tanto, se desarrollará un modelo causal para estas semejanzas, para luego vincularlo con el modelo observacional y de esta forma alcanzar nuestro objetivo de estimar los componentes de varianza. Finalmente, discutiremos las diferencias entre los conceptos de parentesco estadístico (todos los que veremos hasta el final) y parentesco genómico, el derivado de conocer la información genómica de los individuos.

OBJETIVOS DEL CAPÍTULO

\(\square\) Discutir el concepto de parentesco en términos generales.

\(\square\) Ver cómo el parentesco aditivo se relaciona con nuestro modelo genético básico.

\(\square\) Analizar formas de calcular el parentesco aditivo y de representar las relaciones entre individuos.

\(\square\) Discutir el concepto de consanguinidad y su relación con el parentesco aditivo.

\(\square\) Presentar el concepto de parentesco de dominancia y analizar en qué relaciones de parentesco se observa el mismo.

9.1 Parentesco

Todos tenemos una idea bastante desarrollada de lo que significa el término parentesco, en especial cuando nos referimos a nuestra especie. En este caso, de acuerdo a la acepción más común, se trata de un vínculo, tanto por “sangre” como por relaciones de afinidad estable entre personas. Esto pone sobre el tapete, al menos en lo que refiere al término parentesco, una distinción clara entre las construcciones sociales y lo que vamos a desarrollar como concepto genético de parentesco. Por ejemplo, a nadie se le ocurriría pensar que nuestro cónyuge no es nuestro pariente, aunque desde el punto de vista genético posiblemente tengamos lo mismo o menos en común que con cualquier miembro al azar de la población. En todo caso, pese a la distinción, lo que queda claro es que cuando hablamos de parentesco nos referimos a alguna clase de similitud o afinidad especial entre miembros de un grupo, mayor que con el resto de la población no-emparentada.

En nuestro caso, estamos interesados exclusivamente en el parentesco genético entre los individuos, ya que el mismo será un indicador de la constitución genética compartida entre los mismos. Esto, a su vez, nos permitirá determinar el “mérito” genético de los animales, predecir el mismo para sus parientes, así como estimar los parámetros genéticos más relevantes para determinar la base genética de una característica y las estrategias para mejorarla. Como vimos previamente, en nuestro modelo genético básico los componentes genéticos son varios (aditivos, de dominancia, epistáticos) y por lo tanto el parentesco debería reflejar estos distintos aportes a la base genética común entre dos individuos. Como veremos más adelante, la partición en componentes aditivos, de dominancia y epistáticos para la parte genética del fenotipo nos llevará a la necesidad de definir coeficientes de parentesco específicos a cada componente. Es decir, entre dos individuos tendremos un valor para el parentesco aditivo, otro valor para el parentesco de dominancia y otro para el parentesco epistático.

La pregunta que nos podemos hacer entonces es qué consideramos como parentesco y qué característica tiene que tener el o los índices que lo representen. Claramente, cuando entre dos individuos no exista parentesco de ningún tipo sería ideal que los coeficientes de parentesco fuesen iguales a cero. Por otra parte, desde un punto de vista intuitivo, resulta natural esperar que el parentesco de un inviduo consigo mismo sea igual al \(100\%\), es decir igual a \(1\). Dicho de otra forma, cuando un individuo comparte con otro (o con él mismo) todo su genoma, entonces esperaríamos que comparta el \(100\%\) de su base genética. Por ejemplo, en el caso de los gemelos monocigóticos, despreciando el impacto de la epigenética (algo cada vez más discutible), los mismos comparten exactamente el mismo genoma y por lo tanto esperaríamos que nuestros índices o coeficientes de parentesco lo reflejaran indicándolo con un valor de \(1\).

Finalmente, hay un punto muy relevante a destacar antes de comenzar nuestra jornada con el tema de parentesco genético. Históricamente, desde el comienzo de la genética hasta hace relativamente poco tiempo, el genoma de los individuos era completamente desconocido e imposible de conocer. No es hasta mediados del siglo XX que se logra dilucidar la estructura del ADN y conocer el sistema de codificación de la información (código genético). Recién hacia el último cuarto del siglo pasado se logra entender la organización de los genes en procariotas y eucariotas, así como desarrollar los primeros métodos de secuenciación genética, notablemente reducido a unas pocas centenas de bases nucleotídicas. Sin embargo, desde el comienzo de la genética de poblaciones y cuantitativa quedaron en claro las bases de la transmisión de la información genética de progenitores a descendientes. En este capítulo nos referiremos, excepto mención específica, a individuos diploides en especies sexuales. Es decir, en estas especies un padre transmite la mitad de su información genética a sus hijos y partir de esto podemos derivar las expectativas de compartir una fracción de su genoma que tenemos para cada par de individuos para los que conocemos su relación. Esto es, estamos refiriéndonos a una definición de parentesco que es estadística (o probabilística) en su base.

Por ejemplo, como veremos más adelante, el parentesco aditivo entre hermanos enteros (lo que normalmente llamamos hermanos en poblaciones humanas) es igual a \(\frac{1}{2}\). Sin embargo, todos sabemos que dentro de cada grupo de hermanos existen algunos más parecidos entre sí que con el resto. Si bien el “parecido” es apenas una característica exterior que no podemos asociar directamente al genoma, es una clara indicación de que no necesariamente todos los hermanos comparten exactamente la misma fracción del genoma. De hecho, aunque totalmente improbable, teóricamente dos hermanos enteros podrían no compartir ningún alelo IBD de su genoma, y también con la misma implausibilidad podrían compartir todos, aún no siendo gemelos monocigóticos. Al tratarse el parentesco estadístico de una variable aleatoria, esto introduce una fuente de variabilidad en las estimaciones posteriores. Afortunadamente, desde fines del siglo XX es posible genotipar un gran número de loci en cada individuo, o aún secuenciar el genoma completo de ambos, por lo que la comparación de similaridad genética puede ser derivada directamente. Dicho de otra forma, el parentesco aditivo entre dos hermanos en particular no tendrá la necesidad de ser igual a \(\frac{1}{2}\) y ahora será sustituido por la fracción realmente compartida del genoma, tema que veremos al final de este capítulo.

9.2 Parentesco aditivo

En el capítulo anterior discutimos que en nuestro modelo genético podíamos descomponer el aporte de la genética en distintos componentes (\(G=A+D+I\)), uno de los cuales era el que correspondía a los efectos aditivos, es decir, aquellos que podemos describir sumando los aportes de cada uno de los alelos presentes. Por lo tanto, desde el punto de vista intuitivo, una medida de similaridad entre individuos que refleje este aspecto sería la proporción de alelos idénticos por ascendencia (IBD) compartidos por los individuos. En la Figura 9.1 podemos ver representadas un par de situaciones que reflejan distintos grados de parentesco entre individuos, así como las posibles configuraciones de los alelos heredados. A la izquierda tenemos la relación que existe entre un progenitor A y su descendencia, representada por el individuo C. El individuo A posee dos alelos, que llamaremos en forma arbitraria \(A_1\) y \(A_2\), por ahora independientemente de si son distintos, idénticos en estado o idénticos por ascendencia. Claramente, el descendiente de A (B) debe recibir de este uno de sus dos alelos, sí o sí. De hecho, como veremos más adelante, la relación entre progenitor y descendiente es la única en la que la proporción de alelos compartidos está totalmente determinada (es decir, no es aleatoria). Dicho de otra forma, para cada posición del genoma o loci, un hijo recibirá la mitad de la información de su padre y la mitad de su madre, por lo que compartirá con ellos \(\frac{1}{2}\) de los alelos.

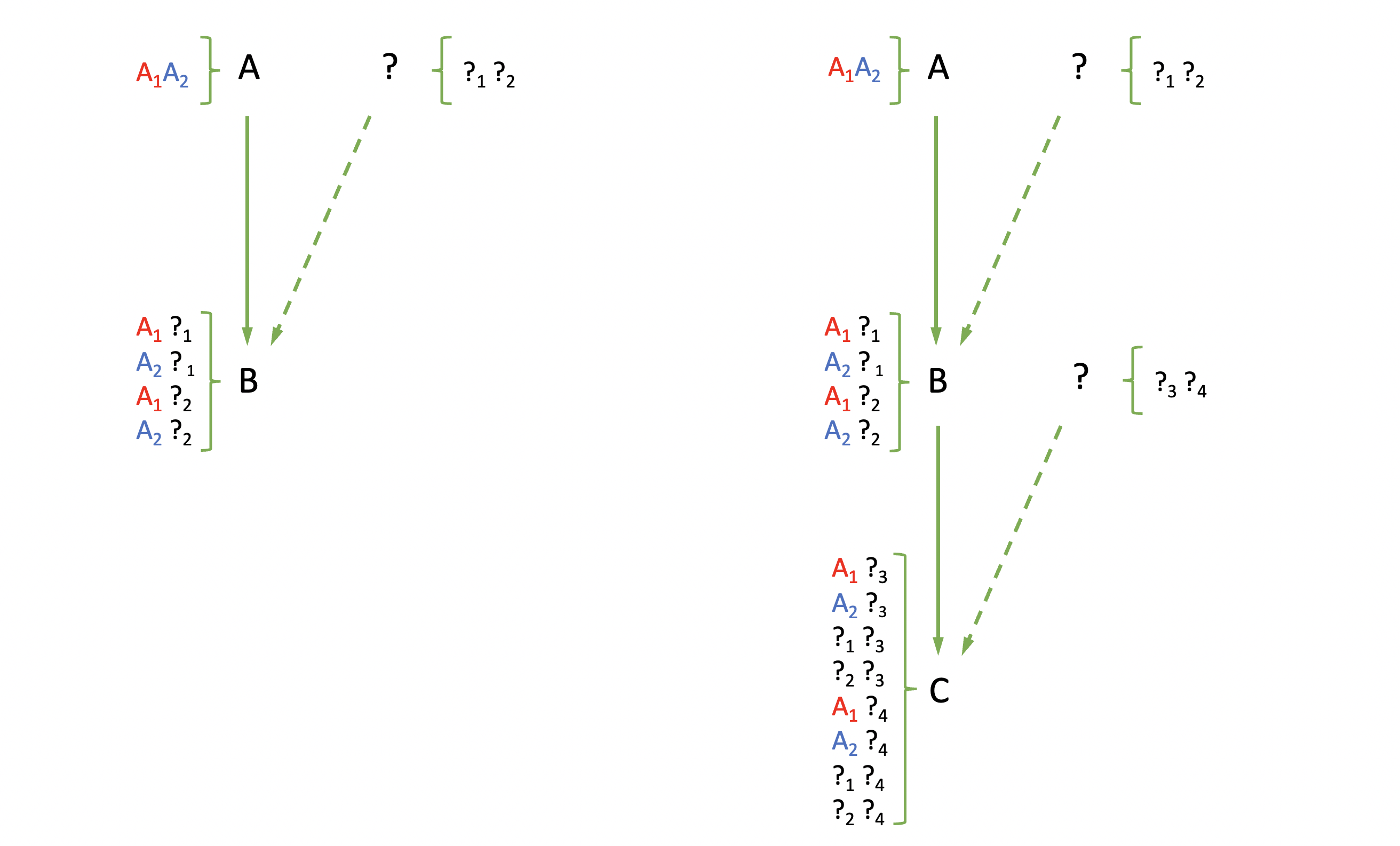
Figura 9.1: Representación de la relación entre alelos en el caso de parentesco aditivo directo. A la izquierda la relación entre padre e hijo, mientras que a la derecha agregamos una nueva generación, lo que nos permite ver la relación entre un individuo (A) y su nieto (C).

Esto lo podemos ver más explícitamente en el diagrama de la figura. El progenitor A, que para un locus determinado tiene los dos alelos \(A_1\) y \(A_2\) se aparea con un progenitor desconocido o irrelevante para nosotros y que por lo tanto marcamos con ? y a sus alelos como \(?_1\) y \(?_2\). Al existir dos posibles gametos producidos por el progenitor de nuestro interés (\(A_1\) y \(A_2\)) y dos gametos por el otro progenitor (\(?_1\) y \(?_2\)), tenemos entonces 4 posibles genotipos que surgen de combinarlos: \(A_1?_1\), \(A_2?_1\), \(A_1?_2\) y \(A_2?_2\). Veamos ahora cuál sería la proporción promedio de alelos compartidos entre un progenitor y su progenie. El progenitor será siempre \(A_1A_2\), pero la descendencia podrá ser de cualquiera de los 4 tipos mencionado previamente. Si ponemos esta información en un cuadro podemos entender mejor por qué en cualquiera de los 4 posibles genotipos del descendiente la proporción de alelos IBD es \(\frac{1}{2}\) y por lo tanto su promedio es también \(\frac{1}{2}\).

	\(\text{Alelos compartidos con progenitor } (A_1A_2)\)	\(\text{Proporción}\)
\(A_1?_1\)	\(A_1\)	\(\frac{1}{2}\)
\(A_2?_1\)	\(A_2\)	\(\frac{1}{2}\)
\(A_1?_2\)	\(A_1\)	\(\frac{1}{2}\)
\(A_2?_2\)	\(A_2\)	\(\frac{1}{2}\)
\(\textbf{Promedio}\)		\(\frac{1}{2}\)

Por ejemplo, si el descendiente tiene el genotipo \(A_1?_1\) entonces compartirá con el progenitor A el alelo \(A_1\), es decir un alelo de los dos que tiene. En el caso de que sea \(A_2?_1\) su genotipo, entonces será el alelo \(A_2\) el que compartirá, pero también será uno de los dos alelos, es decir, una proporción de \(\frac{1}{2}\). Como las 4 combinaciones (genotipos) del descendiente todas comparten \(\frac{1}{2}\) de los alelos con su progenitor, entonces la proporción promedio será también igual a \(\frac{1}{2}\).

Veamos lo que ocurre ahora en el caso de un individuo con su nieto (o nieta), como ocurre en la Figura 9.1 a la derecha. En este caso, el progenitor A tiene una descendencia B, como ya vimos, con los 4 genotipos posibles \(A_1?_1\), \(A_2?_1\), \(A_1?_2\) y \(A_2?_2\). Este individuo B se apareará con otro individuo desconocido de la población, al que le asignamos por lo tanto los alelos \(?_3\) y \(?_4\), y el resultado será ahora de 8 genotipos posibles en la descendencia de B, es decir C. Para conocer el promedio de alelos idénticos por ascendencia entre A y C (es decir, su parentesco aditivo), los volvemos a colocar en un cuadro donde comparar cada una de las combinaciones posibles.

	\(\text{Alelos compartidos con progenitor } (A_1A_2)\)	\(\text{Proporción}\)
\(A_1?_3\)	\(A_1\)	\(\frac{1}{2}\)
\(A_2?_3\)	\(A_2\)	\(\frac{1}{2}\)
\(?_1?_3\)	\(-\)	\(\frac{0}{2}=0\)
\(?_2?_3\)	\(-\)	\(\frac{0}{2}=0\)
\(A_1?_4\)	\(A_1\)	\(\frac{1}{2}\)
\(A_2?_4\)	\(A_2\)	\(\frac{1}{2}\)
\(?_1?_4\)	\(-\)	\(\frac{0}{2}=0\)
\(?_2?_4\)	\(-\)	\(\frac{0}{2}=0\)
\(\textbf{Promedio}\)		\(\frac{4}{16}=\frac{1}{4}\)

De las 8 combinaciones posibles en C, es decir \(8 \times 2=16\) alelos en consideración, hay 4 combinaciones que comparten 1 alelo y otras 4 que no comparten ninguno. En total, \(\frac{4 \times 1+4 \times 0}{16}=\frac{4}{16}=\frac{1}{4}\) de los alelos son compartidos en la relación abuelo-nieto. Tanto en este caso como en el del padre-hijo, los alelos compartidos son claramente IBD y por lo tanto estamos en condiciones ahora de introducir una definición formal del parentesco aditivo.

Para dos individuos \(X\) e \(Y\), llamamos parentesco aditivo entre ellos (que notamos como \(a_{XY}\)) a la proporción esperada de alelos en común, idénticos por ascendencia entre los genotipos de \(X\) e \(Y\). De otra forma, como vimos en el capítulo Apareamientos no-aleatorios el parentesco aditivo es igual a el doble de la probabilidad de que al extraer al azar un alelo en cada individuo, los mismos sean IBD, es decir \(f_{XY}=\frac{1}{2}a_{XY} \therefore a_{XY}=2f_{XY}\). La relación entre ambas descripciones se debe a que cuando lo miramos desde la proporción en los genotipos hacemos 2 comparaciones en lugar de una.

Una de las cosas a remarcar que observamos en el parentesco abuelo-nieto y que no se observaba en el padre-hijo es el carácter aleatorio del número de alelos idénticos, de acuerdo al genotipo del nieto (en nuestro caso). Es decir, ya no todas las combinaciones tienen la misma proporción de coincidencias como en padre-hijo, que eran \(\frac{1}{2}\). Ahora, en abuelo-nieto tenemos 4 genotipos que coinciden en un alelo de dos (\(\frac{1}{2}\)), pero otros 4 genotipos que no tienen coincidencia, lo que resalta el hecho de que este enfoque de parentesco es puramente estadístico. Cuando el número de descendientes tiende a infinito, entonces observaremos la misma proporción de cada uno de los 8 genotipos y por lo tanto el promedio tenderá al valor teórico, \(\frac{1}{4}\) en nuestro caso. El otro aspecto relacionado que podemos notar es la razón por la que requerimos la condición de idéntico por ascendencia, algo que ya hemos tratado en abundancia en el capítulo Apareamientos no-aleatorios. Dado de que en general asumimos que existe un número limitado de formas alternativas de secuencias (alelos) en la población, la presencia de dos secuencias idénticas en dos individuos no necesariamente habla de parentesco, al menos en el intervalo de tiempo relevante para nuestra población. Si recordamos del capítulo Apareamientos no-aleatorios, a esas secuencias le llamábamos idénticas en estado y no eran informativas de parentesco. Por lo tanto, para que la identidad de secuencias sea informativa de parentesco debemos exigir que la mismas correspondan a IBD.

Hasta ahora los dos casos que hemos examinado corresponde a un tipo de relacionamiento entre individuos que conocemos como parentesco directo, donde se puede trazar un camino de una sola dirección del flujo de información genética. Es decir, la información genética va de padres a hijos, pero no al revés. Estos hijos la transmitirán, a su vez, a sus propios hijos, por lo que el flujo sigue la dirección de abuelo \(\Rightarrow\) padre \(\Rightarrow\) hijo. Una situación diferente ocurre cuando queremos analizar el parentesco aditivo entre medio hermanos (comparten solo un progenitor) o hermanos enteros (comparten los dos progenitores). En cualquiera de estos dos casos, representados en la Figura 9.2, la información fluye desde los ancestros (progenitores) a los descendientes, pero la información fluye en paralelo por dos ramas distintas, la que lleva a un hermano (o medio) y la que lleva al otro hermano (o medio).

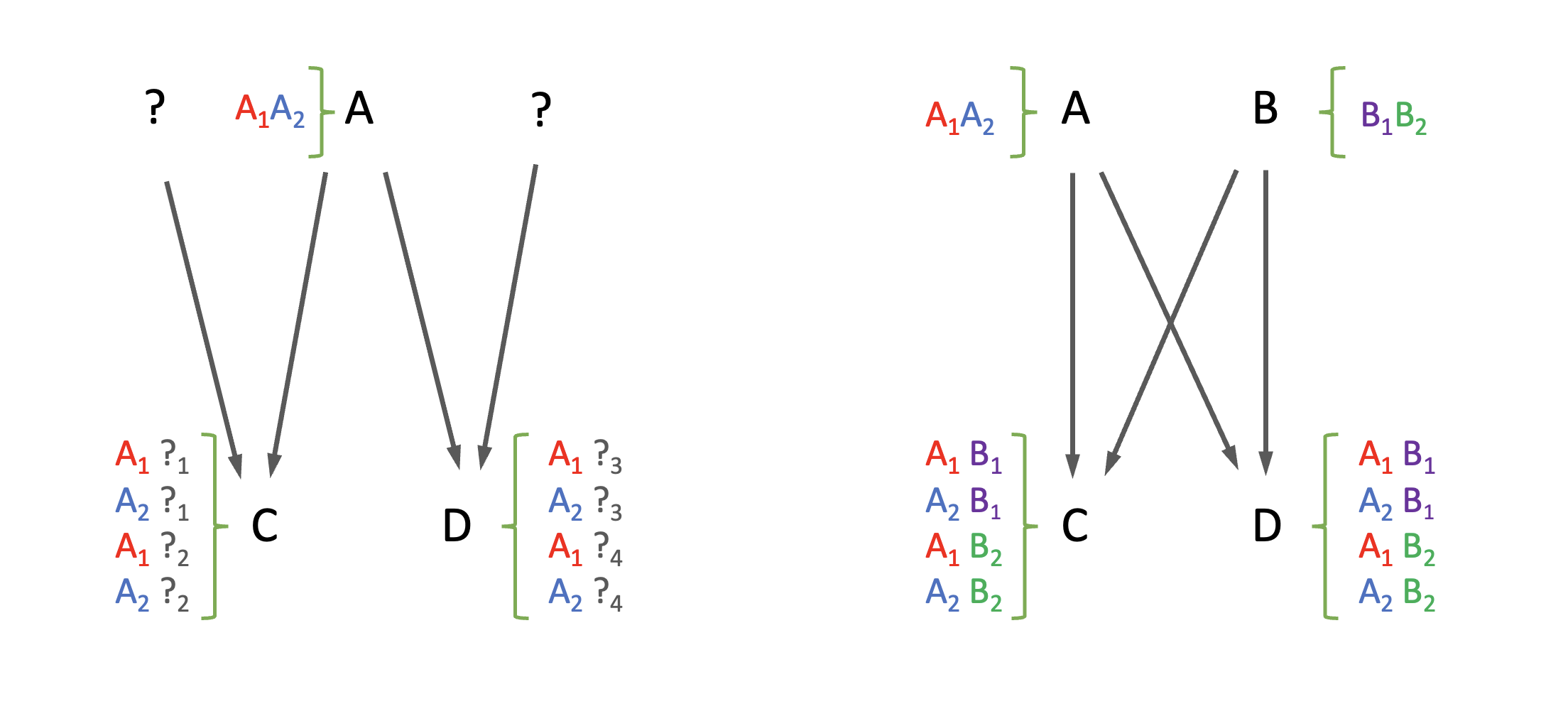
Figura 9.2: Representación de la relación entre alelos en el caso de parentesco aditivo colateral. A la izquierda la relación entre medios hermanos (MH), mientras que a la derecha observamos la relación de alelos entre hermanos enteros (HE).

Para analizar el parentesco aditivo entre medios hermanos, podemos hacer un cuadro con todas las combinaciones de genotipos en cada uno de los medios hermanos. Como los mismos tienen un progenitor en común (por ejemplo, el padre suele ser lo usual en especies domésticas donde un macho puede aparearse con varias hembras en el mismo período reproductivo) pero el otro es diferente, elegimos nuevamente marcar los progenitores que no pueden aportar alelos IBD con el signo de interrogación y sus alelos con subíndices correspondientes. De acuerdo con esto, si colocamos los genotipos posibles (de los individuos C y D en la Figura 9.2 izquierda) en filas y columnas y contamos el número de coincidencias, tenemos

	\(A_1?_1\)	\(A_2?_1\)	\(A_1?_2\)	\(A_2?_2\)
\(A_1?_3\)	\(A_1=1\)	\(0\)	\(A_1=1\)	\(0\)
\(A_2?_3\)	\(0\)	\(A_2=1\)	\(0\)	\(A_2=1\)
\(A_1?_4\)	\(A_1=1\)	\(0\)	\(A_1=1\)	\(0\)
\(A_2?_4\)	\(0\)	\(A_2=1\)	\(0\)	\(A_2=1\)
\(\textbf{Suma}\)	\(2\)	\(2\)	\(2\)	\(2\)
\(\textbf{Promedio}\)	\(\frac{2}{8}\)	\(\frac{2}{8}\)	\(\frac{2}{8}\)	\(\frac{2}{8}\)

Esto nos deja con 4 promedios, todos iguales a \(\frac{2}{8}=\frac{1}{4}\), que debemos a su vez promediar, lo que al ser todos iguales nos lleva a que su promedio sea igual a \(\frac{1}{4}\). Otra forma de verlo es a partir de la suma de todas las coincidencias, que son \(4 \times 2=8\), en un total de \(4 \times 4 \times 2=32\) (4 genotipos en cada medio hermano y con dos alelos cada uno). Por lo tanto, el parentesco aditivo entre medios hermanos será \(\frac{8}{32}=\frac{1}{4}\), idéntico resultado al anterior.

En el caso de hermanos enteros (los individuos C y D en la Figura 9.2 derecha), los hermanos comparten a los dos padres y por lo tanto las posibles configuraciones de los alelos serán iguales para ambos individuos. Esto nos deja con el siguiente cuadro

	\(A_1B_1\)	\(A_2B_1\)	\(A_1B_2\)	\(A_2B_2\)
\(A_1B_1\)	\(A_1,B_1=2\)	\(B_1=1\)	\(A_1=1\)	\(0\)
\(A_2B_1\)	\(B_1=1\)	\(A_2,B_1=2\)	\(0\)	\(A_2=1\)
\(A_1B_2\)	\(A_1=1\)	\(0\)	\(A_1,B_2=2\)	\(B_2=1\)
\(A_2B_2\)	\(0\)	\(A_2=1\)	\(B_2=1\)	\(A_2,B_2=2\)
\(\textbf{Suma}\)	\(4\)	\(2\)	\(2\)	\(2\)
\(\textbf{Promedio}\)	\(\frac{4}{8}\)	\(\frac{4}{8}\)	\(\frac{4}{8}\)	\(\frac{4}{8}\)

El promedio de cada columna (o fila) es de \(\frac{4}{8}=\frac{1}{2}\), por lo que el promedio general será también igual a \(\frac{1}{2}\) y por lo tanto el parentesco aditivo entre hermanos enteros será de \(\frac{1}{2}\).

Parentesco directo y colateral. Llamamos parentesco directo al que se da entre un individuo y su descendencia, sin importar el número de generaciones entre ellos (por ejemplo, hijos, nietos, bisnietos, tataranietos, choznos, bichoznos, etc.). Llamamos parentesco colateral al que no es directo, es decir, que se da entre individuos no directamente vinculados entre sí por una relación de ascendencia (por ejemplo, entre medio hermanos, entre hermanos, tío-sobrino, etc.).

Consanguinidad

Hasta ahora hemos asumido, en forma implícita, que el ancestro de referencia (padre, abuelo, etc.) no era consanguíneo. Como vimos en el capítulo Apareamientos no-aleatorios, cuando un individuo es consanguíneo la probabilidad de que los alelos en cualquier loci sean IBD se ve incrementada, precisamente en una cantidad igual al coeficiente de consanguinidad \(F\). Como nuestra definición de parentesco aditivo hace referencia directa a la probabilidad de que los alelos en dos individuos sean IBD, la consanguinidad del ancestro (y solo esta) incrementará el parentesco aditivo en la misma proporción. Por ejemplo, en el caso de medios hermanos, si el ancestro A (el padre, por ejemplo) posee una consanguinidad \(F_A=\frac{1}{8}\), el parentesco aditivo entre C y D será ahora \(a_{CD}=\frac{1}{4}(1+F_A)=\frac{1}{4}(1+\frac{1}{8})=\frac{1}{4}(\frac{8}{8}+\frac{1}{8})=\frac{1}{4}\frac{9}{8}=\frac{9}{32}\). Este proceso afectará la probabilidad de IBD para cada uno de los ancestros, por lo que debemos encontrar una forma de aplicar este esquema a situaciones que involucren más de un ancestro.

La consanguinidad de un individuo es igual a la mitad del parentesco aditivo de sus padres. Si A y B son los padres de C, entonce \(F_C=\frac{1}{2} a_{AB}\). Esto refuerza el concepto de que un individuo es consanguíneo sí y solo sí sus padres son parientes (es decir, el parentesco aditivo entre ellos es mayor a 0). Otra forma de verlo, en conexión con lo visto en el capítulo Apareamientos no-aleatorios es que \(F_C=\frac{1}{2} a_{AB}=f_{AB}=F_C\), es decir, el coeficiente de consanguinidad de un individuo es igual al coeficiente de coancestría de sus padres.

Veamos cómo llegamos al cálculo del coeficiente de consanguinidad en el caso de un hijo entre medios hermanos, como se aprecia en la Figura 9.3. El coeficiente de consanguinidad de E es igual a la probabilidad de que ambos alelos en el mismo sean IBD, que al tener solo un progenitor en común (A) es igual a la probabilidad de que los dos alelos sean \(A_1\) (es decir \(A_1A_1\) el genotipo de E) o los dos sean \(A_2\). Si la consanguinidad de A es cero, es decir \(F_A=0\), entonces la probabilidad de que \(A_1\) llegue a E por la izquierda es \(\frac{1}{2}\frac{1}{2}=\left(\frac{1}{2}\right)^2\) y la que llegue por la derecha también es igual a \(\frac{1}{2}\frac{1}{2}=\left(\frac{1}{2}\right)^2\). Esto se debe a que, por la rama izquierda, la probabilidad de que \(A_1\) pase de A a C es \(\frac{1}{2}\) y la probabilidad de que de C pase a E también es un medio y como los dos eventos deben darse, entonces multiplicamos sus probabilidades. Idéntico razonamiento podemos hacer para la rama derecha, en este caso pasando por D en lugar de C. Por lo tanto, para que los dos eventos se den a la vez, es decir llegar con \(A_1\) por la izquierda y por la derecha, ambos deben también darse y por lo tanto tenemos que multiplicar las probabilidades de los dos eventos y entonces

\[ \begin{split} {Pr}(E_1=A_1,E_2=A_1)=\left(\frac{1}{2}\right)^2\left(\frac{1}{2}\right)^2=\left(\frac{1}{2}\right)^4=\frac{1}{16} \end{split} \]

Exactamente lo mismo podemos también razonar para el alelo \(A_2\), por lo que

\[ \begin{split} {Pr}(E_1=A_2,E_2=A_2)=\left(\frac{1}{2}\right)^2\left(\frac{1}{2}\right)^2=\left(\frac{1}{2}\right)^4=\frac{1}{16} \end{split} \]

Como los dos eventos son mutuamente excluyentes podemos sumar las probabilidades de ambos y por lo tanto

\[ \begin{split} F_E= {Pr}(E_1=A_1,E_2=A_1)+ {Pr}(E_1=A_2,E_2=A_2)=\frac{1}{16}+\frac{1}{16}=\frac{1}{8} \end{split} \]

que es igual además, como es de esperar a la mitad del parentesco entre sus padres, ya que como vimos \(a_{CD}=\frac{1}{4} \therefore F_E=\frac{1}{2}a_{CD}=\frac{1}{2}\frac{1}{4}=\frac{1}{8}\). En el caso de que \(F_A > 0\), entonces se seguirá cumpliendo \(F_E=\frac{1}{2}a_{CD}\), pero ahora \(a_{CD}\) será mayor a \(\frac{1}{4}\) ya que la probabilidad de que los alelos sean IDB debe incrementarse en la proporción \(F_A\).

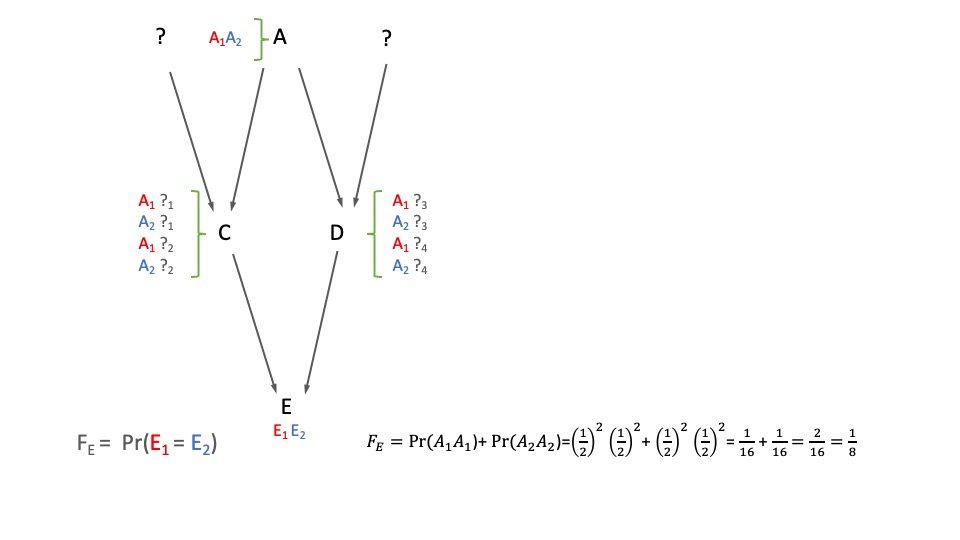
Figura 9.3: Derivación del coeficiente de consanguinidad para el hijo de medios hermanos. El coeficiente de consanguinidad de E es igual a la probabilidad de que ambos alelos en el mismo sean IBD, que al tener solo un progenitor en común (A) es igual a la probabilidad de que los dos alelos sean \(A_1\) (es decir \(A_1A_1\) el genotipo de E) o los dos sean \(A_2\). Si la consanguinidad de A es cero, es decir \(F_A=0\), entonces la probabilidad de que \(A_1\) llegue a E por la izquierda y también por la derecha es igual a \(2\times \left(\frac{1}{2}\right)^2\left(\frac{1}{2}\right)^2=\frac{1}{8}\).

PARA RECORDAR

• Para dos individuos X e Y , llamamos parentesco aditivo (\(a_{XY}\)) entre ellos a la proporción esperada de alelos en común, idénticos por ascendencia (IDB) entre los genotipos de X e Y.

• La relación entre progenitor y descendiente es la única en la que la proporción de alelos compartidos está totalmente determinada.

• Parentesco directo es aquel que se da entre un individuo y su descendencia, sin importar el número de generaciones entre ellos. Parentesco colateral es aquel que no es directo, es decir, que se da entre individuos no directamente vinculados entre sí por una relación de ascendencia.

• La consanguinidad de un individuo es igual a la mitad del parentesco aditivo de sus padres, que es lo mismo que decir que es igual al coeficiente de coancestría de sus padres.

Diagramas de flechas

Una forma sencilla y práctica de calcular el parentesco aditivo a partir de pedigrees es considerar que cada pasaje de información de un individuo a su descendencia es de la mitad de su genoma, por lo que los alelos compartidos entre padre-hijo(a) o madre-hijo(a) es siempre de \(\frac{1}{2}\). Es decir, cada flecha que une un individuo con su descendencia implica una reducción a la mitad de la información compartida. Veamos como esto se aplica en términos prácticos a las relaciones que ya hemos estudiado. Si nos fijamos en la Figura 9.1 a la izquierda, tenemos la relación entre un progenitor A y su descendencia B. Entre ellos hay una sola flecha que marca el flujo de información de A hacia B y por lo tanto podemos representar esto como \(A \rightarrow B\). Cada pasaje de información (flecha) la misma se reduce a la mitad (porque el individuo diploide sexual tiene dos progenitores y cada uno aporta la mitad del nuevo genoma), por lo que si llamamos \(n\) al número de flechas entre los dos individuos a los que les queremos calcular el parentesco aditivo (\(n=1\) en este caso), tenemos ahora

\[ \begin{split} a_{AB}=\left(\frac{1}{2}\right)^n=\left(\frac{1}{2}\right)^1=\frac{1}{2} \end{split} \]

Lo anterior presupone que el ancestro (A) no es consanguíneo, es decir que \(F_A=0\). Como ya vimos antes, si \(F_A \ne 0\), entonces debemos incluir este incremento en la ecuación, la que quedaría

\[ \begin{split} a_{AB}=\left(\frac{1}{2}\right)^n(1+F_A)=\left(\frac{1}{2}\right)^1(1+F_A)=\frac{1}{2}(1+F_A) \end{split} \]

Claramente, la ecuación anterior también se aplica cuando \(F_A=0\), ya que en ese caso \(a_{AB}=\left(\frac{1}{2}\right)^n(1+F_A)=\left(\frac{1}{2}\right)^n(1+0)=\left(\frac{1}{2}\right)^n\).

En el caso de un individuo A y su nieto C, como aparece representado en la Figura 9.1 derecha, tenemos ahora que el pasaje de información (genética) se puede representar como \(A \rightarrow B \rightarrow C\), es decir, hay dos flechas en el camino de la información de A hacia C. Por lo tanto, teniendo en cuenta que la consanguinidad de A es \(F_A\), tenemos ahora

\[ \begin{split} a_{AC}=\left(\frac{1}{2}\right)^n(1+F_A)=\left(\frac{1}{2}\right)^2(1+F_A)=\frac{1}{4}(1+F_A) \end{split} \]

para el caso de la relación abuelo-nieto.

Veamos ahora qué ocurre en el caso de parentesco colateral. En la Figura 9.2 izquierda podemos ver la relación entre dos medios hermanos, C y D, que podemos representar de acuerdo al diagrama de flechas como \(C \leftarrow A \rightarrow D\). Notar que las flechas tienen distintas direcciones ahora, ya que la información fluye desde A, tanto hacia C como hacia D. Dicho de otra forma, en el parentesco colateral hay (al menos) un punto (ancestro) donde las flechas cambian de sentido. Sin embargo, algo que se mantiene es que en cada una de las ramas, cada transferencia de información (flecha) la misma se reduce a la mitad, por lo que si llamamos \(n_1\) a una de las dos ramas (por ejemplo, la que lleva a C) y \(n_2\) a la otra rama (la que lleva a D), entonces, teniendo en cuenta la consanguinidad del ancestro A podemos escribir el parentesco entre C y D como

\[ \begin{split} a_{CD}=\left(\frac{1}{2}\right)^{n_1+n_2}(1+F_A)=\left(\frac{1}{2}\right)^{1+1}(1+F_A)=\left(\frac{1}{2}\right)^2(1+F_A)=\frac{1}{4}(1+F_A) \end{split} \]

La pregunta que sigue es cómo incorporamos la existencia de otros ancestros en común en el caso del parentesco colateral. La situación la vemos representada en el parentesco aditivo entre hermanos enteros, como aparece en la Figura 9.2 derecha. Ahora ya no tenemos un solo ancestro en común entre C y D, como teníamos en medios hermanos, sino los dos progenitores de ambos que son los mismos. Claramente tenemos dos fuentes de información genética compartida, A y B y cada una con un camino propio. Es decir, tenemos los caminos independientes \(C \leftarrow A \rightarrow D\) y \(C \leftarrow B \rightarrow D\), ambos aportando alelos que podrían ser IBD entre C y D, por lo que debemos sumar los aportes de ambas trayectorias. Además, como vimos más arriba, tanto A como B pueden tener consanguinidades distintas de cero, por lo que debemos considerarlas. En este caso particular nuestro, el parentesco aditivo entre ambos hermanos enteros podemos escribirlo

\[ \begin{split} a_{CD}=\left(\frac{1}{2}\right)^{n_{1A}+n_{2A}}(1+F_A)+\left(\frac{1}{2}\right)^{n_{1B}+n_{2B}}(1+F_B)=\left(\frac{1}{2}\right)^2(1+F_A)+\left(\frac{1}{2}\right)^2(1+F_B) \therefore \\ a_{CD}=\frac{1}{4}(2+F_A+F_B) \end{split} \]

En el caso particular de que ni A ni B sean consanguíneos, es decir \(F_A=F_B=0\), entonces el parentesco entre hermanos enteros queda reducido a

\[ \begin{split} a_{CD}=\frac{1}{4}(2+F_A+F_B)=\frac{1}{4}(2+0+0)=\frac{1}{4} \times 2=\frac{1}{2} \end{split} \]

Este análisis que realizamos primero para padres-hijos, abuelos-nietos y luego para medios hermanos y hermanos enteros podemos ahora generalizarlo a cualquier tipo de relación de parentesco entre dos individuos X e Y. Para ello debemos seguir una breve serie de pasos (es decir, un algoritmo):

1. Transformar el “pedigree” en un diagrama de flechas, donde cada individuo aparecerá una sola vez. Del individuo pueden salir tantas flechas como descendientes tenga en consideración, pero podrán entrar solo 0, 1 o 2 flechas (el primer caso si no conocemos ningún progenitor, luego si conocemos 1, o ambos en el último caso). Las flechas irán dirigidas desde el progenitor al descendiente.

2. Identificar a todos los ancestros comunes a X e Y, es decir, que sean ancestros de ambos. Para cada ancestro, si existe la información necesaria (ancestros de los mismos) calcular la consanguinidad (que es igual a un medio del parentesco aditivo entre sus padres).

3. Establecer todos los caminos independientes que vayan desde un individuo de interés al otro. En el caso de parentesco directo, el camino irá de un individuo al otro directamente, con las flechas en la misma dirección. En el caso de parentesco colateral, cada camino de un individuo de interés al otro pasará por un ancestro en común entre ambos, donde ocurrirá el único cambio de dirección de las flechas. Un individuo ocurre solo una vez en cada camino.

4. En caso de existir varios caminos diferentes, los resultados de los mismos se suman. Solo se tiene en cuenta en cada caso la consanguinidad del ancestro, no la de los individuos intermedios en el camino.

5. Si llamamos \(A_i\) a los distintos ancestros en común entre los dos individuos, X e Y, a calcularles el parentesco aditivo, teniendo en cuenta los pasos anteriores aplicamos luego la fórmula

\[ \begin{split} a_{XY}=\sum_{A_{i}} \left(\frac{1}{2}\right)^{n_{i1}+n_{i2}}(1+F_{A_i}) \end{split} \tag{9.1} \]

con \(n_{i1}\) y \(n_{i2}\) las flechas en cada una de las dos ramas en el caso del parentesco colateral o directamente \(n_i\) en el caso de parentesco directo.

Ejemplo 9.1

Un excelente ejemplo, involucrando tanto parentesco directo como parentesco colateral, es el que figura en el Manual de Prácticas del curso de Zootecnia (Echeverrı́a et al. (2012)), página 31 y cuyo diagrama de flechas reproducimos en la Figura 9.4.

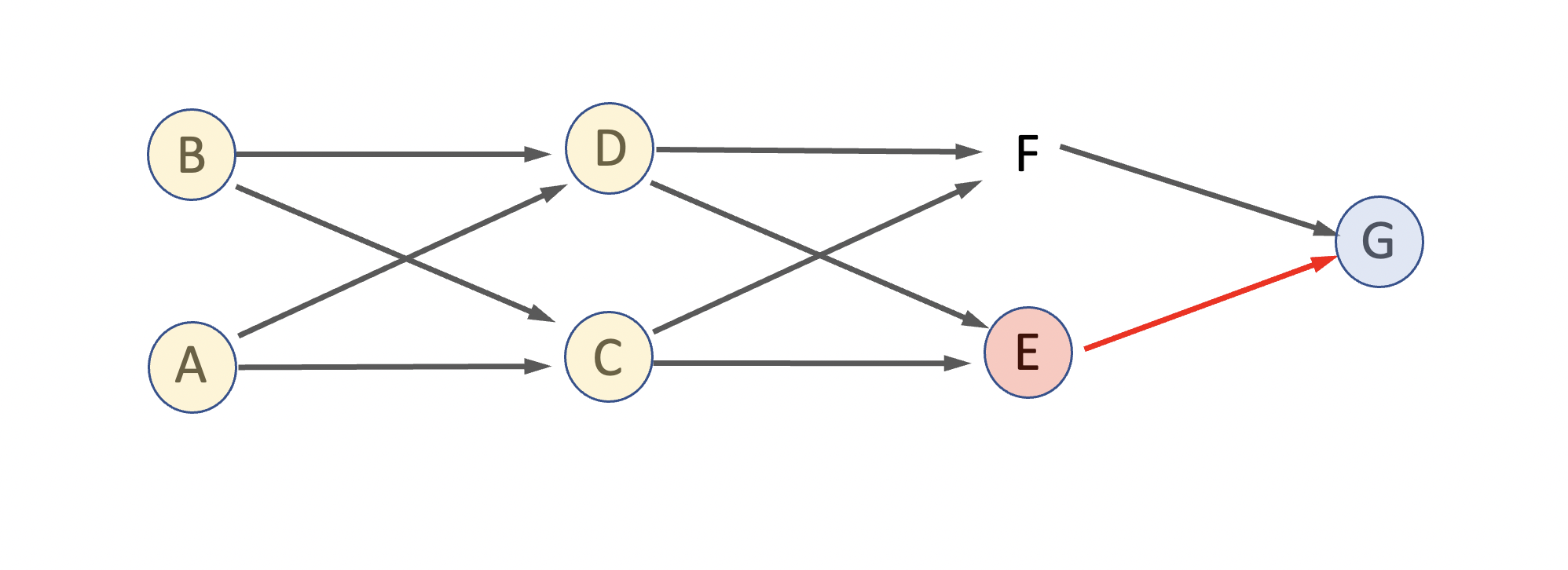
Figura 9.4: Diagrama de flechas con un cruzamiento recurrente entre hermanos. El objetivo es calcular \(a_{EG}\). La flecha roja indica una relación de parentesco directo entre los dos individuos a los que les queremos calcular el parentesco aditivo (E y G), mientras que el círculo rojo indica el ancestro de esa relación. Los círculos amarillos indican ancestros comunes a ambos candidatos.

La idea es calcular el parentesco aditivo entre los individuos E y G, que son entre ellos padre e hijo respectivamente. De lo que vimos más arriba sabemos que normalmente un padre transmite a su hijo la mitad de su información genética, por lo que en ausencia de otra información (consanguinidad o relación con el otro progenitor) el parentesco entre padre e hijo será de \(\frac{1}{2}\).

Sin embargo, solo de observar la figura podemos sospechar que en algunos individuos la consanguinidad no será cero, ya que son hijos de parientes. Por ejemplo, C y D son hermanos enteros, así como E y F, por lo que deberemos proceder a realizar los cálculos con cuidado.

El primer paso, de acuerdo a nuestro algoritmo, consiste en transformar el “pedigree” en un diagrama de flechas y ya está realizado. El segundo paso consiste en identificar todos los ancestros comunes a ambos individuos. En la figura aparecen marcados con un círculo amarillo todos los ancestros comunes a ambos que forman parte de algún parentesco colateral, mientras que el círculo rojo identifica el ancestro en el único camino de parentesco directo (E es padre de G). Para calcular la consanguinidad de cada ancestro recurrimos a la ecuación que nos indica que la misma es igual a la mitad del parentesco aditivo de los padres. Como de A y B no poseemos información, asumimos que no poseen consanguinidad y que además no son parientes entre ellos. Esto nos deja con \(F_A=F_B=0\). Además, como supusimos que A y B no son parientes, entonces sus hijos (C y D) no serán consanguíneos, por lo que \(F_A=F_B=F_C=F_D=0\). Como el parentesco aditivo entre C y D es de hermanos enteros sin consanguinidad en sus ancestros, es decir \(a_{CD}=\frac{1}{2}\), entonces \(F_E=F_F=\frac{1}{2}a_{CD}=\frac{1}{2}\frac{1}{2}=\frac{1}{4}\).

El tercer paso consiste en identificar todos los caminos por los ancestros comunes. Estos son

\[E \rightarrow G\] \[E \leftarrow C \rightarrow F \rightarrow G\] \[E \leftarrow D \rightarrow F \rightarrow G\] \[E \leftarrow C \leftarrow A \rightarrow D \rightarrow F \rightarrow G\] \[G \leftarrow F \leftarrow C \leftarrow A \rightarrow D \rightarrow E\] \[E \leftarrow C \leftarrow B \rightarrow D \rightarrow F \rightarrow G\] \[G \leftarrow F \leftarrow C \leftarrow B \rightarrow D \rightarrow E\]

Contando el número de flechas en cada camino y aplicando la ecuación (9.1) tenemos

\[a_{EG}=\left(\frac{1}{2}\right)^{1}(1+F_E) + \left(\frac{1}{2}\right)^{1+2}(1+F_C) + \left(\frac{1}{2}\right)^{1+2}(1+F_D) + \left(\frac{1}{2}\right)^{2+3}(1+F_A) + \left(\frac{1}{2}\right)^{3+2}(1+F_A) + \left(\frac{1}{2}\right)^{2+3}(1+F_B) +\] \[\left(\frac{1}{2}\right)^{3+2}(1+F_B)\]

Como \(F_E=\frac{1}{4}\) y \(F_A=F_B=F_C=F_D=0\), aplicando los pasos 4 y 5 del algoritmo y sustituyendo estos valores en la ecuación precedente (arriba) tenemos

\[a_{EG}=\left(\frac{1}{2}\right)^{1}(1+\frac{1}{4})+\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^3 +\left(\frac{1}{2}\right)^5+\left(\frac{1}{2}\right)^5+\left(\frac{1}{2}\right)^5+\left(\frac{1}{2}\right)^5 \therefore\] \[a_{EG}=\left(\frac{1}{2}\right)^{1}(\frac{5}{4})+2 \left(\frac{1}{2}\right)^3+4 \left(\frac{1}{2}\right)^5 =\frac{1}{2}\frac{5}{4}+\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^3\ \therefore \] \[a_{EG}=\frac{5}{8}+\frac{1}{4}+\frac{1}{8}=\frac{5}{8}+\frac{2}{8}+\frac{1}{8}=\frac{5+2+1}{8}=1\]

Es decir, el parentesco aditivo entre E y G ya no es típico entre padre e hijo (\(\frac{1}{2}\)), y ahora es \(a_{EG}=1\), lo que se explica tanto por la consanguinidad de E como por la existencia de varios otros ancestros comunes entre padre e hijo (A, B, C y D).

PARA RECORDAR

• Podemos calcualar el parentesco aditivo a partir de pedigrees considerando que cada pasaje de información de un individuo a su descendencia es de la mitad de su genoma.

• Para determinar el parentesco aditivo entre dos individuos X e Y debemos:

1. Transformar el “pedigree” en un diagrama de flechas, donde cada individuo aparecerá una sola vez.
2. Identificar a todos los ancestros comunes a X e Y, es decir, que sean ancestros de ambos.
3. Establecer todos los caminos independientes que vayan desde un individuo de interés al otro.
4. En caso de existir varios caminos diferentes, los resultados de los mismos se suman.
5. Por último, si llamamos \(A_i\) a los distintos ancestros en común entre los dos individuos, X e Y, podemos aplicar la siguiente fórmula: \(a_{XY}=\sum_{A_{i}} \left(\frac{1}{2}\right)^{n_{i1}+n_{i2}}(1+F_{A_i})\)

con \(n_{i1}\) y \(n_{i2}\) las flechas en cada una de las dos ramas en el caso del parentesco colateral o directamente \(n_i\) en el caso de parentesco directo.

El método tabular

Los métodos descritos más arriba dejan de ser prácticos cuando tenemos decenas, centenas o miles de animales, como es usual en las evaluaciones genética de reproductores o cuando queremos estimar parámetros como la consanguinidad promedio de una población; para estos casos debemos buscar una alternativa que sea escalable. Una alternativa conocida y práctica es lo que se conoce como el método tabular (porque se trata de completar una “tabla” o matriz), que se sustenta en un par de principios básicos del parentesco aditivo y que nos permite implementar un algoritmo muy sencillo.

Los dos principios en los que se basa son los siguientes:

1) Si dos animales son parientes, entonces uno o ambos progenitores de uno deben ser parientes del otro individuo. Dicho de otra forma, si un individuo X es pariente de un individuo Y, que tiene padres A y B, entonces X debe ser pariente de A o de B (o de ambos). Como se trata de parentesco aditivo y los padres transmiten a sus hijos la mitad del mismo, entonces

\[ \begin{split} a_{XY}=\frac{1}{2}(a_{XA}+a_{XB}) \end{split} \]

con A y B padres de Y.

2) Como vimos antes, el coeficiente de consanguinidad de un individuo es igual a la mitad del parentesco aditivo entre sus padres. Es decir, si A y B son los padres de Y, entonces

\[ \begin{split} F_{Y}=\frac{1}{2}a_{AB} \end{split} \]

A estos dos principios del parentesco aditivo debemos agregar la base algorítmica que hace funcionar al método tabular: el método de programación dinámica. Este método es ampliamente utilizado en informática y se basa en que para completar las celdas de una tabla en la que las mismas siguen alguna dependencia con otras celdas, debo organizar las filas y columnas de tal forma que al recorrer la tabla de forma ordenada siempre cuente con la información que precise para calcular el valor de cada celda que me va quedando.

Veamos a través de un ejemplo concreto y una serie de pasos o reglas que iremos describiendo cómo funciona el método tabular. El ejemplo que tomaremos será el del diagrama de flechas que aparece en el Ejemplo 9.1.

PASO 1: Ordene todos los animales que participan de la “genealogía” o “pedigree” de acuerdo a su fecha de nacimiento, los más viejos al principio, los más jóvenes al final. En caso de no tener las fechas de nacimiento (como en el ejemplo), determine qué animales son los más ancestrales y utilice las flechas para describir “generaciones”. En el ejemplo, A y B son los más viejos, seguidos de C y D, seguidos de E y F, para finalmente tener a G. No importa si A es más viejo que B o viceversa, así como tampoco entre C y D, o entre E y F.

PASO 2: En una planilla o tabla (puede ser una “hoja de cálculo”), coloque en la primera columna (a partir de la tercera celda) y en la segunda fila (a partir de la segunda celda) los nombres de los animales tal cuál fueron ordenados en el PASO 1.

PASO 3: Coloque en la primera fila de la tabla, encima de cada animal, los progenitores del mismo, como aparece en la Figura 9.5. En caso de no conocer a alguno de los progenitores coloque un signo de interrogación en su lugar. En nuestro ejemplo, los padres de A y B son desconocidos, por lo que encima de ambos colocamos ? ?. En el caso de C y D sus progenitores son A y B, por lo que encima de ambos colocamos esta información. Para E y F sus progenitores son C D, mientras que para G, sus progenitores serán E F.

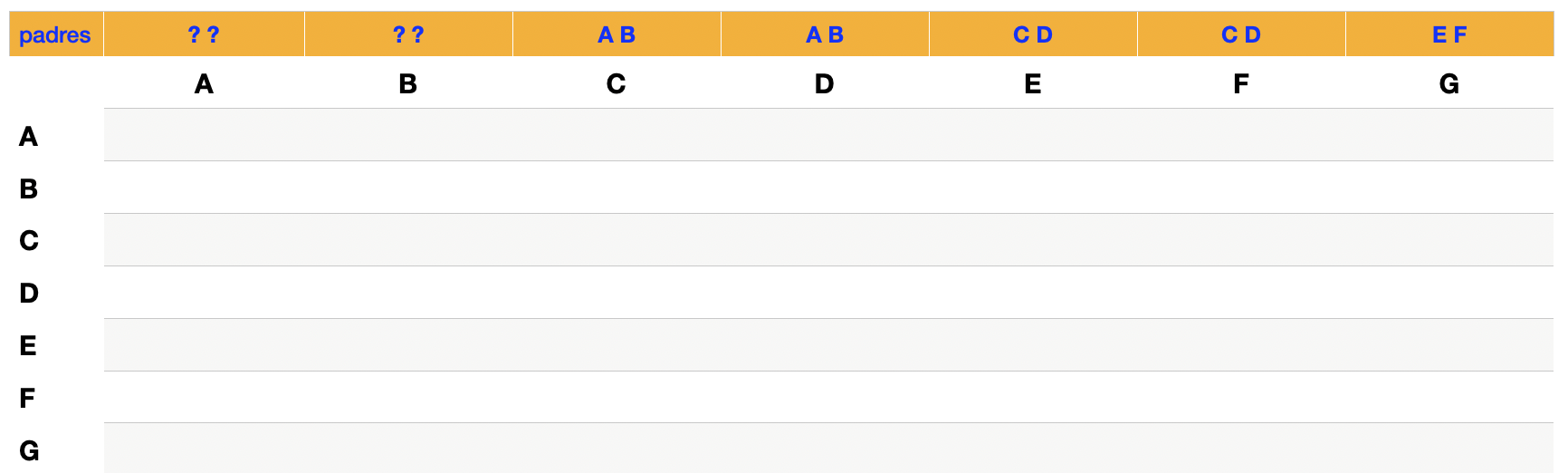
Figura 9.5: Forma de ordenar los animales y sus progenitores para el cálculo de parentescos aditivos y consanguinidades mediante el método tabular para el diagrama de flechas del Ejemplo 9.1.

PASO 4: Coloque un \(1\) en cada celda de la diagonal. El valor de \(1\) sera el parentesco aditivo del animal consigo mismo, excepto si el animal es consanguíneo, en cuyo caso debemos sumarle luego (en un paso siguiente) la consanguinidad (que es igual a la mitad del parentesco entre sus padres)-

PASO 5: Cálculo del parentesco entre animales a partir del principio 1 y de la consanguinidad a partir del principio 2. Para que el algoritmo funcione debemos trabajar en forma ordenada. Como la matriz debe ser simétrica pues el parentesco de A con B debe ser igual al del B con A (\(a_{AB}=a_{BA}\)), nosotros vamos a completar solo la matriz triangular superior y luego, al finalizar todo el proceso, copiaremos los valores a la triangular inferior. Es decir, vamos a ir recorriendo desde la primera fila, la primer celda a la izquierda hasta la última a la derecha, antes de pasar a la segunda fila. Lo mismo para ésta, de izquierda a derecha hasta el final, antes de pasar a la tercera fila, etc.

Cada fila a completar comienza con la celda de la diagonal correspondiente y utilizando el principio 2 calculamos la consanguinidad que debemos sumarle al \(1\) de la celda como la mitad del parentesco entre sus padres. En general, si esa información existe (el parentesco entre los padres del individuo) ya la vamos a tener calculada en alguna celda y bastará con multiplicarla por \(\frac{1}{2}\). En nuestro caso, el primer animal es A si sus padres son desconocidos, por lo que no vamos a poder saber si son parientes y por lo tanto debemos asumir que la consanguinidad de A es cero (\(F_A=0\)).

La siguiente celda corresponde al parentesco aditivo entre A (fila) y B (columna). Como no conocemos tampoco los padres de B, entonces el principio 1 debemos aplicarlo como \(a_{AB}=\frac{1}{2}(a_{A?}+a_{A?})=\frac{1}{2}(0+0)=0\), como podemos ver en la Figura 9.6.

La próxima celda a calcular es la del parentesco entre A (fila) y C (columna). En este caso si conocemos a los padres de C, que son A y B, por lo que aplicando el principio 1, tenemos que \(a_{AC}=\frac{1}{2}(a_{AA}+a_{AB})\). El parentesco de A consigo mismo está en la intersección de la primera fila con la diagonal (es decir, la primera celda de esta fila) y vimos que era \(a_{AA}=1\). En el caso de A con B vimos que era \(a_{AB}=0\), por lo que \(a_{AC}=\frac{1}{2}(a_{AA}+a_{AB})=\frac{1}{2}(1+0)=\frac{1}{2}\). Lo mismo se aplica para el parentesco entre A y D ya que es hermano entero de C.

En el caso del parentesco de A con E (cuyos padres son C y D), aplicando nuevamente el principio 1, tenemos \(a_{AE}=\frac{1}{2}(a_{AC}+a_{AD})=\frac{1}{2}(\frac{1}{2}+\frac{1}{2})=\frac{1}{2}(1)=\frac{1}{2}\). Obviamente, lo mismo se aplica para su hermano entero F, por lo que \(a_{AF}=a_{AE}=\frac{1}{2}\).

Nos queda entonces la última celda de esta fila que es el parentesco aditivo de A con G (cuyos padres son E y F). Aplicando el principio 1, tenemos que \(a_{AG}=\frac{1}{2}(a_{AE}+a_{AF})=\frac{1}{2}(\frac{1}{2}+\frac{1}{2})=\frac{1}{2}(1)=\frac{1}{2}\).

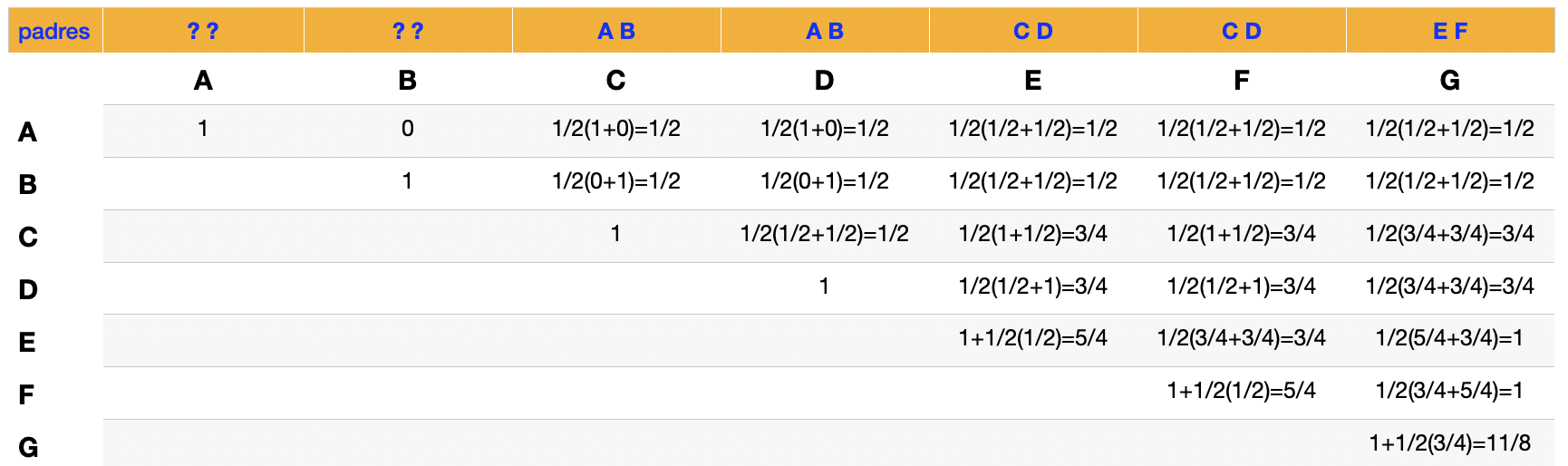
Figura 9.6: Cálculo de parentescos aditivos y consanguinidades mediante el método tabular para el diagrama de flechas del Ejemplo 9.1. Cada celda aparece con el cálculo correspondiente usando los principios 1 y 2.

Podemos pasar ahora a la segunda fila, donde aplicamos el mismo procedimiento que para la primera y no encontraremos ninguna novedad (cosa que es razonable porque las etiquetas de A y B son intercambiables). Tampoco aparecerán novedades hasta la fila correspondiente a E, en la que aparece la primera consanguinidad distinta de cero. Aplicando el principio 2, debemos sumarle al \(1\) del PASO 4 la consanguinidad del individuo, que es igual a la mitad del parentesco aditivo de sus padres. Como los padres de E son C y D, vamos hasta la celda intersección de la fila correspondiente a C con la columna correspondiente a D y observamos que su valor es \(a_{CD}=\frac{1}{2}\), por lo que \(F_E=\frac{1}{2}a_{CD}=\frac{1}{2}\frac{1}{2}=\frac{1}{4}\), valor que sumamos a \(1\) para obtener \(a_{EE}=1+\frac{1}{4}=\frac{5}{4}\).

Si seguimos con estos procedimientos iremos completando la matriz triangular superior.

PASO 6: El último paso consiste en completar los valores de la triangular inferior con los valores correspondientes de la triangular superior, es decir

\[ \begin{split} a_{ji}=a_{ij} \forall j>i \end{split} \]

lo que nos permite llegar al resultado final (Figura 9.7), que es la matriz de parentesco entre los individuos del Ejemplo 9.1. Podemos verificar con lo calculado explícitamente en dicho ejercicio que el parentesco aditivo entre E y G es \(a_{EG}=1\), lo que coincide con lo obtenido por el método tabular.

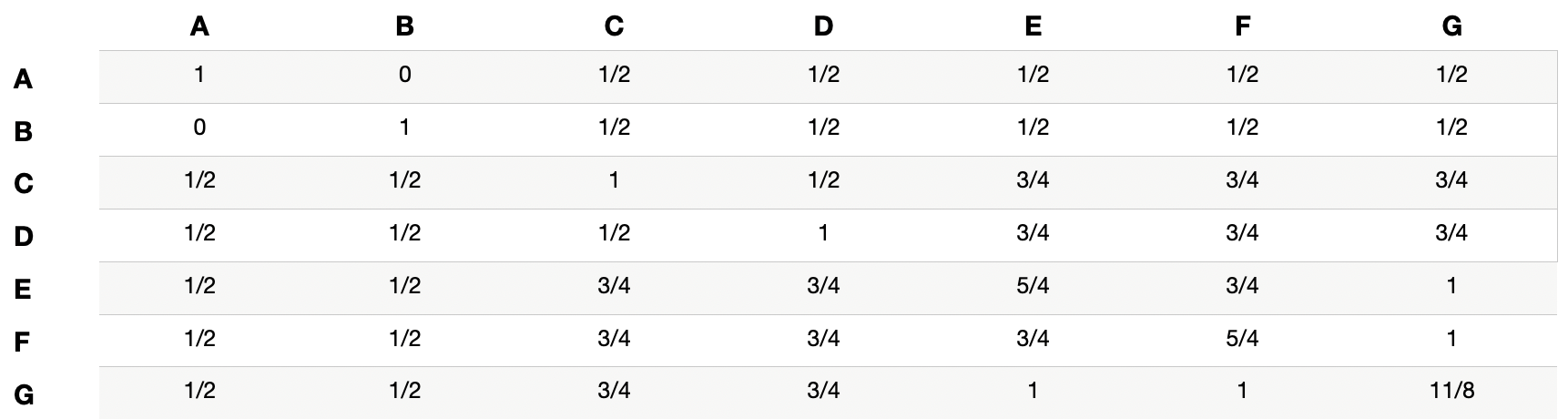
Figura 9.7: Resultado final de la matriz de parentesco aditivo entre los individuos del Ejemplo 9.1, usando el método tabular para calcularla.

Como veremos más adelante y en otros cursos más avanzados, la matriz de parentesco aditivo, de tamaños \(n \times n\) (con \(n\) el número de individuos) y usualmente notada con \(\mathbf A\), juega un papel fundamental en la estimación de los valores de cría de animales en las evaluaciones genéticas. Por ejemplo, tanto en la metodología en uso desde los años 70 del siglo XX, el llamado BLUP (Best Linear Unbiased Prediction), como en las metodologías más modernas que hacen uso del parentesco genómico (que discutiremos más adelante), la matriz de parentesco aditivo “estadística” es un elemento clave para dar cuenta de la dependencia entre observaciones y obtener estimados con buenas propiedades estadísticas.

Ejemplo 9.2

Verificar que el resultado del parentesco entre D y F obtenido de la matriz de parentesco es idéntico al correspondientes del diagrama de flechas del Ejemplo 9.1.

De acuerdo al diagrama de flechas, los ancestros comunes son D (parentesco directo), A y B (parentesco colateral). Los caminos posibles por los ancestros son los siguientes

\[ \begin{split} D \rightarrow F \\ D \leftarrow A \rightarrow C \rightarrow F\\ D \leftarrow B \rightarrow C \rightarrow F\\ \end{split} \]

Por lo tanto, podemos escribir el parentesco aditivo entre D y F como

\[ \begin{split} a_{DF}=(\frac{1}{2})^1(1+F_D)+(\frac{1}{2})^3(1+F_A)+(\frac{1}{2})^3(1+F_B) \\ \end{split} \]

Como \(F_A=F_B=F_D=0\) en nuestro caso, los dos primeros porque no tenemos información de los padres ni de ellos mientras que para \(F_D\) los padres no son parientes, la ecuación anterior se reduce a

\[ \begin{split} a_{DF}=(\frac{1}{2})^1+(\frac{1}{2})^3+(\frac{1}{2})^3=\frac{1}{2}+2 (\frac{1}{2})^3=\frac{1}{2}+\frac{1}{4} \therefore \\ a_{DF}=\frac{3}{4} \end{split} \]

que es el mismo resultado que aparece en la matriz de parentesco calculada por el método tabular (cuarta fila, sexta columna o al revés).

PARA RECORDAR

• El método tabular constituye una alternativa escalable a los diagramas de flechas para calcular el parentesco. El mismo se basa en dos principios:

1. Si un individuo X es pariente de un individuo Y (que tiene padres A y B), entonces X debe ser pariente de A o de B (o de ambos). Como se trata de parentesco aditivo y los padres transmiten a sus hijos la mitad del mismo, entonces: \(a_{XY}=\frac{1}{2}(a_{XA}+a_{XB})\)

2. El coeficiente de consanguinidad de un individuo es igual a la mitad del parentesco aditivo entre sus padres. Es decir, si A y B son los padres de Y, entonces: \(F_{Y}=\frac{1}{2}a_{AB}\)

• Los siguientes pasos constituyen la guía para utilizar el método tabular:

PASO 1: Ordenar todos los animales que participan de la “genealogía” o “pedigree” de acuerdo a su fecha de nacimiento: los más viejos al principio y los más jóvenes al final.

PASO 2: En una planilla o tabla, colocar en la primera columna (a partir de la tercera celda) y en la segunda fila (a partir de la segunda celda) los nombres de los animales tal cuál fueron ordenados en el PASO 1.

PASO 3: Coloque en la primera fila de la tabla, encima de cada animal, los progenitores del mismo. En caso de no conocer a alguno de los progenitores coloque un signo de interrogación en su lugar.

PASO 4: Colocar un “1” en cada celda de la diagonal. El valor de 1 sera el parentesco aditivo del animal consigo mismo, excepto si el animal es consanguíneo, en cuyo caso debemos sumarle luego (en un paso siguiente) la consanguinidad.

PASO 5: Cálculo del parentesco entre animales a partir del principio 1 y de la consanguinidad a partir del principio 2.

PASO 6: Completar los valores de la triangular inferior con los valores correspondientes de la triangular superior.

9.3 Parentesco de dominancia

En nuestra descomposición de los efectos genéticos del modelo genético básico teníamos que \(G=A+D+I\). Para representar la relación de los efectos aditivos entre individuos construimos el parentesco aditivo, que definimos como la proporción de alelos IBD en la comparación entre los genotipos de dos individuos. Los efectos de dominancia los habíamos manejado como las desviaciones de la aditividad intra-locus y por lo tanto deben corresponderse a los genotipos compartidos de alelos IBD, en lugar de a los alelos compartidos entre esos individuos.

Si recapitulamos las relaciones entre individuos que aparecen en la Figura 9.1, vemos que en ninguno de los casos, padre-hijo y abuelo-nieto, podemos compartir el genotipo entre dos individuos ya que los otros progenitores son desconocidos y aparentemente sin relación. Es decir, si nos fijamos en la relación padre-hijo, tenemos que el genotipo del padre es \(A_1A_2\) y el del hijo puede ser una cualquiera de las combinaciones \(A_1?_1\), \(A_1?_2\), \(A_2?_1\), \(A_2?_2\). Claramente, ninguna de estas es \(A_1A_2\), por lo que el parentesco de dominancia entre A y B será \(d_{AB}=\frac{0}{4}=0\). Lo mismo para la relación abuelo-nieto, donde para el abuelo \(A_1A_2\) tenemos ahora 8 posibles combinaciones en el nieto, que serán \(A_1?_3\), \(A_1?_4\), \(A_2?_3\), \(A_2?_4\), \(?_1?_3\), \(?_1?_4\), \(?_2?_3\), \(?_2?_4\). Como ninguna de ellas es igual a \(A_1A_2\), entonces \(d_{AC}=\frac{0}{8}=0\). Obviamente, lo mismo se puede decir de cualquier otro parentesco directo donde los apareamientos provengan de individuos siempre diferentes y no emparentados entre ellos.

La situación en la Figura 9.2 izquierda representa la relación entre medios hermanos. En este caso, uno de los medios hermanos pertenece a alguna de las combinaciones \(A_1?_1\), \(A_1?_2\), \(A_2?_1\), \(A_2?_2\), mientras que el otro pertenece a las combinaciones \(A_1?_3\), \(A_1?_4\), \(A_2?_3\), \(A_2?_4\). Como en el primer hermano uno de los alelos es siempre \(?_1\) o \(?_2\) y en el otro hermano siempre uno de los alelos es \(?_3\) o \(?_4\), entonces nunca coincidirán plenamente los genotipos, entre las 16 combinaciones posibles de \(4 \times 4\). Por lo tanto, también en este caso \(d_{BC}=\frac{0}{16}=0\).

La situación va a cambiar para el caso de hermanos enteros, como vemos en la Figura 9.8. Tenemos ahora también 16 pares de genotipos posibles, producto de 4 combinaciones para cada uno de los hermanos. En este caso, sin embargo, si nos fijamos con atención las 4 posibilidades de genotipo para cada hermano son las mismas, es decir \(A_1B_1\), \(A_1B_2\), \(A_2B_1\) y \(A_2B_2\). Por lo tanto, para cualquiera de las combinaciones del “primer” hermano que elijamos, siempre habrá una de las cuatro del segundo hermano que sea idéntica, como se puede apreciar en la tabla de la derecha de la figura. Es decir, de los 16 pares de genotipos correspondientes a tomar uno en un hermano y el otro en el otro hermano, en 4 de esos pares los genotipos son idénticos, por lo que ahora \(d_{CD}=\frac{4}{16}=\frac{1}{4}\).

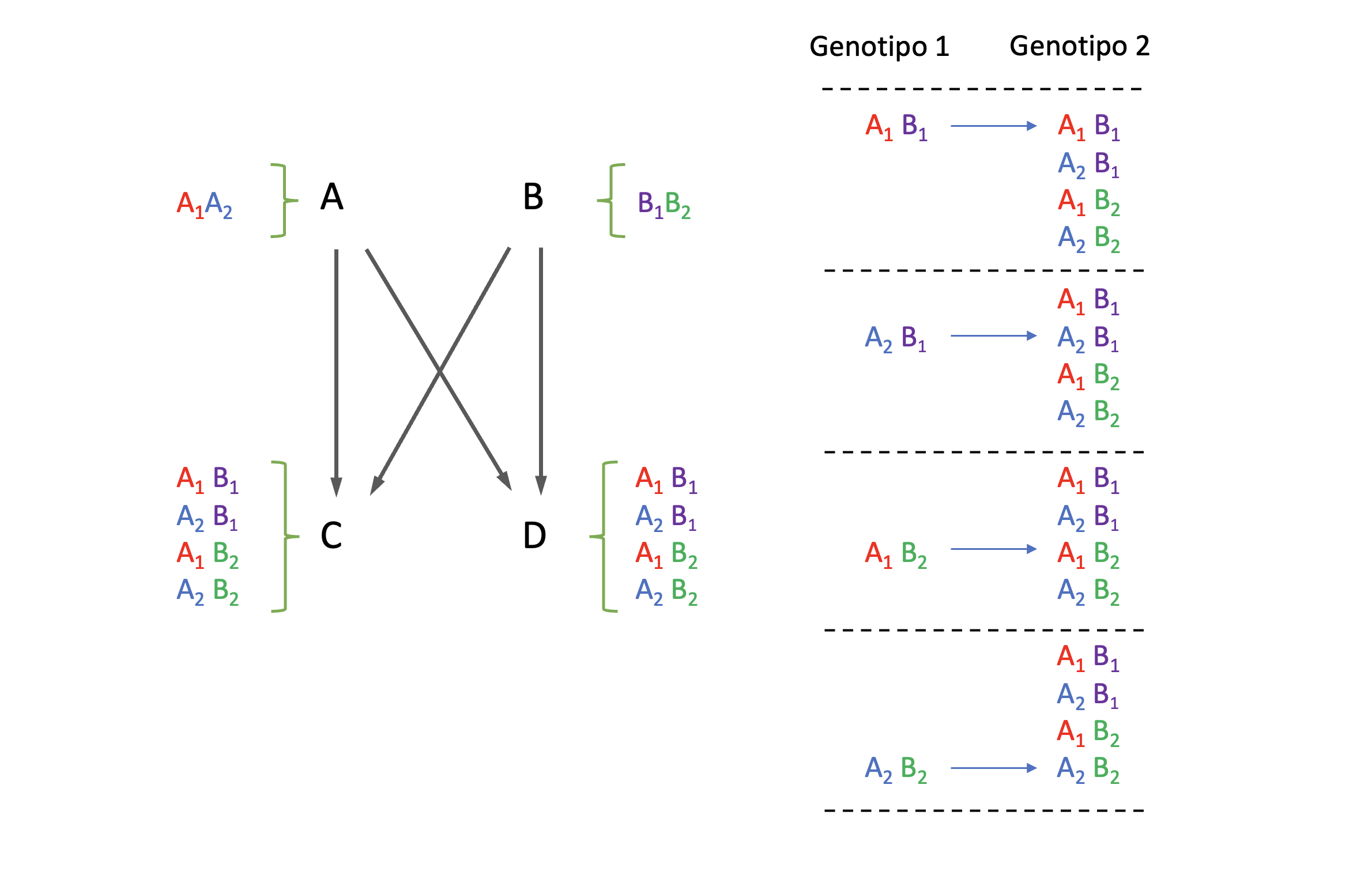
Figura 9.8: Representación de la relación entre hermanos enteros que lleva a un parentesco de dominancia distinto de cero. Dada la elección de cualquiera de los cuatro genotipos posibles en uno de los hermanos, la probabilidad de que el segundo hermano posea el mismo genotipo es de 1 en 4, es decir \(d_{CD}=\frac{1}{4}\).

En estructuras de parentesco más complejas es en general más difícil realizar el desarrollo de todas las combinaciones posibles y es necesario recurrir a otras formas de calcular el parentesco de dominancia, pero a los fines de este curso introductorio nos alcanzará con estas relaciones que vimos. Finalmente, los conceptos que acá hemos desarrollado para un locus pueden extenderse con facilidad conceptual (aunque no analítica) a las relaciones entre loci, definiendo un parentesco epistático o de interacción, que apenas mencionaremos llegado el caso.

PARA RECORDAR

• Los efectos de dominancia los habíamos manejado como las desviaciones de la aditividad intra-locus y por lo tanto deben corresponderse a los genotipos compartidos de alelos IBD, en lugar de a los alelos compartidos entre esos individuos.

• Cualquier parentesco directo donde los apareamientos provengan de individuos diferentes y no emparentados entre ellos tendrán un \(d_{XY}=0\) debido a que los pradres no trasmiten a sus hijos combinaciones de alelos.

• Tomando como ejemplo de parentesco colateral los casos de medios hermanos y hermanos enteros, el parentesco de dominancia será \(d_{XY}=0\) y \(d_{XY}=\frac{1}{4}\).

9.4 Semejanza entre parientes

Como vimos antes, a partir de nuestro modelo genético básico podemos particionar la varianza fenotípica en sus componentes genético y ambiental, y a su vez los primeros en sus componentes aditivos, de dominancia y de epistasis. Sin embargo, al no tratarse cada uno de estos componentes de entidades observables, no tenemos forma de calcular su valor directamente y debemos recurrir a diferentes estrategias para poder estimar su valor. Dicho de otra forma, lo único que nosotros observamos directamente es el fenotipo y por lo tanto, lo único que podemos calcular directamente es la varianza fenotípica, por lo que si queremos conocer la varianza genética o aún sus componentes vamos a tener que contar con otra información que nos permita separarla. En este proceso, resulta fundamental entender las diferencias entre componentes causales de la varianza y componentes observables de la misma, así como la relación entre ellos.

Para comenzar a pensar en términos de componentes observables de la varianza veamos un ejemplo sencillo, que aparece representado en la Figura 9.9.

En dicha figura tenemos representadas tres situaciones distintas, identificadas por los colores de los trazos continuos que las envuelven (gris, violeta y marrón). En cada una de las situaciones tenemos a su vez 3 potreros, en los que pastan 3 ovejas. Las ovejas pueden ser de 3 tamaños diferentes, \(1\), \(2\) o \(3\). En cada una de las situaciones hay el mismo número de ovejas de cada tamaño, 3 de cada una, pero varía como se distribuyen en cada potrero. En la situación de la izquierda, cada uno de los potreros tiene una oveja de cada tamaño, por lo que el contenido de los potreros es idéntico. Obviamente, la media de tamaño de cada potrero, \(\bar{x}\), es igual en los tres (ya que son idénticos), por lo que toda la variación observada en el tamaño de la ovejas corresponde a variación dentro del potrero.

Por otro lado, la situación de la derecha es, de alguna manera, la opuesta. El potrero de la izquierda tiene todas las ovejas de tamaño \(1\), el del centro todas de tamaño \(2\) y el de la derecha todas de tamaño \(3\). Por lo tanto, dentro de cada potrero los tamaños será uniformes y no existirá variación (lo que se refleja en que las medias, \(\bar{x}\), son idénticas a los valores de las ovejas del potrero correspondiente). Esto nos deja con el hecho de que toda la variación de tamaños observada se corresponde a variación entre potreros.

Finalmente, en la situación del medio, las ovejas fueron asignadas al azar entre los 3 potreros. Mientras que en el potrero de la izquierda tenemos una oveja de cada tamaño, en el potrero del centro hay 2 ovejas de tamaño \(2\) y falta la de tamaño \(3\), y en el potrero de la derecha hay 2 ovejas de tamaño \(3\), faltando la oveja de tamaño \(2\). Por un lado, ahora los potreros son son homogéneos internamente (en todos hay variación dentro), pero tampoco son idénticos entre ellos, por lo que también tenemos variación entre potreros, lo que se ve reflejado en las diferencias de las medias.

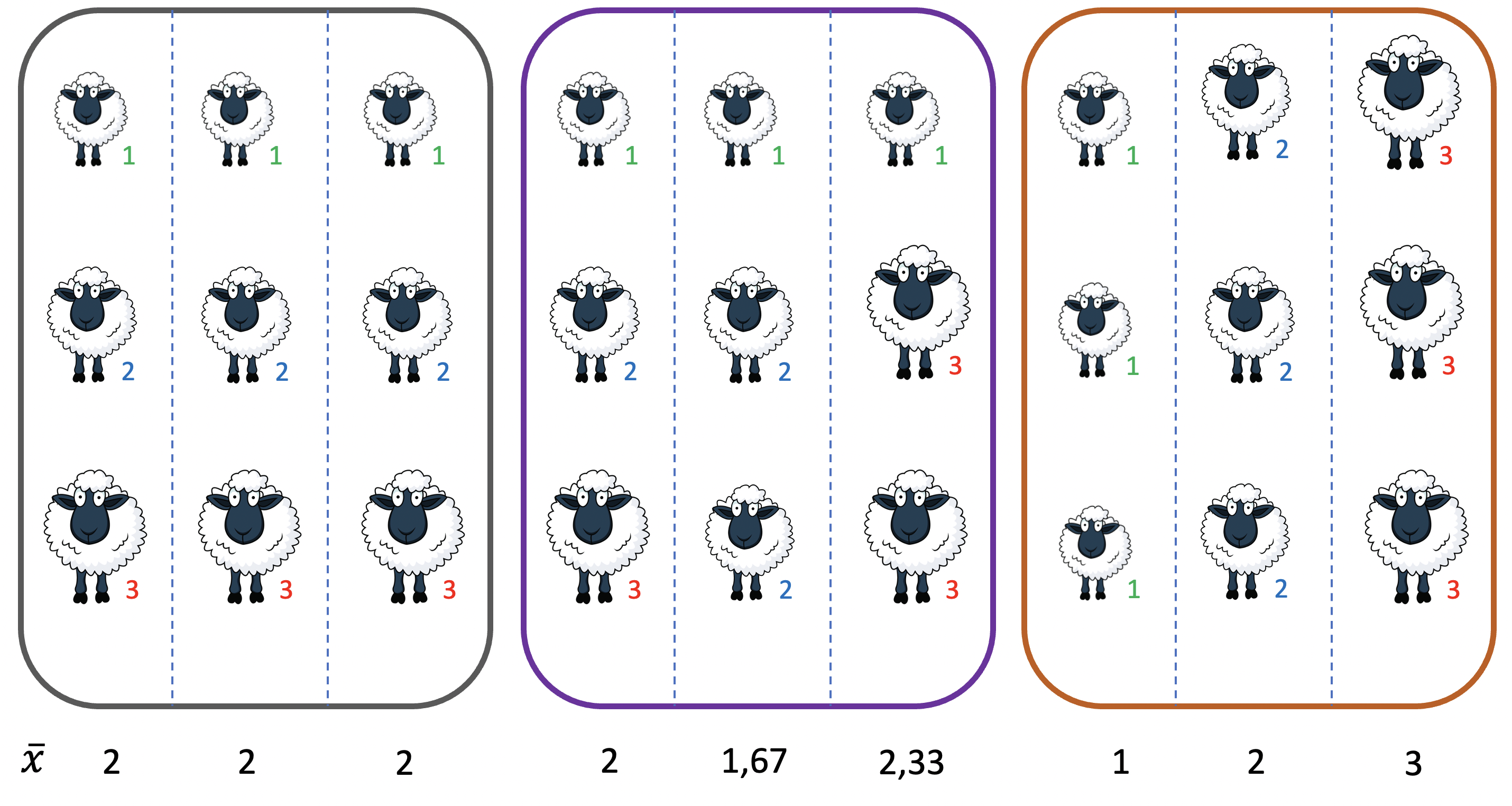
Figura 9.9: Distribución de la variabilidad dentro de grupos y entre grupos. En cada uno de las tres situaciones hay un mismo número de ovejas de cada uno de los 3 valores (o sea, 3 ovejas de valor 1, 3 de valor 2 y 3 de valor 3). Sin embargo en la situación de la izquierda, cada corral tiene una oveja de cada tipo, por lo que los 3 corrales son idénticos y no existe por lo tanto variabilidad entre grupos (corrales), concentrándose toda la variabilidad dentro de los grupos. En la situación de la derecha nos encontramos con que no existe variación dentro de los corrales (ya que el primero tiene todas las ovejas con valor 1, el del medio todas con valor 2 y el último todas con valor 3), por lo que toda la variación está concentrada entre los grupos. La situación del medio es intermedia, las ovejas asignadas al azar, con variabilidad dentro y variabilidad entre. En la línea de abajo, la media de cada grupo (diseño de las ovejas de http://cliparts.co/clipart/2377087 Fuente: Cliparts.co).

Claramente, la distinción de la fuente de variación en componentes entre y dentro de grupos (potreros) es observable, ya que podemos medir, contar y calcular directamente la varianza (por ejemplo) que se corresponde a cada una de las fuentes. Si llamamos \(\sigma^2_B\) a la varianza entre grupos y \(\sigma^2_W\) a la varianza dentro de grupos, una forma de distinguir la importancia relativa de las dos fuentes de variación es el coeficiente de correlación intra-clase, que definimos como

\[ \begin{split} t=\frac{\sigma^2_B}{\sigma^2_B+\sigma^2_W} \end{split} \tag{9.2} \]

Al tratarse de una relación entre una varianza y la suma de varianzas (la varianza total), el coeficiente de correlación intra-clase podrá variar entre \(0\) y \(1\). En la situación de la izquierda de la Figura 9.9 tenemos que no existe variación entre grupos (ya que son idénticos entre ellos), por lo que \(\sigma^2_B=0\) y por lo tanto \(t=\frac{\sigma^2_B}{\sigma^2_B+\sigma^2_W}=\frac{0}{0+\sigma^2_W}=0\). Por otra parte, en la situación de la derecha no existe variación dentro de grupos, por lo que \(\sigma^2_W=0\) y por lo tanto \(t=\frac{\sigma^2_B}{\sigma^2_B+\sigma^2_W}=\frac{\sigma^2_B}{\sigma^2_B+0}=1\).

Un concepto adicional a entender, es la relación que existe entre las fuentes de variación observables y la similaridad de los individuos dentro de los grupos. La similaridad entre los miembros de cada uno de los grupos, para características métricas, la podemos identificar con la co-variación, o en términos estadísticos, con la covarianza entre los miembros del grupo. A medida de que los miembros de cada grupo son más similares entre sí, disminuye el efecto de variación dentro del grupo, aumentando en consiguiente la proporción que corresponde a entre grupos. Por lo tanto, podemos asimilar la covarianza dentro de grupos a la varianza entre grupos, algo que será fundamental en breve.

La razón por la que la covarianza entre individuos del mismo grupo es igual a la varianza entre grupos se puede demostrar fácilmente. Por ejemplo, en el caso de Hermanos Enteros, si asumimos un modelo en el que el fenotipo de un individuos \(j\), perteneciente a una familia \(i\) se corresponde con el siguiente modelo

\[ \begin{split} z_{ij}=\mu+f_i+w_{ij} \end{split} \tag{9.3} \]

entonces la covarianza entre dos individuos \(j\) y \(k\) pertenecientes a la misma familia (\(i\)), es decir Hermanos Enteros, estará dada por

\[Cov_{HE}={Cov}(z_{ij},z_{ik})= {Cov}[(\mu+f_i+w_{ij}),(\mu+f_i+w_{ik})]=\] \[{Cov}(f_i,f_i)+ {Cov}(f_i,w_{ik})+ {Cov}(w_{ij},f_i)+ {Cov}(w_{ij},w_{ik})= {Cov}(f_i,f_i) \therefore\] \[ \begin{split} {Cov_{HE}=\sigma_f^2} \end{split} \tag{9.4} \]

Por lo tanto, la covarianza entre individuos del mismo grupo (familia) es igual a la varianza entre grupos (familias), que es lo que queríamos demostrar.

En la situación de la izquierda, los individuos son todos diferentes dentro de cada grupo, por lo que la similaridad (covarianza) dentro de grupos será nula y la proporción de varianza que corresponde a entre grupos también. Por el contrario, en la situación de la derecha todos los individuos de cada grupo son idénticos entre sí (máxima covarianza dentro) y por lo tanto la varianza entre grupos será igual a la total. En el ejemplo de la figura, aún no aportamos la información de cómo se formaron cada uno de los grupos, pero pronto vamos a comprender que si los mismos se constituyen en base a determinadas relaciones de parentesco entre los integrantes, la causa de la similaridad tendrá que ver con la base genética común entre ellos.

Pasemos ahora a intentar entender la base causal del parecido fenotípico entre parientes, ya que esto nos dará los elementos que nos hacen falta para poder comprender el rol que juega el parentesco en la estimación de los componentes de varianza del modelo genético básico. Asumamos aquí que \(X\) e \(Y\) son pares de individuos entre los cuales existe un parentesco determinado, el mismo para cada par (por ejemplo, un padre y un hijo, o dos medio hermanos, o dos hermanos enteros, etc.). Como tenemos datos fenotípicos de los dos, el cálculo de la covarianza fenotípica es directo (aplicando la fórmula para la covarianza, \(\mathrm{Cov_{XY}}=\frac{1}{(n-1)}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})\)). O sea, esta covarianza tendrá un número, en las mismas unidades que la varianza de la característica (las unidades al cuadrado) ya que se trata de la suma del producto de los desvíos de \(X\) e \(Y\) respecto a sus medias, ambas medidas para la misma característica. Como, de acuerdo a nuestro modelo genético, \(\mathrm{P_X= A_X+D_X+I_X+E_X}\) y \(\mathrm{P_Y= A_Y+D_Y+I_Y+E_Y}\), la covarianza entre medidas en cada par de individuos será igual a

\[\mathrm{Cov(P_X,P_Y)= Cov([A_X+D_X+I_X+E_X],[A_Y+D_Y+I_Y+E_Y])}\] \[\mathrm{Cov(P_X,P_Y)= Cov(A_X,A_Y)+Cov(A_X,D_Y)+...+Cov(D_X,A_Y)+Cov(D_X,D_Y)+...}\]

En general, en nuestro modelo genético, los terminos de covarianza entre componentes de un tipo en un individuo y de otro tipo en otro individuo son cero. Por ejemplo, como vimos antes, por construcción \(\mathrm{Cov(A_X,D_X)}=0\), \(\mathrm{Cov(A_X,I_X)=0}\) y por las mismas razones lo podemos extender a \(\mathrm{Cov(A_X,D_Y)=0}\), \(\mathrm{Cov(A_X,I_Y)=0}\) (no es de esperar que el valor aditivo en un individuo se correlacione o covaríe con desvíos en el otro individuo).

De esta manera,

\[ \begin{split} \mathrm{Cov(P_X,P_Y)= Cov(A_X,A_Y)+Cov(D_X,D_Y)+Cov(I_X,I_Y)+Cov(E_X,E_Y)} \end{split} \]

Por otro lado, vimos que las definiciones de parentesco aditivo que corresponden a Gustave Malecot y Sewall Wright son equivalentes cuando asumimos que ambos individuos no poseen consanguinidad (\(F_X=0\), \(F_Y=0\)). Es decir, de acuerdo a Sewall Wright (1922), el parentesco aditivo es igual

\[ \begin{split} R_{XY}= \frac{ {Cov(A_X,A_Y)}}{\sqrt{ {Var(A_X) Var(A_Y)}}}=\frac{a_{XY}}{\sqrt{a_{XX} . a_{YY}}}=\frac{a_{XY}}{\sqrt{(1+F_X)(1+F_Y})} \end{split} \tag{9.5} \]

por lo que si \(F_X=0\) y \(F_Y=0\) ambas definiciones son equivalentes (\(a_{XY}=R_{XY}\)). Entonces, de acuerdo a esto, si además asumimos que \({Var(A_X)=Var(A_Y)}\) (atención, claramente puede no ser cierto en algunas relaciones de parentesco), entonces

\[ \begin{split} a_{XY}= \frac{ {Cov(A_X,A_Y)}}{ {\sqrt{Var(A_X) Var(A_Y)}}}=\frac{ {Cov(A_X,A_Y)}}{ {Var(A)}} \iff {Cov(A_X,A_Y)}=a_{XY} . {Var(A)} \\ \end{split} \]

De la misma manera, para el parentesco de dominancia (probabilidad de compartir el genotipo en un locus dado entre dos individuos, correlación de los desvíos de dominancia), asumiendo ahora que que \(\mathrm{Var(D_X)=Var(D_Y)}\), tenemos

\[ \begin{split} d_{XY}= \frac{ {Cov(D_X,D_Y)}}{ {\sqrt{Var(D_X) Var(D_Y)}}}=\frac{ {Cov(D_X,D_Y)}}{ {Var(D)}} \iff {Cov(D_X,D_Y)}=d_{XY} . {Var(D)} \end{split} \]

O sea, de ambas deducciones podemos observar que en general el tipo de covarianza entre individuos representa una determinada fracción de la correspondiente varianza y que esa fracción, el coeficiente, es un número que indica la correlación esperada para ese componente del modelo genético entre los dos individuos considerados. De esta forma, podemos extender esa relación a los otros componentes, como epistasis y la parte no genética (ambiental). Sin pérdida de generalidad, asumimos también que la epistasis es usualmente despreciable en las características de interés para nosotros, por lo que, si consideramos que la fracción de la varianza ambiental compartida entre los dos individuos es la varianza del ambiente en común (\(e_{XY}\mathrm{Var(E)=Var(EC)}\), con \(\mathrm{Var(EC)}\) varianza del ambiente en común, por las siglas en inglés), sustituyendo llegamos a la ecuación general:

\[\mathrm{Cov(P_X,P_Y)= Cov(A_X,A_Y)+Cov(D_X,D_Y)+Cov(I_X,I_Y)+Cov(E_X,E_Y)}\] \[ \begin{split} \mathrm{Cov(P_X,P_Y)}= a_{XY} {Var(A)} + d_{XY} {Var(D)} + {Var(EC)} \end{split} \tag{9.6} \]

Por ejemplo, para padres e hijos, utilizando los subíndices \(_P\) para padre y \(_H\) para hijo, podríamos haber derivado explícitamente la relación entre la covarianza fenotípica y los componentes de varianza:

\[\mathrm{Cov(P_P,P_H)= Cov(A_P+D_P+I_P+E_P,A_H+D_H+I_H+E_H)}\] \[\mathrm{Cov(P_P,P_H)= Cov(A_P+D_P+I_P+E_P,}\frac{1}{2} {A_P+D_H+I_H+E_H)}\] \[\mathrm{Cov(P_P,P_H)}= {Cov(A_P,}\frac{1}{2} {A_P)}=\frac{1}{2} {Cov(A_P,A_P)}=\frac{1}{2} {Var(A)}\] \[ \begin{split} \mathrm{Cov(P_P,P_H)}=\frac{1}{2} {Var(A)} \end{split} \tag{9.7} \]

Sin embargo, recordando que el parentesco aditivo entre un padre y su hijo es de \(\frac{1}{2}\), mientras que el parentesco de dominancia es de \(0\) (los hijos no comparten ninguna de las combinaciones alélicas del padre por vía de descendencia), mientras que en general padres e hijos no comparten ambiente (en un sentido amplio), sustituyendo en la ecuación general (ecuación (9.6)) arribamos al mismo resultado.

Veamos que ocurre en el caso de hermanos enteros, ahora utilizando directamente la ecuación general. Si recordamos que el parentesco aditivo entre hermanos enteros es \(a_{XY}=\frac{1}{2}\) y el parentesco de dominancia \(d_{XY}=\frac{1}{4}\), mientras que por definición comparten todo el ambiente común, sustituyendo estos valores en la ecuación (9.6) tenemos

\[ \begin{split} {Cov(P_X,P_Y)=} a_{XY} {Var(A) +} d_{XY} {Var(D) + Var(EC)} \\ {Cov_{P_{HE}}=}\frac{1}{2} {Var(A) +} \frac{1}{4} {Var(D) + Var(EC)} \\ \end{split} \tag{9.8} \]

Ejemplo 9.3

Para nuestras amigables ovejas verdes la varianza aditiva del color (verde) fue de \(3,2 \text{ unidades}^2\), la varianza de dominancia de \(0,4 \text{ unidades}^2\) y la varianza del ambiente común de \(1,2 \text{ unidades}^2\). Determinar la covarianza esperada para medios hermanos y para hermanos enteros.

De acuerdo a la ecuación (9.6), sustituyendo el valor de los coeficientes de parentesco aditivo, de dominancia y del ambiente común para cada caso tenemos que para medios hermanos

\[ \begin{split} {Cov}_{P_{MH}}=\frac{1}{4} \mathbb{V}_A=\frac{1}{4} 3,2 =0,8\text{ unidades}^2 \end{split} \]

mientras que en el caso de hermanos enteros

\[ \begin{split} {Cov}_{P_{HE}}=\frac{1}{2} \mathbb{V}_A+\frac{1}{4} \mathbb{V}_D+\mathbb{V}_{EC}= \frac{1}{2} 3,2+\frac{1}{4} 0,4+1,2 =2,9\text{ unidades}^2 \end{split} \]

PARA RECORDAR

• La distinción de la fuente de variación en componentes entre y dentro de grupos es observable. Si llamamos \(\sigma^2_B\) a la varianza entre grupos y \(\sigma^2_W\) a la varianza dentro de grupos, una forma de distinguir la importancia relativa de las dos fuentes de variación es el coeficiente de correlación intra-clase, que definimos como: \(t=\frac{\sigma^2_B}{\sigma^2_B+\sigma^2_W}\)

• Al tratarse de una relación entre una varianza y la suma de varianzas (la varianza total), el coeficiente de correlación intra-clase podrá variar entre 0 y 1.

• La similaridad entre los miembros de cada uno de los grupos, para características métricas, la podemos identificar con la covarianza entre los miembros del grupo. A medida de que los miembros de cada grupo son más similares entre sí, disminuye el efecto de variación dentro del grupo, aumentando en consiguiente la proporción que corresponde a entre grupos. Por lo tanto, podemos asimilar la covarianza dentro de grupos a la varianza entre grupos.

9.5 Estimación de las varianzas aditiva y de dominancia

Vimos más arriba que es posible relacionar la covarianza fenotípica entre individuos con un grado de parentesco determinado y los distintos componentes de varianza de nuestro modelo genético básico. En particular, usualmente es de nuestro interés poder estimar algún componente de varianza en particular, por ejemplo la varianza aditiva. Como veremos más adelante, la varianza aditiva es el numerador de ecuación que define la heredabilidad como relación de varianzas, \(h^2=\hat \sigma^{2}_A / \hat \sigma^{2}_P\), posiblemente uno de los parámetros más relevantes a la hora de decidir una estrategia de mejora, además de ser la fuente de variación sobre la que actúa normalmente la selección.

De acuerdo a la ecuación general (9.6) vista más arriba,

\[ \begin{split} {Cov(P_X,P_Y)}= a_{XY}\ \sigma^2_A + d_{XY}\ \sigma^2_D + \sigma^2_{EC} \end{split} \tag{9.9} \]

Si prestamos atención, en la ecuación (9.9) hicimos algún cambio de notación respecto a la versión original para remarcar algunos aspectos importantes de esta última fórmula. Por un lado, mezclamos letras griegas (sigma, \(\sigma\)) con nuestra notación más tradicional hasta ahora (\({Cov_{P_{XY}}}\) en lugar de \(\sigma_{XY}\), mucho más sencilla). El objetivo de esta doble notación es remarcar la existencia de una única cantidad directamente estimable de los datos, que es la covarianza fenotípica. Además, introdujimos el acento circunflejo (^) como símbolo de algo que queremos estimar (a lo que le llamamos estimador del “verdadero valor”).

A partir del resultado de la ecuación (9.9) resulta sencillo derivar un estimador de la varianza aditiva, “despejando” \(\hat \sigma^2_A\) de dicha ecuación:

\[ \begin{split} {Cov(P_X,P_Y)}= a_{XY}\ \sigma^2_A + d_{XY}\ \sigma^2_D + \sigma^2_{EC} \therefore \\ a_{XY}\ \sigma^2_A = {Cov(P_X,P_Y)} - [d_{XY}\ \sigma^2_D + \sigma^2_{EC}] \therefore \\ \hat \sigma^2_A =\frac{ {Cov_{P_{XY}}}-d_{XY}\ \hat \sigma^{2}_D - \hat \sigma^{2}_{EC}}{a_{XY}} \end{split} \tag{9.10} \]

Básicamente, nuestro estimador general de la varianza aditiva se construye restando la fracción del estimado de varianza de dominancia y de la varianza del ambiente común que correspondan, al valor obtenido de estimar la covarianza entre observaciones en los pares de individuos (es decir, la covarianza fenotípica), y luego dividiendo entre el parentesco aditivo entre esos pares. De todos estos números, los parentescos aditivos y de dominancia son usualmente conocidos, así como la presencia o ausencia de varianza de ambiente en común, aunque no -obviamente- su valor. Claramente, se trata de muchas incógnitas para una sola ecuación. Sin embargo, a partir de los datos fenotípicos, es bastante obvio que podemos utilizar el estimador clásico de la covarianza a partir de una muestra (\(\hat \sigma_{XY}=[\sum (x-\bar{x})(y-\bar{y})] /(n-1)\)) para obtener un estimado de la covarianza fenotípica (que más arriba notamos como \(\mathrm{Cov_{P_{XY}}}\) especialmente para que se entienda que es la única cantidad que podemos estimar directamente de los datos).

Esto nos deja con una herramienta de estimación muy interesante, pero a la que generalmente le faltarán insumos (información) para explotar todo su potencial. Veamos lo que ocurre con tres estructuras de parentesco que son usuales en diseños experimentales relacionados a la genética cuantitativa: a) padre-hijo (PH), b) medios-hermanos (MH) y c) hermanos enteros (HE). En el primer caso, tenemos que el parentesco aditivo vale \(1/2\) (un padre comparte exactamente la mitad de su información genética aditiva con su hijo, es el único parentesco que es determinístico en este sentido) y nada de parentesco de dominancia (no es posible que comparta ninguna combinación de sus alelos), así como nada del ambiente es común (en general, para mediciones realizadas en la misma edad en dos generaciones el ambiente ha cambiado lo suficiente como para no estar correlacionado). Por lo tanto, si sustituimos esos coeficientes en la fórmula general, tenemos

\[ \begin{split} \hat \sigma^{2}_A =\frac{[\mathrm{Cov_{P_{PH}}}- 0\ \hat \sigma^{2}_D -0\ \hat \sigma^{2}_{EC}]}{\frac{1}{2}} = 2\ \mathrm{Cov_{P_{PH}}} \\ \end{split} \tag{9.11} \]

o lo que es lo mismo, 2 veces la covarianza fenotípica entre parejas de un padre y su hijo (uno) es un estimador insesgado de la varianza aditiva (ya veremos un poquito más adelante cuales son algunas propiedades deseables de los estimadores).

Repitiendo el procedimiento para el caso de medios-hermanos, el coeficiente de parentesco aditivo es ahora de \(1/4\), mientras que el de dominancia es \(0\) y no hay un ambiente en común (porque, por ejemplo, son criados por distintas madres), lo que nos lleva a:

\[ \begin{split} \hat \sigma^{2}_A =\frac{[ \mathrm{Cov_{P_{MH}}}- 0\ \hat \sigma^{2}_D -0\ \hat \sigma^{2}_{EC}]}{\frac{1}{4}} = 4\ \mathrm{Cov_{P_{MH}}} \\ \end{split} \tag{9.12} \]

En este caso, 4 veces la covarianza fenotípica entre medio-hermanos es un estimador insesgado de la varianza aditiva (en la medida de que se cumpla lo que asumimos, por ejemplo que no comparten un ambiente en común).

Finalmente, en el caso de hermanos enteros (aquellos que comparten padre y madre), la situación se vuelve un poco más complicada. Ahora el parentesco aditivo es de \(1/2\), pero el de dominancia ya no es de \(0\) sino de \(1/4\) y en las características que tienen relación con la etapa de crecimiento el ambiente en común es considerable (pensemos, por ejemplo, en los lechones de la misma camada, donde además de compartir el ambiente uterino, los lechones comparten la madre durante la etapa de crecimiento, así como el chiquero). Esto nos lleva a que ahora

\[ \begin{split} \hat \sigma^{2}_A =\frac{[\mathrm{Cov_{P_{HE}}}-\frac{1}{4}\ \hat \sigma^{2}_D -\hat \sigma^{2}_{EC}]}{\frac{1}{2}} =2\ \mathrm{Cov_{P_{HE}}}-\frac{1}{2}\ \hat \sigma^{2}_D -2\ \hat \sigma^{2}_{EC} \leq 2\ \mathrm{Cov_{P_{HE}}} \\ \end{split} \tag{9.13} \]

ya que las varianzas deben ser mayores o iguales a \(0\). Dicho de otra forma, 2 veces la covarianza fenotípica entre hermanos enteros sobrestima consistentemente el “verdadero valor” de la varianza aditiva, excepto en el caso de que se trate de una característica en la que no exista varianza de dominancia y no exista ambiente en común. Como no tenemos forma de separar los aportes de los distintos componentes causales de varianza que quedan, \(2\ \mathrm{Cov_{P_{HE}}}\) es un estimador sesgado (hacia arriba) de la varianza aditiva.

Ejemplo 9.4

En un estudio realizado para obtener estimados de componentes genéticos de la varianza de diámetro de fibras en ovejas verdes se realizaron mediciones bajo dos diseños experimentales: 1) un diseño de medios hermanos y 2) un diseño de hermanos enteros. En el primer diseño se obtuvo un estimado de la covarianza fenotípica de \(\mathrm{Cov_{P_{MH}}}=0,45\ \mu\text{m}^2\), mientras que en el segundo se obtuvo un estimado de la covarianza fenotípica de \(\mathrm{Cov_{P_{HE}}}=1,25\ \mu\text{m}^2\). En los dos diseños los hermanos fueron separados de sus madres al nacer y alimentados y criados todos juntos (por lo tanto no compartieron un ambiente especial a las parejas de hermanos). Obtener un estimado de la varianza aditiva, así como un estimado de la varianza de dominancia a partir de los datos anteriores.

Usando la ecuación (9.6), en el caso de hermanos enteros tenemos que la covarianza fenotípica, en nuestro caso (\(\hat \sigma^{2}_{EC}=0\)) es igual a

\[ \begin{split} \mathrm{Cov_{P_{HE}}}=\frac{1}{2}\hat \sigma^{2}_A + \frac{1}{4}\ \hat \sigma^{2}_D + \hat \sigma^{2}_{EC}=\frac{1}{2}\hat \sigma^{2}_A + \frac{1}{4}\ \hat \sigma^{2}_D=1,25\ \mu\text{m}^2 \end{split} \]

Multiplicando por 2, tenemos entonces que

\[ \begin{split} 2\ \mathrm{Cov_{P_{HE}}}=\hat \sigma^{2}_A + \frac{1}{2}\ \hat \sigma^{2}_D=2 \times 1,25=2,50\ \mu\text{m}^2 \end{split} \]

Para el caso de medios hermanos, la covarianza fenotípica es igual a

\[ \begin{split} \mathrm{Cov_{P_{MH}}}=\frac{1}{4}\hat \sigma^{2}_A =0,45\ \mu\text{m}^2 \therefore \\ 4\ \mathrm{Cov_{P_{MH}}}=\hat \sigma^{2}_A =4 \times 0,45=1,80\ \mu\text{m}^2 \end{split} \]

Esto último nos da un estimado directo e insesgado de la varianza aditiva, que es por lo tanto \(\hat \sigma^{2}_A =1,80\ \mu\text{m}^2\).

Por otro lado, restando las dos ecuaciones de covarianzas multiplicadas por sus respectivos coeficientes para que en ambas el coeficiente que multiplica \(\hat \sigma^{2}_A\) sea \(1\) (y así se eliminen al restarlos), tenemos ahora

\[ \begin{split} 2\ \mathrm{Cov_{P_{HE}}}-4\ \mathrm{Cov_{P_{MH}}}=\hat \sigma^{2}_A + \frac{1}{2}\ \hat \sigma^{2}_D - \hat \sigma^{2}_A=\frac{1}{2}\ \hat \sigma^{2}_D=(2,50-1,80)\ \mu\text{m}^2 \therefore \\ \frac{1}{2}\ \hat \sigma^{2}_D=0,70\ \mu\text{m}^2 \therefore \hat \sigma^{2}_D=2 \times 0,70\ \mu\text{m}^2=1,40\ \mu\text{m}^2 \end{split} \]

Por lo tanto, para el diámetro de fibras en ovejas verdes, la varianza de dominancia es \(\hat \sigma^{2}_D=1,40\ \mu\text{m}^2\).

Propiedades deseables de los estimadores

En varias partes del libro hemos hablado de estimadores y en algunos casos hemos apelado a alguna propiedad deseable de los mismos, pero sin explicar demasiado nuestras pretensiones o siquiera qué es un estimador. Para entender mejor de lo que estamos hablando podemos poner un ejemplo sencillo: deseamos estimar la proporción varones en la población uruguaya, obviamente sin acceder a los datos censales. En un instante dado del tiempo esta proporción tendrá un valor fijo, por ejemplo, si hay 1.707.176 mujeres y 1.579.138 varones, la proporción de varones en la población total es igual a \(\frac{1.579.138}{1.579.138+1.707.176 }=0,4805195\). Claramente esta proporción variará en forma ínfima en los lapsos de tiempo de días o aún meses, por lo que podemos asumirla fija. Desafortunadamente, censar a toda la población es un trabajo enorme, que se realiza cada varios años y nosotros queremos obtener un estimado actual de la proporción de varones.

Para acometer esta tarea se nos ocurre un procedimiento sencillo (entre muchos posibles): contar el número de peatones de cada sexo que pasan por una esquina concurrida de Montevideo durante un intervalo de tiempo pre-definido (por ejemplo, una hora). Al cabo de esa hora, tendremos una tabla con conteos para varones y mujeres y por lo tanto podemos sacar de la misma la fracción correspondiente de varones. Claramente, en una hora nunca va a pasar toda la población de Uruguay por esa esquina, por lo que la fracción que salga de nuestro conteo no será otra cosa que un estimador del “verdadero” valor poblacional. Un estimador es por lo tanto un estadístico (un procedimiento de cálculo a realizar con los datos) que pretende estimar el verdadero valor del parámetro.

Los estimadores son en sí mismo variables aleatorias ya que su valor dependerá, en general, de la muestra extraída. Al tratarse de variables aleatorias, si realizamos el experimento de repetir el muestreo muchas veces, en nuestro caso podría ser realizar el conteo todos los días durante un mes, por ejemplo, los valores del estimador variarán consecuentemente. Una forma sencilla de imaginarnos el impacto de la variación aleatoria en la repetición del muestreo es hacer un histograma con los valores del estimador obtenido cada día. De hecho, si pensamos un poco, es posible que nuestro estimador previo se encuentre afectado por el día de la semana (los domingos casi nadie pasa por esa esquina y luego de una hora apenas habremos registrado de 10 a 15 personas), por lo que podemos pensar en el mismo estimador (fracción de varones en la muestra) pero basado en un procedimiento de muestreo diferente: contar los sexos en las primeras \(N\) personas que pasen a partir de las 8 de la mañana. Este estimador nos lleva a preguntarnos cómo afectará el tamaño de la muestra el comportamiento del estimador. Si \(N=1\) el estimador solamente podrá decir que la población está constituida \(100\%\) por mujeres o \(100\%\) por varones. Si \(N=2\), los valores posibles del estimador serán \(0\), \(50\%\), o \(100\%\). Con \(N=3\), los valores posibles serán \(0\), \(33\%\), \(66\%\) o \(100\%\). ¿Qué ocurriría si en realidad el verdadero valor en la población es de \(50\%\) y nuestro \(N=3\)? En este caso, el estimador siempre le erraría al verdadero valor al menos en \(17\%\), por arriba o por abajo. Claramente, no parece un estimador que funcione muy bien con este tamaño muestral.

Lo anterior nos lleva a preguntarnos qué características serían deseables en un estimador, para luego ver si nuestro estimador cumple con las mismas. Existen varias características que podrían ser deseables en determinados casos, pero en general las siguientes son siempre deseables:

1. Insesgado Un estimador es insesgado cuando el valor medio de las estimaciones obtenidas al repetir el experimento sucesivamente para diferentes muestras es igual al valor del parámetro. De otra forma, si \(\theta\) es el parámetro que queremos estimar, entonces \(\mathbb{E}(\hat \theta)=\theta\).

2. Consistente Un estimador es consistente cuando el valor estimado se aproxima al del parámetro desconocido al aumentar el tamaño de la muestra arbitrariamente. En términos matemático \(\hat{\theta}_{n \to \infty} \to \theta\).

3. Eficiente Un estimador es eficiente cuando su varianza es tan pequeña como sea posible.

4. Suficiente Un estimador es suficiente cuando aprovecha toda la información existente en la muestra.

Claramente, varias de estas propiedades es necesario analizarlas y demostrarlas en forma matemática para los estimadores de interés, pero solamente como ejemplo, podemos ver que nuestro estimador de la proporción de varones en la población uruguaya es (al menos) insesgado y consistente. Por ejemplo, aún con tamaños muestrales pequeños, si bien el valor derivado de cada muestra se puede apartar en forma sustantiva del verdadero valor, el valor promedio obtenido de repetir el muestreo en forma consistente coincidirá con el valor del parámetro poblacional. Por otro lado, si aumentamos el tamaño muestral de \(N=3\) a \(N=100\), los resultados podrán aproximarse al verdadero valor con una diferencia de \(0,5\%\), y si lo aumentamos aún más, a \(N=1000\), se podrán aproximar más aún (a \(0,05\%\)), por lo que el estimador es consistente.

PARA RECORDAR

• Podemos describir la covarianza fenotípica mediante: \({Cov(P_X,P_Y)}= a_{XY}\ \sigma^2_A + d_{XY}\ \sigma^2_D + \sigma^2_{EC}\)

• El estimador general de la varianza aditiva se construye restando la fracción del estimado de varianza de dominancia y de la varianza del ambiente común que correspondan, al valor obtenido de estimar la covarianza entre observaciones en los pares de individuos (es decir, la covarianza fenotípica), y luego dividiendo entre el parentesco aditivo entre esos pares.

• Los estimadores son estadísticos que pretenden estimar el verdadero valor del parámetro, son en sí mismo variables aleatorias ya que su valor dependerá, en general, de la muestra extraída.

• Las propiedades deseables en un estimador es que el mismo sea: insesgado, consistente, eficiente y suficiente.

Estimación de la varianza aditiva a partir del análisis de varianza (ANOVA)

El análisis de varianza, desarrollado por Ronald Fisher, es un método que nos permite estimar y comparar diferentes fuentes de variación. En una de sus versiones usuales, que seguramente hayas estudiado, es una herramientas que nos permite comparar las medias de diferentes tratamientos, así como la significación estadística de estas diferencias (Modelo I, o de efectos fijos). En otra versión (Modelo II, o de efectos aleatorios), los niveles del factor relevante se consideran una muestra aleatoria de todos los niveles posibles y por lo tanto los resultados se pueden extrapolar al resto de la población. Esto va a resultar particularmente atractivo para nosotros porque a partir de un diseño experimental con algunos animales vamos a poder estimar la varianza aditiva en toda la población y no solo restringiéndonos a los animales incluidos en el experimento.

Consideremos un diseño experimental de medios hermanos, en donde cada macho de los incluídos en el experimento se aparea con varias hembras, que dejan cada una una cría, como se puede apreciar en la Figura 9.10.

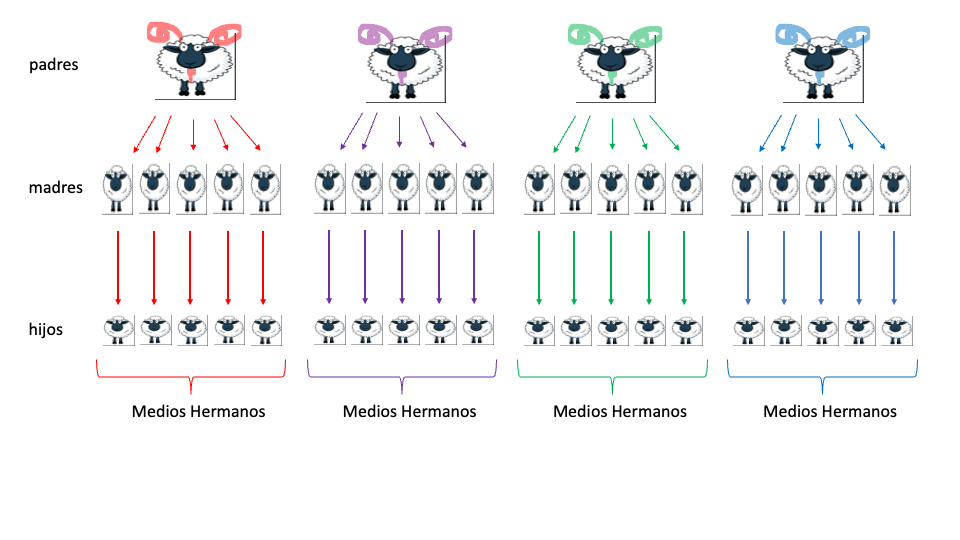
Figura 9.10: Representación de un experimento de estimación de la varianza aditiva mediante un diseño de medios hermanos. Cada carnero (padres, línea superior) se aparea con varias ovejas (madres, línea del medio), formando cada padre un grupo de medios hermanos entre sí (línea de abajo). Fuente del diseño de las ovejas: cliparts.co, modificado para este trabajo.

En la misma, cada uno de los 4 carneros (padres) se aparea con 5 ovejas (madres) y el resultado es, a partir de una cría por madre, grupos de 5 medios hermanos. En estos animales será donde realizaremos las mediciones fenotípicas de nuestro interés, por ejemplo peso al destete, peso del primer vellón o la característica de interés. Como los grupos se forman a partir del padre en común, las madres se eligen al azar, a este modelo también se le conoce como modelo padre.

Desde el punto de vista estadístico podemos escribir el modelo como

\[ \begin{split} Y_{ij}=\mu+s_i+e_{ij} \end{split} \tag{9.14} \]

donde \(Y_{ij}\) representa el fenotipo del animal \(j\) dentro del padre \(i\), \(\mu\) es la media de la característica en la población, \(s_i\) representa el desvío de la media correspondiente al padre \(i\) (\(s\) por “sire”) y \(e_{ij}\) representa el “residuo” del animal \(j\) dentro del padre \(i\). Si suponemos que el diseño del experimento es balanceado, entonces el número de hijos por padre será igual (\(k\) medios hermanos) en todos los \(s\) grupos. En este diseño es muy fácil identificar las dos fuentes de variación: por un lado la variación producida por diferencias entre padres y por el otro lado las diferencias de los animales dentro del grupo de medios hermanos. Como no tenemos ninguna hipótesis particular ni factor asociado a ella que explique los desvíos de los hijos respecto al valor del padre, tratamos a estos desvíos como el residuo del modelo (que puede contener tanto errores de medición, efectos no explicados por el padre y otras fuentes de variación no relevante para nosotros). Dado que una fuente de variación es entre grupos y la otra dentro de grupos, llamamos a sus varianzas respectivamente \(\sigma^2_B=\sigma^2_S\) (la \(_B\) es de “between”, entre, mientras que la \(_S\) es por “sire”) y \(\sigma^2_W\) (por “within”, dentro). Cuando vimos más arriba el coeficiente de correlación intra-clase le llamamos \(\sigma^2_B\) a la varianza entre grupos, mientras que acá vamos a notarla con \(\sigma^2_S\) para reforzar la idea de que es el efecto de los padres. Teniendo en cuenta todo lo anterior, podemos organizar la información en una tabla de ANOVA como la siguiente:

\(\text{Fuente de variación}\)	\(\text{G. L.}\)	\(\text{Cuadrado medio}\)	\(\mathrm{E(MS)}\)
Entre padres (grupos de medios hermanos)	\(s-1\)	\(\mathrm{MS_S}\)	\(\sigma^2_W+k\sigma^2_S\)
Dentro de grupos (medios hermanos)	\(s(k-1)\)	\(\mathrm{MS_W}\)	\(\sigma^2_W\)
Total	\(sk-1\)

Los cuadrados medios se calculan directamente de los datos fenotípicos, de acuerdo a

\[ \begin{split} \mathrm{MS_S}=\frac{\sum_{i=1}^s n_i (\bar x_i - \bar x)^2}{s-1} \end{split} \]

y

\[ \begin{split} \mathrm{MS_W}=\frac{\sum_{i=1}^s \sum_{j=1}^{n_i} (x_{ij}-\bar x_i)^2 }{sk-s} \end{split} \]

Si observamos la última columna de la tabla de ANOVA, la misma contiene la esperanza de los cuadrados medios, es decir, su valor teórico. Si igualamos el valor teórico esperado al valor del cuadrado medio correspondiente podemos despejar estimadores para las varianzas entre y dentro. Por ejemplo, si operamos con la línea correspondiente a la fuente de variación dentro de grupo, tenemos que

\[ \begin{split} \sigma^2_W= {MS_W} \end{split} \tag{9.15} \]

Es decir, el cuadrado medio \(\mathrm{MS_W}\) es un estimador insesgado de la varianza dentro (\(\sigma^2_W\)). Igualando el cuadrado medio entre grupos a su esperanza y sustituyendo \(\sigma^2_W\) por \(\mathrm{MS_W}\) tenemos

\[ \begin{split} \mathrm{MS_S}=\sigma^2_W+k\sigma^2_S=\mathrm{MS_W}+k\sigma^2_S \therefore \\ k\sigma^2_S=\mathrm{MS_S}-\mathrm{MS_W} \therefore \\ \sigma^2_S=\frac{\mathrm{MS_S-MS_W}}{k} \end{split} \tag{9.16} \]

En el caso de que el diseño sea desbalanceado, es decir que el número de hijos por padre (\(n_i\)) no sea el mismo, si llamamos \(N=\sum n_i\) al número total de hijos de todos los toros, entonces el factor \(k\) corregido se calcula como

\[ \begin{split} k=\frac{1}{s-1}\left(N-\frac{\sum n_i^2}{N}\right) \end{split} \tag{9.17} \]

Pero en nuestro modelo, las diferencias entre grupos de medios hermanos (varianza \(\sigma^2_S\)) se corresponden con la similaridad dentro de cada grupo de medios hermanos, es decir su covarianza (\(\mathrm{Cov_{P_{MH}}}\)), es decir

\[ \begin{split} \sigma^2_S= {Cov_{P_{MH}}} \end{split} \tag{9.18} \]

Pero, de acuerdo a la ecuación (9.12), en el caso de medios hermanos la relación entre la covarianza (observable) de medios hermanos y la varianza aditiva (a estimar) está dada por

\[ \begin{split} \hat \sigma^{2}_A =4\ {Cov_{P_{MH}}} \end{split} \]

Por lo tanto, uniendo el resultado de esta última ecuación con la ecuación (9.18), tenemos que nuestro estimador de la varianza aditiva a partir del análisis de varianza está dado por

\[ \begin{split} \hat \sigma^{2}_A =4\ {Cov_{P_{MH}}} =4 \sigma^{2}_S\\ \end{split} \tag{9.19} \]

Ejemplo 9.5

En la población de ovejas verdes que han estado presentes en varias partes del libro se realizó un experimento para estimar la varianza aditiva del peso del vellón verde limpio (PVVL). Teniendo en cuenta las condiciones de la población se trabajó con un diseño de medios hermanos balanceado, donde los segundos vellones de 4 medios hermanos por carnero (con 4 carneros) fueron medidos. Los resultados de la medición se encuentran en la tabla siguiente.

Padre	MH	Peso vellón limpio (kg)
p1	mh1.1	\(3,5\)
p1	mh1.2	\(3,4\)
p1	mh1.3	\(3,9\)
p1	mh1.4	\(3,7\)
p2	mh2.1	\(4,0\)
p2	mh2.2	\(4,1\)
p2	mh2.3	\(4,4\)
p2	mh2.4	\(3,7\)
p3	mh3.1	\(2,9\)
p3	mh3.2	\(2,8\)
p3	mh3.3	\(4,1\)
p3	mh3.4	\(3,5\)
p4	mh4.1	\(4,3\)
p4	mh4.2	\(3,6\)
p4	mh4.3	\(3,1\)
p4	mh4.4	\(3,4\)

Estimar la varianza aditiva de peso de vellón verde limpio a partir de los datos.

De acuerdo a lo que vimos previamente, podemos organizar una tabla de ANOVA con los estimadores derivados de los cuadrados medios y luego igualar estos resultados a las esperanzas. El cuadrado medio de los padres se calcula como

\[ \begin{split} {MS_S}=\frac{\sum_{i=1}^s n_i (\bar x_i - \bar x)^2}{s-1} \end{split} \]

por lo que debemos calcular antes la media general y las medias para cada padre. Las mismas son

Padre	Media PVVL (kg)	Media general (kg)	Desvío padre (kg)	Desvío cuadrado (\(kg^2\))
p1	\(3,625\)	\(3,65\)	\(-0,025\)	\(0,000625\)
p2	\(4,050\)	\(3,65\)	\(0,400\)	\(0,160000\)
p3	\(3,325\)	\(3,65\)	\(-0,325\)	\(0,105625\)
p4	\(3,600\)	\(3,65\)	\(-0,050\)	\(0,002500\)
Suma			\(0\)	\(0,268750\)

Por lo tanto, tomado los valores de la tabla anterior, tenemos que el cuadrado medio de padres es

\[ \begin{split} {MS_S}=\frac{\sum_{i=1}^s n_i (\bar x_i - \bar x)^2}{s-1}=\frac{4 \times 0,268750}{4-1} \therefore \\ {MS_S}=0,3583333\ \text{kg}^2 \end{split} \]

Por otro lado, para el cuadrado medio del error necesitamos los desvíos de cada observación respecto a la media de su padre y elevar esa diferencia al cuadrado, es decir

Padre	MH	PVLL (kg)	Desvío (kg)	Desvío cuadrado (\(kg^2\))
p1	mh1.1	\(3,5\)	\(-0,125\)	\(0,015625\)
p1	mh1.2	\(3,4\)	\(-0,225\)	\(0,050625\)
p1	mh1.3	\(3,9\)	\(0,275\)	\(0,075625\)
p1	mh1.4	\(3,7\)	\(0,075\)	\(0,005625\)
p2	mh2.1	\(4,0\)	\(-0,050\)	\(0,002500\)
p2	mh2.2	\(4,1\)	\(0,050\)	\(0,002500\)
p2	mh2.3	\(4,4\)	\(0,350\)	\(0,122500\)
p2	mh2.4	\(3,7\)	\(-0,350\)	\(0,122500\)
p3	mh3.1	\(2,9\)	\(-0,425\)	\(0,180625\)
p3	mh3.2	\(2,8\)	\(-0,525\)	\(0,275625\)
p3	mh3.3	\(4,1\)	\(0,775\)	\(0,600625\)
p3	mh3.4	\(3,5\)	\(0,175\)	\(0,030625\)
p4	mh4.1	\(4,3\)	\(0,700\)	\(0,490000\)
p4	mh4.2	\(3,6\)	\(0,000\)	\(0,000000\)
p4	mh4.3	\(3,1\)	\(-0,500\)	\(0,250000\)
p4	mh4.4	\(3,4\)	\(-0,200\)	\(0,040000\)
Suma		\(58,4\)	\(0\)	\(2,265\)

Por lo tanto, poniendo estos valores en la fórmula y con \(s=4\), \(k=4\) y \(sk-s=12\) tenemos

\[ \begin{split} {MS_W}=\frac{\sum_{i=1}^s \sum_{j=1}^{n_i} (x_{ij}-\bar x_i)^2 }{sk-s}=\frac{2,265}{12}=0,18875\ \text{kg}^2 \end{split} \]

Ahora, usando los resultados de las ecuaciones (9.16) y (9.19),

\[ \begin{split} \sigma^2_S=\frac{ {MS_S-MS_W}}{k}=\frac{0,3583333-0,18875}{4}=0,04239583\ \text{kg}^2 \\ \sigma^2_A=4\ \sigma^2_S=4 \times 0,04239583= 0,1695833\ \text{kg}^2 \end{split} \]

que es el resultado que buscábamos.

Estimaciones basadas en modelos mixtos lineales

Los procedimientos de estimación de los componentes de varianza que vimos hasta ahora se basan en diseños de estructuras de parentesco determinadas, algo que puede ser relativamente sencillo o práctico de hacer en determinadas especies y casi imposible en otras. Más aún, el plantear este tipo de experimentos para la determinación de componentes de varianza suele traer aparejado costos y complejidades importantes, lo que limita en general el número de individuos que participan del estudio. A su vez, esto implica errores importantes en las estimaciones de los componentes de varianza que muchas veces reducen en forma sustantiva la utilidad de los resultados obtenidos.

Como veremos más adelante en el curso y en cursos específicos más avanzados, el procedimiento normalmente utilizado en la estimación de varianzas para las evaluaciones genéticas se basa en procedimientos iterativos de ajuste a los datos, “frecuentistas” o “bayesianos”, a partir de las ecuaciones del modelo mixto lineal, que usualmente se conocen como BLUP (por Mejor Predictor Lineal Insesgado, en inglés). Para que este procedimiento funcione se precisa, aparte de los datos fenotípicos de la característica a la que le queremos estimar los componentes de varianza, la matriz de parentesco aditivo entre los animales que participan de la evaluación. La idea básica en el procedimiento “frecuentista” es que si bien las varianzas (por ejemplo genética aditiva y ambiental) son desconocidas, es posible introducir valores arbitrarios para las mismas y ver el ajuste del modelo con esa prueba (por ejemplo, a través de la función de verosimilitud). El paso siguiente será cambiar ligeramente esos valores y recalcular la verosimilitud a cada vez que cambiamos los valores de las varianzas. Al repetir este proceso, con suerte se encontrará una tendencia a que crezca la verosimilitud hasta determinado punto en que comienza a bajar nuevamente: en este caso, el último punto de crecimiento sería el máximo de la función de verosimilitud y por lo tanto el valor de las varianzas que lo produjeron el mejor estimador puntual de las mismas. En algunos casos, es posible derivar formas explícitas para la varianza asintótica de los estimadores de varianza, lo que servirá para determinar los intervalos de confianza asintóticos de los mismos.

Los procedimientos “bayesianos MCMC” (Cadenas de Markov Monte Carlo) difieren del anterior en que hacen uso de información a priori sobre la distribución de los parámetros a estimar (las varianzas, por ejemplo) y que el resultado es la distribución a posteriori de los parámetros (que son también considerados variables aleatorias), por lo que se puede realizar inferencia directamente sobre estas distribuciones (sin caer en la consideración de “asintótico”).

En cualquier caso, es de destacar que si bien no existe un experimento diseñado para estimar los componentes y que por lo tanto las relaciones entre individuos son variadas, la clave de la estimación sigue siendo la relación esperada (parentesco) entre individuos. Esta información se encuentra ahora especificada en la matriz de parentesco aditivo \(\mathbf A\), que también se conoce como matriz del numerador del parentesco. La razón de este nombre es que si recordamos la ecuación (9.5) con la relación entre la definición del coeficiente de parentesco de Sewall Wright (1922) y el parentesco aditivo, para los individuos \(i\) y \(j\) la misma era

\[ \begin{split} R_{ij}= \frac{a_{ij}}{\sqrt{(1+F_i)(1+F_j})} \end{split} \]

y por lo tanto los elementos de \(\mathbf A\), que para los individuos \(i\) y \(j\) son \(A_{i,j}=A_{j,i}=a_{ij}\), son los elementos del numerador del coeficiente de parentesco de Sewall Wright (1922). Más adelante, en el Ejemplo 9.6 una de las preguntas nos permitirá vincular más claramente estas dos formas de ver el parentesco.

PARA RECORDAR

• Estadísticamente, podemos definir el modelo padre como: \(Y_{ij}=\mu+s_i+e_{ij}\) dónde \(Y_{ij}\) representa el fenotipo del animal \(j\) dentro del padre \(i\), \(\mu\) es la media de la característica en la población, \(s_i\) representa el desvío de la media correspondiente al padre \(i\) y \(e_{ij}\) representa el “residuo” del animal \(j\) dentro del padre \(i\).

• En este tipo de diseño podemos identificar dos fuentes de variación: la producida por diferencias entre padres y por el otro lado las diferencias de los animales dentro del grupo de medios hermanos. Determinadas estas fuentes, llamamos a sus varianzas respectivamente \(\sigma^2_B=\sigma^2_S\) (la \(_B\) es de “between”, entre, mientras que la \(_S\) es por “sire”) y \(\sigma^2_W\) (por “within”, dentro).

• En el caso de medios hermanos la relación entre la covarianza (observable) de medios hermanos y la varianza aditiva (a estimar) está dada por: \(\hat \sigma^{2}_A =4\ \mathrm{Cov_{P_{MH}}}\)

• Podemos realizar estimaciones a través de modelos mixtos lineales mediante el BLUP, para este procedimiento necesitamos, además de los datos fenotípicos de la característica a la que le queremos estimar los componentes de varianza, la matriz de parentesco aditivo entre los animales que participan de la evaluación.

9.6 Parentesco genómico

Hasta el momento nos hemos manejado con los parentescos esperados a partir de las reglas básicas de transmisión de la información de progenitores a descendencia, pero sin posibilidad de atender en alguna medida la verdadera proporción del genoma compartido por dos individuos. Es por esta razón que hemos llamado de parentesco estadístico (o probabilístico) al tratamiento basado en la esperanza matemática de la fracción del componente del genoma de nuestro interés (aditivo, dominancia, etc.) compartido entre dos individuos. Como vimos más arriba, la única relación de parentesco que comparte siempre exactamente la misma fracción con otro es el de progenitor-progenie, en cuyo caso la mitad del genoma es compartido y por lo tanto el parentesco aditivo es igual a \(\frac{1}{2}\). En el resto de las relaciones entre individuos, la fracción del genoma compartido será una variable aleatoria, con una distribución determinada, con su media y con su varianza.

Sin embargo, los avances en la genómica durante los últimos 20 años han permitido que el genotipado de animales, plantas, etc. sea una práctica rutinaria en diferentes programas de mejoramiento genético y aún una poderosa herramienta para el estudio de las poblaciones humanas. En el caso del mejoramiento genético, conocer la información del genotipo de los individuos mejora sustancialmente la predicción de las evaluaciones genéticas, aportando información adicional tanto para los individuos genotipados como para sus parientes no genotipados. La información aportada por el genotipado puede ayudar, por ejemplo, a entender las diferencias en “performance” entre dos hermanos, que a priori tendrían el mismo parentesco con sus padres (que son los que aportan el material genético en la misma proporción para ambos). Una forma de ver la relación entre el parentesco estadístico que vimos previamente y el genómico es la de considerar al primero como el parentesco esperado y al segundo como el parentesco realizado (u observado).

Veamos entonces de qué se trata el parentesco genético. Lo primero es definir de qué se trata el genotipado y qué es lo que usualmente obtenemos de un chip de genotipado. El genotipado consiste básicamente en determinar el genotipo, es decir el par de alelos concretos, presentes en cada uno de los loci de interés. Normalmente se trata de SNPs, es decir, variantes de un solo nucleótido. Si bien en cada posición del genoma usualmente podemos encontrar cualquiera de las 4 bases (A, C, G o T) y por lo tanto \(\frac{k(k+1)}{2}=\frac{4\times5}{2}=10\) pares posibles, en general, los chips de genotipado se construyen sobre loci que son mayoritariamente bi-alélicos, es decir, loci para los cuales solo vamos a encontrar una de dos posibilidades. Esto reduce el número de pares posibles a \(\frac{k(k+1)}{2}=\frac{2\times 3}{2}=3\). Por ejemplo, si se trata de un locus en el que los dos alelos presentes son A y G, podremos tener cualquiera de los siguientes tres genotipos: AA, AG o GG. Como en cada locus tenemos 3 posibilidades (con marcadores bi-alélicos), en principio, si los marcadores se encuentran a suficiente distancia entre ellos, tendremos \(3^m\) combinaciones distintas posibles, con \(m\) el número de marcadores. Pese a que no parezca muy llamativo, este número de combinaciones posibles es impactante. Por ejemplo, si \(m=10\) marcadores, entonces \(3^{10}=59.049\) combinaciones diferentes posibles (individuos que podríamos distinguir), pero si pasamos a \(m=20\), entonces \(3^{20}=3.486.784.401\), es decir casi \(3.500\) millones de combinaciones diferentes posibles. Los chips que se utilizan normalmente (densidad media) en mejoramiento genético animal contienen del orden de los \(50.000\) marcadores y el número \(3^{50.000}\) escapa a la representación por la mayor parte de las computadoras disponibles (que indican que el mismo es igual a infinito para ellas).

En el cuadro siguiente vemos un ejemplo de uno de los formatos típicos para el genotipado, el formato conocido como tped, para 3 individuos. Las primeras 4 columnas corresponden a información sobre cada locus genotipado: 1) el cromosoma, 2) la identificación del SNP, 3) la posición en el genoma en centi-Morgans (usualmente sustituida por un \(0\) cuando no se conoce) y 4) la posición en el cromosoma, en bases. A partir de la quinta columna en adelante, cada par de columnas se corresponde a un individuo, siendo cada columna la correspondiente a uno de los dos alelos y la otra columna al otro alelo. Por ejemplo, para el primer SNP, su identificación es “snp1”, el mismo se encuentra en el cromosoma 1, en la posición \(50.123\) (respecto a algún genoma de referencia). El primer individuo (columnas 5 y 6) posee el genotipo \(AA\), el segundo individuo (columnas 7 y 8) el genotipo \(AG\) y el tercer individuo (columnas 9 y 10) el genotipo \(GG\). Obviamente, los dos alelos posibles son A y G para este SNP. Para el segundo SNP (cromosoma 1, posición \(61.230\)), los genotipos son \(CT\), \(CC\) y \(CT\). De acuerdo al último SNP que aparece en la tabla, el chip tendría del orden de los 52 mil SNPs.

Cromosoma	ID	Pos (cM)	Bases
1	snp1	0	50123	A	A	A	G	G	G
1	snp2	0	61230	C	T	C	C	C	T
1	snp3	0	97333	G	G	T	T	G	T
…	…	0	…	…	…	…	…	…	…
22	snp52125	0	235243	A	A	A	A	A	G

La pregunta que podemos hacernos ahora es cómo transformar la información de secuencias en cada individuo, los genotipos, en alguna forma numérica que nos sirva para calcular similaridades entre individuos. Como veremos enseguida, existen muchas alternativas posible para esta conversión, aunque la idea de base es siempre la misma. Una distinción muy importante a conservar en mente es que mientras en el caso de parentesco estadístico estamos hablando siempre de alelos IBD, en el caso de parentesco genómico nos vamos a enfocar en alelos IBS (idénticos en estado), ya que no conocemos las relaciones entre los individuos y apenas el genotipo observado para cada locus.

Contenido génico

Al observar el cuadro de arriba, posiblemente haya pasado por nuestra mente si no podíamos reducir la información para cada individuo de dos columnas a una sola columna. De hecho, al existir para cada SNP solamente 3 combinaciones posibles, si despreciamos la información de fase⁸⁴ (que por otra parte, en el genotipado no disponemos de ella), claramente alcanzaría con colocar un número distinto para cada combinación. Si pensamos un poco más la idea, en lugar de colocar un número arbitrario a cada combinación (por ejemplo 1 para un homocigoto, 7 para el otro y 9 para el heterocigoto), podríamos pensar en el marco de nuestro modelo genético básico, y el parentesco aditivo. Si el efecto de los alelos es aditivo, entonces cuando tengo dos alelos del mismo tipo debería tener el doble de efecto. Entonces, si pensamos en el número de copias de uno de los dos alelos elegido en forma arbitraria, por ejemplo el segundo en orden alfabético, tenemos que para un locus con alelos posibles A y G, las combinaciones y el número de copias del alelo G (el segundo por orden alfabético entre A y G) estarían dadas por

Cromosoma	Cantidad de copias de \(\mathrm{G}\)
\(\mathrm{AA}\)	\(0\)
\(\mathrm{AG}\)	\(1\)
\(\mathrm{GG}\)	\(2\)

Con esta información, podemos convertir los genotipos de los 3 individuos para el primer SNP de la tabla con los genotipados en \(AA=0\) (primer individuo), \(AG=1\) (segundo individuo) y \(GG=2\) para el tercer individuo.

Para el segundo SNP tenemos los alelos C y T, por lo que alfabéticamente el segundo es T y el cuadrito resumen de las combinaciones y su valor de contenido génico sería

Genotipo	Cantidad de copias de \(\mathrm{T}\)
\(\mathrm{CC}\)	\(0\)
\(\mathrm{CT}\)	\(1\)
\(\mathrm{TT}\)	\(2\)

y por lo tanto, los valores para los 3 individuos serían \(CT=1\) (individuo 1), \(CC=0\) (individuo 2) y \(CT=1\) (individuo 3). Obviamente, como la elección del alelo de referencia fue completamente arbitaria, para marcadores bi-alélicos el conteo para el otro alelo es igual a dos menos el conteo del alelo de referencia.

Si aplicamos el método anterior a cada SNP de la tabla de genotipado, tenemos ahora que podemos escribirla como

Cromosoma	ID	Pos..cM.	Bases	Individuo.1	Individuo.2	Individuo.3
1	snp1	0	50123	\(0\)	\(1\)	\(2\)
1	snp2	0	61230	\(1\)	\(0\)	\(1\)
1	snp3	0	97333	\(0\)	\(2\)	\(1\)
…	…	0	…	…	…	…
22	snp52125	0	235243	\(0\)	\(0\)	\(1\)

Claramente, además de reducir el número de columnas necesarias para representar cada genotipo, tenemos ahora una representación numérica que se asocia claramente a nuestro modelo genético básico, en particular a los efectos aditivos del mismo. Es más, ahora queda muy claro que podemos descomponer la tabla de genotipado en dos partes, aquella con información sobre los marcadores (columnas 1 a 4) y aquella con información de los genotipos de los individuos (columna 5 en adelante). Con esta segunda parte podemos formar una matriz numérica de contenido génico, a la que por comodidad le ponemos nombres de filas (los identificadores de cada marcador) y de columnas (identificación de individuo), lo que nos deja con algo así

	Individuo 1	Individuo 2	Individuo 3
snp1	\(0\)	\(1\)	\(2\)
snp2	\(1\)	\(0\)	\(1\)
snp3	\(0\)	\(2\)	\(1\)
…	…	…	…
snp52125	\(0\)	\(0\)	\(1\)

Al tratarse de una tabla (matriz) numérica, podemos aplicar sobre ella distintas operaciones, como veremos más adelante. Como cada celda de la tabla es una variable aleatoria de conteo, si llamamos \(z_i\) al conteo del alelo de referencia para el individuo \(i\), entonces podemos calcular para el mismo estadísticos resumen, como la media y la varianza. Si asumimos que cada marcador se encuentra en equilibrio de Hardy-Weinberg (algo que es bastante común para la mayor parte de los marcadores) y llamamos \(A_1\) al alelo de referencia y \(A_2\) al alternativo, entonces podemos resumir la información para el cálculo de la media y la varianza en el siguiente cuadro

Genotipo	Frecuencia	\(z\)	\(z^2\)
\(A_1A_1\)	\(p^2\)	\(2\)	\(2^2=4\)
\(A_1A_2\)	\(2pq\)	\(1\)	\(1^2=1\)
\(A_2A_2\)	\(q^2\)	\(0\)	\(0^2=0\)
\(\mathbb{E}()\)		\(2p\)	\(4p^2+2pq\)

La esperanza de cada una de las variables aleatorias (\(\mathbb{E}(z)\) y \(\mathbb{E}(z^2)\)) se calculan como de costumbre, sumando los productos de los valores por sus frecuencias correspondientes. Es decir

\[ \begin{split} \mathbb{E}(z)=2 \times p^2 + 1 \times 2pq + 0 \times q^2=2p^2+2pq=2p(p+q)=2p\\ \mathbb{E}(z^2)=4 \times p^2 + 1 \times 2pq + 0 \times q^2=4p^2+2pq \end{split} \]

De lo anterior surge claramente que la media del contenido génico es igual a \(2p\), lo que era de esperar ya que \(p\) es la frecuencia del alelo de referencia y en cada genotipo hay dos alelos, por lo que el conteo esperado es dos veces la frecuencia del alelo de referencia. Para calcular la varianza del contenido podemos recurrir a la relación \(\mathbb{V}(z)=\mathbb{E}(z^2)-\mathbb{E}(z)^2\), por lo que

\[ \begin{split} \mathbb{V}(z)=\mathbb{E}(z^2)-\mathbb{E}(z)^2=(4p^2+2pq)-(2p)^2=4p^2+2pq-4p^2=2pq \end{split} \tag{9.20} \]

Es decir, la varianza en contenido génico (el número de alelos de referencia) es igual a \(2pq\).

Si recordamos la definición de parentesco aditivo como correlación entre valores de cría de dos inviduos, entonces para calcular el coeficiente de correlación vamos a precisar conocer la covarianza primero. Como vimos previamente, para dos individuos \(i\) y \(j\), al extraer un alelo en cada uno de ellos al azar, la probabilidad de que los mismos sean IBD es \(f_{ij}=\Theta_{ij}=A_{ij}/2\), que es el coeficiente de coancestría de Malécot. Para calcular la covarianza de conteo génico entre dos individuos podemos recurrir a la fórmula de covarianza

\[ \begin{split} {Cov}(z_i,z_j)=\mathbb{E}(z_iz_j)-\mathbb{E}(z_i)\mathbb{E}(z_j) \end{split} \tag{9.21} \]

Por otro lado, las esperanzas de \(z_i\) y \(z_j\) son iguales a \(\mathbb{E}(z)=2pq\).

Para calcular la esperanza del producto cruzado \(\mathbb{E}(z_iz_j)\) podemos razonar de la siguiente forma: tenemos cuatro formas de elegir un alelo en cada uno de los dos individuos; la única forma en que el producto \(z_iz_j\) sea igual a 1 es que \(z_i\) sea \(A_1\) y \(z_j\) también lo sea. O sea, el primer alelo debe ser \(A_1\), con probabilidad de extracción \(p\) y el segundo también, pero como ya vimos antes, esto puede ocurrir por dos razones: que los dos alelos extraídos sean IBD, con probabilidad \(\Theta_{ij}=A_{ij}/2\), o que los dos alelos no sean IBD pero que por azar se extraiga otro alelo \(A_1\) (IBS), esta segunda posibilidad entonces con probabilidad \((1-\Theta_{ij})p=(1-A_{ij}/2)p\). Multiplicando ambas por la probabilidad \(p\) de que el primer alelo sea \(A_1\) y multiplicando por 4 (por las cuatro posibles combinaciones), tenemos

\[\mathbb{E}(z_iz_j)=4p[\frac{A_{ij}}{2}+\left(1-\frac{A_{ij}}{2}\right)p]=2pA_{ij}+4p^2-2p^2A_{ij} \therefore\] \[\mathbb{E}(z_iz_j)=2A_{ij}(p-p^2)+4p^2=2p(1-p)A_{ij}+4p^2 \therefore\] \[ \begin{split} \mathbb{E}(z_iz_j)=2pqA_{ij}+4p^2 \end{split} \tag{9.22} \]

Sustituyendo el resultado de la ecuación (9.22) en la ecuación (9.21) tenemos

\[ \begin{split} {Cov}(z_i,z_j)=\mathbb{E}(z_iz_j)-\mathbb{E}(z_i)\mathbb{E}(z_j)=2pqA_{ij}+4p^2-[(2p)(2p)] \therefore \\ {Cov}(z_i,z_j)=2pqA_{ij}+4p^2-4p^2=2pqA_{ij} \end{split} \tag{9.23} \]

Este es el resultado de la covarianza en contenido génico entre dos individuos para un locus determinado. La correlación entre los contenidos génicos de los individuos \(i\) y \(j\) es igual a la covarianza entre \(z_i\) y \(z_j\) divida entre el producto de las raíces cuadradas de las varianzas, es decir \(\sqrt{\mathbb{V}(z_i)\mathbb{V}(z_j)}=\sqrt{(2pq)(2pq)}=\sqrt{(2pq)^2}=2pq\), por lo que, poniendo todo junto, tenemos

\[ \begin{split} r_{ij}=\frac{ {Cov}(z_i,z_j)}{\sqrt{\mathbb{V}(z_i)\mathbb{V}(z_j)}}=\frac{2pqA_{ij}}{2pq} \therefore \\ r_{ij}=A_{ij} \end{split} \tag{9.24} \]

o lo que es lo mismo, el valor esperado de la correlación de contenido génico en dos individuos es igual al parentesco aditivo entre los mismos.

Extender el resultado previo de la ecuación (9.23) a la covarianza en contenido génico entre más individuos es inmediato si entendemos que \(A_{ij}\) es un elemento de la matriz de parentesco aditivo entre individuos (\(\mathbf{A}\)). Si ahora utilizamos la notación vectorial/matricial, entonces los resultados previos pueden resumirse como

\[ \begin{split} \mathbb{E}(\mathbf{z})=\mathbf{2}p \\ \mathbb{V}(\mathbf{z})=2pq\mathbf{A} \end{split} \tag{9.25} \]

La matriz de similaridad genómica

En un artículo notable, VanRaden (2008) plantea tres alternativas para representar la similaridad (parentesco) genómica entre individuos, de las que solo consideraremos la primera. Es claro que la matriz de conteo que vimos previamente y que en este trabajo se nombra \(\mathbf M\) es el elemento clave para determinar la similaridad entre individuos. Sin embargo, de la métrica elegida dependerán las propiedades de la matriz genómica. En lo que sigue asumiremos que la matriz \(\mathbf M\) posee \(n\) filas representando los individuos y \(m\) columnas representando los marcadores, por lo que sería la matriz transpuesta respecto a como la habíamos visto previamente. Por ejemplo, si en lugar de utilizar los valores \(\{0,1,2\}\) para los tres genotipos utilizamos \(\{-1,0,1\}\) los elementos de la diagonal de \(\mathbf{[MM']_{nxn}}\) representan el número de loci homocigotos para cada individuo, mientras que los elementos fuera de la diagonal representan el número de alelos compartidos menos \(m\).

Consideremos ahora la matriz \(\mathbf M\) tomando los valores de los genotipos como \(\{0,1,2\}\). La matriz \(\mathbf{[MM']_{nxn}}\) es una matriz cuadrada de \(n \times n\) elementos. Para cada par de individuos \(i_1\) y \(i_2\) esta matriz contiene el resultado de \(\sum_{j=1}^m z_{i_{1},j} z_{i_{2},j}\). Claramente, con esta codificación, si todos los loci en los dos individuos son homocigotos para el alelo alternativo , entonces \(\sum_{j=1}^m z_{i_{1},j} z_{i_{2},j}=\sum_{j=1}^m 0 \times 0=0\). En cambio, si ambos son completamente homocigotos para el alelo de referencia, entonces \(\sum_{j=1}^m z_{i_{1},j} z_{i_{2},j}=\sum_{j=1}^m 2 \times 2=4m\). Sin embargo, ambas situaciones deberían indicar exactamente lo mismo ya que la elección de qué alelo es el de referencia y cuál el alternativo es algo totalmente arbitrario, sin significado biológico hasta ahora. Por otro lado, es claro que con este producto matricial la similaridad entre individuos es función directa del número de marcadores, lo que no parece una buena idea (por ejemplo, en el caso anterior \(4m\)), por lo que deberíamos considerar su estandarización.

La alternativa propuesta por VanRaden (2008) consiste en transformar los conteos génicos restándole el doble de la frecuencia media del alelo de referencia en cada locus y luego dividiendo entre la suma de varianzas de conteo de todos los loci. Para eso, si \(p_j\) es la frecuencia de base del alelo de referencia en el locus \(j\), vamos a definir una matriz \(\mathbf P\) cuyas columnas están dadas por

\[ \begin{split} \mathbf{P}_{.,j}=2(p_j) \end{split} \tag{9.26} \]

Es decir, cada columna \(j\) de \(\mathbf P\) contiene exactamente \(n\) elementos idénticos a \(p_j\). A partir de esto, basta sustraer esta matriz de la matriz de conteo para obtener una matriz \(\mathbf Z\):

\[ \begin{split} \mathbf{Z}=\mathbf{M}-\mathbf{P} \end{split} \tag{9.27} \]

La matriz \(\mathbf Z\) tendrá los conteos, pero ahora “centrados” de alguna manera, tal que la \(\mathbb{E}(Z_{.,j})=0\), es decir, la esperanza de cada marcador en esta matriz es cero. Esta resta, además de centrar pone el énfasis en aquellos alelos raros, más que en los comunes. Supongamos, por ejemplo que para un marcador determinado \(j\) la frecuencia del alelo de referencia es \(0,99\). Entonces, mientras que para los homocigotos \(A_1A_1\) el valor de \(Z_{.,j}=2-(2 \times 0,99)=0,02\), el otro homocigoto (\(A_2A_2\)) tendrá un valor de \(Z_{.,j}=0-(2 \times 0,99)=1,98\), cuyo valor absoluto es \(99\) veces mayor que el valor absoluto del \(A_1A_1\). Ahora podemos hacer con comodidad el producto de \(\mathbf{ZZ'}\) como un buen indicador de similaridad entre individuos, aunque aún dependiente del número de loci.

Finalmente, el último paso consiste en dividir el producto \(\mathbf{ZZ'}\) entre la suma de las varianzas en conteo para todos los loci (ecuación (9.20)),

\[ \begin{split} \mathbf{G}=\frac{\mathbf{Z}\mathbf{Z}'}{2 \sum_{i=1}^m (p_i)(1-p_i)} \end{split} \tag{9.28} \]

De acuerdo a VanRaden (2008), con la estandarización propuesta el coeficiente de consanguinidad observado de un individuo \(i\) es igual a \(F_i=G_{ii}-1\) y las relaciones de parentesco genómico entre dos individuos \(i\) y \(j\), análogas al coeficiente de parentesco de Sewall Wright (1922) que ya vimos en la ecuación (9.5), se obtienen como \(\frac{G_{ij}}{\sqrt{G_{ii}G_{jj}}}\).

Ejemplo 9.6

Cuatro individuos fueron secuenciados para los 8 marcadores siguientes:

Marcador	Alelo.1	Alelo.2
\(\textbf{snp1}\)	C	G
\(\textbf{snp2}\)	A	C
\(\textbf{snp3}\)	C	T
\(\textbf{snp4}\)	G	T
\(\textbf{snp5}\)	A	G
\(\textbf{snp6}\)	A	T
\(\textbf{snp7}\)	C	T
\(\textbf{snp8}\)	A	C

La tabla de genotipado, con la información relevante para el cálculo de la similaridad genómica para los 4 individuos (en formato tped, excluyendo los datos de posicionamiento de cada marcador) fue la siguiente:

Marcador
snp1	G	G	G	G	G	G	G	G
snp2	C	C	C	C	C	C	C	C
snp3	C	T	C	T	T	T	T	T
snp4	G	T	G	G	G	T	G	T
snp5	A	A	A	G	A	G	A	G
snp6	T	T	A	A	A	A	A	T
snp7	T	T	T	T	T	T	C	T
snp8	A	C	A	C	C	C	A	C

Por otra parte, las frecuencias de base de los alelos de referencia (el segundo por orden alfabético) para cada SNP es la siguiente: \(\mathrm{snp1}=0,45\); \(\mathrm{snp2}=0,47\); \(\mathrm{snp3}=0,47\); \(\mathrm{snp4}=0,5\); \(\mathrm{snp5}=0,5\); \(\mathrm{snp6}=0,75\); \(\mathrm{snp7}=0,75\); \(\mathrm{snp8}=0,65\).

A partir de la información provista, calcular la matriz de similaridad genómica de acuerdo a VanRaden (2008). Calcular para cada uno de los indiviudos el coeficiente de consanguinidad genómico (observado). ¿Qué individuos se encuentran más emparentados, de acuerdo a VanRaden (2008) (siguiendo a Sewall Wright (1922)) usando la matriz \(\mathbf G\)?

El primer paso consiste en pasar la tabla de genotipado en una matriz de conteo alélico. Para eso debemos recordar que cada dos columnas indican el genotipo de un individuo. Utilizando la regla arbitraria de contar el número de copias del segundo alelo en orden alfabético (para los que tenemos a su vez las frecuencias de los alelos), contando en cada par de columnas y transponiendo obtenemos la siguiente matriz de conteo \(\mathbf M\):

Individuo	snp1	snp2	snp3	snp4	snp5	snp6	snp7	snp8
Indiv 1	2	2	1	1	0	2	2	1
Indiv 2	2	2	1	0	1	0	2	1
Indiv 3	2	2	2	1	1	0	2	2
Indiv 4	2	2	2	1	1	1	1	1

Para armar la matriz \(\mathbf P\) alcanza con repetir tantas veces como individuos tengamos los valores de las frecuencias de base de los alelos multiplicadas por \(2\), es decir

Individuo	snp1	snp2	snp3	snp4	snp5	snp6	snp7	snp8
Indiv 1	\(0,90\)	\(0,94\)	\(0,94\)	\(1,00\)	\(1,00\)	\(1,50\)	\(1,50\)	\(1,30\)
Indiv 2	\(0,90\)	\(0,94\)	\(0,94\)	\(1,00\)	\(1,00\)	\(1,50\)	\(1,50\)	\(1,30\)
Indiv 3	\(0,90\)	\(0,94\)	\(0,94\)	\(1,00\)	\(1,00\)	\(1,50\)	\(1,50\)	\(1,30\)
Indiv 4	\(0,90\)	\(0,94\)	\(0,94\)	\(1,00\)	\(1,00\)	\(1,50\)	\(1,50\)	\(1,30\)

Ahora, utilizando la ecuación (9.27), calculamos \(\mathbf Z=\mathbf M-\mathbf P\)

Individuo	snp1	snp2	snp3	snp4	snp5	snp6	snp7	snp8
Individuo 1	\(1,10\)	\(1,06\)	\(0,06\)	\(0,00\)	\(-1,00\)	\(0,50\)	\(0,50\)	\(-0,30\)
Individuo 2	\(1,10\)	\(1,06\)	\(0,06\)	\(-1,00\)	\(0,00\)	\(-1,50\)	\(0,50\)	\(-0,30\)
Individuo 3	\(1,10\)	\(1,06\)	\(1,06\)	\(0,00\)	\(0,00\)	\(-1,50\)	\(0,50\)	\(0,70\)
Individuo 4	\(1,10\)	\(1,06\)	\(1,06\)	\(0,00\)	\(0,00\)	\(-0,50\)	\(-0,50\)	\(-0,30\)

El cálculo de \(\mathbf{ZZ'}\) no es difícil (ver Apéndice A: Conceptos matemáticos básicos para refrescar como se realiza la multiplicación de matrices) pero algo tedioso de hacer a mano, por lo que nosotros utilizamos el software estadístico R para realizarla, pero también puedes hacer esta operación utilizando páginas web que lo realizan. El resultado de la multiplicación \(\mathbf{ZZ'}\) es

	Individuo 1	Individuo 2	Individuo 3	Individuo 4
Individuo 1	\(3,9272\)	\(1,9272\)	\(1,6872\)	\(1,9872\)
Individuo 2	\(1,9272\)	\(5,9272\)	\(4,6872\)	\(2,9872\)
Individuo 3	\(1,6872\)	\(4,6872\)	\(6,4472\)	\(3,7472\)
Individuo 4	\(1,9872\)	\(2,9872\)	\(3,7472\)	\(4,0472\)

Notar que la matriz \(\mathbf{ZZ'}\) es una matriz cuadrada y simétrica, de dimensiones \(n \times n\) (con \(n\) el número de individuos). Finalmente, la matriz de similaridad genómica se calcula de acuerdo a la ecuación (9.28), es decir

\[ \begin{split} \mathbf{G}=\frac{\mathbf{Z}\mathbf{Z}'}{2 \sum_{i=1}^m (p_i)(1-p_i)} \end{split} \]

Por lo tanto, necesitamos calcular el denominador de la misma, que teniendo en cuenta los valores de las frecuencias de base de los SNPs es \(2 \sum_{i=1}^m (p_i)(1-p_i)=3,6964\). Dividiendo \(\mathbf{Z}\mathbf{Z}'\) entre este último valor tenemos la matriz \(\mathbf G\) deseada

	Individuo 1	Individuo 2	Individuo 3	Individuo 4
Individuo 1	\(1,0624391\)	\(0,5213721\)	\(0,4564441\)	\(0,5376042\)
Individuo 2	\(0,5213721\)	\(1,6035061\)	\(1,2680446\)	\(0,8081376\)
Individuo 3	\(0,4564441\)	\(1,2680446\)	\(1,7441835\)	\(1,0137431\)
Individuo 4	\(0,5376042\)	\(0,8081376\)	\(1,0137431\)	\(1,0949031\)

Para el cálculo de los coeficientes de consanguinidad de los individuos recordamos que \(F_i=G_{ii}-1\), por lo que extraemos los valores de la diagonal en \(\mathbf G\) y les restamos 1 a cada uno (o lo que es lo mismo \(\mathbf F=\mathbf G - \mathbf 1\)). Esto nos deja con

	\(G_{ii}\)	\(F_i\)
Individuo 1	\(1,0624391\)	\(0,0624391\)
Individuo 2	\(1,6035061\)	\(0,6035061\)
Individuo 3	\(1,7441835\)	\(0,7441835\)
Individuo 4	\(1,0949031\)	\(0,0949031\)

Para determinar qué individuos se encuentran más emparentados de acuerdo a la matriz de parentesco genómico y VanRaden (2008) calculamos \(\frac{G_{ij}}{\sqrt{G_{ii}G_{jj}}}\) para cada celda fuera de la diagonal y observamos qué valor es el mayor. La matriz resultante de este cálculo es

	Individuo 1	Individuo 2	Individuo 3	Individuo 4
Individuo 1	\(-\)	\(0,3994482\)	\(0,3353046\)	\(0,4984513\)
Individuo 2	\(0,3994482\)	\(-\)	\(0,7582338\)	\(0,6099050\)
Individuo 3	\(0,3353046\)	\(0,7582338\)	\(-\)	\(0,7335741\)
Individuo 4	\(0,4984513\)	\(0,6099050\)	\(0,7335741\)	\(-\)

por lo que el parentesco genómico mayor sería entre el individuo 3 y el individuo 2

PARA RECORDAR

• Una forma de ver la relación entre el parentesco estadístico y el genómico es la de considerar al primero como el parentesco esperado y al segundo como el parentesco realizado (u observado).

• Mientras que en el parentesco estadístico estamos siempre hablando de alelos IBD, en el caso de parentesco genómico nos vamos a enfocar en alelos IBS (idénticos en estado), ya que no conocemos las relaciones entre los individuos y apenas el genotipo observado para cada locus.

• El valor esperado de la correlación de contenido génico en dos individuos es igual al parentesco aditivo entre los mismos, tal que:

\[r_{ij}=\frac{ {Cov}(z_i,z_j)}{\sqrt{\mathbb{V}(z_i)\mathbb{V}(z_j)}}=\frac{2pqA_{ij}}{2pq}r_{ij}=A_{ij}\]

9.7 Estudios de ascendencia (“ancestría”)

⁸⁵

Las tecnologías de genotipado masivo, así como las de secuenciación masiva han permitido extender los estudios de relaciones entre individuos y poblaciones al nivel comercial, por lo que en la actualidad resulta fácil y económico conocer nuestros “orígenes”. Sin embargo, al interpretación de los resultados de dichos estudios no es tan trivial como parece y debemos ser bastante cautelosos a la hora de interpretarlos.

Ascendencia (correspondiente a la palabra inglesa “ancestry”), puede definirse como el conjunto de los ancestros para un individuo, un grupo o un linaje dados. En el presente contexto nos referiremos a ella como la proporción de alelos (variantes genéticas) de un individuo que corresponden a diferentes grupos étnicos ancestrales.

Si bien la información contenida en el ADN de un individuo es relativamente inmutable a lo largo de la vida (con pequeñas variaciones debidas a mutaciones somáticas o a errores en el proceso de lectura de la secuencia), el proceso de asignación de la fracciones correspondiente a distintos grupos genéticos (o etnias) no lo es. Para entender la razón de esto, es necesario entender como funciona el proceso de transmisión de información genética a lo largo de las generaciones. Para ello usaremos una simple analogía que simplifica muchísimo el complejo proceso por detrás, eliminando varios detalles que por ahora no nos serán necesarios.

Supongamos que podemos representar la información del ADN de cada individuo en una población con un par de cajas que cada una contiene 50 bolitas de colores. Estás cajas vienen a representar un juego de cromosomas, heredado uno del padre (una caja) y el otro de la madre (la otra caja). Cada bolita correspondería entonces a la información en un locus (alelo) en cada cromosoma paterno o materno. Ahora, supongamos que al comienzo del experimento todas las bolitas de todas las cajas son rojas. Nuestra población es homogénea genéticamente. En nuestro modelo muy simplificado, para crear un nuevo individuo (un hijo), elegimos un padre y una madre, cada uno de los cuales aporta la copia de una caja (o sea, elige las mismas bolitas que tiene en una de las cajas de una reservorio con infinitas bolitas de todos los colores). Cada progenitor (padre o madre) aporta la mitad de las bolitas que tendrá el nuevo individuo, es decir, le aporta la mitad de su ADN, que a su vez será la mitad del ADN del nuevo individuo. Como todos los individuos solo tienen bolitas rojas, sus hijos solo tendrán información roja.

Ahora, supongamos que por error al copiar la información para hacer un nuevo individuo, uno de los padres introduce una pelota verde en su caja copia. En cada proceso de copia hay una probabilidad mayor que cero de cometer un error. Si la tasa de error es de 2% (1 en 50), en promedio en cada copia el padre introducirá un pelota de color diferente al original en la caja. A esto, en genética le llamamos una mutación. Esto hace que el individuo hijo reciba una caja de 50 bolitas rojas y otra con 49 rojas y una verde. En promedio, considerando que este hijo tiene muchos descendientes, la mitad de estos recibirá una caja con una pelota verde y 49 rojas, mientras que la otra mitad recibirá una caja con todas rojas.

En realidad, el proceso de segregación genética (elegir la mitad del material genético del individuo para transmitirlo a la siguiente generación) es un poco más complejo que elegir una de las dos cajas para copiar su contenido. Existe un proceso llamado recombinación, que lo podemos ejemplificar de la siguiente manera: elegimos una bolita de cada caja y las retiramos. Luego, al azar elegimos una de las dos para copiarla en la caja del hijo. Repetimos el proceso hasta que no queden más bolitas en las cajas de los padres (50 veces en nuestro ejemplo). Obviamente debemos devolverle al padre sus dos cajas con las bolitas, tal cual las tenía antes de comenzar el proceso. De esta forma, la caja que el padre armó para su hijo es una combinación del contenido de sus dos cajas.

Supongamos ahora que repetimos el procedimiento de construcción de hijos y luego de varias generaciones muestreamos dos individuos. Uno de ellos, que llamaremos I1 tiene una caja con 35 bolitas rojas, 5 azules, 5 verdes y 5 amarillas, mientras que la otra caja tiene 30 rojas, 6 azules, 7 verdes y 7 amarillas. El otro individuo, I2, tiene 47 bolitas rojas en una caja, dos azules y una amarilla, mientras que en la otra caja tiene 49 rojas y una amarilla. Podríamos suponer incluso que los individuos que tienen una pelota verde en esta población confunden más a menudo los colores que copian, lo que explica en cierta forma la diferencia en el número de bolitas “no rojas” en las 4 cajas.

Hagamos algunos cálculos en este momento. Si no supiéramos de donde vinieron estos individuos, pero suponemos que en algún momento todas las poblaciones que existían eran de un solo color, cualquiera fuera este, diríamos que los dos individuos tienen diferentes proporciones de genes (bolitas) de las poblaciones originales o ancestrales (a veces lo escuchamos como porcentaje de sangre, por más que no tenga nada que ver con la realidad biológica). Para I1 el cálculo nos daría:

\(35+30=65\) rojas, en 100 bolitas totales, o \(65\%\) de genes de una población roja \(5+6=11\) azules, en 100 bolitas totales, o \(11\%\) de genes de una población azul \(5+7=12\) verdes, en 100 bolitas totales, o \(12\%\) de genes de una población verdes \(5+7=12\) amarillas, en 100 bolitas totales, o \(12\%\) de genes de una población amarillas

Además, \(65\%+11\%+12\%+12\%=100\%=1\) (el total de los genes del individuo fueron asignados a alguna población ancestral).

Por otra parte, para I2 el cálculo nos daría:

\(47+49=96\) rojas, en 100 bolitas totales, o \(96\%\) de genes de una población roja \(2+0=2\) azules, en 100 bolitas totales, o \(2\%\) de genes de una población azul \(1+1=2\) amarillas, en 100 bolitas totales, o \(2\%\) de genes de una población amarillas

\(96\%+2\%+2\%=100\%=1\) (el total de los genes del individuo fueron asignados a alguna población ancestral).

Pese a que estos dos individuos los muestreamos de la misma población, si no conocemos cuantas poblaciones ancestrales realmente existían y confiamos que cada color se correspondía con una población homogénea para ese color (despreciamos la mutación como el mecanismo que introduce la variabilidad), entonces llegaremos a la conclusión de que el individuo I1 tiene un \(65\%\) de sus ancestros de la población roja, mientras que el I2 tiene un \(96\%\) de ancestros originarios de esa población. A su vez, arribamos a la conclusión de que I1 tiene \(11\%\) de ancestros azules y \(12\%\) de cada uno de amarillos y verdes, mientras que I2 solo tiene \(2\%\) de ancestros azules y amarillos. Lo que usamos en este proceso fue asumir que las diferencias en colores se corresponden enteramente a poblaciones originales diferentes, lo que es equivalente a asumir que el mestizaje y no la mutación explican enteramente el proceso.

Pero supongamos que ahora tenemos información “histórica” que refiere que originalmente, solo existían dos poblaciones ancestrales, una roja y otra azul. Ahora nuestro modelo puede ser un poco más complejo. Vamos a asignar la variabilidad roja y azul a esas poblaciones ancestrales y vamos a suponer que verde y amarillo son en realidad mutaciones. Eso nos llevará a que para I1 tenemos:

• \(35+30=65\) rojas, en \(76\) bolitas no verdes ni amarillas, o \(85,5\%\) de genes de una población roja

• \(5+6=11\) azules, en \(76\) bolitas no verdes ni amarillas, o \(14,5\%\) de genes de una población azul

Como verificación, \(85,5\%+14,5\%=100\%=1\). Esto es, solo pudimos asignar \(76\) bolitas, de las 100 que tenemos, a alguna de las poblaciones ancestrales. Además, tenemos (\(5+7=12\)) verdes + (\(5+7=12\)) amarillas, en \(100\) bolitas totales (es decir, \(24\%\) de “genes” mutados que no pudimos asignar).

Para el otro individuo, el cálculo nos daría:

• \(96\) rojas, en \(98\) bolitas no verdes ni amarillas, o \(\approx 98\%\) de genes de población roja
• \(2\) azules, en \(98\) bolitas no verdes ni amarillas, o \(\approx 2\%\) de genes de población azul.
• Además (\(1+1=2\)) amarillas en \(100\) bolitas totales, o \(2\%\) de genes mutados.

De esto, es fácil inferir que la proporción de genes que corresponden a cada población ancestral depende del número de poblaciones ancestrales que coloquemos en el modelo. Usualmente, cuanto menos poblaciones ancestrales asumamos, mayor porcentaje de lo asignado le corresponderá a cada una. Además, es muy importante entender los procesos biológicos que existen por detrás de la variabilidad, así como sus parámetros, ya que de lo contrario nuestras conclusiones podrían ser completamente equivocadas (como en nuestro ejemplo, que asignamos la variabilidad a la existencia de distintas poblaciones ancestrales, cuando solo existía una).

Como dijimos más arriba, nuestro primer modelo era extremadamente simple y es tiempo de agregarle un poco más de realismo. Normalmente, aún los grupos étnicos más cerrados suelen tener algún contacto con sus vecinos, lo que produce que algunos hijos no reciban dos cajas de bolitas del mismo color que la población en las que les tocará vivir. Es más, las poblaciones vecinas suelen compartir una parte muy importante de los colores de sus cajas, ya que si nos remontamos un poco en el tiempo probablemente las dos surgieron de una población más ancestral (no hay que olvidarse que originalmente solo existía una población de Homo sapiens, que habitaba en África).

Supongamos entonces que tenemos dos poblaciones ancestrales vecinas A y B, la primera cuyas cajas tienen en promedio \(70\) bolitas rojas y \(30\) azules, mientras que en la segunda poseen en promedio \(50\) bolitas rojas, \(40\) azules y \(10\) amarillas. Dentro de cada población sin duda existirá variación a nivel individual. Es decir, en la población A nos podemos encontrar con individuos 60r+40az, 80r+20az y hasta algún extraño (e insignificante en número) 70r+29az+1am, etc. Lo que cuenta es que el promedio de la población es, como dijimos 70r+30az. Supongamos ahora, que tenemos un individuo que fue encontrado en algún lugar en el espacio geográfico de las dos poblaciones. Cuando analizamos su ADN, nos encontramos que posee la fórmula 60r+35az+5am. ¿A cuál de estas dos poblaciones pertenece, si es que pertenece a alguna? Si fuese el producto de una cruza entre individuos de las poblaciones A y B, ¿cuántas generaciones atrás ocurrió ese mestizaje?

Lo primero que se nos viene a la mente, teniendo en cuenta que solo en una de las poblaciones (B) la frecuencia de las bolitas (alelos) amarillas es significativa y que este individuo tiene una proporción no despreciable de las mismas, es que este individuo probablemente venga de dicha población B. Como comentamos antes, si bien la frecuencia promedio de una población es única, existe variabilidad individual en torno a la misma y las frecuencias que observamos en este individuo desconocido no parece alejarse demasiado de las frecuencias promedios de B. Más exactamente, dada la forma de muestreo de las bolitas, podemos asumir razonablemente que la distribución del número de cada color sigue una ley multinomial (una versión de la conocida binomial, para más de dos categorías). Pero dejemos, por ahora estos cálculos para otro momento.

En realidad, si bien el razonamiento anterior no parece desacertado, no es la única alternativa razonable. De hecho, posiblemente tampoco sea la más parsimoniosa, si consideramos que el individuo puede ser el producto (descendiente) de un cruzamiento entre individuos de la poblaciones parentales A y B. Supongamos que un labrador de la población A (población que tiene en promedio la fórmula 70r+30az) se encuentra con una pastora de la población B (población que tiene en promedio la fórmula 50r+40az+10am), que está llevando a pastar a sus ovejas verdes en los límites de las tierras de la población B y deciden (romance de por medio) establecerse en esas nuevas tierras limítrofes. Simplemente por casualidad, ambos son individuos muy representativos de sus poblaciones, es más, las frecuencias de bolitas en sus cajas se corresponde exactamente con los promedios de cada población. La esperanza matemática es que pasen a sus hijos la mitad de sus bolitas, es decir:

el Labrador (A) transmitirá 35r+15az, mientras que la Pastora (B) pasará 25r+20az+5am (en promedio).

Un hijo promedio de ambos tendrá entonces la suma, 60r+35az+5am, lo que es idéntico a la composición de las cajas de nuestro individuo desconocido. Más aún, las dos alternativas que manejamos más arriba para explicar el posible origen genético de nuestro individuo (que provenga de una de las dos poblaciones o que sea el producto del apareamiento entre un individuo de una y el otro de la otra población) no son más que unos casos particulares de una solución general donde las proporciones de cada una de las poblaciones varían entre 0 y 1, con la restricción de que la suma de las proporciones debe dar 1 (\(100\%\) del origen identificado). Por ejemplo, un individuo producto del apareamiento de un individuo de la población B y un individuo hijo de un individuo de A y otro de B, tendrá \(0,25\) de A y \(0,75\) de B (hablaremos de esto más adelante en el capítulo Endocría, exocría, consanguinidad y depresión endogámica). A medida que pasa el tiempo, en generaciones de individuos, mayor el espectro real de proporciones de mezcla posibles y mayor la dificultad de reconocer con claridad el verdadero origen genético de los individuos.

Podemos preguntarnos a esta altura, ¿de donde vino tanta complejidad? De hecho, si las poblaciones fueran todas homogéneas y de colores diferentes entre ellas, distinguir las proporciones de las diferentes poblaciones en un individuo cualquiera sería una tarea trivial: contamos cuantas bolitas de cada color hay en las cajas de este individuo y las dividimos entre el total. Eso no dará la frecuencia de cada población (si multiplicamos los resultados por \(100\) los tendremos en porcentaje). La complejidad aparece cuando las poblaciones que consideramos como referencia tienen variabilidad interna, que hace que se solapen los colores que tienen. Cuanto mayor el solapamiento, es decir mayor similitud en las frecuencias de los colores de las bolitas, mayor la dificultad para discernir en forma clara las proporciones de cada una en un nuevo individuo.

Consideremos, como ejemplo dos poblaciones X e Y, en dos escenarios: en el primer escenario, X tiene una frecuencia de rojas de \(0,99\) y \(0,01\) de azules, mientras que Y tiene \(0,01\) de rojas y \(0,99\) de azules (asumamos que todos los individuos son idénticos entre ellos). Ahora, en este escenario, si encontramos un individuo cualquiera en el mundo y tenemos que asignar que proporción tiene de cada una de las poblaciones X e Y, la situación será muy fácil. Simplificando mínimamente, podemos asignar todas las bolitas rojas en el nuevo individuo como provenientes de X y todas las azules como provenientes de Y y tendremos las proporciones deseadas.

Ahora, en el segundo escenario, X tiene una frecuencia de rojas de \(0,99\) y \(0,01\) de azules, mientras que Y tiene \(0,97\) de rojas y \(0,03\) de azules (asumamos que todos los individuos son idénticos entre ellos). En este segundo escenario, aplicar la estrategia anterior no tiene sentido ya que las diferencias de frecuencias entre las poblaciones es mínima y solo podremos conjeturar, con enorme probabilidad de equivocarnos que si el individuo tiene más de \(0,98\) de rojas es más probable que venga de X, y si tiene menos de ese valor que provenga de Y.

El asunto aquí es entonces el solapamiento de frecuencias (de colores) entre las distintas poblaciones. Una alternativa muy interesante, es cambiar nuestra definición de poblaciones de referencia. Es decir, si en lugar de considerar como poblaciones de referencia X e Y (en cualquiera de los escenarios), consideramos que las mismas son a su vez producto de mestizaje entre las verdaderas poblaciones ancestrales, la roja y azul (que por definición, serán ahora completamente homogéneas). Esto simplifica enormemente el problema de determinar las frecuencias, ya que nuevamente solo se trata de contar en el nuevo individuo la proporción de las bolitas de cada uno de los colores. ¿Cuál es el problema entonces de esta aproximación en la realidad?

Consideremos en primer lugar lo que sucedería si en lugar de dos colores tenemos una paleta 80 millones de colores reales, es decir que tenemos algún individuo que tiene al menos una bolita con ese color (en realidad la paleta teórica es mucho mayor, del orden de los billones a cifras astronómicas, dependiendo de cómo consideremos los colores). Ahora el problema no aparece con la heterogeneidad de las poblaciones sino en como identificamos los colores. Nuestra capacidad de distinguir colores está claramente por debajo de estas cifras, lo que nos imposibilitaría distinguir con seguridad las poblaciones posibles. Afortunadamente, también sabemos que las posibles poblaciones humanas que existen o existieron en nuestro planeta están claramente por debajo de este número. Digamos que tal vez podemos agrupar colores por similitud, de tal forma que nos quedemos con un número manejable de los mismos, pongamos por ejemplo, unos 25 y nos quedamos con un representante de cada grupo como “prototipo” de dicho grupo. Ahora, dado un individuo cualquiera del que queremos saber las proporciones de las poblaciones “originales” el problema se trata simplemente de asignar las bolitas con colores reales del mismo a las categorías de los colores prototípicos y contar cuantas entran en cada uno.

El proceso real de asignación de proporciones de ascendencia, en alguna de sus versiones, es bastante parecido a lo que describimos hasta acá. Se trata en una primera etapa de identificar un conjunto de poblaciones, que llamaremos de referencia, a las que se le realiza el genotipado (determinación de las variantes en el ADN) de varios individuos representativos de cada una. El genotipado es un proceso caro, si bien su costo disminuye en forma continua, por lo que el número de poblaciones para las que se cuenta con esta información es (era) relativamente bajo. Si bien, idealmente, las poblaciones que integran el conjunto debieran ser seleccionadas para representar de la mejor manera posible la diversidad genética humana del planeta entero, esto dista muchísimo de ser la realidad. Por ejemplo, en el proyecto “1000 genomes” (1000 genomas, aunque superaron los 2 mil), posiblemente el más exhaustivo en cobertura del genoma y número de poblaciones (26), existe una clara sub-representación de los nativos americanos. Además, este panel de poblaciones está integrado en muchos casos por poblaciones que pretenden representar un grupo étnico al que ya no pertenecen geográfica e históricamente, simplemente porque es mucho más fácil de extraer las muestras en ellos. Por ejemplo, los centro-europeos del panel (CEU), son residentes del estado de Utah en EEUU, con ascendencia del norte y oeste de Europa. En otros casos, las poblaciones sobre las que se muestrea presentan un alto grado de mestizaje con otros grupos completamente diferentes en la evolución humana, lo que hace muy difícil de interpretar los resultados cuando aparece una proporción significativa de estas poblaciones de referencia. Un ejemplo es el grupo MXL, que podría intentar interpretarse como nativos de México, pero que solo representa individuos con algo de ascendencia mexicana, viviendo en el área de Los Ángeles (EEUU). En la tabla que sigue se observan las poblaciones de referencia que hay disponibles en proyecto “1000 genomes” (ver tabla más abajo).

Para cada una de las poblaciones del proyecto “1000 genomes” se realizó el secuenciado de varios individuos (del orden de los 100 por población) y se determinó por lo tanto que estado (base o nucleótido) existían en cada individuo. A partir de ahí es fácil obtener una estimación para cada población de cuál es la frecuencia de cada base (A,C,G,T) en cada posición del genoma. Como usualmente solo consideramos marcadores di-mórficos (que en las poblaciones solo hay dos variantes), esta tabla tiene tantas filas como marcadores di-mórficos y tantas columnas como poblaciones, con cada celda conteniendo el valor del alelo de referencia.

La segunda parte del proceso de determinar los porcentajes de ascendencia de un individuo consiste en obtener la información genética del mismo. Para esto existen varias alternativas; las más simples y baratas consisten en genotipar (identificar variantes) un juego muy reducido y definido previamente de marcadores (posiciones en el genoma). Los marcadores más usuales para ascendencia son del tipo polimorfismos de un solo nucleótido (SNPs en inglés). Las alternativas de mayor complejidad consisten en la secuenciación del exoma o aún del genoma completo de un individuo. Estos últimos enfoques permiten además de estimar las frecuencias de ascendencia obtener valiosa información médica, por lo que al bajar el costo de secuenciación en forma dramática, cada vez son más usados. Si bien las aproximaciones de secuenciación masiva permiten distinguir diferentes tipos de variaciones, no solo SNPs, dada la enorme cantidad de los mismos que se obtienen con estas técnicas y la simplicidad de su comparación, suelen ser el conjunto de información más usado para ascendencia.

Luego de que tenemos un conjunto de poblaciones de referencia y que tenemos la información genómica del individuo (marcadores), el proceso consiste intentar determinar que proporciones de cada una de esas poblaciones de referencia mejor explican el genotipo del individuo. Una de las estrategias para esto, eficiente y suficientemente rápida, es considerar cada marcador como una pieza independiente de información (una simplificación sobre la que abundaremos más adelante) y utilizar el enfoque estadístico de máxima verosimilitud. Básicamente, el enfoque de máxima verosimilitud consiste en describir una función de verosimilitud, que se relaciona con la probabilidad de observar los datos dados diferentes valores de los parámetros del modelo, y hallar el máximo de esta función. En nuestro caso, los parámetros del modelo serían las distintas proporciones de cada una de las poblaciones de referencia y por lo tanto, lo que buscamos es cuál combinación de los mismos permiten maximizar la probabilidad de observar el conjunto de marcadores que observamos en el individuo. Para hallar este máximo, existen algoritmos eficientes que nos garantizan la solución óptima si se cumplen una serie de requerimientos.

Código	Descripción	Grupo
CHB	Han Chinese en Bejing, China	EAS
JPT	Japoneses en Tokio, Japón	EAS
CHS	Han Chinese del sur	EAS
CDX	Chinese Dai en Xishuangbanna, China	EAS
KHV	Kinh en ciudad Ho Chi Minh, Vietnam	EAS
CEU	Residentes de Utah (CEPH) con ascendencia de Europa del norte y el oeste	EUR
TSI	Toscanos en Italia	EUR
FIN	Fineses en Finlandia	EUR
GBR	Británicos in Inglaterra y Escocia	EUR
IBS	Iberian Population in Spain	EUR
YRI	Yoruba en Ibadan, Nigeria	AFR
LWK	Luhya en Webuye, Kenia	AFR
GWD	Gambian en Divisiones Oeste en Gambia	AFR
MSL	Mende en Sierra Leona	AFR
ESN	Esan en Nigeria	AFR
ASW	Americanos de ascendencia Africana en el suroeste de EEUU	AFR
ACB	Caribeños Africanos en Barbados	AFR
MXL	Ascendencia Mexicana en Los Angeles EEUU	AMR
PUR	Puertorriqueños de Puerto Rico	AMR
CLM	Colombianos de Medellín, Colombia	AMR
PEL	Peruanos de Lima, Perú	AMR
GIH	Gujarati Indian de Houston, Texas	SAS
PJL	Punjabi de Lahore, Pakistán	SAS
BE	B Bengalíes de Bangladesh	SAS
STU	Tamiles (Sri Lanka) del Reino Unido	SAS
ITU	Indian Telugu del Reino Unido	SAS

Estas poblaciones corresponden a su vez a los siguiente 5 grupos:

AFR, Africanos AMR, Mestizos Americanos EAS, Asiáticos del este EUR, Europeos SAS, Asiáticos del Sur

¿Cuáles son los principales problemas con esta aproximación tan simple y elegante? Primero, las que tienen que ver con las violaciones a lo asumido por el algoritmo. En particular, la no independencia de las observaciones, algo que está asociado al proceso de muestreo genético, el desequilibrio de ligamiento. Desequilibrio de ligamiento es el término usado para describir el hecho de que el proceso de selección de bolitas no es independiente como lo describimos nosotros más arriba; es decir, al seleccionar una bolita de las dos cajas del padre para copiarla al hijo, la siguiente bolita a escoger tiene mayor probabilidad de ser de la misma caja del padre que lo que correspondería al azar (\(50\%\) de cada caja). Esto se debe, en nuestro genoma, a que los genes están físicamente organizados en forma lineal en los cromosomas y por lo tanto, los que están cerca tienen mayor probabilidad de “ir juntos” en el muestreo. Si bien este es un problema real, su impacto a nivel práctico parece ser bastante menor y en todo caso relativamente fácil de solucionar, muestreando marcadores lo suficientemente espaciados como para que el desequilibrio de ligamiento entre los mismos sea mínimo o inexistente. Un problema más real (de casi todos los métodos), es la dependencia de los resultados del conjunto de poblaciones de referencia usados.

El primer problema y más obvio es que si en el conjunto de poblaciones de referencia no se encuentran las “verdaderas” de origen del individuo, el método le asignará de cualquier manera frecuencias a las poblaciones de las que dispone, de tal manera que su suma dará 1 (\(100\%\)). Si la(s) población(es) de donde desciende no se encuentran, pero están algunas muy cercanas (en términos de similitud genética), entonces el problema no será muy importante; cuanto mayor la distancia entre las poblaciones de origen real y las que se encuentran representadas, mayor también la posibilidad de diferencias en las frecuencias estimadas. Además, dependiendo del origen del individuo a analizar, los resultados pueden resultar demasiado “coarse grain” para nuestros conocimientos genealógicos; por ejemplo, en Uruguay una parte importante de la población tiene origen francés, pero esta población no se encuentra entre las de referencia para el proyecto “1000 genomes”, lo que hará que la proporción de ese origen aparezca inflando otras poblaciones de Europa que si están (GBR, CEU, IBS, TSI, FIN).

Otro problema, menos obvio pero no menos importante, es el que genera la introducción de poblaciones de referencia con un alto grado de mestizaje, en particular las que tienen aportes de otras poblaciones de referencia. Este problema puede sesgar en forma importante las estimaciones de los coeficientes de ascendencia de un individuo y es difícil de distinguir el origen del problema. Por esta razón, una estrategia un poco cruda pero efectiva consiste en eliminar del conjunto de poblaciones de referencia a estas poblaciones con una proporción importante de mestizaje. Dependiendo del criterio utilizado, unas 19 poblaciones del proyecto “1000 genomes” muestran poca proporción de mestizaje y estarían aptas para ser usadas en el método de máxima verosimilitud. En el caso de las poblaciones pertenecientes al grupo AMR, solamente PEL (peruanos de Lima) presenta un nivel de mestizaje suficientemente bajo para ser incluida como población de referencia. Esto produce que, en general, toda la variabilidad de un individuo correspondiente a nativos americanos vaya a ser asignada a PEL, aunque en la mayor parte de los casos se corresponda a otros grupos étnicos bien distantes (en nuestro país la proporción esperable de ascendencia de nativos andinos es muy baja, aún entre los descendientes de nativos americanos, que se corresponden más a la macro-etnia charrúa y/o a los guaraníes). Otro grupo con grandes problemas es el SAS, pero en nuestro país suele tener poca relevancia ya que pocos individuos presentan ascendencia cercana de estos grupos.

9.8 Conclusión

La semejanza entre parientes es uno de los hechos que más relacionamos con la disciplina de la genética. En este capiulo nos acercamos al fenómeno utilizando la aproximación de la genética cuantitativa, la cual desarrollamos en el capiulo anterior. Conceptos como la consanguinidad y el análisis de diagramas de parentesco nos permiten realizar un análisis sistemático del grado de similitud genética que poseen individuos emparentados. Pero, ¿cómo se vincula la similitud genética con la fenotípica? ¿Cumple la herencia de los caracteres fenotípicos las mismas regularidades que se pueden plantear en el caso genético? En el siguiente capítulo entraremos en estas cuestiones, presentando el concepto de heredabilidad. Este es clave, en tanto el objetivo del mejoramiento genético es en última instancia realizar selección sobre caracteres fenotípicos de interés; la viabilidad de dicha selección depende de cuánto se hereda un caracter fenotípico de una generación a la siguiente, ya que la selección solo puede operar en caracteres heredables (como vimos en la primera parte de este libro).

9.9 Actividades

9.9.1 Control de lectura

1. Dos individuos emparentados comparten material genético. ¿Cómo se relaciona esto con el concepto de parentesco entre ambos? ¿Y con el concepto de consanguinidad?

2. ¿Pueden dos medios hermanos tener todos sus alelos idénticos por ascendencia? ¿E idénticos en estado?

3. Bajo el modelo genético básico, la covarianza fenotípica entre parientes se puede desglosar en diferentes componentes de varianza. ¿Cuáles son los mismos en los siguientes casos? i) Caso padre-hijo, ii) abuelo-nieto, iii) hermanos enteros, y iv) medios hermanos.

4. Defina el concepto de parentesco aditivo y discuta su importancia en el contexto del mejoramiento genético.

5. ¿Por qué pares de medios hermanos no pueden compartir varianza de dominancia? Desarrolle teniendo en cuenta que la varianza de dominancia se relaciona con la probabilidad de heredar un mismo genotipo.

9.9.2 ¿Veradero o falso?

1. Los individuos pertenecen a poblaciones finitas, por lo cual siempre comparten cierta cantidad de material genético. Por lo tanto, el coeficiente de parentesco entre dos individuos de una misma población debe ser distinto de cero.

2. El parentesco de dominancia entre dos hermanos es distinto de cero.

3. La consanguinidad entre dos individuos emparentados siempre es mayor a cero.

4. Consideremos la distribución de la variabilidad dentro de grupos y entre grupos de individuos. Cuanto mayor es la covarianza entre individuos pertenecientes a un mismo grupo, mayor es la proporción de la variabilidad total que se explica por la varianza entre grupos (y vice versa).

5. Es posible estimar la varianza aditiva a través de la covarianza y otros componentes de varianzas.

Soluciones

1. Verdadero. Recordemos que el coeficiente de parentesco se vincula conceptualmente con la probabilidad de que dos alelos de dos individuos distintos sean idénticos por ascendencia. En una población finita, debido al efecto de la deriva, en última instancia todos los individuos comparten alelos (recordar la teoría del coalescente y su relación con la endocría en una población, capítulo 6). Durante el cálculo del coeficiente de consanguinidad de un individuo se asume que los últimos ancestros del mismo poseen un coeficiente de parentesco de cero solo por motivos prácticos.

2. Falso. La afirmación es falsa ya que esto no aplica para todos los casos: en el caso de hermanos enteros sí ocurre esto, pero para medios hermanos el coeficiente de parentesco es siempre cero (ya que no es posible que los individuos compartan genotipos).

3. Falso. El coeficiente de consanguinidad sólo se puede calcular para un individuo. El concepto no aplica a relaciones entre individuos, sean estos parientes o no.

4. Verdadero. Esto se puede ver en el ejemplo de la Figura 9.9. Dicho de otra forma, mayor covarianza entre individuos implica mayor similitud entre los mismos. Por lo tanto, una mayor proporción de la variabilidad total estará explicada por la diferencia entre los grupos (ya que dentro de cada grupo la variabilidad es baja). En el caso contrario una menor covarianza implica mayor diferencia entre los individuos de un mismo grupo, por lo que una mayor proporción de la variabilidad total estará explicada por estas diferencias dentro de los grupos (y no entre los mismos).

5. Verdadero. Si bien la covarianza fenotípica es la única cantidad directamente medible a partir de los datos, es posible estimar otros componentes (como la variabilidad aditiva) partiendo del modelo genético básico y realizando algunas asunciones razonables (ver sección Estimación de las varianzas aditiva y de dominancia).

9.9.3 Ejercicios

Ejercicio 9.1

A continuación se presenta un diagrama de parentesco de caballos criollos:

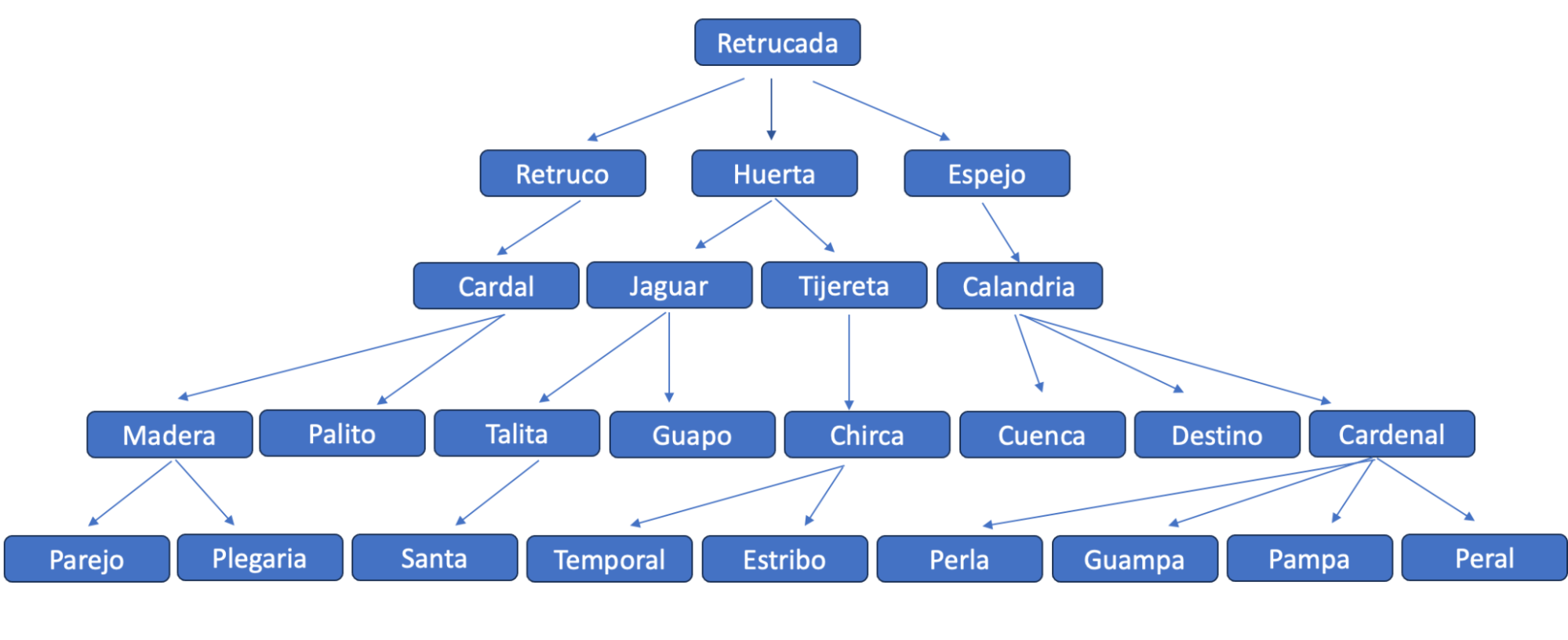
Basados en el mismo:

a. ¿Cuál es el parentesco entre Tijereta y Plegaria?

b. ¿Cuánto valdría la consanguinidad de un hijo de Guampa y Cuenca?

Solución

a. Podemos constatar que Tijereta y Plegaria comparten un único ancestro común (que es Retrucada), por lo que podremos expresar la ecuación 9.10 cómo:

\[a_{TP}=\frac{1}{2}^n(1+F_{Retrucada})\]

En primera instancia, podremos asumir que \(F_{Retrucada} = 0\), debido a que no tenemos información de que el animal posea consanguinidad (no tenemos la información y no podemos determinarla a través del pedigree). Por lo tanto:

\[a_{TP}=\frac{1}{2}^n\]

El único dato que necesitaremos entonces es el valor de \(n\), el cual obtendremos contando las flechas que separan a ambos individuos.

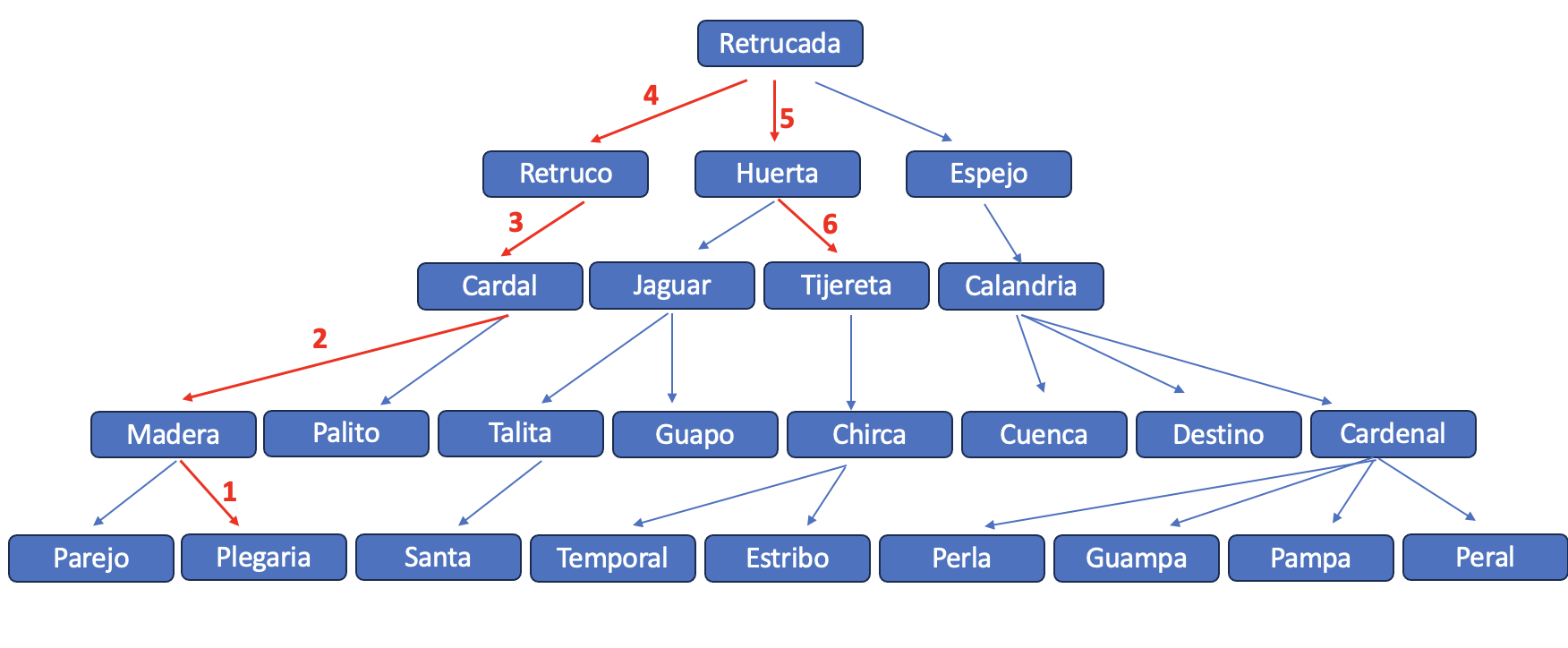
Procediendo con el método determinamos que \(n=6\), por lo tanto el parentesco entre Tijereta y Plegaria es de:

\[a_{TP}=\frac{1}{2}^6 = \frac{1}{64} = 0,015625\]

b. En primera instancia, podemos recordar que el coeficiente de consanguinidad (\(F\)) de un individuo equivale a la mitad del parentesco de sus padres. Por este motivo, para determinar la consanguinidad de un hijo entre Guampa y Cuenca deberemos determinar el parentesco entre los mismos.

Podremos comprobar, al igual que en el caso anterior, que ambos animales comparten un único ancestro en común (Calandria). Repetiremos entonces lo aplicado en la parte \(a\), tal que \(a_{GC}=\frac{1}{2}^n(1+F_{Calandria})\).

Nuevamente asumimos que \(F_{Calandria} = 0\) por las mismas consideraciones detalladas en el caso anterior, por lo que sólo resta determinar \(n\):

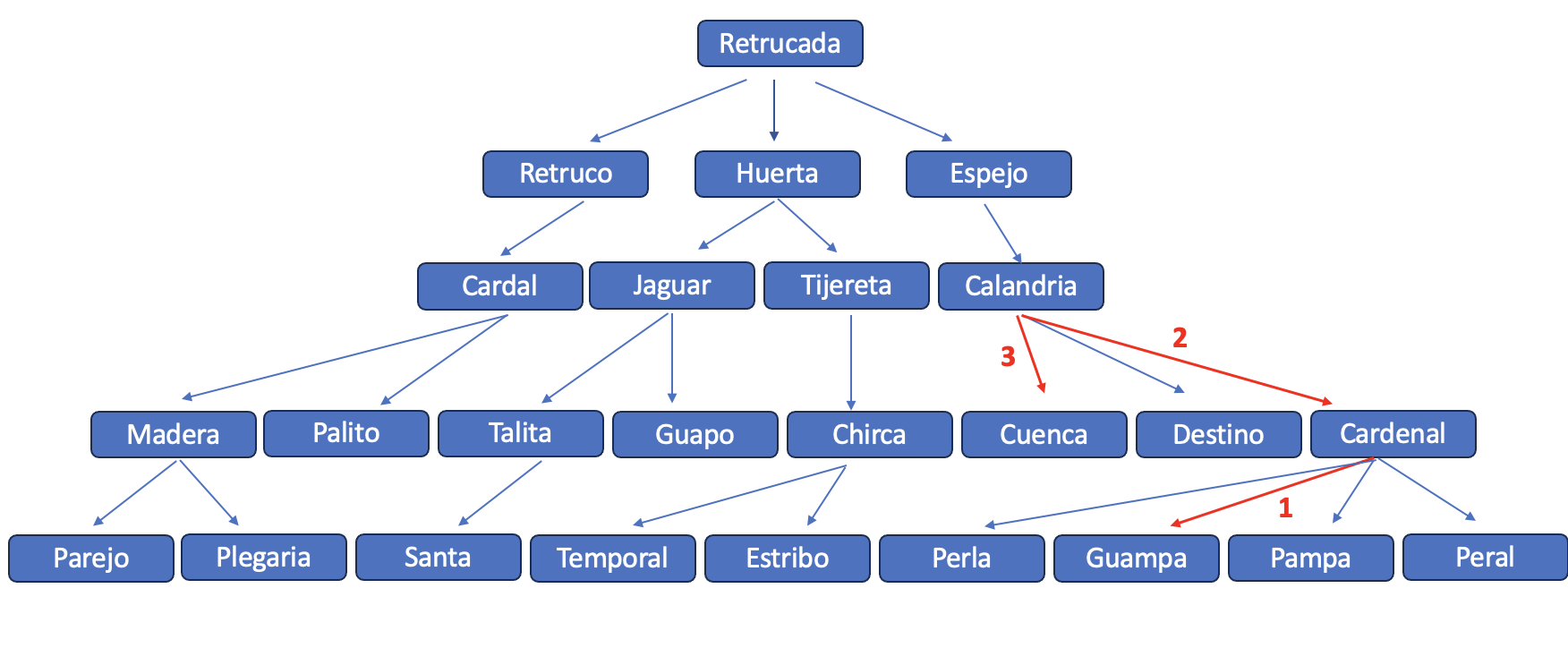
Comprobamos entonces que \(n=3\) por lo que:

\[a_{GC}=\frac{1}{2}^3 = \frac{1}{8} = 0,125\]

Entonces, la consanguinidad de un hijo de Guampa y Cuenca valdría:

\[F_{Hijo}=\frac{1}{2}a_{GC} = 0,0625\]

Ejercicio 9.2

A continuación se presenta un diagrama de pedigree de una familia de ratones:

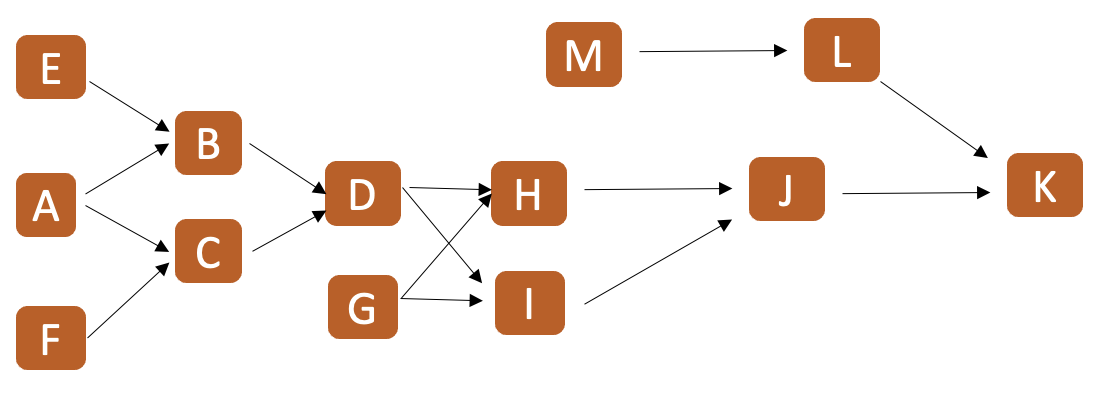
Basados en el mismo:

a. ¿Cuánto vale el parentesco entre \(H\) e \(I\)?

b. ¿Cuánto vale la consanguinidad de \(J\)?

c. ¿Cuánto vale la consanguinidad de \(K\)?

Solución

a. Como podemos observar en el esquema, \(H\) e \(I\) poseen dos ancestros en común que son \(D\) y \(G\), por lo que:

\[a_{HI}=\frac{1}{2}^n(1+F_D) + \frac{1}{2}^n(1+F_G)\]

En este sentido, \(F_G = 0\) mientras que observando el esquema, podemos ver que los padres de \(D\) están emparentados por lo que \(F_D\) no será \(0\).

Calculemos entonces \(F_D\):

\[F_D=\frac{1}{2}a_{BC}\]

\[a_{BC}=\frac{1}{2}^n(1+F_A) = \frac{1}{2}^2(1+ 0) = \]

\[F_D=\frac{1}{2} \frac{1}{4} = \frac{1}{8}\]

Por lo que ahora contamos con esta información para poder calcular el parentesco entre \(H\) e \(I\):

\(a_{HI}=\frac{1}{2}^2(1+ \frac{1}{8}) + \frac{1}{2}^2 = \frac{1}{4} \frac{9}{8} + \frac{1}{4} = \frac{9}{32} + \frac{8}{32} = \frac{17}{32} = 0,53125\)

b. Como hemos visto, la consanguinidad de de \(J\) será equivalente a la mitad del parentesco de sus padres y que sabemos del punto anterior que vale \(\frac{17}{32}\). Entonces, podemos calcular la consanguinidad de \(J\) como:

\[F_J=\frac{1}{2} \frac{17}{32} = \frac{17}{64} = 0,265625\]

c. Como nos ha sucedido en otras ocasiones, podemos comprobar que \(F_K=0\) ya que no existe relación de parentesco entre \(J\) y \(L\) (padres de \(K\)).

Ejercicio 9.3

En una población finita un individuo \(A\) se reproduce con un individuo \(B\) no emparentado, teniendo como progenie al individuo \(C\). Un estudio revela que el coeficiente de consanguinidad en el individuo \(C\) es de \(0,13\). ¿Cómo es esto posible? Nota: calcule teniendo en cuenta que nos encontramos estudiando una población finita (donde la deriva opera generando endocría).

Solución

Notemos que \(A\) y \(B\) son individuos no emparentados. La aproximación usual al momento de evaluar el coeficiente de consanguinidad en \(C\) es asumir que el parentesco aditivo \(a_{AB} = 0\), lo cual implica también que el coeficiente de consanguinidad \(F_C = 0\), ya que \(F_C = \frac{1}{2} a_{AB}\). No obstante, esto es una simplificación de la realidad: \(A\) y \(B\) pertenecen a una población real de tamaño finito, y como vimos en la segunda parte de este libro esto implica que compartirán alelos idénticos por ascendencia simplemente por efecto de la deriva genética (capítulos Deriva genética y Apareamientos no-aleatorios, recordar además el concepto del modelo del coalescente). ¿Cuál es la probabilidad de que dos alelos tomados al azar de \(A\) y \(B\) sean idénticos por ascendencia? Justamente el coeficiente de fijación de la población, que será a su vez igual al coeficiente de parentesco aditivo, si repasamos su definición (i.e., \(a_{AB} = F = 0,13\)). Por lo tanto, el coeficiente de consanguinidad de \(C\) no será de cero, si no de \(F_C = \frac{1}{2} 0,13 = 0,625\)

Ejercicio 9.4

A continuación se muestra una genealogía que detalla las relaciones de parentesco entre 8 individuos.

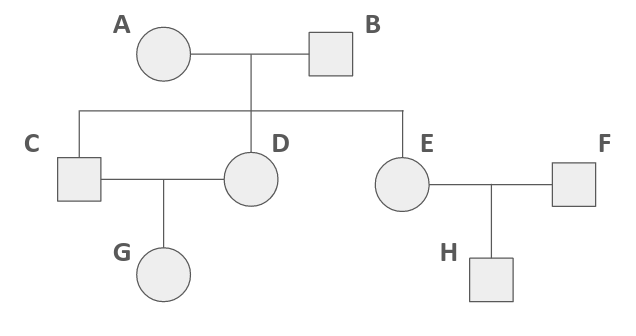
a. Calcule el coeficiente de consanguinidad para el individuo \(G\).

b. Un estudio poblacional muestra que en la población el coeficiente de fijación para la población es de aproximadamente \(F = 0,14\). Teniendo este dato responda: ¿cuál es el coeficiente de consanguinidad para el individuo \(H\)? ¿Cuál es la probabilidad de que dos alelos sean IBD en el individuo \(G\)?

Solución

a. Recordemos que el coeficiente de consanguinidad de \(G\) equivale a \(\frac{1}{2} a_{CD}\), donde \(a_{CD}\) es el parentesco aditivo de \(C\) y \(D\). Para calcular \(a_{CD}\) se puede recurrir al método del “diagrama de flechas”, según el cual el parentesco aditivo entre dos individuos \(X\) e \(Y\) equivale a

\[ a_{XY} = \sum_{A_i} (\frac{1}{2})^{n_{i1} + n_{i2}} (1 + F_{A_i}) \]

Notemos no obstante que los individuos \(C\) y \(D\) se encuentran emparentados, y son hermanos completos. El coeficiente de parentesco en este caso ya fue desarrollado en el capítulo (siendo \(a_{CD} = \frac{1}{2}\)), por lo que no nos extenderemos nuevamente el su cálculo. No obstante, remarcaremos (ya que es importante para la siguiente parte del ejercicio) que esta aproximación tiene en cuenta que dicho cálculo tiene en cuenta que \(A\) y \(B\) son individuos no emparentados (i.e. sin alelos IBD).

De lo anterior se tiene que el coeficiente de consanguinidad de \(G\) es de \((\frac{1}{2}) \cdot (\frac{1}{2}) = \frac{1}{4}\)

b. ¿Qué sucede en el caso del individuo \(H\)? Notemos que sus progenitores, \(E\) y \(F\), no están emparentados. Esto implica, en principio, que el coeficiente de consanguinidad de \(H\) debería ser de \(0\) (razonamiento análogo al utilizado para calcular los coeficientes de consanguinidad de los individuos \(C\) o \(D\) en el ejercicio anterior). No obstante, se reporta que el \(F\) en la población es de \(0,14\). Si recordamos de capítulos anteriores, la probabilidad de que dos alelos tomados al azar en la población sean IBD; ya que los individuos \(E\) y \(F\) son técnicamente dos individuos tomados al azar de la población, \(F\) debería ser también la probabilidad de que dos alelos de estos individuos sean IBD. Es decir, \(F\) es en efecto equivalente a lo que antes definimos como \(a_{EF}\). Teniendo esto en cuenta tenemos que la consanguinidad de \(H\) es de \((\frac{1}{2}) \cdot a_{EF} = (\frac{1}{2}) \cdot 0,14 = 0,07\).

Notemos que el dato de que \(F \neq 0\) afecta también a la estimación que hicimos en la primer parte del ejercicio. Por razonamiento análogo al empleado entre los individuos \(E\) y \(F\), el coeficiente de parentesco \(a_{AB} = 0,14\). Esto implica a su vez que los individuos \(C\) y \(D\) tienen coeficiente de consanguinidad de \(0,07\) cada uno. Esto debe contemplarse al momento de calcular el parentesco aditivo entre \(C\) y \(D\) para calcular la consanguinidad en \(G\). La consanguinidad entre \(C\) y \(D\) ya no es de \(\frac{1}{2}\), si no que

\[ \begin{split} a_{CD} = \frac{1}{2}^2(1+F_A) + \frac{1}{2}^2(1+F_B) \\ a_{CD} = \frac{1}{2}^2(1+0,07) + \frac{1}{2}^2(1+0,07) \\ a_{CD} = 0,535 \end{split} \]

De esto se desprende a su vez que \(F_G \neq \frac{1}{4}\), sino que ahora aproximamos que \(F_G = (\frac{1}{2}) \cdot a_{CD} = (\frac{1}{2}) \cdot 0,535 = 0,2576\)

Ejercicio 9.5

Se conoce que la varianza aditiva del peso de carcasa en corderos pesados es \(2,4 kg^2\) a la vez que la varianza de dominancia es \(1,2 kg^2\) y la de ambiente común es \(2,7 kg^2\).

¿Cuál es la covarianza entre medios hermanos para esta característica? ¿Cuál es la covarianza entre hermanos enteros para esta característica?

Solución

En el caso de medios hermanos \(\text{Cov}_{ME}=\frac{1}{4}V_A\), mientras que en hermanos enteros la \(\text{Cov}_{HE}=\frac{1}{2}V_A +\frac{1}{4}V_D + V_{E\text{común}}\). Por lo tanto, en este caso \(\text{Cov}_{ME}= \frac{1}{4} \cdot 2,4 = 0,6 kg^2\) y \(\text{Cov}_{HE}= \frac{1}{2} \cdot 2,4 +\frac{1}{4} \cdot 1,2 + 2,7 = 4,2 kg^2\).

---

Bibliografía

Echeverrı́a, Pı́a, Ana Espasandin, Paola Gaiero, Ana Laura Sánchez, and Jorge I Urioste. 2012. Manual de Prácticas Del Curso de Zootecnia. Facultad de Agronomı́a.

VanRaden, P. M. 2008. “Efficient methods to compute genomic predictions.” J Dairy Sci 91 (11): 4414–23.

Wright, Sewall. 1922. “Coefficients of inbreeding and relationship.” American Naturalist 56: 330–38.

---

84. Llamamos información de fase a la que nos indica qué alelo de un locus va junto en el cromosoma con qué alelo de otro locus, o de otra forma, la que nos permite reconstruir los haplotipos.↩︎

85. La siguiente sección fue inicialmente escrita para explicar los estudios de ascendencia en humanos y utilizada por la empresa genLives (https://wwww.genlives.com) para facilitar la comprensión del alcance de los mismos Aquí es usada y modificada con conocimiento y autorización de dicha empresa.↩︎