Capítulo 13 Selección Artificial II

En capítulos anteriores hemos avanzado en la construcción de las estrategias para mejorar desde el punto de vista genético características de interés para nosotros, primero basados en el fenotipo de los individuos que son candidatos a la selección en la misma característica de interés y luego a través de otras características correlacionadas, pero siempre basados en la información fenotípica del candidato. Una excepción a esto fue nuestra definición de valor de cría de un individuo, cuando la consideramos la mitad del desvío fenotípico promedio de los hijos del candidato, cuando este se apareaba con un número importante de individuos del otro sexo escogidos al azar. En este caso, estamos utilizando la información de la progenie del candidato (el criterio de selección) para mejorar una determinada característica.

En el presente capítulo vamos a extender nuestros conocimientos sobre las estrategias de selección posibles, en una primera parte utilizando información proveniente de parientes del individuo, mientras que en la segunda parte vamos a discutir cómo seleccionar por diferentes características a la vez. Cerraremos el capítulo discutiendo sobre métodos “modernos” para la predicción del valor de cría, los que permiten incorporar de forma “automática” la información aportada por parientes del candidato, así como la evaluación de muchas características a la vez.

Como lo notarás en breve, el eje articulador del capítulo son los índices de selección, en particular los índices lineales. Hay una extensa teoría disponible sobre ellos, son sencillos de comprender, fáciles de usar y su interpretación es intuitiva. Para ello haremos uso extensivo de herramientas básicas de álgebra lineal ya que trabajaremos con las matrices de varianza-covarianza, tanto fenotípica como genética, que vimos en la sección Matrices de varianza-covarianza del capítulo Correlaciones y Respuesta Correlacionada.

Muchos de los métodos de selección que discutiremos en el capítulo no se utilizan actualmente en la práctica ya que han sido ampliamente superados por metodologías más modernas de selección, que permiten trabajar en forma unificada los datos. Ejemplos de esto son la selección familiar y la selección dentro de familias. Sin embargo, su presentación aquí sigue jugando un papel muy importante en comprender cómo los distintos grados de parentesco aportan información diferente y si bien como métodos de selección han sido superados, su comprensión facilita la comprensión futura de las técnicas más avanzadas, como los modelos lineales mixtos y los estimados BLUP.

OBJETIVOS DEL CAPÍTULO

$\square$ Entender los criterios, objetivos fundamentales y el uso de información en el proceso de selección genética.

$\square$ Integrar la información proveniente de diferentes parientes para mejorar la precisión de la selección.

$\square$ Estudiar cómo se calculan las matrices de varianza-covarianza fenotípica y genética.

$\square$ Analizar la utilidad y limitaciones de las pruebas de progenie en la selección genética.

$\square$ Evaluar la precisión del valor de cría derivado de índices de selección.

$\square$ Comprender los métodos de selección para múltiples características y cómo se combinan estas en índices.

$\square$ Explorar técnicas avanzadas para la predicción del valor de cría, como BLUP y modelos mixtos lineales, y su aplicación en la mejora genética.

13.1 Criterios y objetivos de selección

En parte importante de este capítulo vamos a trabajar con la selección por varias características, mientras que en el resto trabajaremos con selección en una característica a partir de información obtenida de parientes de los candidatos. En ambos casos es importante entender la distinción que existe entre objetivos de selección y criterios de selección.

Objetivo de selección define a la característica que queremos mejorar a través de la selección, aquella característica que presenta relevancia propia para nosotros.

En el caso de la producción agropecuaria, los objetivos de selección se vinculan, en general, directamente a los ingresos o egresos del establecimiento. Por ejemplo, si se trata de producción lechera, el sistema de pago en nuestro país incluye los kilogramos de proteína y los kilogramos de grasa en la paramétrica de pago. Por lo tanto, si queremos incrementar los ingresos del establecimiento una buena opción sería mejorar la cantidad de grasa y proteína que genera cada vaca en una lactancia. Como ambas características, producción de grasa y de proteína, poseen una fuerte base genética, entonces resulta razonable plantearse mejorar genéticamente dichas características. Por lo tanto, en caso de elegirlas, las mismas constituyen objetivos de selección claros.

En algunos casos será posible hacer selección directamente por la característica, basados en el fenotipo del candidato. En otros casos esto resultará imposible, por ejemplo, en el caso de que una característica se exprese en el otro sexo (respecto a los candidatos a la selección). En este caso, será necesario recurrir a otras características correlacionadas, a información de parientes o ambas combinadas. En ese caso, los objetivos de selección y los criterios de selección no son los mismos.

Criterios de selección son los criterios que se utilizan como fuente de información para mejorar los objetivos de selección. Pueden coincidir o no con los objetivos de selección.

En muchos casos, los criterios de selección no tienen ningún valor per se para los ingresos y egresos del establecimiento y simplemente se trata de fuentes de información disponibles para mejorar los objetivos de selección. En otros casos se trata del mismo objetivo de selección, lo que simplifica muchísimos la tarea de seleccionar. En general, en las características fáciles de observar y registrar, que se expresan en ambos sexos y que poseen una heredabilidad razonable el objetivo de selección coincide con el criterio de selección.

Para que un criterio de selección sea usable para mejorar otras características es fundamental que el mismo sea relativamente fácil y barato de medir, que posea una heredabilidad razonable, pero fundamentalmente que se encuentre correlacionado desde el punto de vista genético con el objetivo que se desea mejorar.

Ejemplo 13.1

Objetivos y criterios de selección suelen ser diferentes. En general, la razón de esto es que la característica de interés es difícil de medir directamente en los individuos candidatos. Por ejemplo, porque el animal no expresa la característica (leche en machos). En ese caso, una alternativa es realizar la medición en parientes.

En la siguiente tabla, solo a modo de ejemplo, se presentan algunas alternativas para mejorar una característica mediante información de parientes (medio-hermanas o hijas) de los candidatos a la selección ($h^2=0,20$):

$\text{Alternativa}$	$i$	$r_{AC}$	$IG$	$\frac{i \times r_{AC}}{IG}$
Medir 5 medio-hermanas	$1,03$	$0,228$	$4,3$	$0,055$
Medir 10 medio-hermanas	$0,88$	$0,294$	$4,3$	$0,060$
Medir 20 medio-hermanas	$0,70$	$0,358$	$4,3$	$0,058$
Medir 30 medio-hermanas	$0,58$	$0,391$	$4,3$	$0,053$
Medir 5 hijas	$1,03$	$0,456$	$6,3$	$0,075$
Medir 10 hijas	$0,88$	$0,587$	$6,3$	$0,082$
Medir 20 hijas	$0,70$	$0,716$	$6,3$	$0,080$
Medir 30 hijas	$0,58$	$0,782$	$6,3$	$0,072$

Como la respuesta anual depende de $\frac{i\ r_{AC}\ \sigma_A}{IG}$, pero $\sigma_A$ es igual para todas las alternativas, entonces nos alcanza con optimizar $\frac{i \times r_{AC}}{IG}$ (última columna de la tabla).

PARA RECORDAR

El objetivo de selección define a la característica que queremos mejorar a través de la selección, aquella característica que presenta relevancia propia para nosotros. Generalmente los mismos estan directamente vinculados a los ingresos o egresos del establecimiento.
Los criterios de selección son los criterios que se utilizan como fuente de información para mejorar los objetivos de selección. Pueden coincidir o no con los objetivos de selección. En muchos casos, los criterios de selección no tienen ningún valor en sí para los ingresos y egresos del establecimiento y simplemente se tratan de fuentes de información disponibles para mejorar los objetivos de selección.
En algunos casos será posible hacer selección directamente por la característica, basados en el fenotipo del candidato, en otros casos esto resultará imposible. Entonces, será necesario recurrir a otras características correlacionadas, a información de parientes o ambas combinadas. En ese caso, los objetivos de selección y los criterios de selección no son los mismos.
En general, en las características fáciles de observar y registrar, que se expresan en ambos sexos y que poseen una heredabilidad razonable el objetivo de selección coincide con el criterio de selección.
Para que un criterio de selección sea usable para mejorar otras características es fundamental que el mismo sea relativamente fácil y barato de medir, que posea una heredabilidad razonable, pero fundamentalmente que se encuentre correlacionado desde el punto de vista genético con el objetivo que se desea mejorar.

13.2 Selección basada en un solo tipo de fuente de información

En el método de selección individual la idea es utilizar la información fenotípica aportada por el individuo como criterio para la decisión sobre el valor reproductivo del mismo. Este método es extremadamente sencillo de implementar y es el método sobre el que construimos el capítulo Selección Artificial I, donde trabajamos con la selección por umbral y que a veces llamamos selección masal. Se trata de un método que funciona muy bien cuando la información fenotípica es fácil de colectar y la heredabilidad de la característica es media o alta. Sin embargo, en situaciones donde el fenotipo individual es difícil o aún imposible de obtener (por ejemplo, cuando la característica se expresa en solo un sexo), o cuando la heredabilidad de la característica es baja, aún podemos recurrir a la selección usando otras fuentes de información. En el capítulo Correlaciones y Respuesta Correlacionada vimos cómo utilizar la información de una característica fuertemente correlacionada medida en el mismo individuo para mejorar la eficiencia de la selección. En lo que sigue veremos como utilizar la información brindada por algunas estructuras de parentesco particulares y más adelante en este capítulo veremos como combinar la información de diferentes relaciones de parentesco. Esta sección está basada en el tratamiento del tema dado por Douglas S. Falconer and Mackay (1996), que es además una excelente referencia sobre el tema.

La idea por detrás de la presente sección (y de otras) es que el fenotipo de un individuo podemos descomponerlo en la suma de dos fuentes diferentes, una la correspondiente al desvío de la media familiar respecto a la media de la población, que llamaremos ${P_f}$ y otra que corresponde al desvío fenotípico del individuo respecto a la media familiar, que llamaremos ${P_w}$ (la ${_w}$ correspondiendo al inglés “within”, dentro). Por lo tanto, el fenotipo de un individuo será

\[ \begin{split} {P=P_f+P_w} \end{split} \tag{13.1} \]

Ambos componentes aportan cosas diferentes, dependiendo de las relaciones familiares y de los parámetros genéticos, por lo que la idea a continuación será ver los distintos tipos de selección posibles usando estructuras de parentesco definidas y la respuesta a la selección consiguiente. En el caso de selección individual le hemos dado un peso equivalente a ambos componentes, ${P_f}$ y ${P_w}$. Veremos entonces que existe un tipo de selección que llamaremos selección familiar donde solo ponderaremos el aporte de ${P_f}$, mientras que en otro tipo de selección, que llamaremos selección intrafamiliar solo ponderaremos el aporte de ${P_w}$.

Diferentes tipos de selección basados en estructuras de parentesco definidas

Selección familiar La idea en selección familiar es darle todo el peso a ${P_f}$, dejando de lado el aporte de ${P_w}$ y de esta manera eligiendo familias enteras como reproductores. Si bien podría parecer una idea terrible a primera vista, la lógica de este tipo de selección es que los efectos ambientales tienden a cancelarse dentro de la familia, lo que llevaría a que la media fenotípica de la misma sea similar a la media genotípica. Esto es particularmente interesante cuando los efectos ambientales son una parte importante de la variabilidad fenotípica, es decir, la heredabilidad es baja, ya que el fenotipo individual no es un buen indicador del mérito genético. En el caso de que existan efectos del ambiente común, estos afectarán los promedios familiares, por lo que los promedios familiares tampoco serían una buena indicación del mérito genético. Claramente, además, el funcionamiento de esta lógica es dependiente del número de individuos evaluados por familia, ya que un número bajo dará promedios familiares con mucho error, reduciendo las ventajas del método. Este tipo de selección es bastante común en peces, donde se crían numerosas familias y se eligen, por ejemplo, aquellas de mayor rendimiento.

La respuesta esperada a este tipo de selección la podemos escribir como

\[ \begin{split} {R_f=i\ \sigma_f\ h^2_f} \end{split} \tag{13.2} \]

donde ${\sigma_f}$ representa el desvío estándar de las medias fenotípica familiares y ${h^2_f}$ es la heredabilidad de los promedios familiares, algo que calcularemos un poco más adelante.

El mayor problema con este tipo de selección es, obviamente, el incremento en la consanguinidad esperada en la población y la depresión endogámica consiguiente en las características que la muestren, algo que discutiremos en el capítulo Endocría, exocría, consanguinidad y depresión endogámica.

Selección fraternal La misma podría considerarse como un caso especial de selección familiar en el que el fenotipo del candidato no es incluido en las mediciones. Este tipo de selección es clásico para características que se expresan en un solo sexo, como podrían ser las de producción lechera que solo se expresan en hembras. En este caso, es frecuente utilizar la información proveniente de grupos de hermanos (enteros o medio hermanos, uno de los dos). A medida de que el número de individuos medidos por grupo se incrementa, el incluir o no el fenotipo del individuo deja de tener relevancia y los resultados de ambos tipos de selección convergen. Este tipo de selección a su vez es típica en el mejoramiento genético de características de carcasa donde se sacrifican hermanos del candidato, el cual por obvios motivos no podemos medir.

Selección dentro de familia La idea es exactamente la opuesta a la idea de selección familiar, en lugar de seleccionar por la media familiar, seleccionamos por el desvío respecto a la media familiar. La lógica subyacente de esto es que si el ambiente común familiar juega un papel muy importante en la similaridad de los individuos, entonces las diferencias respecto a la media de la familia pueden representar mejor las diferencias genéticas entre individuos. Un ejemplo claro de características de este tipo son las de crecimiento inicial en especies multíparas de mamíferos, como los cerdos, donde toda la camada se cría junta y su “performance” depende en gran medida de las habilidades maternas. En el caso particular de que se seleccione un individuo de cada sexo en cada familia, en lugar de uno solo, esto permite asegurar tamaños de familia exactamente iguales, llevando a cero la varianza en el número de progenies efectivo por familia y de esta manera incrementando al doble el tamaño efectivo poblacional (algo que a fines prácticos es mayormente aplicable en poblaciones de laboratorio). De esta forma, con un número no muy elevado de individuos podemos mantener relativamente controlada la consanguinidad.

En forma análoga a la selección familiar, la respuesta esperada a la selección dentro de familias vamos a calcularla como

\[ \begin{split} {R_w=i\ \sigma_w\ h^2_w} \end{split} \tag{13.3} \]

donde ${R_w}$ es la respuesta a la selección dentro de familias, ${\sigma_w}$ es el devío estándar fenotípico de los desvíos respecto a la media familiar y ${h^2_w}$ es la heredabilidad correspondiente a este tipo de selección.

Pruebas de progenie En este tipo de selección la idea es evaluar el valor reproductivo a partir de los fenotipos de su progenie. De hecho, la definición de valor de cría como el doble del desvío fenotípico observado en la progenie es exactamente esto. Claramente, en la definición recurríamos al concepto de apareamiento con una muestra aleatoria de tamaño infinito de individuos del otro sexo, cosa que en la práctica es imposible. Sin embargo, evaluando a los futuros reproductores a partir de un gran número de hijos, producto de apareamientos al azar, suele ser una buena aproximación a ese concepto. En principio, podría parecer que se trata de una alternativa óptima, pero presenta serias dificultades que lo hacen apenas una alternativa razonable para manejos a gran escala y esfuerzos centralizados. Por un lado, existe un incremento importante en el intervalo generacional, ya que debemos esperar a que los hijos del candidato crezcan hasta el momento de poder ser evaluados para la característica de interés y luego esperar un período reproductivo entero del candidato elegido (en el que es usado en forma masiva) para que nazcan sus hijos. Esto enlentece en una medida importante el mejoramiento genético anual, algo que discutiremos en la sección Límites de la eficiencia en pruebas de progenie. Por otra parte, cuantos más individuos tengamos que mantener para evaluar a cada candidato (aumentando la precisión de la evaluación del candidato), menos candidatos podremos evaluar y por lo tanto también bajaremos la intensidad de selección. Se trata de un balance delicado y no-lineal, por lo que la evaluación de las mejores combinaciones es algo complicada.

Cálculo de las heredabilidades en los distintos tipos de selección

Como ${\sigma^2_T=\sigma^2_B+\sigma^2_W}$ y ${t=\frac{\sigma^2_B}{\sigma^2_T}}$ y por lo tanto ${\sigma^2_B=t\ \sigma^2_T}$, entonces ${\sigma^2_W=(1-t)\sigma^2_T}$. Esta es la partición de la varianza observada en componentes observables, donde la varianza total ${\sigma^2_T}$ es la varianza fenotípica y que, como de costumbre, notaremos con ${V_P}$.

De la misma manera, podemos particionar la varianza aditiva en componentes entre familias y dentro de familias, como ya discutimos en el capítulo 9. En el mismo, vimos que la covarianza dentro de familias (similaridad) era igual a la varianza entre familias. Si, para mantener la consistencia con Douglas S. Falconer and Mackay (1996) usamos ${r}$ como notación para el coeficiente de parentesco aditivo (${r}=2f$), en lugar de $a$ que habíamos usado, entonces la varianza aditiva entre familias será ${r\ V_A}$ y la varianza aditiva dentro de familias, por lo tanto, ${(1-r)\ V_A}$.

Organizando la información anterior en una tabla de partición de las varianzas aditivas y fenotípica y su relación con los componentes observacionales, tenemos:

Componente.observacional	Varianza.Aditiva	Varianza.Fenotípica
Entre familias ${\sigma^2_B}$	${r\ V_A}$	${t\ V_P}$
Dentro de familias ${\sigma^2_W}$	${(1-r)\ V_A}$	${(1-t)\ V_P}$

Si ${\sigma^2_f}$ y ${\sigma^2_w}$ son las varianzas observadas sin error, es decir con muestras de tamaño infinito, el observarlas con muestras de tamaño reducido introducirá errores en las medias de grupos (familias) y por lo tanto las varianzas observadas realmente. De esta forma, la varianza entre medias familiares se verá incrementada en la cantidad ${\frac{1}{n}\sigma^2_W}$ (que es la varianza en la estimación de la media familiar), mientras que la varianza de los desvíos intrafamiliares se verá reducida de la misma manera (la varianza total es la misma).

Entonces, teniendo en cuenta el tamaño de muestras no-infinito, tenemos que la relación entre los componentes observacionales y causales, utilizando los resultados que están en la tabla anterior, para las varianzas aditivas están dadas ahora por

\[ \begin{split} {\sigma^2_B+\frac{1}{n}\sigma^2_W=r V_A+\frac{1}{n}(1-r)V_A=\left[\frac{nr+(1-r)}{n}\right]V_A=\left[\frac{1+(n-1)r}{n}\right]V_A} \end{split} \tag{13.4} \]

\[ \begin{split} {\sigma^2_W-\frac{1}{n}\sigma^2_W=\frac{(n-1)}{n}\sigma^2_W=\frac{(n-1)}{n}(1-r)V_A=\frac{(n-1)(1-r)}{n}V_A} \end{split} \tag{13.5} \]

Con el mismo procedimiento, para las varianzas fenotípicas, tenemos ahora que

\[ \begin{split} {\sigma^2_B+\frac{1}{n}\sigma^2_W=t V_P+\frac{1}{n}(1-t)V_P=\left[\frac{nt+(1-t)}{n}\right]V_P=\left[\frac{1+(n-1)t}{n}\right]V_P} \end{split} \tag{13.6} \]

y en forma correspondiente

\[ \begin{split} {\sigma^2_W-\frac{1}{n}\sigma^2_W=\frac{(n-1)}{n}\sigma^2_W=\frac{(n-1)}{n}(1-t)V_P=\frac{(n-1)(1-t)}{n}V_P} \end{split} \tag{13.7} \]

La información anterior podemos organizarla en una tabla como la siguiente, que nuevamente relaciona los componentes observacionales con los causales:

Varianza observada	Componentes observacionales	Aditiva (causal)	Fenotípica (causal)
$\text{de medias familiares } \sigma^2_f$	$\sigma^2_B + \frac{1}{n} \sigma^2_W$	$\frac{1+(n-1)r}{n}\ V_A$	$\frac{1+(n-1)t}{n}\ V_P$
$\text{desvíos intrafamiliares } \sigma^2_w$	$\sigma^2_W - \frac{1}{n} \sigma^2_W$	$\frac{(n-1)(1-r)}{n}\ V_A$	$\frac{(n-1)(1-t)}{n}\ V_P$

A partir de esto, la heredabilidad de la selección familiar podemos calcularla directamente como la relación entre las varianzas aditiva y fenotípica correspondientes, es decir

\[ \begin{split} {h^2_f=\frac{\left[\frac{1+(n-1)r}{n}\right]V_A}{\left[\frac{1+(n-1)t}{n}\right]V_P}=\left(\frac{1+(n-1)r}{1+(n-1)t}\right)\frac{V_A}{V_P}=\left(\frac{1+(n-1)r}{1+(n-1)t}\right)h^2} \end{split} \tag{13.8} \]

De la misma manera, la heredabilidad de las desviaciones intrafamiliares será

\[ \begin{split} {h^2_w=\frac{\frac{(n-1)(1-r)}{n}V_A}{\frac{(n-1)(1-t)}{n}V_P}=\frac{(1-r)}{(1-t)}\frac{V_A}{V_P}=\frac{(1-r)}{(1-t)}h^2} \end{split} \tag{13.8} \]

En el caso de selección fraternal, donde nos vamos a guiar por la información de los hermanos del candidato, la principal diferencia con la selección familiar es que el individuo candidato no es medido. En este caso, resulta más sencillo obtener la heredabilidad apropiada a este tipo de selección como la regresión de los valores de cría de los individuos candidatos (no medidos) en la media fenotípica de sus hermanos medidos. La covarianza entre hermanos (medio o enteros) es igual ${r\ V_A}$, lo que no se ve afectado por el número de hermanos medidos en el grupo. Por otro lado, la varianza fenotípica en el grupo de medios hermanos sí se ve afectada y su valor, como vimos antes es ${\frac{1+(n-1)t}{n}V_P}$, por lo que poniendo todo junto, tenemos

\[ \begin{split} {h^2_s=\frac{r\ V_A}{\frac{1+(n-1)t}{n}V_P}=\frac{nr}{1+(n-1)t}h^2} \end{split} \tag{13.9} \]

Si recordamos del capítulo Parámetros Genéticos: Heredabilidad y Repetibilidad que un estimador obtenido como regresión del valor de cría del individuo a partir de su información fenotípica era el producto de la heredabilidad por el desvío fenotípico (respecto a la media de la población), entonces resulta natural extender este concepto a otros tipos de selección, como por ejemplo con estructuras de parentesco definidas. En el caso de selección individual teníamos

\[ \begin{split} {\hat A=b_{AC}(z_i - \bar z)=h^2(z_i - \bar z)} \end{split} \tag{13.10} \]

Aplicando la misma idea a selección fraternal, que se puede aplicar a estructuras de parentesco definidas y que no contengan la información del propio candidato, tenemos que el coeficiente de regresión es

\[ \begin{split} {b_{AC}=\frac{r\ n\ h^2}{1+(n-1)t}} \end{split} \tag{13.11} \]

y por lo tanto, el estimador del valor de cría del individuo, evaluado a través de sus parientes será

\[ \begin{split} {\hat A=b_{AC}(z_i - \bar z)=h^2_s(z_i - \bar z)=\frac{n\ r\ h^2}{1+(n-1)t}(z_i - \bar z)} \end{split} \tag{13.12} \]

Para obtener la precisión del método de selección fraternal (y de los otros que tengan relación fija de parentesco y no incluyan al candidato) alcanza con calcular la correlación entre el valor de cría del candidato y el criterio (la media fenotípica de $n$ hermanos). Usando la misma lógica que para derivar la ecuación (13.9), pero ahora recordando que la varianza aditiva de la población de donde sale el candidato es ${V_A}$, tenemos

\[{r_{AC}=\frac{r\ V_A}{\sqrt{V_A}\sqrt{\frac{1+(n-1)t}{n}V_P}}=\frac{V_A}{\sqrt{V_A}\sqrt{V_P}}\frac{r}{\sqrt{\frac{1+(n-1)t}{n}}}=}\] \[{\frac{\sqrt{V_A}\sqrt{V_A}}{\sqrt{V_A}\sqrt{V_P}}\frac{r}{\sqrt{\frac{1+(n-1)t}{n}}}=\frac{\sqrt{V_A}}{\sqrt{V_P}}\frac{r}{\sqrt{\frac{1+(n-1)t}{n}}}=\sqrt{\frac{V_A}{V_P}}\frac{r}{\sqrt{\frac{1+(n-1)t}{n}}}}\ \therefore\]

\[ \begin{split} {r_{AC}=r\ h\sqrt{\frac{n}{1+(n-1)t}}} \end{split} \tag{13.13} \]

Utilizando la misma aproximación de regresión, en el caso de las pruebas de progenie, teniendo en cuenta que ${r=\frac{1}{2}}$ y ${t=r_{A_1A_2}\ h^2=\frac{1}{4}h^2}$

\[ \begin{split} {b_{AC}=r\ \frac{n\ h^2}{1+(n-1)t}=\frac{1}{2}\left[\frac{n\ h^2}{1+(n-1) \frac{1}{4}h^2}\right]=\frac{1}{2}\left[\frac{4\ n\ h^2}{4+(n-1)h^2}\right]=\frac{2\ n\ h^2}{4+(n-1)h^2}} \end{split} \tag{13.14} \]

que es el mismo resultado que vamos a obtener más adelante en la ecuación (13.40) de la sección Pruebas de progenie usando la aproximación de los índices de selección.

PARA RECORDAR

En la selección individual la idea es utilizar la información fenotípica aportada por el individuo como criterio para la decisión sobre el valor reproductivo del mismo. Sin embargo, en situaciones donde el fenotipo individual es difícil o aún imposible de obtener, o cuando la heredabilidad de la característica es baja, aún podemos recurrir a la selección usando otras fuentes de información.
El fenotipo de un individuo podemos descomponerlo en la suma de dos fuentes diferentes, una la correspondiente al desvío de la media familiar respecto a la media de la población, que llamaremos $P_f$ y otra que corresponde al desvío fenotípico del individuo respecto a la media familiar, que llamaremos $P_w$.
Cuando realizamos selección familiar la idea es darle todo el peso a $P_f$, dejando de lado el aporte de $P_w$ y de esta manera eligiendo familias enteras como reproductores. La lógica de este tipo de selección es que los efectos ambientales tienden a cancelarse dentro de la familia, lo que llevaría a que la media fenotípica de la misma sea similar a la media genotípica. La respuesta esperada será: ${R_f=i\ \sigma_f\ h^2_f}$ dónde donde ${\sigma_f}$ representa el desvío estándar de las medias fenotípica familiares y ${h^2_f}$ es la heredabilidad de los promedios familiares.
El problema más notable de este tipo de selección es el incremento en la consanguinidad esperada en la población y la depresión endogámica consiguiente en las características que la muestren.
Podemos definir la selección fraternal como un caso particular de selección familiar en el que el fenotipo del candidato no es incluido en las mediciones. En este caso, es frecuente utilizar la información proveniente de grupos de hermanos. A medida de que el número de individuos medidos por grupo se incrementa, el incluir o no el fenotipo del individuo deja de tener relevancia y los resultados de ambos tipos de selección convergen.
Cuando realizamos selección dentro de la familia, la idea es la opuesta a la de selección familiar, en lugar de seleccionar por la media familiar, seleccionamos por el desvío respecto a la media familiar. Este tipo de selección se aplica cuando el ambiente común familiar juega un papel muy importante en la similaridad de los individuos, entonces las diferencias respecto a la media de la familia pueden representar mejor las diferencias genéticas entre individuos. La respuesta esperada será: ${R_w=i\ \sigma_w\ h^2_w}$ dónde ${R_w}$ es la respuesta a la selección dentro de familias, ${\sigma_w}$ es el devío estándar fenotípico de los desvíos respecto a la media familiar y ${h^2_w}$ es la heredabilidad correspondiente a este tipo de selección.
La idea detrás de las pruebas de progenie es evaluar el valor reproductivo a partir de los fenotipos de su progenie. Teóricamente parece una alternativa óptima a la evaluación, pero al tener que esperar que los hijos crezcan para realizar la evaluación de la característica, el $IG$ se ve aumentado. Por otra parte, cuánto mas individuos evaluemos aumentaremos la precision del método pero estaremos disminuyendo la cantidad de candidatos a evaluar y por lo tanto también bajaremos la intensidad de selección.
Podemos calcular la heredabilidad de la selección familiar directamente como la relación entre las varianzas aditiva y fenotípica correspondientes: ${h^2_f=\left(\frac{1+(n-1)r}{1+(n-1)t}\right)h^2}$
De la misma manera, la heredabilidad de las desviaciones intrafamiliares será: ${h^2_w=\frac{(1-r)}{(1-t)}h^2}$
En el caso de la selección fraternal, la heredabilidad podemos calcularla como: ${h^2_s=\frac{nr}{1+(n-1)t}h^2}$
El estimador del valor de cría del individuo, evaluado a través de sus parientes será: ${\hat A=\frac{n\ r\ h^2}{1+(n-1)t}(z_i - \bar z)}$ y su correspondiente precisión será: ${r_{AC}=r\ h\sqrt{\frac{n}{1+(n-1)t}}}$

13.3 Combinando la información proporcionada por diferentes tipos de parientes

Hasta ahora hemos visto selección fenotípica individual en el capítulo Selección Artificial I, selección por una característica correlacionada con fenotipo en el mismo individuo en el capítulo Correlaciones y Respuesta Correlacionada y en la sección precedente selección basada en estructuras de parentesco definidas. En el último caso, vimos que se podía tratar como la ponderación de la información fenotípica proveniente de medias familiares y de desvíos respecto a esas medias, pero nunca hicimos un esfuerzo por buscar la combinación óptima de esas dos fuentes. En esta sección vamos a comenzar a remediar ese punto, buscando combinaciones óptimas desde el punto de vista de la respuesta a la selección. Las mismas provienen de la aplicación de la teoría de índices de selección y vamos a basar buena parte de esta sección en las notas del curso de Werf (2000).

Un índice de selección (lineal) es una combinación (lineal) de diferentes valores, usualmente fenotípicos, tal que me permite asignar un valor reproductivo único a cada individuo. En el contexto de esta sección, la idea es cómo combinar de manera óptima la información, de tal manera que la correlación del índice con el valor de cría sea máxima. Dicho de otra forma, nuestro índice será

\[ \begin{split} {I=EBV=\hat A=b_1\ z_1+b_2\ z_2+...+b_k\ z_k} \end{split} \tag{13.15} \]

donde utilizamos los ${z_i}$ para identificar los fenotipos de cada tipo de fuente de información. Los tipos de fuentes de información pueden incluir el fenotipo propio del candidato, el promedio de hermanos enteros, promedio de medios hermanos, fenotipo de un progenitor, etc. De la teoría de modelos lineales, sabemos que los coeficientes correspondientes serán iguales a

\[ \begin{split} {b_i=\frac{Cov(z_i,A)}{Var(z_i)}} \end{split} \tag{13.16} \]

Por lo tanto, para estimar estos coeficientes la información que vamos a precisar es:

Covarianzas entre los valores fenotípicos y el valor de cría que nos interesa, es decir ${Cov(z_i,A)}$.
Varianzas fenotípicas en las diferentes fuentes de información, es decir ${Var(z_i)}$.
Como las fuentes de información covarían, para no superponer información (es decir, contar dos veces la misma información), debemos tener en cuenta esas covarianzas, es decir ${Cov(z_i,z_j)}$.

La información de los puntos 2 y 3 la podemos organizar en una matriz de varianza-covarianza, como vimos en la sección Matrices de varianza-covarianza del capítulo Correlaciones y Respuesta Correlacionada, es decir, la matriz $\mathbf{P}$.

Como los elementos $b_i$ forman un vector de largo $k$, que llamaremos $\mathbf{b}$ y las informaciones fenotípicas correspondientes a las distintas fuentes de información forman un vector $\mathbf{z}$ con elementos $z_i$, la ecuación (13.15) podemos escribirla como

\[ \begin{split} {EBV=\hat A=b_1\ z_1+b_2\ z_2+...+b_k\ z_k=\mathbf{b'z}} \end{split} \tag{13.17} \]

Más aún, las covarianzas entre las distintas fuentes de información fenotípica y el valor de cría, es decir las que describe el punto 1, ${Cov(z_i,A)}$, las podemos organizar en un vector. Como en realidad se trata de varianzas y covarianzas genéticas, usando la misma notación que usamos previamente en el capítulo anterior, llamaremos a esto $\mathbf{G}$, aunque teniendo en cuenta que en este caso particular se trata de un vector de varianzas-covarianzas genéticas.

Por lo tanto, usando la notación matricial, el vector de coeficientes del índice se reduce a

\[ \begin{split} \mathbf{b=P^{-1}G} \end{split} \tag{13.18} \]

por lo que debemos construir $\mathbf{G}$ y $\mathbf{P}$ para poder calcular los pesos de las distintas fuentes de información.

Cálculo de los elementos de la matriz de varianzas-covarianzas fenotípica

Recordemos que las características fenotípicas de las que estamos hablando en este contexto son en realidad siempre las mismas, pero provenientes desde diferentes fuentes de información. Tenemos, por lo tanto, diferentes situaciones a considerar:

Información generada a partir de una sola medición, donde la varianza de la misma está dada por

\[ \begin{split} {Var(z_i)=\sigma^2_P} \end{split} \tag{13.19} \]

Información generada a partir de la media de ${n}$ individuos, relacionados entre sí de tal manera que el coeficiente de correlación intraclase sea ${t}$ y donde por lo tanto la varianza del promedio será

\[ \begin{split} {Var(\bar z_i)=t \sigma^2_P+\frac{(1-t)}{n}\sigma^2_P=\sigma^2_P \left[t+\frac{(1-t)}{n}\right]=\sigma^2_P \left[\frac{nt+(1-t)}{n}\right] \therefore} \\ {Var(\bar z_i) =\sigma^2_P\left[\frac{1+(n-1)t}{n}\right]} \end{split} \tag{13.20} \]

Esto es equivalente a lo que vimos en la sección La reducción en la varianza fenotípica con varias medidas, resultado de promediar $n$ observaciones, algo que vimos en el capítulo Parámetros Genéticos: Heredabilidad y Repetibilidad. El coeficiente de correlación intraclase, habíamos visto que podía ser igual a la Repetibilidad, es decir ${t}=\rho$, cuando teníamos varias medidas repetidas en el mismo individuo o ${t=r_{A_{1}A_{2}}\ h^2}$ cuando teníamos medidas en distintos individuos con el mismo grado de parentesco.

La covarianza entre dos fuentes de información que consiste cada una en una sola medida, tomadas en individuos diferentes, es igual a

\[ \begin{split} {Cov(z_i,z_j)=a_{ij}\ \sigma^2_A=a_{ij}\ h^2\ \sigma^2_P} \end{split} \tag{13.21} \]

En los casos en que las observaciones entre individuos compartan una fracción del ambiente en común, por ejemplo, si ${c^2}$ es la proporción de varianza en común que corresponde al ambiente compartido, entonces adicionamos ${c^2\ \sigma^2_P}$ (ignorando los efectos de dominancia).

La covarianza entre dos fuentes de información, una de ellas una sola medida en el candidato a la selección y la otra el promedio de $n$ medidas en individuos que tienen el mismo parentesco entre sí y también el mismo parentesco con el candidato, es igual a

\[ \begin{split} {Cov(z_i,\bar z_j)=a_{ij}\ \sigma^2_A=a_{ij}\ h^2\ \sigma^2_P} \end{split} \tag{13.21} \]

con ${a_{ij}}$ el parentesco aditivo entre el candidato y cualquiera de los integrantes del grupo a promediar (todos tienen el mismo parentesco con el candidato).

Cálculo de los elementos del vector de varianzas-covarianzas genéticas

En este caso, solo tenemos dos posibilidades en el vector:

La covarianza entre una sola medida fenotípica y el valor de cría del individuo, que está dada por

\[ \begin{split} {Cov(z_i,A)=a_{ij}\ \sigma^2_A=a_{ij}\ h^2\ \sigma^2_P} \end{split} \tag{13.21} \]

La covarianza entre entre el promedio de $n$ medidas fenotípicas y el valor de cría del individuo, que está dada por

\[ \begin{split} {Cov(\bar z_i,A)=a_{ij}\ \sigma^2_A=a_{ij}\ h^2\ \sigma^2_P} \end{split} \tag{13.21} \]

Nuevamente, es importante acá que todos los individuos con información fenotípica sean con el mismo grado de parentesco entre sí y a su vez, con el mismo grado de parentesco (puede ser diferente al anterior) con el candidato.

Información propia y de un progenitor

Supongamos que queremos construir un índice utilizando la información propia y de un progenitor a fin de predecir el valor de cría de un individuo. En ese caso, usando la ecuación (13.15), nuestro índice sería

\[ \begin{split} {I=EBV_{ind}=\hat A=b_{ind}\ z_{ind}+b_{pro}\ z_{pro}} \end{split} \tag{13.22} \]

Por otra parte, de acuerdo a la ecuación (13.18), el índice será igual a

\[ \begin{split} \mathbf{b=P^{-1}G} \end{split} \]

por lo que debemos determinar dichas matrices. Aplicando las “reglas” que vimos más arriba para los elementos de $\mathbf{P}$, tenemos que la misma quedará determinada por

\[ \begin{split} \mathbf{P}= \left( \begin{matrix} {Var(z_{ind})} & {Cov(z_{ind},z_{pro})} \\ {Cov(z_{pro},z_{ind})} & {Var(z_{pro})} \end{matrix} \right) = \left( \begin{matrix} {\sigma^2_P} & {\frac{1}{2}h^2\sigma^2_P} \\ {\frac{1}{2}h^2\sigma^2_P} & {\sigma^2_P} \end{matrix} \right) = \left( \begin{matrix} {1} & {\frac{1}{2}h^2} \\ {\frac{1}{2}h^2} & {1} \end{matrix} \right) {\sigma^2_P} \end{split} \tag{13.23} \]

Por otra parte, aplicando las reglas para el vector $\mathbf{G}$, dado que ${a_{ind,ind}=1}$, ${a_{ind,pro}=\frac{1}{2}}$, tenemos que el mismo es igual a

\[ \begin{split} \mathbf{G}= \left( \begin{matrix} {Cov(z_{ind},A)} \\ {Cov(z_{pro},A)} \end{matrix} \right) = \left( \begin{matrix} {a_{ind, ind}\ \sigma^2_A} \\ {a_{ind, pro}\ \sigma^2_A} \end{matrix} \right) = \left( \begin{matrix} {h^2\ \sigma^2_P} \\ {\frac{1}{2}\ h^2\ \sigma^2_P} \end{matrix} \right) = \left( \begin{matrix} {h^2} \\ {\frac{1}{2}\ h^2} \end{matrix} \right) \sigma^2_P \end{split} \tag{13.24} \]

Utilizando los resultados de las ecuaciones (13.23) y (13.24), tenemos que el índice estará dado por

\[ \begin{split} \mathbf{b=P^{-1}G}= \left[ \left( \begin{matrix} {1} & {\frac{1}{2}h^2} \\ {\frac{1}{2}h^2} & {1} \end{matrix} \right) {\sigma^2_P} \right]^{-1} \left( \begin{matrix} {h^2} \\ {\frac{1}{2}\ h^2} \end{matrix} \right) \sigma^2_P = \left( \begin{matrix} {1} & {\frac{1}{2}h^2} \\ {\frac{1}{2}h^2} & {1} \end{matrix} \right)^{-1} \left( \begin{matrix} {h^2} \\ {\frac{1}{2}\ h^2} \end{matrix} \right) \end{split} \tag{13.25} \]

Más aún, la inversión de matrices de 2x2 es directa, ya que si la misma tiene coeficientes $a,b,c,d$, su inversa es

\[ \begin{split} \left( \begin{matrix} a & b \\ c & d \end{matrix} \right)^{-1} = \frac{1}{ad-bc} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right) \end{split} \tag{13.26} \]

por lo que aplicando esto a la ecuación (13.25) tenemos que

\[ \begin{split} \mathbf{b} = \left[ \begin{matrix} {1} & {\frac{1}{2}h^2} \\ {\frac{1}{2}h^2} & {1} \end{matrix} \right]^{-1} \left[ \begin{matrix} {h^2} \\ {\frac{1}{2}\ h^2} \end{matrix} \right] = \left( {\frac{1}{1-\frac{1}{4}h^4}}\right) \left[ \begin{matrix} {1} & {-\frac{1}{2}h^2} \\ {-\frac{1}{2}h^2} & {1} \end{matrix} \right] \left[ \begin{matrix} {h^2} \\ {\frac{1}{2}\ h^2} \end{matrix} \right] \therefore \\ \mathbf{b} = \left( {\frac{4}{4-h^4}}\right) \left[ \begin{matrix} {h^2-\frac{1}{4}h^4} \\ {\frac{1}{2}h^2-\frac{1}{2}h^4} \end{matrix} \right] \end{split} \tag{13.27} \]

Es decir, tenemos ahora los coeficientes del índice, para la información que aporta el individuo y para la información que aporta su progenitor (uno de ellos), que sería

\[ \begin{split} {EBV=\hat A=\mathbf{b'z}=\left(\frac{4}{4-h^4}\right)[(h^2-\frac{1}{4}h^4)\ z_{ind}+(\frac{1}{2}h^2-\frac{1}{2}h^4)\ z_{pro}]} \end{split} \tag{13.28} \]

En la Figura 13.1 podemos apreciar el comportamiento de los dos coeficientes, el de color rojo para el coeficiente correspondiente a la información aportada por el individuo, el de color azul correspondiente a la información que aporta su progenitor.

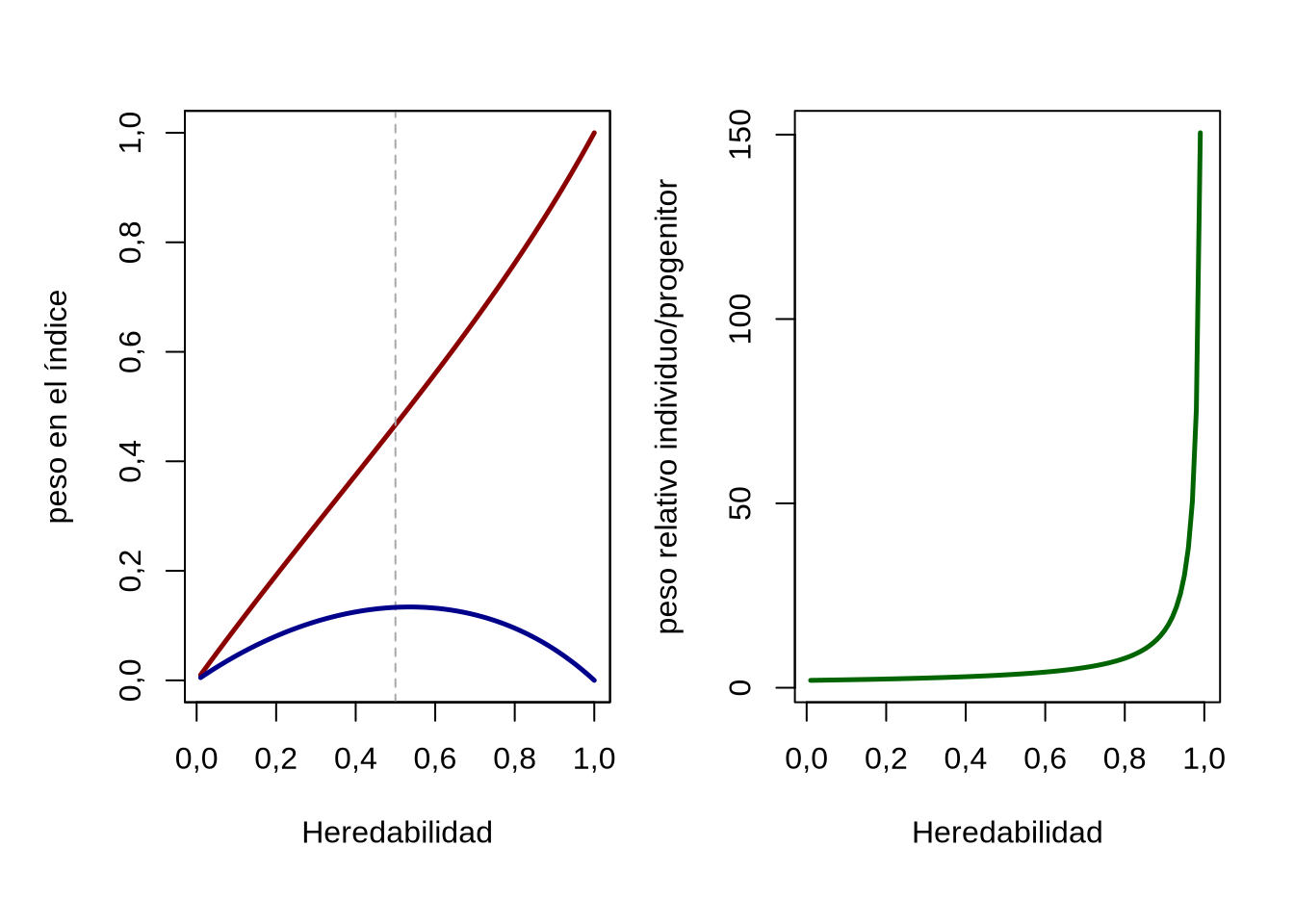
$Pesos en el índice con información del individuo y un progenitor en función de la heredabilidad de la característica. A la izquierda, en rojo el coeficiente correspondiente al individuo, mientras que en azul el correspondiente al peso de la información en el progenitor. A la derecha (en verde), la relación entre los dos coeficientes, es decir ${b_{ind}/b_{pro}}$, donde se aprecia claramente que a mayor heredabilidad mayor es el peso relativo de la información individual respecto a la del progenitor. De hecho, si se observa el gráfico de la izquierda, el máximo del coeficiente para la información aportada por el progenitor está en ${h^2=\frac{1}{2}}$, ya que la derivada de ${\frac{1}{2}h^2-\frac{1}{2}h^4}$ respecto a la heredabilidad se anula en ese valor y la derivada segunda tiene signo negativo, aunque la relación entre el coeficiente del individuo y del progenitor es una función monotónica creciente.$

Figura 13.1: Pesos en el índice con información del individuo y un progenitor en función de la heredabilidad de la característica. A la izquierda, en rojo el coeficiente correspondiente al individuo, mientras que en azul el correspondiente al peso de la información en el progenitor. A la derecha (en verde), la relación entre los dos coeficientes, es decir ${b_{ind}/b_{pro}}$, donde se aprecia claramente que a mayor heredabilidad mayor es el peso relativo de la información individual respecto a la del progenitor. De hecho, si se observa el gráfico de la izquierda, el máximo del coeficiente para la información aportada por el progenitor está en ${h^2=\frac{1}{2}}$, ya que la derivada de ${\frac{1}{2}h^2-\frac{1}{2}h^4}$ respecto a la heredabilidad se anula en ese valor y la derivada segunda tiene signo negativo, aunque la relación entre el coeficiente del individuo y del progenitor es una función monotónica creciente.

De la ecuación (13.28) resulta claro que tanto los coeficientes del índice, como sus pesos relativos, solo dependen del valor de la heredabilidad. A heredabilidades muy altas la predicción del ínidice es casi idéntica a la predicción a partir del fenotipo individual, mientras que a heredabilidades más bajas el papel de la información aportada por el progenitor puede ser mucho más relevante.

Ejemplo 13.2

En el rebaño experimental de ovejas verdes se están buscando los mejores carneros para mejorar el índice de esfericidad. Para ello se cuenta con la información de algunos borregos candidatos y la misma información de sus padres, cuando tenían la misma edad, de acuerdo a la siguiente tabla

Caravana Borrego	$I_e$	Caravana Padre	$I_e$
$\text{J117}$	$-17$	$\text{H034}$	$-11$
$\text{J432}$	$11$	$\text{F404}$	$4$
$\text{J521}$	$-7$	$\text{G009}$	$1$
$\text{J707}$	$4$	$\text{E009}$	$13$

Si la heredabilidad de la característica Índice de Esfericidad ${I_e}$ es de ${h^2=0,50}$, estimar un índice para los valores de cría esperados de estos borregos y ordenarlos de acuerdo a dicho índice.

De acuerdo a la ecuación (13.28), el índice correspondiente a esta característica sería

\[{EBV=\hat A=\mathbf{b'z}=\left(\frac{4}{4-h^4}\right)[(h^2-\frac{1}{4}h^4)\ z_{ind}+(\frac{1}{2}h^2-\frac{1}{2}h^4)\ z_{pro}]=}\] \[{=\left(\frac{4}{4-0,50^2}\right)[(0,50-\frac{1}{4}0,50^2)\ z_{ind}+(\frac{1}{2}0,50-\frac{1}{2}0,50^2)\ z_{pro}]=}\] \[{=\frac{4}{3,75}[0,4375\ z_{ind}+0,125\ z_{pro}]}\ \therefore\] \[{EBV=\hat A=0,4667\ z_{ind}+0,1333 \ z_{pro}}\]

Utilizando este índice, podemos calcularlo directamente para cada animal, o hacerlo para cada fuente de información por separado y luego sumar ambos valores de cada animal, como en la tabla siguiente

Caravana Borrego	$I_e$	$I_e\text{ Padre}$	$b_{ind}\ z_{ind}$	$b_{pro}\ z_{pro}$	EBV
$\text{J117}$	$-17$	$-11$	$-7,93$	$-1,47$	$-9,4$
$\text{J432}$	$11$	$4$	$5,13$	$0,53$	$5,7$
$\text{J521}$	$-7$	$1$	$-3,26$	$0,13$	$-3,1$
$\text{J707}$	$4$	$13$	$1,87$	$1,73$	$3,6$

De acuerdo a la tabla, recordando que queremos disminuir la esfericidad del rebaño, el orden de los borregos de acuerdo a su valor de cría esperado (EBV) es: J117, J521, J707 y J432.

PARA RECORDAR

Un índice de selección es una combinación de diferentes valores, usualmente fenotípicos, tal que permiten asignar un valor reproductivo único a cada individuo, podemos construirlo tal que: ${I=EBV=\hat A=b_1\ z_1+b_2\ z_2+...+b_k\ z_k}$ donde utilizamos ${z_i}$ para identificar los fenotipos de cada tipo de fuente de información que pueden incluir el fenotipo propio del candidato, el promedio de hermanos enteros, promedio de medios hermanos, fenotipo de un progenitor,etc.
Podemos describir el vector de coeficientes del índice usando la notación matricial como: ${b=P^{-1}G}$
Calcularemos los elementos de la matriz $P$ dependiendo de la información de la que dispongamos, tal que: 1)Si disponemos de información generada a partir de una sola medición, la varianza de la misma está dada por ${Var(z_i)=\sigma^2_P}$

Si disponemos de información generada a partir de la media de ${n}$ individuos, relacionados entre sí de tal manera que el coeficiente de correlación intraclase sea ${t}$, la varianza del promedio será:${Var(\bar z_i)=\sigma^2_P\left[\frac{1+(n-1)t}{n}\right]}$
Además, la covarianza entre dos fuentes de información que consiste cada una en una sola medida, tomadas en individuos diferentes, es igual a ${Cov(z_i,z_j)=a_{ij}\ h^2\ \sigma^2_P}$
Consigueintemente, la covarianza entre dos fuentes de información, una de ellas una sola medida en el candidato a la selección y la otra el promedio de $n$ medidas en individuos que tienen el mismo parentesco entre sí y también el mismo parentesco con el candidato, es igual a ${Cov(z_i,\bar z_j)=a_{ij}\ h^2\ \sigma^2_P}$ siendo ${a_{ij}}$ el parentesco aditivo entre el candidato y cualquiera de los integrantes del grupo a promediar (todos tienen el mismo parentesco con el candidato).

De la misma manera, alcularemos los elementos de la matriz $G$ dependiendo de la información de la que dispongamos, tal que:

La covarianza entre una sola medida fenotípica y el valor de cría del individuo, está dada por ${Cov(z_i,A)=a_{ij}\ h^2\ \sigma^2_P}$
La covarianza entre entre el promedio de $n$ medidas fenotípicas y el valor de cría del individuo, está dada por ${Cov(\bar z_i,A)=a_{ij}\ h^2\ \sigma^2_P}$

En el caso que quisiéramos construir un índice utilizando la información propia y de un progenitor a fin de predecir el valor de cría de un individuo. El mismo sería: ${I=EBV_{ind}=\hat A=b_{ind}\ z_{ind}+b_{pro}\ z_{pro}}$ donde podemos expresar los coeficientes como ${EBV=\hat A=\mathbf{b'z}=\left(\frac{4}{4-h^4}\right)[(h^2-\frac{1}{4}h^4)\ z_{ind}+(\frac{1}{2}h^2-\frac{1}{2}h^4)\ z_{pro}]}$
Podemos notar que a heredabilidades muy altas la predicción del ínidice es casi idéntica a la predicción a partir del fenotipo individual, mientras que a heredabilidades más bajas el papel de la información aportada por el progenitor puede ser mucho más relevante.

Información propia y de varios hermanos enteros

En este caso, la información de la que disponemos es, además del registro fenotípico en el individuo, la media de $n$ hermanos enteros del candidato (y por lo tanto, hermanos enteros entre sí, ya que los padres de todos deben ser los mismos que los del candidato). Como antes, vamos a armar primero las matrices $\mathbf{P}$ y (el vector) $\mathbf{G}$ para luego proceder a obtener los coeficientes.

Para obtener la matriz $\mathbf{P}$ alcanza con utilizar las reglas, recordando que ahora tenemos, la varianza de la información individual, igual a

\[ \begin{split} {Var(z_{ind})=\sigma^2_P} \end{split} \tag{13.29} \]

mientras que la varianza del promedio de $n$ medidas es

\[ \begin{split} {Var(z_{HE})=t\ \sigma^2_P+ \frac{(1-t)}{n}\sigma^2_P=\left[\frac{1+(n-1)t}{n}\right]\sigma^2_P} \end{split} \tag{13.30} \]

con ${t=a_{ind,HE}\ h^2+c^2=\frac{1}{2}\ h^2+c^2}$.

Por otro parte, la covarianza entre ambas medidas (la individual y el promedio de $n$ hermanos enteros) será

\[ \begin{split} {Cov(z_{ind},z_{HE})=t \sigma^2_P} \end{split} \tag{13.31} \]

Poniendo todo junto, la matriz $\mathbf{P}$ nos queda

\[ \begin{split} \mathbf{P}= \left[ \begin{matrix} {Var(z_{ind})} & {Cov(z_{ind},z_{HE})} \\ {Cov(z_{HE},z_{ind})} & {Var(z_{HE})} \end{matrix} \right] = \left[ \begin{matrix} {\sigma^2_P} & {t\ \sigma^2_P} \\ {t\ \sigma^2_P} & {t\ \sigma^2_P+\frac{(1-t)}{n}\sigma^2_P} \end{matrix} \right] = \left[ \begin{matrix} {1} & {t} \\ {t} & {\frac{1+(n-1)t}{n}} \end{matrix} \right] {\sigma^2_P} \end{split} \tag{13.32} \]

Por otro lado, los elementos del vector $\mathbf{G}$ son

\[ \begin{split} {Cov(z_{ind},A)=a_{ind,ind}\ \sigma^2_A=\sigma^2_A} \end{split} \tag{13.33} \]

\[ \begin{split} {Cov(z_{HE},A)=a_{HE,ind}\ \sigma^2_A=\frac{1}{2}\sigma^2_A} \end{split} \tag{13.33} \]

por lo que

\[ \begin{split} \mathbf{G}= \left[ \begin{matrix} {Cov(z_{ind},A)} \\ {Cov(z_{HE},A)} \end{matrix} \right] = \left[ \begin{matrix} {\sigma^2_A} \\ {\frac{1}{2} \sigma^2_A} \end{matrix} \right] = \left[ \begin{matrix} {1} \\ {\frac{1}{2}} \end{matrix} \right] {\sigma^2_A} \end{split} \tag{13.34} \]

Ahora, poniendo las dos matrices juntas para armar el índice, recordando que tenemos que invertir $\mathbf{P}$, tenemos que

\[ \begin{split} \mathbf{b=P^{-1}G} = \left( \left[ \begin{matrix} {1} & {t} \\ {t} & {\frac{1+(n-1)t}{n}} \end{matrix} \right] {\sigma^2_P} \right) ^{-1} \left[ \begin{matrix} {1} \\ {\frac{1}{2}} \end{matrix} \right] {\sigma^2_A} =\\ =\left[ \begin{matrix} {1} & {t} \\ {t} & {\frac{1+(n-1)t}{n}} \end{matrix} \right]^{-1} \left[ \begin{matrix} {1} \\ {\frac{1}{2}} \end{matrix} \right] {\frac{\sigma^2_A}{\sigma^2_P}} = \left[ \begin{matrix} {1} & {t} \\ {t} & {\frac{1+(n-1)t}{n}} \end{matrix} \right]^{-1} \left[ \begin{matrix} {1} \\ {\frac{1}{2}} \end{matrix} \right] {h^2} \end{split} \tag{13.35} \]

Haciendo la inversión de la matriz $\mathbf{P}$ escalada por ${1/\sigma^2_P}$ (que sacamos de factor común) y multiplicando por $\mathbf{G}$, tenemos entonces que

\[ \begin{split} \mathbf{b=} \left[ \begin{matrix} {1} & {t} \\ {t} & {\frac{1+(n-1)t}{n}} \end{matrix} \right]^{-1} \left[ \begin{matrix} {1} \\ {\frac{1}{2}} \end{matrix} \right] {h^2} = \left( {\frac{n}{1+(n-1)t-nt^2}}\right) \left[ \begin{matrix} {\frac{1+(n-1)t}{n}} & {-t}\\ {-t} & {1} \end{matrix} \right] \left[ \begin{matrix} 1 \\ {\frac{1}{2}} \end{matrix} \right] {h^2} \therefore \\ \mathbf{b} = \left( {\frac{nh^2}{1+(n-1)t-nt^2}}\right) \left[ \begin{matrix} {\frac{2+(n-2)t}{2n}} \\ {\frac{1}{2}-t} \end{matrix} \right] \end{split} \tag{13.36} \]

Tenemos por lo tanto el índice, como aparece en la ecuación (13.36), para el caso en que contamos con la información propia del individuo y del promedio de $n$ hermanos enteros del mismo. Ahora, a diferencia de lo que ocurría en el caso de individuo y progenitor (que solo dependía de ${h^2}$), ahora nuestro índice depende de varios parámetros: ${h^2}$, ${n}$ y ${t}$ (que a su vez depende de ${h^2}$ y ${c^2}$). Por lo tanto, resulta algo complejo el estudio analítico de esta función y vamos solamente a realizar una exploración gráfica del comportamiento de los coeficientes en distintas situaciones.

Como se ilustra en la Figura 13.2, el aporte relativo y absoluto de los coeficientes de aporte individual y del promedio de ${n}$ hermanos enteros varía ampliamente de acuerdo a la heredabilidad, la proporción de varianza debida al ambiente común y el número de hermanos evaluados.

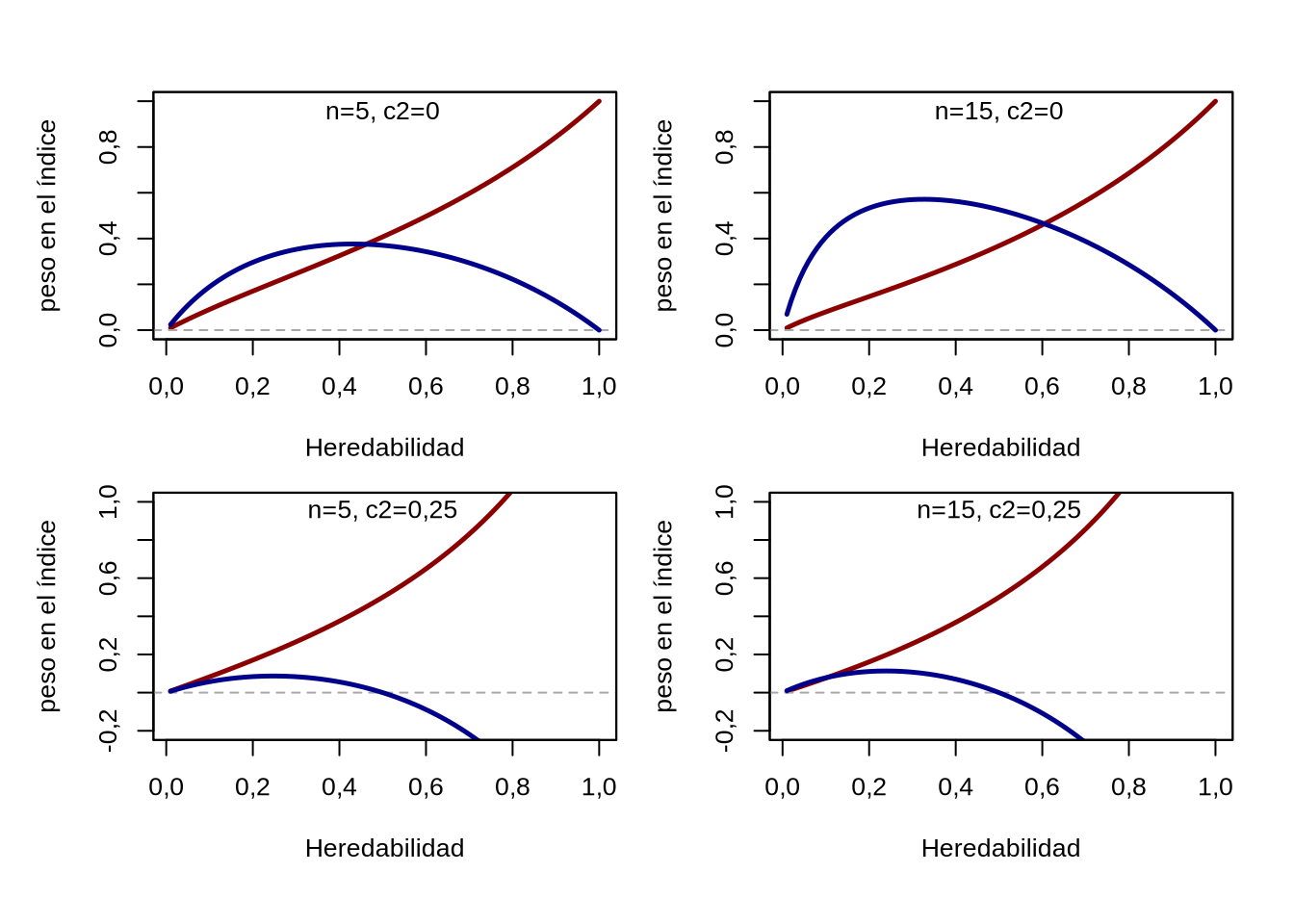
$Comportamiento de los coeficientes para el aporte del fenotipo individual (en azul) y del promedio de ${n}$ hermanos enteros del candidato, de acuerdo a la heredabilidad ${h^2}$ y la proporción de varianza del ambiente común ${c^2}$. A medida de que crece la heredabilidad, crece el coeficiente del aporte individual, mientras que el aporte de los hermanos tiene un máximo a hededabilidades intermedias. A medida de que crece el número de hermanos evaluados (gráficos de la izquierda versus los correspondientes a la derecha) aumenta el peso relativo del aporte de la media de hermanos enteros. Mientras que cuando ${c^2=0}$ ambos coeficientes son siempre positivos, cuando ${c^2>0}$ a partir de determinados valores de ${h^2}$ el aporte del promedio de los hermanos enteros comienza a ser negativo (gráficos de la parte inferior).$

Figura 13.2: Comportamiento de los coeficientes para el aporte del fenotipo individual (en azul) y del promedio de ${n}$ hermanos enteros del candidato, de acuerdo a la heredabilidad ${h^2}$ y la proporción de varianza del ambiente común ${c^2}$. A medida de que crece la heredabilidad, crece el coeficiente del aporte individual, mientras que el aporte de los hermanos tiene un máximo a hededabilidades intermedias. A medida de que crece el número de hermanos evaluados (gráficos de la izquierda versus los correspondientes a la derecha) aumenta el peso relativo del aporte de la media de hermanos enteros. Mientras que cuando ${c^2=0}$ ambos coeficientes son siempre positivos, cuando ${c^2>0}$ a partir de determinados valores de ${h^2}$ el aporte del promedio de los hermanos enteros comienza a ser negativo (gráficos de la parte inferior).

Las gráficas de la parte superior representan la situación donde la proporción de la varianza que corresponde al ambiente común es cero, es decir, los hermanos enteros no comparten ambiente especial (materno, etc.). En este caso, ambos coeficientes son positivos siempre; mientras que el correspondiente al fenotipo individual del candidato crece en forma monotónica, el aporte del promedio de los ${n}$ hermanos enteros posee máximos a frecuencias intermedias y que dependen de ${n}$. Por ejemplo, se observa claramente que a mayor ${n}$, el máximo se desplaza hacia la izquierda, es decir, se da con menores heredabilidades.

Por otra parte, cuando la proporción de la varianza debida al ambiente común es mayor a cero, es decir ${c^2>0}$, el signo del coeficiente correspondiente al aporte del promedio de los hermanos aumenta hasta cierta heredabilidad y luego decrece, pasando a ser negativo incluso. Este efecto se debe a que si una mayor parte de la similaridad entre hermanos se debe al ambiente, entonces una menor proporción será genética. De hecho, cuando el signo es negativo la covarianza entre hermanos enteros sirve como una corrección por el ambiente común.

En este punto resulta claro que si usamos los índices de selección para incorporar la información de dos fuentes, una individual y la otra familiar, estamos dándole mayor o menor importancia a la información individual o a la familiar. En el caso de heredabilidades altas le daremos mayor importancia a la información individual (el peso relativo del coeficiente correspondiente es mayor), mientras que si la heredabilidad es baja tenderemos a favorecer la información familiar. En este último caso, además, al seleccionar basados en información familiar (que es casi idéntica para todos los hermanos que componen el grupo) estaremos tendiendo a seleccionar como reproductores individuos fuertemente emparentados, lo que puede llevar a un importante aumento de la consanguinidad promedio de la población y de la consiguiente depresión endogámica (que veremos en el capítulo Endocría, exocría, consanguinidad y depresión endogámica).

PARA RECORDAR

Cuando disponemos además del registro fenotípico en el individuo, la media de $n$ hermanos enteros del candidato, las matrices $P$ y $G$ serán:

\[ \begin{split} \mathbf{P}= \left[ \begin{matrix} {1} & {t} \\ {t} & {\frac{1+(n-1)t}{n}} \end{matrix} \right] {\sigma^2_P} \end{split} \]

\[ \begin{split} \mathbf{G}= \left[ \begin{matrix} {1} \\ {\frac{1}{2}} \end{matrix} \right] {\sigma^2_A} \end{split} \]

Sabiendo además que $\mathbf{b=P^{-1}G}$, entonces: \[ \begin{split} \mathbf{b} = \left( {\frac{nh^2}{1+(n-1)t-nt^2}}\right) \left[ \begin{matrix} {\frac{2+(n-2)t}{2n}} \\ {\frac{1}{2}-t} \end{matrix} \right] \end{split} \]
Como diferencia respecto a lo que ocurría en el caso de individuo y progenitor (que solo dependía de $h^2$), ahora nuestro índice depende de varios parámetros: $h^2$, $n$ y $t$ (que a su vez depende de $h^2$ y $c^2$).
Podemos concluir que si usamos los índices de selección para incorporar la información de dos fuentes, una individual y la otra familiar, estamos dándole mayor o menor importancia a la información individual o a la familiar. En el caso de heredabilidades altas le daremos mayor importancia a la información individual, mientras que si la heredabilidad es baja tenderemos a favorecer la información familiar. En este último caso, además, al seleccionar basados en información familiar estaremos tendiendo a seleccionar como reproductores individuos fuertemente emparentados, lo que puede llevar a un importante aumento de la consanguinidad promedio de la población y de la consiguiente depresión endogámica.

Pruebas de progenie

Muchas veces, la mejor alternativa para evaluar a un futuro reproductor es a través de su progenie. Un caso típico de esto es cuando la característica no se expresa en el sexo del reproductor, como por ejemplo en la producción lechera. Más importante aún, como veremos más adelante, las pruebas de progenie son el único mecanismo que permite alcanzar una precisión cercana a uno, al menos cuando el número de progenies a evaluar no es limitante. En las pruebas de progenie se aparea cada uno de los candidatos a evaluar (sin pérdida de generalidad, supongamos que son machos) con un número determinado de hembras, escogidas al azar de la población. Esto es un punto fundamental en las derivaciones, por lo que supongamos no tenemos problema en resolverlo.

La idea es sencilla: para obtener estimados de los futuros valores de cría de los candidatos vamos a regresar el valor de cría del progenitor en el promedio de los valores fenotípicos de la progenie, es decir, nuestro índice será

\[ \begin{split} {EBV_{sire}=b_1\ P_1} \end{split} \tag{13.37} \]

con ${P_1}$ igual al promedio de la progenie expresado como desvío de la media de la población y $b_1$ el coeficiente de regresión del valor de cría del progenitor en la media del fenotipo de su progenie.

Como vimos en la sección Semejanza entre parientes del capítulo [Parentesco y Semenjanza entre Parientes], como un padre con sus hijos comparte solo la mitad del genoma (siempre, es algo “determinístico”, del mecanismo de herencia, despreciando la contribución de los genomas de organelos, etc.), la covarianza entre el valor aditivo del progenitor y el promedio de la progenie será igual a la covarianza aditiva entre padre y la progenie, que es

\[ \begin{split} {Cov(A,P_1)=Cov(A,\frac{1}{2}A)=\frac{1}{2}V_A} \end{split} \tag{13.38} \]

Por otra parte, ya que en el promedio de $n$ medidas realizadas en la progenie va a aparecer $n$ el efecto aditivo ${\frac{1}{2}A}$, el aporte a la varianza va a ser ${Var(\frac{1}{2}A)=\frac{1}{4}V_A}$. El resto de la varianza fenotípica, es decir ${(V_P-\frac{1}{4}V_A)}$ va a estar promediado entre $n$ observaciones, por lo que sumando ambos aportes (que son ortogonales), tenemos que la varianza en la media de la progenie será igual a

\[ \begin{split} {Var(P_1)=\frac{1}{4}V_A+\frac{(V_P-\frac{1}{4}V_A)}{n}} \end{split} \tag{13.39} \]

Tenemos entonces lo que precisamos para derivar el coeficiente de regresión, que será

\[b_1=\frac{Cov(A,P_1)}{Var(P_1)}=\frac{\frac{1}{2}V_A}{\frac{1}{4}V_A+\frac{(V_P-\frac{1}{4}V_A)}{n}}=\frac{\frac{1}{2}V_A\ n}{\frac{1}{4}V_A\ n+V_P-\frac{1}{4}V_A}=\] \[\frac{\frac{1}{2}V_A\ n}{\frac{1}{4}V_A\ (n-1)+V_P}=\frac{\frac{1}{2}V_A\ n}{\frac{1}{4}V_P\ h^2\ (n-1)+V_P}=\] \[\frac{V_A}{V_P}\frac{\frac{1}{2}\ n}{\frac{1}{4}\ h^2\ (n-1)+1}=h^2 \frac{1}{2}\frac{4n}{h^2(n-1)+4}\ \therefore\]

\[ \begin{split} b_1=\frac{2\ n\ h^2}{h^2(n-1)+4} \end{split} \tag{13.40} \]

13.3.1 Límites de la eficiencia en pruebas de progenie

Las pruebas de progenie tienen un uso muy importante cuando se evalúan reproductores que van a ser utilizados en forma masiva. De hecho, es el único método que permite alcanzar precisiones cercanas a 1, cuando el número de hijos a evaluar no es una limitante (es decir, es muy grande). Esto puede ser un factor importante para la venta de reproductores o en algunos casos una de las pocas posibilidades si la característica se expresa en hembras, por ejemplo. Sin embargo, el uso en establecimientos que generan sus propios reproductores puede presentar importantes limitaciones. Una de ellas es la proveniente del incremento en el intervalo generacional asociado a tener que esperar a que la progenie pueda ser evaluada antes de usar el futuro reproductor en forma “masiva”. Este intervalo suele ser de más de 2 y usualmente más de 3 años. Por otro lado, la intensidad de selección suele verse disminuida ya que necesariamente se ensayan pocos animales. Por lo tanto, la pregunta que nos hacemos es ¿Cuándo es mejor la prueba de progenie que la selección fenotípica individual?

En principio, igual que para respuesta correlacionada en general, podemos evaluar la eficiencia de un método respecto al otro evaluando el cociente entre ambos, que suele eliminar algunos términos de la comparación (por ejemplo la intensidad de selección o el desvío aditivo). Un caso particular es la comparación entre un método de selección directa y uno basado en información de parientes, por ejemplo la prueba de progenie. Sin pérdida de generalidad, pongamos que la característica por la que nos interesa seleccionar es una que se mide antes del primer año de vida del animal, por ejemplo peso al destete. En ese caso, el intervalo generacional para selección fenotípica individual es de 3 años, mientras en el caso de la prueba de progenie es de 5 años. Para que la prueba de progenie sea más fenotípica individual, el cociente deber ser mayor que 1. Es decir,

\[ \begin{split} {\frac{r_{AA'} h \sqrt{\frac{n}{1+(n-1) r_{A_1A_2} h^2}}}{h} \frac{IG_1}{IG_m} \geqslant 1} \end{split} \tag{13.41} \]

Simplificando y elevando al cuadrado ambos lados (numerador y denominador de la izquierda son necesariamente positivos), tenemos

\[ \begin{split} {r_{AA'}^2 \frac{n}{1+(n-1) r_{A_1A_2} h^2} \left(\frac{IG_1}{IG_m}\right)^2 \geqslant 1} \\ {r_{AA'}^2\ n\ \left(\frac{IG_1}{IG_m}\right)^2 \ge 1+(n-1) r_{A_1A_2} h^2}\\ {\frac{r_{AA'}^2\ n\ \left(\frac{IG_1}{IG_m}\right)^2\ -1}{(n-1) r_{A_1A_2} }\geqslant h^2} \end{split} \tag{13.42} \]

Pero en nuestro caso ${r_{AA'}^2=1/4}$ y ${r_{A_1A_2} =1/4}$, por lo que

\[ \begin{split} {\frac{n\ \left(\frac{IG_1}{IG_m}\right)^2\ -1}{(n-1) }\geqslant h^2} \end{split} \tag{13.43} \]

Cuando $n$ tiende a infinito, o sea que el número de hijos por candidato no es limitante,

\[ \begin{split} {\lim_{n \to \inf} \frac{n\ \left(\frac{IG_1}{IG_m}\right)^2\ -1}{(n-1) } = \left(\frac{IG_1}{IG_m}\right)^2\ \ge h^2} \end{split} \tag{13.44} \]

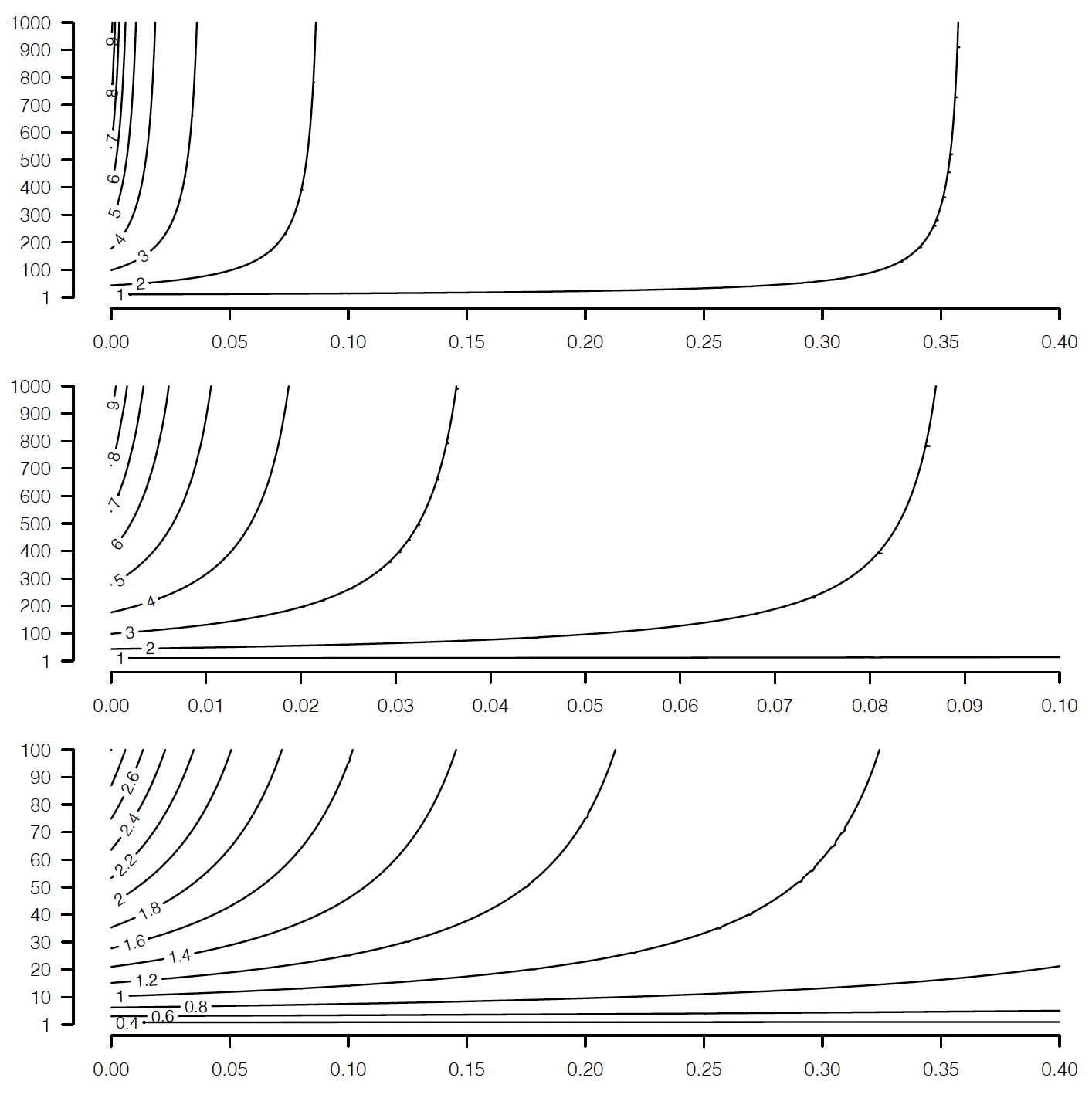
Eficiencia relativa de la prueba de progenie sobre la selección fenotípica individual. Las curvas de nivel mayores a 1 indican mayor eficiencia de la prueba de progenie. La heredabilidad se muestra en las abcisas y el número de hijos por candidato en las ordenadas.

Figura 13.3: Eficiencia relativa de la prueba de progenie sobre la selección fenotípica individual. Las curvas de nivel mayores a 1 indican mayor eficiencia de la prueba de progenie. La heredabilidad se muestra en las abcisas y el número de hijos por candidato en las ordenadas.

Por lo tanto, si bien la precisión de la prueba de progenie se incrementa con el número de hijos, la misma nunca superará en eficiencia a la selección fenotípica individual cuando la heredabilidad sea superior a ${\left(\frac{IG_1}{IG_m}\right)^2}$. Con los intervalos generacionales de 3 y 5 años, esto significa que la prueba de progenie solo podrá ser más eficiente para características en que ${h^2 \leqslant \left( \frac{IG_1}{IG_m}^2 \right) = \left( \frac{3}{5} \right)^2 =0,36}$.

Otra forma de ver esto es a partir de un gráfico de curvas de nivel de la eficiencia relativa, de acuerdo a las diferentes heredabilidades y número de hijos por candidato. En la figura 13.3 podemos ver qué ocurre a diferentes escalas del problema. El panel superior muestra el comportamiento de la eficiencia relativa en toda la escala de heredabilidad donde puede ser igual o mayor a 1, donde se aprecia claramente como la eficiencia aumenta con el número de hijos (para eso puedes imaginar una línea vertical que a medida que subes va cortando curvas de nivel cada vez más altas) y disminuye con ${h^2}$ (lo mismo, ahora con una línea horizontal). En el panel del medio redujimos el límite superior de la heredabilidad para poder apreciar claramente lo que ocurre a heredabilidades muy bajas, donde la eficiencia relativa puede ser muy importante. Finalmente, en el panel de abajo mostramos lo que ocurrre con un número de hijos por candidatos bastante más acordes a la realidad, donde se aprecia que las eficiencias relativas razonables están entre 1 y 3.

Precisión del valor de cría a partir del índice

La precisión de los valores de cría esperados a partir de la información en el índice la podemos estimar como la correlación entre los valores del índice y el valor de cría, es decir

\[ \begin{split} {r_{IA}=\frac{Cov(I,A)}{\sqrt{\sigma^2_I \sigma^2_A}}} \end{split} \tag{13.45} \]

La covarianza entre el índice y el valor de cría, el numerador de la ecuación (13.45), usando notación matricial es igual a

\[ \begin{split} {Cov(I,A)=Cov(\mathbf{b'z},A)=\mathbf{b'}Cov(\mathbf{z},A)=\mathbf{b'G}} \end{split} \tag{13.46} \]

Por otra parte, la varianza en el índice (recordar que el índice es un escalar), usando nuevamente la notación matricial, la obtenemos como

\[ \begin{split} {\sigma^2_I=Var(\mathbf{b'z})=\mathbf{b'}Var(\mathbf{z})\mathbf{b=b'Pb}} \end{split} \tag{13.47} \]

Observar que $\mathbf{b'Pb}$ es un escalar (un número, no una matriz o un vector). De acuerdo a la ecuación (13.18)

\[ \begin{split} {\mathbf{b=P^{-1}G \therefore Pb=PP^{-1}G=IG=G}} \end{split} \tag{13.48} \]

y por lo tanto

\[ \begin{split} {\mathbf{b'G=b'Pb}} \end{split} \tag{13.49} \]

lo que es idéntico al resultado obtenido en la ecuación (13.47). Por lo tanto, combinando las ecuaciones (13.46), (13.47) y (13.49), tenemos que

\[ \begin{split} {Cov(A,I)=\sigma^2_I} \end{split} \tag{13.50} \]

Si ahora volvemos al punto inicial, la precisión en el valor de cría obtenido a partir del índice, de acuerdo a la ecuación (13.45) será

\[ \begin{split} {r_{IA}=\frac{Cov(I,A)}{\sqrt{\sigma^2_I \sigma^2_A}}=\frac{\sigma^2_I}{\sqrt{\sigma^2_I \sigma^2_A}}=\frac{\sigma^2_I}{\sigma_I \sigma_A}=\frac{\sigma_I}{\sigma_A}} \end{split} \tag{13.51} \]

PARA RECORDAR

Muchas veces, la mejor alternativa para evaluar a un futuro reproductor es a través de su progenie. El principio básico del método es que para obtener los futuros valores de cría de los candidatos, se regresa el valor de cría del progenitor en el promedio de los valores fenotípicos de la progenie, es decir, el índice será: ${EBV_{sire}=b_1\ P_1}$ con $P_1$ igual al promedio de la progenie expresado como desvío de la media de la población y $b_1$ el coeficiente de regresión del valor de cría del progenitor en la media del fenotipo de su progenie.
El coeficiente de la regresión será: $b_1=\frac{2\ n\ h^2}{h^2(n-1)+4}$
Para que la prueba de progenie sea más eficiente que la relección individual: ${\frac{r_{AA'} h \sqrt{\frac{n}{1+(n-1) r_{A_1A_2} h^2}}}{h} \frac{IG_1}{IG_m} \geqslant 1}$
Si bien la precisión de la prueba de progenie se incrementa con el número de hijos, la misma nunca superará en eficiencia a la selección fenotípica individual cuando la heredabilidad sea superior a ${\left(\frac{IG_1}{IG_m}\right)^2}$.
La precisión en el valor de cría obtenido a partir del índice será: ${r_{IA}=\frac{\sigma_I}{\sigma_A}}$

13.4 Métodos de selección para varias características

Hasta ahora nos hemos manejado en el presente capítulo con la selección de una característica sola, aportando información de otras fuentes que son los parientes. Sin embargo, en la práctica del mejoramiento genético es difícil encontrar situaciones donde exista un solo objetivo a mejorar desde el punto de vista genético. Por ejemplo, en producción de lana siempre queremos aumentar el peso de vellón por animal ya que es lo que producimos, pero al mismo tiempo el diámetro de las fibras (el menor es el mejor pago) es crucial para el precio y apenas podremos comercializarlas a partir de determinado punto. En la producción lechera, vamos a procurar aumentar la producción de sólidos (proteína y grasa) ya que el pago está directamente asociado a los volúmenes de los mismos (de hecho, proteína y grasa son dos características con pago diferente), pero al mismo tiempo vamos a querer reducir el volumen de leche producida (porque es castigado por la industria, que debe concentrar) y reducir el recuento de células somáticas en leche (que es un indicador de la calidad sanitaria de la misma). En producción de carne vamos a querer, como siempre, aumentar la producción de kilos por animal, pero también mejorar características de palatabilidad de la misma. En todos estos casos se trata de características que tienen una fuerte base genética y por lo tanto son buenos objetivos para plantearnos la mejora de los mismos por vía genética.

La selección por más de una característica presenta complejidades importantes, como veremos en el resto del capítulo, tanto desde el punto de vista conceptual como desde el punto de vista práctico. Afortunadamente, para las razas que poseen una buena organización y buenos registros, los métodos “modernos” de evaluación genética nos permiten realizar selección por varias características (las características evaluadas) de manera muy sencilla a partir de los catálogos.

En lo que resta de esta sección veremos tres métodos alternativos de selección, selección en tandem, selección por niveles independientes de rechazo e índices de selección, mientras que dejaremos para las secciones finales el desarrollo de las bases teóricas de los índices de selección aplicados a muchas características y a una introducción del BLUP y los métodos modernos de evaluación.

Selección en tandem

El primer método que vamos a presentar es el más sencillo de implementar en la práctica, la selección en tandem y de hecho no presenta ninguna diferencia con las estrategias de selección que usamos para una sola característica. En este método, la idea es muy sencilla: seleccionar cada vez por una sola característica, como haríamos usualmente, y luego de un tiempo cambiar a otra característica de interés. Si bien el método se representa usualmente con los métodos de selección a partir del fenotipo del individuo, en principio no hay restricciones mayores a aplicarlo con fuentes de información diferentes, como las provenientes de parientes.

La lógica de este método se presenta en la Figura 13.4, donde los ejes coordenados representan dos características de interés. En la imagen de la izquierda se representa la población total (círculo azul), que sin pérdida de generalidad podría tener una distribución del tipo normal bivariada y sobre la que vamos a hacer selección por umbral en la característica 1 primero. Por lo tanto, definimos un valor de la misma a partir del cual los animales que lo superen serán los reproductores (área roja). Otra posibilidad análoga es seleccionar determinada proporción de animales, de acuerdo a los requisitos para generar los reemplazos necesarios y ambas opciones son equivalentes en caso de normalidad de la característica. Luego de algún número de generaciones o de años, después de haber observado el desplazamiento de la media de la característica lo suficiente como para “descuidarla” por un tiempo, pasamos a mejorar la segunda característica. Decimos “descuidar” porque no le vamos a prestar atención durante el siguiente período, donde el foco estará en la segunda característica, como se muestra en la imagen de la derecha en la Figura 13.4. Ahora le prestaremos atención a la característica 2, donde realizaremos selección nuevamente por el método de elección (umbral, por ejemplo). Obviamente, todo el ciclo se puede repetir el número de veces que sea necesario si los objetivos de selección continúan siendo los mismos, o se pueden agregar más características en el ciclo.

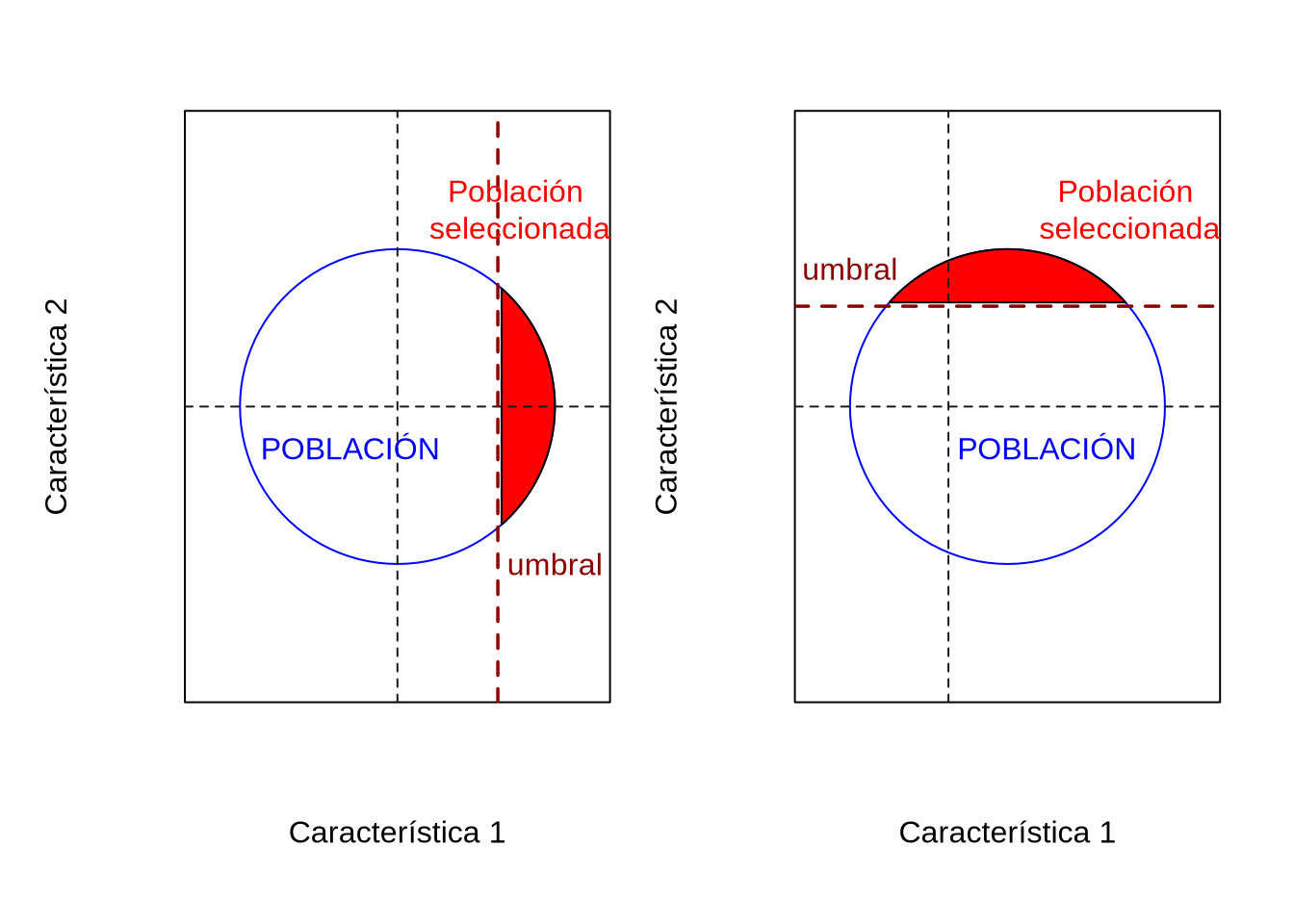
Selección en tandem. Durante la primera fase (imagen de la izquierda) se selecciona por la característica 1, de la manera usual en selección fenotípica individual para una sola característica (por ejemplo, selección umbral). El proceso se repite durante un determinado período de generaciones o años, para luego pasar a seleccionar por la segunda característica (imagen de la derecha), de la misma manera que lo hicimos en la primera fase. Notar el desplazamiento de la media de la población de la característica 1 hacia la derecha, antes de empezar el proceso de selección por la segunda característica. El proceso entero se repite todas las veces que sea necesario.

Figura 13.4: Selección en tandem. Durante la primera fase (imagen de la izquierda) se selecciona por la característica 1, de la manera usual en selección fenotípica individual para una sola característica (por ejemplo, selección umbral). El proceso se repite durante un determinado período de generaciones o años, para luego pasar a seleccionar por la segunda característica (imagen de la derecha), de la misma manera que lo hicimos en la primera fase. Notar el desplazamiento de la media de la población de la característica 1 hacia la derecha, antes de empezar el proceso de selección por la segunda característica. El proceso entero se repite todas las veces que sea necesario.

La complejidad de este método es muy baja ya que no requerimos nada adicional a lo que ya acostumbramos a trabajar en selección por una sola característica, alcanza con definir los momentos en que realizaremos los cambios de objetivos de selección, lo que puede realizarse a priori o luego de observar la respuesta a la selección. Claramente la eficiencia de este método es generalmente baja o muy baja, en particular si las características poseen una fuerte correlación genética en sentido desfavorable. Por ejemplo, si mejoramos primero peso de vellón durante años, solo prestando atención a esa característica, lo más probable es que el grosor de la lana se incremente en forma sustantiva. Pasamos ahora a seleccionar por diámetro de las fibras y lentamente recuperamos la finura que habíamos perdido, pero ahora el peso del vellón volvió a bajar. Luego de un ciclo entero posiblemente estemos muy cerca del punto de partida, lo que no parece una buena estrategia. Por otro lado, para características donde la correlación genética es favorable, como vimos en el capítulo Correlaciones y Respuesta Correlacionada, la selección por una característica ““arrastrará” a la otra en sentido correcto y luego, al cambiar a seleccionar por la segunda característica, también la selección por la segunda mejorará la primera. En este caso, lo que consigue este método de selección es, de alguna manera, balancear el avance en las dos características, en relación a seleccionar solo por una de ellas.

Niveles Independientes de Rechazo

Una alternativa al método de selección por tandem es la selección por el método de Niveles Independientes de Rechazo (o NIR, por sus siglas). La idea, esquematizada en la Figura 13.5, es muy sencilla: establecer un umbral independiente para cada característica y seleccionar como reproductores solamente a aquellos individuos que superen los dos criterios (el área en rojo en la figura).

A diferencia del método de selección en tandem, en el método NIR el foco se pone siempre en las dos características, lo que evita el comportamiento “en dientes de sierra” que presenta el método del tandem (cuando funciona).

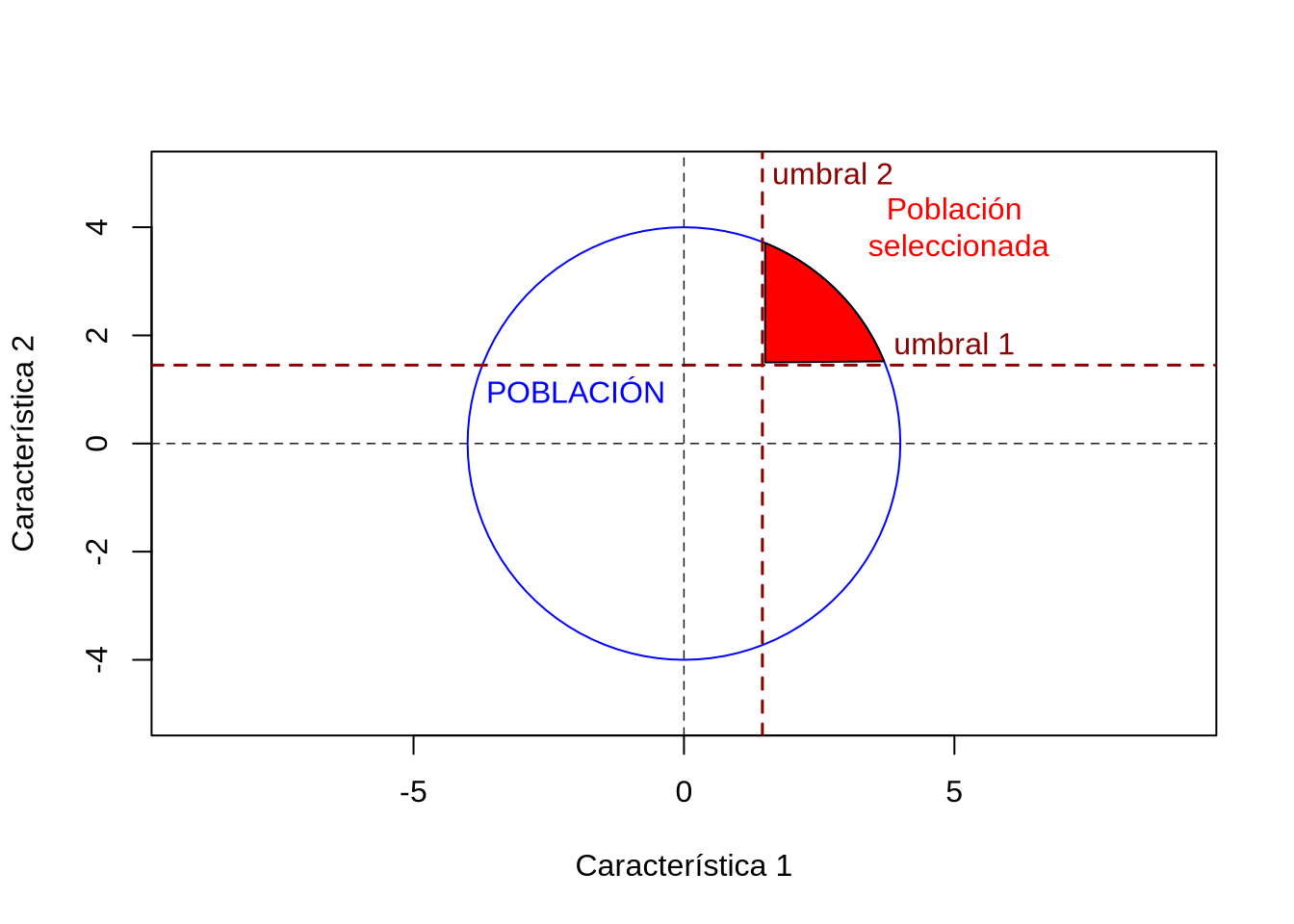
Niveles Independientes de Rechazo (NIR). Para dos características se fijan previamente los umbrales (líneas a trazos rojos) en forma independiente y los animales que “pasen” dichos umbrales serán los futuros reproductores. La proporción de animales seleccionados disminuye rápidamente a medida de que incorporamos más características independientes.

Figura 13.5: Niveles Independientes de Rechazo (NIR). Para dos características se fijan previamente los umbrales (líneas a trazos rojos) en forma independiente y los animales que “pasen” dichos umbrales serán los futuros reproductores. La proporción de animales seleccionados disminuye rápidamente a medida de que incorporamos más características independientes.

El principal problema que aparece en forma obvia con este método es que a medida de que establecemos umbrales para diferentes características, el número de individuos que pasa todos los filtros es cada vez menor. De hecho, si en todas las características seleccionamos la misma proporción de individuos y las características son independientes entre sí, la proporción total seleccionada estará dada por $p=p_i^{k}$. Por lo tanto, si definimos una proporción $p$ determinada de individuos que necesitamos como reproductores (algo que estará dado por la eficiencia reproductiva alcanzada y por la estructura de edades de la población), la proporción $p_i$ seleccionada para cada característica estará dada por

\[ \begin{split} p=p_i^{k} \therefore p_i=\sqrt[k]{p} \end{split} \tag{13.52} \]

con $p_i=p_j\ \forall\ i,j$.

Veamos un ejemplo que ilustra las implicancias prácticas de esto. Supongamos que tenemos 4 características de nuestro interés, que son totalmente independientes entre ellas y con distribución normal todas. Precisamos retener una proporción de $20\%$ de los animales como reproductores, por lo que $p=0,20$. Aplicando la ecuación (13.52), tenemos que la proporción seleccionada en cada características sería

\[ \begin{split} p_i=\sqrt[k]{p}=\sqrt[4]{p}=p^{\frac{1}{4}}=0,6687 \end{split} \]

Por lo tanto, reteniendo una proporción $p=0,20$ de animales, que en una característica sola me conduciría a una intensidad de selección de $i=1,40$, en cada una de las características solo selecciono una proporción $p_i=0,6687$, lo que me conduce a una intensidad en cada una de $i \approx 0,545$.

Por otro lado, como veremos enseguida, este método puede eliminar individuos excepcionalmente buenos en una característica, pero que estén levemente por debajo del umbral en cualquiera de las otras características, o aún individuos excelentes en todas las características excepto una.

Índices de selección

El comentario precedente sobre los inconveniente del método NIR abre las puertas para considerar algún método que no presente el inconveniente de excluir buenos candidatos en muchas características por el resultado relativamente malo en una sola de ellas. Esto nos lleva al concepto de mérito global o mérito agregado del candidato. Es decir, debemos encontrar una combinación de los valores en las distintas características que pueda resumirse en un solo valor, el cuál será entonces nuestro nuevo valor fenotípico del candidato.

Dicho de otra manera, construimos un nuevo fenotipo, de forma relativamente arbitraria y vamos a seleccionar por ese nuevo fenotipo que es el índice. En general, por simplicidad, se utilizan índices que son una combinación lineal de los fenotipos de las características de interés, aunque también existen índice no-lineales en las características. Vamos a dedicar toda la sección Índices de selección para múltiples características a describir las bases de la teoría de índices de selección aplicados al mejoramiento de varias características, pero antes de pasar a eso vamos a describir brevemente la idea y su aplicación en mejoramiento genético.

Como vimos antes, uno de los problemas de considerar los caracteres como independientes es la reducción en la eficiencia producto de la necesidad de definir límites arbitrarios (los umbrales) para las distintas características. Si encontramos una forma racional de ponderar la incidencia de cada una de las $k$ características en la función de mérito global del individuo, entonces el fenotipo agregado del individuo será igual a

\[ \begin{split} I=b_1\ z_1+b_2\ z_2+...+b_k\ z_k=\sum_{i=1}^k b_i\ z_i=\mathbf{b^{T}\mathbf{z}} \end{split} \]

Esto es una función lineal de todas las características, con pesos fenotípicos $b_i$. Supongamos que resolvimos el problema de cómo determinar los pesos, cosa que veremos cómo hacer en la sección Índices de selección para múltiples características. En ese caso, si tenemos los fenotipos como desvío de la media para cada característica, alcanza con multiplicar cada fenotipo $z_i$ por su correspondiente ponderación $b_i$ y sumar todos los resultados para tener el mérito agregado del individuo, que será su nuevo fenotipo. A partir de esto podemos aplicar el criterio de selección individual que sea de nuestro agrado.

En la Figura 13.6 se representa el funcionamiento del índice. Para dos características el mismo será una combinación lineal de ambas, cuya dirección está descrita por la recta a trazos de color rojo. Conociendo la proporción de animales que necesitamos seleccionar, alcanza con ordenar los individuos por el índice y determinar el corte en el punto en que haya esa proporción con índice igual o mayor,

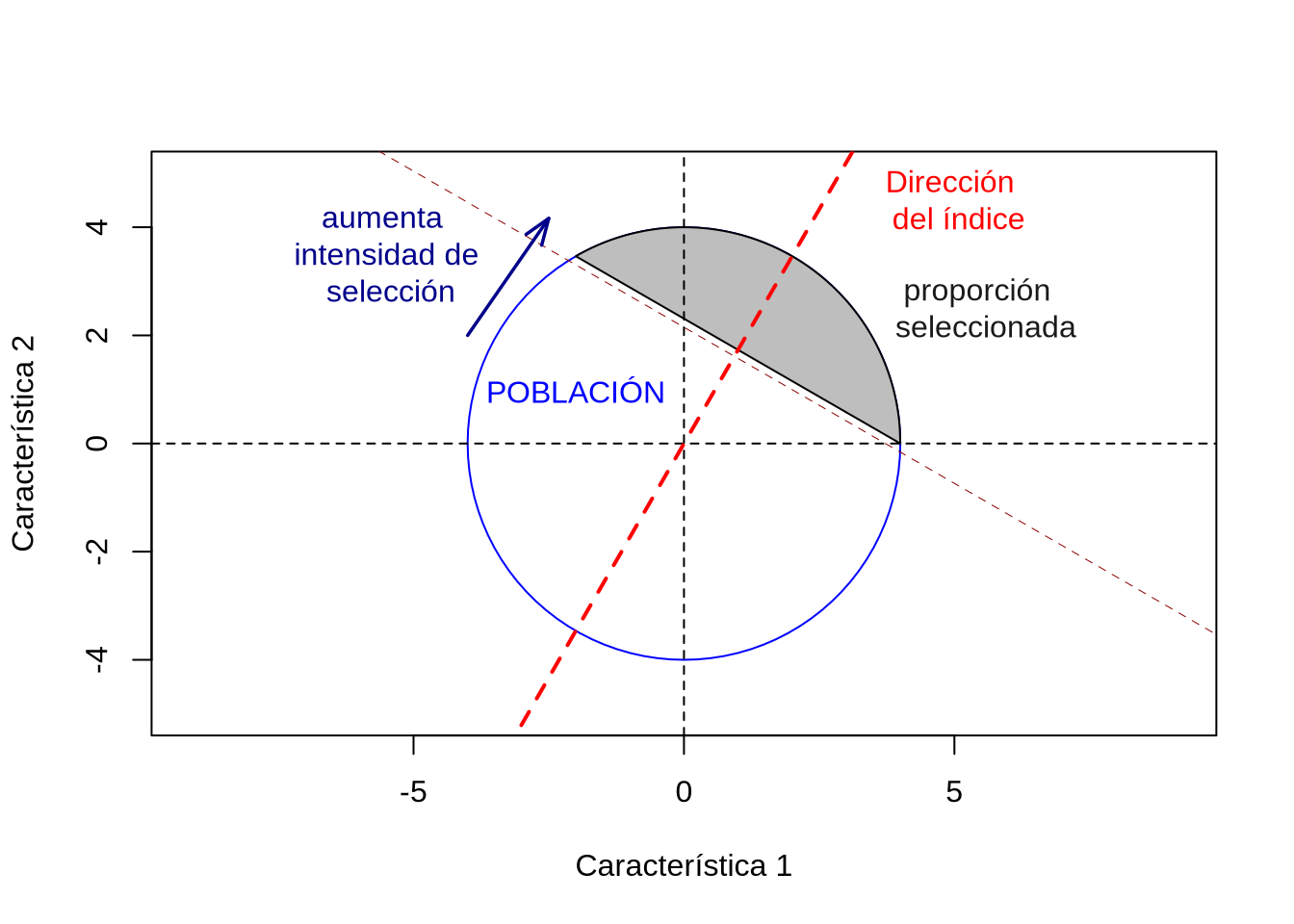
Índice de selección para dos características. El índice es una combinación lineal de ambas carcaterísticas y tiene la dirección de la línea roja a trazos gruesos. Pasamos de tener dos valores fenotípicos para cada individuo a un solo valor que representa el mérito global o agregado del mismo.

Figura 13.6: Índice de selección para dos características. El índice es una combinación lineal de ambas carcaterísticas y tiene la dirección de la línea roja a trazos gruesos. Pasamos de tener dos valores fenotípicos para cada individuo a un solo valor que representa el mérito global o agregado del mismo.

Dentro de las ventajas que posee esta combinación lineal está la de no dejar afuera fenotipos (genotipos) de alto valor en una característica porque no pasan en otra. Si nos fijamos en la Figura 13.6 nuevamente, veremos que hay una proporción de individuos seleccionados (sombreado en gris) que se encuentran a la izquierda del eje de las ordenadas. Es decir, para la característica 1 son peores que la media de los individuos de la población. Sin embargo, para la característica 2 son excepcionalmente valiosos. Posiblemente, en NIR hubiesen quedado por el camino. Sin embargo, el mérito global de los mismos es suficientemente elevado como para que justifique retenerlos, cosa que hace el índice.

Otra de las ventajas que presenta un índice es la simplicidad de uso. En lugar de tener que inspeccionar para cada posible reproductor el mérito en $k$ características, alcanza con el valor en una sola. En el caso de que se trate de semen, por ejemplo, donde existe una gran oferta de reproductores, dentro del mismo intervalo de valores del índice es posible luego “afinar” el criterio y elegir los reproductores mejores en las características que más nos interesan. Por ejemplo, si un rodeo presenta problema de baja cantidad de proteínas, dentro de los toros con determinado valor del índice puedo elegir aquellos que tengan ese valor porque son excelentes en proteína (en general puedo hacerlo sin empeorar otras características).

En la actualidad, existen índices de seleccción para muchas razas, lo que permite obtener un avance eficiente en la selección. Para esto se requiere, no solamente contar con grandes volúmenes de datos que permitan obtener estimaciones adecuadas de los parámetros genéticos (algo que veremos enseguida), sino también alcanzar un acuerdo entre los productores acerca de tipos de sistemas de producción para los que se desea que el índice de selección sea una fiel representación del sistema de ingresos y egresos de los establecimientos. Como suele ser imposible que un solo índice represente a diferentes tipos de establecimientos, en muchos casos se tendrán tantos índices como situaciones los datos y el esfuerzo permitan generar, cada uno de ellos eficiente para su propio sistema de producción. Un ejemplo típico de esto es en producción lechera, donde dependiendo del tipo de producción (estabulada, pastoril, etc.) y dependiendo del destino de la leche (industria, producción de quesos, etc.) se deben desarrollar diferentes índices que representen esas combinaciones. En lo que sigue veremos la teoría que sustenta el desarrollo de índices de selección como forma de mejorar la eficiencia y simplificar la selección.

Ejemplo 13.3

Supongamos que tenemos rodeo lechero y queremos mejorar simultáneamente las siguientes características: producción de leche, producción de grasa, producción de proteína, puntaje de células somáticas y tasa de preñez en hijas. Para esto, nos ofrecen a la venta el semen de $7$ toros disponibles, con la siguiente información:

Toro	Leche		Grasa		Proteína		$\text{cs}^1$		$\text{THP}^2$		$\text{Índice de selección}^3$
$\text{}$	$\text{DEP}^4$	$r_{AC}$	$\text{DEP}^4$	$r_{AC}$	$\text{DEP}^4$	$r_{AC}$	$\text{DEP}^4$	$r_{AC}$	$\text{DEP}^4$	$r_{AC}$	$\text{}$
$\text{HOLDNKM000000260548}$	$57$	$0,59$	$12,8$	$0,57$	$13,2$	$0,57$	$-0,50$	$0,62$	$0,67$	$0,56$	$51,75$
$\text{HOL840M003147224052}$	$288$	$0,58$	$19,6$	$0,57$	$17,5$	$0,57$	$-0,49$	$0,60$	$-0,42$	$0,58$	$50,30$
$\text{HOLNLDM000580616806}$	$31$	$0,60$	$10,1$	$0,59$	$9,4$	$0,59$	$-0,62$	$0,63$	$-1,21$	$0,60$	$45,90$
$\text{HOLFRAM002933738576}$	$48$	$0,63$	$18,2$	$0,62$	$8,9$	$0,62$	$-0,35$	$0,67$	$-0,82$	$0,64$	$36,42$
$\text{HOLNLDM000694388754}$	$154$	$0,62$	$15,4$	$0,61$	$11,5$	$0,62$	$-0,36$	$0,67$	$-2,85$	$0,65$	$33,78$
$\text{HOL840M003150687270}$	$328$	$0,56$	$17,7$	$0,55$	$17,6$	$0,55$	$-0,04$	$0,58$	$0,23$	$0,57$	$30,93$
$\text{HOLCANM000012529241}$	$308$	$0,59$	$21,0$	$0,59$	$14,5$	$0,59$	$-0,10$	$0,65$	$-1,85$	$0,59$	$25,69$

$^1$células somáticas; $^2$tasa de preñez en hijas;

$^3$ Índice de selección $=-0,05\times DEP(L)+0,33\times DEP(G)+2,25\times DEP(P)+1,31\times DEP(TPH)-39,6\times DEP(SCS)$;

$^4$$DEP=1/2\times\hat A$

Para tomar la decisión de selección, nos planteamos los siguientes niveles de exigencia:

leche: DEP menor a $100$ litros
grasa: DEP mayor a $10$ kg
proteína: DEP mayor a $9$ kg
células somáticas: DEP menor a $-0,40$
tasa de preñez en hijas: DEP mayor a $-1,5$.

a. De acuerdo con el método de selección NIR, ¿a cuáles toros seleccionaríamos? b. Si en lugar de aplicar el método de selección NIR, aplicáramos el método de Índice de selección, ¿seleccionaríamos a los mismos toros? c. Interpretar el índice de selección utilizado.

a. El método NIR implica que cada criterio es excluyente de por sí. Es decir, alcanza con que no cumpla uno solo como para que el candidato quede eliminado.

Por leche, eliminaríamos a los toros HOL840M003147224052, HOLNLDM000694388754, HOL840M003150687270 y HOLCANM000012529241. Luego, por grasa no eliminaríamos a ningún toro.

Por proteína eliminaríamos al toro HOLFRAM002933738576. Por células somáticas y tasa de preñez en hijas no eliminaríamos a ningún toro (los que no cumplen con el nivel de exigencia, ya fueron eliminados por las características anteriores).

Por lo tanto, seleccionaríamos a los toros HOLDNKM000000260548 y HOLNLDM000580616806.

b. Si aplicáramos el método de Índice de selección, los dos toros que seleccionaríamos serían HOLDNKM000000260548 y HOL840M003147224052.

La diferencia se da en que mediante el método de selección NIR el toro HOL840M003147224052 es eliminado debido a su mal desempeño en producción de leche. Sin embargo, el método Índice de selección compensa el mal desempeño en unos caracteres con el buen desempeño en otros caracteres, además de tener en cuenta el coeficiente de ponderación de cada carácter.

c. El Índice de selección utilizado es igual a $-0,05\times DEP(L)+0,33\times DEP(G)+2,25\times DEP(P)+1,31\times DEP(TPH)-39,6\times DEP(SCS)$, por lo tanto:

Pondera en forma negativa el volumen de leche (coeficiente $-0,05$), lo que es típico de mercados que priorizan los sólidos (destino queso, manteca, leche en polvo, etc.).
Favorece la producción de Grasa (coeficiente $+0,33$) y Proteína (coeficiente $+2,25$). La relación entre ambas ponderaciones refleja una visión “antigua” que no se condice en l actualidad con los precios de ambos productos (el valor de la grasa de leche se ha incrementado notoriamente en los últimos años).
La tasa de preñez en hijas del candidato es fundamental para mantener el nivel de reemplazos en el rodeo y para poder hacer selección en hembras (coeficiente $+1,31$).
El recuento de células somáticas representa, junto con el conteo microbiológico, uno de los parámetros claves en la calidad de la leche y es un factor clave en el pago (con bonificaciones por número reducido y castigo por elevado). El score de células somáticas es la medida que se utiliza en las evaluaciones y por lo tanto su ponderación es fuertemente negativa (coeficiente $-39,6$).

PARA RECORDAR

La selección en tandem se basa en seleccionar primero por una sola característica y luego de un tiempo cambiar a otra característica de interés. Es de destacar que la complejidad de este método es baja, aunque también lo es su eficiencia, particularmente si las características poseen una fuerte correlación genética en sentido desfavorable.
La selección por Niveles Independientes de Rechazo (NIR) se basa en establecer un umbral independiente para cada característica y seleccionar como reproductores solamente a aquellos individuos que superen todos los criterios. El principal problema que aparece con este método es que a medida de que establecemos umbrales para diferentes características, el número de individuos que pasa todos los filtros es cada vez menor. A su vez, este método puede eliminar individuos excepcionalmente buenos en una característica, pero que estén levemente por debajo del umbral en cualquiera de las otras características, o aún individuos excelentes en todas las características excepto una.
Los Índices de selección evalúan el mérito global o mérito agregado de los candidatos. Si encontramos una forma racional de ponderar la incidencia de cada una de las $k$ características en la función de mérito global del individuo, entonces el fenotipo agregado del individuo será igual a $I=b_1\ z_1+b_2\ z_2+...+b_k\ z_k=\sum_{i=1}^k b_i\ z_i=\mathbf{b^{T}\mathbf{z}}$. Esto es una función lineal de todas las características, con pesos fenotípicos $b_i$. Dentro de las ventajas que posee esta combinación lineal está la de no dejar afuera fenotipos (genotipos) de alto valor en una característica porque no pasan en otra además de la simplicidad del uso del índice una vez calculado.

13.5 Índices de selección para múltiples características

Previamente, en la sección [Información proporcionada por diferentes tipos de parientes], discutimos acerca del uso de los índices de selección como una manera de combinar información fenotípica proveniente de diferentes relaciones de parentesco a fin de obtener una mejor estimación del valor de cría de un individuo. En esta sección vamos a ver el tema de los índices de selección nuevamente, pero desde una perspectiva diferente: la combinación de la información de diferentes características en un solo valor a partir del cual elegir los mejores reproductores.

Vamos a usar la misma notación que usamos al final del capítulo anterior para las matrices de varianza-covarianza genética ($\mathbf{G}$) y fenotípica ($\mathbf{P}$), mientras que usaremos la notación, que ya usamos antes, de ${\sigma(,)}$ para la covarianza, tanto escalar como vectorial. Las ideas de de esta sección se basan en las notas de Bruce Wfalsh y Michael Lynch, disponibles en (2000), que constituyen un excelente material para ampliar lo tratado aquí.

Nuevamente, al tratarse de un índice lineal sobre medidas fenotípicas, nuestro índice será de la forma

\[ \begin{split} {I=b_1\ z_1+b_2\ z_2+...+b_k\ z_k=\mathbf{b'z}} \end{split} \tag{13.53} \]

donde ahora los distintos ${z_i}$ serán diferentes características fenotípicas. Por ejemplo, en producción lechera es de nuestro interés aumentar la producción de grasa y proteína, al mismo tiempo que reducir el volumen de leche y el recuento de células somáticas. Todas estas características (grasa, proteína, volumen de leche, recuento de células somáticas) serían los ${z_i}$.

Al ser el índice una combinación lineal de otras características, podemos considerarlo al mismo como una nueva característica fenotípica. Como ya vimos antes (en otro contexto) en la sección Precisión del valor de cría a partir del índice, la varianza del índice es igual a

\[ \begin{split} {\sigma^2_I=\sigma(\mathbf{b'z},\mathbf{b'z})=\mathbf{b'}\sigma(\mathbf{z},\mathbf{z})\mathbf{b}=\mathbf{b'Pb}} \end{split} \tag{13.54} \]

mientras que la varianza genética-aditiva del mismo sería

\[ \begin{split} {\sigma^2_{A_I}=\sigma_A(\mathbf{b'z},\mathbf{b'z})=\mathbf{b'}\sigma_A(\mathbf{z},\mathbf{z})\mathbf{b}=\mathbf{b'Gb}} \end{split} \tag{13.55} \]

Por lo tanto, combinando las ecuaciones (13.54) y (13.55), tenemos que la heredabilidad del índice es igual a

\[ \begin{split} {h^2_I=\frac{\sigma^2_{A_I}}{\sigma^2_I}=\frac{\mathbf{b'Gb}}{\mathbf{b'Pb}}} \end{split} \tag{13.56} \]

A riesgo de mencionar lo obvio, tanto $\mathbf{b'Gb}$ como $\mathbf{b'Pb}$ son escalares (números), ya que si tenemos $k$ características las dimensiones de ambos productos son ${[1 \times k][k \times k][k \times 1]}$ y de acuerdo a las reglas de multiplicación de matrices los índices internos “colapsan”, quedando las dimensiones del resultado ${[1 \times 1]}$, es decir un escalar.

Asumiendo que la distribución de los valores de cría $\mathbf{g}$ y los fenotipos $\mathbf{z}$ es conjuntamente normal multivariada, como ya vimos previamente, entonces se aplica la ecuación del criador a la respuesta esperada del índice y utilizando los resultados de las ecuaciones (13.54) y (13.56), con una intensidad de selección ${i}$, tenemos

\[ \begin{split} {R_I=i\ h^2_I\ \sigma_I=i\ \frac{\mathbf{b'Gb}}{\mathbf{b'Pb}} \sqrt{\mathbf{b'Pb}}=i\ \frac{\mathbf{b'Gb}}{\sqrt{\mathbf{b'Pb}}}} \end{split} \tag{13.57} \]

La pregunta que nos surge ahora es ¿cómo cambian las diferentes características que conforman el índice cuando seleccionamos por este? Para eso, bajo los supuestos usuales para que se cumpla la ecuación del criador, tenemos que el cambio en la media será igual a

\[ \begin{split} \Delta \mu=\mathbf{G}\mathbf{P}^{-1}\mathbf{s} \end{split} \tag{13.58} \]

Debemos pues encontrar el vector del diferencial de selección $\mathbf{s}$. Consideremos un caracter, por ejemplo el caracter $j$ y su diferencial $s_j$. Como la correlación entre el fenotipo del caracter $j$ y el fitness lo podemos expresar como

\[ \begin{split} \rho_{z_j,w}=\rho_{z_j,I}\cdot\rho_{I,w} \end{split} \tag{13.59} \]

entonces, expresado en términos de varianzas y covarianzas, tenemos que

\[ \begin{split} \frac{\sigma(z_j,w)}{\sigma_{z_j} \sigma_w}=\left(\frac{\sigma(z_j,I)}{\sigma_{z_j} \sigma_I}\right)\left(\frac{\sigma(I,w)}{\sigma_I \sigma_w}\right) \end{split} \tag{13.60} \]

Al mismo tiempo, si recordamos la identidad de Robertson-Price que vimos en la sección El diferencial de selección direccional y la identidad de Robertson-Price, la misma establecía que el diferencial de selección era igual a la covarianza entre el fenotipo y el fitness correspondiente a ese fenotipo, es decir $\sigma(z_j,w=s_j$. En forma análoga, si el fenotipo es el índice, entonces $\sigma(I,w)=s_I=i \sigma_I$, con $i$ la intensidad de selección en el índice. La última igualdad proviene, obviamente, de $i=\frac{s}{\sigma_P} \Leftrightarrow s=i\ \sigma_P$.
Utilizando estos resultados y resolviendo para $\sigma(z_j,w)$ en la ecuación (13.60), que como vimos es igual al diferencial de selección que nos interesa, tenemos

\[ \begin{split} \sigma(z_j,w)=\sigma_{z_j} \sigma_w \left(\frac{\sigma(z_j,I)}{\sigma_{z_j} \sigma_I}\right)\left(\frac{\sigma(I,w)}{\sigma_I \sigma_w}\right)=\frac{\sigma(z_j,I)\sigma(I,w)}{\sigma^2_I}=i\ \frac{\sigma(z_j,I)}{\sigma_I} \end{split} \tag{13.61} \]

Por otro lado, también podemos escribir

\[ \begin{split} \sigma(z_j,I)=\sigma(z_j,\sum_k b_k z_k)=\sum_k b_k P_{jk} \end{split} \tag{13.62} \]

donde $P_{ij}$ es el elemento de la fila $i$ y columna $j$ en la matriz $\mathbf{P}$. De esta forma, podemos ahora escribir el resultado de la ecuación (13.60) como

\[ \begin{split} \sigma(z_j,w)=s_j=\left(\frac{i}{\sigma_I}\right) \cdot \sum_k b_k P_{jk} \end{split} \tag{13.63} \]

lo que para el conjunto de características pasa a ser entonces el vector de diferenciales de selección

\[ \begin{split} \mathbf{s}=\left(\frac{i}{\sigma_I}\right) \cdot \mathbf{Pb} \end{split} \tag{13.64} \]

Finalmente, combinando el resultado de la ecuación (13.58) con este vector de diferenciales de selección, tenemos que la respuesta a la selección será

\[ \begin{split} \Delta \mu=\mathbf{G}\mathbf{P}^{-1}\mathbf{s}=\left(\frac{i}{\sigma_I}\right) \cdot \mathbf{G}\mathbf{P}^{-1} \mathbf{Pb}=\left(\frac{i}{\sigma_I}\right) \cdot \mathbf{G}\mathbf{b} \end{split} \tag{13.65} \]

y como $\sigma_I=\sqrt{\sigma^2_I}=\sqrt{\mathbf{b}^{T}\mathbf{Pb}}$, la ecuación anterior se puede escribir como

\[ \begin{split} \Delta \mu=\left(\frac{i}{\sigma_I}\right) \frac{\mathbf{G}\mathbf{b}}{\sqrt{\mathbf{b}^{T}\mathbf{Pb}}} \end{split} \tag{13.66} \]

El índice de Smith-Hazel

En esta sección vamos a introducir un cambio en la notación para indicar la transpuesta de una matriz o un vector, ya que usaremos $^{T}$ p, dejando el uso de $'$ para las derivadas. Normalmente, la idea de usar índices de selección es resumir en un valor el mérito general del individuo. Si tenemos un conjunto de valores económicos para cada una de la características, entonces podemos ordenar estos pesos relativos en un vector $\mathbf{a}$ y por lo tanto, el mérito general del individuo (a partir de su fenotipo en las distintas características) es

\[ \begin{split} J=\mathbf{a^{T}z} \end{split} \tag{13.67} \]

Claramente, $J$ nos habla del mérito fenotípico del individuo, pero nuestro objetivo es seleccionar a los mejores reproductores, por lo que si llamamos $g_i$ al valor de cría en la característica $_i$, entonces el correspondiente mérito genético agregado será

\[ \begin{split} H=\sum_i a_i g_i=\mathbf{a^{T}g} \end{split} \tag{13.68} \]

\[ \begin{split} H-\mu_H=H-\mathbf{a^{T}\mu} \end{split} \tag{13.69} \]

será el valor de cría del individuo. Debido a las estructura de dependencias entre características (varianzas y covarianzas genéticas y fenotípicas), por lo general $J$ no es el mejor predictor del mérito genético agregado $H$.

Como vimos antes, bajo los supuestos tradicionales de ausencia de interacción genotipo-ambiente, epistasis, etc., la media de valores de cría de los reproductores seleccionados será igual a la media esperada en los valores fenotípicos de la progenie. Es decir, el cambio en $H$ dentro de la misma generación será igual al cambio esperado en $J$ en la siguiente generación. Este cambio se maximiza seleccionando entonces a los individuos con mayores valores de $H$ y nuestra tarea será entonces encontrar un índice $I_s=\mathbf{b_s^{T}z}$ tal que maximice la correlación con $H$.

La correlación entre un índice arbitrario $I=\mathbf{b^{T}z}$, y el mérito genético agregado $H$ es

\[ \begin{split} \rho_{I,H}=\frac{\sigma_{I,H}}{\sigma_I \sigma_H} \end{split} \tag{13.70} \]

La varianza en el mérito genético agregado será igual a

\[ \begin{split} \sigma^2_H=\sigma(\mathbf{a^{T}z},\mathbf{a^{T}z})=\mathbf{a^{T}Ga} \end{split} \tag{13.71} \]

mientras que, como ya vimos antes en la ecuación (13.54), la varianza del índice es igual a

\[ \begin{split} \sigma^2_I=\mathbf{b^{T}Pb} \end{split} \]

Por otra parte, la covarianza entre el mérito genético agregado y el índice es

\[ \begin{split} \sigma_{I,H}=\sigma(\mathbf{a^{T}g},\mathbf{b^{T}z})=\mathbf{a}^{T}\sigma(\mathbf{g},\mathbf{z})\mathbf{b}=\mathbf{a}^{T}\sigma(\mathbf{g},\mathbf{g+e})\mathbf{b}=\mathbf{a}^{T}\sigma(\mathbf{g},\mathbf{g})\mathbf{b}=\mathbf{a^{T}Gb} \end{split} \tag{13.72} \]

Poniendo todo junto, tenemos que la correlación entre el índice arbitrario y el mérito genético agregado es igual a

\[ \begin{split} \rho_{I,H}=\frac{\sigma_{I,H}}{\sigma_I \sigma_H}=\frac{\mathbf{a^{T}Gb}}{\sqrt{\mathbf{b^{T}Pb}}\sqrt{\mathbf{a^{T}Ga}}} \end{split} \tag{13.73} \]

Para hallar el máximo de esta función (función de $\mathbf{b}$) debemos hacer la derivada e igualarla a cero. Para esto, una ayuda importante viene de notar que el término $\mathbf{a^{T}Ga}$ es una constante, por lo que la optimización no dependerá de él, es decir, debemos optimizar $\frac{\mathbf{a^{T}Gb}}{\sqrt{\mathbf{b^{T}Pb}}}$. Además, tanto el numerador como el denominador son productos cuadráticos que como ya vimos son simples escalares, por lo que aplicaremos las técnicas estándar de derivación sobre ellos y solo luego utilizaremos derivación sobre vectores y matrices. En primer lugar, podemos usar la regla de la cadena para el cociente en la ecuación (13.73), es decir $\left(\frac{u(x)}{v(x)}\right)'=\frac{u'v-v'u}{v^2}$. Además, sabemos que la derivada de una forma cuadrática $x^{T}Ax$ donde además la matriz es simétrica es igual a $2x^{T}A$. Por lo que utilizando la regla de la cadena y la derivada de una forma cuadrática, tenemos que $(\sqrt{\mathbf{b}^{T}\mathbf{Pb})}'=\frac{\mathbf{b}^{T}\mathbf{P}}{\sqrt{\mathbf{b}^{T}\mathbf{Pb}}}$ y entonces, luego de igualar a cero la derivada, si llamamos $\tilde {\mathbf{b}}$ a las soluciones para $\mathbf{b}$, entonces

\[ \begin{split} \left(\frac{\mathbf{a^{T}Gb}}{\sqrt{\mathbf{b^{T}Pb}}}\right)'=\frac{\mathbf{a}^{T}\mathbf{G}(\sqrt{\mathbf{b}^{T}\mathbf{Pb}})-[\sqrt{\mathbf{b}^{T}\mathbf{Pb}}]'(\mathbf{a}^{T}\mathbf{Gb})}{\mathbf{b}^{T}\mathbf{Pb}} \end{split} \tag{13.74} \]

La derivada que tenemos en el numerador, como ya vimos, es la derivada de una forma cuadrática, por lo que

\[ \begin{split} [\sqrt{\mathbf{b}^{T}\mathbf{Pb}}]'=\frac{2\mathbf{b}^{T}\mathbf{P}}{2\sqrt{\mathbf{b}^{T}\mathbf{Pb}}}=\frac{\mathbf{b}^{T}\mathbf{P}}{\sqrt{\mathbf{b}^{T}\mathbf{Pb}}} \end{split} \tag{13.75} \]

por lo que sustituyendo en la ecuación (13.74) e igualando a cero, teniendo solo en cuenta el numerador porque para que sea cero el denominador no importa, tenemos

\[\mathbf{a}^{T}\mathbf{G}(\sqrt{\mathbf{b}^{T}\mathbf{Pb}})-\frac{\mathbf{b}^{T}\mathbf{P}}{\sqrt{\mathbf{b}^{T}\mathbf{Pb}}}(\mathbf{a}^{T}\mathbf{Gb})=0 \Leftrightarrow\] \[\mathbf{a}^{T}\mathbf{G}(\sqrt{\mathbf{b}^{T}\mathbf{Pb}})(\sqrt{\mathbf{b}^{T}\mathbf{Pb}})=\mathbf{b}^{T}\mathbf{P}(\mathbf{a}^{T}\mathbf{Gb}) \Leftrightarrow\] \[ \begin{split} \mathbf{G}^{T}\mathbf{a}(\mathbf{b}^{T}\mathbf{Pb})=\mathbf{P}^{T}\mathbf{b}(\mathbf{a}^{T}\mathbf{Gb}) \end{split} \tag{13.76} \]

Si llamamos $\tilde{\mathbf{b}}$ al vector en su solución, entonces

\[ \begin{split} (\tilde{\mathbf{b}}^{T}\mathbf{P}\tilde{\mathbf{b}})\mathbf{Ga}=(\mathbf{a}^{T}\mathbf{G}\tilde{\mathbf{b}})\mathbf{P}\tilde{\mathbf{b}} \end{split} \tag{13.77} \]

Por lo tanto, como $(\tilde{\mathbf{b}}^{T}\mathbf{P}\tilde{\mathbf{b}})$ y $(\mathbf{a}^{T}\mathbf{G}\tilde{\mathbf{b}})$ son escalares, la solución para $\mathbf{b}$ será de la forma

\[ \begin{split} \mathbf{P}\tilde{\mathbf{b}}=c \cdot \mathbf{Ga} \end{split} \tag{13.78} \]

con $c=\frac{\tilde{\mathbf{b}}^{T}\mathbf{P}\tilde{\mathbf{b}}}{\mathbf{a}^{T}\mathbf{G}\tilde{\mathbf{b}}}$ y por lo tanto

\[ \begin{split} \tilde{\mathbf{b}}=c \cdot \mathbf{P}^{-1}\mathbf{Ga} \end{split} \tag{13.79} \]

donde $c$ es un escalar que es irrelevante para el peso relativo de los distintos componentes en el índice. Finalmente, utilizando este resultado, tenemos que el índice de Smith-Hazel es

\[ \begin{split} I_s=\mathbf{b}^{T}_s\mathbf{z}=(\mathbf{P}^{-1}\mathbf{Ga})^{T}\mathbf{z} \end{split} \tag{13.80} \]

El índice de Smith-Hazel necesita conocer con precisión ambas matrices de varianza-covarianza, $\mathbf{G}$ y $\mathbf{P}$, así como el vector de pesos $\mathbf{a}$. En general las matrices de varianza-covarianza deben estimarse a partir de los datos y por lo tanto no son conocidas sin error, lo que tiene implicancias para la optimalidad del índice. Por otra parte, el índice parece ser relativamente resistente a los errores de estimación en $\mathbf{a}$.

El índice de Smith-Hazel posee algunas propiedades que lo hacen muy interesante:

1- Provee la mayor respuesta posible en el mérito cuando la intensidad de selección es fija.

2- El índice esta estrechamente relacionado con la solución de mínimos cuadrados para la regresión del mérito en los valores fenotípicos $z$ y con las soluciones del método BLUP, que veremos más adelante en este capítulo.

3- Para una muestra dada, el índice de Smith-Hazel da la probabilidad máxima de seleccionar al individuo con mayor mérito agregado.

La respuesta a la selección utilizando el índice de Hazel-Smith estará dada por

\[ \begin{split} R_H=i\ \frac{\mathbf{a}^{T}\mathbf{Gb}_s}{\sqrt{\mathbf{b}^{T}_s\mathbf{P}\mathbf{b}_s}}=i\ \sqrt{\mathbf{a}^{T}\mathbf{Gb}_s}=i\ \sqrt{\mathbf{a}^{T}\mathbf{G}\mathbf{P}^{-1}\mathbf{Ga}} \end{split} \tag{13.81} \]

El índice de Smith-Hazel se puede extender fácilmente a un número diferentes de características fenotípicas que las consideradas en el mérito genético agregado y de hecho ni siquiera hace falta que tengan solapamiento las mismas, aportando la información la estructura de varianza-covarianza genética entre características.

Para esto definimos $\mathbf{P}$ como la matriz de varianza-covarianza fenotípica para el vector $\mathbf{z}$, de dimensiones $[m \times m]$ y $\mathbf{G}$, de dimensiones $[m \times n]$, cuyos elementos son $G_{kj}=\sigma(z_k,g_j)$ para $1\leqslant k \leqslant m,\ 1\leqslant j \leqslant n$, a la matriz de covarianzas genéticas entre los $m$ valores fenotípicos y los $n$ caracteres comprendidos en $H$.

Esto nos lleva a un mérito genético agregado igual a

\[ \begin{split} H=\sum_{j=1}^n a_j\ g_j \end{split} \tag{13.82} \]

y un índice fenotípico

\[ \begin{split} I_s=\sum_{k=1}^m b_k\ z_k \end{split} \tag{13.83} \]

A partir de estas definiciones, la solución para el índice sigue siendo de la forma $\mathbf{b}_s=\mathbf{P}^{-1}\mathbf{Ga}$, pero dado que $\mathbf{G}$ ya no es más simétrica, en este caso la respuesta estará dada por

\[ \begin{split} R_H=i\ \sqrt{\mathbf{a}^{T}\mathbf{G}^{T}\mathbf{P}^{-1}\mathbf{Ga}} \end{split} \tag{13.84} \]

PARA RECORDAR

La heredabilidad del índice es igual a ${h^2_I=\frac{\sigma^2_{A_I}}{\sigma^2_I}=\frac{\mathbf{b'Gb}}{\mathbf{b'Pb}}}$ con una respuesta a la selección equivalente a $\Delta\mu=\left(\frac{i}{\sigma_I}\right)\frac{\mathbf{G}\mathbf{b}}{\sqrt{\mathbf{b}^{T}\mathbf{Pb}}}$
Si tenemos un conjunto de valores económicos para cada una de la características, entonces podemos ordenar estos pesos relativos en un vector $\mathbf{a}$ y por lo tanto, el mérito general del individuo (a partir de su fenotipo en las distintas características) es $J=\mathbf{a^{T}z}$
El índice de Smith-Hazel $I_s=\mathbf{b}^{T}_s\mathbf{z}=(\mathbf{P}^{-1}\mathbf{Ga})^{T}\mathbf{z}$ necesita conocer con precisión ambas matrices de varianza-covarianza, $\mathbf{G}$ y $\mathbf{P}$, así como el vector de pesos $\mathbf{a}$. El mismo:

Provee la mayor respuesta posible en el mérito cuando la intensidad de selección es fija.
El índice esta estrechamente relacionado con la solución de mínimos cuadrados para la regresión del mérito en los valores fenotípicos $z$ y con las soluciones del método BLUP.
Para una muestra dada, el índice de Smith-Hazel da la probabilidad máxima de seleccionar al individuo con mayor mérito agregado.

La respuesta a la selección utilizando el índice de Smith-Hazel estará dada por $R_H=i\ \sqrt{\mathbf{a}^{T}\mathbf{G}\mathbf{P}^{-1}\mathbf{Ga}}$

13.6 Métodos y técnicas avanzadas de selección

En la primera parte de este capítulo discutimos diferentes tipos de selección utilizando información de parientes, selección familiar, selección intrafamiliar, selección fraternal, pruebas de progenie, todas utilizando un solo tipo de relaciones de parentesco único. Más adelante, extendimos los tipos posibles de fuentes de información a través de la integración en índices de selección y vimos que era necesario desarrollar un índice para cada tipo de combinación. Esto, sin dudas, resulta extremadamente impráctico ya que es necesario estudiar individuo a individuo las fuentes de información disponibles u optar por no utilizar todas las fuentes disponibles.

Por otra parte, en la segunda parte del capítulo vimos que usualmente debemos trabajar con varias características a la vez para obtener una respuesta que se adecue a las ecuaciones de ingresos y egresos de los establecimientos. Si nos vamos un momento a la sección La forma generalizada de la ecuación del criador del capítulo Correlaciones y Respuesta Correlacionada, recordaremos que la extensión de la ecuación del criador a la selección multivariada involucraba el uso de las matrices de varianza-covarianza genética y fenotípica y vimos en este capítulo el papel de traspaso de información de una característica a otra a través de dichas matrices.

Afortunadamente, desde mediados del siglo XX contamos con los desarrollos, primero teóricos y luego gracias a la computación prácticos, que nos permiten resolver casi todos estos problemas de manera “automática”. En ese sentido, uno de los avances más importantes se debe a Charles R. Henderson, que en una serie de artículos sentó las bases de lo que actualmente conocemos como las ecuaciones del modelo mixto lineal o el BLUP directamente y que es la metodología de base en las evaluaciones genéticas.

BLUP: las ecuaciones del modelo mixto lineal

Un modelo mixto lineal es un modelo mixto que combina efectos fijos y efectos aleatorios. Existen muchas definiciones para estos dos tipos de efectos, pero en nuestro contexto unas pocas consideraciones prácticas nos permitirán distinguirlos:

Efectos fijos son aquellos que nos puede interesar contrastar sus niveles, que usualmente tienen pocos niveles y que en otros casos usaremos para compensar diferencias sistemáticas entre niveles. Por ejemplo, en sexo de los animales suele ser considerado un efecto fijo con dos niveles y su inclusión en los modelos compensa las diferencias entre machos y hembras. Normalmente, queremos estimar su valor.
Efectos aleatorios son efectos donde asumimos que los datos observados son una muestra aleatoria de una población mayor. Normalmente poseen muchos niveles y los usamos, en nuestro caso, para modelar el valor de cría de los animales, los efectos maternales, etc. y obviamente, los efectos ambientales y del error. En general, el objetivo es predecir su valor ya que se trata de un efecto aleatorio.

La idea de combinar las ecuaciones del modelo mixto en forma matricial aparece por primera vez en Charles Roy Henderson (1949), Charles Roy Henderson (1950) y fue posteriormente extendida por Charles Roy Henderson (1959), entre otros, demostrando alguna de las “propiedades” de este método. Más adelante, el propio Henderson bautizó el método con el acrónimo BLUP, por “Best Linear Unbiased Predictor”. El signficado de cada una de estas palabras, de acuerdo con Henderson sería:

Mejor: Significa que la varianza del error de predicción ${Var(a-\hat a)}$ (que es la diferencia entre los valores “verdaderos” y los predichos) se minimiza, o que, en forma equivalente, la correlación entre ellos se maximiza
Lineal: Significa que los ${EBV}$ predichos son funciones lineales de los datos (que normalmente se denota como ${L'y}$)
Insesgado: Significa que el valor esperado de los ${EBV}$ predichos y de los ${EBV}$ “verdaderos” son iguales, es decir ${E(a=\hat a)}$
Predictor: Como ya vimos, significa que implica una predicción del verdadero valor de cría (ya que este es tratado como un efecto aleatorio).

Varias de estas propiedades solo se cumplen si el modelo asumido es el modelo verdadero, un problema filosófico difícil de resolver (por ejemplo la condición de Mejor), aunque se trata de un modelo robusto frente a este supuesto, o el Insesgado, que solo es condicional a los hiperparámetros del modelo. Sin embargo, pese a esto, se trata de un modelo que ha sido muy exitoso como forma de modelar las evaluaciones genéticas y de incrementar la respuesta a la selección.

Nosotros no vamos a extendernos en la base teórica, que corresponde a cursos más avanzados, pero comenzaremos a dejar las bases acerca de cómo funciona para que en próximos cursos puedas usar los resultados y entender mejor la teoría.

En mejoramiento genético tenemos información de un número determinado de animales, tanto el fenotipo de las características de interés, como las relaciones de parentesco entre los animales (usualmente en un pedigree) y de los distintos efectos que incidieron en la manifestación del fenotipo. Sin pérdida de generalidad, asumamos que poseemos información completa para $n$ animales (incluyendo su pedigree completo), que serán los que pretendemos evaluar. Los efectos fijos vamos a codificarlos en una matrix $\mathbf{X}$, que tendrá tantas filas como individuos con fenotipo, es decir $n$ y tantas columnas como el número total de niveles de los factores considerados, menos el número de factores (para eliminar la dependencia lineal entre columnas). También en la matriz $\mathbf{X}$ podemos incluir las covariables (variables continuas) que sean necesarias (por ejemplo kilogramos de alimento que recibió, temperaturas promedio o lo que se nos ocurra que explica el fenotipo). Por otra parte, vamos a considerar por simplicidad solamente dos efectos aleatorios, el genético-aditivo de los individuos y el error. Teniendo en cuenta la matriz $\mathbf{A}$ de parentesco aditivo entre los individuos (que si no consideramos a los progenitores de los individuos con registros será de dimensiones $[n \times n]$), la forma usual de especificar nuestro modelo mixto será

\[\mathbf{y = Xb + Zu + e},\] \[\mathbf{u} \sim (0, \mathbf{G}), \mathbf{G}=\mathbf{A}\sigma_A^2,\] \[\mathbf{e} \sim (0, \mathbf{R}), \mathbf{R}=\mathbf{I}\sigma_E^2,\] \[ \begin{split} {cov(\mathbf{u}, \mathbf{e'}) = 0} \end{split} \tag{13.85} \]

El aporte sustantivo de Henderson fue demostrar que las ecuaciones correspondientes a este modelo se podían escribir en forma matricial como

\[ \begin{split} \begin{bmatrix} \mathbf{X'R^{-1}X} & \mathbf{X'R^{-1}Z}\\ \mathbf{Z'R^{-1}X} & \mathbf{Z'R^{-1}Z+G^{-1}} \end{bmatrix} \begin{bmatrix} \mathbf{\hat b}\\ \mathbf{\hat u} \end{bmatrix} = \begin{bmatrix} \mathbf{X'R^{-1}y} \\ \mathbf{Z'R^{-1}y} \end{bmatrix} \end{split} \tag{13.86} \]

La solución de dicho sistema de ecuaciones se corresponde con la estimación de los efectos fijos (BLUE) y aleatorios (BLUE) del modelo mixto.

De hecho, en sistemas de tamaño pequeño, para obtener la solución alcanza con invertir la matriz del lado izquierdo de la ecuación (13.86) y luego premultplicar por dicha inversa a ambos lados de la ecuación, es decir

\[ \begin{bmatrix} \mathbf{X'R^{-1}X} & \mathbf{X'R^{-1}Z}\\ \mathbf{Z'R^{-1}X} & \mathbf{Z'R^{-1}Z+G^{-1}} \end{bmatrix}^{-1} \begin{bmatrix} \mathbf{X'R^{-1}X} & \mathbf{X'R^{-1}Z}\\ \mathbf{Z'R^{-1}X} & \mathbf{Z'R^{-1}Z+G^{-1}} \end{bmatrix} \begin{bmatrix} \mathbf{\hat b} \mathbf{\hat u} \end{bmatrix}= \] \[ \begin{bmatrix} \mathbf{X'R^{-1}X} & \mathbf{X'R^{-1}Z}\\ \mathbf{Z'R^{-1}X} & \mathbf{Z'R^{-1}Z+G^{-1}} \end{bmatrix}^{-1} \begin{bmatrix} \mathbf{X'R^{-1}y} \mathbf{Z'R^{-1}y} \end{bmatrix}\ \therefore \] \[ \begin{split} \begin{bmatrix} \mathbf{\hat b} \mathbf{\hat u} \end{bmatrix}= \begin{bmatrix} \mathbf{X'R^{-1}X} & \mathbf{X'R^{-1}Z}\\ \mathbf{Z'R^{-1}X} & \mathbf{Z'R^{-1}Z+G^{-1}} \end{bmatrix}^{-1} \begin{bmatrix} \mathbf{X'R^{-1}y} \mathbf{Z'R^{-1}y} \end{bmatrix} \end{split} \tag{13.87} \]

En las evaluaciones genéticas los sistemas de ecuaciones suelen tener cientos, miles o aún millones de lineas, por lo que los métodos computacionales involucrados son mucho más sofisticados que la inversión directa. Además, para obtener las soluciones de acuerdo a las ecuaciones del BLUP es necesarion conocer las varianzas genéticas y del error, cosa que usualmente se desconoce. Como forma de solucionar esto se suele recurrir a métodos iterativos que ya discutimos en capítulos previos y que permiten la resolución iterativa de los dos problemas a la vez.

Finalmente, desde el punto de vista conceptual, el BLUP posee conexión directa con dos temas que trabajamos en este capítulo. Por un lado, la integración de la información de parientes se realiza en forma “automática”, en lugar de considerar cada situación particular (de combinación de distintas fuentes de información). Por el otro, el método se extiende fácilmente a la predicción de los valores de cría en diferentes características, C. R. Henderson and Quaas (1976), “apilando” los vectores de características fenotípicas y usando el producto Kronecker entre la matriz de parentesco y la matriz de varianza-covarianza genética entre características.

Ejemplo 13.4

Supongamos que contamos con la información de peso al destete de $6$ animales pertenecientes a $2$ rodeos:

Animal	Padre	Madre	Rodeo	Peso.al.destete
$1$			$1$	$185$
$2$			$1$	$180$
$3$			$2$	$175$
$4$	$1$	$2$	$1$	$188$
$5$	$1$	$3$	$2$	$182$
$6$	$1$	$3$	$2$	$187$

El modelo que describe las observaciones es:

\[ \begin{split} y_{ij}=r_i+a_j+e_{ij} \end{split} \]

donde:

$y_{ij}$ = observación (peso al destete);
$r_i$ = efecto fijo (rodeo);
$a_j$ = efecto aleatorio (animal);
$e_{ij}$ = efecto aleatorio (error)

Por otra parte, si utilizamos la notación matricial, el modelo que describe las observaciones es:

\[ \begin{split} \mathbf{y=Xb+Zu+e}\\ \mathbf{u} \sim N(\mathbf{0}, \mathbf{G}), \mathbf{G}=\mathbf{A}\sigma_A^2\\ \mathbf{e} \sim N(\mathbf{0}, \mathbf{R}), \mathbf{R}=\mathbf{I}\sigma_E^2, cov(\mathbf{u}, \mathbf{e}') = 0 \end{split} \]

donde:

$\mathbf{y}$ = vector de observaciones (peso al destete) $n \times 1$, siendo $n$ el número de observaciones:

\[ \begin{split} \mathbf{y} = \left[\begin{array} {r} 185\\ 180\\ 175\\ 188\\ 182\\ 187 \end{array}\right] \end{split} \]

$\mathbf{b}$ = vector de efecto fijo (rodeo) $p \times 1$, siendo $p$ el número de niveles de efecto fijo;
$\mathbf{u}$ = vector de efecto aleatorio (animal) $q \times 1$, siendo $q$ el número de niveles de efecto aleatorio;
$\mathbf{e}$ = vector de efecto aleatorio (error) $n \times 1$, siendo $n$ el número de observaciones;
$\mathbf{X}$ = matriz de incidencia de efecto fijo (rodeo) $n \times p$:

\[ \begin{split} \mathbf{X} = \left[\begin{array} {rr} 1 & 0\\ 1 & 0\\ 1 & 1\\ 1 & 0\\ 1 & 1\\ 1 & 1 \end{array}\right] \end{split} \]

En esta matriz, la primera columna representa la media (ya que vamos a trabajar nuestros resultados como desvío de la media), mientras que la segunda columna representa el rodeo. Como en este tipo de modelos debemos especificar la pertenencia a un efecto fijo u otro con ceros y unos (cero quiere decir que no tiene ese nivel del efecto y uno que sí lo tiene), en general vamos a precisar de tantas columnas para cada efecto como niveles menos uno (eso porque uno de los niveles podemos incluirlo en la media). En nuestro caso, como tenemos solamente dos rodeos, alcanza con una sola columna para indicar a que rodeo pertenece. Supongamos que usamos la columna para especificar el nivel “rodeo 2”. Por lo tanto, la tercera, quinta y sexta observación pertenecen al rodeo $2$ (por eso hay un $1$ en dichas observaciones); por lo que la primera, segunda y cuarta observación pertenecen al rodeo $1$ (y por lo tanto hay un $0$ en la columna “rodeo 2”).

$\mathbf{Z}$ = matriz de incidencia de efecto aleatorio (animal) $n \times q$:

\[ \begin{split} \mathbf{Z} = \left[\begin{array} {rrrrrr} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{array}\right] \end{split} \]

La primer columna indica que la primer observación pertenece al animal $1$; la segunda columna indica que la segunda observación pertenece al animal $2$; la tercer columna indica que la tercer observación pertenece al animal $3$; la cuarta columna indica que la cuarta observación pertenece al animal $4$; la quinta columna indica que la quinta observación pertenece al animal $5$; la sexta columna indica que la sexta observación pertenece al animal $6$.

$\mathbf{A}$ = matriz de parentesco aditivo entre los animales $n$ x $n$:

\[ \begin{split} \mathbf{A} = \left[\begin{array} {rrrrrr} 1.0 & 0.0 & 0.0 & 0.50 & 0.50 & 0.50\\ 0.0 & 1.0 & 0.0 & 0.50 & 0.00 & 0.00\\ 0.0 & 0.0 & 1.0 & 0.00 & 0.50 & 0.50\\ 0.5 & 0.5 & 0.0 & 1.00 & 0.25 & 0.25\\ 0.5 & 0.0 & 0.5 & 0.25 & 1.00 & 0.50\\ 0.5 & 0.0 & 0.5 & 0.25 & 0.50 & 1.00\\ \end{array}\right] \end{split} \]

En esta matriz la primer columna indica que el primer animal es padre de los animales $4$, $5$ y $6$ (por eso el valor de $0,5=\frac{1}{2}$, el valor correspondiente al parentesco aditivo dentre un progenitor y su progenie si no hay consanguinidad en el progenitor); la segunda columna indica que el segundo animal es padre del animal $4$; la tercer columna indica que el tercer animal es padre de los animales $5$ y $6$; la cuarta columna indica que el cuarto animal es hijo de los animales $1$ y $2$, y medio hermano de los animales $5$ y $6$; la quinta columna indica que el quinto animal es hijo de los animales $1$ y $3$, medio hermano del animal $4$, y hermano entero del animal $6$; la sexta columna indica que el sexto animal es hijo de los animales $1$ y $3$, medio hermano del animal $4$, y hermano entero del animal $5$.

La diagonal indica el parentesco aditivo de cada animal consigo mismo: ninguno de seis los animales es consanguíneo.

Siguiendo el sistema de ecuaciones propuesto por Henderson (Charles Roy Henderson (1949); Charles Roy Henderson (1950); Charles Roy Henderson (1959)), obtenemos las estimaciones de los efectos fijos y aleatorios del modelo mixto. Primero, con todas la matrices y vectores que especificamos previamente armamos las matrices del lado izquierdo y del lado derecho del sistema de ecuaciones:

Luego, asumiendo que podemos invertir directamente la matriz del lado izquierdo de las ecuaciones BLUP, de acuerdo con las ecuaciones en (13.87), tenemos que la solución está dada por

\[ \begin{split} \begin{bmatrix} \mathbf{X'R^{-1}X} & \mathbf{X'R^{-1}Z}\\ \mathbf{Z'R^{-1}X} & \mathbf{Z'R^{-1}Z+G^{-1}} \end{bmatrix}^{-1} \begin{bmatrix} \mathbf{X'R^{-1}X} & \mathbf{X'R^{-1}Z}\\ \mathbf{Z'R^{-1}X} & \mathbf{Z'R^{-1}Z+G^{-1}} \end{bmatrix} \begin{bmatrix} \mathbf{\hat b}\\ \mathbf{\hat u} \end{bmatrix} = \end{split} \] \[ \begin{split} \begin{bmatrix} \mathbf{X'R^{-1}X} & \mathbf{X'R^{-1}Z}\\ \mathbf{Z'R^{-1}X} & \mathbf{Z'R^{-1}Z+G^{-1}} \end{bmatrix}^{-1} \begin{bmatrix} \mathbf{X'R^{-1}y} \\ \mathbf{Z'R^{-1}y} \end{bmatrix}\ \therefore \begin{bmatrix} \mathbf{\hat b}\\ \mathbf{\hat u} \end{bmatrix} = \end{split} \] \[ \begin{split} \begin{bmatrix} \mathbf{X'R^{-1}X} & \mathbf{X'R^{-1}Z}\\ \mathbf{Z'R^{-1}X} & \mathbf{Z'R^{-1}Z+G^{-1}} \end{bmatrix}^{-1} \begin{bmatrix} \mathbf{X'R^{-1}y} \\ \mathbf{Z'R^{-1}y} \end{bmatrix} \end{split} \]

lo que en nuestro caso nos deja con la siguiente solución:

\[ \begin{split} \mathbf{ \begin{bmatrix} \mathbf{\hat b}\\ \mathbf{\hat u} \end{bmatrix} } = \left[\begin{array} {r} 183.7098802 \\ -2.5482036 \\ 1.3952096 \\ -0.5149701 \\ -0.8802395 \\ 0.9901198 \\ 0.3404619 \\ 1.0547476 \\ \end{array}\right] \end{split} \]

Como nuestro modelo tenía dos efectos fijos, la media y el desvío del segundo rodeo respecto al primero, la primer fila indica la media general, mientras que la segunda fila nos indicará la media del rodeo $2$ (como desvío del “rodeo 1”). A partir de acá, el resto de las filas representarán los “niveles” de los efectos aleatorios: la tercer fila indica el valor de cría del animal $1$; la cuarta fila indica el valor de cría del animal $2$; la quinta fila indica el valor de cría del animal $3$; la sexta fila indica el valor de cría del animal $4$; la séptima fila indica el valor de cría del animal $5$; la octaba fila indica el valor de cría del animal $6$.

PARA RECORDAR

Un modelo mixto lineal es un modelo mixto que combina efectos fijos y efectos aleatorios:

Efectos fijos son aquellos que nos puede interesar contrastar sus niveles, que usualmente tienen pocos niveles y que en otros casos usaremos para compensar diferencias sistemáticas entre niveles. Normalmente, queremos estimar su valor.
Efectos aleatorios son efectos donde asumimos que los datos observados son una muestra aleatoria de una población mayor. Normalmente poseen muchos niveles y en general, el objetivo es predecir su valor ya que se trata de un efecto aleatorio.

El método BLUP (“Best Linear Unbiased Predictor”) implica que si poseemos información completa para $n$ animales (incluyendo su pedigree completo), que serán los que pretendemos evaluar, los efectos fijos serán codificados en una matrix $\mathbf{X}$, que tendrá tantas filas como individuos con fenotipo, es decir $n$ y tantas columnas como el número total de niveles de los factores considerados, menos el número de factores (para eliminar la dependencia lineal entre columnas). También en la matriz $\mathbf{X}$ se podrá incluir las covariables (variables continuas) que sean necesarias. Por otra parte, se considerarán por simplicidad solamente dos efectos aleatorios, el genético-aditivo de los individuos y el error. Teniendo en cuenta la matriz $\mathbf{A}$ de parentesco aditivo entre los individuos (que si no consideramos a los progenitores de los individuos con registros será de dimensiones $[n \times n]$). De tal manera que podemos describir el modelo mixto de forma matricial como:

13.7 Conclusión

En este capítulo hemos ahondado nuestros conocimientos sobre la metodología empleada para llevar a cabo el proceso de selección artificial de forma efectiva. En particular se ha tenido en cuenta el problema planteado en el capítulo anterior, la existencia de respuestas correlacionadas entre caracteres fenotípicos. La existencia de dicha correlación plantea cuestiones estratégicas al momento de seleccionar: ¿el órden de selección altera el producto obtenido? ¿Cómo podemos realizar el proceso de la forma más eficiente? Además de algunos métodos intuitivos (e.g., selección en tándem), hemos visto también cómo la aplicación de algunos resultados que pueden parecer más abstractos y matemáticamente complejos (como el teorema de Robertson-Price) pueden ser de suma utilidad para plantear una aproximación cuantitativa a estos problemas. Nuevamente la aproximación a través del modelado y la estadística resultan útiles en nuestro proceso de intentar entender y moldear la diversidad genética que observamos en la naturaleza, un mensaje central que es transversal a lo largo de las tres secciones de este libro.

13.8 Actividades

13.8.1 Control de lectura

Defina objetivos y criterio de selección. ¿Cuál es la diferencia entre ambos conceptos?
Agregar información fenotípica de varios individuos genéticamente relacionados permite realizar estimaciones más precisas del valor de cría de un individuo comparado a utilizar solo la información fenotípica de este. ¿A qué se debe esta mejora en la estimación?
¿En qué casos es necesaria la selección por parientes? ¿A qué se debe esta necesidad?
¿Cuándo es mejor la prueba de progenie que la selección fenotípica individual?
¿Qué métodos de selección multicaracter conoce? ¿Qué ventajas presenta cada uno?

13.8.2 ¿Verdadero o falso?

La prueba de progenie siempre brinda mejores resultados que la selección individual.
Con tamaño finito de progenies es necesario considerar el balance existente entre el número de candidatos a evaluar y el número de registros por candidato.
La precisión del valor de cría de una característica siempre es una función de la heredabilidad de la misma.
Los valores de cría (EBV) combinan varias características fenotípicas de un individuo a la vez.
Los índices de selección ponderan según el valor económico de cada característica contemplada.

Soluciones

Falso. Si bien las pruebas de progenie brindan la ventaja de que nos permiten obtener una mejor precisión al momento de hacer estimados, conllevan la desventaja de incrementar considerablemente el intervalo generacional. Esto puede implicar una disminución en el progreso genético anual obtenido. Por lo tanto, es necesario calcular los coeficientes de eficiencia a efectos de determinar qué método brinda un mayor progreso genético anual.
Verdadero. Trabajar con tamaños de progenie finitos implica que al aumentar el número de registros (hijos medidos) por candidato se disminuye el número de candidatos a evaluar. Esto disminuye la capacidad de ejercer presión selectiva, en tanto se seleccionan menos individuos. Por lo tanto, es necesario optimizar estas relaciones para obtener el mayor progreso genético posible.
Verdadero. [Aprovechar y bajar línea sobre por qué tiene sentido esto; intuitivamente tiene sentido: si tenés heredabilidad de cero la estimación que vas a poder hacer con fenotipo claramente está errada (se basa en efectos ambientales) y tiene precisión de cero, si en cambio la heredabilidad es de uno la estimación a partir de fenotipo se ve totalmente alineada con el valor de cría “real”, y por tanto la precisión total.]
Falso. El valor de cría de un individuo refiere siempre a una única característica fenotípica de interés. La estimación del mismo se realiza con datos fenotípicos de uno o varios individuos genéticamente relacionados, referentes a este caracter de interés.
Verdadero. En los índices de selección cada carácter o fuente de información (criterio de selección) considerado es ponderado a través de un coeficiente parcial de regresión que toma en cuenta los parámetros genéticos intervinientes (varianzas fenotípicas, heredabilidades, correlaciones genéticas y fenotípicas, y valor económico de aquellas características incluidas en el objetivo). Este coeficiente parcial de regresión define la importancia relativa de cada fuente de información. Para estimar el índice de selección se reúne la información de distintas fuentes y para distintos caracteres, finalmente logrando un solo valor para cada candidato. Los individuos son posteriormente ordenados según el valor de su índice, para luego elegir a los de mayor puntaje, como si se tratara de una sola característica. [Adaptado del “Manual de Práctica de Zootecnia” (Facultad de Agronomía, edición 2014)]

13.8.3 Ejercicios

Ejercicio 13.1

Se desea seleccionar 3 toros con el fin de mejorar el contenido de proteína de la leche en ganado Jersey y con este objetivo se plantea realizar una prueba de progenie utilizando hembras medias hermanas entre sí. Con este fin se manejan tres alternativas: probar 20, 30 o 50 candidatos. Sabiendo que la capacidad de medición es de 3000 hembras y que la heredabilidad de la característica es de $0,31$, ¿con qué alternativa se lograría el mayor progreso genético?

Solución

En primer lugar, debemos recordar que un aumento en el número de candidatos a probar implica una disminución en la proporción de los animales seleccionados lo que significa un aumento en la intensidad de selección. Sin embargo, al mismo tiempo, este aumento en el número de candidatos a probar implica una disminución del número de individuos medidos por candidato (menor $n$), por lo que no existe una respuesta evidente en cuanto a qué opción es más conveniente. Entonces, dado que el $IG$ no varía entre alternativas, deberemos evaluar cuál relación $i*r_{AC}$ es mayor, lo que implicará un mayor progreso genético.

Candidatos evaluados	p	i	n	$r_{AC}$	$i \cdot r_{AC}$
$20$	$3/20=0,15$	$1,5544$	$3000/20=150$	$0,963$	$1,497$
$30$	$3/30=0,10$	$1,7550$	$3000/30=100$	$0,945$	$1,469$
$50$	$3/50=0,06$	$1,9854$	$3000/50=60$	$0,913$	$1,419$

Como podemos notar, la alternativa que nos permite lograr el mayor progreso genético es evaluar 20 candidatos. Es decir, en este caso en particular, el aumento en la intensidad de selección, producto de probar más candidatos, no compensa la pérdida de exactitud por evaluar menos hijas por candidato.

Ejercicio 13.2

Un mago posee una población de conejos y tiene como objetivo mejorar el peso adulto ($h^2=0,38$) de los mismos ya que si son muy pequeños es más difícil sacarlos de la galera. La media poblacional actual es de $4,1$ kg, y para mejorarla en la próxima generación el mago ha evaluado dos animales como reproductores:

Conejo Cartas: el peso promedio de $7$ medios hermanos es $4,3 \text{ kg}$
Conejo Varita: el peso promedio de $3$ hermanos enteros es $4,4 \text{ kg}$

¿Qué animal seleccionaría como reproductor?

Solución

Para evaluar a estos animales como reproductores, deberemos calcular el valor de cría con cada uno con su correspondiente precisión.

\[\hat A_{cartas}=\frac{r_{AA'}\times n\times h^2}{1+(n-1)\times t}\times (\bar x_i- \mu)=\frac{\frac{1}{4}\times 7\times 0,38}{1+(7-1)\times \frac{1}{4}\times 0,38}\times (4,3-4,1)=0,08 \text{kg}\] \[r_{AC_{cartas}}=r_{AA'}\times h\times \sqrt{\frac{n}{1+(n-1)\times t}}=\frac{1}{4}\times \sqrt{0,38}\times \sqrt{\frac{7}{1+(7-1)\times \frac{1}{4}\times 0,38}}=0,325\] \[\hat A_{varita}=\frac{r_{AA'}\times n\times h^2}{1+(n-1)\times t}\times (\bar x_i- \mu)=\frac{\frac{1}{2}\times 3\times 0,38}{1+(3-1)\times \frac{1}{2}\times 0,38}\times (4,4-4,1)=0,12 \text{kg}\] \[r_{AC_{varita}}=r_{AA'}\times h\times \sqrt{\frac{n}{1+(n-1)\times t}}=\frac{1}{2}\times \sqrt{0,38}\times \sqrt{\frac{3}{1+(3-1)\times \frac{1}{2}\times 0,38}}=0,454\]

El valor de cría del conejo varita es superior, al igual que la precisión del mismo, por lo tanto será el animal seleccionado por el mago para utilizar como reproductor.

Ejercicio 13.3

En una población de bovinos se tiene como objetivo mejorar el tamaño del músculo del lomo ya que el frigorífico estaría dispuesto a pagar un sobreprecio en los animales que muestren un mayor tamaño del mismo. Dado que es una característica cuya medición implica el sacrificio de los animales, se propone medir a 18 medios hermanos (medios hermanos entre sí) de los candidatos a la selección. Se ha determinado a la vez que la $h^2=0,33$ y que la varianza aditiva de la característica es $\sigma^2=0,8$. Por otra parte, la proporción de machos seleccionados es del 20% mientras que no se realiza selección en las hembras.

¿Cuál es el progreso genético generacional logrado en estas condiciones?

Solución

Recordemos en primer lugar la fórmula de progreso genético generacional:

\[\text{PGG}=i\times r_{AC}\times \sigma_A\]

En primer lugar, podremos despejar la intensidad de selección a partir de la información de la proporción de animales seleccionados:

\[p=20% \implies i = 1,3998\]

\[i=\frac{i_m+i_h}{2}=\frac{1,3998+0}{2}=0,6999 \]

A continuación deberemos calcular la exactitud $r_{AC}$ y el desvío aditivo:

$r_{AC}=r_{AA'}\times h\times \sqrt{\frac{n}{1+(n-1)\times t}}=\frac{1}{4}\times \sqrt{0,33}\times \sqrt{\frac{18}{1+(18-1)\times \frac{1}{4}\times 0,33}}=0,3931$

\[\sigma_A=\sqrt{\sigma^2_A}=\sqrt{0,8}=0,8944\]

Por último podremos aplicar la fórmula de PGG:

\[\text{PGG}=0,6999 \times 0,3931 \times 0,8944 = 0,246\]

Es decir que por generación, se podrá aumentar en 0,246 kg el peso del músculo del lomo.

Ejercicio 13.4

(Adaptado de Miglior, Muir, and Van Doormaal 2005)

En una revisión del año 2005 Miglior y colaboradores (Miglior, Muir, and Van Doormaal 2005) analizaron los índices de selección de utilizados para producción con ganado bovino de la raza Holstein de quince países elegidos por posición geográfica, tamaños de las poblaciones productivas consideradas y otros aspectos de relevancia

A continuación se muestra una selección de algunas de estas características en tres países (Dinamarca, Estados Unidos e Israel)

	$\text{Índice}$	$\text{Prod. leche}$	$\text{Prod. grasa}$	$\text{Prod. proteína}$	$\text{Longevidad}$	$\text{Tamaño corporal}$	$\text{Fertilidad}$
$\text{Dinamarca}$	$\text{S-index}$	$-8,4$	$1,2$	$2,4$	$6,0$	$-2,0$	$9,0$
$\text{Estados Unidos}$	$\text{TPI/Net Merit}$	$-6,0$	$18,0$	$36,0$	$4,0$	$-3,0$	$7,0$
$\text{Israel}$	$\text{PD01}$	$-11,0$	$18,0$	$51,0$	$11,0$	$-2,5$	$9,0$

Nota: la fertilidad constituye un índice en sí (índice de fertilidad), el cual pondera variables relacionadas a la capacidad de dejar progenie de una vaca.

a. Un individuo que presenta las siguientes características

	$\text{Prod. leche}$	$\text{Prod. grasa}$	$\text{Prod. proteína}$	$\text{Longevidad}$	$\text{Tamaño corporal}$	$\text{Fertilidad}$
$\text{Vaca}_1$	$27,5 \text{ L/día}$	$1,17 \text{ kg/día}$	$0,98 \text{ kg/día}$	$18 ext{años}$	$615 ext{ kg}$	$6$

Calcule el índice de selección en cada país.

b. ¿A qué atribuye las diferencias observadas? ¿Esperaría que un índice de selección uruguayo sea igual a alguno de los presentados?

Solución

a. Para calcular el índice de selección en cada país realizaremos una combinación lineal de los valores presentados para la $\text{Vaca}_1$ y los pesos dados en cada índice de selección según la primera tabla. Es decir, para calcular el índice índice de selección operamos según

\[I = w_1 \times x_1 + w_2 \times x_2 + \ldots + w_n \times x_nI\]

donde $w_i$ son los pesos dados y $x_i$ son los valores fenotípicos de la vaca.

Tenemos entonces

\[I_{\text{Dinamarca}} = (-8,4 \times 27,5) + (1,2 \times 1,17) + (2,4 \times 0,98) + (6,0 \times 18) + (-2,0 \times 615) + (9,0 \times 6) = -1295,244\] \[I_{\text{Estados Unidos}} = (-6,0 \times 27,5) + (18,0 \times 1,17) + (36,0 \times 0,98) + (4,0 \times 18) + (-3,0 \times 615) + (7,0 \times 6) = -1839,66\] \[I_{\text{Israel}} = (-11,0 \times 27,5) + (18,0 \times 1,17) + (51,0 \times 0,98) + (11,0 \times 18) + (-2,5 \times 615) + (9,0 \times 6) = -1516,96\]

Aclaración: Tener presente que, a efectos de simplificar el ejercicio, no se utilizaron todas las componentes contempladas en cada índice de selección; esto puede explicar el por qué se obtuvieron valores negativos.

b. Notemos que existen diferencias sustanciales en los valores de índice de selección: la diferencia entre el valor obtenido según el índice estadounidense y el danés es de $\approx 600$, que es cerca de la mitad del valor estimado con este último. Es importante recordar que cada índice pondera en base a las necesidades que plantea el mercado de cada país, por lo que es de esperar que lugares con culturas y mercados tan disímiles den importancias diferentes a iguales características fenotípicas. En principio es razonable esperar, por lo tanto, que un índice uruguayo también muestre diferencias. Además, debe contemplarse que este estudio es de hace 20 años (al momento de publicación de este libro), por lo que incluso los índices actuales empleados en cada país pueden variar actualmente.

Bibliografía

2000. http://nitro.biosci.arizona.edu/zdownload/Volume2/Chapter23.pdf.

Falconer, Douglas S, and Trudy FC Mackay. 1996. Quantitative Genetics. Benjamin-Cummings Pub Co.

Henderson, C. R., and R. L. Quaas. 1976. “Multiple Trait Evaluation Using Relatives’ Records.” Journal of Animal Science 43 (6): 1188–97. https://doi.org/10.2527/jas1976.4361188x.

Henderson, Charles Roy. 1949. “Estimation of Changes in Herd Environment.” Journal of Dairy Science 32: 706.

———. 1950. “Estimation of Genetic Parameters.” Ann Math Stat 21: 309–10.

———. 1959. “The Estimation of Environmental and Genetic Trends from Records Subject to Culling.” Biometrics 15 (2): 192–218.

Miglior, F., B. L. Muir, and B. J. Van Doormaal. 2005. “Selection Indices in Holstein Cattle of Various Countries.” Journal of Dairy Science 88 (3): 1255–63. https://doi.org/10.3168/jds.s0022-0302(05)72792-2.

Werf, Julius van der. 2000. “Genetic Evaluation and Breeding Program Design.” https://jvanderw.une.edu.au/gene422.htm.

\(\text{Alternativa}\)	\(i\)	\(r_{AC}\)	\(IG\)	\(\frac{i \times r_{AC}}{IG}\)
Medir 5 medio-hermanas	\(1,03\)	\(0,228\)	\(4,3\)	\(0,055\)
Medir 10 medio-hermanas	\(0,88\)	\(0,294\)	\(4,3\)	\(0,060\)
Medir 20 medio-hermanas	\(0,70\)	\(0,358\)	\(4,3\)	\(0,058\)
Medir 30 medio-hermanas	\(0,58\)	\(0,391\)	\(4,3\)	\(0,053\)
Medir 5 hijas	\(1,03\)	\(0,456\)	\(6,3\)	\(0,075\)
Medir 10 hijas	\(0,88\)	\(0,587\)	\(6,3\)	\(0,082\)
Medir 20 hijas	\(0,70\)	\(0,716\)	\(6,3\)	\(0,080\)
Medir 30 hijas	\(0,58\)	\(0,782\)	\(6,3\)	\(0,072\)

Componente.observacional	Varianza.Aditiva	Varianza.Fenotípica
Entre familias \({\sigma^2_B}\)	\({r\ V_A}\)	\({t\ V_P}\)
Dentro de familias \({\sigma^2_W}\)	\({(1-r)\ V_A}\)	\({(1-t)\ V_P}\)

Varianza observada	Componentes observacionales	Aditiva (causal)	Fenotípica (causal)
\(\text{de medias familiares } \sigma^2_f\)	\(\sigma^2_B + \frac{1}{n} \sigma^2_W\)	\(\frac{1+(n-1)r}{n}\ V_A\)	\(\frac{1+(n-1)t}{n}\ V_P\)
\(\text{desvíos intrafamiliares } \sigma^2_w\)	\(\sigma^2_W - \frac{1}{n} \sigma^2_W\)	\(\frac{(n-1)(1-r)}{n}\ V_A\)	\(\frac{(n-1)(1-t)}{n}\ V_P\)

Caravana Borrego	\(I_e\)	Caravana Padre	\(I_e\)
\(\text{J117}\)	\(-17\)	\(\text{H034}\)	\(-11\)
\(\text{J432}\)	\(11\)	\(\text{F404}\)	\(4\)
\(\text{J521}\)	\(-7\)	\(\text{G009}\)	\(1\)
\(\text{J707}\)	\(4\)	\(\text{E009}\)	\(13\)

Caravana Borrego	\(I_e\)	\(I_e\text{ Padre}\)	\(b_{ind}\ z_{ind}\)	\(b_{pro}\ z_{pro}\)	EBV
\(\text{J117}\)	\(-17\)	\(-11\)	\(-7,93\)	\(-1,47\)	\(-9,4\)
\(\text{J432}\)	\(11\)	\(4\)	\(5,13\)	\(0,53\)	\(5,7\)
\(\text{J521}\)	\(-7\)	\(1\)	\(-3,26\)	\(0,13\)	\(-3,1\)
\(\text{J707}\)	\(4\)	\(13\)	\(1,87\)	\(1,73\)	\(3,6\)

Toro	Leche		Grasa		Proteína		\(\text{cs}^1\)		\(\text{THP}^2\)		\(\text{Índice de selección}^3\)
\(\text{}\)	\(\text{DEP}^4\)	\(r_{AC}\)	\(\text{DEP}^4\)	\(r_{AC}\)	\(\text{DEP}^4\)	\(r_{AC}\)	\(\text{DEP}^4\)	\(r_{AC}\)	\(\text{DEP}^4\)	\(r_{AC}\)	\(\text{}\)
\(\text{HOLDNKM000000260548}\)	\(57\)	\(0,59\)	\(12,8\)	\(0,57\)	\(13,2\)	\(0,57\)	\(-0,50\)	\(0,62\)	\(0,67\)	\(0,56\)	\(51,75\)
\(\text{HOL840M003147224052}\)	\(288\)	\(0,58\)	\(19,6\)	\(0,57\)	\(17,5\)	\(0,57\)	\(-0,49\)	\(0,60\)	\(-0,42\)	\(0,58\)	\(50,30\)
\(\text{HOLNLDM000580616806}\)	\(31\)	\(0,60\)	\(10,1\)	\(0,59\)	\(9,4\)	\(0,59\)	\(-0,62\)	\(0,63\)	\(-1,21\)	\(0,60\)	\(45,90\)
\(\text{HOLFRAM002933738576}\)	\(48\)	\(0,63\)	\(18,2\)	\(0,62\)	\(8,9\)	\(0,62\)	\(-0,35\)	\(0,67\)	\(-0,82\)	\(0,64\)	\(36,42\)
\(\text{HOLNLDM000694388754}\)	\(154\)	\(0,62\)	\(15,4\)	\(0,61\)	\(11,5\)	\(0,62\)	\(-0,36\)	\(0,67\)	\(-2,85\)	\(0,65\)	\(33,78\)
\(\text{HOL840M003150687270}\)	\(328\)	\(0,56\)	\(17,7\)	\(0,55\)	\(17,6\)	\(0,55\)	\(-0,04\)	\(0,58\)	\(0,23\)	\(0,57\)	\(30,93\)
\(\text{HOLCANM000012529241}\)	\(308\)	\(0,59\)	\(21,0\)	\(0,59\)	\(14,5\)	\(0,59\)	\(-0,10\)	\(0,65\)	\(-1,85\)	\(0,59\)	\(25,69\)

Animal	Padre	Madre	Rodeo	Peso.al.destete
\(1\)			\(1\)	\(185\)
\(2\)			\(1\)	\(180\)
\(3\)			\(2\)	\(175\)
\(4\)	\(1\)	\(2\)	\(1\)	\(188\)
\(5\)	\(1\)	\(3\)	\(2\)	\(182\)
\(6\)	\(1\)	\(3\)	\(2\)	\(187\)

Candidatos evaluados	p	i	n	\(r_{AC}\)	\(i \cdot r_{AC}\)
\(20\)	\(3/20=0,15\)	\(1,5544\)	\(3000/20=150\)	\(0,963\)	\(1,497\)
\(30\)	\(3/30=0,10\)	\(1,7550\)	\(3000/30=100\)	\(0,945\)	\(1,469\)
\(50\)	\(3/50=0,06\)	\(1,9854\)	\(3000/50=60\)	\(0,913\)	\(1,419\)

	\(\text{Índice}\)	\(\text{Prod. leche}\)	\(\text{Prod. grasa}\)	\(\text{Prod. proteína}\)	\(\text{Longevidad}\)	\(\text{Tamaño corporal}\)	\(\text{Fertilidad}\)
\(\text{Dinamarca}\)	\(\text{S-index}\)	\(-8,4\)	\(1,2\)	\(2,4\)	\(6,0\)	\(-2,0\)	\(9,0\)
\(\text{Estados Unidos}\)	\(\text{TPI/Net Merit}\)	\(-6,0\)	\(18,0\)	\(36,0\)	\(4,0\)	\(-3,0\)	\(7,0\)
\(\text{Israel}\)	\(\text{PD01}\)	\(-11,0\)	\(18,0\)	\(51,0\)	\(11,0\)	\(-2,5\)	\(9,0\)