Capítulo 5 Dinámica de 2 loci
En los capítulos anteriores hemos sentado las bases matemáticas del análisis de la evolución de las frecuencias alélicas en la poblaciones, considerando tanto los fenómenos sistemáticos como los estocásticos. Sin embargo, hasta el momento nuestro modelo fue simplificado en extremo y el tratamiento quedó reducido casi siempre a un locus con un par de alelos. En principio, podríamos pensar que para el tratamiento de más loci alcanzaría con considerar para cada uno de ellos un modelo como el de un locus con dos alelos, como los que hemos trabajado. Eso significaría que nuestros loci son todos independientes unos de otros. Desafortunadamente para el modelado matemático, aunque afortunadamente para nosotros, la meiosis produce un barajado de los alelos en diferentes loci, el cual que puede ocurrir en varios puntos del genoma. Obviamente, la probabilidad de que esos eventos discretos que producen el intercambio de cromátidas ocurran entre dos loci en particular es una función de la distancia de mapeo entre ellos (cuanto mayor es dicha distancia, mayor la probabilidad de que ese evento ocurra entre los dos loci).
Es momento entonces de comenzar a extender nuestros modelos a la interacción con otro locus cercano y analizar el tipo de dinámicas que pueden surgir de esta interacción. En general, aún los modelos más simplificados de interacción entre dos loci agregan una complejidad importante al análisis, por lo que nos limitaremos a tratar analíticamente los casos más sencillos, mientras que recurriremos a aproximaciones basadas en el modelado computacional en aquellos casos que se complique más allá de nuestras posibilidades. Una nota de advertencia antes de empezar: gran parte del material de este capítulo se encuentra basado en el libro de John H. Gillespie (John H. Gillespie 2004), que es uno de los pocos textos que lo trata como un tema mereciendo un capítulo, la mayoría de ellos apenas considerándolo en alguna sección. Si bien la decisión de qué temas tratar y su profundidad es algo arbitraria, las posibles consecuencias evolutivas de los fenómenos asociados no son despreciables y por lo tanto entendimos que merece este tratamiento preferencial.
OBJETIVOS DEL CAPÍTULO
\(\square\) Introducir el concepto de desequilibrio de ligamiento entre loci y discutir su relevancia biológica.
\(\square\) Plantear un modelo para la relación entre el desequilibrio de ligamiento y la tasa de recombinación \(r\) entre dos loci, así como su evolución en el tiempo.
\(\square\) Presentar medidas para determinar la significancia del desequilibrio de ligamiento entre dos loci, analizando las ventajas y desventajas de los mismos.
\(\square\) Analizar la relación entre selección y desequilibrio de ligamiento. Se planteará un modelo matemático explícito para un caso sencillo: selección en un locus e impacto en el desequilibrio de ligamiento con un segundo locus neutral.
\(\square\) Discutir diferentes escenarios biológicos, además de la proximidad física, que pueden dar como resultado el desequilibrio de ligamiento entre dos o más loci.
5.1 Desequilibrio de ligamiento y recombinación
En los organismos diploides y con ploidías mayores, durante la meiosis se produce un fenómeno fundamental para la evolución: la recombinación. Este proceso se encuentra esquematizado en la Figura 5.1. En los organismos diploides todas las células nucleadas, con excepción de los gametos, cuentan con una dotación aproximadamente duplicada, la mitad proveniente de la hembra y la otra mitad del macho. Como recordarás del curso de Genética I, durante la meiosis I ocurre ocasionalmente (frecuentemente) la unión física de los cromosomas homólogos en algunos puntos (e.g., en mamíferos usualmente en el orden del número de brazos cromosómicos) llamados quiasmas y mediante un proceso complejo se produce un intercambio entre cromátidas no-hermanas. Esto lleva a combinar de una manera diferente los alelos respecto a su arreglo original hembra-macho, existiendo ahora fragmentos de uno y de otro en los gametos recombinados.
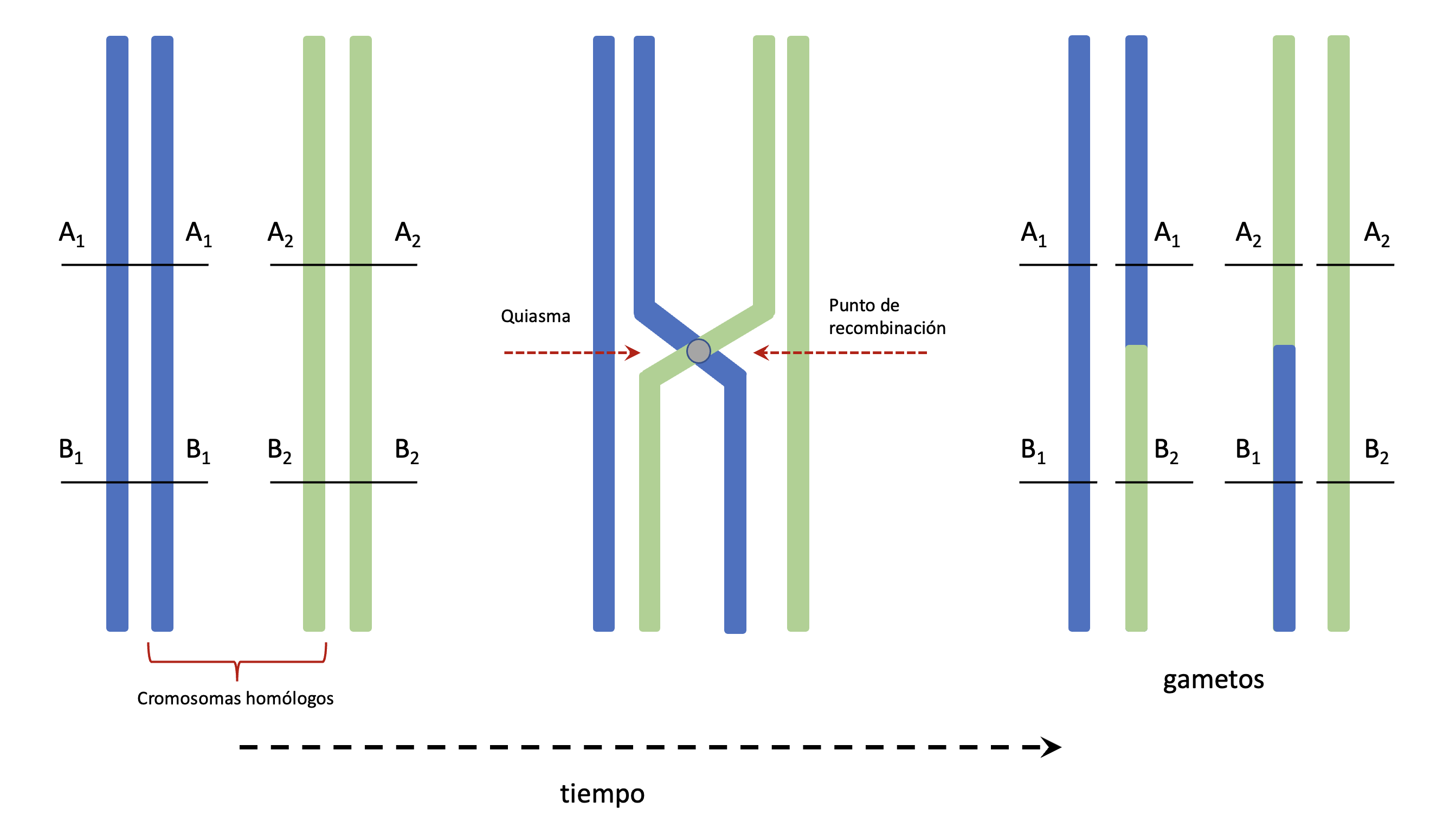
Figura 5.1: Proceso de recombinación durante la meiosis. Durante la meiosis los cromosomas homólogos se aparean y se dan intercambios entre crómatidas no-hermanas, a partir de una unión física de los mismos llamada quiasma. En esta representación dos loci, A y B, se encuentran a los lados del punto de recombinación. Los alelos son para cada uno de ellos dos posibles (alelos \(1\) en azul, alelos \(2\) en verde). Luego de finalizada la meiosis contamos con 4 gametos haploides, en nuestro caso dos recombinantes y dos idénticos a los parentales..
Este es un proceso aleatorio y los lugares donde ocurren los quiasmas también lo son, aunque no necesariamente con la misma probabilidad para cada punto o región del genoma. La importancia evolutiva de este fenómeno es evidente: la posibilidad de combinar en diferentes formas alelos beneficiosos surgidos en diferentes lugares del mismo cromosoma nos aporta tanto en el efecto aditivo de los mismos como en el efecto agregado de la combinación; este último (estadísticamente el efecto de la interacción entre loci), es desde el punto de vista genético la epistasis, algo que veremos en el capítulo El Modelo Genético Básico.
En la Figura 5.2 se presenta el modelo simplificado con el que vamos a trabajar en la mayor parte de este capítulo.
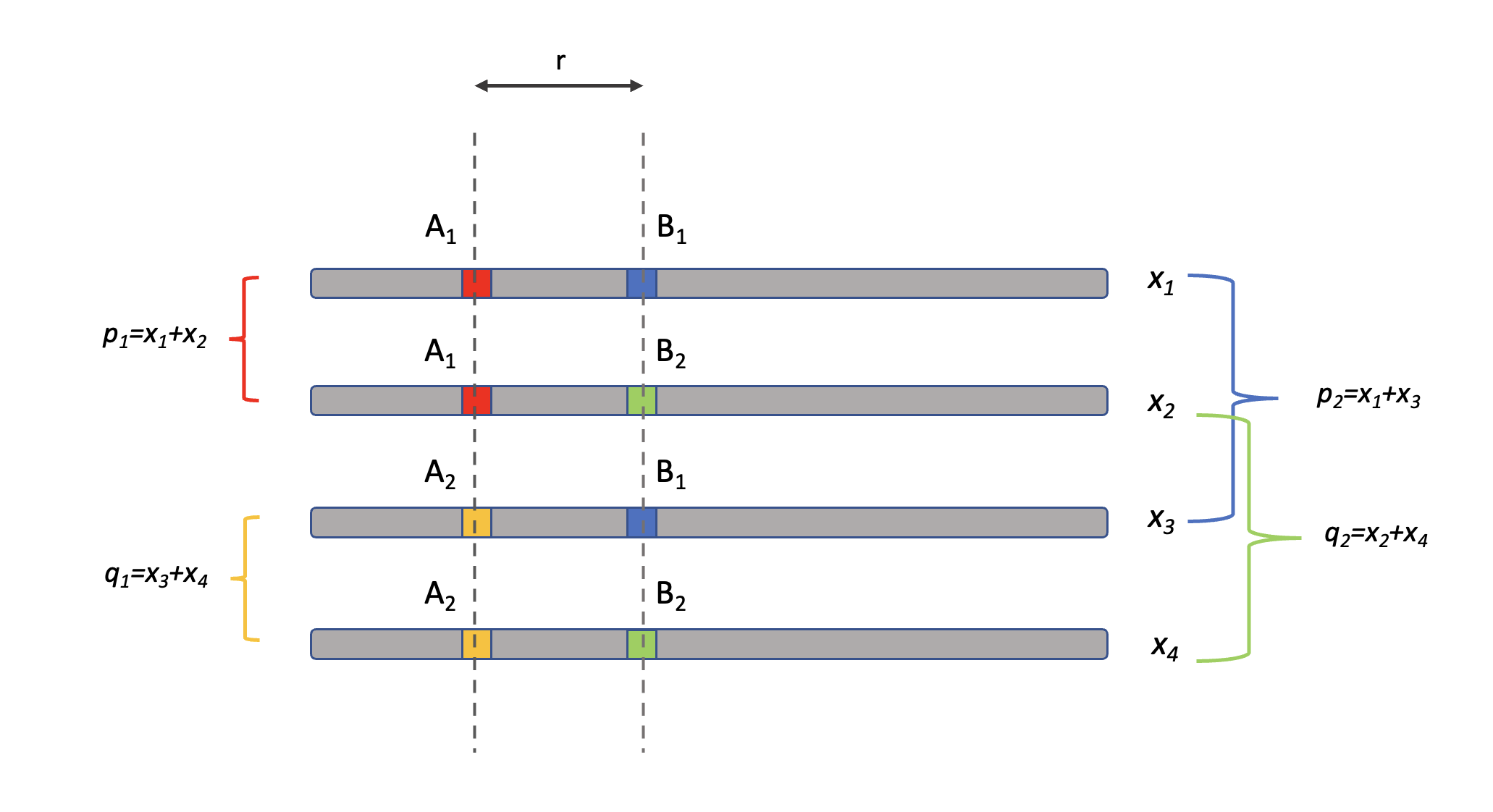
Figura 5.2: Modelo de dos loci con dos alelos cada uno. Las frecuencias de las 4 combinaciones posibles aparecen a la derecha. Los gametos que aparecen en fase de acoplamiento son el 1 y el 4, mientras que el 2 y 3 están en fase de repulsión. El parámetro \(r\) es la probabilidad de producir un gameto recombinante por meiosis. \(p_1=x_1+x_2\) es la frecuencia del alelo \(A_1\) en el primer locus, mientras que \(p_2=x_1+x_3\) es la frecuencia del alelo \(B_1\), en el segundo locus.
Tenemos dos loci que asumimos en un principio relativamente cerca en el mismo cromosoma. El primer locus que denotaremos con la letra \(A\) tiene dos alelos, \(A_1\) y \(A_2\), con frecuencias \(p_1\) y \(q_1=1-p_1\). El segundo locus, que llamaremos \(B\), tiene también dos alelos, \(B_1\) y \(B_2\), con frecuencias \(p_2\) y \(q_2=1-p_2\). Notar que el subíndice en las frecuencias se refiere al locus, mientras que usamos las letras \(p\) y \(q\) para los alelos existentes en cada locus.
A las frecuencias de los \(2\)x\(2=4\) gametos posibles las denominamos \(x_1\) (gameto \(A_1B_1\)), \(x_2\) (gameto \(A_1B_2\)), \(x_3\) (gameto \(A_2B_1\)) y \(x_4\) (gameto \(A_2B_2\)), de modo que \(x_1+x_2+x_3+x_4=1\). A la fracción de gametos recombinantes en la meiosis le llamamos \(r\), con \(0 \leqslant r \leqslant \frac{1}{2}\). Si bien en teoría \(r\) puede ser mayor a \(0,50\) (si la recombinación ocurre en los dos pares de cromátidas no-hermanas), se trataría de un fenómeno bastante infrecuente y de ahí la restricción. Más aún, en este capítulo vamos a despreciar la posibilidad de los dobles recombinantes. Si bien es una aproximación, la misma es razonable ya que vamos a trabajar básicamente con loci a relativamente poca distancia. A los gametos que poseen los mismos subíndices en los dos loci los llamamos gametos en fase de acoplamiento y a los que poseen distintos subíndices los llamamos en fase de repulsión. Tengamos en cuenta que se trata de una distinción arbitraria y simplemente la tomamos para poder describir mejor nuestro modelo, pero en la realidad no existe tal distinción (los alelos no tienen subíndices en la realidad, y a cuál de ellos le asignamos el 1 y a cuál el 2 es completamente arbitrario).
Como vemos en la Figura 5.2, la frecuencia de los gametos \(A_1B_1\) está definida por \(x_1\). Si entre los dos loci no existiese ningún tipo de asociación física ni estadística (i.e., si no estuviesen ligados) o se encontrasen en equilibrio de ligamiento, entonces la probabilidad de obtener un gameto \(A_1B_1\) sería simplemente el producto de tener un alelo \(A_1\) multiplicado por la probabilidad de tener un \(B_1\), es decir \(x_1=p_1p_2\) (recordar que \(p_1\) es la frecuencia de \(A_1\) y \(p_2\) es la frecuencia de \(B_1\)). Como ya sabemos, si nuestros loci se encuentran en el mismo cromosoma la probabilidad de que ocurra un “crossover” entre ellos, y por lo tanto una recombinación, no es en general despreciable, pero claramente también existe la probabilidad de que ello no ocurra y que por lo tanto vayan a los gametos en la configuración existente en la generación actual.
Veamos ahora cómo podemos expresar la frecuencia del gameto \(A_1B_1\) en la siguiente generación, después de una ronda de apareamiento al azar, en función de la frecuencia en la generación anterior. Existen dos posibilidades mutuamente excluyentes para que en la nueva generación aparezca un gameto \(A_1B_1\): a) que se trate de gametos \(A_1B_1\) en la generación previa y que no recombinaron (con probabilidad \((1-r) x_1\)), y b) que se trate de un evento de recombinación (con probabilidad \(r\)) que arroje \(A_1B_1\) (cuya probabilidad es \(p_1p_2\)); como dichos eventos son independientes, su probabilidad conjunta es \(rp_1p_2\). Poniendo en conjunto las consideraciones de los escenarios a) y b), tenemos que la probabilidad de \(A_1B_1\) en la generación siguiente (que llamaremos \(x'_1\)) es
\[\begin{equation} x'_1=(1-r)x_1+rp_1p_2 \tag{5.1} \end{equation}\]
Claramente, aplicando la misma lógica, las ecuaciones para el resto de las combinaciones de alelos serán
\[ \begin{split} x'_2=(1-r)x_2+rp_1q_2\\ x'_3=(1-r)x_3+rq_1p_2\\ x'_4=(1-r)x_4+rq_1q_2 \end{split} \tag{5.2} \]
En palabras, la lógica que siguen estas ecuaciones es: a la fracción del mismo gameto que no recombinó le sumamos la proporción de recombinantes del producto de los alelos que forman el gameto.
Veamos ahora qué ocurre con el cambio de frecuencia del gameto \(A_1B_1\). La nueva frecuencia es \(x'_1\) y la anterior \(x_1\), por lo que sustituyendo el resultado de (5.1), la diferencia será
\[ \begin{split} \Delta_r x_1=x'_1-x_1=(1-r)x_1+rp_1p_2-x_1= x_1 -rx_1 + rp_1p_2 - x_1 \Leftrightarrow \\ \Delta_r x_1=-r(x_1-p_1p_2) \end{split} \tag{5.3} \]
Esta formulación nos permite una primera definición del desequilibrio de ligamiento
\[\begin{equation} D=x_1-p_1p_2 \tag{5.4} \end{equation}\]
cuya lógica es sencilla: la diferencia entre la frecuencia real del gameto \(A_1B_1\) y la frecuencia esperada si los dos loci fuesen independientes (que es el producto de la frecuencia de los alelos \(A_1\) y \(B_1\), \(p_1\) y \(p_2\)). Sustituyendo en la ecuación (5.3) la definición de \(D\), tenemos ahora
\[\begin{equation} \Delta_r x_1=-rD \tag{5.5} \end{equation}\]
La interpretación de esta ecuación es intuitiva: la frecuencia de los gametos en fase de acoplamiento disminuirá en proporción al producto de la fracción de recombinación y del desequilibrio de ligamiento. Por lo tanto, la diferencia respecto a lo esperado bajo independencia irá disminuyendo en cada generación. Otra forma sencilla de verlo es la siguiente. En el equilibrio, no habrá más cambios en la frecuencia de los gametos de generación a generación, o lo que es lo mismo \(\Delta_r x_1=-rD=0\). Excepto el caso trivial de \(r=0\) (i.e., en ausencia de recombinación), \(\Delta_r x_1=0 \Leftrightarrow D=0\), o lo que es lo mismo
\[\begin{equation} D=0 \Leftrightarrow x_1-p_1p_2=0 \Leftrightarrow x_1=p_1p_2 \tag{5.6} \end{equation}\]
Es decir, la condición de equilibrio es que la frecuencia del gameto (en este caso \(A_1B_1\), con frecuencia \(x_1\)), sea igual al producto de las frecuencias de los alelos que lo componen, en nuestro caso \(A_1\) (frecuencia \(p_1\)) y \(B_1\) (frecuencia \(p_2\)).
Si trabajamos sobre la ecuación (5.4), podemos ahora definir la frecuencia del gameto \(A_1B_1\) como
\[\begin{equation} x_1=p_1p_2+D \tag{5.7} \end{equation}\]
Es decir, la frecuencia de cada gameto será lo esperado de las frecuencias de los alelos que lo conforman (en este caso \(A_1\) y \(B_1\)), más el aporte del desequilibrio de ligamiento \(D\). Naturalmente este concepto se puede extender a los otros gametos, por lo que las frecuencias serán
\[ \begin{split} x_1 = p_1q_1+D \\ x_2=p_1q_2-D \\ x_3=q_1p_2-D \\ x_4=q_1q_2+D \end{split} \tag{5.8} \]
El signo negativo para \(D\) en los gametos que están en fase de repulsión se explica porque el exceso de los gametos que están en fase de acoplamiento debe provenir de algún lado.
Para entender mejor la relación entre los gametos en fases de acoplamiento y repulsión con el desequilibrio de ligamiento, veamos si podemos probar la siguiente conjetura
\[\begin{equation} D=x_1x_4-x_2x_3 \tag{5.9} \end{equation}\]
En palabras, nuestra conjetura es que el desequilibrio de ligamiento es igual al producto de las frecuencias de los gametos en fase de acoplamiento menos el producto de las frecuencias de los gametos en fase de repulsión. Para probarlo, podemos igualar la expresión de la ecuación (5.9) con nuestra anterior definición en función de \(x_1\), como aparece en la ecuación (5.4)
\[\begin{equation} D=x_1x_4-x_2x_3\overset{?}{=}x_1-p_1p_2=D \tag{5.10} \end{equation}\]
Si recordamos que \(p_1=x_1+x_2\) y que \(p_2=x_1+x_3\), reemplazando en la expresión \(x_1 - p_1p_2\), llegamos a que
\[\begin{equation} x_1-p_1p_2=x_1-(x_1+x_2)(x_1+x_3)=x_1-x_1^2-x_1x_3-x_1x_2-x_2x_3 \tag{5.11} \end{equation}\]
Si sacamos factor común \(x_1\) en esta última expresión, tenemos
\[\begin{equation} x_1-x_1^2-x_1x_3-x_1x_2-x_2x_3=x_1(1-x_1-x_2-x_3)-x_2x_3 \tag{5.12} \end{equation}\]
Como la suma de frecuencias de los gametos debe ser igual a uno (i.e., \(x_1+x_2+x_3+x_4=1\)), tenemos que \(x_4=1-x_1-x_2-x_3\). Sustituyendo en la ecuación (5.12) los términos entre paréntesis, tenemos
\[\begin{equation} x_1(1-x_1-x_2-x_3)-x_2x_3=x_1x_4-x_2x_3 \tag{5.13} \end{equation}\]
Es decir, hemos probado la conjetura de la ecuación (5.10) y por lo tanto se confirma la validez de plantear
\[\begin{equation} D=x_1x_4-x_2x_3 \tag{5.14} \end{equation}\]
Veamos si este resultado nos sirve para verificar alguna de las ecuaciones que aparecen en (5.8), la primera de ellas, por ejemplo. Si sustituimos en la misma \(D=x_1x_4-x_2x_3\) y utilizamos algunas de las identidades planteadas anteriormente, tenemos
\[x_2=p_1q_2-D=p_1q_2-x_1x_4+x_2x_3=(x_1+x_2)(x_2+x_4)-x_1x_4+x_2x_3\] \[\begin{equation} x_2=x_1x_2+x_2^2+ x_1x_4 +x_2x_4 - x_1x_4 +x_2x_3=x_2(x_1+x_2+x_3+x_4) \tag{5.15} \end{equation}\]
Y recordando que \(x_1+x_2+x_3+x_4=1\), entonces
\[\begin{equation} x_2=x_2 \cdot (x_1+x_2+x_3+x_4)=x_2 \cdot (1)=x_2 \tag{5.16} \end{equation}\]
que es lo que queríamos verificar. El procedimiento es el mismo para el resto de las ecuaciones.
Resumiento, las formas de expresar las frecuencias de los gametos en función de \(p_i\), \(q_i\) y \(D\) aparecen en el siguiente cuadro que resume las ecuaciones (5.7) y (5.8).
| Gametos | \(A_1B_1\) | \(A_1B_2\) | \(A_2B_1\) | \(A_2B_2\) |
|---|---|---|---|---|
| $ $ (\(D\)) | \(p_1p_2+D\) | \(p_1q_2-D\) | \(q_1p_2-D\) | \(q_1q_2+D\) |
Puesto en conjunto con la ecuación (5.14), los resultados del cuadro anterior nos confirman que cuando \(D\) es positivo el desequilibrio de ligamiento produce un exceso de gametos en fase de acoplamiento respecto a lo esperado si no existiese ese ligamiento. Este exceso debe compensarse con un déficit de gametos en fase de repulsión. Cuando \(D\) es negativo, se trata de la situación inversa (recordar que la definición de que pares de gametos consideramos en en fase de acoplamiento o en en fase de repulsión es algo completamente arbitrario a nivel molecular).
El otro resultado importante que se desprende del cuadro es el que tiene que ver con los máximos y mínimos para \(D\). Como \(x_i \geqslant 0\) para todos los \(i \in {1 \cdots 4}\) ya que son la frecuencias de los gametos, entonces
\[0 \leqslant x_1=p_1p_2+D \Leftrightarrow D \geqslant -p_1p_2\] \[0 \leqslant x_2=p_1q_2-D \Leftrightarrow D \leqslant p_1q_2\] \[0 \leqslant x_3=q_1p_2-D \Leftrightarrow D \leqslant q_1p_2\] \[\begin{equation} 0 \leqslant x_4=q_1q_2+D \Leftrightarrow D \geqslant -q_1q_2 \tag{5.17} \end{equation}\]
Los resultados de (5.17) implican que, agrupándolos por condición,
\[\begin{equation} \begin{cases} D_\text{mín}=\text{máximo}(-p_1p_2,-q_1q_2) \\ D_\text{máx}=\text{mínimo}(p_1q_2,q_1p_2) \end{cases} \tag{5.18} \end{equation}\]
Claramente, \(D_\text{máx}\) y \(D_\text{mín}\) dependen ambas de las frecuencias de los alelos, \(p_1\) y \(p_2\), que son específicas a cada situación. Sin embargo, podríamos variar \(p_1\)y \(p_2\) a nuestro antojo para ver cuáles son el máximo y el mínimo teóricos de \(D\). La función bivariada (porque depende de \(p_1\) y \(p_2\)) para \(D_\text{máx}\) tiene un máximo cuando \(p_1=\frac{1}{2}=q_1;\ p_2=\frac{1}{2}=q_2\) y el valor es entonces \(D_\text{máx}=0,25\), como se aprecia en la Figura 5.3. A su vez, para \(D_\text{mín}\) su valor mínimo teórico es también cuando \(p_1=\frac{1}{2}=q_1;\ p_2=\frac{1}{2}=q_2\) y equivale a \(D_\text{mín}=-0,25\). En palabras, el valor absoluto del desequilibrio de ligamiento puede ser máximo cuando las frecuencias de los dos alelos equivalen a \(0,5\) en ambos loci.
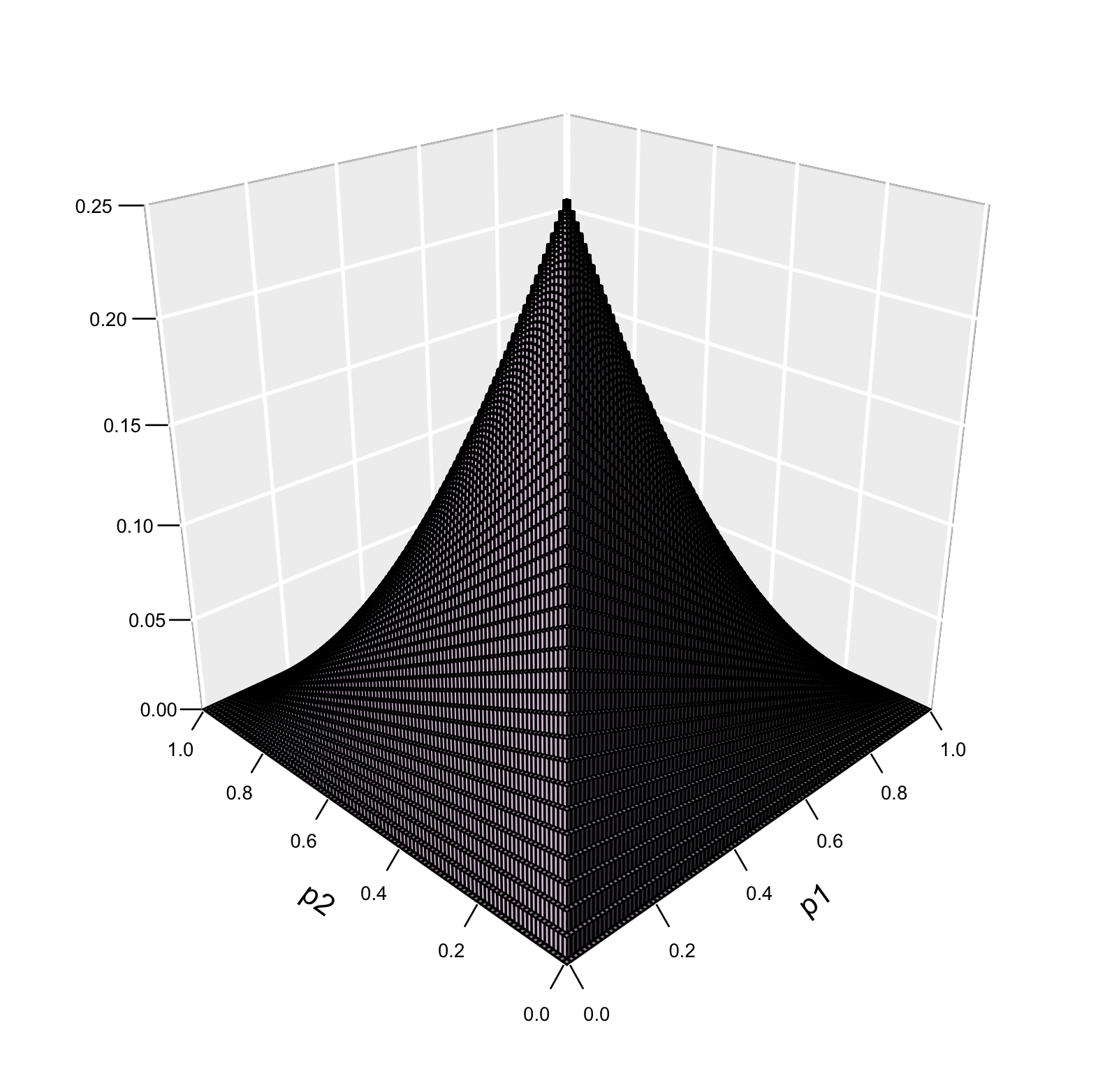
Figura 5.3: Superficie para el valor de \(D_\text{máx}\) en función de las frecuencias del alelos \(A_1\) (\(p_1\)) y \(B_1\) (\(p_2\)). Se aprecia claramente la simetría de la figura, así como el máximo único en \(p_1=q_1=p_2=q_2=\frac{1}{2}\).
Ejemplo 5.1
En un análisis genómico de dos loci (A y B) físicamente cercanos en el mismo cromosoma autosomal, ambos con dos alelos, de una especie diploide se encontraron los siguientes conteos para los haplotipos posibles
\[\bf{A_1B_1}=300\] \[\bf{A_1B_2}=140\] \[\bf{A_2B_1}=260\] \[\bf{A_2B_2}=280\]
Calcular las frecuencias de los alelos. ¿Es la frecuencia de los haplotipos la esperada en base a estas frecuencias? ¿Hay desequilibrio de ligamiento entre estos loci y si es así cuánto vale? ¿Hay exceso o déficit de los gametos en fase de acomplamiento? ¿Cuánto es el \(D_\text{máx}\) posible para este par de loci?
Llamemos \(x_1\) a la frecuencia de \(A_1B_1\), \(x_2\) a la de \(A_1B_2\), \(x_3\) a la de \(A_2B_1\) y \(x_4\) a la de \(A_2B_2\), con \(x_i=N_i/N\). La frecuencia de \(A_1\) (primer locus), \(p_1=x_1+x_2\), es decir
\[\begin{equation} p_1=x_1+x_2=\frac{N_1}{N}+\frac{N_2}{N}=\frac{300}{980}+\frac{140}{980} \approx 0,449 \end{equation}\]
Por lo tanto, \(q_1=1-p_1=1-0,449=0,551\). Para el alelo \(B_1\) (segundo locus ) será
\[\begin{equation} p_2=x_1+x_3=\frac{N_1}{N}+\frac{N_3}{N}=\frac{300}{980}+\frac{260}{980}=0,571 \end{equation}\]
y entonces \(q_2=1-p_2=1-0,571=0,429\).
Las frecuencias “reales” de los 4 gametos (haplotipos) posibles son
\[ \begin{split} x_1=\frac{N_1}{N}=\frac{300}{980} = 0,306 \\ x_2=\frac{N_2}{N}=\frac{140}{980} = 0,143 \\ x_3=\frac{N_3}{N}=\frac{260}{980} = 0,265 \\ x_4=\frac{N_4}{N}=\frac{280}{980} = 0,286 \end{split} \]
mientras que las esperadas si no existiese desequilibrio de ligamiento serían los productos de las frecuencias de los alelos que los forman, es decir
\[ \begin{split} \mathbb{E}_1=p_1p_2=0,449 \cdot 0,571 = 0,256 \\ \mathbb{E}_2=p_1q_2=0,449 \cdot 0,429 = 0,193 \\ \mathbb{E}_3=q_1p_2=0,551 \cdot 0,571 = 0,315 \\ \mathbb{E}_4=q_1q_2=0,551 \cdot 0,429 = 0,236 \end{split} \]
Un chequeo obvio es que tanto la suma \(\sum_i \mathbb{E}_i=1\) (\(0,256+0,193+0,315+0,236=1\)), así como \(\sum_i x_i=1\) (\(0,306+0,143+0,265+0,286=1\)).
Ahora, podemos armar un cuadro con las frecuencias esperadas y observadas
| \(\text{Gametos}\) | \(A_1B_1\) | \(A_1B_2\) | \(A_2B_1\) | \(A_2B_2\) |
|---|---|---|---|---|
| \(\text{Frecuencia esperada}\) | \(0,256\) | \(0,193\) | \(0,315\) | \(0,236\) |
| \(\text{Diferencia } (D\text{ o } -D)\) | \(0,050\) | \(-0,050\) | \(-0,050\) | \(0,050\) |
A partir de este cuadro vemos claramente las diferencias entre las frecuencias esperadas y las observadas, que se corresponden con un valor de \(D=0,05\). Los gametos en fase de acoplamiento, es decir \(A_1B_1\) y \(A_2B_2\) están en exceso respecto a lo esperado.
De acuerdo a la ecuación (5.18), \(D_\text{máx}=\text{mínimo}(p_1q_2,q_1p_2)\), por lo que en nuestro caso
\[ \begin{split} D_\text{máx}=\text{mínimo}(p_1q_2;q_1p_2)= \text{mínimo}(0,449 \cdot 0,429 ; 0,551 \cdot 0,571) \\ D_\text{máx}=\text{mínimo}(0,1926 ; 0,3146) = 0,1926 \end{split} \]
El conteo de los distintos gametos está influido por el azar y por lo tanto lo podemos considerar producto de alguna distribución de probabilidad subyacente. A partir de un conteo de haplotipos (o gametos, por ejemplo) normalmente vamos a derivar no solo las frecuencias de cada uno de ellos, sino que también de los alelos en los distintos loci. En general, al tratarse de un muestreo aleatorio siempre vamos a encontrar valores de \(D\) no exactamente iguales a cero, aunque estas diferencias puedan ser mínimas. Eso nos lleva a preguntarnos cómo podemos distinguir cuáles diferencias son estadísticamente significativas, es decir, que si muestreamos toda la población (o con \(N \to \infty\)) detectemos aquellas que “realmente” existen. Para eso debemos antes que nada definir que cuál es nuestra hipótesis nula a evaluar, o dicho de otra forma, que esperaríamos nosotros “por defecto”.
En el caso de desequilibrio de ligamiento, la hipótesis nula usual es que los loci considerados se encuentran en equilibrio, o lo que es equivalente, que las frecuencias de los alelos en cada locus son independientes de los resultados en otros loci. Por ejemplo, para el caso de dos loci con dos alelos cada uno, usando la notación anterior, la frecuencia esperada para un gameto \(A_1B_1\) sería el producto de la frecuencia de \(A_1\) en el primer locus (\(p_1\)) por la frecuencia de \(B_1\) en el segundo locus (\(p_2\)) (i.e., bajo la hipótesis nula \(\mathbb{E}(x_1)=p_1p_2\)). Dado un conteo total de \(N\) haplotipos (o gametos), entonces el número esperado de los mismos que sean \(A_1B_1\) es \(\mathbb{E}(n_1)=p_1p_2N\). Claramente, siguiendo esta lógica, el conteo esperado (bajo nuestra hipótesis nula) para los otros gametos será \(\mathbb{E}(n_2)=p_1q_2N\), \(\mathbb{E}(n_3)=q_1p_2N\) y \(\mathbb{E}(n_4)=q_1q_2N\), con \(n_1+n_2+n_3+n_4=N\). Los conteos observados para nuestros haplotipos (gametos) los hemos notado como \(x_1\), \(x_2\), \(x_3\) y \(x_4\) respectivamente, por lo que tenemos un conteo observado y uno esperado. Si recuerdas de los cursos de estadística, las anteriores parecen ser las condiciones para la aplicación de un test de independencia. Más aún seguramente recuerdes de esos mismos cursos el test de chi-cuadrado (\(\chi^2\)), cuya fórmula lucía
\[\begin{equation} \chi_{gl}^2=\sum_i \frac{(O_i-E_i)^2}{E_i} \tag{5.19} \end{equation}\]
siendo \(gl\) los grados de libertad del test, \(O_i\) el conteo observado para la “celda” \(i\), y \(E_i\) el esperado para esa misma celda. En nuestro caso, podemos arreglar los datos que observamos en una tabla como la siguiente
| \(\text{Gametos}\) | \(B_1\) | \(B_2\) | \(\textbf{Marginal}\) |
|---|---|---|---|
| \(A_2\) | \(x_3N\) | \(x_4N\) | \((x_3+x_4)N=q_1N\) |
| \(\textbf{Marginal}\) | \((x_1+x_3)N=p_2N\) | \((x_2+x_4)N=q_2N\) | \(N\) |
Es de notar que los \(x_1N,...,x_4N\) representan los conteos observados de los 4 haplotipos posibles (ya que \(x_1,...,x_4\) son la frecuencias relativas de los mismos). Al mismo tiempo, los conteos esperados estarán dados por el siguiente cuadro
| \(\text{Gametos}\) | \(B_1\) | \(B_2\) | \(\textbf{Marginal}\) |
|---|---|---|---|
| \(A_2\) | \(q_1p_2N\) | \(p_2q_2N\) | \(q_1N\) |
| \(\textbf{Marginal}\) | \(p_2N\) | \(q_2N\) | \(N\) |
Con esta configuración de las celdas en una tabla podemos volver a formular la ecuación (5.19) para considerar la sumatoria en las \(i\) filas y \(j\) columnas de la siguiente forma
\[\begin{equation} \chi_{gl}^2=\sum_{i,j} \frac{(O_{i,j}-E_{i,j})^2}{E_{i,j}}=\sum_{i,j} \frac{[O_{i,j}-(m_i*m_j/N)]^2}{(m_i*m_j/N)} \tag{5.20} \end{equation}\]
donde \(m_i,\ (i=1,2)\) y \(m_j,\ (j=1,2)\) son los conteos marginales de filas y columnas, respectivamente. En una tabla de 2x2 como la que estamos trabajando, los grados de libertad son \(gl=2\)x\(2=4-1=3\), menos \(1\) para estimar \(p_1\) (\(3-1=2\)), menos otro grado de libertad para estimar \(p_2\) (\(2-1=1\)), por lo que \(gl=1\), con lo que ya tenemos casi todo para nuestro test de independencia. Lo único que nos estaría faltando es definir el valor umbral para \(p\) que vamos a usar para determinar si la diferencia observada es estadísticamente significativa (a veces conocido como \(\alpha\)).
Ejemplo 5.2
Con los datos del Ejemplo 5.1 determinar si el desequilibrio de ligamiento observado es estadísticamente significativo al valor de \(\alpha=1\%\).
Ordenando los haplotipos observados en una tabla tenemos
| \(\text{Gametos}\) | \(B_1\) | \(B_2\) | \(\textbf{Marginal}\) |
|---|---|---|---|
| \(A_2\) | \(260\) | \(280\) | \(540\) |
| \(\textbf{Marginal}\) | \(560\) | \(420\) | \(980\) |
El valor esperado para la celda \(i,j\) podemos calcularlos de acuerdo a \(E_{i,j}=\frac{m_1*m_j}{N}\). Por ejemplo, para el haplotipo \(A_1B_1\) sería \(E_{1,1}=\frac{440*560}{980}=251,43\) Por lo tanto, si lo calculamos para las celdas restantes, los esperados serían
| \(\text{Gametos}\) | \(B_1\) | \(B_2\) | \(\textbf{Marginal}\) |
|---|---|---|---|
| \(A_2\) | \(308,57\) | \(231,43\) | \(540\) |
| \(\textbf{Marginal}\) | \(560\) | \(420\) | \(980\) |
Ahora, aplicando la ecuación (5.20),
\[\begin{equation} \chi_{gl}^2=\sum_{i,j} \frac{(O_{i,j}-E_{i,j})^2}{E_{i,j}} \end{equation}\]
por lo que tenemos que calcular primero los valores de \(\frac{(O_{i,j}-E_{i,j})^2}{E_{i,j}}\) y luego sumarlos. Para \(i=1,j=1\) tenemos \(\frac{(O_{1,1}-E_{1,1})^2}{E_{1,1}}=\frac{(300-251,43)^2}{251,43}=9,38\). Para \(i=1,j=2\) tenemos \(\frac{(140-188,57)^2}{188,57}=12,51\). Para \(i=2,j=1\) tenemos \(\frac{(260-308,57)^2}{308,57}=7,65\). Finalmente, para \(i=2,j=2\) tenemos \(\frac{(280-231,43)^2}{231,43}=10,19\). Sumando estos valores, tenemos el valor del estadístico
\[\begin{equation} \chi^2=9,38+12,51+7,65+10,19=39,73 \end{equation}\]
Si ahora entramos en una tabla de valores del estadístico \(\chi^2\) con \(gl=1\), tenemos que el valor del estadístico correspondiente a \(\alpha=0,01\) es \(6,635\). Como nuestro resultado es claramente superior a este valor, es decir está a la derecha de este punto de corte, la diferencia de frecuencias entre lo observado y lo esperado (bajo la hipótesis de independencia de los loci) es estadísticamente significativa y podemos rechazar la hipótesis nula.
PARA RECORDAR
- Si \(x_1\), \(x_2\), \(x_3\) y \(x_4\) son las frecuencias de los gametos, con \(x_1\) y \(x_4\) la de los gametos en fase de acoplamiento, entonces el desequilibrio de ligamiento es
\[\begin{equation} D=x_1x_4-x_2x_3 \end{equation}\]
- Si \(p_1=x_1+x_2\) y \(p_2=x_1+x_3\) son las frecuencias de los alelos \(A_1\) y \(B_1\) respectivamente, entonces
\[ \begin{split} x_1=p_1p_2+D \\ x_2=p_1q_2-D \\ x_3=q_1p_2-D \\ x_4=q_1q_2+D \end{split} \]
- El rango de \(D\) posibles para cada par de loci depende de las frecuencias de los alelos en los mismos y en particular \(D_\text{mín}\) y \(D_\text{máx}\) quedan definidos por
\[ \begin{split} D_\text{mín}=\text{máximo}(-p_1p_2,-q_1q_2) \\ D_\text{máx}=\text{mínimo}(p_1q_2,q_1p_2) \end{split} \]
5.2 La evolución en el tiempo del desequilibrio de ligamiento
A esta altura podemos preguntarnos cómo evolucionará el desequilibrio de ligamiento con el tiempo, en nuestro caso en generaciones. Para eso podemos ver lo que ocurre en una generación. Si llamamos con \(x'_1\) a la frecuencia del gameto \(A_1B_1\) en la siguiente generación, entonces de acuerdo a lo la ecuación (5.7) (poniendo “primas” donde corresponda)
\[\begin{equation} x'_1=p'_1p'_2+D'=(1-r)(p_1p_2+D)+rp_1p_2 \tag{5.21} \end{equation}\]
trabajando un poco la ecuación, para despejar \(D'\) (el desequilibrio de ligamiento en la siguiente generación) llegamos a
\[ \begin{split} D'=(1-r)(p_1p_2+D)+rp_1p_2-p'_1p'_2 \Leftrightarrow \\ D'=p_1p_2 - rp_1p_2 +D-rD + rp_1p_2 -p'_1p'_2 \end{split} \tag{5.22} \]
Si asumimos que la frecuencia de los alelos no depende de sus combinaciones y que el equilibrio de Hardy-Weinberg no se ve afectado por la inclusión de otros loci, entonces podemos asumir \(p'_1=p_1\) y \(p'_2=p_2\), por lo que podemos simplificar la expresión anterior
\[ \begin{split} D'=p_1p_2 + D-rD - p_1p_2\ \therefore D'=D-rD\\ D'=D(1-r) \end{split} \tag{5.23} \]
Es decir, el desequilibrio de ligamiento en la siguiente generación será una fracción (\(1-r\)) del desequilibrio de ligamiento en la anterior. El cambio en el desequilibrio de ligamiento será entonces la diferencia entre \(D'\) y \(D\), es decir
\[ \begin{split} \Delta_rD=D'-D=D(1-r)-D\ \therefore \\ \Delta_rD=-rD \end{split} \tag{5.24} \]
Claramente, si en cada generación el desequilibrio de ligamiento es el producto de \((1-r)\) por el desequilibrio en la anterior (que a su vez es la fracción \((1-r)\) de dos generaciones atrás), entonces luego de \(t\) generaciones será el producto de \((1-r)\), \(t\) veces por sí mismo. Es decir, será equivalente a \((1-r)^t\) multiplicado por el desequilibrio en la primera generación considerada, que llamamos \(D_0\). Por lo tanto, el desequilibrio de ligamiento en la generación \(t\) será
\[\begin{equation} D_t=(1-r)^t D_0 \tag{5.25} \end{equation}\]
Este patrón de decrecimiento es geométrico, y se aproxima razonablemente bien al patrón de decrecimiento exponencial, ya que \((1-r)^t \approx e^{-rt}\) (esta aproximación ya la hemos visto en capítulos previos). Por lo tanto, tenemos
\[\begin{equation} D_t \approx e^{-rt} D_0 \end{equation}\]
En la Figura 5.4 se puede apreciar la evolución del desequilibrio de ligamiento a medida que transcurren sucesivas generaciones, para distintos valores de \(r\). Como \(D_t=(1-r)^t D_0\), para independizar el comportamiento de las curvas del valor \(D_0\) expresamos está gráfica considerando \(D_0=D_\text{máx}=0,25\). En esta figura se aprecia que la fracción del desequilibrio de ligamiento que permanece con el paso de las generaciones decrece en general rápidamente, dependiendo de \(r\): cuanto menor es la fracción de recombinantes entre los dos loci, más tarda en reducirse el desequilibrio. Esto es totalmente intuitivo, ya que cuanto menos probable sea la aparición de un evento de recombinación, menos probable es que los gametos recombinen y por lo tanto que se rompa el desequilibrio de ligamiento. El corte con la línea gris horizontal representa el número de generaciones necesario para reducir el desequilibrio a la mitad.
Veamos si podemos determinar analíticamente el número de generaciones necesarias para llegar a una proporción determinada de \(D_0\) (e.g., \(f\)). Tendremos \(D_t=D_0 f\), con \(0<f<1\). Si operamos con la ecuación (5.25), sustituyendo \(D_t\), tenemos
\[\begin{equation} D_t = D_0 f = (1-r)^t D_0\ \therefore\ f=(1-r)^t \tag{5.26} \end{equation}\]
Aplicando logaritmo a ambos lados la ecuación (5.26) se transforma en
\[\begin{equation} \ln(f)=\ln{(1-r)^t}=t \ln (1-r) \Leftrightarrow \end{equation}\]
\[\begin{equation} t=\frac{\ln(f)}{\ln (1-r)} \tag{5.27} \end{equation}\]
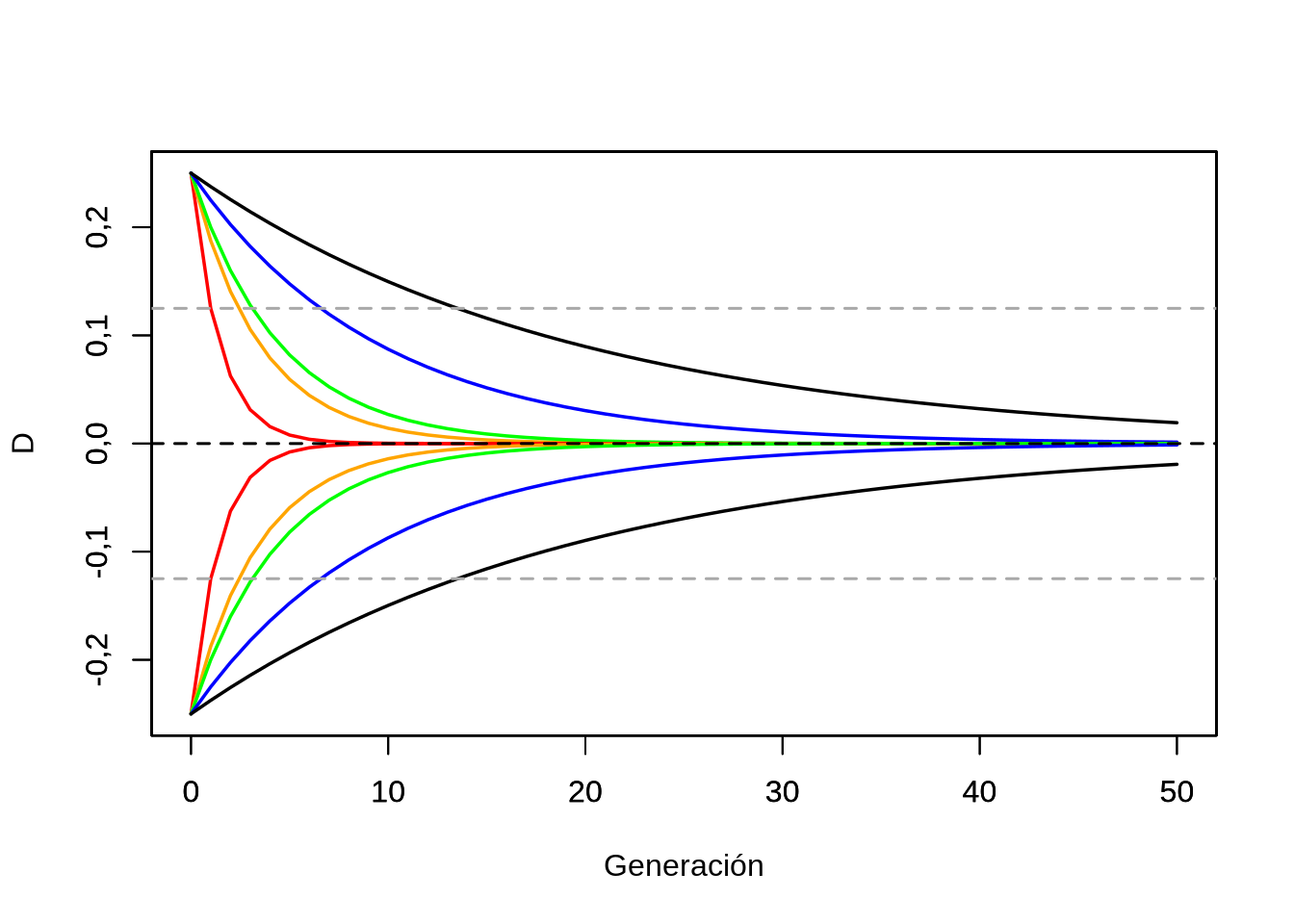
Figura 5.4: Evolución del desequilibrio de ligamiento respecto de \(D_0=D_\text{máx}=0,25\). Rojo \(r=0,50\), anaranjado \(r=0,25\), verde \(r=0,20\), azul \(r=0,10\) y negro \(r=0,05\)
El resultado de aplicar la ecuación (5.27) a distintas combinaciones de la fracción \(f=\frac{D_t}{D_0}\) y \(r\) se puede apreciar en la Tabla ??. Claramente, a medida de que disminuye la fracción de gametos recombinantes \(r\) (de izquierda a derecha en la tabla), mayor se hace el número de generaciones necesarias para alcanzar una fracción determinada \(f\). Por ejemplo, mientras que para reducir el desequilibrio de ligamiento inicial a la mitad con un \(r=0,50\) se precisa una generación, para lograrlo con un \(r=0,01\) se precisan \(\approx 69\) generaciones.
| r=0,50 | r=0,40 | r=0,30 | r=0,25 | r=0,20 | r=0,10 | r=0,05 | r=0,01 | |
|---|---|---|---|---|---|---|---|---|
| f=0,75 | 0,42 | 0,56 | 0,81 | 1,00 | 1,29 | 2,73 | 5,61 | 28,62 |
| f=0,50 | 1,00 | 1,36 | 1,94 | 2,41 | 3,11 | 6,58 | 13,51 | 68,97 |
| f=0,40 | 1,32 | 1,79 | 2,57 | 3,19 | 4,11 | 8,70 | 17,86 | 91,17 |
| f=0,30 | 1,74 | 2,36 | 3,38 | 4,19 | 5,40 | 11,43 | 23,47 | 119,79 |
| f=0,25 | 2,00 | 2,71 | 3,89 | 4,82 | 6,21 | 13,16 | 27,03 | 137,94 |
| f=0,20 | 2,32 | 3,15 | 4,51 | 5,59 | 7,21 | 15,28 | 31,38 | 160,14 |
| f=0,10 | 3,32 | 4,51 | 6,46 | 8,00 | 10,32 | 21,85 | 44,89 | 229,11 |
| f=0,05 | 4,32 | 5,86 | 8,40 | 10,41 | 13,43 | 28,43 | 58,40 | 298,07 |
El comportamiento general de la función se puede apreciar en la Figura 5.5. Claramente el comportamiento es aproximadamente exponencial en los dos ejes, lo cual hace extremadamente lenta la reducción final del desequilibrio de ligamiento si la tasa de recombinación es muy baja, algo que suele ocurrir entre loci muy cercanos físicamente.
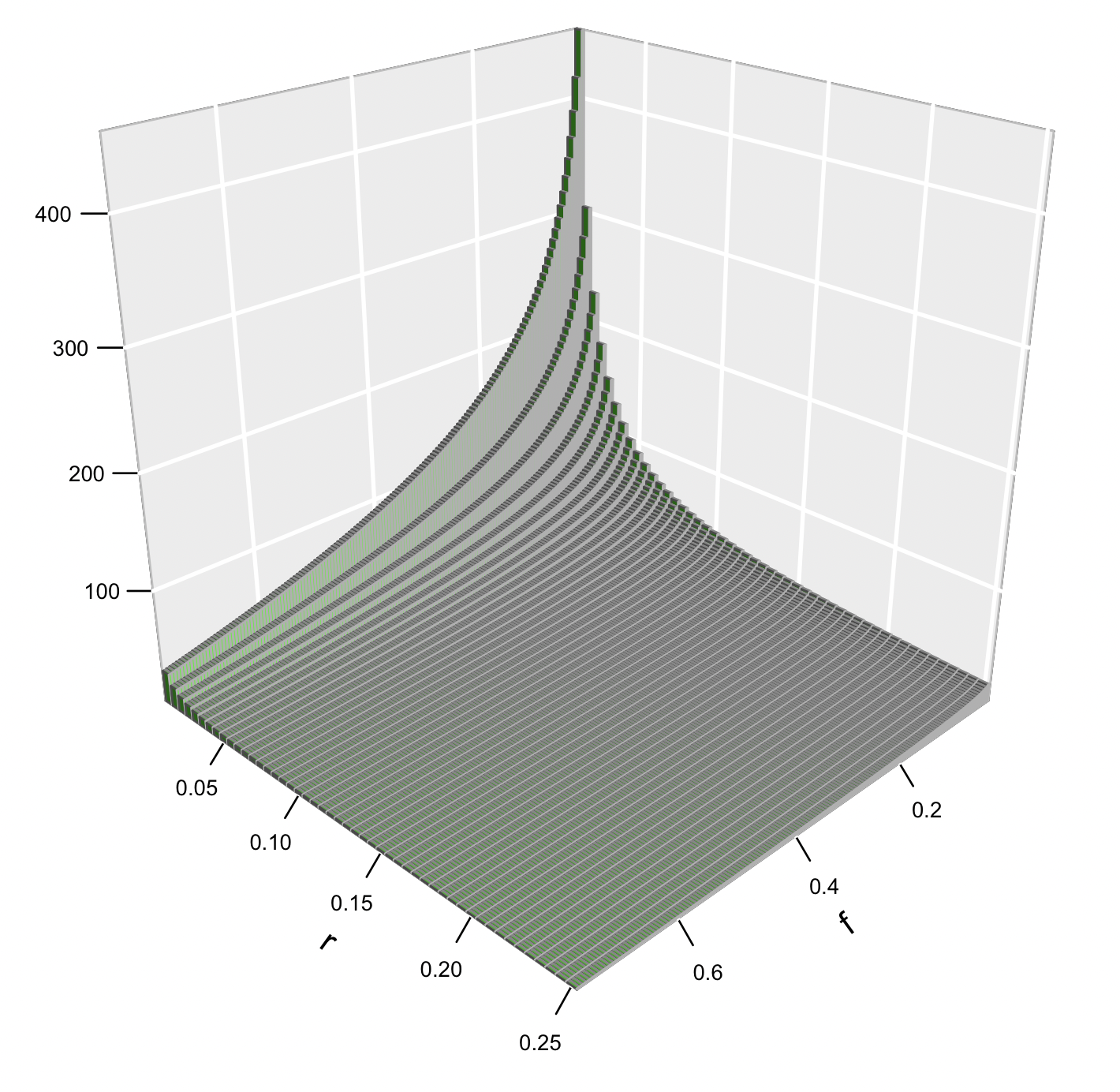
Figura 5.5: Superficie de la función bivariada que nos devuelve el número de generaciones requeridas para alcanzar una fracción \(f=\frac{D_t}{D_0}\) del desequilibrio de ligamiento inicial en función de la fracción de recombinación \(r\). Los límites fueron elegidos (\(f \leqslant 0,75\), \(r \leqslant 0,25\)) para poder observar mejor el comportamiento general de la función (fuera de estos límites la superficie es mucho más plana)..
Por último, notemos que la aproximación exponencial nos permite estimar el número \(t\) de generaciones necesarias para alcanzar una fracción \(f\) del desequilibrio de ligamiento inicial \(D_0\):
\[ \begin{split} D_t = D_0 f \approx e^{-rt} D_0 \Leftrightarrow \\ ln(f) = -rt \Leftrightarrow \\ \end{split} \]
\[\begin{equation} t=\frac{\ln(f)}{-r} \tag{5.27} \end{equation}\]
PARA RECORDAR
- Si partimos de un desequilibrio de ligamiento \(D_0\) en la generación \(0\), el desequilibrio en la generación \(t\) será
\[\begin{equation} D_t=(1-r)^t D_0 \end{equation}\]
- Esto muestra un comportamiento de función geométrica, que se aproxima razonablemente bien por una exponencial ya que \((1-r)^t \approx e^{-rt}\), por lo que
\[\begin{equation} D_t \approx e^{-rt} D_0 \end{equation}\]
- Si \(f=\frac{D_t}{D_0}\) es la fracción del desequilibrio de ligamiento inicial que permanece después de un tiempo, el número de generaciones requerido para alcanzarlo es
\[\begin{equation} t=\frac{\ln f}{\ln (1-r)} \end{equation}\]
- Nuevamente, una aproximación del número de generaciones requerido, a partir de la aproximación exponencial es
\[\begin{equation} t=\frac{\ln f}{-r} \end{equation}\]
5.3 Otras medidas de asociación
Como vimos previamente, en la ecuación (5.18) el rango de valores posibles de \(D\) es claramente dependiente de las frecuencias de los alelos en ambos loci, ya que este rango se encuentra dado por
\[\begin{equation} \begin{cases} D_\text{mín}=\text{máximo}(-p_1p_2,-q_1q_2) \\ D_\text{máx}=\text{mínimo}(p_1q_2,q_1p_2) \end{cases} \end{equation}\]
Una alternativa para hacer \(D\) independiente de las frecuencias es dividir su valor por su máximo (o mínimo) valor posible en relación a las frecuencias (dependiendo del signo se utiliza \(D_\text{máx}\) o \(D_\text{mín}\)). Es decir,
\[ \begin{split} D'=\frac{D}{D_\text{máx}} \text{ si } D>0 \\ D'=\frac{D}{D_\text{mín}} \text{ si } D<0 \end{split} \tag{5.28} \]
De esta manera, el estadístico \(D'\) nos permite comparar el desequilibrio de ligamiento de una manera independientemente de la historia de evolución de las frecuencias en distintas regiones del genoma o aún entre organismos diferentes. El rango de valores para \(D'\) es entonces \(0 \leqslant D' \leqslant 1\), ya que tanto en el caso de que normalicemos según \(D=D_\text{máx}\) o \(D=D_\text{mín}\) tendremos \(D'=1\).
Otro estadístico usual es el \(r^2\), definido como
\[\begin{equation} r^2=\frac{D^2}{p_1q_1p_2q_2} \tag{5.29} \end{equation}\]
Es importante tener en cuenta que en este contexto \(r\) no se refiere a la tasa de recombinación, la cual también fue denotada con \(r\) en secciones previas. \(r^2\) es el cuadrado del coeficiente de correlación de Pearson, a veces llamado el coeficiente de determinación, que recordarás de los cursos de estadística. En nuestro contexto \(r=\sqrt{r^2}\) es la correlación entre estados alélicos dentro del mismo gameto. Por otro lado, \(r^2\) es útil para el cálculo de \(\chi^2\) a partir de las frecuencias de haplotipos ya que el valor numérico que usamos en el test es igual a \(r^2N\). Igual que para \(D'\), \(0 \leqslant r^2 \leqslant 1\), ya que se trata del cuadrado del coeficiente de correlación (que por definición está limitado a \(-1 \leqslant r \leqslant 1\)). Tanto \(D'\) como \(r^2\) tienen signo positivo por definición, por lo que desafortunadamente no es posible tener el sentido del desequilibrio a partir de ellos (pero si a partir de \(D\), del que ambos parten usualmente).
Ejemplo 5.3
A partir del resultado \(\chi^2=r^2N\) calcular el valor de este estadístico con los datos del Ejemplo 5.1.
Usando las frecuencias calculadas para \(p_1,q_1, p_2, q_2\) y el valor de \(D\) del ejemplo, sustituyendo, tenemos
\[\begin{equation} \chi^2=0,05^2/(0,551 \cdot 0,449 \cdot 0,571 \cdot 0,429) \cdot (300+140+260+280) \approx 40,43 \end{equation}\]
que es un poco superior al resultado obtenido en el Ejemplo 5.2. Si en lugar de eso partimos directamente del hecho de que \(D=x_1x_4-x_2x_3\), usando los números
\[\begin{equation} \chi^2=980 \cdot \frac{\left[\frac{(300 \cdot 280)}{980^2}-\frac{(140 \cdot 260)}{980^2}\right]^2}{\frac{440}{980} \cdot \left(1-\frac{440}{980}\right) \cdot \frac{560}{980} \cdot \left(1-\frac{560}{980}\right)}=39,73 \end{equation}\]
que es un valor idéntico al calculado usando el formato de tabla de 2x2, pero ahora por un procedimiento más abreviado.
La relación entre los dos estadísticos, \(D'\) y \(r^2\) se puede observar en la Figura 5.6.
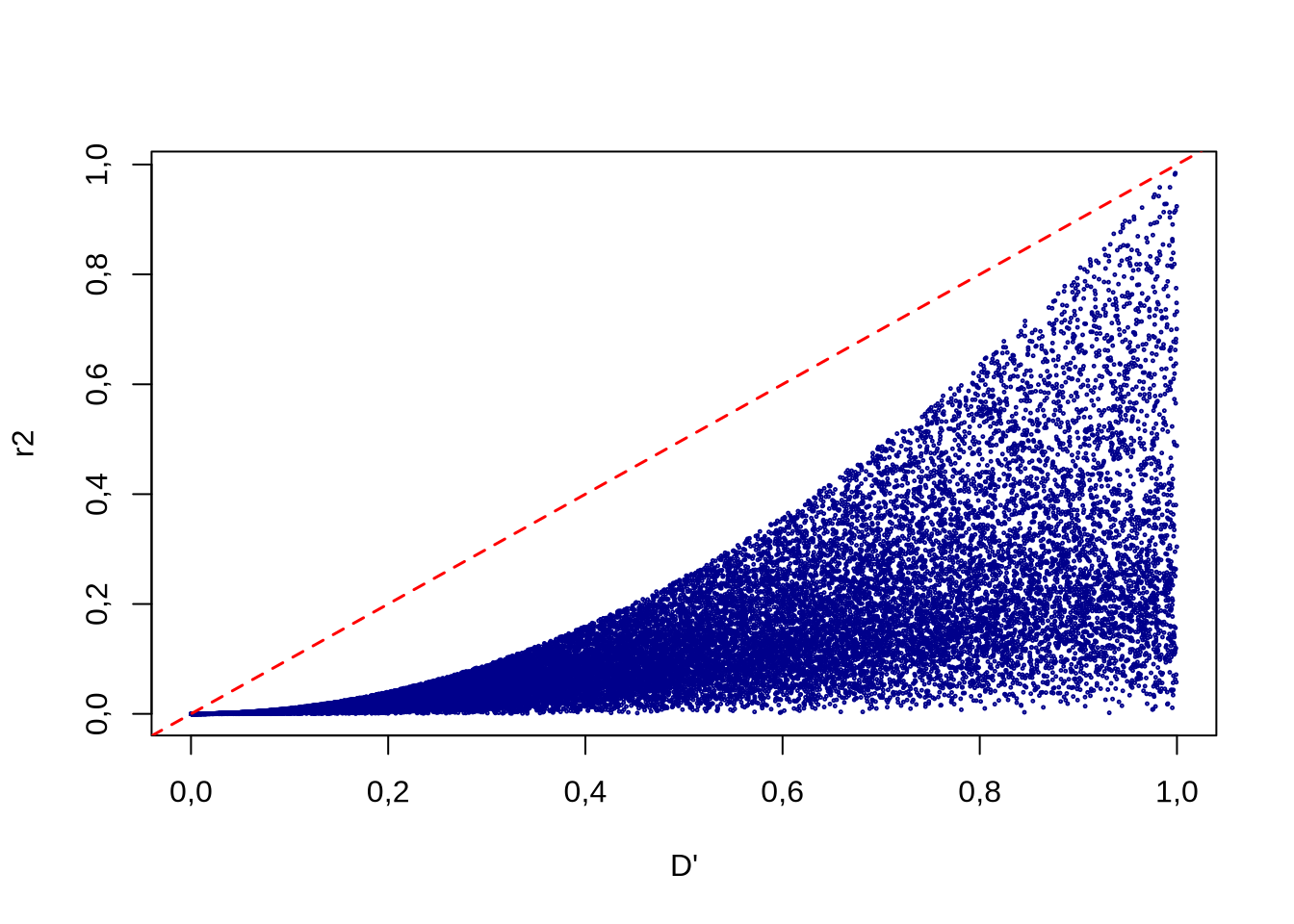
Figura 5.6: Relación entre los estadísticos \(D'\) y \(r^2\) para realizaciones al azar de los 4 haplotipos en dos loci con dos alelos. Mientras que para valores bajos de \(r^2\) es posible encontrar cualquier valor de \(D'\), no ocurre lo mismo en el sentido contrario (valores bajos de \(D'\) implican valores más bajos de \(r^2\)). Realización propia sobre idea en Hartl and Clark (2007).
La misma representa 30 mil realizaciones al azar de las 4 frecuencias de los gametos, muestreados de una distribución uniforme y escalados (para que sumen a uno) en cada realización del experimento. A partir de esos muestreos se calcularon los dos estadísticos. Mientras que para valores bajos de \(r^2\) se pueden encontrar todos los valores posibles de \(D'\), lo contrario no se cumple. Es más, los valores de \(r^2\) son siempre menores que los de \(D'\), lo que se aprecia claramente ya que los puntos están por debajo de la línea de identidad (diagonal en rojo). De hecho, \(r^2\) puede tomar cualquier valor entre \(0 \leqslant r^2 \leqslant (D')^2\) (recordar que el cuadrado de un número entre cero y uno es menor que el número mismo).
Una diferencia importante entre el estadístico \(D'\) y el \(r^2\) tiene que ver con la afectación de ambos frente a la historia que produce el desequilibrio de ligamiento. Mientras que \(r^2\) es relativamente sensible al momento en que, por ejemplo, aparece una nueva variante, \(D'\) es relativamente independiente y su principal dependencia es la tasa de recombinación. Por ejemplo, un alelo que entra “temprano” en la historia evolutiva de la asociación tendrá, a medida de que pase el tiempo, una alta correlación con el alelo en el otro locus con el que fue a dar en el inicio. En cambio, si la introducción de este alelo es “reciente” la correlación será baja. Eso explica en gran medida por qué para un valor determinado de \(D'\) el rango de valores posibles de \(r^2\) es importante. Otras diferencias que favorecen el uso de \(r^2\) sobre \(D'\) son que primero presenta mayor estabilidad en el caso de loci con alelos en baja frecuencia cuando los tamaños muestrales son pequeños, y que favorece la interpretación como la proporción explicada de varianza debida al desequilibrio de ligamiento en relación a la varianza explicada por QTLs (Quantitative Trait Loci) (Van Inghelandt et al. (2011)). Finalmente, existen otros estadísticos alternativos con mejores propiedades en ciertas condiciones o más fáciles de obtener. Por ejemplo, D. Gianola, Qanbari, and Simianer (2013) introducen el estadístico \(\rho^2\) que además de buenas propiedades de muestreo es mucho más sencillo de calcular que los estimados por máxima-verosimilitud o bayesianos de la correlación tetracórica (correlación para tablas de 2x2, por ejemplo).
PARA RECORDAR
Dos medidas alternativas para el desequilibrio de ligamiento, menos sensibles a las frecuencias de los alelos son \(D'\) y \(r^2\).
El estadístico \(D'\) es el valor de \(D\) estandarizado al valor máximo (mínimo) posible, dependiendo del signo de \(D\), es decir \(D'=\frac{D}{D_\text{máx}} \text{ si } D>0;\ D'=\frac{D}{D_\text{mín}} \text{ si } D<0\).
El estadístico \(r^2\) es la correlación entre estados alélicos dentro del mismo gameto y se calcula como \(r^2=\frac{D^2}{(p_1q_1p_2q_2)}\).
Para cada valor de \(D'\) \(r^2\) puede variar entre \(0 \leqslant r^2 \leqslant (D')^2\), lo que refleja aspectos diferentes de ambos estadísticos: mientras \(D'\) es principalmente afectado por la tasa de recombinación, \(r^2\) refleja también de alguna manera la historia de los alelos.
El valor de \(r^2\) es útil también para calcular la significación estadística del desequilibrio de ligamiento, ya que \(\chi^2=r^2N\) (con \(N\) igual al número de gametos).
5.4 Selección en modelos de dos loci
En esta sección vamos a estudiar qué ocurre con la selección cuando tenemos dos loci en los que la tasa de recombinación entre ellos no es \(r=\frac{1}{2}\) (i.e., cuando no podemos considerar a ambos loci como estadísticamente independientes). Nuestro estudio va a ser somero, ya que las complicaciones posibles son inmediatas y muchas, lo que escapa al alcance del presente libro. Para el modelado de este fenómenos vamos a suponer que entre los dos loci la tasa de recombinación \(0 \leqslant r < \frac{1}{2}\) (aunque teóricamente \(r\) pueder ser mayor a \(\frac{1}{2}\)). La idea central de esta sección aparece representada en la Figura 5.7.
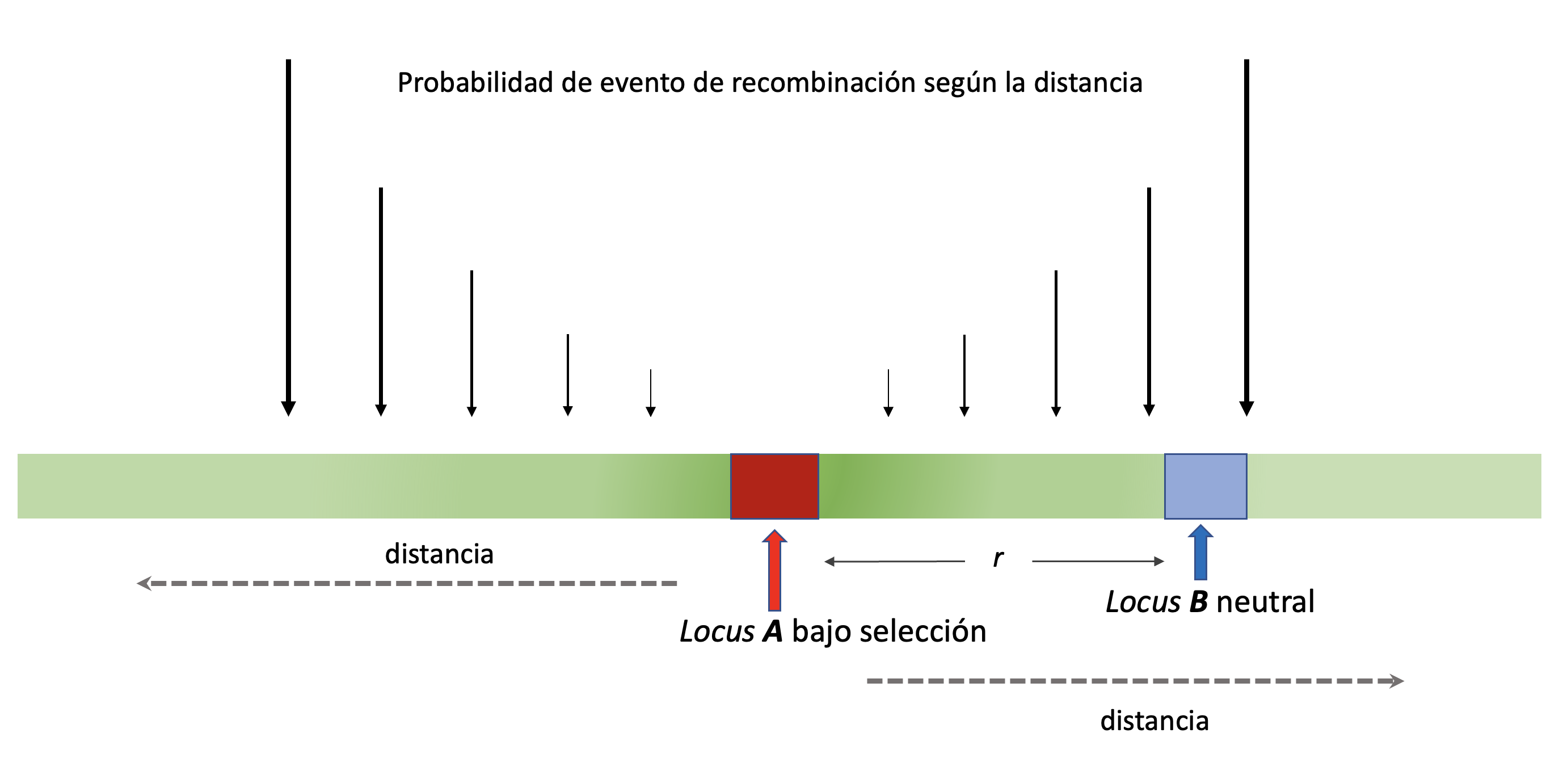
Figura 5.7: Ilustración del modelo de selección que vamos a analizar. Mientras que vamos a tratar con la selección en un solo locus (en rojo) de acuerdo al modelo que vimos en el capítulo Selección Natural, observaremos qué ocurre en algún otro locus que se encuentre en desequilibrio de ligamiento con el primero. A medida que crece la distancia respecto al locus seleccionado, aumenta la probabilidad de recombinación y por lo tanto la pérdida del efecto asociado a la selección en el primer locus.
Tenemos un locus bajo selección, el locus A, y un locus “cercano” B “neutral” (i.e., que no está sujeto a selección). En el presente contexto el término “cercano” refiere a que \(r<\frac{1}{2}\), es decir, que ambos loci no se comportan desde el punto de vista de la recombinación como totalmente independientes. A medida de que nos alejamos del locus bajo selección la probabilidad de que aparezca un quiasma entre el locus A y el B se incrementa (lo que representamos por flecha de tamaño creciente). En forma ingenua podríamos pensar que la dinámica del locus A sería la de selección de acuerdo a lo que ya vimos mientras que el comportamiento de B (no sujeto a la selección) sería complemante al azar y dominado exclusivamente por fenómenos como la mutación y la deriva. Sin embargo, en esta sección vamos a ignorar los efectos de estas dos últimas fuerzas evolutivas y vamos a estudiar si en ausencia de esas fuerzas las frecuencias de los alelos en B siguen imperturbables.
Tenemos dos loci con dos alelos cada uno, \(A_1\) y \(A_2\) en el locus A, \(B_1\) y \(B_2\) en el B. Imaginemos ahora que en lugar de asignar fitness a los gametos (como hicimos en el capítulo Selección Natural) vamos a asignarle ese fitness a los genotipos (i.e., a la combinación específica de gametos). Para ello vamos a hacer una matriz con las frecuencias de los distintos genotipos luego del apareamiento aleatorio y la selección por viabilidad. El cuadro siguiente resume estos resultados. La primer columna y el encabezado representan los gametos, mientras que cada celda de la matriz representa la frecuencia esperada para dicho genotipo (el constituido por el gameto de fila con el de columna).
| \(\text{Gametos}\) | \(A_1B_1\) | \(A_1B_2\) | \(A_2B_1\) | \(A_2B_2\) |
|---|---|---|---|---|
| \(A_1B_2\) | \(-\) | \(x_2^2w_{22}\) | \(2x_2x_3w_{23}\) | \(2x_2x_4w_{24}\) |
| \(A_2B_1\) | \(-\) | \(-\) | \(x_3^2w_{33}\) | \(2x_3x_4w_{34}\) |
| \(A_2B_2\) | \(-\) | \(-\) | \(-\) | \(x_4^2w_{44}\) |
El número de parámetros de fitness es ahora de \(n(n+1)/2=4 \cdot 5/2=10\). La lógica de la notación es sencilla. Las frecuencias de los gametos (haplotipos) son \(x_1\), \(x_2\), \(x_3\) y \(x_4\), con los subíndices haciendo referencia a los gametos \(A_1B_1\), \(A_1B_2\), \(A_2B_1\) y \(A_2B_2\). Entonces \(w_{ij}\) es el fitness asociado a la combinación del gameto \(i\) con el gameto \(j\). En la matriz (cuadro) de arriba tenemos las posibles combinaciones de gametos y los fitness asociados a cada combinación (fila \(i\), columna \(j\)). La matriz sería simétrica (por eso la ausencia de valores en el triángulo inferior izquierdo), los valores ausentes están contemplados en su simétrico (de ahí que exista un factor 2 cuando \(i \ne j\)).
Si recordamos, por ejemplo, \(x_1\) es la frecuencia del gameto \(A_1B_1\). Veamos cuántos de esos aparecen en la siguiente generación (\(x'_1\)), luego de un apareamiento al azar. Analicemos la primera fila del cuadro anterior que corresponde a este gameto. Por ejemplo, la primera fila con la primera columna representa un genotipo \(A_1B_1/A_1B_1\) que en la meiosis producirá gametos. Más allá de que haya o no recombinación todos los gametos serán \(A_1B_1\) en este caso, por lo que la frecuencia de este genotipo en la edad adulta y produciendo gametos será \(x_1^2w_{11}\). El caso de la primera fila con la segunda columna es aún más ilustrativo. El genotipo \(A_1B_1/A_1B_2\), más allá de la recombinación o ausencia de ella, producirá la mitad de los gametos \(A_1B_1\) y la otra mitad \(A_1B_2\). La frecuencia de este genotipo que llega a la reproducción es \(2x_1x_2w_{12}\), por lo que la mitad de nuestro interés (la que genera \(A_1B_1\)) será \(\frac{1}{2}2x_1x_2w_{12}=x_1x_2w_{12}\). Para la tercera fila el genotipo a considerar es \(A_1B_1/A_2B_1\), que producirá la mitad de los gametos \(A_1B_1\) y la mitad \(A_2B_1\), por lo que su aporte a \(x'_1\) será \(x_1x_3w_{13}\) (por razonamiento análogo al planteado en el caso anterior). Finalmente, de esta fila solo nos queda el genotipo \(A_1B_1/A_2B_2\), que solo producirá gametos \(A_1B_1\) en el caso de que no haya recombinación, que serán en ese caso la mitad. Como la probabilidad de no-recombinación es \((1-r)\), entonces todo junto es \(\frac{1}{2}(1-r)2x_1x_4w_{14}=(1-r)x_1x_4w_{14}\). De todos los otros genotipos en el resto de las filas, el único que puede producir gametos \(A_1B_1\) es el \(A_1B_2/A_2B_1\) (fila \(i=2\), columna \(j=3\)), pero solamente si ocurre recombinación, lo que acontece con probabilidad \(r\), en cuyo caso la mitad de los gametos serán del tipo \(A_1B_1\). Poniendo todo junto para este caso, obtenemos \(\frac{1}{2}r(2x_2x_3w_{23})=rx_2x_3w_{23}\).
Ahora, combinando los resultados de todas las posibilidades de obtener gametos \(A_1B_1\) en la siguiente generación y recordando de dividir por el fitness medio (\(\bar{w}\)), tenemos que la frecuencia de este gameto en la siguiente generación será
\[\begin{equation} x'_1=\frac{x_1^2w_{11}+x_1x_2w_{12}+x_1x_3w_{13}+(1-r)x_1x_4w_{14}+rx_2x_3w_{23}}{\bar{w}} \tag{5.30} \end{equation}\]
Antes de continuar veamos el concepto de fitness marginal de un gameto. El mismo es el fitness medio de todos los genotipos en los que participa ese gameto, justo antes de que la selección ocurra, es decir
\[\begin{equation} \bar{w}_i=\frac{\sum_{j=1}^{4} x_ix_jw_{ij}}{x_i}=\sum_{j=1}^{4} x_jw_{ij} \tag{5.31} \end{equation}\]
y por lo tanto el fitness medio de todos los gametos, el promedio de los fitness marginales, es
\[\begin{equation} \bar{w}=\sum_{i=1}^{i=4} x_i\bar{w}_{i} \tag{5.32} \end{equation}\]
Prosigamos con el caso de nuestro gameto \(A_1B_1\). En ese caso, la ecuación (5.31) se transforma en
\[\begin{equation} \bar{w}_1=x_1w_{11}+x_2w_{12}+x_3w_{13}+x_4w_{14} \tag{5.33} \end{equation}\]
Ahora asumamos además que \(w_{14}=w_{23}\), lo cual implica que no hay un efecto diferencial cis-trans, es decir que el fitness depende de la combinación de alelos pero no de cómo ellos están organizados en los cromosomas homólogos56. Si hacemos explícita la multiplicación en el numerador de (5.30) tenemos, sustituyendo además \(w_{23}\) por \(w_{14}\)
\[x'_1=\frac{x_1^2w_{11}+x_1x_2w_{12}+x_1x_3w_{13}+x_1x_4w_{14}-rx_1x_4w_{14}+rx_2x_3w_{23}}{\bar{w}} \Leftrightarrow\] \[x'_1=\frac{x_1^2w_{11}+x_1x_2w_{12}+x_1x_3w_{13}+x_1x_4w_{14}-r(x_1x_4-x_2x_3)w_{14}}{\bar{w}} \Leftrightarrow\] \[x'_1=\frac{x_1(x_1w_{11}+x_2w_{12}+x_3w_{13}+x_4w_{14})-rDw_{14}}{\bar{w}} \Leftrightarrow\] \[\begin{equation} x'_1=\frac{x_1\bar{w}_1-rDw_{14}}{\bar{w}} \tag{5.34} \end{equation}\]
Veamos ahora el cambio en las frecuencias de los gametos, es decir \(\Delta x_i\), que lo obtenemos como de costumbre, \(\Delta x_i = x'_i-x\). Por ejemplo, para el gameto \(A_1B_1\), el cambio de frecuencia será
\[\Delta x_1=x'_1-x_1=\frac{x_1\bar{w}_1-rDw_{14}}{\bar{w}}-x_1 \therefore =\frac{x_1\bar{w}_1-rDw_{14}}{\bar{w}}-x_1\frac{\bar{w}}{\bar{w}}\] \[\Delta x_1=\frac{x_1\bar{w}_1-rDw_{14}-x_1\bar{w}}{\bar{w}}\ \therefore\ \] \[\begin{equation} \Delta x_1=\frac{x_1(\bar{w}_1-\bar{w})-rw_{14}D}{\bar{w}} \tag{5.35} \end{equation}\]
En principio, podemos aplicar la misma lógica para el resto de las ecuaciones, lo que nos lleva a
\[\begin{equation} \begin{cases} \Delta x_1=\frac{x_1(\bar{w}_1-\bar{w})-rw_{14}D}{\bar{w}} \\ \Delta x_2=\frac{x_2(\bar{w}_2-\bar{w})+rw_{14}D}{\bar{w}} \\ \Delta x_3=\frac{x_3(\bar{w}_3-\bar{w})+rw_{14}D}{\bar{w}} \\ \Delta x_4=\frac{x_4(\bar{w}_4-\bar{w})-rw_{14}D}{\bar{w}} \tag{5.36} \end{cases} \end{equation}\]
Finalmente, podemos interpretar los resultado de las ecuaciones (5.35) y (5.36) mediante una aproximación (recordar la ecuación (5.5))
\[\begin{equation} \Delta x_i \approx \Delta_s x_i + \Delta_r x_i \tag{5.36} \end{equation}\]
Es decir, el cambio en la frecuencia de los gametos es aproximadamente suma del cambio debido a la selección y el cambio debido a la recombinación. Más aún, el conflicto entre las direcciones de ambos aportes es evidente (notar los signos de cada término en la ecuación): la selección tiende a favorecer la asociación de los alelos en gametos, mientras que la recombinación actúa destruyendo esa asociación.
Selección en un locus: impacto en loci en desequilibrio de ligamiento
Un ejemplo de la aplicación del análisis previo es el de un locus bajo selección en desequilibrio de ligamiento con un locus cercano, neutral este último (i.e., sin ventaja selectiva ninguno de sus alelos o combinaciones) aparece en el libro de John H. Gillespie (John H. Gillespie 2004). ¿Qué ocurrirá con las frecuencias alélicas bajo estas condiciones? Utilizaremos la misma notación del capítulo Selección Natural. Para el primer locus, los fitness relativos quedan definidos por \(1\), \(1-hs\) y \(1-s\), y entonces nuestro cuadro de fitness \(w_{ij}\) estará dado por
| \(\text{Gametos}\) | \(A_1B_1\) | \(A_1B_2\) | \(A_2B_1\) | \(A_2B_2\) |
|---|---|---|---|---|
| \(A_1B_2\) | \(-\) | \(1\) | \(1-hs\) | \(1-hs\) |
| \(A_2B_1\) | \(-\) | \(-\) | \(1-s\) | \(1-s\) |
| \(A_2B_2\) | \(-\) | \(-\) | \(-\) | \(1-s\) |
La matriz anterior es fácil de entender. Como solo el primer locus se encuentra bajo selección, todos los genotipos que compartan los mismos dos alelos en el locus A tendrán el mismo fitness. Por ejemplo, \(A_1B_1/A_1B_1\) será equivalente a \(A_1B_1/A_1B_2\) y a \(A_1B_2/A_1B_2\), ya que en los tres casos se trata de genotipos homocigotas \(A_1/A_1\) para el primer locus. Con este cuadro y los resultados previos vamos a ver qué ocurre con las frecuencias alélicas luego de una generación de selección.
Calculemos primero los fitness marginales y el fitness medio. Para los fitness marginales usamos la ecuación (5.31)
\[\begin{equation} \bar{w}_i=\frac{\sum_{j=1}^{4} x_ix_jw_{ij}}{x_i}=\sum_{j=1}^{4} x_jw_{ij} \end{equation}\]
que, sustituyendo los \(w_{ij}\) por los valores en la matriz de arriba, nos da para \(\bar{w}_1\)
\[ \begin{split} \bar{w}_1=x_1w_{11}+x_2w_{12}+x_3w_{13}+x_4w_{14}=x_1 \cdot (1)+x_2 \cdot (1)+x_3 \cdot (1-hs)+x_4 \cdot (1-hs)\ \therefore \\ \bar{w}_1=(x_1+x_2)+(1-hs) \cdot(x_3+x_4) \end{split} \tag{5.37} \]
pero \(x_1+x_2=p_1\), mientras que \(x_3+x_4=q_1\), por lo que
\[\begin{equation} \bar{w}_1=p_1+(1-hs)q_1=p_1+q_1-q_1hs \Leftrightarrow \bar{w}_1=1-q_1hs \tag{5.38} \end{equation}\]
En forma similar, teniendo en cuenta que \(w_{21}\) es en realidad equivalente al \(w_{12}\), porque en nuestra matriz es un requisito que \(i \leqslant j\), entonces
\[ \begin{split} \bar{w}_2=x_1w_{12}+x_2w_{22}+x_3w_{23}+x_4w_{24}=(x_1+x_2)+(x_3+x_4)(1-hs) \therefore \\ \bar{w}_2=1-q_1hs \end{split} \tag{5.39} \]
Por otro lado, para \(\bar{w}_3\) tenemos
\[\bar{w}_3=x_1w_{13}+x_2w_{23}+x_3w_{33}+x_4w_{34}=(x_1+x_2)(1-hs)+(x_3+x_4)(1-s)\ \therefore \] \[\begin{equation} \bar{w}_3=p_1-p_1hs+q_1-q_1s = p_1 + q_1 -p_1hs -q_1s = 1-p_1hs-q_1s \tag{5.40} \end{equation}\]
Finalmente, para \(\bar{w}_4\) tenemos
\[\bar{w}_4=x_1w_{14}+x_2w_{24}+x_3w_{34}+x_4w_{44}=(x_1+x_2)(1-hs)+(x_3+x_4)(1-s)\ \therefore \] \[\begin{equation} \bar{w}_4=p_1-p_1hs+q_1-q_1s = p_1+q_1-p_1hs-q_1s = 1-p_1hs-q_1s \tag{5.40} \end{equation}\]
Resumiendo, tenemos que \(\bar{w}_1=\bar{w}_2=1-q_1hs\) y \(\bar{w}_3=\bar{w}_4=1-p_1hs-q_1s\).
Para calcular el fitness medio usamos la ecuación (5.32)
\[\begin{equation} \bar{w}=\sum_{i=1}^{i=4} x_i\bar{w}_{i} \end{equation}\]
y, sustituyendo en ella los valores de los fitness marginales obtenidos más arriba, nos dejan
\[\bar{w}=x_1\bar{w}_1+x_2\bar{w}_2+x_3\bar{w}_3+x_4\bar{w}_4 = \] \[x_1 (1-q_1hs) + x_2 (1-q_1hs) + x_3(1-p_1hs-q_1s) + x_4(1-p_1hs-q_1s)\] \[(x_1+x_2)(1-q_1hs)+(x_3+x_4)(1-p_1hs-q_1s)\ \therefore\] \[\bar{w}=p_1(1-q_1hs)+q_1(1-p_1hs-q_1s)=p_1-p_1q_1hs+q_1-p_1q_1hs-q_1^2s\ \therefore\] \[\begin{equation} \bar{w}=1-2p_1q_1hs-q_1^2s \tag{5.41} \end{equation}\]
Este fitness medio es equivalente al que vimos en el capítulo anterior, cosa que no sorprende ya que en última instancia estamos trabajando con selección en un locus mientras consideramos que el otro es neutral. Veamos ahora el cambio en la frecuencia del alelo \(A_1\). Como \(p_1=x_1+x_2\), tenemos que \(\Delta p_1=\Delta x_1 + \Delta x_2\). A partir de las ecuaciones (5.35) y (5.36), tenemos
\[\Delta x_1+\Delta x_2=\frac{x_1(\bar{w}_1-\bar{w})-rw_{14}D}{\bar{w}}+\frac{x_2(\bar{w}_2-\bar{w})+rw_{14}D}{\bar{w}} \Leftrightarrow\] \[\Delta x_1+\Delta x_2=\frac{x_1(\bar{w}_1-\bar{w})-rw_{14}D+x_2(\bar{w}_2-\bar{w})+rw_{14}D}{\bar{w}} \Leftrightarrow\] \[\begin{equation} \Delta x_1+\Delta x_2=\frac{x_1(\bar{w}_1-\bar{w})+x_2(\bar{w}_2-\bar{w})}{\bar{w}} \tag{5.42} \end{equation}\]
Como \(x_1+x_2=p_1\) y \(\bar{w}_1=\bar{w}_2\), sustituyendo en la ecuación (5.42) tenemos que
\[\begin{equation} \Delta x_1+\Delta x_2=\frac{p_1(\bar{w}_1-\bar{w})}{\bar{w}}=\Delta p_1 \tag{5.43} \end{equation}\]
Sustituyendo ahora por los correspondientes valores de fitness marginal \(\bar{w}_1\) y fitness medio \(\bar{w}\) en la ecuación (5.43), tenemos
\[\Delta p_1=\frac{p_1[(1-q_1hs)-(1-2p_1q_1hs-q_1^2s)]}{\bar{w}} \Leftrightarrow \Delta p_1=\frac{p_1[1-q_1hs-1+2p_1q_1hs+q_1^2s]}{\bar{w}} \Leftrightarrow\] \[\Delta p_1=\frac{p_1[-q_1hs+2p_1q_1hs+q_1^2s]}{\bar{w}} \Leftrightarrow \Delta p_1=\frac{p_1q_1s[-h+p_1h+p_1h+q_1]}{\bar{w}} \Leftrightarrow\] \[\Delta p_1=\frac{p_1q_1s[-h+p_1h+(1-q_1)h+q_1]}{\bar{w}} \Leftrightarrow \Delta p_1=\frac{p_1q_1s[-h+p_1h+h-hq_1+q_1]}{\bar{w}} \Leftrightarrow\]
\[\begin{equation} \Delta p_1=\frac{p_1q_1s[p_1h+q_1(1-h)]}{\bar{w}} \tag{5.44} \end{equation}\]
El resultado final en (5.44) es idéntico al cambio en frecuencia \(\Delta_s p\) que obtuvimos en el capítulo Selección Natural, cuando desarrollamos el caso para un solo locus. Esto tampoco nos debería extrañar, ya que continuamos trabajando considerando que la selección selección opera en un solo locus (el \(A\)). Pasemos ahora a analizar el efecto en el segundo locus (que es neutral). Para observar qué ocurre respecto al cambio de frecuencia en este locus debemos recordar que \(p_2=x_1+x_3\).
Luego, partir de las ecuaciones (5.36)
\[\Delta p_2=\Delta x_1+\Delta x_3=\frac{x_1(\bar{w}_1-\bar{w})-rDw_{14}}{\bar{w}}+\frac{x_3(\bar{w}_3-\bar{w})+rDw_{14}}{\bar{w}} \Leftrightarrow\] \[\Delta p_2=\frac{x_1(\bar{w}_1-\bar{w})+x_3(\bar{w}_3-\bar{w})-rDw_{14}+rDw_{14}}{\bar{w}} \Leftrightarrow\] \[\Delta p_2=\frac{x_1(\bar{w}_1-\bar{w})+x_3(\bar{w}_3-\bar{w})}{\bar{w}}\]
Como \(p_2=x_1+x_3\), tenemos
\[\Delta p_2=\frac{x_1\bar{w}_1+x_3\bar{w}_3-(x_1+x_3)\bar{w}}{\bar{w}} \Leftrightarrow\] \[\begin{equation} \Delta p_2=\frac{x_1\bar{w}_1+x_3\bar{w}_3-p_2\bar{w}}{\bar{w}} \tag{5.45} \end{equation}\]
De acuerdo a las ecuaciones (5.7) y (5.8), \(x_1=p_1p_2+D\) y \(x_3=q_1p_2-D\), mientras que las ecuaciones (5.38) y (5.40) indican que \(\bar{w}_1=1-q_1hs\) y \(\bar{w}_3=1-p_1hs-q_1s\), por lo que sustituyendo en (5.45) tenemos
\[\Delta p_2=\frac{(p_1p_2+D)[1-q_1hs]+(q_1p_2-D)[1-p_1hs-q_1s]-p_2\bar{w}}{\bar{w}} =\] \[\frac{p_1p_2-p_1p_2q_1hs+D-Dq_1hs+q_1p_2-p_1p_2q_1hs-p_2q_1^2s-D+Dp_1hs+Dq_1s-p_2\bar{w}}{\bar{w}} \Leftrightarrow \] \[\Delta p_2=\frac{p_1p_2-2p_1p_2q_1hs-Dq_1hs+q_1p_2-p_2q_1^2s+Dp_1hs+Dq_1s-p_2\bar{w}}{\bar{w}} \Leftrightarrow\] \[\Delta p_2=\frac{p_2(p_1+q_1)-2p_1p_2q_1hs-Dq_1hs-p_2q_1^2s+Dp_1hs+Dq_1s-p_2\bar{w}}{\bar{w}} \Leftrightarrow\] \[\begin{equation} \Delta p_2=\frac{p_2[1-2p_1q_1hs-q_1^2s]-Dq_1hs+Dp_1hs+Dq_1s-p_2\bar{w}}{\bar{w}} \tag{5.46} \end{equation}\]
Pero de acuerdo a la ecuación (5.41) tenemos que \(\bar{w}=1-2p_1q_1hs-q_1^2s\), por lo que sustituyendo en la ecuación (5.46) tenemos ahora
\[ \begin{split} \Delta p_2=\frac{p_2\bar{w}-Dq_1hs+Dp_1hs+Dq_1s-p_2\bar{w}}{\bar{w}} \Leftrightarrow \\ \Delta p_2=\frac{-Dq_1hs+Dp_1hs+Dq_1s}{\bar{w}} \Leftrightarrow \\ \Delta p_2=\frac{Ds[p_1h-q_1h+q_1]}{\bar{w}} \Leftrightarrow \end{split} \tag{5.47} \]
Finalmente, como \(-q_1h+q_1=q_1(1-h)\), sustituyendo en (5.47) tenemos
\[\begin{equation} \Delta p_2=\frac{Ds[p_1h+q_1(1-h)]}{\bar{w}} \tag{5.48} \end{equation}\]
El resultado de la ecuación (5.48) es de fundamental importancia. Si \(D \ne 0\), entonces pese a que el locus \(B\) no está directamente bajo ninguna presión selectiva, la frecuencia del alelo \(B_1\) cambiará de acuerdo a la ecuación (5.48). Si \(D > 0\), entonces crecerá la frecuencia del alelo \(B_1\) que se encuentra en fase de acoplamiento, y si \(D<0\) entonces decrecerá \(B_1\) (al aumentar \(A_1\)), o lo que es lo mismo aumentará \(B_2\) que se encuentra en fase de repulsión.
PARA RECORDAR
- El cambio en la frecuencias de los gametos en una generación está dado por las ecuaciones
\[\Delta x_1=\frac{x_1(\bar{w}_1-\bar{w})-rw_{14}D}{\bar{w}}\] \[\Delta x_2=\frac{x_2(\bar{w}_2-\bar{w})+rw_{14}D}{\bar{w}}\] \[\Delta x_3=\frac{x_3(\bar{w}_3-\bar{w})+rw_{14}D}{\bar{w}}\] \[\Delta x_4=\frac{x_4(\bar{w}_4-\bar{w})-rw_{14}D}{\bar{w}}\]
- En el modelo en que un locus se encuentra bajo selección pero no los loci vecinos (en desequilibrio de ligamiento), el cambio de frecuencia del alelo \(A_1\) será igual que en modelo de un solo locus bajo selección, es decir
\[\begin{equation} \Delta p_1=\frac{p_1q_1s[p_1h+q_1(1-h)]}{\bar{w}} \end{equation}\]
- Bajo este mismo modelo, el cambio de frecuencia del alelo \(B_1\) en el locus que no está bajo selección directa (segundo locus) está dado por la ecuación
\[\begin{equation} \Delta p_2=\frac{Ds[p_1h+q_1(1-h)]}{\bar{w}} \end{equation}\]
En todos los casos, el fitness medio está dado por \(\bar{w}=1-2p_1q_1hs-q_1^2s\)
5.5 Arrastre genético (“genetic hitchhiking” o “genetic draft”)
A esta altura te estarás preguntando ¿qué consecuencias tiene el fenómeno descrito al final de la sección anterior? Desde un punto de vista evolutivo el fenómeno anterior tiene la enorme importancia de que aún las regiones del genoma que no se encuentran bajo selección directa por ninguna característica (tanto a nivel nucleotídico, aminoacídico o en ningún otro nivel) y que por lo tanto podrían considerarse neutrales pueden estar sujetas a las consecuencias de la selección si están asociadas (en desequilibrio de ligamiento) con algún locus bajo selección. Una analogía para esto sería que para las regiones que están cerca del locus bajo selección los alelos viajan (se da un cambio en sus frecuencias alélicas) “sin pagar” (el precio de la selección), y por lo que al fenómeno anterior se lo conoce como hitchhiking genético (del inglés, “hacer dedo” o “autostop”). El término fue acuñado por John Maynard Smith 57 y John Haigh (Maynard Smith and Haigh 1974), pese a no ser los primeros en trabajar la idea. De cualquier manera, pese al atractivo del nombre, la idea continuó relativamente desatendida hasta que el artículo de John Gillespie (J. H. Gillespie 2000) resaltó su posible papel como la fuerza estocástica dominante sobre la deriva.
Claramente, a partir de lo anterior, un locus bajo selección puede arrastrar todo un segmento del cromosoma en que se encuentra en la dirección en que opera la selección sobre dicho locus. Para ello es necesario que exista un desequilibrio de ligamiento con las regiones asociadas estadísticamente, usualmente las colindantes. En el caso de que el desequilibrio de ligamiento inicial sea relativamente importante, con una tasa de recombinación \(r\) baja en relación al coeficiente de selección \(s\), como es poco probable la aparición de recombinación en ese fragmento entonces el alelo más asociado en el segundo locus al alelo favorecido en el primero seguirá su camino. Esto, como una función continua de la distancia, implica que todo lo que esté asociado en otras posiciones del genoma a ese alelo favorecido sufrirá cambios en la misma dirección. Si el destino del alelo favorecido es la fijación, las regiones del genoma que estén suficientemente ligadas al mismo tendrán también una ventaja para ir hacia la fijación que no ganaron por derecho propio. El fenómeno dependerá del alcance de la relación \(r/s\). La consecuencia directa de esto es la pérdida de heterocigosidad, o el aumento de homocigosidad en los loci asociados estadísticamente.
El caso típico es aquel en que una nueva mutación que llega a un locus (llamémosle \(A\)), que hasta el momento no tenía alelos (al menos alelos que no fuesen neutrales). Este nuevo alelo \(A_1\) se encontrará en frecuencia \(\frac{1}{2N}\), y por lo tanto los alelos viejos (todos los que no son el \(A_1\)) se encontrarán en frecuencia \(1-(\frac{1}{2N})\). Supongamos que el locus \(A\) se encuentra relativamente cerca de otro, \(B\), con dos alelos \(B_1\) y \(B_2\) selectivamente neutros. Nuestro nuevo alelo \(A_1\) le confiere ventajas a los genotipos en los que se encuentra, por lo que siguiendo el modelo que vimos en la sección previa estos tendrán un fitness relativo de \(1\) (\(A_1A_1\)), \(1-hs\) (\(A_1A_2\)) y \(1-s\) (\(A_2A_2\)). ¿Qué ocurrirá en el locus \(B\) si la fracción de recombinantes entre \(A\) y \(B\) es \(r\)?. En principio, el alelo \(A_1\) puede haber caído en un cromosoma que tenía el alelo \(B_1\) en el otro locus (con probabilidad \(p_2\)), o en un cromosoma conteniendo el alelo \(B_2\) (con probabilidad \(q_2=1-p_2\)). En función de esto se puede calcular el desequilibrio de ligamiento \(D\), así como el cambio en frecuencia \(p_2\) (y obviamente en \(p_1\)). Sin embargo, no existe una forma fácil y cerrada de describir la trayectoria de esta evolución a lo largo de las generaciones, siendo la aproximación más fácil la simulación en una computadora.
En la Figura 5.8 podemos ver el resultado de la reducción de heterocigosidad al simular la situación anterior para 3 tamaños poblacionales, de \(N=100\), \(N=1000\) y \(N=5000\) individuos, con un coeficiente de selección \(s=0,1\) y variando \(r\) desde \(0\) a \(0,001\) para variar la relación \(r/s\) (con signo negativo a la izquierda del locus seleccionado) y con frecuencias iniciales en el locus \(B\) (antes de la mutación en el \(A\)) de \(p_2=q_2=\frac{1}{2}\). Como \(p_2=q_2=\frac{1}{2}\), es indistinto el análisis de las dos situaciones (i.e. el estado del alelo en el locus \(B\) próximo a donde surge \(A_1\)). A medida de que el tamaño poblacional aumenta, menos se extiende el efecto de la reducción de heterocigosidad con la distancia. Esto se podría asociar directamente con el valor del desequilibrio de ligamiento (\(D=x_1x_4-x_2x_3\)), el cual se puede calcular directamente a partir \(x_1=\frac{1}{2N}\), \(x_2=0\), \(x_3=1-\frac{1}{2N}\), \(x_4=0,5\), donde modelamos la situación planteando arbitrariamente que \(A_1\) surge en proximidad de un alelo \(B_1\)58. Notemos que esto implica \(D=x_1x_4-x_2x_3=(\frac{1}{2})(\frac{1}{2N}) - 0 \cdot (1-\frac{1}{2N})=\frac{1}{4N}\). En efecto, a medida que aumenta \(N\) se incremente el denominador y decrece el desequilibrio inicial.
La otra cosa importante que apreciamos en la figura es que la reducción no opera en forma lineal con la distancia, al menos cuando esta es medida a partir de la tasa de recombinación (en la figura \(s=0,1\) se mantuvo constante, por lo que el cambio en \(r/s\) se debe solo al cambio de \(r\) en nuestro ejemplo). Más allá del cambio en el desequilibrio de ligamiento inicial, en las tres gráficas de la figura se observa un patrón similar: en el entorno muy cercano al locus bajo selección se observa una reducción de la heterocigosidad muy importante, pero la misma tiende a desaparecer rápidamente a medida que nos alejamos del mismo. De hecho, ni siquiera para el tamaño poblacional más pequeño el efecto se extiende más allá del entorno \(\left|\frac{r}{s}\right| < 0,10\). Esto puede parecer, en principio, un efecto muy pequeño. Sin embargo, en humanos un estimado general es del orden de 1 Mb/cM (centi-Morgan59), es decir 1 millón de nucleótidos por cada \(0,01=1\%\) de recombinación. Tomando en cuenta este número (que, repetimos, es una primera aproximación) en el gráfico de la derecha, notemos que el corte con la línea verde (reducción del \(25\%\)) ocurre en \(r/s=0,042\), y como \(s=0,10\) entonces la tasa de recombinación es de \(r=0,0042=0,42\%\). Traducido a nucleótidos, esta estimación nos da en el entorno de \(400\)Kb (400 mil bases). Dicho de otra forma, si tenemos una nueva mutación con coeficiente de selección \(s=0,10\), a 400Kb del locus donde ocurre la misma se esperaría ver una reducción de la heterocigosidad del \(25\%\). Si pudiésemos afinar más en la gráfica (nosotros lo hicimos ya en forma numérica), a los \(100\)Kb del locus seleccionado, con el mismo coeficiente de selección \(s=0,10\) y el mismo tamaño poblacional (\(N=5000\)), la reducción de la heterocigosidad es \(>70\%\), mientras que a \(10\)Kb la reducción es \(>95\%\). Obviamente un tamaño poblacional de \(N=5000\) es extremadamente pequeño en poblaciones humanas modernas, aunque no necesariamente en el pasado.
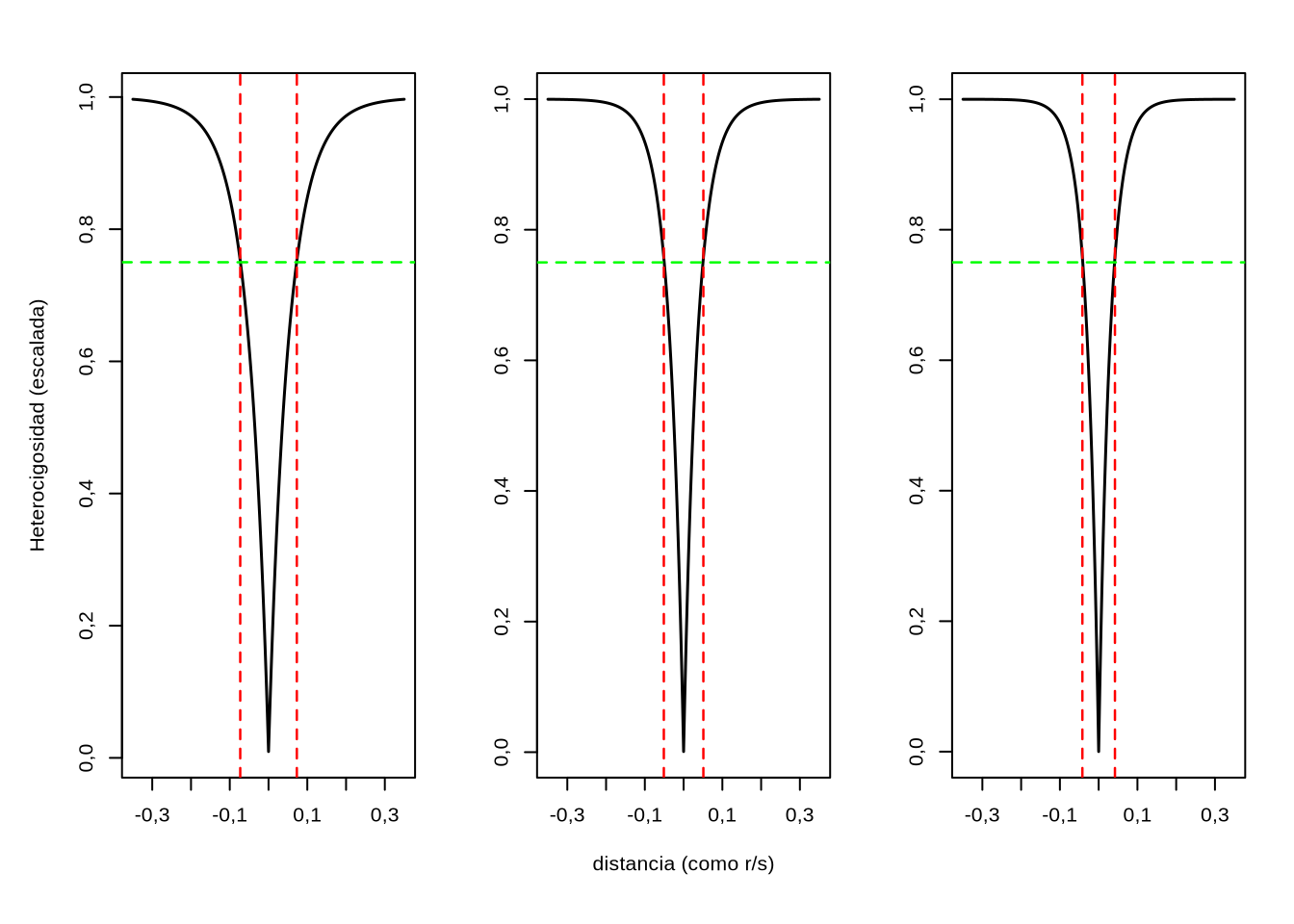
Figura 5.8: Heterocigosidad final (relativa a la inicial) en función de la distancia a un locus bajo selección direccional. La distancia al locus bajo selección se muestra como \(r/s\) a ambos lados del mismo (el cero corresponde al locus bajo selección). Los parámetros para esta simulación fueron, \(N=100\), \(N=1000\) y \(N=5000\) individuos (de izquierda a derecha), \(h=\frac{1}{2}\), \(s=0,1\) y variando \(r\) desde \(0\) a \(0,001\) para variar la relación \(r/s\) (con signo negativo a la izquierda del locus seleccionado). Se aprecia claramente que el efecto fuerte del hitchhiking es bastante local, del entorno de \(|r/s|<0,05\), aunque esto puede significar miles de pares de bases. En rojo la distancia (como \(r/s\)) en la que se alcanza una reducción del \(25\%\) de la heterocigosidad (es decir, la misma es el \(75\%\) del valor inicial).
Las tasas de recombinación varían entre géneros, y aún dentro de los géneros entre especies, entre cromosomas y más aún dentro de los mismos en distintas regiones. Existen estudios variados sobre la tasa de recombinación a estas distintas escalas. Por ejemplo, en un mapa de ligamiento del genoma bovino Arias y colaboradores concluyen que para los cromosomas autosomales la distancia genética por cM es de \(1,25\) Mb, o al revés \(\approx 0,8\) Mb/cM (Arias et al. 2009). Estimaciones más precisas para el genoma humano son del orden de \(0,75\) Mb/cM, lo que coincide razonablemente con el genoma bovino del que no estamos tan lejos en términos evolutivos. Kong y colaboradores estimaron que el total del genoma humano en mujeres abarca 4460 cM, mientras que el de los varones es de 2590 cM (Kong et al. 2002). Sardell y Kirkpatrick encuentran que en general, en distintas especies, los hotspots de recombinación se encuentran distribuidos hacia los telómeros, mientras que en hembras la distribución es más uniforme (Sardell and Kirkpatrick 2020). Si bien se desconoce el mecanismo molecular que se encuentra por detrás de este fenómeno, se sabe que los paisajes de la cromatina (“chromatin landscapes”, en inglés) juegan un rol importante. Kong y colaboradores, utilizando datos de 15.257 pares padre-hijo, encontraron que aproximadamente \(15\%\) de los hotspots son específicos de cada sexo (Kong et al. 2010). Por otro lado, Baudat y colaboradores demostraron que el gen PRDM9 es un determinante mayor de los sitios de recombinación en humanos y en ratón, con sus variantes alélicas asociadas a variación en el número de los mismos, lo que contribuiría a explicar variaciones dentro y posiblemente entre especies (Baudat et al. 2010).
Si bien hasta ahora hemos visto el rol de dos fuerzas estocásticas en el cambio de las frecuencias aleĺicas, su importancia relativa está sujeta a diferentes factores. En el caso de la deriva genética la dependencia es inversa respecto al tamaño poblacional efectivo, el factor del que depende. A tamaños poblacionales efectivos moderados su importancia es baja. Por el contrario, en el genetic draft existe una dependencia respecto al coeficiente de selección en el locus bajo selección y al desequilibrio de ligamiento entre este y los loci adyacentes (factor que a su vez tiene una cierta dependencia con el tamaño poblacional, como vimos). Sin embargo, a medida de que crece el tamaño poblacional se llega a un punto donde el draft domina al drift como fuerza estocástica.
PARA RECORDAR
El efecto de genetic draft o hitchhiking es el que corresponde a un locus bajo selección que en razón del desequilibrio de ligamiento con loci vecinos arrastra a los mismos en el proceso selectivo, más allá de que los mismos sean selectivamente “neutros”.
Eventualmente, si la relación \(r/s\) es relativamente grande, se producirán recombinaciones entre los loci (el locus seleccionado y el neutral), lo que llevará a un equilibrio distinto a la fijación en el locus neutral.
Cuando aparece un nuevo alelo ventajoso en un locus que hasta el momento solo presentaba alelos neutrales, el fenomeno de hitchhiking suele implicar una reducción importante de la heterocigosidad en la vecindad del locus seleccionado. La importancia y extensión de este efecto depende de la relación \(r/s\) y del tamaño poblacional.
En general resulta difícil o imposible encontrar soluciones explícitas a varios de los problemas asociados al draft, por lo que una buena aproximación es la simulación computacional.
5.6 Causas del desequilibrio de ligamiento
Hasta ahora hemos manejado el desequilibrio de ligamiento como una condición mecanísticamente asociada a la cercanía física de los loci en el mismo cromosoma, y por lo tanto a la probabilidad de que alelos en los mismos compartan destino en los gametos. En este sentido, vimos la influencia de la selección en un locus y una fracción de recombinantes menor a \(\frac{1}/{2}\) con otros loci como la causa de “arrastre” de esos otros loci y, en ciertas condiciones, el desarrollo de un desequilibrio de ligamiento. Cuando arriba un nuevo alelo en un locus determinado siempre lo hace en alguna configuración particular con los loci vecinos al mismo (i.e., una combinación particular de alelos en estos). Ya estudiamos previamente su devenir si el nuevo alelo tiene ventajas selectivas. Sin embargo, la selección no es la única causa posible asociada a una fracción de recombinación menor a \(\frac{1}/{2}\); en principio, en poblaciones pequeñas el efecto de la deriva puede ocasionalmente incrementar la frecuencia del alelo nuevo y aún llevarlo a la fijación (aunque con baja probabilidad). ¿Cómo sucede esto? Dado que el alelo se origina para alguna configuración particular de alelos en otros loci, si el alelo incrementa su frecuencia por azar (i.e., deriva genética), en la medida que exista una ausencia relativa de recombinación también se espera un aumento de la frecuencia para los alelos de los otros loci que comparten configuración con él. Esto, al aumentar la correlación de estados alélicos compartidos, incrementará el valor de \(r^2\) y también de \(D\).
Si en lugar de considerar el fenómeno del desequilibrio de ligamiento desde el punto de vista de los mecanismos de transmisión de la información genética lo consideramos simplemente desde el punto de vista estadístico como la no-independencia de las frecuencias entre loci, entonces desaparece la necesidad de una explicación estrictamente asociada a estos mecanismos. Un ejemplo claro de esto es cuando aparecen correlaciones entre estados alélicos en diferentes cromosomas. En este caso ya no podemos usualmente apelar a la cercanía física, y es necesario invocar otros mecanismos. Uno de los procesos poblacionales que pueden explicar este “desequilibrio” (en realidad, apenas la no-independencia) es la existencia de determinadas estructuras poblacionales, como veremos a continuación.
Desequilibrio debido al mestizaje
Supongamos que tenemos dos poblaciones de la misma especie que han evolucionado en paralelo durante un tiempo relativamente importante respecto al tamaño poblacional como para que la deriva pueda hacer su trabajo en el cambio de las frecuencias alélicas. Supongamos también que vamos a estudiar dos loci bi-alélicos en particular en ambas poblaciones, que además se encuentran en equilibrio de Hardy-Weinberg. Luego del análisis genómico logramos determinar las frecuencias de los 4 haplotipos posibles, que son las que aparecen en el siguiente cuadro (bajo las columnas Población 1 y Población 2):
| \(\textbf{Gameto/estadístico}\) | \(\textbf{Frecuencia}\) | \(\textbf{Población 1}\) | \(\textbf{Población 2}\) | \(\textbf{Población mezcla}\) |
|---|---|---|---|---|
| \(A_1B_2\) | \(x_2\) | \(0,09\) | \(0,09\) | \(0,09\) |
| \(A_2B_1\) | \(x_3\) | \(0,09\) | \(0,09\) | \(0,09\) |
| \(A_2B_2\) | \(x_4\) | \(0,01\) | \(0,81\) | \(0,41\) |
| \(p_1\) | \(x_1+x_2\) | \(0,90\) | \(0,10\) | \(0,50\) |
| \(p_2\) | \(x_1+x_3\) | \(0,90\) | \(0,10\) | \(0,50\) |
| \(D\) | \(-\) | \(0\) | \(0\) | \(0,16\) |
| \(D_\text{max}\) | \(-\) | \(0,09\) | \(0,09\) | \(0,25\) |
| $D$ | \(-\) | \(0\) | \(0\) | \(0,64\) | | \(r^2\) | \(-\) | \(0\) | \(0\) | \(0,41\) | |
A partir de las frecuencias de los haplotipos podemos calcular las frecuencias de los alelos, como ya lo hemos hecho antes. Por ejemplo, la frecuencia del alelo \(A_1\) la calculamos como \(p_1=x_1+x_2\). Como vemos a partir de las líneas de \(p_1\) y \(p_2\) en el cuadro de arriba, mientras que en la Población 1 la frecuencia del alelo \(A_1\) es \(p_1=0,9\), en la Población 2 \(p_1=0,10\). Curiosamente (en realidad, a fin de mostrar el punto con número claros) para el alelo \(B_1\) (del segundo locus) las frecuencias son también \(p_2=0,9\) para la Población 1 y \(p_2=0,1\) para la Población 2.
Veamos ahora qué ocurre con el desequilibrio de ligamiento dentro de ambas poblaciones. Si recordamos que \(D=x_1x_4-x_2x_3\), haciendo los cálculos tenemos que para la Población 1, \(D=0,81 \cdot 0,01 - 0,09 \cdot 0,09=0\), mientras que para la Población 2, \(D=0,01 \cdot 0,81 - 0,09 \cdot 0,09=0\). Es decir, llegamos a la conclusión de que dentro de ambas poblaciones el desequilibrio de ligamiento para estos dos loci es cero. Como \(D=0\), entonces también lo será \(D'=\frac{D}{D_\text{máx}}\) (no importa si usamos \(D_\text{máx}\) o \(D_\text{mín}\) en el denominador, ya que el numerador es cero) y también tenemos \(r^2=\frac{D^2}{p_1q_1p_2q_2} = 0\). Solo para chequear de que no se trata de un artefacto producto de que dadas las frecuencias sea imposible que se encuentren en desequilibrio de ligamiento, calculamos el \(D_\text{máx}=mín(p_1q_2,q_1p_2)\) para ambas poblaciones, que es igual a \(0,09\) en ambas.
Hasta aquí nada sorprendente. Veamos qué ocurre si ahora formamos una nueva población, mezclando la mitad de los individuos de la Población 1 con la mitad de los individuos de la Población 2. Los resultados de mezclar estas dos poblaciones se encuentran en la última columna del cuadro de arriba. Como mezclamos mitad y mitad los individuos, las frecuencias de los haplotipos y de los alelos serán simplemente la media aritmética de las frecuencias en ambas poblaciones. Por ejemplo, para la frecuencia del haplotipo \(A_1B_1\) tenemos \(x_1=\frac{0,81 + 0,01}{2}=0,41\), mientras que las del \(A_1B_2\) es de \(x_2=\frac{0,09 + 0,09}{2}=0,09\) (el mismo cálculo para los restantes). Lo mismo para las frecuencias alélicas, donde \(p_1=\frac{0,9 + 0,1}{2}=0,5\) y \(p_2=\frac{0,9 + 0,1}{2}=0,5\). Veamos entonces qué ocurre con el desequilibrio de ligamiento. Usando las frecuencias de los haplotipos calculadas para la población mezcla, tenemos que \(D=x_1x_4-x_2x_3=0,41 \cdot 0,41 - 0,09 \cdot 0,09=0,16\). Este es un resultado por lo menos sorprendente, considerando que en ambas poblaciones ambos loci se encontraban en equilibrio de ligamiento. Si ahora calculamos los otros dos estadísticos de desequilibrio para esta población mezcla, tenemos \(D'= \frac{0,16}{0,25} = 0,64\) y \(r^2= \frac{0,16^2}{0,5 \cdot 0,5 \cdot 0,5 \cdot 0,5} = 0,41\). O sea, en la nueva población no solo tenemos un desequilibrio de ligamiento distinto de cero, sino que además el mismo es del \(64\%\) de su valor máximo posible para las frecuencias alélicas en ambos loci. ¿De dónde sale este desequilibrio?
Si prestamos atención al cuadro veremos que las diferencias de frecuencias en los alelos entre poblaciones es muy importante para ambos loci. Pese a esto, dentro de cada población las frecuencias de los haplotipos simplemente siguen lo esperado para la independencia (e.g., \(p_1p_2\) para el haplotipo \(A_1B_1\)). Sin embargo, pese a que en cada población uno de los haplotipos en fase de acoplamiento presenta una frecuencia muy alta, el descenso en la frecuencia del otro haplotipo en la misma fase es tan importante como para hacer que el producto de las frecuencias de los gametos en fase de acoplamiento sea idéntico al de las frecuencias de los gametos en fase de repulsión (i.e., \(x_1x_4=x_2x_3\)). En nuestro caso \(0,81 \cdot 0,01=0,081\) compensa perfectamente \(0,09 \cdot 0,09=0,081\). Ahora, cuando mezclamos las dos poblaciones que tienen cada una frecuencia alta para uno de los dos gametos en fase de acoplamiento (pero \(A_1B_1\) en una y \(A_2B_2\) en la otra), el promedio son dos frecuencias relativamente altas de los dos gametos en fase de acoplamiento (\(0,41\) para ambos, en nuestro caso). Es decir, la frecuencia alta en \(A_1B_1\) no es acompañado por una reducción suficiente en \(A_2B_2\). Ya que, en nuestro caso, el promedio de las frecuencias de los gametos en fase de repulsión se mantuvo en \(0,09\), se tiene que \(x_2x_3=0,09 \cdot 0,09=0,081\). Para que existiese equilibrio de ligamiento en la nueva población mezcla \(x_1x_4\) también debería ser \(0,081\), cosa que no ocurre ya que \(0,41 \cdot 0,41=0,1681\), y de ahí el desequilibrio de ligamiento observado.
Es de notar que al invocar este mecanismo no hicimos uso de la fracción de recombinantes ni en forma explícita ni implícita, por lo que el mismo proceso podría haberse adjudicado a dos loci que se encontrasen a suficiente distancia para que se cumpla \(r=\frac{1}{2}\) e incluso, con alguna modificación leve al ejemplo, que estuviesen en cromosomas diferentes.
Desequilibrio inducido por el sistema de apareamiento
En algunas especies de plantas la auto-fertilización es moneda corriente, variando la tasa de la misma. Cuando se produce auto-fertilización se produce una reducción de los heterocigotas, ya que la misma es un caso extremo de inbreeding, concepto que veremos en más detalle en el capítulo Apareamientos no-aleatorios. La lógica es igual sencilla: los loci en los que una planta dada son heterocigotas tienen una probabilidad de \(50\%\) en auto-fertilización de dejar descendencia heterocigota, mientras que el otro \(50\%\) será homocigota. Los homocigotas de la nueva generación solo podrán dejar descendencia homocigota, pero lo heterocigotas tendrán nuevamente un \(50\%\) de chance de dejar heterocigotas (es decir, \(50\%\) del \(50\%\) de la generación anterior). Claramente, de continuar esa progresión la fracción de heterocigotas decaerá en función de \(\left(\frac{1}{2}\right)^t\), siendo \(t\) el número de generaciones.
Supongamos ahora dos loci que son homocigotos en la misma planta. Los eventos de recombinación entre ellos para la producción de gametos serán completamente irrelevantes (para estos dos loci) ya que los gametos producidos siempre serán del mismo tipo (porque para cada loci hay un solo alelo, dado que son homocigotos). Más aún, el efecto de la auto-fertilización disminuye el número de dobles heterocigotas, \(A_1B_2\) y \(A_2B_1\), fundamentales para reducir el desequilibrio de ligamiento. Por lo tanto, en función de la proporción de auto-fertilización esperamos una reducción de la eficiencia en el proceso que elimina el desequilibrio. Pese a la importancia de este fenómeno en el mantenimiento del desequilibrio de ligamiento, aún pequeñas tasas de outcrossing (i.e., cruzamiento con otras plantas no emparentadas) reduce rápidamente el efecto ya que quiebra los bloques haplotípicos formados. Un bloque haplotípico es una serie de variantes (e.g., SNPs) que se encuentran en fuerte desequilibrio de ligamiento entre todos ellos, siendo usualmente definido por un valor de \(r^2\) (todos los marcadores tienen al menos ese valor con los adyacentes). Al romperse un bloque por un evento de recombinación, a ambos lados se sigue manteniendo el desequilibrio pero ya no entre las variantes de lados diferentes. A modo de ejemplo, en Arabidopsis thaliana, una planta modelo para la experimentación que normalmente experimenta más del \(95\%\) de auto-fertilización, los bloques haplotípicos son del orden de las 100 kb (Nordborg et al. 2002), mientras que en especies como el maíz (que normalmente no experimenta auto-fertilización) los bloques haplotípicos son del orden de algunas decenas de miles de bases (Van Inghelandt et al. 2011).
El cromosoma Y
En mamíferos cromosoma Y representa una situación particular. Al no tener un homólogo para recombinar este proceso no forma parte del repertorio de mecanismos moleculares en su evolución, a diferencia del cromosoma X que sí puede recombinar con su homólogo en el caso de las hembras. Esto hace del cromosoma Y un cromosoma muy particular. De hecho, se trata de un cromosoma con muy pocos genes, habiendo perdido más del \(95\%\) de los mismos durante su evolución.
La ausencia de recombinación (en realidad hay un \(5\%\) del mismo que se recombina con el X), como ya vimos, implica la imposibilidad de “barajar” los alelos en diferentes loci para que el tamiz de la selección pueda “elegir” los mejores. Es decir, si una nueva mutación beneficiosa aparece en un locus determinado, su suerte será siempre acompañar a la configuración de alelos en otros loci del gameto en el que apareció. Si está configuración era ya beneficiosa, la misma posiblemente incrementará el fitness del portador, pero si la configuración era detrimental el riesgo de perder esta mutación es grande. A esto se suma que el cromosoma Y está sujeto a una mayor tasa de deriva genética que el resto, puesto que su aporte es solo \(\frac{1}{4}\) del aporte del resto (es la mitad de la información de los gametos sexuales en los machos, que son la mitad de los individuos, \((\frac{1}{2}) \cdot (\frac{1}{2}) =\frac{1}{4}\)).
La imposibilidad de recombinar impide en principio eliminar por selección los errores generados en la replicación, a lo cual se suma alta tasa mutacional de este cromosoma en particular. Eso llevaría a una situación catastrófica, con acumulación continua de errores y casi sin posibilidad de liberarse de ellos. Sin embargo, existe un mecanismo que en principio funcionaría en el cromosoma Y y que permite la reparación de algunos de ellos. Este mecanismo se llama conversión génica, y fue propuesto para el cromosoma Y por Rozen y colaboradores (Rozen et al. 2003). Su funcionamiento se basa en la existencia de secuencias palindrómicas (una secuencia repetida pero en el sentido contrario), las cuales permitirían la recombinación del cromosoma Y con sí mismo. Estos autores plantean que 8 palíndromos ocuparían la cuarta parte de la eucromatina de la región específica del macho (MSY, \(95\%\) del largo total) en el cromosoma humano y que unos 600 nucleótidos por recién nacido habrían experimentado recombinación Y-Y.
Desequilibrio debido a recombinación reducida
Los rearreglos cromosómicos son una de las fuentes importantes de evolución a nivel genómico. Una de ellas se relaciona con la inversión de segmentos cromosómicos alrededor de los centrómeros, por ejemplo en las moscas Drosophila pseudoobscura y D. subobscura. La inversión de un segmento de cromosoma en general inhibe la recombinación en el mismo por lo que todos los genes en el mismo están de alguna manera ligados físicamente. Igual que en el caso del cromosoma Y, esto conlleva la imposibilidad de “barajar” los alelos entre loci buscando las mejores combinaciones, pero al mismo tiempo las mutaciones beneficiosas que se acumulen tampoco serán separadas por eventos de recombinación. Finalmente, el mecanismo de conversión génica permite de alguna manera el flujo de información de un cromosoma al otro, sin recurrir a la recombinación, erosionando la estructura fija del bloque invertido.
PARA RECORDAR
El desequilibrio de ligamiento entre loci vecinos es un fenómeno cuya ocurrencia es esperable por los mecanismos subyacentes a la transmisión de la información genética. Los eventos de recombinación, que ocurren en forma aleatoria a lo largo de los cromosomas (aunque no con distribución uniforme) tienden a romper ese desequilibrio.
Más allá de las causas mecanísticas directas, como la vecindad en el cromosoma, otras veces el desequilibrio de ligamiento es producto de fenomenos a nivel poblacional, como por ejemplo cuando existe una estructuración de las poblaciones de la misma especie. Si existen diferencias importante en las frecuencias alélicas entre las subpoblaciones (producto por ejemplo de la deriva), aunque no exista desequilibrio de ligamiento en cada una de ellas, al considerarlas en su conjunto (una mezcla, por ejemplo), sí se puede observar desequilibrio de ligamiento bajo determinadas condiciones.
El cromosoma Y presenta una situación particular ya que en la mayor parte de su extensión no tiene posibilidad de recombinar con un homólogo (por ejemplo \(95\%\) en humano, el restante \(5\%\) con el X). Esto lleva a la imposibilidad de “barajar” los alelos en diferentes loci y por lo tanto el éxito de los nuevos alelos depende en gran medida de la “suerte” con la que cuenten al arribar a una determinada configuración de alelos en el cromosoma. El mecanismo de conversión génica Y-Y (o sea, dentro del mismo cromosoma) permite reducir el número de errores que se acumulan en el mismo por su escasa probabilidad de recombinación y de conversión génica con el homólogo.
En algunas especies, como las moscas Drosophila pseudoobscura y D. subobscura, la inversión de un segmento de cromosoma en torno al centrómero es frecuente. Esto inhibe la recombinación en ese segmento y todos los genes dentro del mismo van de alguna manera asociados en su destino, de forma análoga a lo que ocurre con el cromosoma Y. En este caso, sin embargo, es posible el mecanismo de conversión génica con el homólogo, que no depende de la recombinación, permitiendo un flujo de información entre ambos cromosomas y erosionando la estructura de bloque en el segmento.
5.7 Conclusión
Si dos o más loci se encuentran segregando de forma independiente en una población, podemos recurrir a las frecuencias alélicas en los mismos para calcular las frecuencias esperadas para combinaciones alélicas. En las poblaciones naturales esta expectativa de independencia no se cumple, observándose en muchos casos, en mayor o menor medida, un grado de asociación entre los alelos de diferentes loci. Diferentes métricas nos permiten cuantificar este fenómeno (tales como \(D\), el coeficiente \(D'\) o el estadístico \(r^2\)). Los motivos detrás del fenómeno de desequilibrio de ligamiento pueden ser variados, siendo quizá el más evidente la proximidad física (inversamente proporcional a la recombinación entre dos loci). La selección natural, e incluso la deriva genética, son fuerzas evolutivas que tenderán a generar este fenómeno de no-independencia. Según la historia poblacional, pueden tender a existir diferentes combinaciones alélicas con mayor o menor frecuencia, afectando así el fenotipo de los individuos portadores y las trayectorias evolutivas observadas. En contraposición, la recombinación gamética es una fuerza que tenderá a favorecer la independencia entre loci, disminuyendo la magnitud del desequilibrio de ligamiento con el tiempo.
5.8 Actividades
5.8.1 Control de lectura
Tanto la selección natural como la recombinación pueden influir en las frecuencias observadas para combinaciones de alelos de dos o más loci. Describa cómo la combinación de estas fuerzas influye en las frecuencias haplotípicas observadas.
El valor de desequilibrio de ligamiento \(D\) es dependiente de las frecuencias alélicas presentes en una población. Discuta: a) el rango de valores que se pueden observar en función de las frecuencias presentes en una población; y b) la utilidad del coeficiente \(D'\) al momento de comparar la magnitud de desequilibrio de ligamiento observado en distintas poblaciones o condiciones.
Desde un punto de vista estadístico el desequilibrio de ligamiento implica la no-independencia entre las frecuencias alélicas entre loci. Nombre al menos un escenario biológico que genere este fenómeno (además de los mecanismos de transmisión de la información genética).
Describa el fenómeno denominado “genetic hithchiking”. ¿Aumenta o disminuye su relevancia a medida que aumenta el tamaño de la población considerada?
Las ecuaciones para calcular los máximos y mínimos teóricos esperados para el desequilibrio de ligamiento \(D\) son diferentes según exista un exceso de gametos en fase de acoplamiento (\(D > 0\)) o en fase de repulsión (\(D < 0\)). ¿A qué se debe esta diferencia? (Pista: Tenga en cuenta cómo se expresan las frecuencias haplotípicas esperadas en función de las frecuencias alélicas y el valor \(D\)).
5.8.2 ¿Verdadero o falso?
Las tasas de recombinación varían entre especies de un mismo género. Esto se debe a que son constantes y características para cada cromsoma de las especies.
Las frecuencias alélicas de los loci que no tienen consecuencias directas sobre el fitness de los organismos portadores en un ambiente dado (i.e., loci selectivamente neutros) pueden apartarse de las frecuencias esperadas debido a los efectos de la selección.
La evolución del desequilibrio de ligamiento \(D\) depende de la tasa de recombinación \(r\). Ésta dependencia está dada por la ecuación \(r^2 = \frac{D^2}{p_1q_1p_2q_2}\).
El fenómeno de genetic hithchiking lleva a una reducción abrupta de la heterocigosidad en los loci cercanos al locus seleccionado. Esta disminución de la heterocigosidad se extiende de forma no lineal al rededor de este locus.
La estructuración poblacional puede generar desequilibrio de ligamiento, aún cuando las subpoblaciones consideradas se encuentren en equilibrio de ligamiento.
Solución
Falso. Las tasas de recombinación son altamente variables, pudiendo diferir entre especies de un mismo género. No obstante, las tasas de recombinación no son características y constantes en cada cromosoma de una especie; diferentes zonas de un mismo cromosoma pueden presentar grandes diferencias en sus tasas de recombinación (pensar, por ejemeplo, en la existencia de hotspots de recombinación).
Verdadero. Un ejemplo claro es el fenómeno denominado “genetic hitchhiking”: si un alelo selectivamente neutro se encuentra ligado físicamente a otro que posee una variante alélica que se ve seleccionada, su frecuencia aumentará junto a la de este alelo.
Falso. El desequilibrio de ligamiento \(D\) si presenta una dependencia con la tasa de recombinación \(r\), pero no corresponde a la ecuación presentada (que corresponde al estadístico de asocación entre alelos \(r^2\)). El desequilibrio de ligamiento \(D\) cambia en magnitud según \(D_t = (1-r)^t D_0\) (donde \(D_t\) es el desequilibrio luego de \(t\) generaciones, partiendo de un valor \(D_0\)), donde claramente se observa la dependencia con la tasa de recombinación \(r\).
Verdadero. En un escenario de “genetic hitchhiking” las frecuencias alélicas presentes en loci vecinos al locus seleccionado también aumentan su frecuencia. Existirá por lo tanto un aumento de la homocigosidad en dichos loci, o lo que es igual una disminución de la heterocigosidad. Simulaciones computacionales muestran que este descenso de la heterocigosidad es no-lineal, y que su extensión en torno al locus seleccionado depende tanto de la relación \(r/s\) como del tamaño poblacional.
Verdadero. La estructuración de una población en subpoblaciones implica una ruptura del régimen de apareamientos aleatorios de la población global. De esta forma las frecuencias eséradas para las combinaciones de alelos de diferentes loci para cada población pueden desviarse de lo esperado para la población general, llevando a la no-independencia para los estados alélicos de estos loci (i.e., desequilibrio de ligamiento). Un caso extremo que grafica esto es el de una población que se estructura en dos poblaciones, cada una de las cuales fijando un haplotipo distinto (e.g. una solo presenta el haplotipo \(A_1B_2\) y la otra el \(A_2B_1\)).
Ejercicios
 Ejercicio 5.1
Ejercicio 5.1
Dos loci bi-alélicos \(A\) y \(B\) se encuentran a una distancia estimada de \(2,3\) centi-Morgans. En un momento dado las frecuencias alélicas para ambos alelos son las siguientes:
\[ \begin{cases} f(A_1B_1) = 0,09 \\ f(A_1B_2) = 0,51 \\ f(A_2B_1) = 0,21 \\ f(A_2B_2) = 0,19 \end{cases} \]
a. Determine si las frecuencias genotípicas son las esperadas bajo equilibrio de Hardy-Weinberg. Discuta sus resultados teniendo en cuenta el valor del desequilibrio de ligamiento \(D\).
b. Determine las frecuencias genotípicas esperadas en la siguiente generación, si se asume que ambos loci evolucionan bajo régimen neutral.
Solución
a. La estimación de las frecuencias alélicas esperadas bajo equilibrio de Hardy-Weinberg requiere tener en cuenta los valores de las frecuencias alélicas de \(A_1\), \(A_2\), \(B_1\) y \(B_2\) (las cuales llamaremos de ahora en más \(p_1\), \(q_1\), \(p_2\) y \(q_2\) de ahora en más). Notemos que
\[ \begin{cases} p_1 = f(A_1B_1) + f(A_1B_2) = 0,09 + 0,51 = 0,60\\ q_1 = f(A_2B_1) + f(A_2B_2) = 0,21 + 0,19 = 0,40\\ p_2 = f(A_1B_1) + f(A_2B_1) = 0,09 + 0,21 = 0,30\\ q_2 = f(A_1B_2) + f(A_2B_2) = 0,51 + 0,19 = 0,70 \end{cases} \]
Bajo equilibrio Hardy-Weinberg se asume independencia en la segregación de los loci, por lo que las frecuencias genotípicas esperadas corresponden al producto de las frecuencias alélicas correspondientes. Las frecuencias genotípicas esperadas (que denotaremos con subíndice \(_{HW}\)) son por lo tanto:
\[ \begin{cases} f(A_1B_1)_{HW} = p_1p_2 = 0,6 \cdot 0,3 = 0,18 \\ f(A_1B_2)_{HW} = p_1q_2 = 0,6 \cdot 0,7 = 0,42 \\ f(A_2B_1)_{HW} = q_1p_2 = 0,4 \cdot 0,3 = 0,12 \\ f(A_2B_2)_{HW} = q_1q_2 = 0,4 \cdot 0,7 = 0,28 \end{cases} \]
Se observa por lo tanto una desviación sustancial de las frecuencias esperadas bajo segregación independiente de los loci (i.e. existe desequilibrio de ligamiento). La magnitud del desequilibrio de ligamiento es equivalente a la magnitud de esta diferencia. Considerando la frecuencia de gametos en fase de acoplamiento con haplotipo \(A_1B_1\) podemos calcular \(D\), según
\[ f(A_1B_1) = f(A_1B_1)_{HW} + D \Rightarrow 0,09 = 0,18 + D \]
por lo que \(D = 0,09 - 0,18 = -0,09\). Notemos que \(D < 0\) implica que existe un déficit en estos gametos en fase de acoplamiento, el cual debería ser compensado por un exceso de gametos en fase de repulsión \(A_1B_2\). En efecto, vemos que el valor esperado \(f(A_1B_2)_{HW} = 0,42\) y el valor observado para gametos en fase de repulsión \(f(A_1B_2) = 0,51\), siendo la diferencia \(D=0,09\) y con signo opuesto al observado para gametos en fase de acoplamiento. Se puede corroborar lo mismo para los gametos en fase de acoplamiento y repulsión \(A_2B_2\) y \(A_2B_1\).
b. Por efecto de la recombinación las frecuencias haplotípicas cambiarán, disminuyendo generación a generación el valor de desequilibrio de ligamiento. Se espera un cambio de magnitud \(rD\) para cada haplotipo de una generación a la siguiente, donde el signo estará determinado según el haplotipo se encuentre en exceso o déficit según lo esperado bajo equilibrio de ligamiento. Por lo tanto, teniendo en cuenta que los loci se encuentran a una distancia de \(2,3\) centi-Morgas (i.e. la tasa de recombinación es \(r = 2,3/100 = 0,023\)) los cambios esperados para las frecuencias haplotípicas serán
\[ \begin{cases} \Delta_r f(A_1B_1) = -0,023 \cdot (-0,09) = 0,00207 \\ \Delta_r f(A_1B_2) = -0,023 \cdot (0,09) = -0,00207 \\ \Delta_r f(A_2B_1) = -0,023 \cdot (0,09) = -0,00207 \\ \Delta_r f(A_2B_2) = -0,023 \cdot (-0,09) = 0,00207 \end{cases} \]
Por lo tanto, las frecuencias genotípicas esperadas en la siguiente generación son
\[ \begin{cases} f(A_1B_1) = 0,09 + 0,00207 = 0,09207\\ f(A_1B_2) = 0,51 + (-0,00207) = 0,50793\\ f(A_2B_1) = 0,21 + (-0,00207) = 0,20793\\ f(A_2B_2) = 0,19 + 0,00207 = 0,19207 \\ \end{cases} \]
 Ejercicio 5.2
Ejercicio 5.2
Dos loci se encuentran segregando en una población de D. melanogaster bajo un desequilibrio de ligamiento de \(D = 0,36\). Se logra determinar que luego de 20 generaciones este valor a \(D=0,20\).
a. Estime la tasa de recombinación entre los dos loci.
b. Estime el número de generaciones esperado para que el desequilibrio de ligamiento \(D\) pase a ser la mitad de su valor inicial.
Solución
a. El desequilibrio de ligamiento \(D\) entre dos loci decae en función de la tasa de recombinación \(r\) entre los mismos luego de considerar \(t\) generaciones según
\[ D_t = (1-r)^t D_0 \]
donde \(D_0\) es el desequilibrio de ligamiento a tiempo inicial y \(D_t\) el observado luego de este intervalo generacional.
Tenemos entonces
\[ 0,20 = (1-r)^{20} \cdot 0,36 \]
\[ \frac{0,20}{0,36} = (1-r)^{20} \Rightarrow 1-r = \sqrt[20]{\frac{0,20}{0,36}} \]
\[ r = 1-\sqrt[20]{\frac{0,20}{0,36}} \]
\[ r = 1-\sqrt[20]{\frac{0,20}{0,36}} \]
Por lo tanto, se deduce que existe una tasa de recombinación de \(r \approx 0,029\) entre ambos loci.
b. La relación \(D_t = (1-r)^t D_0\) aproxima razonablemente bien a la función exponencial \(D_t \approx e^{-rt} D_0\). A partir de este resultado, se puede estimar el número de generaciones requerido para que se alcance una fracción \(f = \frac{D_t}{D_0}\) del valor inicial de desequilibrio de ligamiento \(D_0\) según la ecuación
\[ t = \frac{ln(f)}{ln(1-r)} \]
En el caso planteado se tiene \(f = 0,5\), y anteriormente estimamos \(r = 1-\sqrt[20]{\frac{0,20}{0,36}}\), por lo que se tiene
\[ t = \frac{ln(0,5)}{ln(1-(1-\sqrt[20]{\frac{0,20}{0,36}}))} = \frac{ln(0,5)}{ln(\sqrt[20]{\frac{0,20}{0,36}})} \]
\[ t \approx 23,6 \]
Por lo tanto, se estima se requieren aproximadamente 24 generaciones para que el valor de desequilibrio de ligamiento \(D\) decaiga a la mitad de su valor inicial.
 Ejercicio 5.3
Ejercicio 5.3
Una población de 50 individuos diploides se encuentra segregando dos loci, \(A\) y \(B\), los cuales presentan una baja tasa de recombinación. Inicialmente sólo segregan tres alelos en la población, que llamaremos \(A_1\), \(B_1\) y \(B_2\). En un momento dado surge un nuevo alelo por una mutación espontánea \(A_1 \rightarrow A_2\). Los conteos haplotípicos en dicho momento son
| \(A_1B_1\) | \(A_1B_2\) | \(A_2B_1\) | \(A_2B_2\) |
|---|---|---|---|
| 50 | 49 | 1 | 0 |
a. Calcule el valor de \(D'\) y \(r^2\) en esta situación, discutiendo en función de los máximos y mínimos teóricos esperados para dichos estadísticos.
b. Un tiempo después, algunos organismos portadores de los haplotipos \(A_1B_2\) y \(A_2B_1\) migran hacia otra región geográfica, fundando una nueva población. Algunas generaciones después se realiza un muestreo, observándose los siguientes conteos haplotípicos en la población resultante.
| \(A_1B_1\) | \(A_1B_2\) | \(A_2B_1\) | \(A_2B_2\) |
|---|---|---|---|
| 5 | 43 | 46 | 6 |
Recalcule los valores de \(D'\) y \(r^2\), discutiendo las diferencias observadas en la nueva población respecto al momento en que surge el haplotipo \(A_2B_1\) en la población original.
Solución
a. Notemos que al surgir una nueva variante alélica (en este caso, \(A_2\)) se observará siempre desequilibrio de ligamiento, ya que hasta que ocurra un evento de recombinación una de las cuatro variantes haplotípicas posibles no será observada. En este caso puntual, existe un déficit de gametos con haplotipo \(A_2B_2\) (en fase de acoplamiento). Las frecuencias esperadas (en función de \(D\) y las frecuencias alélicas) y las frecuencias haplotípicas observadas son
| Haplotipo | Frecuencia.esperada | Frecuencia.observada |
|---|---|---|
| \(A_1B_1\) | \(p_1p_2 + D\) | \(\frac{50}{50+49+1+0} = 0,50\) |
| \(A_1B_2\) | \(p_1q_2 - D\) | \(\frac{49}{50+49+1+0} = 0,49\) |
| \(A_2B_1\) | \(q_1p_2 - D\) | \(\frac{1}{50+49+1+0} = 0,01\) |
| \(A_2B_2\) | \(q_1q_2 + D\) | \(\frac{0}{50+49+1+0} = 0\) |
donde \(p_1,\ q_1,\ p_2,\ q_2\) son las frecuencias de los alelos \(A_1\), \(A_2\), \(B_1\) y \(B_2\) respectivamente. Recordemos que las frecuencias alélicas son calculables a partir de las haplotípicas, siendo
\[ \begin{cases} p_1 = f(A_1B_1) + f(A_1B_2) = 0,50 + 0,49 = 0,99 \Rightarrow q_1 = 1 - p_1 = 1 - 0,99 = 0,01\\ p_2 = f(A_1B_1) + f(A_2B_1) = 0,50 + 0,01 = 0,51 \Rightarrow q_2 = 1 - p_2 = 1 - 0,51 = 0,49 \end{cases} \]
Podemos entonces calcular \(D\) en base al déficit de frecuencia que observamos para el haplotipo \(A_2B_2\),
\[ \begin{split} f(A_2B_2) = q_1q_2 + D \Rightarrow D = f(A_2B_2) - q_1q_2 \\ D = 0 - q_1q_2 \\ D = -0,01 \cdot0,49 \\ D = -0,0049 \end{split} \]
donde vemos que \(D < 0\), acorde a lo esperado cuando existe un exceso de gametos en fase de repulsión (o lo que es igual, déficit de gametos en fase de acoplamiento).
En este caso \(D' = \frac{D}{D_\text{mín}}\), donde
\[D_\text{\text{mín}} = \text{máximo}(-p_1p_2,-q_1q_2)\] \[D_\text{\text{mín}} = \text{máximo}(-0,99 \cdot 0,51,-0,01\cdot0,49)\] \[D_\text{\text{mín}} = \text{máximo}(-0,5049,-0,0049)\] \[D_\text{\text{mín}} = -0,0049\]
Por lo tanto tenemos \(D' = \frac{-0,0049}{-0,0049} = 1\). En otras palabras, se observa el máximo desequilibrio de ligamiento posible para las frecuencias alélicas dadas. Esto es lógico, ya que el desequilibrio de ligamiento no puede ser mayor que en la situación en la que ya no se observa un haplotipo (claramente, no pueden existir frecuencias haplotípicas negativas). A esta situación se le suele denominar desequilibrio de ligamiento completo.
¿Qué sucede con el estadístico \(r^2\)? Recordemos que \(r^2 = \frac{D^2}{p_1q_1p_2q_2} \Rightarrow r^2 = \frac{(-0,0049)^2}{0,99 \cdot 0,01 \cdot 0,51 \cdot 0,49} = 0,0097\), siendo su mínimo teórico de \(0\) y su máximo de \(1\). Por lo tanto, mientras que \(D'\) se encuentra en su máximo teórico, el estadístico \(r^2\) se encuentra cerca de su mínimo teórico. ¿A qué se debe esto? Recordemos que este estadístico refiere a la correlación entre los estados alélicos; podríamos pensarlo como la capacidad de predecir el estado alélico de un locus dada la información del estado alélico en el otro. En este caso particular, si bien el alelo \(A_2\) se encuentra exclusivamente asociado al alelo \(B_2\), el alelo \(A_1\) se encuentra asociado casi por igual a los alelos \(B_1\) y \(B_2\), por lo que la correlación entre estados alélicos entre los loci es muy baja.
b. Para la nueva población fundada tenemos
| Haplotipo | Frecuencia.esperada | Frecuencia.observada |
|---|---|---|
| \(A_1B_1\) | \(p_1p_2 + D\) | \(\frac{5}{5+43+46+6} = 0,050\) |
| \(A_1B_2\) | \(p_1q_2 - D\) | \(\frac{43}{5+43+46+6} = 0,43\) |
| \(A_2B_1\) | \(q_1p_2 - D\) | \(\frac{46}{5+43+46+6} = 0,46\) |
| \(A_2B_2\) | \(q_1q_2 + D\) | \(\frac{6}{5+43+46+6} = 0,060\) |
Tenemos por lo tanto ahora \(p_1 = 0,05 + 0,43 = 0,48 \Rightarrow q_1 = 1-0,48 = 0,52\) y \(p_2 = 0,05 + 0,46 = 0,51 \Rightarrow q_2 = 1-0,51 = 0,49\). Calculemos \(D\) a partir las frecuencias del haplotipo \(A_1B_2\),
\[ \begin{split} f(A_1B_2) = p_1q_2 - D \Rightarrow D = p_1q_2 - f(A_1B_2) \\ D = (0,48 \cdot 0,49) - 0,43 \\ D = -0,1948 \end{split} \]
Nuevamente, \(D < 0\) es coherente con el exceso de haplotipos en fase de repulsión observado. En este caso
\[D_\text{\text{min}} = \text{máximo}(-p_1q_1,-p_2q_2)\] \[D_\text{\text{min}} = \text{máximo}(-0,48 \cdot 0,51,- 0,52 \cdot 0,49)\] \[D_\text{\text{min}} = \text{máximo}(-0,2448,-0,2548) \Rightarrow\] \[D_\text{\text{min}} = -0,2448\]
por lo que \(D' = \frac{-0,1948}{-0,2448} = 0,80\). Por otro lado \(r^2 = \frac{D^2}{p_1q_1p_2q_2} \Rightarrow r^2 = \frac{(-0,1948)^2}{0,48 \cdot 0,52 \cdot 0,51 \cdot 0,49} = 0,61\). Vemos que en este caso sigue existiendo un desequilibrio de ligamiento considerable (\(80\%\) del máximo esperado para las frecuencias alélicas existentes), aunque menor al máximo teórico dado que se observan todos los haplotipos posibles. En cuanto al estadístico \(r^2\), vemos que la correlación entre los alelos ahora es considerablemente mayor al de la población inicial. Esto es atribuible al efecto fundador. La nueva población se fundó con individuos que únicamente portaban los haplotipos \(A_2B_1\) y \(A_1B_2\), existiendo una correlación perfecta entre los estados alélicos de ambos loci. Si bien la recombinación generó otras combinaciones alélicas (disminuyendo la correlación de \(r^2 = 1\) observable en la generación fundadora), al momento de sampleo de haplotipos la correlación sigue siendo apreciable (\(60\%\) del máximo teórico).
 Ejercicio 5.4
Ejercicio 5.4
Poco después de que se redescubrieran las leyes de Mendel, William Bateson, Edith Saunders y Reginald Punnett se dispusieron a estudiar la herencia de caracteres en Lathyrus odoratus. En particular, se centraron en el estudio de dos caracteres: color de flor (alelo \(V\) dominante, color violeta; alelo \(v\) recesivo, color rojo) y forma del grano de polen (alelo \(A\) dominante, forma alargada; alelo \(a\) recesivo, redondo).
Los investigadores realizaron cruces entre líneas homocigotas \(VV/AA\) (flor violeta, grano de polen alargado) y \[vv/aa\] (flor roja, grano de polen redondo).
La distribución de la generación resultante fue la siguiente
| Fenotipo | Genotipo | Número observado |
|---|---|---|
| \(\text{Flor violeta; grano alargado}\) | \(V\_/A\_\) | \(1528\) |
| \(\text{Flor violeta; grano redondo}\) | \(V\_/aa\) | \(106\) |
| \(\text{Flor roja: grano alargado}\) | \(vv/A\_\) | \(117\) |
| \(\text{Flor roja; grano redondo}\) | \(vv/aa\) | \(381\) |
| \(\textbf{Total}: 2132\) |
¿Se encuentran los loci segregando de forma independiente?
Solución
Bajo equilibrio de Hardy-Weinberg la hipótesis nula es que los loci segregan de forma independiente. Realizando un doble cuadro de Punnett (recuerda tus cursos de Genética básica y la sección de ejemplos del capítulo Variación y equilibrio de Hardy-Weinberg) se puede concluir que la proporción esperada para los cuatro fenotipos posibles es de \(9:3:3:1\) (correspondientes a los genotipos \(V\_/A\_;\ V\_/aa;\ vv/A\_; vv/aa\), respectivamente). Por lo tanto, podemos deducir los números esperados para cada fenotipo en una progenie de \(2132\) individuos, siendo
\[ \begin{cases} N_{V\_/A\_} = 2132 \cdot (\frac{9}{16}) \approx 1199 \\ N_{V\_/aa} = 2132 \cdot (\frac{3}{16}) \approx 400 \\ N_{vv/A\_} = 2132 \cdot (\frac{3}{16}) \approx 400 \\ N_{vv/aa} = 2132 \cdot (\frac{1}{16}) \approx 133 \end{cases} \]
Notemos que existe un exceso de fenotipos donde se dan las combinaciones alélicas de los fenotipos parentales (i.e., con genotipos que incluyen combinación de alelos \(V\) y \(A\) o \(v\) y \(a\)), y un déficit para los fenotipos que involucran las otras combinaciones alélicas posibles. Esto parece indicar la existencia de desequilibrio de ligamiento (i.e. existencia de asociación estadística entre alelos).
Mediante un test de \(\chi^2\) podemos determinar si las diferencias observadas son estadísticamente significativas al valor de \(\alpha = 1\%\).
Tenemos \(\chi^2 = (\frac{(1528-1199)^2}{1199}) + (\frac{(106-400)^2}{400}) + (\frac{(117-400)^2}{400}) + (\frac{(381-133)^2}{133}) = 969,02\), lo cual es estadísticamente significativo a \(\alpha = 1%\) para \(g.l. = 1\). Por lo tanto se rechaza la hipótesis nula de independencia para la segregación de los loci considerados.
 Ejercicio 5.5
Ejercicio 5.5
(Inspirado en Ma et al. 2019)
La raza de ganado bovino Holstein-Frisia ha sido sometida a un intenso proceso de selección en América del Norte, a efectos de aumentar las tasas de producción o modificar el contenido nutricional de la leche producida. El locus \(\text{DGAT1}\) codifica para la enzima diacilglicerol O-aciltransferasa 1, y se ha visto asociado a la relación grasa-proteína de la leche vacuna, así como a el volúmen de producción. Adyacente al locus \(\text{DGAT1}\) se encuentra el locus \(\text{SCRT1}\), el cual asumiremos es selectivamente neutro en el contexto dado.
a. En una población segregan dos alelos en el locus \(\text{DGAT1}\) (\(\text{DGAT1}_A\) y \(\text{DGAT1}_G\), frecuencias \(p_1 = 0,75;\ q_1 = 0,25\) respectivamente) y dos alelos en el locus \(\text{SCRT1}\) (\(\text{SCRT1}_T\) y \(\text{SCRT1}_G\), frecuencias \(p_2 = 0,45;\ q_2 = 0,55\) respectivamente). El locus \(\text{DGAT1}\) se encuentra bajo un régimen de selección direccional donde el alelo \(\text{DGAT1}_A\) se ve seleccionado, con \(s = 0,2\). Se asume un modo de acción génica completamente aditivo. Si el desequilibrio de ligamiento entre los loci es \(D = 0,22\). ¿Cual es la frecuencia \(p'_2\) esperada para la siguiente generación?
b. En las cercanías de varios de los loci sujetos a selección direccional en líneas de la raza Holstein se encuentran loci codificantes para proteínas relevantes para procesos como la espermatogénesis, la morfología y movilidad de esperma, y el desarrollo de ovocitos y embriones, entre otros. En un estudio comparativo entre líneas sujetas a selección y ganado silvestre, Ma y colaboradores observaron un aumento de variantes alélicas que son letales en homocigosidad para varios de estos loci (Ma et al. 2019). ¿Cómo explica este fenómeno, teniendo en cuenta que tales variantes alélicas deberían estar sujetas a selección negativa? ¿Qué impacto espera en la fecundidad de las líneas de ganado sujetas a selección conforme pasa el tiempo?
Solución
a. El cambio en la frecuencia del alelo \(p_2\) del locus neutral \(\text{SCRT}\) se puede calcular utilizando la ecuación
\[ \Delta p_2 = \frac{Ds[p_1h + q_1(1-h)]}{\bar{w}} \]
donde \(\bar{w} = 1 - 2 p_1 q_1 hs - q_1^2s\), y dado que el modo de acción génica planteado es completamente aditivio \(h = 0,5\). Remplazando en la ecuación con los valores dados se tiene por tanto
\[ \begin{split} \Delta p_2 = \frac{0,22 \cdot 0,2 \cdot [0,75 \cdot 0,5 + 0,25 \cdot (1-0,5)]}{1 - 2 \cdot 0,75 \cdot 0,25 \cdot 0,5 \cdot 0,2 - 0,25^2 \cdot 0,2} \\ \Delta p_2 \approx 0,0232 \end{split} \]
Tenemos entonces
\[ \begin{split} p'_2 = p_2 + \Delta p_2 \\ p'_2 = 0,45 + (\frac{0,22 \cdot 0,2 \cdot [0,75 \cdot 0,5 + 0,25 \cdot (1-0,5)]}{1 - 2 \cdot 0,75 \cdot 0,25 \cdot 0,5 \cdot 0,2 - 0,25^2 \cdot 0,2}) \\ p'_2 \approx 0,47 \end{split} \]
Vemos que, aún siendo un alelo neutral, se espera un aumento de la frecuencia para \(\text{SCRT1}_T\) debido al desequilibrio de ligamiento con un alelo seleccionado positivamente.
b. Dependiendo de la cercanía física y la tasa de recombinación entre los loci, puede existir un mayor o menor grado de desequilibrio de ligamiento entre los loci sujetos a selección y los loci codificantes para proteínas relevantes para los procesos de desarrollo mencionados. Si en los individuos seleccionados por poseer características deseadas (e.g. mayor tasa de producción de leche) se encuentran ligados a los loci seleccionadas variantes alélicas letales desde el punto de vista del desarrollo (en heterocigosis), estas también aumentarán de frecuencia en la población. En otras palabras, las variantes alélicas letales para el desarrollo pueden aumentar en frecuencia en la población debido al fenómeno de “genetic hitchhiking” (igual que el alelo \(\text{SCRT1}_T\) en la primer parte de este ejercicio). A medida que aumentan en frecuencia los haplotipos que poseen estas variantes en la población, es de esperar que la fecundidad del ganado disminuya, ya que aumentan las probabilidades de que las combinaciones gaméticas sean homocigotas para los alelos letales, afectando o bien la producción o calidad del esperma, o el desarrollo embrionario. En efecto, el descenso en la fecundidad conforme se seleccionan líneas con mayor capacidad productiva es una problemática que ha sido observada en poblaciones de Holstein-Frisia.
Bibliografía
Esta aproximación es bastante razonable en general, pero no siempre. Un contraejemplo es el caso de reguladores de expresión en cis.↩︎
John Maynard Smith (6 enero 1920 – 19 abril 2004) fue un teórico de la biología evolutiva y la genética matemática. Estudió en Eton, un colegio de la elite británica y frente a la ausencia de una educación formal en ciencia se basó en los trabajo de JBS Haldane (quién también había asistido a Eton). Prosiguió sus estudios en ingeniería aeronáutica en el Trinity College en donde se graduó. Después de finalizada la II Guerra Mundial abandonó la ingeniería para estudiar biología y genética, guiado por el propio Haldane. Entre sus principales contribuciones se encuentra la aplicación de la “teoría del juego” a la evolución, junto con George R Price, en particular de las estrategias evolutivamente estables.↩︎
Recordemos que esto no afecta nuestro análisis, ya que se plantea una situación con igual frecuencia de alelos \(B_1\) y \(B_2\). Si \(A_1\) surgiera en proximidad del otro alelo, sólo deberiamos cambiar la notación para realizar un análisis análogo.↩︎
Recuerda de tus cursos de genética que Sturtevant definió la unidad en un mapa genético como la distancia entre genes a la cual, en promedio, se observa un 1% de productos de recombinación meiótica. En honor a Thomas Hunt Morgan, dicha unidad se define como 1 centi-Morgan, pudiendo ser extendida a dos puntos cuales quiera en un cromsoma (correspondan o no a genes).↩︎