Capítulo 3 Deriva genética

En el capítulo anterior (Variación y equilibrio de Hardy-Weinberg) comenzamos a entender los procesos que hay por detrás del mantenimiento de la variabilidad genética en las poblaciones de distintas especies. En particular, a partir de las reglas mecanísticas de la herencia mendeliana³² vimos que una vez alcanzado el equilibrio, si no aparecen otras fuerzas, las frecuencias alélicas y genotípicas se mantienen constantes generación tras generación. Para esto hemos asumido varias cosas (Supuestos que asumimos se cumplen para H-W), algunas más razonables que otras. En particular, una de las cosas que asumimos es que el tamaño de nuestra población es prácticamente infinito (con esto queremos decir un número realmente muy alto de individuos), una situación que no siempre se cumple en la práctica. Más aún, esto nos lleva al concepto de población en nuestro contexto: el conjunto de individuos que potencialmente podrían aparearse en igualdad de condiciones con cualquier otro de la misma población para dejar descendencia fértil. Se trata de un concepto fácil de comprender, pero en la práctica suele ser bastante más complejo delimitar sus alcances. Pensemos, por ejemplo, en las poblaciones de Corriedale (ovinos), Angus (bovino de carne) o de Holando (bovino de leche) del Uruguay. ¿Se cumplen los supuestos del equilibrio de Hardy-Weinberg?. ¿Cuál sería mi población si el rebaño o rodeo es cerrado (i.e., produce sus propios reemplazos)?.

Habiendo definido en forma operativa lo que consideramos una población, rápidamente podemos llegar a ver que en muchas poblaciones asumir un tamaño casi infinito para las mismas es algo absurdo. Veremos que en las poblaciones donde se deja de lado esta asunción empieza a jugar una de las fuerzas siempre presentes en biología: el azar.

OBJETIVOS DEL CAPÍTULO

\(\square\) Comprender como el azar puede ser una fuerza evolutiva de relevancia en poblaciones de tamaño finito.

\(\square\) Modelar este fenómeno a través de modelos matemáticos; esto nos permitirá derivar predicciones respecto a qué se espera de la evolución de las frecuencias alélicas en un conjunto de poblaciones iguales. En particular, veremos el modelo de Wright-Fisher y la aplicación de cadenas de Markov en este problema.

\(\square\) Describir la evolución de la homocigosidad en poblaciones de tamaño finito conforme pasan las generaciones. Se presentará al coeficiente de fijación, y su tendencia según el modelo de Wright-Fisher.

\(\square\) Presentar el concepto de tamaño poblacional efectivo, el cual permite tratar a una población que se desvía de lo ideal con las herramientas matemáticas presentadas hasta ahora en dinstintos contextos biológicos.

\(\square\) Ver la aproximación por difusión, una herramienta matemática que permite integrar los procesos azarosos de cambio en las frecuencias alélicas con los procesos direccionados. Este modelado conjunto es más realista, en tanto en las poblaciones naturales es de esperar que los dos fenómenos tengan influencia.

\(\square\) Presentar el modelo de coalescente, un modelo clave en genética de poblaciones. Este nos permitirá nos permitirá indagar en la historia de una muestra de alelos, yendo hacia atrás en el tiempo (hasta identificar su último ancestro común en una población), estimando los tiempos esperados en el proceso.

3.1 El rol de los procesos estocásticos en la genética

Para estudiar el alcance del azar en nuestro contexto propongamos un experimento conceptual sencillo, que cada persona puede reproducir en su casa. Tomemos una jarra o vaso grande y coloquemos 20 bolitas de vidrio azules y 20 bolitas de vidrio rojas, idénticas excepto por el color. Si, como es de esperar, no tienes tantas bolitas de diferentes colores, alcanza con hacer bolitas de papel coloreado o cosas similares, aunque nosotros nos seguiremos refiriendo en nuestro ejemplo a las bolitas. Por lo tanto, el estado inicial de nuestro experimento (la jarra) es:

	Azul	Roja
Cantidad	20	20
Proporción	\(\frac{20}{40}\)	\(\frac{20}{40}\)

Si sacas una bolita sin mirar el color, ¿qué esperas que ocurra? ¿Será roja o será azul? La extracción de una bolita de nuestra jarra se trata de un fenómeno aleatorio (no podemos saber el resultado con certeza), aunque en algunos casos podemos hacer conjeturas razonables. Por ejemplo, en nuestra jarra hay 20 bolitas azules y 20 rojas (\(20+20=40\) bolitas en total), por lo que la proporción de azules es \(p_{azul}=\frac{20}{40}=\frac{1}{2}=0,5\) y lo mismo para las rojas \(p_{roja}=\frac{20}{40}=\frac{1}{2}=0,5\) ³³. Por lo tanto, como elegimos al azar qué bolita agarramos y no existe nada (en principio) que lleve a tener preferencias por el color al elegirlas (recordar que las estamos agarrando sin verlas) la probabilidad de tomar unas u otras será esencialmente la proporción de las mismas. Como la proporción de azules es igual a la de rojas (\(\frac{1}{2}\) en cada caso), lo único que podría conjeturar razonablemente es que hay tanta probabilidad de que aparezca una roja como una azul. Además, si reponemos la bolita elegida en la jarra la situación vuelve a ser como al principio (20 rojas y 20 azules), por lo que podemos repetir la lógica tantas veces como queramos.

Supongamos ahora que la bolita que sacamos antes fue azul y que en lugar de reponerla la dejamos afuera del juego (la puedes colocar en una caja). Tenemos ahora como estado del sistema antes de extraer la siguiente bolita:

.	Azul	Roja
Cantidad	19	20
Proporción	\(\frac{19}{39}\)	\(\frac{20}{39}\)

¿Cuál será la probabilidad, en una nueva extracción de la jarra, de sacar una bolita azul? ¿Será nuevamente equiprobable sacar una bolita roja que una azul? Para responder a estas preguntas debemos volver a hacer las cuentas. La probabilidad de sacar una bolita azul en la segunda extracción, dado que la primera fue azul y que no la repusimos es de \(p_{azul}=\frac{19}{39} \sim 0,4872\), y la probabilidad de sacar una roja será por lo tanto \(p_{roja}=\frac{20}{39} \sim 0,5128\) (notar que ahora en lugar de 40 bolitas solo teníamos 39 antes de sacar la segunda). La diferencia de probabilidades respecto al experimento original es relativamente pequeña, pero aún así real: \(p_{azul}=0,5\) en la primer extracción, mientras que \(p_{azul} \sim 0,4872\) en la segunda.

Supongamos que, una vez más, en la segunda extracción volvió a aparecer una bolita azul, algo nada extraño ya que existían aún en la jarra casi tantas bolitas rojas como azules. Nuevamente, la dejamos afuera de la jarra (la guardamos en la caja, junto a la primera). El estado actual de nuestro sistema es, por lo tanto:

	Azul	Roja
Cantidad	18	20
Proporción	\(\frac{18}{38}\)	\(\frac{20}{38}\)

Ahora, si volvemos a hacer las cuentas previas a una tercer extracción, tenemos que \(p_{azul}=\frac{18}{38} \sim 0,47372\), y la probabilidad de sacar una roja será por lo tanto \(p_{roja}=\frac{20}{38} \sim 0,5263\) (siempre la suma de \(p_{azul}+p_{roja}=1\)). Claramente, si empezamos (por azar) a extraer más bolitas azules que rojas (o más rojas que azules) y no reponemos, la probabilidad de volver a sacar una del mismo color que las que venían saliendo tiende a bajar.

Vayamos para atrás en el tiempo (afortundamente podemos hacerlo porque se trata de un experimento conceptual). Supongamos en cambio que luego de haber sacado la primera bolita azul, la segunda hubiese sido roja y, por supuesto, no repusimos ninguna de las dos. En este escenario la probabilidad de sacar una bolita azul en la tercera extracción hubiese sido \(p_{azul}=\frac{19}{38}=\frac{1}{2}=0,5\), y la de sacar una roja hubiese sido también \(p_{roja}=\frac{19}{38}=\frac{1}{2}=0,5\). En otras palabras, como volvimos a igualar las proporciones respecto al estado inicial de la jarra (cuando había 40 bolitas), la probabilidad de extraer alguno de los dos colores hubiese sido la misma.

Hasta ahora habíamos parado nuestro experimento luego de la extracción de dos bolitas. Veamos un experimento real, pero sigámoslo hasta que no queden más bolitas en la jarra. Las extracciones han seguido el orden que aparece en la primer columna (“bolita”) de la Tabla 3.1. Es fundamental entender que este es el resultado de un experimento en particular. Si repetimos el experimento el resultado (orden de salida de las bolitas) posiblemente sea muy distinto. Tenemos solo 39 filas y no 40, porque la última extracción ya no es aleatoria y porque además no tiene sentido calcular las proporciones luego de esa última extracción (ya no quedan más bolitas).

Tabla 3.1: La realización de un experimento en particular. Partimos de 20 bolitas azules y 20 bolitas rojas. En la columna “bolita” aparece qué bolita sacamos (sin reposición) y en las otras columnas cuántas nos quedan luego de esa extracción de cada color, así como su proporción

bolita	rojas	azules	p.roja	p.azul
azul	20	19	0,5128	0,4872
roja	19	19	0,5000	0,5000
roja	18	19	0,4865	0,5135
azul	18	18	0,5000	0,5000
azul	18	17	0,5143	0,4857
azul	18	16	0,5294	0,4706
roja	17	16	0,5152	0,4848
roja	16	16	0,5000	0,5000
azul	16	15	0,5161	0,4839
roja	15	15	0,5000	0,5000
roja	14	15	0,4828	0,5172
azul	14	14	0,5000	0,5000
roja	13	14	0,4815	0,5185
azul	13	13	0,5000	0,5000
roja	12	13	0,4800	0,5200
roja	11	13	0,4583	0,5417
azul	11	12	0,4783	0,5217
azul	11	11	0,5000	0,5000
roja	10	11	0,4762	0,5238
roja	9	11	0,4500	0,5500
roja	8	11	0,4211	0,5789
roja	7	11	0,3889	0,6111
azul	7	10	0,4118	0,5882
roja	6	10	0,3750	0,6250
roja	5	10	0,3333	0,6667
azul	5	9	0,3571	0,6429
azul	5	8	0,3846	0,6154
azul	5	7	0,4167	0,5833
azul	5	6	0,4545	0,5455
azul	5	5	0,5000	0,5000
roja	4	5	0,4444	0,5556
roja	3	5	0,3750	0,6250
azul	3	4	0,4286	0,5714
roja	2	4	0,3333	0,6667
azul	2	3	0,4000	0,6000
azul	2	2	0,5000	0,5000
azul	2	1	0,6667	0,3333
azul	2	0	1,0000	0,0000
roja	1	0	1,0000	0,0000

El resultado de graficar las proporciones de bolitas azules remanentes (probabilidades de extraer una bolita azul) la podemos ver en la Figura 3.1. Claramente, arrancando desde una proporción de \(p_{azul}=\frac{1}{2}\), como tenemos muchas bolitas, al comienzo las variaciones en las proporciones son relativamente pequeñas en cada extracción. A medida que van quedando cada vez menos bolitas (porque se trata de un muestreo sin reposición), las oscilaciones son cada vez mayores hasta que llegamos a una de las dos barreras absorbentes que tiene nuestro experimento: las proporciones de 0 (0%) y de 1 (100%). Se les denomina barreras absorbentes porque luego de llegar a estos valores no podremos escaparnos hacia otros (insistiremos en este concepto en breve). Es decir, luego de que llegamos a la proporción de 0 bolitas azules (y por lo tanto una proporción de 0), no hay forma de incrementar esa proporción. Lo mismo para la proporción de 1, cuando todas las bolitas que quedan son azules: la proporción se mantendrá así hasta el final del experimento.

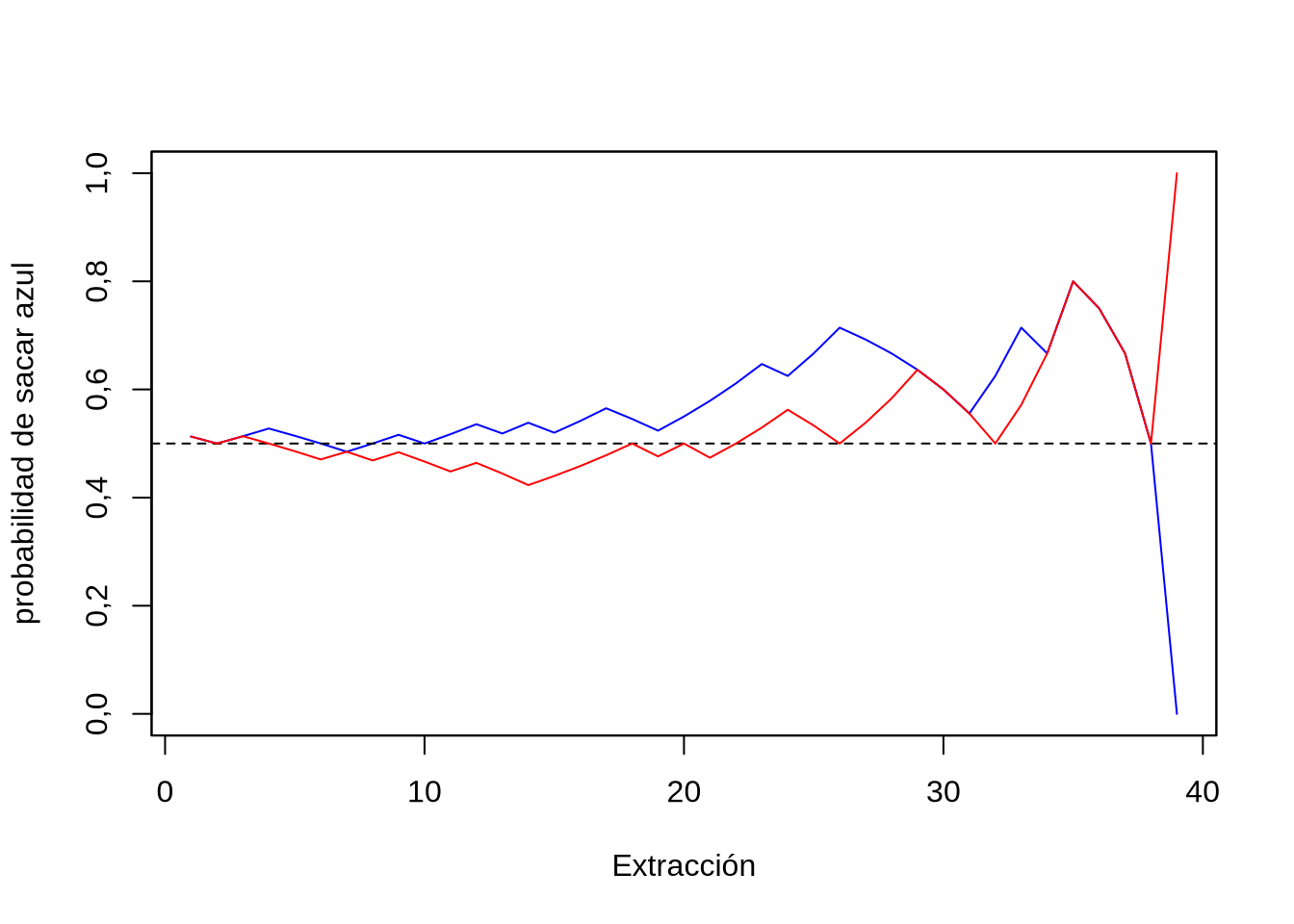
Figura 3.1: Probabilidad de sacar una bolita azul en la próxima extracción, para un nuevo experimento (en rojo), con las mismas condiciones iniciales.

Claramente, el inicio del experimento es igual al del anterior (en los dos partimos de \(p_{azul}=\frac{1}{2}\)), y el mismo debe terminar en una proporción de bolitas azules de 0 o de 1, cuando no queden más bolitas azules o cuando todas las que queden sean azules (esa es la razón también por la que no ploteamos hasta después de la última extracción).

¿Qué ocurriría con nuestro experimento si hubiésemos tomado otro punto de partida (i.e., distinto número de bolitas azules que rojas), o si hubiésemos arrancado desde un número mayor o menor de bolitas?. Afortunadamente, es muy fácil realizar estos experimentos en una computadora y analizar los resultados, al menos para tener una primera impresión del comportamiento cualitativo del sistema. En la Figura 3.2 se observa qué ocurre al variar el número de bolitas en nuestra jarra (columna de la izquierda: 20 bolitas, columna de la derecha: 120 bolitas) y variando la frecuencia (proporción) de bolitas azules al comienzo (fila superior: \(p_{azul}=\frac{1}{2}\), fila inferior: \(p_{azul}=\frac{3}{4}\)).

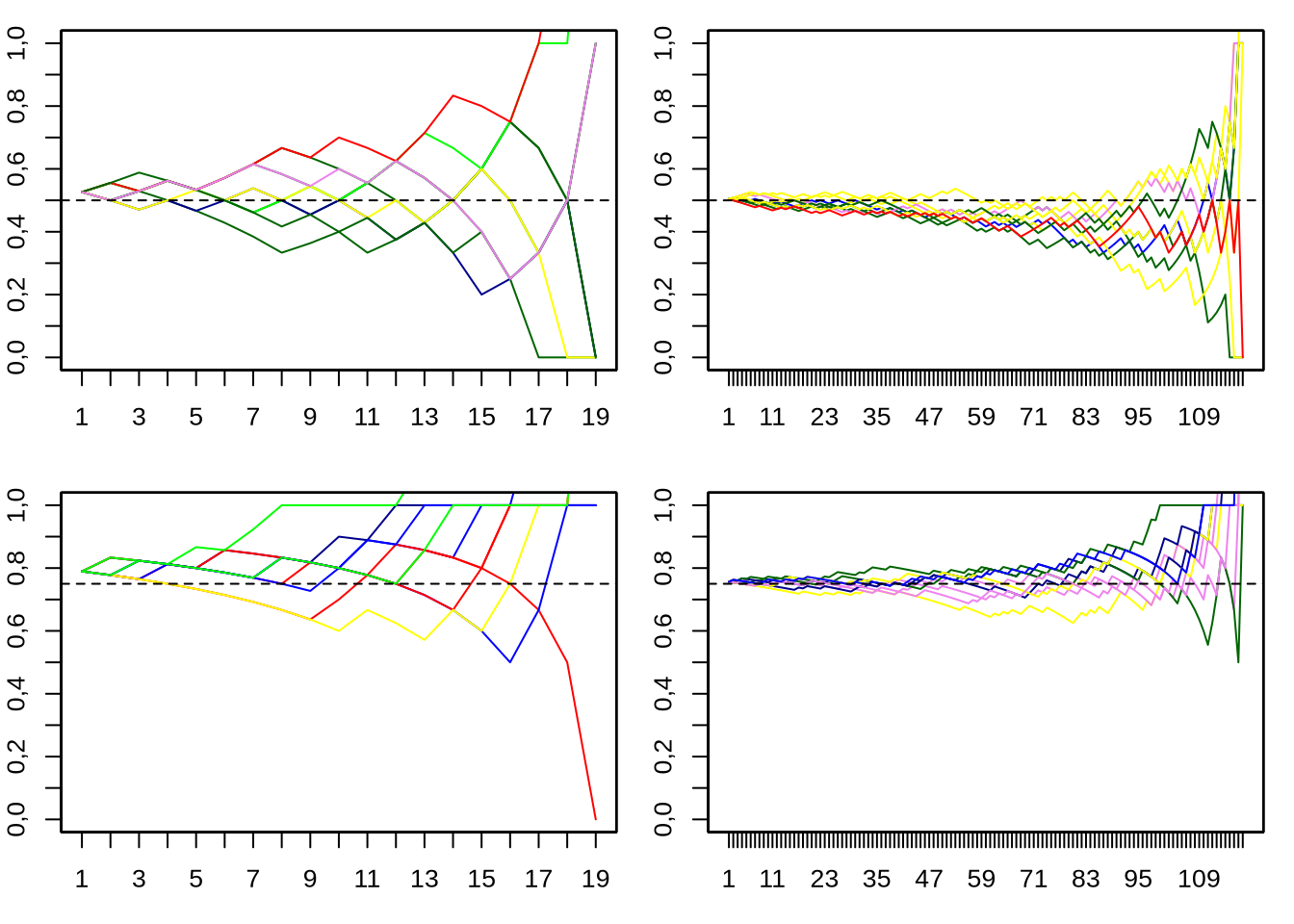
Figura 3.2: Probabilidad de sacar una bolita azul en la próxima extracción, para 10 experimentos, para 4 condiciones: p=1/2 (arriba) y p=3/4 abajo, en 20 (izquierda) y 120 (derecha) bolitas.

A partir de la Figura 3.2 podemos empezar a sacar algunas conclusiones de este experimento aleatorio que nos servirán de referencia en breve. La primera conclusión se relaciona con algo que ya habíamos visto: a medida que quedan menos bolitas en la jarra, ya sea porque se comenzó con pocas o porque el experimento se acerca a su fin, las variaciones en frecuencias suelen ser más drásticas. Esto se puede observar, por ejemplo, en la figura de arriba a la derecha: al principio las variaciones entre distintas réplicas del experimento apenas se apartan de la línea a trazos, pero a medida que quedan menos bolitas (aumenta el número de experimentos que ya realizamos) las proporciones en cada experimento empiezan a ser cada vez más variables (existe mayor dispersión en torno a la línea a trazos). La segunda conclusión refiere al punto de partida del experimento: a medida de que nos alejamos del punto medio (igual proporción de bolitas azules que rojas), mayor es la probabilidad de que la última bolita que quede en la jarra sea una bolita del tipo con mayor proporción inicial. De hecho, la probabilidad de que la última bolita sea de uno de los dos colores, si realizamos repetidas veces el mismo experimento, es la probabilidad inicial del tipo al que pertenece dicha bolita. Podemos ver esto claramente a partir de un ejemplo. Supongamos que tenemos al inicio 10 bolitas en la jarra, 9 de ellas azules y una roja. Para que la roja sea la última en salir, todas las anteriores extracciones deben dar como resultado bolitas azules. La probabilidad de que la bolita roja sobreviva a la primer extracción (o sea, que la primer bolita sea azul) es \(\frac{9}{10}\) (ya que hay 9 bolitas azules y solo una roja). La de la segunda, asumiendo que la primera fue azul y que por lo tanto la bolita roja sobrevivió a la primer tirada, es de \(\frac{8}{9}\). La de la tercera será entonces \(\frac{7}{8}\), y así sucesivamente hasta que queden dos bolitas: una roja y otra azul. En este caso, la probabilidad de elegir nuevamente una bolita azul es de \(\frac{1}{2}\). Considerando estos eventos en conjunto (multiplicando sus respectivas probabilidades), tenemos:

\[\begin{equation} P(\text{última}=\text{roja})=\frac{9}{10} \cdot \frac{8}{9} \cdot \frac{7}{8} \cdot ... \cdot \frac{1}{2}=\frac{\prod_{1}^9}{\prod_{2}^{10}}=\frac{9!}{10!}=\frac{1}{10} \end{equation}\]

que es la proporción de bolitas rojas al inicio ³⁴.

De hecho, podemos generalizar fácilmente el razonamiento anterior a otra proporción de bolitas rojas y azules. Supongamos ahora que tenemos como punto de partida 4 bolitas rojas y 6 azules. ¿Cuál es la probabilidad de que la última bolita sea de color rojo? Llamemos \(n\) al número total de bolitas (\(n=10\), en nuestro experimento) y \(k\) al número de bolitas rojas (\(k=4\), ídem). El total de posibles órdenes en que salen todas las bolitas es igual a las permutaciones de \(n\) elementos, dado por \(\mathbb{P}(n)=n!\). Para que la ultima bolita sea roja, separamos una de ellas del conjunto, por lo que ahora solo tenemos \(n-1=9\) bolitas. Notemos que el orden de salia de las mismas es irrelevante, por lo que hay \(\mathbb{P}{(n-1)}=(n-1)!\) posibilidades (órdenes de salida) de que esto suceda. Por lo tanto, dado que agarramos una bolita roja en particular, la probabilidad de que esa salga última será \(\frac{\mathbb{P}{(n-1)}}{\mathbb{P}{(n)}}=\frac{(n-1)!}{n!}=\frac{\prod_{1}^{n-1}}{\prod_{1}^{n}}=\frac{1}{n}\). Sin embargo, hay \(k\) bolitas rojas diferentes y para cualquiera de ellas este razonamiento es válido, por lo que debemos multiplicar la probabilidad anterior por \(k\) (todos son eventos disjuntos). Considerando esto, tenemos que la probabilidad de que la última bolita sea roja es

\[\begin{equation} \mathbb{P}(\text{última}=\text{roja})=k \frac{\mathbb{P}{(n-1)}}{\mathbb{P}{(n)}}=k \frac{(n-1)!}{n!}=k \frac{\prod_{1}^{n-1}}{\prod_{1}^{n}}=\frac{k}{n} \end{equation}\]

que es la probabilidad inicial de sacar una bolita roja (\(k/n\), \(4/10\) en nuestro caso) o, lo que es lo mismo, la proporción inicial de bolitas rojas. La utilidad de todo este razonamiento lo veremos en la siguiente sección (El modelo de Wright-Fisher ).

PARA RECORDAR

• La importancia de las proporciones de partida puesto que estas determinaran las probabilidades de obtener cierto resultado.
• Las barreras absorbentes serán aquellos valores que no podremos sobrepasar, y representarán los “límites” de los que no podremos escapar hacia otros valores.

3.2 El modelo de Wright-Fisher

A esta altura, ya habrás comenzado a imaginarte la relación entre los experimentos aleatorios de la sección anterior y nuestro modelo de poblaciones con un número relativamente pequeño de individuos. Si bien es posible imaginarse y modelar todo el proceso de gametogénesis, apareamientos al azar para constituir los genotipos de la próxima generación y repetir esto tantas veces como queramos, Sewall Wright ³⁵ y Ronald Fisher ³⁶ imaginaron un procedimiento mucho más sencillo que permite arribar a las misma conclusiones con mucho menos esfuerzo de cálculo.

La primera suposición que hace el modelo de Wright-Fisher es que, más allá del número de individuos, el pool de gametos (el conjunto de todos los gametos en la población) es infinito. Si bien esto puede parecer extraño, es importante recordar que el número de espermatozoides (gametos masculinos) que producen los machos es virtualmente enorme, y el número de óvulos que produce cada hembra es de órdenes de magnitud superior que su descendencia; teniendo esto en cuenta, este no parece un supuesto arriesgado. Los otros supuestos incluyen: i) ausencia de selección, ii) ausencia de mutaciones, iii) ausencia de migración, iv) tiempos de generación no superpuestos, y v) apareamiento aleatorio (panmixia). Si bien no suena realista que se cumplan todas estas condiciones en la vida real, el apartamiento de las mismas suele ser lo suficientemente menor como para considerar el modelo como una buena aproximación inicial. El proceso que plantean Wright-Fisher para el modelo de un gen con dos alelos es el siguiente: para una población de \(N\) individuos de una especie diploide, dada la frecuencia de uno de los alelos muestrear al azar del pool infinito \(2N\) alelos. Está será nuestra nueva población. La lógica del modelo Wright-Fisher se ve graficada para un caso con \(N\) individuos en la Figura 3.3, donde además se hace explícita la analogía con el experimento mental de bolitas que desarrollamos anteriormente.

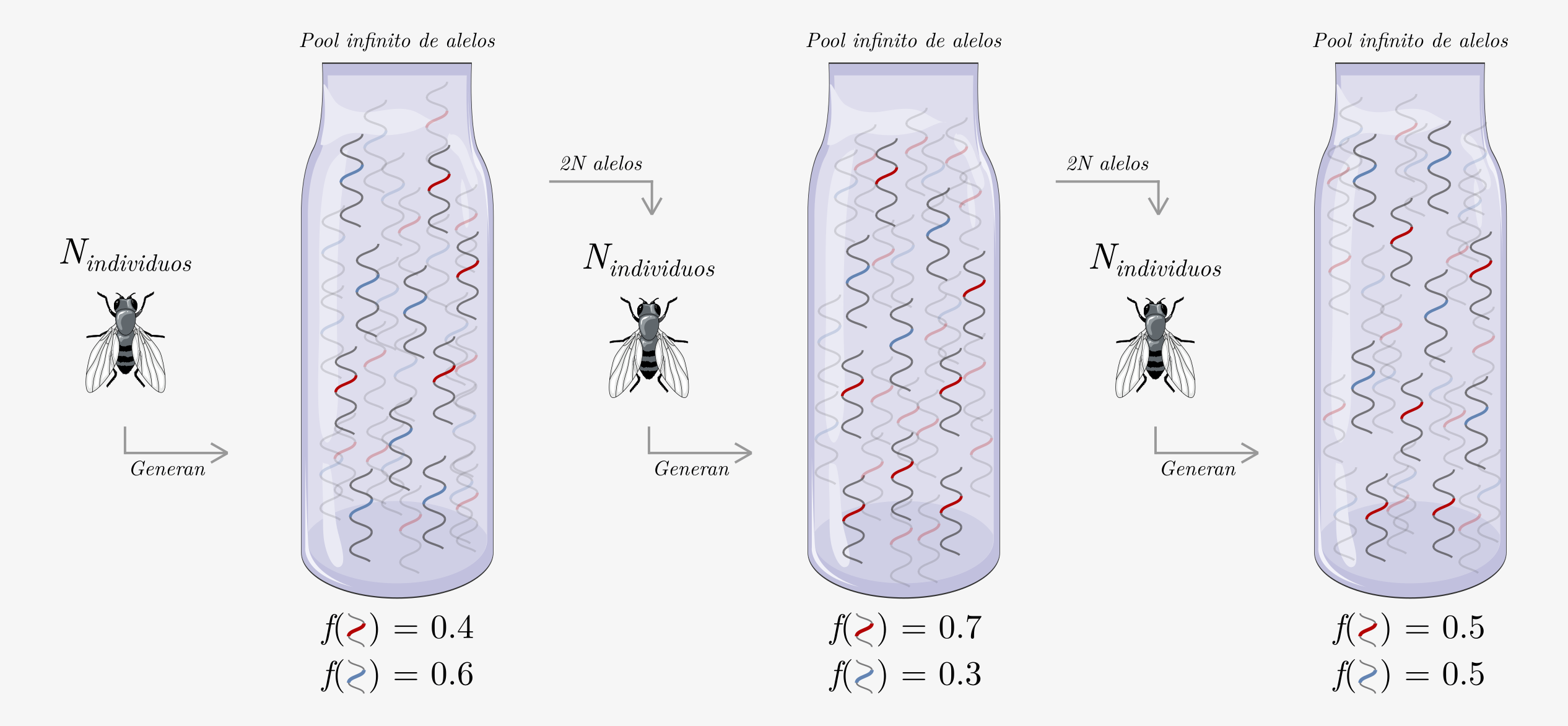
Figura 3.3: Representación esquemática del modelo de Wright-Fisher. Una población finita de N individuos (de la especie , en este ejemplo) generan en cada generación un pool infinito de alelos que mantiene las frecuencias alélicas de la generación. La próxima generación se compone muestreando 2N alelos con reposición, los cuales conformarán a los N individuos de la generación. Imagen creada con elementos gráficos tomados de bioicons (https://bioicons.com/).

Podemos repetir el procedimiento. tantas veces como queramos para estudiar el comportamiento a lo largo del tiempo de nuestro modelo. hora, suponemos que ya te habrás preguntado cómo hacemos para muestrear de un pool infinito a partir de un número limitado de alelos disponibles (\(2N\)). El truco es muy sencillo, la diferencia entre un muestreo con reposición y un muestreo sin reposición (el que hicimos en la sección precedente) es que mientras que en este último las frecuencias van variando a medida de que vamos extrayendo muestras, en el primero (con reposición) las frecuencias permanecen incambiadas definitivamente. Claramente, cuando el muestreo es de a una bolita (o alelo) esto se asemeja a muestrear de un pool infinito de bolitas (o alelos).

Veamos cómo funciona en la práctica. Supongamos que tenemos una población de \(N=5\) individuos. Supongamos además de que se trata de un locus con dos alelos, \(A\) representado por bolitas azules y \(a\) representado por las bolitas rojas. Para simplificar y que se fije la idea del procedimiento vamos a comenzar con una frecuencia inicial de \(p_A=p_{azul}=\frac{1}{2}=p_{roja}=p_a\). Para que nuestro procedimento funcione claramente vamos a tener ahora dos jarras (una inicialmente con igual proporción de bolitas azules y rojas y la otra vacía) y una caja con al menos \(2N\) bolitas de cada color, o sea que en nuestro ejemplo, al menos 10 bolitas azules y 10 bolitas rojas.

La jarra vacía va a representar una nueva generación de nuestra población. Para completarla procederemos extrayendo al azar de la jarra llena una bolita y de acuerdo al color de la misma sacamos de la caja una bolita del mismo color y la colocamos en la jarra vacía, devolviendo la bolita que sacamos a la jarra llena. Repetimos este procedimiento \(2N\) veces, al cabo del cual tendremos \(2N\) bolitas en nuestra antigua jarra vacía (la nueva generación de la población). Para completar el procedimiento y estar prontos para una nueva generación, vaciamos el contenido de la anterior jarra llena en la caja.

En este punto, podemos analizar el contenido de la nueva jarra llena (la población “hija” de la inicial), contando cuántas bolitas de cada color obtuvimos. Ahora, ¿podemos predecir (de alguna manera) el comportamiento de este experimento en una generación? Si llamamos (arbitrariamente) un “éxito” al hecho de sacar una bolita de color azul, entonces la extracción de cada bolita será una variable aleatoria con distribución de Bernoulli³⁷ y probabilidad de éxito \(p_{azul}\) (y por lo tanto, probabilidad de fracaso, bolita roja, \(p_{roja}=1-p\)). Si consideramos el resultado de las \(2N\) extracciones independientes y con la misma probabilidad (recordar que es un muestreo con reposición) como un conjunto, entonces la distribución del número de bolitas azules (éxitos) y rojas (fracasos) entre las \(2N\) tenga una distribución binomial:

\[ \begin{split} P(i \text{ bolitas azules})={2N\choose i} p^i (1-p)^{2N-i},\\ {2N\choose i}=\frac{2N!}{i!(2N-i)!} \end{split} \tag{3.1} \]

Es decir, si bien el número de bolitas en la nueva jarra también es de \(2N=10\), ahora el número de bolitas azules (copias del alelo A) que llamamos \(i\) (y por lo tanto el de bolitas rojas, o alelo a igual a \(2N-i\)) es una variable aleatoria y por lo tanto con resultado incierto de experimento en experimento. En general, si una población tiene \(i\) copias del alelo \(A\) y \(2N-i\) copias del alelo \(a\), la probabilidad de transición de pasar de \(i\) copias a \(j\) copias en el modelo de Wright-Fisher se encuentra dada por la siguiente ecuación:

\[\begin{equation} T_{ij}={2N \choose j}\left(\frac{i}{2N}\right)^{j}\left(\frac{2N-i}{2N}\right)^{2N-j}=\frac{(2N)!}{j!(2N-j)!}p^jq^{2N-j} \tag{3.2} \end{equation}\]

Esta ecuación es bien sencilla de explicar. La probabilidad de éxito (alelo A o bolita azul) varía de generación en generación, y por lo tanto para la generación actual de gametos es igual a la proporción de alelos A (\(i\)) en el total (\(2N\)), por lo que para cada generación de gametos \(p=\frac{i}{2N}\). Concomitantemente, la probabilidad de fracaso (alelo a o bolita roja) es igual a la proporción de alelos a en el total, o sea \(\frac{2N-i}{2N}\). Ahora, al número de éxitos en la siguiente generación le llamamos \(j\) (la cantidad de alelos A que tienen la probabilidad \(T_{ij}\)) y por lo tanto, la cantidad de alelos a será \(2N-j\).

Hasta ahora nos hemos referido a una población en particular y como vimos su evolución es completamente al azar. En la Figura 3.4 podemos ver un ejemplo de la evolución del alelo A en una población de 5 individuos diploides. El punto de partida es de \(p_{A}=\frac{1}{2}\) y el aspecto de “dientes de sierra” se debe a que lo más fino que puede ser el movimiento es de \(\frac{1}{2N}=\frac{1}{10}=0,1\) en nuestro caso. Por otro lado, tanto \(p_A=0\) como \(p_A=1\) son barreras absorbentes ya que \(p_A=0\) quiere decir que no quedan más alelos A (bolitas azules) en la población, mientras que \(p_A=1\) quiere decir que todos los alelos que quedan en la población son A, es decir que este alelo se fijó en la población (y por lo tanto, en ambos casos la frecuencia no variará más en el tiempo; recordar que uno de los supuestos fue que no hay mutación).

Afortunadamente a partir de unas pocas líneas de código podemos explorar a nuestro antojo el comportamiento en varias poblaciones, conjunto que se llama ensemble (del francés, el conjunto de todos los individuos de todas las poblaciones; ver Figura 3.6), variando el número de individuos en ellas, así como la proporción inicial del alelo A. El resultado de probar el comportamiento para poblaciones de 5 y 50 individuos, con proporción inicial de alelo de \(p=\frac{1}{2}\) y \(p=\frac{3}{4}\) lo podemos ver en la Figura 3.5. Claramente podemos apreciar que las poblaciones con mayor número de individuos tienen un comportamiento menos errático. Por otro lado, en las poblaciones que arrancan más cerca de una de las barreras absorbentes la variación es menor en relación a las poblaciones con el mismo número de individuos que arrancan desde la mitad (\(p=\frac{1}{2}\)).

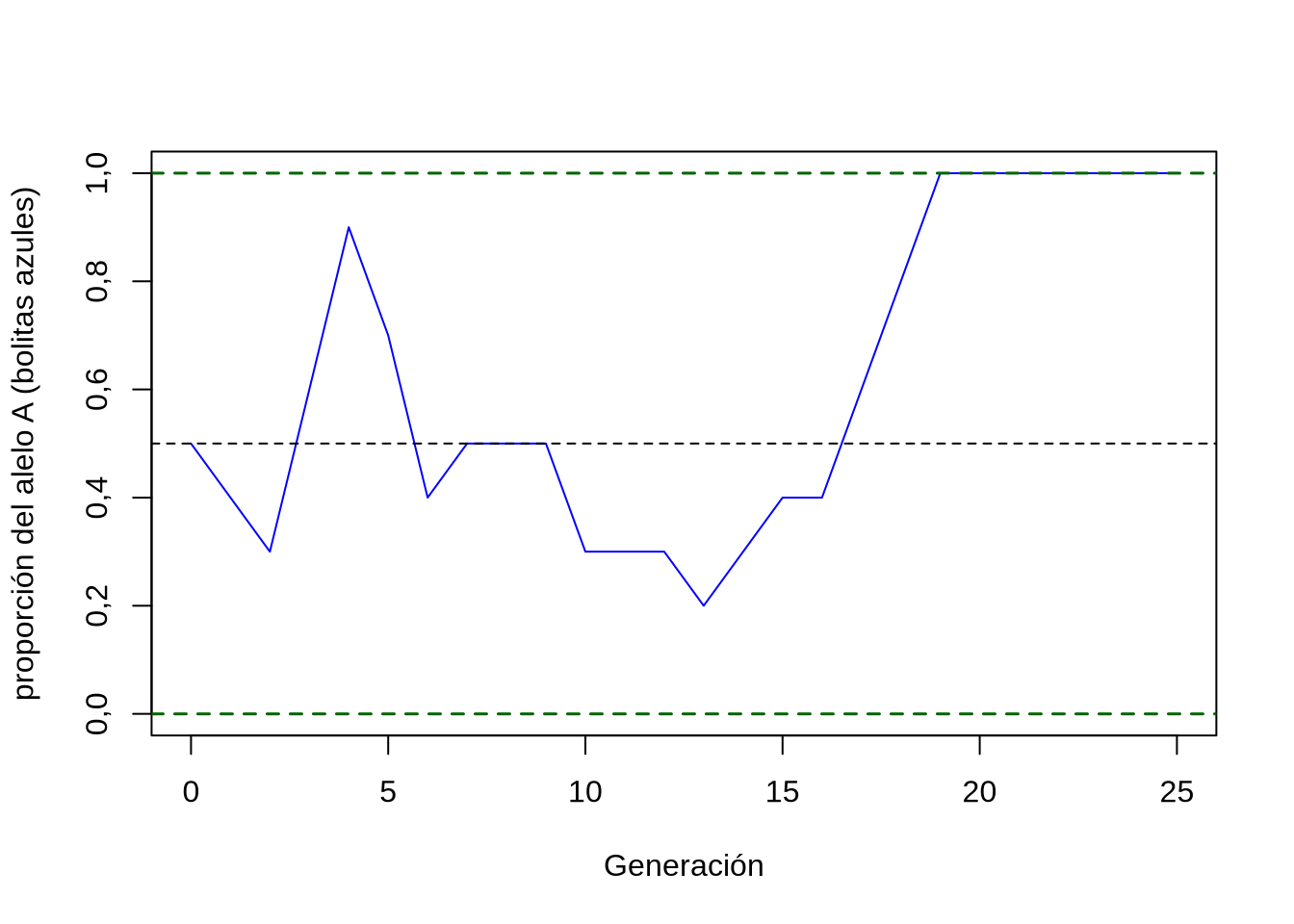
Figura 3.4: Proporción del alelo A (bolitas azules) en una población de 5 individuos diploides. Notar de que se trata de una realización en particular de este experimento y que con seguridad si repetimos el experimento el resultado será diferente.

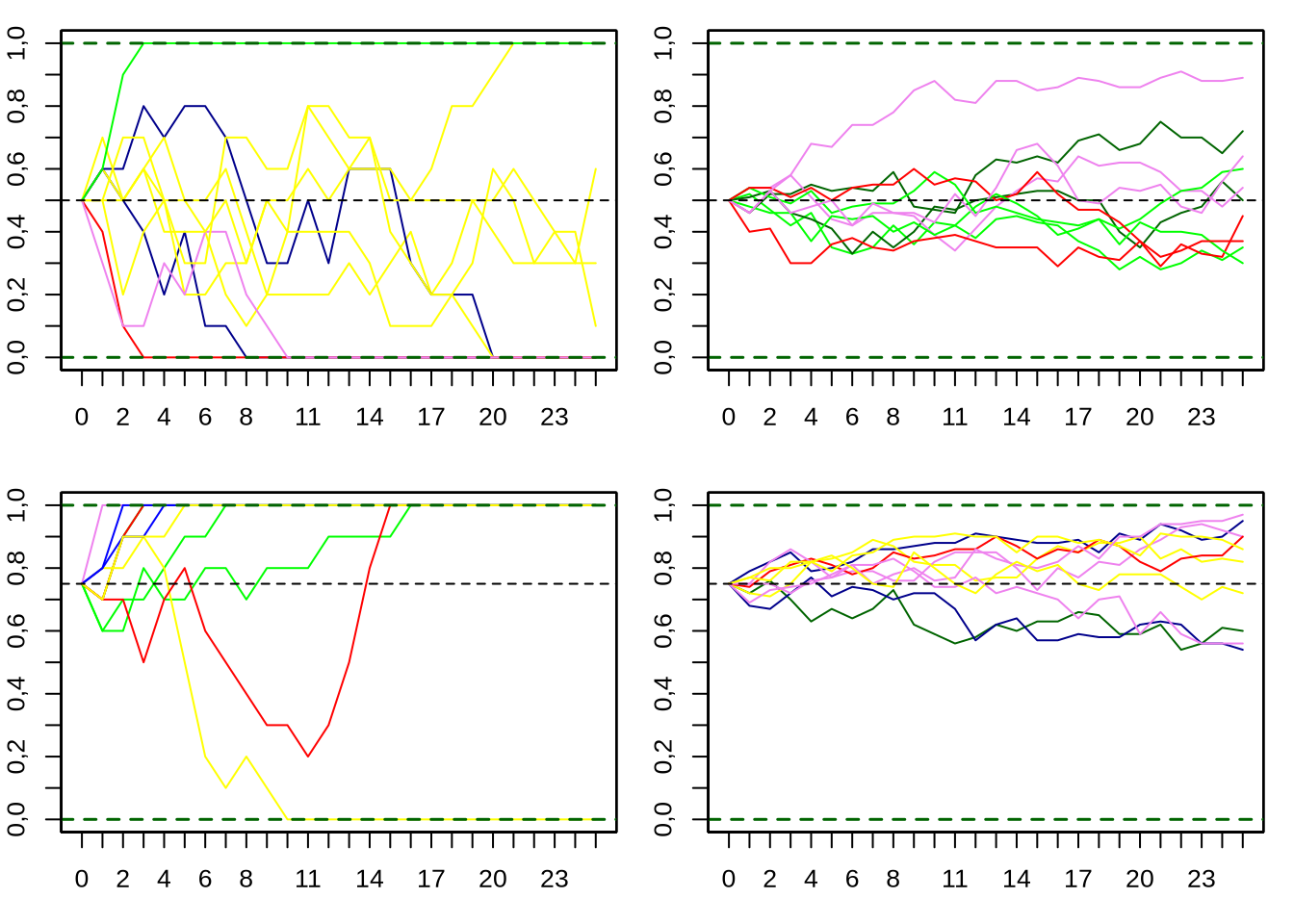
Figura 3.5: Frecuencia del alelo A (bolitas azules) en 10 poblaciones de 5 individuos diploides (a la izquierda) y de 50 individuos diploides (derecha), para frecuencias iniciales de p=1/2 (arriba) y p=3/4 (abajo).

Este comportamiento no debería resultarnos extraño. Los muestreos que estamos realizando en cada población, a cada generación, provienen de distribuciones binomiales. Si recuerdas de tus cursos de matemáticas y estadística, para una variable \(i \sim Binom(2N,p)\) se tiene valor esperado \(E(i)=2Np\) y varianza \(\sigma^2(i)=2Np(1-p)=2Np-2Np^2\), por lo que esperamos que mientras las poblaciones se encuentren segregando, la esperanza (la media) entre la distintas poblaciones sea de \(Np\), o lo que es lo mismo, la proporción del alelo A sea igual a \(p_A=\frac{E(i)}{2N}=\frac{2Np}{2N}=p\) (es decir, en promedio las líneas de poblaciones oscilarán en torno a la frecuencia inicial). Más aún, como vimos antes (H-W: la frecuencia de heterocigotas en función de la frecuencia alélica), \(p(1-p)\) tiene un máximo en \(p=\frac{1}{2}\), por lo que la varianza \(\sigma^2(i)=2Np(1-p)\) también tendrá un máximo en \(p=\frac{1}{2}\) (porque \(p(1-p)\) está multiplicado por \(2N\) que es necesariamente una constante positiva); en otras palabras, la varianza dentro de cada población será máxima cerca de la frecuencia \(p=\frac{1}{2}\). ¿Cómo se condice esto con el comportamiento más variable en poblaciones pequeñas? Si recuerdas de esos mismos cursos, la varianza en la frecuencia por generación en el ensemble viene dada por

\[\begin{equation} \sigma^2(i/(2N_e))= \frac{1}{(2N_e)^2} \cdot \sigma^2(i) \sigma^2(p)=\frac{2 N_e p(1-p)}{4 N_e^2}=\frac{p(1-p)}{2N_e} \Rightarrow \end{equation}\]

\[\begin{equation} \sigma^2(p)=\frac{pq}{2N_e}=\frac{p-p^2}{2N_e} \end{equation}\]

Es decir que al aumentar el tamaño de cada población (\(2N\)) la variación entre poblaciones disminuye. Finalmente, la variación entre poblaciones para las poblaciones que aún se encuentran segregando (o sea, que no llegaron a las barreras absorbentes) se incrementa con el tiempo de manera aproximadamente lineal, por lo que para tiempo \(t\) en las líneas que continúan segregando esperamos una varianza de

\[\begin{equation} \sigma_t^2(p)=t\frac{pq}{2N}=t\frac{(p-p^2)}{2N}. \end{equation}\]

Una última observación es la que hace al número de individuos \(N\) de las distintas poblaciones. Hasta ahora asumimos que cada uno de nuestros individuos era completamente independiente de los otros desde el punto de vista genético (es decir, asumimos condiciones ideales) y por lo tanto no tuvimos en cuenta el efecto de que se puedan ver emparentadas en nuestros cálculos. En realidad, en la práctica, bajo diferentes criterios (apareamientos dirigidos, diferencias en el número de progenie esperada por pareja, etc.), las poblaciones se suelen comportar como si el número de individuos fuese menor y a ese número se lo conoce como tamaño efectivo de la población y se lo representa con el símbolo \(N_e\). Esto lo veremos con más detalle en la sección Tamaño efectivo poblacional y de nuevo en el capítulo Apareamientos no-aleatorios.

En resumen, a partir del modelo sencillo de Wright-Fisher pudimos entender que en ausencia de otras fuerzas evolutivas como la selección, migración o mutación, las frecuencias alélicas pueden variar en forma aleatoria y que con el transcurso del tiempo cada alelo puede fijarse en alguna población mientras que desaparece en otras. Este fenómeno es lo que se conoce como deriva genética o deriva aleatoria, este último término en razón de que el cambio en las frecuencias no tiene una dirección y que por lo tanto no es predecible el sentido para una población en particular.

Ejemplo 3.1

Una población de 1000 individuos es dividida en cuatro subpoblaciones, cada una con un tamaño poblacional efectivo de 250 individuos. Las poblaciones se encuentran segregando un locus bi-alélico, siguiendo todos los supuestos esperados para encontrarse en equilibrio de Hardy-Weinberg (salvo el de tamaño poblacional infinito). Luego de un tiempo, se observan las siguientes frecuencias alélicas (\(p_i\)) para el alelo \(A_1\) en el ensemble de subpoblaciones: \(p_1 = 0,39;\ p_2 = 0,61 ;\ p_3 = 0,57;\ p_4 = 0,42\). Estime el número de generaciones transcurrido desde la formación del ensemble de subpoblaciones.

A partir de las frecuencias alélicas observadas en el ensemble se estima una frecuencia promedio \(\bar{p} = \frac{0.39+0.61+0.57+0.42}{4} = 0.4975\). A su vez, la varianza observada para la frecuencia alélica en el ensemble es de \(\sigma_t^2(p) = \frac{1}{n}\sum_{i=1}^{i=n}(p_i - \bar{p})^2 = \frac{(0.39-0.4975)^2 + (0.61-0.4975)^2 + (0.57-0.4975)^2 + (0.42-0.4975)^2}{4} \Rightarrow \sigma_t^2(p) = 0, 00886875\).

Dado que la varianza para la frecuencia alélica \(p\) aumenta linealmente con el tiempo generacional \(t\) según la ecuación \(\sigma^2_t(p) = t \cdot \frac{pq}{2N_e}\), podemos usar nuestro estimado de \(\bar{p}\) y el tamaño poblacional efectivo \(N_e = 250\) para calcular el número de generaciones transcurrido desde la generación del ensemble:

\[\sigma^2_t(p) = t \cdot \frac{pq}{2N_e} \Rightarrow t = \frac{\sigma^2_t(p) \cdot 2N_e}{\bar{p}\bar{q}}\]

\[ t = \frac{0,00886875 \cdot 2\cdot250}{0,4975 \cdot (1-0,4975)}\]

por lo que inferimos que se estima pasaron \(t \approx 18\) generaciones desde la formación del ensemble poblacional.

PARA RECORDAR

• El modelo de Wright-Fisher asume que de un pool infinito de gametos, con las frecuencias de los alelos proporcionales a lo muestreado para constituir la generación anterior, muestreamos nuevamente \(2N\) alelos, que constituirá a la nueva población.
• La suposición de un pool infinito de gametos es equivalente, desde el punto de vista matemático a un muestreo con reposición.
• Al generarse la nueva población a partir de \(2N\) muestreos independientes de Bernoulli, la distribución de la nueva población será una Binomial con probabilidad \(p\) y tamaño \(2N\).
• La varianza de las frecuencias del alelo A (\(p\)) entre poblaciones, por generación, debida al efecto de la deriva genética es:

\[\begin{equation*} \sigma^2(p)=\frac{pq}{2N_e}=\frac{p-p^2}{2N_e} \tag{3.3} \end{equation*}\]

siendo \(p\) y \(q\) (con \(q=1-p\)) las frecuencias de los alelos y \(N_e\) el tamaño efectivo de las poblaciones que forman el ensemble. Como la varianza crece linealmente con el tiempo (en generaciones), tenemos también que para el tiempo \(t\) para las líneas que continúan segregando:

\[\begin{equation*} \sigma_t^2(p)=t\frac{pq}{2N_e}=t\frac{(p-p^2)}{2N_e} \tag{3.4} \end{equation*}\]

3.3 La subdivisión poblacional y la evolución de las frecuencias alélicas

La sección anterior marcó un cambio importante en nuestras perspectivas. Desde analizar el comportamiento de una o dos poblaciones, a partir de la sección anterior empezamos a apreciar que el azar puede jugar un rol muy importante en la evolución de las frecuencias alélicas en poblaciones relativamente pequeñas y nos empezamos a interesar en la visión en conjunto de las mismas.

El debate acerca del rol de la deriva genética versus la selección en los procesos de especiación (la aparición de nuevas especies) ha sido acalorado (ver, por ejemplo B. Charlesworth, Lande, and Slatkin (1982)). Aunque el debate continúa, pese a reconocer un rol no despreciable a la deriva genética, los actores principales de esta comedia que es la vida parecen ser la mutación (como generador de variabilidad) y la selección, a través de sus diversas formas de acción (algo que veremos en el capítulo de Selección Natural).

Pero veamos cómo podría estar funcionando la deriva genética en los procesos que llevan a la especiación. En efecto, imaginemos un locus con dos alelos que sean neutros respecto a los ambientes (por lo tanto no hay selección). Asumamos también que la tasa mutacional es suficientemente baja como para que resulte improbable la aparición de los mismos alelos. Supongamos también que se trata de una especie con poca movilidad esperada, o sea la relación entre su área potencial de apareamiento y el rango geográfico de la especie (pueden ser especies animales, plantas, hongos, por ejemplo). Si la dispersión a largas distancias en esta especie suele ser algo relativamente raro, por ejemplo semillas llevadas por el viento, es posible imaginar que el ensemble de poblaciones está formado por pequeños parches, cada uno constituyendo una población diferente y que dada la baja movilidad de la especie no es probable que intercambien material genético con otros parches (ver representación en la Figura 3.6).

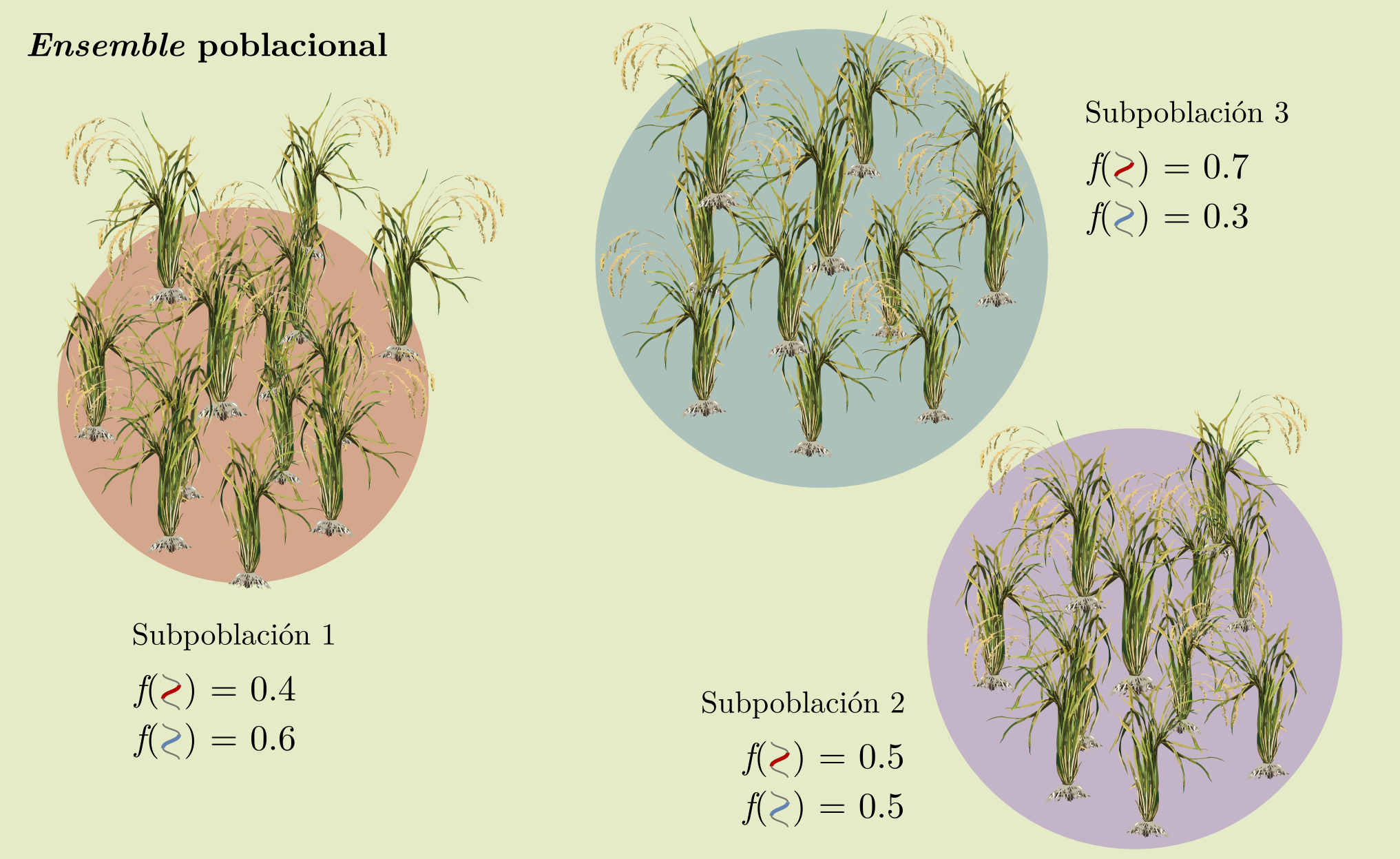
Figura 3.6: Ejemplo de poblacional. Tres poblaciones de arroz () se encuentran distribuídas en parches, a distancias tales que los individuos de cada subpoblación sólo se reproducen entre sí. Por efecto de la deriva genética es esperable que las frecuencias alélicas de las subpoblaciones del ensemble diverjan con el tiempo, lo cual se ejemplifica para un locus bialélico (alelos “rojo” y “azul”, en la figura). Imagen creada con elementos gráficos tomados de bioicons (https://bioicons.com/).

Suponiendo además que el tamaño efectivo (\(N_e\)) es relativamente pequeño, algo muy razonable teniendo en cuenta que los individuos deben reproducirse en su entorno cercano, estamos entonces en una situación como alguna de las representadas en la Figura 3.5. Es decir, mientras que en algunos parches la frecuencia del alelo A crecerá hacia la fijación del mismo, en otras poblaciones posiblemente se pierda (o lo que es lo mismo, quede fijado el alelo a). Pero la deriva genética es un fenómeno que ocurre simultáneamente en todo el genoma (obviamente que en sitios no ligados del genoma el fenómeno es independiente) y por lo tanto aún las poblaciones que terminen con el alelo A fijado serán diferentes en otros loci, donde la deriva ocurre en forma independiente. Todo este proceso, dado simplemente por la “reglas” de la reproducción, producirá un conjunto de poblaciones cada vez más disimiles entre ellas (y cada vez más parecidas dentro), lo que es un buen comienzo para la especiación.

Un fenómeno usual en muchas especies, que magnifica el rol de la deriva genética, es lo que se conoce como cuello de botella poblacional (o “genetic bottleneck”, en inglés). En efecto, en muchas especies es frecuente encontrarse con eventos que llevan a la casi extinción de alguna población en particular, en un momento dado del tiempo, luego de lo cual la población comienza a recuperarse e incrementar el número de individuos. Sin embargo, las huellas de esta momentánea reducción drástica son normalmente imborrables en el genoma. Como en el momento de máxima restricción solo unos pocos individuos sobreviven (constituyendo la base reproductiva de la población a futuro), al ser \(N_e\) muy pequeño la varianza por generación será enorme, además de que la frecuencia inicial de las variantes será posiblemente sesgada respecto a la misma población antes del cuello de botella. Esto último nos lleva directamente a otro fenómeno estrechamente relacionado: el efecto fundador.

El efecto fundador (Figura 3.7) se produce cuando un número relativamente pequeño de individuos funda una nueva población y por efecto de la frecuencia sesgada en esa pequeña muestra más el efecto de la endogamia (o “inbreeding”, el efecto del apareamiento entre parientes que veremos en otro capítulo más adelante) casi obligada por el número reducido de individuos, llevan a medida de que la población va creciendo a una fuerte desviación de las frecuencias alélicas respecto a la población original.

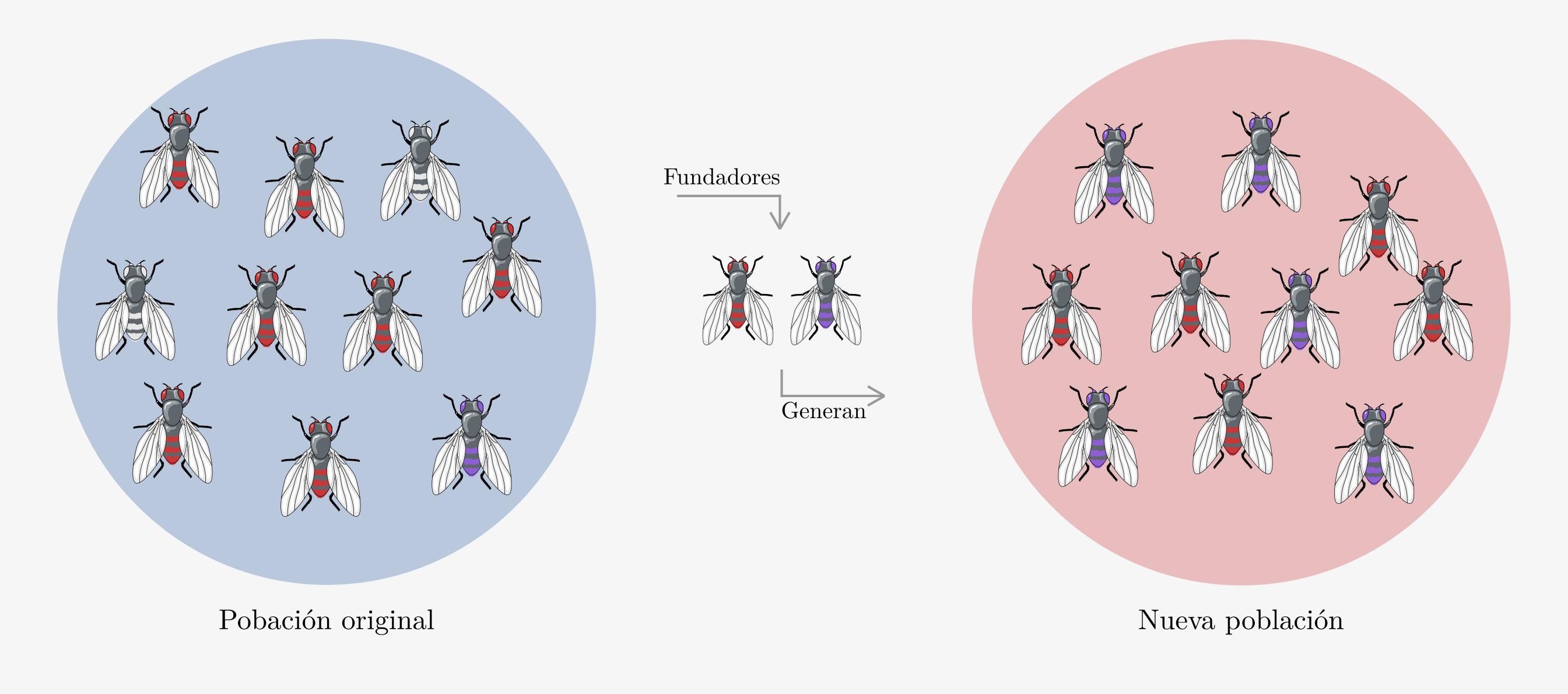
Figura 3.7: Efecto fundador ejemplificado para una población de la mosca de la fruta (D. melanogaster). Cuando una nueva población es formada a partir de una muestra pequeña de individuos, las frecuencias alélicas presentes entre los individuos fundadores tendrán un fuerte impacto en el devenir de las frecuencias alélicas de la nueva población. Debido al efecto de muestreo, las frecuencia alélicas entre los miembros fundadores pueden apartarse considerablemente de las presentes en la población original. En el ejemplo vemos una población original de moscas que presentan diferentes fenotipos para el color de ojo (rojo, blanco y violeta), los cuales se asumen se deben a las variantes alélicas que presenta cada individuo en un locus. La muestra de individuos fundadores se encuentra fuertemente sesgada (la componen en igual proporción individuos con ojos rojos y violetas), lo cual lleva a que la nueva población fundada sea radicalmente diferente a la original. Imagen creada con elementos gráficos tomados de bioicons (https://bioicons.com/).

Un ejemplo notable entre poblaciones humanas lo constituye el pueblo de Cândido Godói, un municipio de Río Grande do Sul (Brasil) de unos 6 mil habitantes. El sobrenombre del pueblo es “Terra dos gêmeos” (tierra de los gemelos), ya que 1 de cada 10 mujeres ha tenido mellizos/gemelos, una cifra muy superior al 1,8% de Río Grande do Sul (y en algún estudio, cerca de la mitad fueron monocigóticos), Figura 3.8.

Figura 3.8: Mellizos/gemelos de Cândido Godoi (imagen sacada de la web, sin crédito de autor).

Si bien se especuló que el origen de este fenómeno serían una serie de experimentos del doctor nazi Josef Mengele, la causa más probable es el estrecho parentesco de sus habitantes, unido al efecto fundador como origen de la colonia (Tagliani-Ribeiro et al. 2011). En particular, en este estudio los autores encuentran una fuerte asociación entre la presencia del alelo P72 en el gen TP53 y el “riesgo” de embarazo gemelar. También los autores reportan una significancia menor para la asociación entre el alelo T del gen MDM4 y en conjunto proponen que ambos alelos (en dos genes distintos) estarían actuando mediante la reducción del mecanismo de apoptosis inducida por p53.

Homocigosidad y heterocigosidad

En las secciones anteriores nos hemos manejado considerando exclusivamente la evolución en el tiempo de las frecuencias alélicas en las distintas poblaciones que conforman nuestro ensemble y dejamos de lado el análisis de lo que ocurriría dentro y entre ellas desde el punto de vista de los genotipos. Consideremos, como una suposición a priori razonable, que dentro de cada población se mantiene el apareamiento al azar y que más allá del número posiblemente pequeño de individuos dentro de ellas que hacen fluctuar las frecuencias alélicas, podemos esperar que las mismas se comporten aproximadamente según lo esperado en el equilibrio de Hardy-Weinberg de generación en generación. Para graficar nuestra situación supongamos que tenemos una gran población, con una frecuencia del alelo A igual a \(p=\frac{1}{2}=0,5\) que en el momento inicial de nuestra historia se divide en 4 poblaciones idénticas en tamaño (cada una de \(1/4\) del tamaño de la grande), como lo representamos en la Figura 3.9. Cada una de estas poblaciones, a medida de que pase el tiempo, por efecto exclusivo de la deriva genética se irá apartando de la frecuencia original \(p=0,5\) y la varianza de frecuencias entre ellas irá creciendo en el tiempo, como vimos más arriba. Es de destacar que nuestra representación en la Figura 3.9 es apenas una configuración posible de infinitas, ya que la evolución de las 4 poblaciones será aleatoria, pero esta configuración en particular, sin pérdida de generalidad, nos ayudará a ilustrar el fenómeno general.

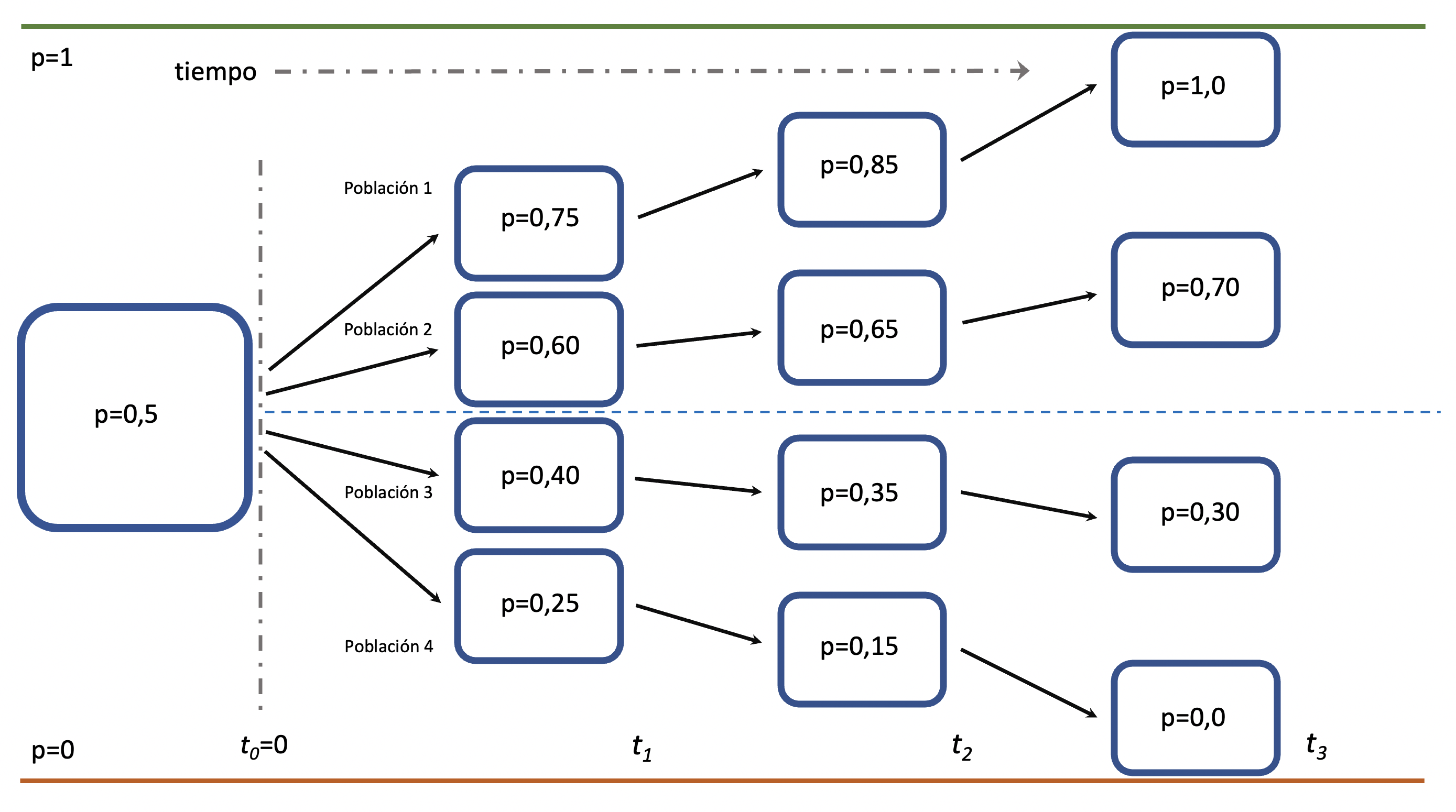
Figura 3.9: Evolución por deriva genética de las frecuencias alélicas en 4 subpoblaciones que parten de la misma frecuencia (el tiempo no está a escala). Las líneas superior e inferior representan las extbf{barreras absorbentes} de fijación y pérdida del alelo. A medida que corre el tiempo las poblaciones se apartan de la frecuencia alélica inicial, aunque se mantiene la frecuencia promedio como el valor inicial.

Si pensamos en la población original, antes de la subdivisión y asumimos que se encontraba en equilibrio de Hardy-Weinberg, ya que \(q=1-p=1-\frac{1}{2}=\frac{1}{2}\), tenemos que la composición de los tres genotipos era la siguiente:

\[ \begin{split} AA=p^2=\left(\frac{1}{2}\right)^2=\frac{1}{4}\\ Aa=2pq=2 \cdot \frac{1}{2} \frac{1}{2}=2 \cdot \frac{1}{4}=\frac{1}{2}\\ aa=q^2=\left(\frac{1}{2}\right)^2=\frac{1}{4} \end{split} \]

Luego, con el paso del tiempo, llegamos a un determinado momento \(t_1\) en que las frecuencias alélicas ya han divergido algo. En la Tabla ?? podemos ver lo que ocurre a nivel de los genotipos en cada una de las 4 poblaciones, así como la media de las 4 poblaciones (que como son todas iguales en tamaño es directamente igual al promedio de los valores). En la última columna tenemos también la frecuencia de los genotipos homocigotos, es decir AA y aa. Claramente, la frecuencia alélica promedio no ha cambiado, era de \(\frac{1}{2}\) en \(t_0=0\) y sigue siendo \(\frac{1}{2}\) en \(t_1\). Sin embargo, dentro de las poblaciones el cambio de frecuencia, sumado al equilibrio Hardy-Weinberg para cada una de ellas se refleja en diferencias importantes entre poblaciones en la proporción de homocigotos. Más aún, el promedio de los homocigotos (el promedio de la suma AA y aa en cada población) se vio incrementado, desde \(fr(AA)+fr(aa)=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}=0,5\) a \(0,5725\). Este hecho no es menor: sin cambiar el promedio de las frecuencias alélicas y manteniendo el equilibrio de Hardy-Weinberg dentro de las poblaciones, si las volviésemos a agrupar a el solo efecto de contar los genotipos, el ensemble ya no se encuentra en el equilibrio de Hardy-Weinberg (porque el equilibrio para \(p=0,5\) es de \(G=\frac{1}{2}=0,5\)) ³⁸.

(#tab:subdivtx1_html)Frecuencias de los genotipos en las 4 poblaciones, manteniendo el equilibrio de Hardy-Weinberg en cada una de ellas, en el primer punto en el tiempo luego del inicio (\(t_1\)).

	p	AA	Aa	aa	Homocigotos
Población 1	0,75	0,5625	0,3750	0,0625	0,6250
Población 2	0,60	0,3600	0,4800	0,1600	0,5200
Población 3	0,40	0,1600	0,4800	0,3600	0,5200
Población 4	0,25	0,0625	0,3750	0,5625	0,6250
Media	0,50	0,2862	0,4275	0,2862	0,5725

Veamos qué ocurre entonces a medida de que nos alejamos del punto inicial en el tiempo. Cuando llegamos al punto \(t_2\), las frecuencias en las poblaciones divergen un poco más, aunque ninguna población ha llegado aún a fijar alguno de los dos alelos. La distribución de los genotipos en las mismas, de acuerdo a las nuevas frecuencias alélicas, se puede apreciar en la Tabla ??. Claramente volvemos a ver un incremento en promedio de homocigotos en la población, que ahora alcanzó el valor \(0,6450\).

(#tab:subdivtx2_html)Frecuencias de los genotipos en las 4 poblaciones, manteniendo el equilibrio de Hardy-Weinberg en cada una de ellas, en el segundo punto en el tiempo luego del inicio (\(t_2\)).

	p	AA	Aa	aa	Homocigotos
Población 1	0,85	0,7225	0,255	0,0225	0,745
Población 2	0,65	0,4225	0,455	0,1225	0,545
Población 3	0,35	0,1225	0,455	0,4225	0,545
Población 4	0,15	0,0225	0,255	0,7225	0,745
Media	0,50	0,3225	0,355	0,3225	0,645

Para ser breves y confirmar la tendencia observada (además de comenzar a imaginar hacia dónde nos lleva ésta), veamos qué ocurre en el instante \(t_3\). Llegado este momento, en la Población 1 se ha fijado el alelo A (\(p=1\)), mientras que en la Población 4 se ha fijado el alelo a (o lo que es equivalente, se ha perdido el A, \(p=0\)). La distribución de genotipos se observa en la Tabla ??.

(#tab:subdivtx3_html)Frecuencias de los genotipos en las 4 poblaciones, manteniendo el equilibrio de Hardy-Weinberg en cada una de ellas, en el tercer punto en el tiempo luego del inicio (\(t_3\)).

	p	AA	Aa	aa	Homocigotos
Población 1	1,0	1,000	0,00	0,000	1,00
Población 2	0,7	0,490	0,42	0,090	0,58
Población 3	0,3	0,090	0,42	0,490	0,58
Población 4	0,0	0,000	0,00	1,000	1,00
Media	0,5	0,395	0,21	0,395	0,79

Ahora, además de haber aumentado nuevamente la proporción de homocigotos respecto al punto anterior en el tiempo, también tenemos un fenómeno nuevo: dos poblaciones solo tienen (y tendrán a futuro) genotipos homocigotos, ya que se ha fijado uno de los dos alelos. Todo esto ocurre sin cambiar la frecuencia alélica media del ensemble. Más aún, si recordamos el comportamiento de las frecuencias alélicas en el tiempo, tarde o temprano las poblaciones terminan cayendo en alguna de las dos “trampas” que son las barreras absorbentes, los estados de fijación o pérdida (fijación del otro alelo), por lo que este comportamiento de la Población 1 y Población 4 es también esperable para las otras dos poblaciones (veremos este fenómeno en detalle más adelante). Llegado ese momento ya no quedarán heterocigotos en el ensemble, pese a que la frecuencia alélica se mantiene como al inicio.

Para entender mejor y poder cuantificar este fenómeno de la reducción del número de heterocigotos debemos pasar a entender primero algunos conceptos sobre los que ahondaremos más adelante (ver capítulo Apareamientos no-aleatorios). Como vimos previamente, el concepto de alelo ha ido variando en el tiempo a medida de que nuestro conocimiento sobre la biología molecular y la genética han llevado a entender las bases de la variación genética. Sin embargo, hay un aspecto en que las cosas no han cambiado mucho: el origen de la similaridad o diferencia entre alelos. En ausencia de mutación³⁹, cuando un alelo es diferente de otro en la presente generación, nos resulta obvio de dónde viene la diferencia: dos alelos son diferentes en esta generación porque provienen de diferentes alelos en la generación previa, y hay poca distinción más que agregar. Sin embargo, cuando dos alelos son “iguales” (decimos que es el mismo alelo) en la presente generación, podemos ser más precisos sobre el origen de esta similitud: los dos alelos “iguales” en la presente generación pueden provenir de dos alelos “iguales” en la generación previa, pero que no sean copias del mismo ADN que los generó, o pueden ser copias del mismo ADN (gametos del mismo individuo y del mismo cromosoma), en cuyo caso los llamamos idénticos por ascendencia. Este concepto es fundamental, así que asegúrate de haberlo entendido. En ambos casos, cuando los dos alelos son “iguales” independientemente del origen, decimos que son idénticos en estado. Claramente, excepto por mutaciones recurrentes en el tiempo, si nos retrotraemos en el pasado lo suficiente, todos los alelos idénticos en estado deberían venir del mismo alelo original, y por lo tanto serían de alguna manera idénticos por ascendencia, por lo que el marco de referencia es fundamental para decidir a partir de cuando se comienza a hacer esta distinción.

La probabilidad de que los dos alelos en un individuo sean idénticos por ascendencia se simboliza comúnmente con la letra \(F\), a partir de Sewall Wright (1922), que lo llamó coeficiente de fijación. Nosotros vamos a utilizar un subíndice para denotar el tiempo desde la generación \(0\), que consideramos la generación inicial. Supongamos que queremos calcular la probabilidad de que dos alelos sean idénticos por ascendencia en la generación \(t\), es decir \(F_t\).

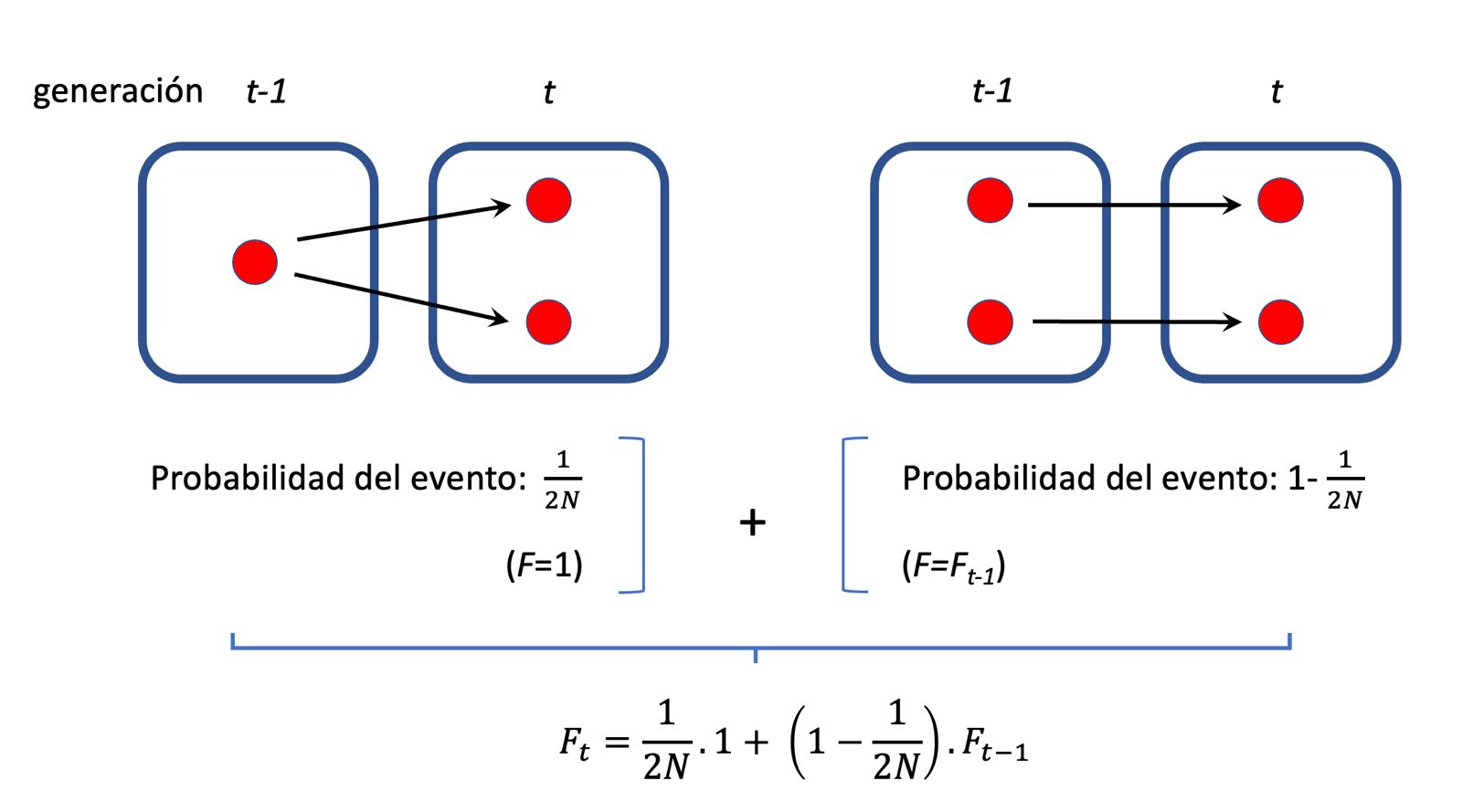
Figura 3.10: Ilustración del razonamiento detrás de la recursión para F en una población de tamaño finito. Existen dos alternativas disjuntas (de ahí la suma) para que un alelo sea idéntico por ascendencia en la generación t: que los alelos provengan del mismo alelo en la generación t-1, cuya probabilidad es \(\frac{1}{2N}\) (y en ese caso \(F=1\), por definición) o que los alelos provengan de distintas copias en la generación t-1, y en cuyo caso la probabilidad de que sean idénticos por ascendencia es por definición \(F_{t-1}\). Por lo tanto, la probabilidad de que dos alelos sean idénticos por ascendencia en la generación \(t\), considerando a la generación \(t-1\), es de \(F_t=\frac{1}{2N}+\left(1-\frac{1}{2N}\right) F_{t-1}\). Aplicando este razonamiento a las sucesivas generaciones anteriores se puede obtener, por recursión, la probabilidad de que dos alelos sean ídénticos por ascendencia a tiempo \(t\) (tomando como referencia la población a tiempo \(t=0\)).

Como se ilustra en la Figura 3.10, existen dos posibilidades mutuamente excluyentes para que dos alelos sean idénticos por ascendencia en la generación \(t\): a) que los dos alelos provengan del mismo alelo en la generación \(t-1\), un evento cuya probabilidad es \(\frac{1}{2N}\) (ya que hay \(2N\) alelos en la población y por lo tanto la probabilidad de volver a muestrear el mismo es \(\frac{1}{2N}\)) y en ese caso \(F=1\), ya que al venir del mismo alelo este es idéntico por ascendencia a sí mismo con probabilidad de 1, y b) que los alelos provengan de distintas copias en la generación \(t-1\), y en ese caso la probabilidad de que sean idénticos por ascendencia es por definición \(F_{t-1}\). Como se trata de dos eventos disjuntos (puede pasar uno u otro, pero no los dos a la vez), puedo sumar sus probabilidades para tener

\[\begin{equation} F_t=\frac{1}{2N}+\left(1-\frac{1}{2N}\right)F_{t-1} \tag{3.5} \end{equation}\]

Se puede calcular así la probabilidad de dos alelos sean idénticos por ascendencia en una generación, asumiendo que se conoce dicha probabilidad para la generación anterior. Veamos ahora si podemos llegar a una expresión general para la probabilidad de dos alelos sean idénticos por ascendencia en una generación basado en el número de generaciones transcurridas desde un momento de referencia (\(t=0\)) y la probabilidad inicial \(F_0\) en dicho momento. Si a ambos lados de la ecuación (3.5) multiplicamos por \(-1\) y le sumamos \(1\) ⁴⁰ tenemos

\[\begin{equation} 1-F_t=1-\frac{1}{2N}-(1-\frac{1}{2N}) F_{t-1} 1-F_t=(1-\frac{1}{2N})(1-F_{t-1}) \tag{3.6} \end{equation}\]

Pero con la misma lógica,

\[\begin{equation} 1-F_{t-1}=\left(1-\frac{1}{2N}\right)(1-F_{t-2}) \tag{3.7} \end{equation}\]

y sustituyendo (3.7) en (3.6), tenemos

\[\begin{equation} 1-F_t=(1-\frac{1}{2N})(1-\frac{1}{2N})(1-F_{t-2})=(1-\frac{1}{2N})^2(1-F_{t-2}) \tag{3.8} \end{equation}\]

Prosiguiendo con la recursión hasta llegar a la generación \(0\) (generación inicial), como transcurren \(t\) generaciones entre la \(0\) y la actual tenemos que la ecuación (3.8) se generaliza a

\[\begin{equation} 1-F_t=\left(1-\frac{1}{2N}\right)^t(1-F_{0}) \tag{3.9} \end{equation}\]

Más aún, si asignamos arbitrariamente \(F_0=0\) por falta de conocimiento acerca de la probabilidad de que dos alelos sean idénticos por ascendencia en la generación inicial, entonces la ecuación (3.9) se transforma en

\[\begin{equation} 1-F_t=\left(1-\frac{1}{2N}\right)^t \end{equation}\]

\[\begin{equation} F_t=1-\left(1-\frac{1}{2N}\right)^t \tag{3.10} \end{equation}\]

Veamos ahora cómo se relaciona todo esto con el problema de la subdivisión poblacional planteado en la Figura 3.9. Por definición, \(F\) es también la reducción en heterocigosis (o el incremento en homocigosis) respecto a la expectativa en equilibrio de Hardy-Weinberg (y sus frecuencias genotípicas) en poblaciones finitas (porque es la probabilidad de que dos alelos sean idénticos por ascendencia en un individuo, por lo tanto homocigoto). Entonces, el paralelismo de \(1-F\) es respecto a los heterocigotos conservados y el apareamiento aleatorio. Si consideramos que la frecuencia esperada de heterocigotas en una población de tamaño finito es una función de \(p\) y \(q\), pero también de esa probabilidad de que los alelos no sean idénticos por ascendencia, entonces si llamamos \(H_t\) a esa frecuencia, tenemos,

\[ \begin{split} H_t=2pq(1-F_{t-1})\\ \therefore 1-F_{t-1}=\frac{H_t}{2pq} \end{split} \]

El \(t-1\) en el término \((1-F_{t-1})\) se corresponde con el hecho de que el efecto de la reducción de los pares de alelos NO idénticos por ascendencia se ve en la generación anterior a la presente. Notemos que \(H_t = 2pq(1-F_{t-1})\), lo cual equivale a decir \(1-F_{t-1} = \frac{H}{2pq}\). Esto nos lleva a

\[ \begin{split} 1-F_t=\left(1-\frac{1}{2N}\right)(1-F_{t-1})=\left(1-\frac{1}{2N}\right)\frac{H_t}{2pq}= \\ =\left(1-\frac{1}{2N}\right)^2\frac{H_{t-1}}{2pq}=\left(1-\frac{1}{2N}\right)^3\frac{H_{t-2}}{2pq} \\ \therefore \left(1-\frac{1}{2N}\right)\frac{H_t}{2pq}=\left(1-\frac{1}{2N}\right)^{t+1}\frac{H_{t-t}}{2pq} \\ H_t=\left(1-\frac{1}{2N}\right)^t H_0= \left(1-\frac{1}{2N}\right)^t[2pq(1-F_{-1})] \end{split} \]

Notemos que en el desarrollo anterior se continuó la recursión planteada hasta alcannzar el tiempo \(t=t\) (de ahí que el exponente que acompaña a \(H_{t-t} = H_0\) sea \(t+1\)). Luego, como en ambos lados de la ecuación se tiene \(2pq\) en el denominador, los términos se cancelan, y como en el lado izquierdo se tiene \(1-\frac{1}{2N}\), al dividir ambos lados por este término el exponente \(t+1\) en el lado derecho pasa a ser \(t\).

En resumen, luego de este desarrollo por recursión se llega a

\[ H_t = (1 - \frac{1}{2N})^t H_0 \tag{3.11} \]

Utilizando la aproximación \((1-a)^b \approx (e^{-a})^b \approx e^{-ab}\) cuando \(a \to 0\) (en nuestro caso, \(a = \frac{1}{2N};\ b = t\)), tenemos

\[\begin{equation} H_t=\left(1-\frac{1}{2N}\right)^t H_0 \approx H_0 e^{\frac{-t}{2N}} \tag{3.12} \end{equation}\]

Es decir, pese a que en cada una de las poblaciones se mantiene el equilibrio de Hardy-Weinberg, como se puede apreciar en la Figura 3.11, la proporción de individuos heterocigotos en el conjunto de ellas, o mejor dicho el promedio en el ensemble, decaerá en forma geométrica respecto al valor inicial a lo largo del tiempo ya que la proporción en cada generación es multiplicada por el factor \(\left(1-\frac{1}{2N}\right)\) al pasar a la siguiente. La aproximación exponencial funciona en general razonablemente bien, y permite resolver algunos problemas en forma más sencilla. El efecto de la reducción en la proporción de heterocigotos es realmente drástico cuando los tamaños poblacionales son extremadamente pequeños, por ejemplo \(N=5\) o \(N=10\) individuos en la Figura 3.11, pero son apenas notables cuando el número de individuos es 50 o más (notar que para 100 individuos el punto de reducción a \(50\%\) de la heterocigosis inicial ni siquiera aparece en la gráfica, ya que llevaría más de 138 generaciones para alcanzarlo).

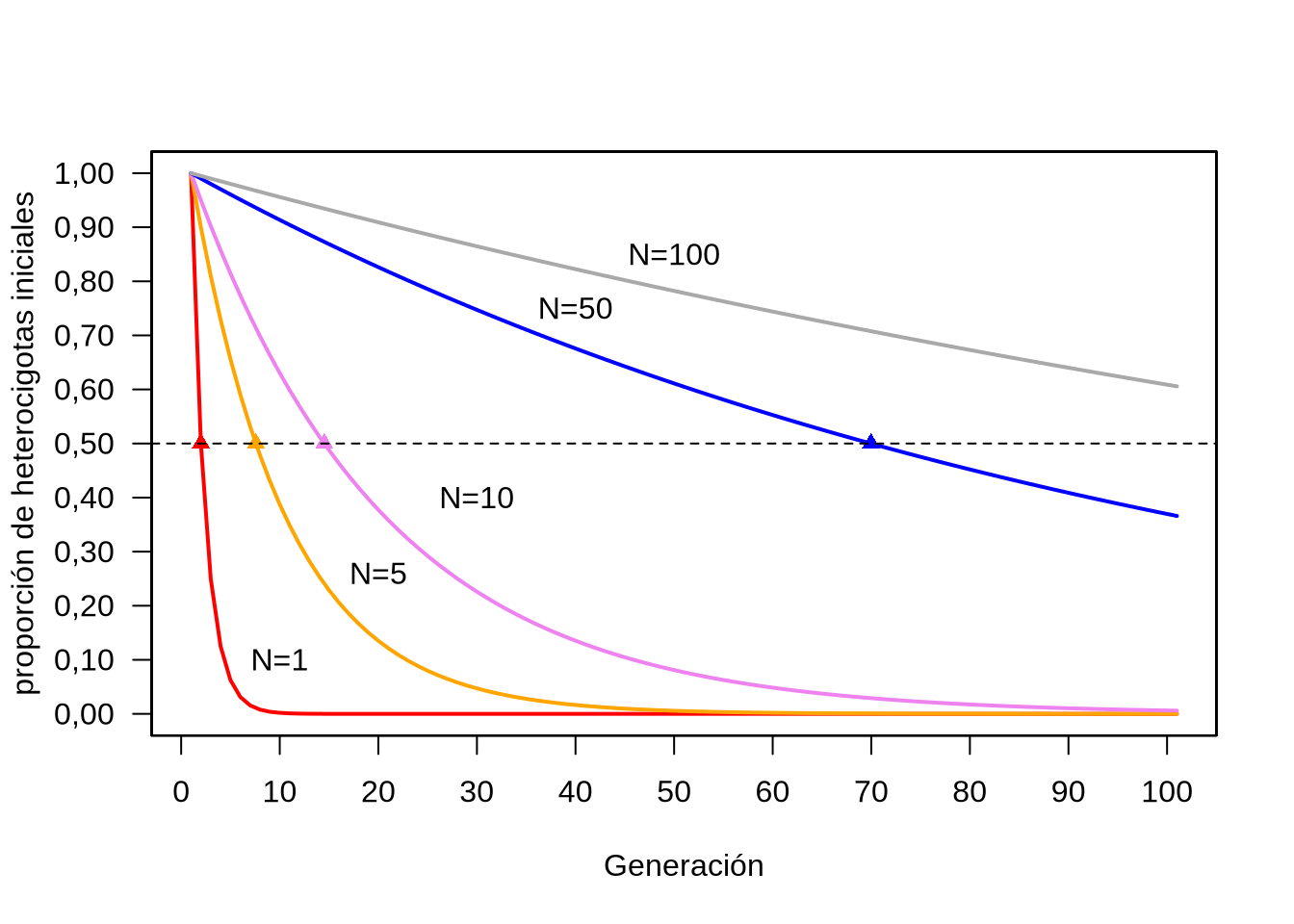
Figura 3.11: Reducción esperada en el número inicial de heterocigotas \(H_0\) de acuerdo al tamaño N de las poblaciones y al número de generaciones transcurridas. La línea negra horizontal marca la reducción a la mitad del valor inicial y los puntos sobre las curvas resaltan el número de generaciones requeridas para esa reducción a la mitad.

Ejemplo 3.2

La ecuación (3.12), en particular la aproximación exponencial, nos permite estimar facilmente los tiempos hasta determinado nivel de reducción de la frecuencia inicial de heterocigotos. Por ejemplo, para alcanzar la mitad del valor inicial (\(H_0\)), con poblaciones de \(N\) individuos puedo hacer \(H_t=\frac{H_0}{2}\). Luego, de acuerdo a la ecuación (3.12) tenemos que

\[ \begin{split} H_t=\frac{H_0}{2}=H_0e^{\frac{-t}{2N}}\\ \therefore \frac{1}{2}=e^{\frac{-t}{2N}} \end{split} \]

Aplicando el logaritmo a ambos lados de la ecuación, tenemos

\[\begin{equation*} \ln\left(\frac{1}{2}\right)=\ln\left(e^{\frac{-t}{2N}}\right)=\frac{-t}{2N} \end{equation*}\]

y finalmente

\[\begin{equation*} t=-2N \ln\left(\frac{1}{2}\right) \approx 1,39N \end{equation*}\]

Es decir, en \(1,39N\) generaciones. Si lo hubiésemos hecho sin la aproximación, el procedimiento es análogo y llegaríamos a

\[\begin{equation*} \frac{H_0}{2}=\left(1-\frac{1}{2N}\right)^t H_0 \therefore t=\frac{\ln{\left(\frac{1}{2}\right)}}{\ln{\left(1-\frac{1}{2N}\right)}} \end{equation*}\]

que si bien es la solución exacta, no es lineal en el número de individuos en cada población.

---

Resumiendo, en esta sección vimos cómo la subdivision poblacional produce el efecto de disminuir el número de heterocigotas respecto a los esperado para las poblaciones del ensemble agregadas en un solo grupo y bajo condiciones de panmixia (es decir, con libertad de aparearse con cualquier otro individuo de la población, sin restricciones genéticas, conductuales o ambientales). Esa disminución de la proporción de heterocigotos esperados ocurre a una tasa constante por generación (en nuestro modelo) y la misma es de \(\left(1-\frac{1}{2N}\right)\), por lo que la reducción total a lo largo de \(t\) generaciones será del orden de \(\left(1-\frac{1}{2N}\right)^t\). Mientras que en la sección El modelo de Wright-Fisher construimos un modelo de evolución de las frecuencias alélicas sin preocuparnos de los genotipos, en esta sección vimos las implicancias para la evolución de los genotipos tiene dicho modelo. En la sección Cadenas de Markov veremos de otra forma una conexión entre los dos fenómenos utilizando una aproximación fundamental para comprender los procesos estocásticos en general.

PARA RECORDAR

• La recursión para el coeficiente de fijación \(F\) en la generación \(t\), \(F_t\) es igual a: \[\begin{equation*} 1-F_t=\left(1-\frac{1}{2N}\right)^t(1-F_0) \end{equation*}\]
• Cuando \(F_0=0\), es decir que asumimos que en la generación inicial la probabilidad de que dos alelos en un locus de un individuo diploide es cero, entonces la recursión anterior se simplifica a:

\[\begin{equation*} F_t=1-\left(1-\frac{1}{2N}\right)^t \end{equation*}\]

• El número de heterocigotos en un ensemble de poblaciones de tamaño finito \(N\) se ve reducido de generación en generación respecto a lo esperado para el equilibrio de Hardy-Weinberg. Esa reducción es a la tasa de \(\left(1-\frac{1}{2N}\right)\) por generación, por lo que la frecuencia de heterocigotos en la generación \(t\) se calcula de acuerdo a la siguiente ecuación:

\[\begin{equation*} H_t=\left(1-\frac{1}{2N}\right)^t H_0 \approx H_0 e^{\frac{-t}{2N}} \end{equation*}\]

3.4 Cadenas de Markov

Si recuerdas la ecuación (3.2) de más arriba establecía la probabilidad de transición de un número \(i\) de copias a un número \(j\) (en un total de \(2N\) alelos) en una generación, y la misma era igual a:

\[\begin{equation} T_{ij}={2N \choose j}\left(\frac{i}{2N}\right)^{j}\left(\frac{2N-i}{2N}\right)^{2N-j}=\frac{(2N)!}{j!(2N-j)!}p^jq^{2N-j} \tag{3.13} \end{equation}\]

Visto de otra forma, como \(i\) puede ir desde \(0\) hasta \(2N\) y lo mismo para \(j\), podemos poner estas probabilidad de transición en una matriz cuadrada con \(2N+1\) filas y \(2N+1\) columnas (el \(+1\) es debido a que un conteo de \(0\) para cada alelo es posible). Por ejemplo, calculemos la matriz para una población con 2 individuos diploides. Para ello vamos a calcular en forma explícita las probabilidades de transición de unas pocas celdas de la matriz y el resto sigue la misma lógica. En particular, vamos a calcular algunas celdas de la fila correspondientes a 2 alelos A en la generación actual (o sea \(p=\frac{2}{4}=\frac{1}{2}=0,5\)). Estas celdas corresponden a la probabilidad de pasar de un número \(i=2\) de alelos A a un número \(j\) determinado en la próxima generación.

De acuerdo a la ecuación (3.13), la probabilidad de transición de 2 copias del alelo A (\(i=2\)) a 1 copia del mismo (\(j=1\)) es de:

\[\begin{equation} T_{2,1}={4 \choose 1}\left(\frac{2}{4}\right)^{1}\left(\frac{4-2}{4}\right)^{4-1}={4 \choose 1}\left(\frac{1}{2}\right)^{1}\left(\frac{1}{2}\right)^{3}=4 \left(\frac{1}{2}\right)^4=0,25 \end{equation}\]

Asimismo, la probabilidad de transición de 2 copias del alelo A (\(i=2\)) a 3 copias del mismo (\(j=3\)) es de:

\[\begin{equation} T_{2,3}={4 \choose 3}\left(\frac{2}{4}\right)^{3}\left(\frac{4-2}{4}\right)^{4-3}={4 \choose 3}\left(\frac{1}{2}\right)^{3}\left(\frac{1}{2}\right)^{1}=4 \left(\frac{1}{2}\right)^4=0,25 \end{equation}\]

De la misma manera, la probabilidad de transición de 2 copias del alelo A (\(i=2\)) a 4 copias del mismo (\(j=4\)) es de:

\[\begin{equation} T_{2,4}={4 \choose 4}\left(\frac{2}{4}\right)^{4}\left(\frac{4-2}{4}\right)^{4-4}={4 \choose 4}\left(\frac{1}{2}\right)^{4}\left(\frac{1}{2}\right)^{0}=1 \left(\frac{1}{2}\right)^4=0,0625 \end{equation}\]

En la tabla ?? puedes ver el resultado de calcular las probabilidades de transición para todos los pares de estados posibles (pares entrada-salida, o generación actual-próxima generación, \(0 \leq i \leq 2N\), \(0 \leq j \leq 2N\)). Llamaremos a esta matriz \(T\), por ser la matriz de probabilidad de transiciones de estado. En las filas tenemos los posibles estados en la generación actual, definidos como el número de alelos A en la generación actual, mientras que en las columnas tenemos el número de alelos A en la generación próxima. Se trata de probabilidades, ya que lo visto hasta ahora es que el apareamiento de acuerdo al modelo de Wright-Fisher generará poblaciones descendientes en forma aleatoria, con una probabilidad dada por esta matriz de transición. Es de notar que los estados actuales de 0 y 4 alelos A se corresponden a lo que definimos como barreras absorbentes de nuestro sistema, pues una vez alcanzado alguno de estos dos estados será imposible abandonarlos (estamos asumiendo la ausencia de mutación). Dicho de otra forma, una vez que se pierde el alelo A en una población (\(0\) copias del mismo), o que el mismo queda fijado en la población (\(2N\) copias, en nuestro ejemplo \(2N=4\) copias), en las próximas generaciones esto no va a cambiar.

(#tab:matrizMarkov_html)(#tab:matrizMarkov_html)Matriz de transición para un locus con dos alelos y dos individuos diploides.

	a 0 alelos A	a 1 alelos A	a 2 alelos A	a 3 alelos A	a 4 alelos A
de 0 alelos A	1,0000	0,0000	0,0000	0,0000	0,0000
de 1 alelos A	0,3164	0,4219	0,2109	0,0469	0,0039
de 2 alelos A	0,0625	0,2500	0,3750	0,2500	0,0625
de 3 alelos A	0,0039	0,0469	0,2109	0,4219	0,3164
de 4 alelos A	0,0000	0,0000	0,0000	0,0000	1,0000

¡Excelente! Tenemos computada nuestra matriz de transiciones. Si observas con cuidado verás que la suma de cada fila es igual a 1, es decir \(\sum_{j=0}^{2N} p_{i,j}=1\). Esto quiere decir que las poblaciones que parten de \(i\) alelos en la generación padre deben distribuirse entre todas las posibilidades \(j\), pero que en última instancia, al tratarse de un probabilidad, la suma de todas las posibilidades disjuntas debe ser igual a 1. Veamos ahora cómo la podemos usar para calcular la evolución de las frecuencias alélicas en un ensemble de poblaciones, todas del mismo tamaño y que parten de la misma frecuencia alélica. Supongamos que todas estas poblaciones parten en tiempo \(t=0\) de \(i=2\) alelos A. Representaremos las frecuencia de poblaciones en las que hay \(i\) alelos con un vector de largo \(2N+1\); la primera posición en el vector representará la frecuencia de poblaciones con 0 alelos A, la segunda la frecuencia de poblaciones con 1 alelo A, la tercera con 2 alelos AA, y así hasta la posición \(2n+1=5\) en nuestro caso. Como todas las poblaciones arrancan desde \(i=2\), nuestro vector de frecuencias será \(\mathbf{I}_0=(0;0;1;0;0)\). Ahora, si multiplicamos este vector fila \(\mathbf{I}_0\) por nuestra matriz \(\mathbf{T}\) de transiciones (si precisas recordar como se multiplican matrices y vectores, recurre al [APENDICE A: Conceptos Matemáticos Básicos]), obtendremos un nuevo vector de probabilidad de que las distintas poblaciones del ensemble posean un número determinado de alelos A, dado por \(\mathbf{I}_1=\mathbf{I}_0 * \mathbf{T}\) (representado en la Tabla ??).

(#tab:vectorProbabilidades1_html)Vector de probabilidades de que una población en nuestro ensemble se encuentre en un estado alélico determinado luego de la primera generación (\(I_1\)).

0 alelos A	1 alelos A	2 alelos A	3 alelos A	4 alelos A
0,0625	0,25	0,375	0,25	0,0625

Es decir, si bien partimos de que todas las poblaciones poseían 2 alelos A, por efecto del azar (deriva genética le llamamos a este efecto), ahora un \(6,25\%\) de ellas poseerán 0 alelos A (se habrá perdido el mismo), un \(25\%\) 1 alelo A, un \(37,5\%\) 2 alelos A, otro \(25\%\) 3 alelos A y finalmente, \(6,25\%\) de ellas tendrán todos los 4 alelos A (habrán fijado ese alelo). Ahora, la misma matriz de transición que aplicamos para pasar de la generación \(t=0 \to t=1\) la podemos aplicar al vector de probabilidades (frecuencias relativas) de poblaciones en la generación \(t=1\) para pasar a la \(t=2\). ⁴¹ Es decir que ahora tenemos \(\mathbf{I}_2=\mathbf{I}_1 * \mathbf{T}\), cuyo resultado podemos apreciar en ??.

(#tab:vectorProbabilidades2_html)Vector de probabilidades de que una población en nuestro ensemble se encuentre en un estado alélico determinado luego de la segunda generación (I2).

0 alelos A	1 alelos A	2 alelos A	3 alelos A	4 alelos A
0,166	0,2109	0,2461	0,2109	0,166

Podemos repetir este procedimiento de generación en generación. Cuando un proceso estocástico depende solamente del estado inmediantamente anterior en el tiempo, como en nuestro caso, decimos que se trata de un proceso Markoviano. Una cadena de Markov⁴² es una secuencia de eventos (usualmente en el tiempo) en la que cada resultado depende exclusivamente del resultado precedente. Dicho de otra manera, para predecir el siguiente resultado del proceso (futuro) solo la información del presente estado es relevante y el pasado (los estados anteriores del sistema) no tienen relevancia. A esto último se le conoce como propiedad markoviana (o de falta de memoria). En nuestro caso, como la distribución de probabilidades de cada nueva generación \(t=k\) es determinada multiplicando el resultado de la anterior (\(\mathbf{I}_{t=(k-1)}\)) por la matriz de transición (\(\mathbf{T}\)), claramente podemos ver por qué se trata de una cadena (de Markov). Si comparamos la evolución de nuestro sistema, tenemos ahora que desde la generación \(t=0\) hasta la generación \(t=5\), la frecuencias han ido cambiando de la manera que se aprecia en la Tabla ??.

(#tab:evolProbabilidades1_html)Evolución del vector de probabilidades de que una población en nuestro ensemble se encuentre en un estado alélico determinado desde la generación 0 a la quinta generación.

0 alelos A	1 alelos A	2 alelos A	3 alelos A	4 alelos A
0,0000	0,0000	1,0000	0,0000	0,0000
0,0625	0,2500	0,3750	0,2500	0,0625
0,1660	0,2109	0,2461	0,2109	0,1660
0,2490	0,1604	0,1813	0,1604	0,2490
0,3117	0,1205	0,1356	0,1205	0,3117
0,3587	0,0904	0,1017	0,0904	0,3587

Otra forma de verlo, más gráfica, aparece en la Figura 3.12. Claramente se aprecia que mientras que las probabilidades de encontrarse en los estados intermedios (\(i=1\) a \(i=3\), en gris) decrece, la de los estados correspondientes a las barreras absorbentes (rojo: pérdida, azul: fijación) crece en la misma medida. La pregunta sería ¿hacia dónde va este movimiento?, o dicho de otra forma, ¿qué ocurre si seguimos de generación en generación?

Antes de abordar esta cuestión, es interesante notar que \(\mathbf{I}_2=\mathbf{I}_1 * \mathbf{T} = (\mathbf{I}_0 * \mathbf{T}) * \mathbf{T} = \mathbf{I}_0 * (\mathbf{T} * \mathbf{T})=\mathbf{I}_0 * \mathbf{T}^2\)⁴³. Claramente, lo anterior se puede generalizar a \(\mathbf{I}_{t=k}=\mathbf{I}_0 * \mathbf{T}^{(k)}\). En palabras, para calcular la distribución de probabilidades de los estados (número de alelos A en nuestro ensemble de poblaciones) en cualquier generación \(k\) (donde consideramos \(t=k\), \(k>0\)) basta con multplicar la distribución en la generación inicial (o sea en \(t=0\), que llamamos \(\mathbf{I}_0\)) por la matriz de transición de probabilidades elevada a la potencia \(k\).

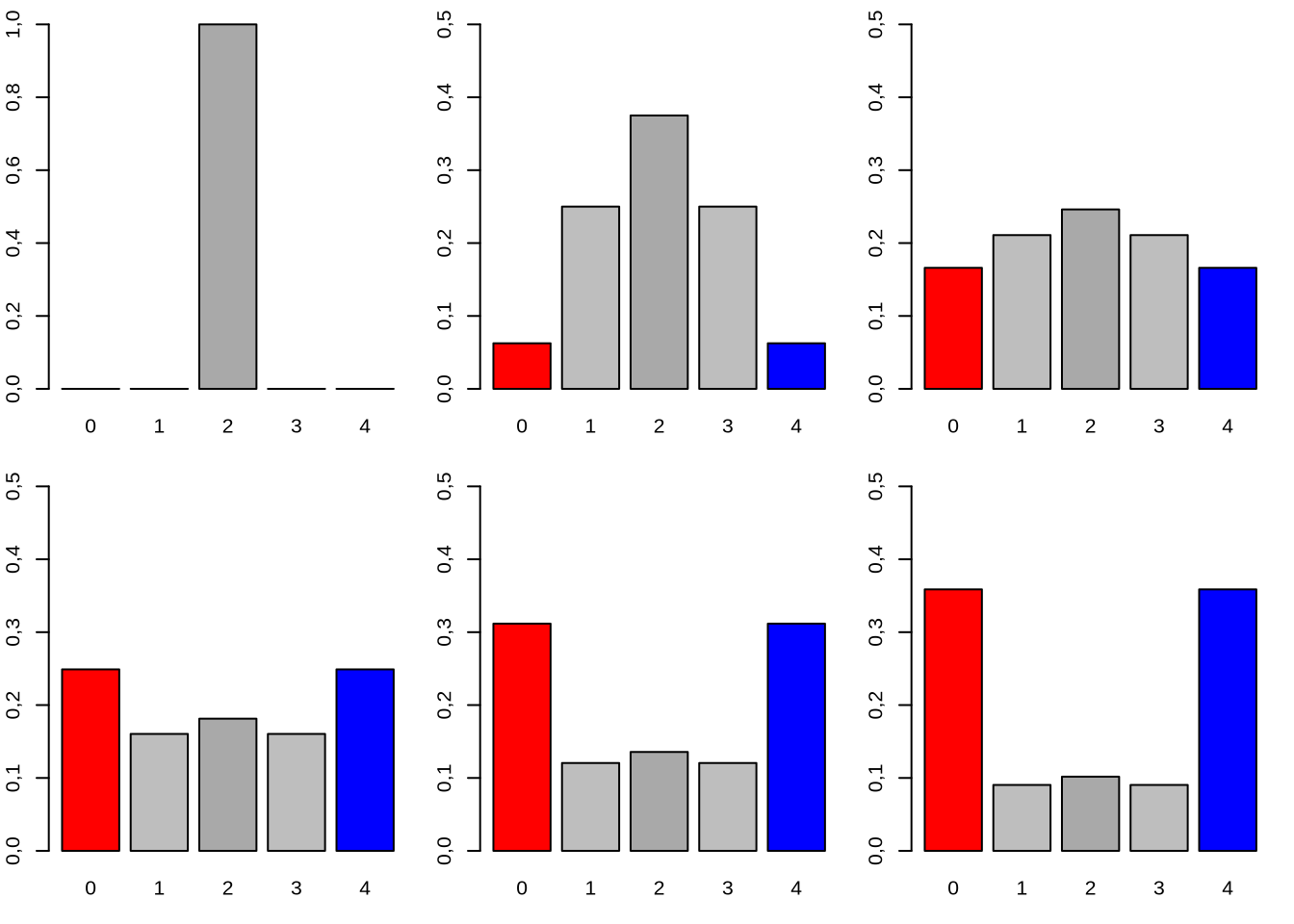
Figura 3.12: Evolución de la probabilidad de encontrar a las poblaciones en un estado alélico determinado desde la generación \(t=0\) a \(t=5\) (desde el costado superior izquierdo al inferior derecho). En rojo el estado de 0 alelos A (pérdida del mismo), en azul 4 alelos A (fijación del mismo) y en gris oscuro 2 alelos (nuestro punto de partida en todas las poblaciones). Notar la diferente escala de la generación \(t=0\) al resto.

Volvamos entonces a la pregunta anterior: ¿hacia dónde va el movimiento de las frecuencias en las distintas poblaciones a largo plazo? Para abordar esta cuestión, tendremos en cuenta el razonamiento de que \(\mathbf{I}_{t=k}=\mathbf{I}_0 * \mathbf{T}^{(k)}\). Resulta interesante ver cómo se comporta \(\mathbf{T}^{(k)}\) cuando \(k \to \infty\), es decir cuando el número de generaciones tiende a infinito. Una aproximación numérica sencilla consiste en elevar \(\mathbf{T}\) a un número suficientemente grande (e.g 50 generaciones) y ver la forma que adquiere la matriz, como aparece en la Tabla ??.

(#tab:matrizMarkov50_html)Matriz de transición para un locus con dos alelos y dos individuos diploides luego de 50 generaciones.

	a 0 alelos A	a 1 alelos A	a 2 alelos A	a 3 alelos A	a 4 alelos A
de 0 alelos A	1,00	0	0	0	0,00
de 1 alelos A	0,75	0	0	0	0,25
de 2 alelos A	0,50	0	0	0	0,50
de 3 alelos A	0,25	0	0	0	0,75
de 4 alelos A	0,00	0	0	0	1,00

Si miramos las columnas de la Tabla ?? podemos apreciar dos situaciones claramente distintas; en las columnas 2, 3 y 4 (que corresponden a pasar de una generación a la siguiente a los estados de 1, 2 y 3 alelos A respectivamente), todas las celdas son 0, es decir más allá del punto de arranque (el vector de frecuencias o probabilidades \(\mathbf{I}_0\)), cuando el tiempo tiende a infinito (en principio lo estaríamos viendo con solo 50 generaciones) estos estados alélicos estarán vacíos (ninguna población tendrá 1, 2 o 3 alelos A), en nuestro modelo de dos individuos diploides. En cambio, las columnas 1 y 5, que se corresponden a la fijación del alelo a (pérdida del alelo A) y la fijación del alelo A respectivamente plantean una distribución que parece en espejo una de otra; claramente estas columnas se corresponden a las dos barreras absorbentes. Si nos fijamos en la columna 1, el único 0 corresponde a la probabilidad de pasar de 4 alelos A a 0 alelos A. Esto es trivial, ya que si el alelo A se encuentra fijado, al no existir mutación es imposible que las poblaciones evolucionen a otro estado alélico. Inversamente, en la columna 5 el único 0 se corresponde a la probabilidad de pasar de 0 a 4 alelos A. Esto también trivial, ya que no existe posibilidad de pasar del alelo a fijado a otro estado alélico. El resto de las celdas es fácil de explicar, si recordamos las probabilidades de fijación de un alelo dada su frecuencia inicial en la población. Cuando se parte de 1 solo alelo A (i.e., 3 alelos a), la probabilidad de fijación del alelo a es \(\frac{3}{4}\); cuando se parte de 2 alelos A, es de \(\frac{2}{4}=\frac{1}{2}\), y cuando se parte de 3 alelos A (i.e. solo 1 alelo a), la probabilidad de fijación del alelo a es \(\frac{1}{4}\). Lo mismo acontece de forma inversa para las transiciones representadas en la columna 5.

La conclusión de todo lo anterior no es menor: con la matriz de probabilidad de transiciones \(\mathbf{T}\) (??) el estado estacionario (cuando \(t \to \infty\)) implica que solo los estados de fijación de alguno de los alelos tienen probabilidad mayor a cero. El punto de partida solo influirá en la distribución entre ellos, pero no en que solo ellos pueden tener probabilidad positiva de fijación. Pongamos un ejemplo: todas las poblaciones inicialmente tienen 1 alelo A de los 4 posibles (recordar que son dos individuos diploides, \(2N=4\)), es decir, \(\mathbf{I}_0=(0;1;0;0;0)\). Si multiplicamos este vector inicial de probabilidades (probabilidades de encontrar poblaciones del ensemble en ese estado), tenemos que \(\mathbf{I}_0*\mathbf{T}^\infty\) (llamamos \(\mathbf{T}^\infty\) a la potencia infinita, aunque en este contexto \(\mathbf{T}^{50} \sim \mathbf{T}^\infty\)), el resultado es \(\mathbf{I}_0*\mathbf{T}^\infty=(0,75;0;0;0;0,25)\), claramente en línea con lo que esperábamos: ninguna población aún segregando (1, 2 o 3 alelos A), \(75\%\) de la poblaciones con el alelo a fijado y \(25\%\) de las poblaciones con el alelo A fijado.

Si en lugar de haber arrancado con todas las poblaciones con 1 solo alelo A, hubiésemos arrancado con \(25\%\) de las poblaciones con 1 alelo A, \(25\%\) con dos alelos y \(50\%\) con 3 alelos A, entonces \(\mathbf{I}_0=(0;0,25;0,25;0,50;0)\). Por lo tanto \(\mathbf{I}_0*\mathbf{T}^\infty=(0,4375;0;0;0;0,5625)\), es decir que el \(43,75\%\) de las poblaciones de nuestro ensemble tendrían fijado el alelo a y el restante \(56,25\%\) tendría fijado el alelo A.

En general, si la deriva genética es la única fuerza evolutiva actuante (sin selección, sin mutación, sin migración), el equilibrio se alcanza cuando más tarde o más temprano todas las poblaciones se encuentran fijadas para uno de los dos alelos.

Un último punto que cabe mencionar acá. Si observamos la forma en la que crece la suma de los estados correspondientes a las barreras absorbentes, es posible demostrar que a partir de determinado punto la tasa de aproximación al estado de equilibrio es igual a \((1-\frac{1}{2N})\). Dicho de otra forma, a partir de determinado momento, a cada generación la proporción de poblaciones aún segregantes se reduce en \(\frac{1}{2N_e}\), proporción que va a parar de los estados correspondientes a las barreras absorbentes.

3.5 Tamaño efectivo poblacional

Un punto que mencionamos antes pero no abundamos fue la diferencia entre el tamaño censal de una población, es decir el número \(N\) de individuos que la conforman y el tamaño efectivo de la misma, que llamamos \(N_e\). A veces resulta claro cuando en determinadas estructuras poblacionales particulares no tiene ningún sentido el número \(N\) como un indicador del comportamiento genético de la población, por ejemplo cuando un solo macho es responsable de todas las crías, pero otras veces no resulta tan claro. En todo caso, dada la dependencia de varias de nuestras ecuaciones de algún número que represente el tamaño poblacional, es necesario definir qué significa ese número a la luz de las cosas que hemos asumido en nuestros modelos.

Un ejemplo claro lo representa el supuesto de tamaño poblacional constante que hemos usado en el modelo de Wright-Fisher. Desafortunadamente, este supuesto es difícil de constatar en la realidad ya que las poblaciones fluctúan de tamaño, algunas en forma de tendencia (al crecimiento o decrecimiento) y otras a través de ciclos (por ejemplo, tamaños poblacionales de presa y predador, que están íntimamente relacionados). En este sentido, podríamos pensar en obtener un número poblacional en una población perfecta (para nuestro modelo) en la que de alguna manera el efecto genético de la deriva fuese equivalente al de nuestra población real. Si el tamaño poblacional fluctúa en el tiempo, podríamos por ejemplo pensar en que la media aritmética (el clásico promedio, que conoces muy bien) del tamaño censal sería un buen resumen del impacto genético de la deriva en la población. Desafortunadamente, el impacto genético de los tamaños poblacionales pequeños es desproporcionadamente alto, como puede verse en la Figura 3.13.

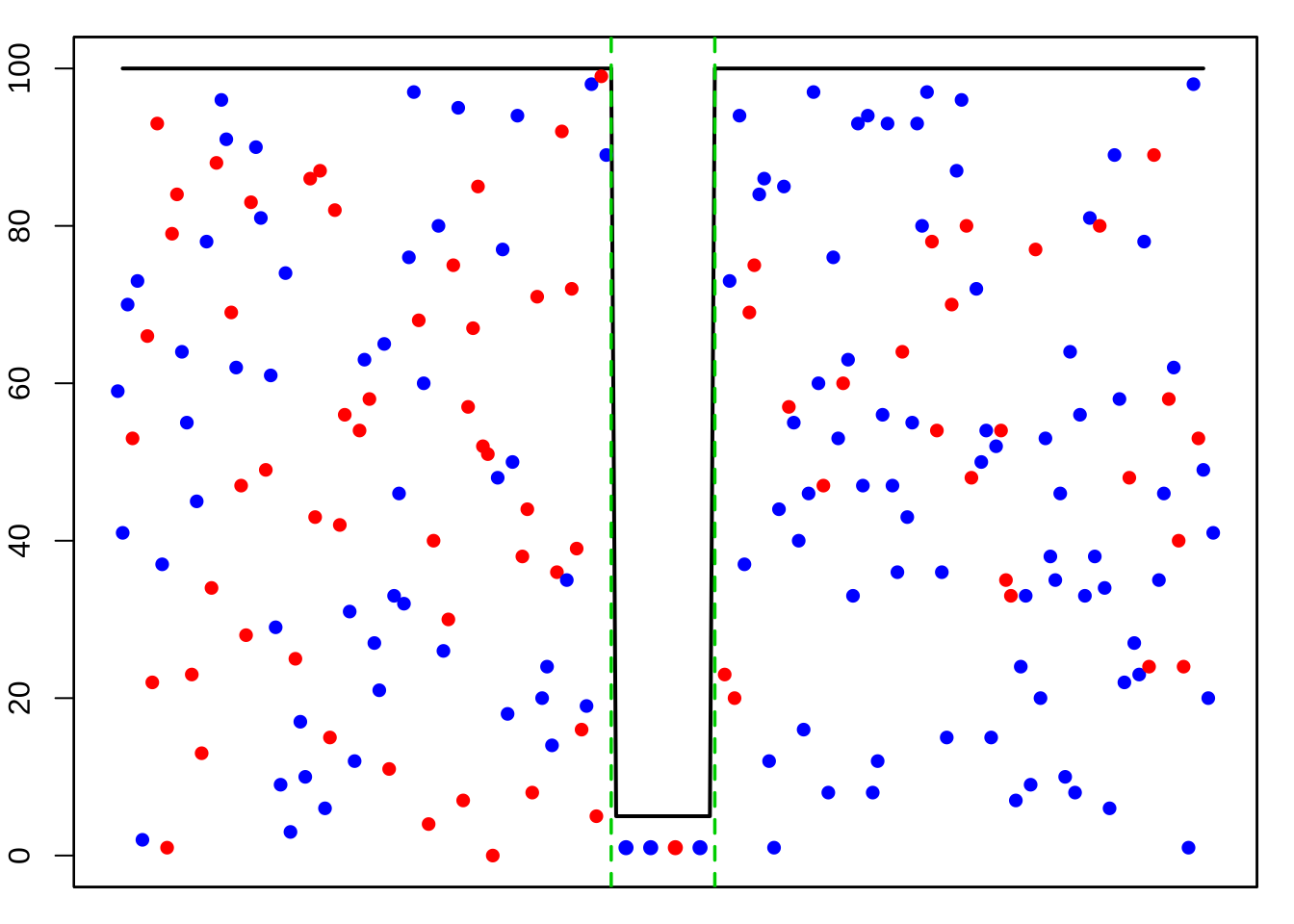
Figura 3.13: Efecto de un cuello de botella poblacional en la frecuencia alélica. La población de 100 alelos, 50 rojos y 50 azules, se ve drásticamente reducida en una generación a 4 alelos (entre las dos líneas verdes), que por muestreo aleatorio son ahora 3 azules y 1 rojo. Luego de ese cuello de botella la población vuelve a expandirse al nivel inicial, pero la frecuencia ya quedó alterada en forma importante (figura propia sobre idea de Hamilton (2009)).

En efecto, pese a que la población inicial era de 50 individuos diploides, o sea 100 alelos, 50 rojos y 50 azules, al sufrir un cuello de botella poblacional (sobreviven 2 individuos diploides, marcado por las dos líneas verdes en la Figura 3.13) se muestrean 3 alelos azules y 1 rojo (un evento que tiene una probabilidad de \(\frac{1}{4}=25\%\)). Al expandirse nuevamente la población a 50 individuos, es decir 100 alelos, lo hará desde la frecuencia del cuello de botella. Resulta clara la influencia desproporcionada (respecto a un promedio simple) que tiene el muestreo durante el cuello de botella poblacional.

Veamos entonces una forma más razonable de estimar el tamaño de una población que fluctúa en número. Para hacer nuestro razonamiento supongamos que la población va de la generación 0 hasta la 2. De acuerdo a lo que vimos en la sección de Homocigosidad y Heterocigosidad,

\[\begin{equation} 1-F_2=\left(1-\frac{1}{2N_1}\right)(1-F_1) \tag{3.14} \end{equation}\]

\[\begin{equation} 1-F_1=\left(1-\frac{1}{2N_0}\right)(1-F_0) \tag{3.15} \end{equation}\]

Sustituyendo (3.15) en (3.14), tenemos:

\[\begin{equation} 1-F_2=\left(1-\frac{1}{2N_1}\right)\left(1-\frac{1}{2N_0}\right)(1-F_0) \tag{3.16} \end{equation}\]

Si el tamaño \(N\) fuese constante, obtendríamos el \(N_e\) generalizando esta expresión para un tiempo \(t\)

\[\begin{equation} 1-F_t = (1-\frac{1}{2N_e})^{t}(1-F_0) \tag{3.17} \end{equation}\]

Por ejemplo, en el caso en que \(t=2\), la ecuación (3.17) se transforma en

\[\begin{equation} 1-F_2=(1-\frac{1}{2N_e})^2 (1-F_0) \tag{3.18} \end{equation}\]

Ahora, si igualamos el resultado “real” (ecuación (3.16)) a la “ideal” (ecuación (3.18)), tenemos:

\[\begin{equation} \begin{split} 1-F_2=(1-\frac{1}{2N_e})^2(1-F_0)=(1-\frac{1}{2N_1})(1-\frac{1}{2N_0})(1-F_0)=1-F_2 \\ (1-\frac{1}{2N_e})^2=(1-\frac{1}{2N_1})(1-\frac{1}{2N_0}) \end{split} \tag{3.19} \end{equation}\]

Desarrollando la ecuación (3.19), tenemos que:

\[\begin{equation} \begin{split} 1-2\frac{1}{2N_e}+\frac{1}{4N_e^2}=1-\frac{1}{2N_0}-\frac{1}{2N_1}+\frac{1}{4N_0N_1} \frac{1}{N_e}-\frac{1}{4N_e^2}=\frac{1}{2}\left(\frac{1}{N_0}+\frac{1}{N_1}\right)-\frac{1}{4N_0N_1} \end{split} \tag{3.20} \end{equation}\]

y considerando que los términos en \(\frac{1}{4N_e^2}\) y \(\frac{1}{4N_0N_1}\) no afectan casi el resultado, porque su orden es casi similar, llegamos a que:

\[\begin{equation} \frac{1}{N_e}=\frac{1}{2}(\frac{1}{N_0}+\frac{1}{N_1}) \tag{3.20} \end{equation}\]

es una muy buena aproximación. De hecho, esto significa que \(N_e\) es la media armónica entre \(N_0\) y \(N_1\). En general, para \(t \ge 2\) la media armónica (el recíproco de la media de recíprocos) es un buen indicador del tamaño efectivo poblacional:

\[\begin{equation} \frac{1}{N_e}=\frac{1}{t}\left(\frac{1}{N_0}+\frac{1}{N_1}+\frac{1}{N_2}+...+\frac{1}{N_{t-1}} \right) \end{equation}\]

\[\begin{equation} N_e=\frac{t}{\left(\frac{1}{N_0}+\frac{1}{N_1}+\frac{1}{N_2}+...+\frac{1}{N_{t-1}} \right)} \tag{3.21} \end{equation}\]

Ejemplo 3.3

El venado de campo (O. bezoarticus) fue una especie típica de nuestro país (“extremadamente abundante” en palabras de Charles Darwin, que al pasar por estas tierras no dudó en llevarse ejemplares en el Beagle). Lamentablemente, la población ha sufrido una disminución importante durante el último siglo. Imaginemos que en un momento una población estaba compuesta por \(50000\) individuos, y que en la actualidad se compone por \(1000\) individuos. Si en un esfuerzo descomunal se lograra recuperar el tamaño de la población, ¿cuál sería su tamaño poblacional efectivo, considerando que pasó por dicho cuello de botella?

El tamaño poblacional efectivo (\(N_e\)) se calcula a partir de la media armónica de los tamaños poblacionales mencionados:

\[ \frac{1}{N_e} = \frac{1}{3}(\frac{1}{50000} + \frac{1}{1000} + \frac{1}{50000}) \Rightarrow \]

\[ N_e = \frac{3}{(\frac{1}{50000} + \frac{1}{1000} + \frac{1}{50000})} \]

lo cual da una estimación de

\[ N_e \approx 2885 \]

---

Otra fuente importante de diferencias entre el tamaño censal y el tamaño efectivo de una población es el desequilibrio entre el número de machos y el número de hembras, como veremos en detalle en otros capítulos. En general, si una población está constituida por \(N_m\) machos y \(N_h\) hembras, el número total de animales (individuos) es \(N_a=N_m+N_h\), mientras que (como deduciremos en otro capítulo), para una generación determinada

\[\begin{equation} N_e=\frac{4N_mN_h}{N_m+N_h} \tag{3.22} \end{equation}\]

Cuando el número de hembras es igual al número de machos (\(N_h=N_m=\frac{N}{2}\)), algo bastante raro en las poblaciones comerciales (al menos de mamíferos), tenemos que para la misma generación la ecuación (3.22) se transforma en

\[ \begin{split} N_e=\frac{4N_mN_h}{N_m+N_h}=\frac{4\frac{N}{2}\frac{N}{2}}{\frac{N}{2}+\frac{N}{2}}=\frac{N^2}{N}=N \end{split} \tag{3.23} \]

Es decir, \(N_e=N\), el tamaño efectivo poblacional es igual al tamaño censal.

Ejemplo 3.4

El león marino (Otaria flavescens) se reproduce de forma estacional, siguiendo una estructura de harén: un macho alfa territorial monopoliza la reproducción, apareándose con varias hembras. Grandi et al. (Grandi et al. 2012) realizaron censos en colonias de O. flavescens en el norte de la Patagonia, contando el número de machos alfa y de hembras sexualmente activas. En el año 2012, el censo de 33 colonias arrojó un conteo de 2534 machos alfa y 12097 hembras sexualmente activas. ¿Cual es el tamaño efectivo poblacional en este caso?

Si se asume que a lo largo de las estaciones existe un apareamiento aproximadamente al azar entre machos alfa y hembras sexualmente activas, se puede estimar el tamaño poblacional efectivo teniendo en cuenta el desbalance de sexos según

\[ N_e = \frac{4N_hN_m}{N_h + N_m} \]

\[ N_e = \frac{4 \cdot 12097 \cdot 2534}{12097 + 2534} \Rightarrow N_e = 8381 \]

---

Finalmente, otra versión del tamaño efectivo poblacional es la que sale de nuestra definición del modelo ideal y de cuanto esperamos que sea su varianza. Si llamamos \(\Delta p=p_t-p_{t-1}\), es decir a la diferencia entre la frecuencia promedio en la generación \(t\) y la generación anterior (\(t-1\)), entonces la varianza de \(\Delta p\) estará dada por

\[\begin{equation} Var(\Delta p)=\frac{p_{t-1}q_{t-1}}{2N} \end{equation}\]

cuando el proceso cumple con todos los requerimientos del modelo de Wright-Fisher. Pero esto mismo podemos usarlo para estimar cuál sería el tamaño efectivo poblacional que generaría la misma varianza empírica que tenemos en \(\Delta p\), \(N_e^v\). Es decir, despejando \(N\), que ahora llamaremos \(N_e^v\), que es nuestra incógnita asumiendo que proviene de un proceso perfecto Wright-Fisher, tenemos

\[\begin{equation} N_e^v=\frac{pq}{2 Var(\Delta p)} \end{equation}\]

En resumen, en esta última forma de calcular el tamaño efectivo poblacional hemos asumido que la varianza entre generaciones en la media de frecuencias alélicas proviene de un proceso de Wright-Fisher y esto nos permite estimar cuál sería el tamaño de las poblaciones que se corresponden con esa varianza.

PARA RECORDAR

• El tamaño efectivo de una población (\(N_e\)) raramente coincide con el tamaño censal de la misma (\(N\)), siendo las razones para esto diversas (variación del tamaño en el tiempo, diferente número de machos que de hembras, diferencias muy importantes en el número de descendientes entre reproductores candidatos, etc.).
• El efecto conocido como cuello de botella (bottleneck) poblacional se refiere a la reducción drástica del número de reproductores en algún momento de la vida de una población determinada y aunque luego la misma experimente una nueva expansión, el cuello de botella dejará huellas indelebles a nivel de la variabilidad genómica.
• El tamaño efectivo poblacional cuando varía el tamaño de la población en el tiempo se puede calcular como la media armónica entre los tamaños a cada generación:

\[\begin{equation*} N_e=\frac{t}{\left(\frac{1}{N_0}+\frac{1}{N_1}+\frac{1}{N_2}+...+\frac{1}{N_{t-1}} \right)} \end{equation*}\]

• Cuando el número de reproductores machos es diferente del número de reproductores hembras, el tamaño efectivo de la población es inferior a la suma de individuos y lo podemos calcular como

\[\begin{equation*} N_e=\frac{4N_mN_h}{N_m+N_h} \end{equation*}\]

• Si asumimos que se trata de un proceso de Wright-Fisher perfecto, podemos obtener un estimado del tamaño efectivo poblacional que se corresponde con la varianza en la media de frecuencias alélicas entre generaciones a partir de la dicha varianza observada mediante

\[\begin{equation*} N_e^v=\frac{pq}{2 Var(\Delta p)} \end{equation*}\]

3.6 Aproximación de difusión

Gran parte de los desarrollos de esta sección siguen directamente el libro Hartl and Clark (2007), que entendemos es de los más claros al nivel del presente curso, mientras que otros siguen el libro de Walsh and Lynch (2018) que posee un apéndice dedicado al tema. Otras fuentes importantes son el libro de Denny and Gaines (2000) para los procesos de difusión en biología y el libro de Hamilton (2009), que seguimos directamente también (más allá de modificaciones mínimas) y que trata con cierto detalle pero a un nivel muy razonable la aproximación por difusión en genética (que a su vez sigue el de Denny and Gaines (2000)).

Inevitablemente, esta sección es bastante técnica y usaremos cálculo diferencial e integral en múltiples variables, así como algunos conceptos básicos de ecuaciones diferenciales en derivadas parciales. Si te sientes un poco oxidado en estos temas, en el [Apéndice B: Cálculo diferencial e integral] podrás repasar los principales conceptos.

Dada la complejidad de esta sección, no pretendemos que seas capaz de reproducir o aún entender cada paso o derivación (aunque nos pondría muy contentos si así fuese). Si te resulta imposible entender no te desanimes ya que podrás seguir el resto del curso en forma independiente de las derivaciones de esta sección. La idea es que puedas entender de dónde surgen algunos resultados muy importantes que veremos en este y otros capítulos. Es muy importante para la mente científica conocer y entender el origen de resultados y fórmulas que utilizarás a lo largo de tu carrera, tanto como estudiante como profesional. ¡Ánimo!

Como vimos más arriba (Cadenas de Markov), la evolución del número de copias de un alelo en poblaciones idénticas es un proceso estocástico discreto y la evolución de los estados puede seguirse a través de la multiplicación de la matriz de probabilidades de transición (cadenas de Markov). Sin embargo, esta aproximación suele ser dificultosa o imposible en la práctica para manejar modelos más complejos y una buena aproximación para comprender el comportamiento a largo plazo viene por el lado de los procesos de difusión. En efecto, si consideramos el tiempo como una variable continua, re-escalando el tiempo en generaciones que habíamos utilizado hasta ahora mediante la transformación \(\tau=\frac{t}{N}\) y escalando el número de copias del alelo A (\(i\)) de tal forma que \(x=\frac{i}{2N}\), cuando \(N \to \infty\) ambas variables pasan a ser continuas.

Caminatas al azar y procesos de difusión

En la sección El modelo de Wright-Fisher vimos el comportamiento de la frecuencia alélica guiada solo por el proceso de deriva genética. Si observamos nuevamente el trazo dejado por cualquiera de las poblaciones no resulta difícil imaginarse el recorrido de alguien que (posiblemente borracho) a cada instante en el tiempo, decide a través del resultado de tirar una moneda si el siguiente paso es a la derecha o a la izquierda. Más aún, podemos pensar que esta persona se encuentra sobre una línea trazada en el piso y que arranca desde una determinada posición inicial decidiendo con la moneda hacia dónde dar el siguiente paso. Lo que nos interesa entonces es estudiar el comportamiento de este tipo de procesos y ver si podemos hacer algunas predicciones al respecto. Más divertido aún y más cercano a lo que vamos a describir ahora sería un experimento donde a la salida de un bar (en un lugar medio desierto) reclutamos a todos los borrachos disponibles, los ponemos en “fila india” y les explicamos que al sonido de la campana (que tañeremos en forma regular) deben tirar una moneda y en función del resultado dar un paso a la derecha (si sale cara) o a la izquierda (si sale cruz); o aún quedarse quietos si no sintieron la campana o estaban distraídos. Bueno, también se podría hacer sin borrachos, pero intuimos que será mucho más divertido en el primer caso.

En realidad, existe una motivación física mucho más potente y que usaremos como analogía para luego pasar a ver cómo esa analogía nos puede ayudar a entender los procesos estocásticos en las frecuencias alélicas de nuestras poblaciones. La motivación es muy sencilla: imaginemos que en el instante \(t=0\) dejamos caer una gota de tinta en la posición central de un canal horizontal abierto conteniendo agua (el canal se extiende a derecha, signo positivo, e izquierda, signo negativo, de \(x=0\)). En ambos extremos del canal tenemos un medio que absorbe las partículas de tinta a medida de que van arribando (es decir, son barreras absorbentes para las partículas de tinta). El papel de nuestros “borrachos” lo representarán ahora las pequeñas partículas de tinta que formaban la gota y que ahora, a partir del instante \(t=0\) comenzarán a dispersarse en ambas direcciones. Para que nuestra analogía tenga cierto sentido físico y poder estudiar su comportamiento vamos a definir una serie de reglas que se aplican al movimiento individual de cada partícula.

Reglas

1. La partícula comienza en la posición \(x=0\) en el instante inicial, \(t=0\).

2. La partícula se mueve una distancia fija \(\delta\) en cada intervalo de tiempo \(\tau\).

3. La partícula se puede mover solo en el eje permitido, con probabilidad \(p=\frac{1}{2}\) hacia la derecha (arbitrariamente, puede ser cualquier dirección) y por lo tanto con probabilidad \(q=1-p=1-\frac{1}{2}=\frac{1}{2}\) hacia la izquierda (o en sentido opuesto al anterior).

4. El sentido en el que se mueve es independiente del sentido en la movida anterior, o lo que es lo mismo, se trata de un proceso sin memoria (recordar lo visto en la sección Cadenas de Markov).

5. Pueden existir tantas partículas como se quiera en la misma posición del eje sin interferir unas con otras (es como si cada una “corriese” por su propio carril, todos los carriles paralelos unos a otros).

En la Figura 3.14 podemos ver una representación esquemática de nuestro diseño. En el instante \(t=0\) consideramos que cae la gota de tinta (roja) al agua al mismo tiempo que las partículas que la constituyen comienzan a difundir hacia izquierda y derecha de acuerdo a las reglas que establecimos más arriba.

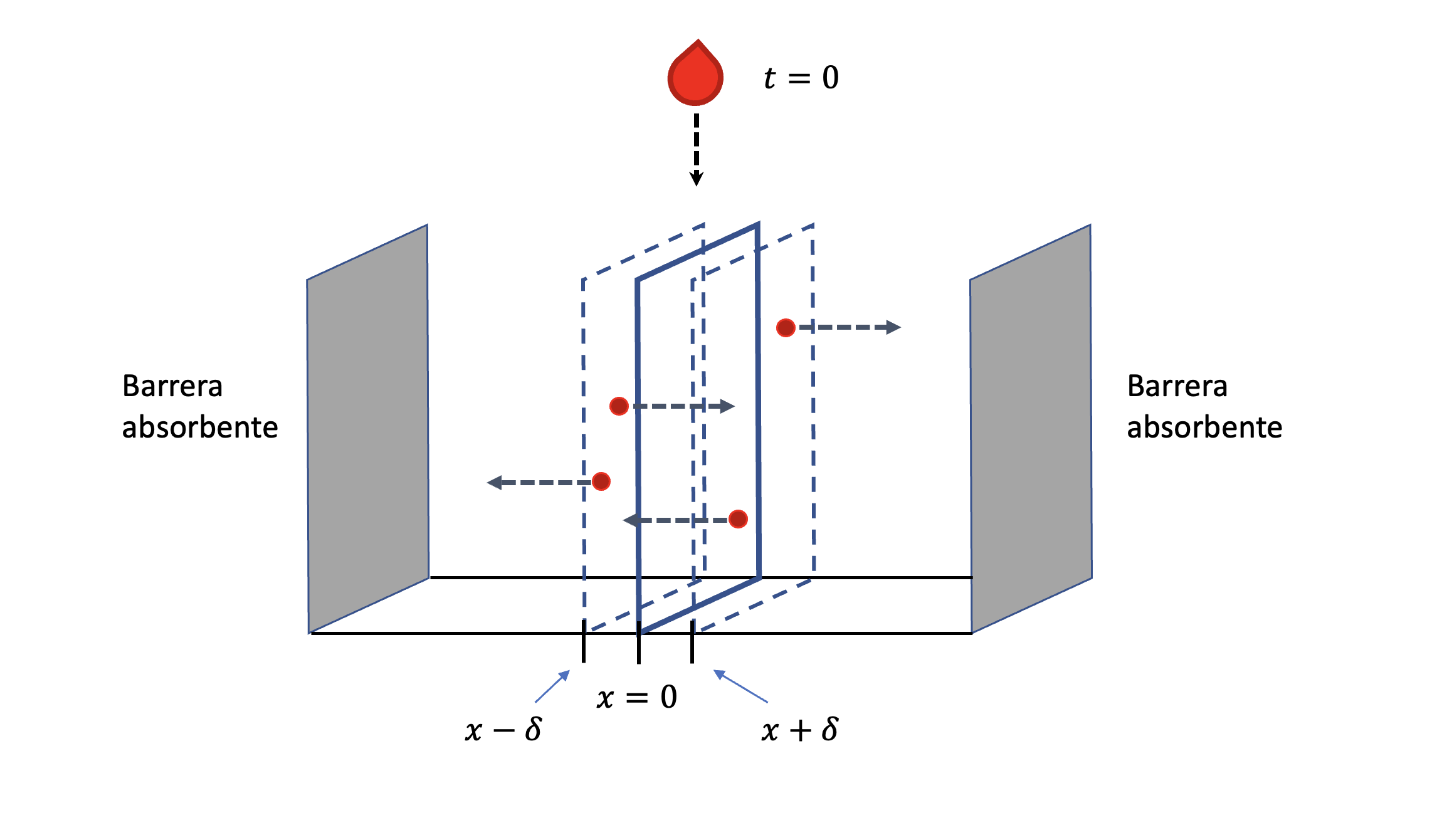
Figura 3.14: Diagrama que representa el escenario para el movimiento de nuestras partículas de tinta. En el instante inicial la gota de tinta cae al mismo tiempo sus partículas constituyentes comienzan a difundir a izquierda y derecha (elaboración propia sobre idea de Hamilton (2009)).

Primero, podríamos analizar qué ocurre con la posición promedio de las partículas a medida de que avanza el tiempo, por ejemplo en una unidad (\(\tau\)). La posición media está dada por

\[\begin{equation} \bar{x}=p(\delta)+q(-\delta) \end{equation}\]

Como las partículas se mueven a derecha e izquierda con la misma probabilidad, \(\delta\) y \(-\delta\) unidades de posición, entonces tenemos que luego de una unidad de tiempo \(\tau\) la posición media será en nuestro caso

\[\begin{equation} \bar{x}=\frac{1}{2}(\delta)-\frac{1}{2}(\delta)=0 \tag{3.24} \end{equation}\]

Es decir, que la posición media de las partículas será la misma que al comienzo. Esto no debería extrañarnos dado de que por simetría del problema tantas partículas se moverán hacia un lado como otras en el sentido opuesto, lo que da un balance neto de cero respecto al desplazamiento del punto medio. Entonces, ¿nada ha cambiado? Si recuerdas el comportamiento de las distintas poblaciones en la Figura 3.5, posiblemente te habrás imaginado que si bien la media del proceso no cambia, la varianza sí lo hace. Si además recuerdas la fórmula para la varianza

\[\begin{equation} Var(x)=E(x^2)-E^2(x) \end{equation}\]

y que además en nuestro caso \(E^2(x)=E(x)E(x)=\bar{x}\bar{x}=0 \cdot 0\), llegaremos enseguida a la conclusión de que la varianza en posición de las partículas es igual a \(E(x^2)\), o lo que es lo mismo el promedio de las posiciones al cuadrado. Como además, en cada intervalo arbitrariamente pequeño de tiempo la partícula solo puede moverse \(\delta\) en uno de los sentidos, la ubicación de la partícula \(i\) en el tiempo 1 será igual a

\[\begin{equation} x_{i,(t=1)}=x_{i,(t=0)}+\delta \end{equation}\]

con \(\delta\) positivo o negativo. O sea, para obtener una expresión de la varianza en las posiciones de las partículas, luego de un intervalo arbitrariamente pequeño (de \(t=0\) a \(t=1\)) debemos comenzar por elevar al cuadrado esta expresión y luego promediar

\[ \begin{split} x_{i,(t=1)}^2=(x_{i,(t=0)}+\delta)^2\\ x_{i,(t=1)}^2=x_{i,(t=0)}^2+2x_{i,(t=0)}\delta+\delta^2 \end{split} \]

Por lo tanto, promediando el resultado anterior para las N partículas obtenemos

\[\begin{equation} \sigma^2(x_{i,(t=1)})=\frac{1}{N} \sum_{i=1}^{N} (x_{i,(t=0)}^2+2x_{i,(t=0)}\delta+\delta^2) \end{equation}\]

La expresión anterior se puede simplificar bastante. En primer lugar, por una razón de simetría, habrá tantas partículas que se muevan a la derecha como a la izquierda (recordar \(\bar{x}=0\), ecuación (3.24)), por lo que el término del medio es igual a cero. Luego

\[ \begin{split} \sigma^2(x_{i,(t=1)})=\frac{1}{N}\sum_{i=1}^{N} x_{i,(t=0)}^2 + \frac{1}{N}N\delta^2\\ \sigma^2(x_{i,(t=1)})=\overline{x^2}_{i,(t=0)}+\delta^2 \end{split} \]

Ahora, suponiendo que a \(t=0\) todas las partículas salen de la posición cero, entonces el promedio del cuadrado de sus distancias será 0 también (\(\overline{x^2}_{i,(t=0)}=0\)), por lo que nos quedamos con \(\delta^2\), es decir el cuadrado del cambio en posición en un intervalo de tiempo, como el incremento en la varianza en un avance arbitrariamente pequeño del tiempo (de \(t=0\) a \(t=1\)). En un intervalo de tiempo de \(t\) unidades, por lo tanto, la varianza de la posición de las partículas será de \(t\delta^2\), o dicho de otra manera, la varianza en la posición de las partículas se incrementa en forma lineal con el tiempo. En el primer instante la varianza será \(1 \cdot\delta^2=\delta^2\), en el segundo instante será \(2\delta^2\), luego \(3\delta^2\), etc. La anterior es una observación más que razonable para describir el fenómeno de cómo una gota de tinta se dispersa en el agua a medida de que pasa el tiempo.

Si definimos el coeficiente de difusión de las partículas (\(D\)) como la velocidad con que la tinta se difunde en el agua, tenemos que

\[\begin{equation} D=\frac{1}{2}\frac{d\sigma^2}{dt} \tag{3.25} \end{equation}\]

La ecuación anterior es fácil de entender, la varianza representa la dispersión de las partículas en un momento dado y por lo tanto su derivada primera respecto del tiempo es su velocidad. Pero la varianza representa dispersión a ambos lados del punto de inicio, por lo que solo la mitad de la misma corresponderá a la magnitud de la velocidad en un sentido (de lo contrario, la velocidad neta siempre sería cero). Como \(\sigma^2=t\delta^2\), entonces

\[\begin{equation} D=\frac{1}{2}\frac{d\sigma^2}{dt}=\frac{1}{2}\frac{d(t\delta^2)}{dt}=\frac{\delta^2}{2} \tag{3.26} \end{equation}\]

Es decir, \(D=\frac{\delta^2}{2}\) es la velocidad de difusión de las partículas, o lo que es lo mismo, un medio del incremento en la varianza en una unidad de tiempo arbitrariamente pequeño.

Volvamos ahora a la genética. ¿Cómo se relaciona esto del proceso de difusión con nuestro tratamiento de la evolución estocástica de las frecuencias alélicas en las poblaciones? En principio es muy sencillo: si consideramos que cada población del ensemble es como una partícula en nuestro modelo de difusión, los “movimientos” que puede realizar nuestras poblaciones son en lugar del movimiento físico de las partículas, los cambios en frecuencia alélica en la población. O sea, si por ejemplo, partimos de \(p_A=0,5\), es equivalente como partir del punto medio en el modelo de difusión. Ahora las barreras absorbentes estarán en \(p_A=0\) y \(p_A=1\). Por otra parte, si recuerdas lo tratado en la sección El modelo de Wright-Fisher, la varianza por generación (o lo que sería un intervalo arbitrariamente pequeño en la difusión) era \(\sigma^2(p)=\frac{pq}{2N}\) y la varianza a lo largo del tiempo, en la generación \(t\), por ejemplo igual a \(\sigma^2_t(p)=t\frac{pq}{2N}\) (ecuación (3.4), para simplificar la notación llamaremos \(\sigma^2\) a \(\sigma^2_t(p)\)), por lo que podemos hacer:

\[\begin{equation} \frac{d\sigma^2}{dt}=\frac{d(t\frac{pq}{2N})}{dt}=\frac{pq}{2N} \tag{3.27} \end{equation}\]

Si recordamos de la ecuación (3.25) que \(D=\frac{1}{2}\frac{d\sigma^2}{dt}\) y substituimos en ella el resultado de la ecuación (3.27), tenemos que el coeficiente de difusión \(D\) es ahora

\[\begin{equation} D=\frac{1}{2}\frac{d\sigma^2}{dt}=\frac{1}{2}\frac{pq}{2N}=\frac{pq}{4N}=\frac{p-p^2}{4N} \tag{3.28} \end{equation}\]

Es decir, el coeficiente de difusión para las frecuencias alélicas de nuestras poblaciones es una función de la frecuencia de los alelos (\(p\) y \(q\)). El denominador de la ecuación (3.28) no depende de las frecuencias ya que se trata de un número \(N\) positivo, multiplicado por una constante positiva (4). En cambio, el numerador depende de la frecuencia del alelo A (\(p\)): si recuerdas de la sección H-W: la frecuencia de heterocigotas en función de la frecuencia alélica, el producto \(p \cdot q\) tiene un máximo cuando \(p=q=\frac{1}{2}\). Es decir la velocidad de difusión (cambio de frecuencias alélicas) será máxima cerca de \(p=\frac{1}{2}\) y tenderá a cero a medida que \(p\) se acerque a las barreras absorbentes de \(0\) y \(1\). Dicho de otra manera, la velocidad de cambio en la frecuencia en cada población será máximo en el entorno de \(p=\frac{1}{2}\), llevando a las poblaciones hacia las regiones donde el coeficiente de difusión es menor, cerca de las barreras absorbentes, donde al ser menor el coeficiente de difusión permanecerá más tiempo. Por otra parte, el coeficiente de difusión también depende del tamaño poblacional efectivo: a mayor número de individuos en cada una de las poblaciones que constituyen el ensemble, menor será el coeficiente de difusión, o lo que es lo mismo menor la velocidad con que cambian las frecuencias de los alelos en cada población.

Procuraremos ahora calcular la probabilidad de que una población se encuentre en una región en particular en el intervalo de frecuencias, o en nuestra analogía de difusión la probabilidad de encontrar una partícula en una posición en particular del eje en que se mueven. Para eso necesitaremos calcular el flujo de partículas en la región de interés, o dicho de otra forma el número neto de partículas que atraviesan un área definida por intervalo de tiempo. Si consideramos un área \(A\) el flujo neto de partículas que atraviesa la misma hacia la derecha (arbitrariamente) es igual a la mitad del número de partículas que están a una distancia \(\delta\) a la izquierda de la misma (recuerda que en cada posición la mitad de las partículas tenderá a moverse a la izquierda y la otra mitad a la derecha), menos la mitad de la partículas que a una distancia \(\delta\) a la derecha del área de referencia (\(\delta\) porque es la distancia a la que se mueven en una unidad de tiempo). Es decir:

\[\begin{equation} N_{neto}(Der)=\frac{1}{2}N(Izq)-\frac{1}{2}N(Der)=-\frac{1}{2}[N(Der)-N(Izq)] \end{equation}\]

Pero el flujo es la cantidad de partículas que atraviesan un área en determinado tiempo, por lo que para obtener una expresión de éste en el punto \(x\), que llamaremos \(J_x\) debemos dividir por área y por tiempo:

\[\begin{equation} J_x=-\frac{1}{2}\frac{[N(Der)-N(Izq)]}{At} \end{equation}\]

Si multiplicamos esta última expresión por 1, bajo la forma de \(\frac{\delta^2}{\delta^2}\), para luego rearreglar los términos, la misma quedará:

\[\begin{equation} J_x=-\frac{\delta^2}{2t}\frac{1}{\delta}\frac{[N(Der)-N(Izq)]}{A\delta}=-\frac{\delta^2}{2t}\frac{1}{\delta}\left[\frac{N(Der)}{A\delta}-\frac{N(Izq)}{A\delta}\right] \tag{3.29} \end{equation}\]

Si observamos los dos términos entre paréntesis rectos de la ecuación anterior, en ambos casos (\(\frac{N(Der)}{A\delta}\) y \(\frac{N(Izq)}{A\delta}\)) se trata de un número de partículas dividido entre el producto de un área (\(A\)) por una distancia (\(\delta\)), es decir dividido entre un volumen (recuerda de la escuela cómo calculábamos los volúmenes). Pero el número de partículas divido entre el volumen que ocupan las mismas es la concentración, por lo que podemos llamar \(C(Der)\) y \(C(Izq)\) a la concentración de partículas a derecha e izquierda de nuestra área. Además, previamente habíamos visto (ecuación (3.26)) que \(\frac{\delta^2}{2}=D\), por lo que en una unidad de tiempo (\(t=1\)), substituyendo en (3.29) tenemos:

\[\begin{equation} J_x=-D\frac{C(Der)-C(Izq)}{\delta} \tag{3.30} \end{equation}\]

Si asumimos que las partículas se encuentran uniformemente distribuidas en el intervalo entre \(x\) y \(x+\delta\) su posición promedio será \(\frac{\delta}{2}\) (lo mismo para el otro lado, pero ahora será \(-\frac{\delta}{2}\)), que tomaremos como posición característica. Entonces \(C(Der)=C(x+\frac{\delta}{2})\) y \(C(Izq)=C(x-\frac{\delta}{2})\), por lo que la ecuación (3.30) la podemos escribir como:

\[\begin{equation} J_x=-D\frac{C(x+\frac{\delta}{2})-C(x-\frac{\delta}{2})}{\delta} \tag{3.31} \end{equation}\]

Si en esta última expresión hacemos el paso al límite cuando las distancias en \(x\) son infinitamente pequeñas), es decir cuando \(\delta \to 0\), tenemos que:

\[\begin{equation} J_x=-D\frac{dC}{dx} \tag{3.31} \end{equation}\]

que se conoce como la primer ecuación de difusión de Fick. Nuevamente, esta ecuación parece sencilla de interpretar. El coeficiente de difusión es un número positivo que indica la velocidad de movimiento de las partículas en el medio. Por otro lado, \(\frac{dC}{dx}\) representa el gradiente de la concentración de partículas (en nuestro caso de poblaciones) y cuando su signo es positivo indica la dirección hacia la mayor concentración de partículas. Como acá el producto tiene un signo negativo, la ecuación nos indica que las partículas (poblaciones) se moverán en dirección a donde hay una menor concentración (recordar la analogía con la gota de tinta en agua; la tinta se moverá hacia donde hay menor concentración). Obviamente, en el equilibrio, para cada posición en el eje de movimiento (nuestras frecuencias alélicas) tantas partículas se moverán hacia un lado como hacia el otro.

Pasemos ahora a intentar entender como esto nos puede aportar a entender el comportamiento de las frecuencias alélicas en nuestro ensemble. Para esto, debemos recordar que estamos tratando con una aproximación continua (las frecuencias alélicas ya no las expresamos como el número de copias de un alelo sino como este número divido entre \(2N\)) y por lo tanto la probabilidad la vamos a sustituir por una densidad de probabilidad, que llamaremos \(\phi(p,x,t)\) (notar la dependencia del punto inicial de partida \(p\), o sea la frecuencia inicial del alelo A). Esta densidad de probabilidad es equivalente a la concentración de partículas. \(\phi(p,x,t)\) representa el balance neto entre las poblaciones que arriban a esa frecuencia alélica \(x\) y aquellas que se alejan de la misma; pero esto, en nuestro razonamiento previo es el flujo neto en el punto \(x\), es decir \(J_x\). De acuerdo a la ecuación de continuidad, ya que el material no se crea o destruye,

\[ \begin{split} \frac{d\phi(p,x,t)}{dt}+\frac{dJ_{x,t}}{dx}=0\\ \frac{d\phi(p,x,t)}{dt}=-\frac{dJ_{x,t}}{dx} \end{split} \tag{3.32} \]

Hasta ahora nos hemos manejado asumiendo que el movimiento de las frecuencias alélicas en las distintas poblaciones se debe exclusivamente al azar (por eso random drift), pero para hacer más general nuestra ecuación debemos entender que las frecuencias alélicas también pueden variar de forma sistemática, por ejemplo a través de la mutación (fuera del equilibrio mutacional) y selección. La analogía con las partículas de tinta sería a través de suponer que las mismas tienen determinada carga eléctrica y que entre las dos barreras absorbentes existe una diferencia de potencial que hará que las partículas se muevan sistemáticamente en una dirección (efecto superpuesto al aleatorio). Otra analogía para intentar entender esta lógica de efectos superpuestos se plantea en la Figura 3.15, en donde se observa el comportamiento de bolitas de diferente densidad al ingresar a un tubo de viento que cuenta a su vez con un sistema de ventilación interno.

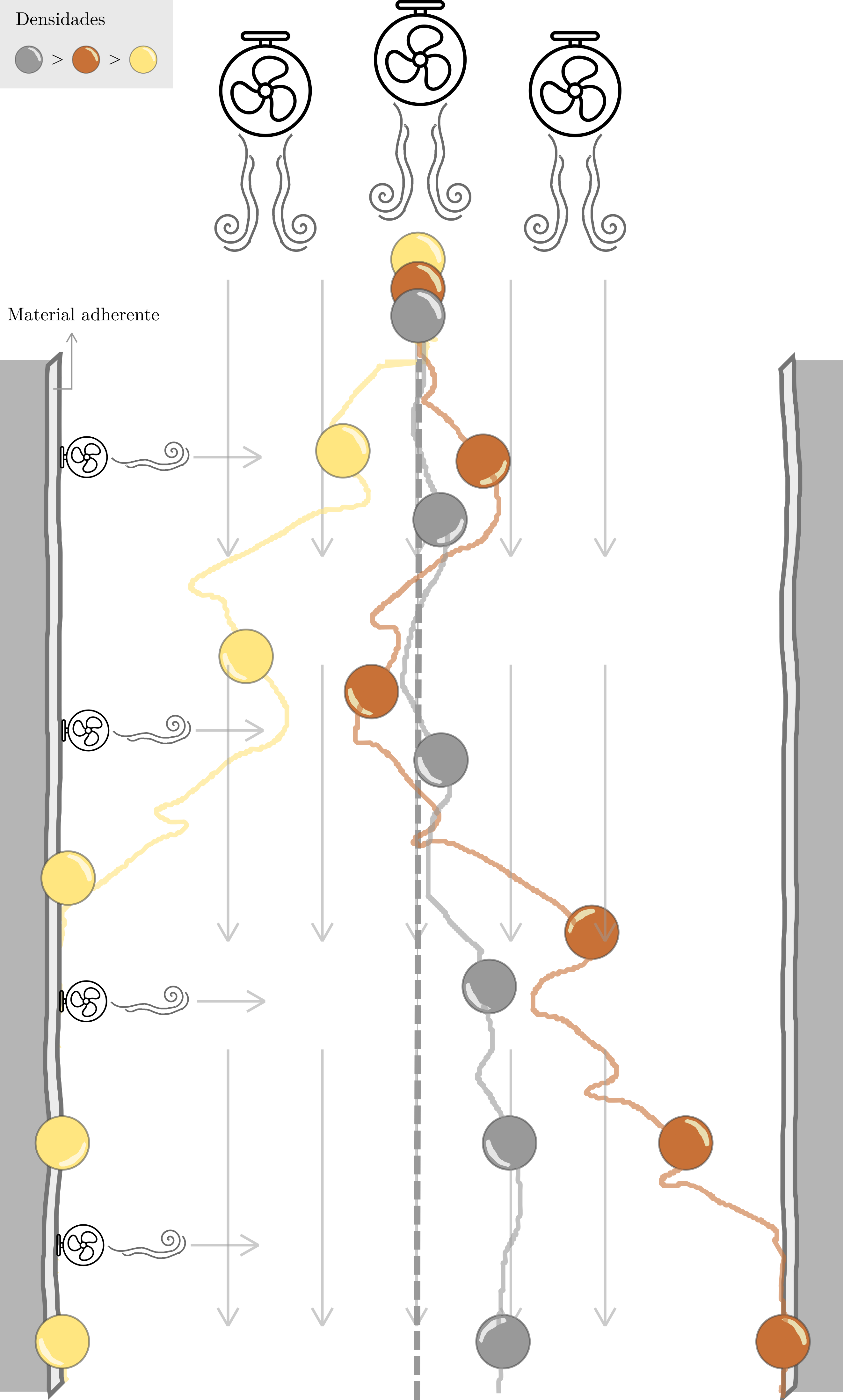
Figura 3.15: Diagrama que representa posibles trayectorias de bolitas de diferente densidad ( una pelotita de ping-pong, una de madera y una de metal) al ingresar a un tubo de viento con un sistema de ventilación interno. El sistema cuenta a su vez con un material adherente sus costados, por lo que las bolitas que entren en contacto con el borde continuarán su trayectoria sobre él. Dos efectos superpuestos influyen sobre la trayectoria de cada bolita: a) el flujo de viento a través del tubo, generado por ventiladores superiores, y b) una corriente de menor intensidad, de izquierda a derecha, generada por un sistema de ventilación interno. El efecto del flujo de viento superior es aleatorio respecto al plano horizontal, pudiendo cada bolita desplazarse a cada lado con igual probabilidad debido a este estímulo. En cambio, el efecto de la ventilación interna es sistemático, favoreciendo un movimiento de izquierda a derecha en cada bolita. Según su densidad, cada bolita responderá a estos estímulos de manera diferente. Notemos como en el ejemplo la bolita de ping-pong se inclinó tempranamente hacia la izquierda, lo cual favoreció su contacto con dicho borde. Las otras bolitas (de mayor densidad), presentan menores varianzas respecto a su movimiento horizontal.

Ahora, si llamamos \(M(x)\) a ese efecto sistemático, tenemos entonces

\[\begin{equation} J_{x,t}=M(x)\phi(p,x,t)-D\frac{d\phi(p,x,t)}{dx} \end{equation}\]

por lo que sustituyendo en la ecuación (3.32) tenemos

\[\begin{equation} \frac{d\phi(p,x,t)}{dt}=-\frac{dJ_{x,t}}{dx}=-\frac{d}{dx}\left[M(x)\phi(p,x,t)-D\frac{d\phi(p,x,t)}{dx}\right] \tag{3.33} \end{equation}\]

Pero la derivación en forma más general de estas ecuaciones, directamente en nuestro dominio, así como las soluciones para casos particulares las veremos en más detalles en las sub-secciones que siguen.

Kolmogorov Forward Equation

Asumiendo que las poblaciones de nuestro ensemble son suficientemente grandes, la frecuencia de los alelos se transforma razonablemente en una variable continua que avanza suvamente en el tiempo, sin grandes saltos. En este sentido, la “Kolmogorov Forward Equation” (KFE) nos permite analizar el comportamiento en el tiempo de la función continua de probabilidad \(\phi(p,x,t)\), es decir de la densidad de probabilidad de encontrar la frecuencia alélica en \(0<x<1\) (notar que es válida solo entre las barreras absorbentes, pero no para ellas, es decir en las poblaciones aún segregantes) en determinado tiempo \(t\), partiendo de una frecuencia inicial \(p\).

Para nuestro desarrollo, análogo a lo que hicimos en Caminatas al azar y procesos de difusión vamos a permitir pequeños desplazamientos de nuestras variables \(x\) y \(t\), es decir \(\Delta x\) y \(\Delta t\). Nuevamente, como vimos más arriba, hay dos fuerzas que pueden hacer que \(x\) cambie en un intervalo \(\Delta t\): una fuerza sistemática que desplace las frecuencias alélicas siempre en una dirección (nuestro análogo era el campo eléctrico para las partículas de tinta) y que llamaremos \(M(x)\) y una fuerza aleatoria, la deriva genética (que en nuestra analogía previa era la difusión por movimiento “Browniano” de las partículas de tinta) que llamaremos \(V(x)\). Sin pérdida de generalidad, vamos a asumir que nuestro alelo favorecido es el A, cuya densidad de probabilidad (frecuencia) está dada por \(x\) (y la inicial del mismo por \(p\)) y que la fuerza sistemática es en el sentido creciente de \(x\) (o sea, en sentido de la fijación del A). En el cuadro que sigue tenemos detallados los posibles movimientos hacia la “posición” \(x\) en un intervalo \(\Delta t\) a partir del momento \(t\) en que estamos (recordar que en un intervalo \(\Delta t\) \(x\) solo puede moverse hacia abajo o hacia arriba, pérdida o fijación, una cantidad \(\Delta x\)), así como las probabilidades asociadas y la causa del movimiento.

\(\text{Posición (generación } t \text{)}\)	\(\text{Prob. de esa frecuencia}\)	\(\text{Posibilidad de cambio a } x \text{ en } \Delta \text{t}\)	\(\text{Prob. del cambio en } \Delta \text{t}\)	\(\text{Fuerza}\)
\(x-\Delta x\)	\(\phi(p,x-\Delta x,t)\)	\(x-\Delta x \to x\)	\(M(x-\Delta x)\)	Sistemática
\(x-\Delta x\)	\(\phi(p,x-\Delta x,t)\)	\(x-\Delta x \to x\)	\(\frac{V(x-\Delta x)}{2}\)	Deriva
\(x+\Delta x\)	\(\phi(p,x+\Delta x,t)\)	\(x+\Delta x \to x\)	\(\frac{V(x+\Delta x)}{2}\)	Deriva
\(x\)	\(\phi(p,x,t)\)	\(x o x\)	\(1-M(x)-V(x)\)	Permanece

Para llegar a \(x\) en el próximo intervalo (\(t+\Delta t\)), como el máximo recorrido posible en \(x\) es \(\Delta x\) debo estar a la distancia \(\|\Delta x\|\) de \(x\), es decir en \(x-\Delta x\) o en \(x+\Delta x\), o una tercera alternativa que es estar ya en \(x\) y quedarme en esa posición. Las probabilidades de estar en esas posiciones en el tiempo \(t\) son las que aparecen en la segunda columna del cuadro anterior. A cada una de ellas le corresponde una probabilidad de movimiento de \(x\) determinada, como aparece en la columna 4 del cuadro. Como asumimos que \(M(x)\) va hacia la fijación, solo participaría en la probabilidad de movernos de \(x-\Delta x\) a \(x\) (y no en el sentido contrario); esa es la razón porque \(x-\Delta x\) aparece en dos filas del cuadro. La razón de por qué el efecto de la deriva es \(\frac{V(x)}{2}\) es que se trata de una fuerza simétrica y por lo tanto la posibilidad de aumentar \(x\) es igual a la de disminuirla y entonces debemos partir a la mitad su efecto para cada lado. Por último, la probabilidad de que \(x\) se quede en donde está es el complemento de las otras probabilidades (\(M(x)\) y \(V(x)\)), ya que al ser probabilidades el conjunto de todos los eventos excluyentes deben sumar \(1\).

Ahora, para analizar el cambio ocurrido entre \(\phi(p,x,t+\Delta t)\) y \(\phi(p,x,t)\), si multiplicamos la columna 2 por la 4, sumamos y reordenamos los términos tenemos:

\[\phi(p,x,t+\Delta t)-\phi(p,x,t)=-[M(x)\phi(p,x,t)-M(x-\Delta x)\phi(p,x-\Delta x,t)]+\] \[\frac{1}{2}[V(x+\Delta x)\phi(p,x+\Delta x,t)-V(x)\phi(p,x,t)]-[V(x)\phi(p,x,t)-V(x-\Delta x)\phi(p,x-\Delta x,t)]\]

Pero el lado izquierdo de la ecuación anterior representa el cambio en \(\phi\) (que podemos representar como \(\Delta \phi\)) a partir de un cambio en \(t\) (por lo tanto \(\Delta t\)). De la misma manera, el primer término del lado derecho de la ecuación representa el cambio en \(M\phi\) para un determinado cambio en \(x\) (\(\Delta x\)). Finalmente, el segundo término es el cambio del cambio en \(V\phi\), notar las dos diferencias en ese término (que representamos como \(\Delta\Delta V\phi\)) para un cambio en dos pasos de \(x\) (por lo tanto \(\Delta\Delta x\)). Poniendo todo junto:

\[\begin{equation} \begin{split} \frac{\Delta \phi(p,x,t)}{\Delta t}=-\frac{\Delta [M(x)\phi(p,x,t)]}{\Delta x}+\frac{1}{2}\frac{\Delta \{\Delta[V(x)\phi(p,x,t)]\}}{\Delta(\Delta x)} \end{split} \end{equation}\]

Pasando al límite, cuando \(\Delta t \to 0\) y \(\Delta x \to 0\), la ecuación en diferencias converge a una ecuación diferencial parcial, que se conoce como Kolmogorov Forward Equation (o KFE)⁴⁴:

\[\begin{equation} \frac{\partial \phi(p,x,t)}{\partial t}=-\frac{\partial [M(x)\phi(p,x,t)]}{\partial x}+\frac{1}{2}\frac{\partial \{\partial[V(x)\phi(p,x,t)]\}}{\partial(\partial x)} \end{equation}\]

\[\begin{equation} \frac{\partial \phi(p,x,t)}{\partial t}=-\frac{\partial [M(x)\phi(p,x,t)]}{\partial x}+\frac{1}{2}\frac{\partial^2[V(x)\phi(p,x,t)]}{\partial x^2} \tag{3.34} \end{equation}\]

Retomando la biología del problema, arriba mencionamos que \(M(x)\) era una fuerza sistemática que llevaba la frecuencia del alelo A en una dirección pero no especificamos mucho más. Esta fuerza podría representar sin problemas la selección, la mutación (o el balance mutacional) y la migración, alguna de ellas las veremos más adelante. Por otro lado, la fuerza aleatoria es igual (en nuestro modelo) a la varianza en las frecuencias alélicas luego de una generación de muestreo al azar en poblaciones de tamaño \(2N\) y por lo tanto \(V(x)=\frac{x(1-x)}{2N_e}\), con \(N_e\) tamaño efectivo según la varianza.

Kolmogorov Backward Equation

Una segunda posibilidad que se nos brinda de analizar lo que ocurre con la función de densidad \(\phi(p,x,t)\) es mirar hacia atrás en el tiempo (de ahí el Backward) y ver lo que podría haber ocurrido con \(p\), la frecuencia inicial (en lugar de \(x\)) en el primer instante en el tiempo. Ahora, como todas las poblaciones del ensemble parten del mismo \(p\), en ese pequeño incremento de tiempo \(\Delta t\), los movimientos posibles serían \(p-\Delta p\), \(p+\Delta p\) o quedarse en \(p\). Las probabilidades correspondientes a esos eventos las vemos en el siguiente cuadro.

\(\text{Cambio en la 1era generación}\)	\(\text{Probabilidad de ese cambio}\)	\(\text{Probabilidad de cambiar a } x \text{ en } t-\Delta t\)	\(\text{Fuerza}\)
\(p \to p+\Delta p\)	\(M(p)\)	\(\phi(p+\Delta p,x,t-\Delta t)\)	Sistemática
\(p \to p+\Delta p\)	\(\frac{V(p)}{2}\)	\(\phi(p+\Delta p,x,t-\Delta t)\)	Deriva
\(p \to p-\Delta p\)	\(\frac{V(p)}{2}\)	\(\phi(p-\Delta p,x,t-\Delta t)\)	Deriva
\(p \to p\)	\(1-M(p)-V(p)\)	\(\phi(p,x,t-\Delta t)\)	Permanece

Para la movida \(p \to p+\Delta p\) hay dos posibilidades, el efecto de la fuerza sistemática y de la aleatoria, por lo que su efecto combinado será \(M(p)+\frac{V(p)}{2}\). Para la movida \(p \to p-\Delta p\) solamente \(\frac{V(p)}{2}\) y para quedarse en \(p\) por lo tanto \(1-M(p)-V(p)\). Ahora, como ya recorrimos un intervalo de tiempo \(\Delta t\), el tiempo remanente para llegar al estado \(x\) en el presente será \(t-\Delta t\) y por lo tanto las probabilidades asociadas a cada evento serán las que aparecen en la columna 3 del cuadro. Por ejemplo, para \(p \to p+\Delta p\), entonces para llegar a \(x\) en el tiempo \(t-\Delta t\) restante, la probabilidad es de \(\phi(p+\Delta p,x,t-\Delta t)\). De la misma manera, para \(p \to p-\Delta p\) la probabilidad es de \(\phi(p-\Delta p,x,t-\Delta t)\) y finalmente para permanecer en \(p\) la probabilidad será de \(\phi(p,x,t-\Delta t)\). Ahora, la diferencia entre \(\phi(p,x,t)\) y \(\phi(p,x,t-\Delta t)\) saldrá de la multiplicación de las columnas 2 y 3 del cuadro, para luego sumarlas, que luego de reordenar los términos nos permite llegar a:

\[\phi(p,x,t)-\phi(p,x,t-\Delta t)=M(p)\left[\phi(p+\Delta p,x,t-\Delta t)-\phi(p,x,t-\Delta t)\right]+\] \[\frac{V(p)}{2}\left\{\left[\phi(p+\Delta p,x,t-\Delta t) - \phi(p,x,t-\Delta t) \right] -\left[\phi(p,x,t-\Delta t) - \phi(p-\Delta p,x,t-\Delta t) \right] \right\}\]

Nuevamente, el lado izquierdo de la ecuación anterior representa el cambio en \(\phi\) (que podemos representar como \(\Delta \phi\)) a parti de un cambio en \(t\) (por lo tanto \(\Delta t\)). Ahora, sin embargo, el primer término del lado derecho de la ecuación es \(M(p)\) (que queda afuera del \(\Delta\)) multiplicado por el cambio en \(\phi\) (\(M\Delta\phi\)) para un determinado cambio en \(p\) (\(\Delta p\)). Notar que ahora, en lugar de \(x\) es en \(p\). Finalmente, el segundo término es ahora \(V(p)\) multiplicado el cambio del cambio en \(\phi\), notar las dos diferencias en ese término (que representamos como \(\Delta\Delta \phi\)) para un cambio en dos pasos de \(p\) (por lo tanto \(\Delta\Delta p\)). Poniendo todo junto:

\[\begin{equation} \frac{\Delta \phi(p,x,t)}{\Delta t}=M(p)\frac{\Delta \phi(p,x,t)}{\Delta p}+\frac{V(p)}{2}\frac{\Delta \{\Delta\phi(p,x,t)\}}{\Delta(\Delta p)} \end{equation}\]

Pasando al límite, cuando \(\Delta t \to 0\) y \(\Delta p \to 0\), la ecuación en diferencias converge a una ecuación diferencial parcial, que se conoce como Kolmogorov Backward Equation (o KBE):

\[\begin{equation} \frac{\partial \phi(p,x,t)}{\partial t}=M(p)\frac{\partial \phi(p,x,t)}{\partial p}+\frac{V(p)}{2}\frac{\partial \{\partial \phi(p,x,t)\}}{\partial(\partial p)} \end{equation}\]

\[\begin{equation} \frac{\partial \phi(p,x,t)}{\partial t}=M(p)\frac{\partial \phi(p,x,t)}{\partial p}+\frac{V(p)}{2}\frac{\partial^2 \phi(p,x,t)}{\partial p^2} \tag{3.35} \end{equation}\]

Solución de las ecuaciones

En el equilibrio, la distribución de probabilidades no cambia con el tiempo, por lo que

\[\begin{equation} \frac{\partial \phi(p,x,t)}{\partial t}=0 \tag{3.36} \end{equation}\]

Cuando una función de este tipo existe la llamamos distribución estacionaria ya que no cambiará con el tiempo y como la misma no depende del punto de partida tampoco (dentro del intervalo abierto de la difusión), la denotamos como \(\phi(x)\) solamente. Cuando se cumple la ecuación (3.36), aplicándolo en la ecuación (3.34), tenemos

\[ \begin{split} \frac{\Delta \phi(x)}{\partial t}=-\frac{\partial [M(x)\phi(x)]}{\partial x}+\frac{1}{2}\frac{\partial^2[V(x)\phi(x)]}{\partial x^2}=0\ \therefore \\ \frac{\partial [M(x)\phi(x)]}{\partial x}=\frac{1}{2}\frac{\partial^2[V(x)\phi(x)]}{\partial x^2} \end{split} \tag{3.37} \]

Si ahora integramos (en \(x\)) ambos lados de esta ecuación, tenemos

\[\begin{equation} 2 M(x)\phi(x)=\frac{\partial [V(x)\phi(x)]}{\partial x} \tag{3.38} \end{equation}\]

que se trata de una ecuación diferencial simple, tratable con técnicas de ecuaciones diferenciales ordinarias, que tiene como solución

\[\begin{equation} \phi(x)=\frac{C}{V(x)G(x)} \tag{3.39} \end{equation}\]

con \(C\) una constante normalizadora tal que \(\int_0^1 \phi(p,x,t) dx=1\), de forma que la ecuación (3.39) pueda considerarse una función de densidad de probabilidad y \(G\) la integral indefinida (conocida como función de escala):

\[\begin{equation} G(x)=exp[-2 \int^x \frac{M(y)}{V(y)}dy] \tag{3.40} \end{equation}\]

Ahora, la pregunta que nos hacemos es ¿cómo se relaciona todo esto con nuestros problemas de genética de poblaciones? Veamos por ejemplo la determinación de la probabilidad de fijación de un alelo bajo deriva genética. Cuando al menos existe una barrera absorbente y la misma es accesible, entonces no existe la distribución estacionaria (ya que en algún momento del tiempo todas las poblaciones terminarán en alguna de esas barreras absorbentes). Sin embargo, cuando existe más de una, conocer la probabilidad de terminar en una de ellas en particular suele ser importante y en nuestro caso, conocer la probabilidad de terminar en la barrera absorbente \(x=1\), es decir la fijación, dado que partimos de una frecuencia \(p\) inicial es algo muy importante. Llamaremos \(u(p,t)\) a la probabilidad de fijación en el tiempo \(t\) del alelo de interés (por ejemplo A), cuando partimos de una frecuencia inicial \(p\). Es posible demostrar que \(u(p,t)\) es una función que cumple con la KBE . En particular, nos interesa conocer esa probabilidad cuando el tiempo \(t \to \infty\), es decir cuando todas las poblaciones hayan fijado algún alelo y llamaremos \(u(p)=\lim_{t \to \infty}u(p,t)\). En esas condiciones \(u(p)\) no variará con el tiempo y por lo tanto su derivada respecto al tiempo será igual a cero, por lo que la ecuación (3.35) quedará:

\[\begin{equation} \frac{\partial u(p)}{\partial t}=0=M(p)\frac{\partial u(p)}{\partial p}+\frac{V(p)}{2}\frac{\partial^2 u(p)}{\partial p^2} \tag{3.41} \end{equation}\]

A veces es posible encontrar esta misma ecuación escrita de la siguiente forma, que reduce un poco el aspecto intimidante de esta última ecuación

\[\begin{equation} 0=M(p)\frac{d u(p)}{d p}+\frac{V(p)}{2}\frac{d^2 u(p)}{d p^2} \tag{3.42} \end{equation}\]

al pasar la notación desde \(\partial\) a \(d\) lo que es posible ya que a esta altura nuestra \(u(p,t)\) ya no depende más del tiempo (no cambiará en el tiempo) y entonces se trata de una función de una sola variable. Tenemos dos formas de ver \(u(p)\), primero como la probabilidad última de fijación de alelo A siendo que partimos desde una frecuencia inicial \(p\); segundo, como la proporción de poblaciones en nuestro ensemble en los que finalmente el alelo A será fijado.

Volviendo a la ecuación (3.41), de acuerdo a Kimura (1962) la misma tiene la siguiente solución

\[\begin{equation} u(p)=\frac{\int_0^p G(x) dx}{\int_0^1 G(x) dx} \tag{3.43} \end{equation}\]

con \(G(x)\) como fue definido previamente en la ecuación (3.40) y con las condiciones de frontera \(u(0)=0\) y \(u(1)=1\), que en términos llanos quiere decir que un alelo que no existe jamás será fijado y que un alelo fijado ya está fijado.

Finalmente, casi llegamos a donde queríamos. Vamos a determinar la probabilidad de fijación de un alelo que solo experimenta la fuerza de la deriva y por lo tanto \(M(x)=0\) y \(V(x)=x(1-x)/(2N_e)\). Sustituyendo estos valores en la ecuación (3.40) tenemos que

\[\begin{equation} G(x)=exp[-2 \int^x \frac{M(y)}{V(y)}dy]=exp[-4N_e \int^x \frac{0}{x(1-x)}dy]=e^{-4N_e0}=1 \tag{3.44} \end{equation}\]

es decir, que bajo estas condiciones \(G(x)=1\). Por lo tanto, sustituyendo este valor en la ecuación (3.43), tenemos ahora

\[\begin{equation} u(p)=\frac{\int_0^p G(x) dx}{\int_0^1 G(x) dx}=\frac{\int_0^p 1 dx}{\int_0^1 1 dx}=\frac{p-0}{1-0}=p \tag{3.45} \end{equation}\]

La ecuación (3.45) nos brinda un resultado así de simple como de importante: la probabilidad de fijación de un alelo que solo experimenta deriva genética es igual a su frecuencia inicial en la población (o en el ensemble de poblaciones) de referencia, algo que usaremos en la próxima sección. Si lo pensamos un poco este resultado tiene bastante sentido intuitivo a partir del comportamiento de las gráficas que vimos en la sección El modelo de Wright-Fisher, en particular la Figura 3.5: como se trata de un proceso aleatorio con la misma probabilidad de ir hacia arriba o hacia abajo en la figura, cuanto más cerca arrancamos del borde superior (la fijación del alelo), mayor será la probabilidad de que las poblaciones caigan en la barrera absorbente de fijación, o dicho de otra forma, una mayor proporción de poblaciones irán a terminar en el estado de fijación. ¿Cuánto o cuántas? Bueno, en principio uno podría pensar que es proporcional al punto de arranque, \(p\), lo que afortunadamente se ve confirmado por los cálculos (algo más complejos) precedentes.

PARA RECORDAR

Bajo la condición de que la deriva sea la única fuerza evolutiva actuando, en una población de \(N\) individuos diploides, en un locus con dos alelos:

• La probabilidad de fijación de un alelo es igual a su frecuencia \(p\)
• La ecuación hacia adelante de Kolmogorov (KFE) analiza el comportamiento de la función de densidad de probabilidad \(\phi(p,x,t)\), es decir la distribución de las frecuencias alélicas \(x\), a medida de que avanza el tiempo y tiene la siguiente forma

\[\begin{equation*} \frac{\partial \phi(p,x,t)}{\partial t}=-\frac{\partial [M(x)\phi(p,x,t)]}{\partial x}+\frac{1}{2}\frac{\partial^2[V(x)\phi(p,x,t)]}{\partial x^2} \end{equation*}\]

• La ecuación hacia atrás de Kolmogorov (KBE) es la generalmente más útil en genética de poblaciones. Analiza el comportamiento de la función de densidad de probabilidad \(\phi(p,x,t)\) respecto a la frecuencia inicial \(p\), a medida de que voy hacia atrás en el tiempo y tiene la siguiente forma

\[\begin{equation*} \frac{\partial \phi(p,x,t)}{\partial t}=M(p)\frac{\partial \phi(p,x,t)}{\partial p}+\frac{V(p)}{2}\frac{\partial^2 \phi(p,x,t)}{\partial p^2} \end{equation*}\]

3.7 Probabilidad de fijación y tiempos de fijación

Como vimos antes, la probabilidad última de fijación de un alelo neutro es igual a la frecuencia inicial de dicho alelo, por ejemplo \(p\) para el alelo A. Inicial, en este contexto, se refiere a cualquier punto en el tiempo que tomemos como referencia, lo que claramente irá variando a medida que avance el tiempo. Más aún, como también vimos antes, cuando la única acción evolutiva es la correspondiente a la deriva genética el estado de equilibrio se corresponderá a cuando no existan poblaciones segregando, por lo que la probabilidad para cualquier punto entre las dos barreras absorbentes (fijación, \(p=1\), pérdida, \(p=0\)) será cero. Pese a esto, hay varios resultados interesantes que surgen a partir de la KBE y que fueron derivados por Kimura y Ohta (Kimura and Ohta 1969). En particular, si bien existían resultados previos para el tiempo de segregación de un alelo (obtenidos a partir de un método diferente), es decir el tiempo hasta que uno de los dos estados absorbentes es alcanzado, no existía una solución para cada uno de los dos tiempos en forma independiente. En particular, asumiendo que el punto de partida es cuando la frecuencia del alelo A es \(p\), el tiempo medio transcurrido hasta la fijación del alelo A (\(\bar{t_1}(p)\), notar la dependencia en \(p\)) viene dado por

\[\begin{equation} \bar{t_1}(p)=-4N \frac{(1-p) \ln(1-p)}{p} \tag{3.46} \end{equation}\]

mientras que el tiempo medio hasta la pérdida del alelo A (\(\bar{t_0}(p)\)) es

\[\begin{equation} \bar{t_0}(p)=-4N \frac{(p) \ln(p)}{(1-p)} \tag{3.47} \end{equation}\]

Por las dudas, los subíndices \(0\) y \(1\) se refieren en esta sección a pérdida (\(p=0\)) y fijación (\(p=1\)), respectivamente. La derivación de estas ecuaciones es un poco más compleja y excede el alcance de este capítulo (y seguramente tu paciencia), pero para los que estén interesados en cómo se llega hasta eso (a partir de los resultados de la sección previa) una excelente explicación se encuentra en el Apendix 1 del libro de Walsh and Lynch (2018), ecuaciones A1.21-A1.28. Volviendo a lo nuestro, los anteriores son los tiempos a la fijación y a la pérdida del alelo. Para calcular el tiempo medio hasta que ocurra alguno de los dos eventos (\(\bar{t}(p)\)), debemos ponderar cada uno de estos dos tiempos por la probabilidad de que ocurra, la fijación con probabilidad \(p\) y la pérdida con probabilidad \(1-p\), por lo que el promedio ponderado de ellos estará dado por \(\bar{t}=p \bar{t_1}(p)+ (1-p) \bar{t_0}(p)\). Sustituyendo los valores correspondientes a \(\bar{t_1}(p)\) (ecuación (3.46)) y \(\bar{t_0}(p)\) (ecuación (3.47)), tenemos:

\[ \begin{split} \bar{t}(p)=p \bar{t_1}(p)+ (1-p) \bar{t_0}(p)=\\ p \left[-4N \frac{(1-p) \ln(1-p)}{ p }\right] + (1-p) \left[-4N \frac{(p) \ln(p)}{ (1-p) }\right] \end{split} \]

\[\begin{equation} \bar{t}(p)=-4N [p \ln(p) + (1-p) \ln(1-p)] \tag{3.48} \end{equation}\]

Las curvas correspondientes a los tres tiempos (\(\bar{t},\bar{t_0}, \bar{t_1}\)) se pueden ver en la Figura 3.16, como función de la frecuencia inicial del alelo A (\(p\)).

Mientras que en \(\bar{t_0}\) y \(\bar{t_1}\) los máximos tiempos se corresponden a la proximidad inmediata a barreras absorbentes (ahora discutiremos cuán cerca), en el caso de \(\bar{t}\) el tiempo máximo ocurre cuando la frecuencia del alelo A es exactamente intermedia entre las barreras (\(p=\frac{1}{2}=0,5\)). En particular, a esta frecuencia \(p=\frac{1}{2}\), la ecuación (3.48) se transforma en

\[ \begin{split} \bar{t}(p=\frac{1}{2})=-4N [\frac{1}{2} \ln(\frac{1}{2}) + \frac{1}{2} \ln(\frac{1}{2})]=-4N [2 \frac{1}{2} \ln(\frac{1}{2})]=-4N \ln(\frac{1}{2})=4N \ln(2)\\ \bar{t}_{max} \sim 2,77N \end{split} \tag{3.49} \]

Figura 3.16: Tiempo medio a la fijación (verde), pérdida (roja) y de segregación (azul) en función de la frecuencia del alelo A. Cuando la frecuencia de A es 1/2 el tiempo medio de segregación es máximo y su valor esperado es de aproximadamente 2,77N generaciones.

Es decir, si partimos de una frecuencia del alelo A de \(p=0,5\) el tiempo medio que llevará hasta la eventual fijación o pérdida del mismo es de \(2,77N\) generaciones. Por otro lado, cuando aparece un nuevo alelo en la población su frecuencia es \(\frac{1}{(2N)}\) ya que en la población hay \(N\) individuos diploides (y por lo tanto un total de \(2N\) alelos). En este caso, lo más cerca que podemos estar de su pérdida antes de que ocurra, el tiempo que le llevará a la fijación será

\[\begin{equation} \bar{t_1}(p=\frac{1}{2N})=-4N \frac{(1-\frac{1}{2N}) \ln(1-\frac{1}{2N})}{\frac{1}{2N}} \sim 4N \tag{3.50} \end{equation}\]

La última aproximación basada en que \(\frac{\ln(1-x)}{x} \to 1\) cuando \(x \to 0\) y que \(1-\frac{1}{2N}=\frac{2N-1}{2N} \to 1\) cuando \(N \to \infty\), en conjunto una buena aproximación aún para valores tan pequeños como \(N=10\). Es decir, al surgir un nuevo alelo en la población su probabilidad de fijación es \(\frac{1}{2N}\) y en la eventualidad de que lo consiga el tiempo requerido será en promedio de \(4N\) generaciones.

Finalmente, la probabilidad de perder ese mismo alelo nuevo es \(1-\frac{1}{2N}\) y el tiempo promedio a la pérdida será de

\[\begin{equation} \bar{t_0}(\frac{1}{2N})=-4N \frac{(\frac{1}{2N}) \ln(\frac{1}{2N})}{(1-\frac{1}{2N})}=-2 \frac{\ln(\frac{1}{2N})}{(1-\frac{1}{2N})} \sim 2 \ln(2N) \tag{3.51} \end{equation}\]

lo que es claramente menor que el tiempo medio a la eventual fijación ya que para \(N>0\), \(2N \gg \ln(2N)\).

Ejemplo 3.5

En la mosca de la fruta (D. melanogaster) se han reportado varias mutaciones en el locus “vestigial” (vg) que alteran la forma de las alas de la mosca portadora. Consideremos una población de \(N=60\) individuos homocigotas para el alelo \(vg_1\), el cual se asume produce alas normales. En un momento dado, se mezcla esta población con otra (de tamaño \(N=20\)), compuesta por individuos homocigotas para el alelo \(vg_2\), el cual genera una pequeña muesca en las alas de las moscas. Asumiendo que ambos alelos son neutros (es decir, la única fuerza evolutiva en juego es la deriva genética), ¿cuál es la probabilidad de fijación del alelo \(vg_2\) en la población resultante? Si el tiempo generacional de D. melanogaster es de 10 días, ¿cuántos años en promedio se espera segregue el alelo en la población? ¿Cuántos años en promedio son necesarios para que se fije en la población?

Una vez se mezclan las poblaciones de moscas, las frecuencias alélicas \(p\) y \(q\) (para los alelos \(vg_1\) y \(vg_2\), respectivamente) son \(p=\frac{120}{160} = \frac{3}{4}\) y \(q=\frac{40}{160} = \frac{1}{4}\). Por lo tanto, la probabilidad de fijación del alelo \(vg_2\) es de \(0.25\). El tiempo medio de segregación para el alelo está dado por

\[ \bar{t}_{vg_2} = -4N[q \cdot ln(q) + (1-q) \cdot ln(1-q)] \]

\[ \bar{t}_{vg_2} = -4 \cdot 80 \cdot [0,25 \cdot ln(0,25) + (1-0,25) \cdot ln(1-0,25)] \approx 180\text{ generaciones} \]

Dado que cada generación ronda los diez días, se espera que el alelo segregue en promedio por

\[\frac{-4 \cdot 80 \cdot [0.25 \cdot ln(0,25) + (1-0,25) \cdot ln(1-0,25)] \text{ (generaciones)} \cdot 10 \text{ (días/generación)}}{365 \text{ (días/año)}} \approx 4,9\text{ años}\].

El tiempo de fijación medio está dado por

\[ \bar{t_1}_{vg_2} = -4 \cdot N \cdot \frac{(1-q) \cdot ln(1-q)}{q} \]

\[ \bar{t_1}_{vg_2} = -4 \cdot 80 \cdot \frac{(1-0,25) \cdot ln(1-0,25)}{0,25} \approx 276 \text{ generaciones} \]

\[\frac{-4 \cdot 80 \cdot \frac{(1-0,25) \cdot ln(1-0,25)}{0,25} \text{ (generaciones)} \cdot 10 \text{ (días/generación)}}{365 \text{ (días/año)}} \approx 7,6\text{ años}\]

---

Para terminar con este tema, un hecho a primera vista curioso. Si ya has tenido un curso de ecología, sin duda te estarás preguntando por la conexión entre la ecuación (3.48) que predice el tiempo medio que un locus con dos alelos se encuentra segregando en un ensemble de poblaciones con el índice de diversidad de Shannon-Weaver (a veces conocido como de Shannon o incluso Shannon-Wiener). Si recuerdas este índice, que nos indicaba la diversidad de especies en un sistema ecológico, el mismo era \(- \sum_{i=1}^{n} p_i \ln{p_i}\), para un conjunto de \(n\) especies diferentes, donde \(p_i\) es la frecuencia de la especie \(i\) en el conjunto (\(\sum_i p_i=1\)). Si consideramos que \(q=1-p\) y \(p+q=1\), podemos llamar \(p_1=p\) y \(p_2=q\), que cumplen \(\sum_i p_i=1\). Más aún, con este cambio de notación podemos reescribir la ecuación (3.48) como: \[\bar{t}(p)=-4N [p \ln(p) + (1-p) \ln(1-p)]=-4N [p_1 \ln(p_1)+p_1 \ln(p_2)]=-4N \sum_i p_i \ln(p_i)\] Excepto por el factor de escala \(4N\), el índice de Shannon-Wiener para \(n=2\) especies es idéntico al tiempo medio de segregación, lo que llama inmediatamente a pensar, como paralelismo, en las distintas poblaciones segregando como la probabilidad de mantener la diversidad genética dentro de las mismas en el tiempo.

PARA RECORDAR

Bajo la condición de que la deriva sea la única fuerza evolutiva actuando, en una población de \(N\) individuos diploides, en un locus con dos alelos:

• La probabilidad de fijación de un alelo es igual a su frecuencia \(p\)
• El tiempo a la eventual fijación de ese alelo es \(\bar{t_1}(p)=-4N \frac{(1-p) \ln(1-p)}{p}\)
• La probabilidad de perder un alelo es igual a \(1-p\)
• El tiempo a la eventual pérdida de ese alelo es \(\bar{t_0}(p)=-4N \frac{(p) \ln(p)}{(1-p)}\)
• El tiempo segregando en ese locus, es decir el tiempo a eventual fijación o pérdida es \(\bar{t}(p)=-4N [p \ln(p) + (1-p) \ln(1-p)]\)
• El tiempo máximo segregando se alcanza cuando el punto de partida es \(p=\frac{1}{2}\) y es igual a \(\sim 2,77N\) generaciones.

3.8 El modelo coalescente

En general, el modelo de Wright-Fisher es una buena aproximación inicial para modelar la evolución de una población, pero las poblaciones reales se suelen apartar de varios de los supuestos, como ya vimos. Un tema del que nos hemos abstenido de tocar hasta ahora es el del número de alelos. Hasta ahora hemos tratado los problemas como un locus con dos alelos, pero se trata de un modelo poco realista desde el punto de vista de la evolución molecular. Es decir, si secuenciamos una región razonable de un gen en varios individuos de la población nos vamos a encontrar con que en la misma existen varias posiciones segregantes (en las que hay variabilidad entre los individuos muestreados). Esto es muy razonable ya que las mutaciones (que son la fuente primaria de variabilidad) ocurren aproximadamente al azar entre las diferentes posiciones posibles en el gen, por lo que en una muestra de secuencias del gen vamos a encontrar muchos alelos diferentes. La idea ahora es ver si podemos trazar y entender la historia hacia atrás, es decir, a partir de una muestra del presente extraer conclusiones sobre la historia de la población de la que extrajimos la muestra. Por ejemplo, nos podemos preguntar si a partir de los datos presentes podemos responder algunas de estas cuestiones: ¿Cuál fue el ancestro común más reciente de las copias genéticas existentes en el presente? ¿Cuál era el tamaño de la población en el momento del evento de coalescencia? ¿Con qué frecuencia se “extinguen” las copias genéticas? ¿Qué régimen migratorio operaba en la población histórica?

Una representación de la situación se puede ver en la Figura 3.17, donde la generación presente (generación \(0\)) aparece en la parte de abajo de la figura y a medida de que nos retrotraemos en el tiempo, generación a generación, vamos subiendo en el gráfico.

En la generación presente, que es lo que usualmente tenemos para muestrear, tenemos 3 alelos diferentes, marcados por los colores (notar que hay 3 colores: verde, magenta y rojo). Cada una de las copias presentes proviene de una copia en la generación anterior. Si conociésemos de cuál exactamente, la podríamos unir con una línea (técnicamente, con una arista en el grafo que representa la evolución de nuestra población de alelos en el tiempo). Notar que el tamaño de la población de alelos es fija, 20 en nuestra figura. A medida de que vamos hacia atrás, las copias de cada generación deben venir de alguna copia de la generación anterior. Sin embargo, como el muestreo en el modelo de Wright-Fisher es con reposición, como vimos antes, con probabilidad \(1/(2N)\) podemos volver a extraer una copia del mismo alelo para la nueva generación. Como el tamaño de la población de alelos es fijo, entonces si alguno de ellos es muestreado en forma repetida, algún otro deberá NO dejar copias, es decir, se perderá para el futuro. Si observas con detenimiento la figura verás que en muchas copias no hay una línea que las una con la generación inmediatamente debajo, que significa que esa copia no ha dejado descendientes y por lo tanto “muere” en nuestra genealogía de los alelos. Más aún, si vuelves a mirar con cuidado, seguramente notarás que varios linajes han desaparecido en el tiempo, por ejemplo el naranja y el azul, que como en general no tenemos muestras del pasado no tendríamos capacidad de verlos o conocerlos hoy en día.

Figura 3.17: Evolución del linaje de los alelos encontrados en la generación presente (generación 0) hacia \(t\) generaciones atrás. Figura propia generada con el paquete “learnPopGen” (Liam Revell) de R (función modificada por nosotros).

Veamos si podemos entender cómo es la distribución de probabilidades asociada con el comportamiento de esta genealogía. De acuerdo con el modelo de Wright-Fisher, si tenemos \(2N\) copias de alelos en cada generación, dado de que extraemos una cualquiera (que viene de una copia en particular en la generación anterior), la probabilidad de una segunda copia que extraemos de la población provenga de la misma ancestral que la de la primera es \(1/(2N)\), por lo que la probabilidad de que vengan de copias ancestrales distintas en la generación previa es de \(1-[1/(2N)]\). Ahora, si deseamos saber cuál es la probabilidad de que la tercera copia que sacamos de la generación presente provenga de una copia diferente a las otras dos, esta copia debe ser primero diferente a la primera (con probabilidad \(1-[1/(2N)]\)), pero también a la segunda, ahora con probabilidad \(1-[2/(2N)]=(2N-2)/(2N)\) (el \(2\) en el numerador de la expresión anterior es porque quedan \(2N-2\) posibilidades de copias diferentes); como deben darse los dos eventos, entonces la probabilidad de que la tercera copia sea diferente a las dos anteriores (también diferentes), es decir que las 3 sean diferentes es \(\left[\left(1-\frac{1}{2N}\right)\right] \cdot \left[\left(1-\frac{2}{2N}\right)\right]\). Claramente la misma lógica se puede aplicar para la cuarta copia, para la quinta y así sucesivamente. Si (siguiendo la notación del libro de Joseph Felsenstein (2004)) llamamos \(G_{kk}\) a la probabilidad de que \(k\) copias vengan de copias diferentes en la generación previa, entonces tenemos que

\[\begin{equation} G_{kk}=\left(1-\frac{1}{2N}\right)\left(1-\frac{2}{2N}\right)\left(1-\frac{3}{2N}\right)...\left(1-\frac{k-1}{2N}\right)=\prod_{i=1}^{k-1}\left(1-\frac{i}{2N}\right) \end{equation}\]

Si operamos un poco, reagrupamos y descartamos los términos del orden \(\frac{1}{N^2}\), tenemos entonces

\[\begin{equation} G_{kk}=1-[1+2+3+..+(k-1)]/(2N)+\text{ términos en }\frac{1}{N^2} \text{ y menores} \end{equation}\]

Como \(\sum_{i=1}^{k-1}=k(k-1)/2\)⁴⁵, entonces,

\[\begin{equation} G_{kk} \approx 1-\frac{k(k-1)}{4N} \end{equation}\]

o visto de otra forma, la probabilidad de coalescer de dos copias en la generación anterior (que es igual a \(1\) menos la probabilidad de que vengan de distintas copias) es de

\[\begin{equation} P(\text{coalescer})=1-G_{kk} \approx \frac{k(k-1)}{4N} \end{equation}\]

Otra forma de ver lo anterior es que la probabilidad de coalescer es el producto de la probabilidad de extraer un alelo idéntico (\(\frac{1}{2N}\)), multiplicada por el número de posibilidades de a dos, que es \(k(k-1)/2\) (despreciando la posibilidad de que 3 o más coalescan en la misma generación, un evento extremádamente improbable cuando \(k \ll N\)),

\[\begin{equation} P(\text{coalescer})= \frac{1}{2N} \cdot \frac{k(k-1)}{2} = \frac{k(k-1)}{4N} \end{equation}\]

Si recuerdas, la distribución geométrica era la que correspondía al número de fracasos hasta obtener el primer éxito. Tiene la forma \(\Pr(X=k)=(1-p)^{k-1}p\), con parámetro \(p\) igual la probabilidad de éxito, media igual a \(1/p\) y varianza \((1-p)/p^2\) (con soporte en \(k \in \{1,2,3,...\}\)). La distribución exponencial tiene forma \(\lambda e^{-\lambda x}\), con soporte en \(x \in [0,\infty )\), media \(1/p\) y varianza \(1/p^2\). Ahora, si llamamos \(u_{k}\) a la variable aleatoria para el tiempo (en generaciones) hasta la primer coalescencia, que me lleva de \(k\) a \(k-1\) alelos, la misma tendrá una distribución geométrica (muy bien aproximada por una exponencial cuando \(k \ll N\)) y como \(p=\frac{k(k-1)}{4N}\), entonces \(\frac{1}{p}=\frac{4N}{k(k-1)}\), por lo tanto con media

\[\begin{equation} \mathbb{E}(u_{k})=\frac{4N}{k(k-1)} \text{ generaciones} \tag{3.52} \end{equation}\]

y varianza

\[\begin{equation} \mathbb{V}(u_{k})=\frac{16N^2}{[k(k-1)]^2} \text{ generaciones}^2 \tag{3.53} \end{equation}\]

Es decir, tenemos la distribución del tiempo hasta el primer evento de coalescencia, que me reducirá el número de alelos diferentes en 1. Por esta razón, el siguiente tiempo de coalescencia tendrá también una distribución aproximadamente exponencial, pero ahora su esperanza será

\[\begin{equation} \mathbb{E}(u_{k-1})=\frac{4N}{(k-1)(k-2)} \text{ generaciones} \tag{3.54} \end{equation}\]

Como el denominador es menor que en (3.52), el tiempo esperado para el próximo evento de coalescencia será mayor. De hecho, si dividimos la ecuación (3.54) entre la ecuación (3.52), tendremos la relación entre los tiempos para el primer evento de coalescencia y para el segundo.

\[\begin{equation} \frac{\mathbb{E}(u_{k-1})}{\mathbb{E}(u_{k})}=\frac{4N}{(k-1)(k-2)} \frac{k(k-2)}{4N}=\frac{k}{k-2} \tag{3.55} \end{equation}\]

El proceso se repite y los tiempos serán cada vez mayores, hasta llegar al último evento de coalescencia que es cuando pasamos de \(k=2\) alelos a \(k=1\) alelo. Para este último evento tendremos entonces que la esperanza es igual a

\[\begin{equation} \mathbb{E}(u_{2})=\frac{4N}{2(2-1)}= \frac{4N}{2} = 2N\text{ generaciones} \tag{3.56} \end{equation}\]

Figura 3.18: Árbol genético representando los tiempos del proceso coalescente, cuya esperanza está dada por \(4N/(k(k-1))\) para \(k\) alelos. Con 5 alelos incialmente el tiempo es \(4N/20=2/10N\) y así sucesivamente. Se aprecia claramente que hacia atrás los tiempos son cada vez mayores. Elaboración propia a partir de idea en Hartl and Clark (2007).

Como se aprecia en la Figura 3.18, en el caso de 5 alelos iniciales, los tiempos de los intervalos hasta el próximo evento de coalescencia van creciendo de acuerdo a la progresión \(\frac{4N}{(5 \cdot 4)}=\frac{2N}{10}=\frac{N}{5}\), \(\frac{4N}{(4 \cdot 3)}=\frac{2N}{6}=\frac{N}{3}\), \(\frac{4N}{(3 \cdot 2)}=\frac{4N}{6}=\frac{2N}{3}\) y \(\frac{4N}{(2 \cdot 1)}=\frac{4N}{2}=2N\).

Para un muestra conteniendo \(k\) alelos diferentes, el tiempo total a la coalescencia, o lo que es lo mismo el tiempo hasta el ancestro más reciente de todos los alelos en la muestra es de

\[\begin{equation} t=4N(1-\frac{1}{k}) \tag{3.57} \end{equation}\]

con varianza

\[\begin{equation} \mathbb{V}(t)=4N^2 \sum_{i=2}^k \frac{1}{ {i \choose 2}^2} \tag{3.58} \end{equation}\]

(según Kingman (1982a); Kingman (1982b); Tajima (1983), ecuaciones 10 y 11).

Un primer resultado de la ecuación (3.57) es que a medida de que el número de alelos se acerca a \(2N\) (el máximo), como \(\frac{1}{(2N)} \to 0\), el tiempo al ancestro común de todos los alelos tenderá a \(4N\). Otro resultado más interesante es provisto por Rosenberg and Nordborg (2002), que muestran que la probabilidad de que el ancestro común a los alelos en la muestra sea el mismo que el ancestro común a todos los alelos de la población se guía por la relación \(\frac{(k-1)}{(k+2)}\), una relación que crece muy rápido (por ejemplo, para \(k=3\), \(\frac{(3-1)}{(3+2)}=\frac{2}{5}=0,40\), pero para \(k=10\) ya es \(\frac{(10-1)}{(10+2)}=\frac{9}{12}=\frac{3}{4}=0,75\)). Esto, de alguna manera, nos da cierta garantía de que aún con una muestra relativamente pequeña es posible identificar correctamente los patrones evolutivos de la población.

Una de las aplicaciones del modelo coalescente tiene que ver con el supuesto de tamaño poblacional constante. Como la sucesión de intervalos de coalescencia (la esperanza) depende del tamaño poblacional, ecuación (3.52), una reducción del tamaño poblacional, por ejemplo a la mitad implicaría también reducir a la mitad el tiempo esperado, o lo que es lo mismo duplicar la velocidad de aparición de estos eventos. Esto tiene dos aristas. Por un lado, si de otra forma conseguimos reconstruir un árbol de alelos, por ejemplo a partir de las secuencias y comparamos los dos árboles, el del coalescente y el molecular (sumado a otra información, usualmente biológica o histórica) podemos en algunos casos asignar estas discrepancias a fluctuaciones del tamaño poblacional. Por el otro lado, si conocemos alguna función del tamaño poblacional en función del tiempo, \(N(t)\), y suponemos por ejemplo que el tiempo en una nueva escala ficticia \(\tau\) pasa proporcional a \(\frac{N(t)}{N(0)}\) (con \(N(0)\) el tamaño poblacional actual), tenemos que para pequeños intervalo de tiempo ficticio

\[\begin{equation} d\tau = \frac{N(0)}{N(t)} dt \tag{3.59} \end{equation}\]

por lo que

\[\begin{equation} \tau = \int d\tau= \int \frac{N(0)}{N(t)} dt = N(0) \int \frac{1}{N(t)} dt \tag{3.60} \end{equation}\]

O sea, si conocemos una función que nos relacione el tamaño de la población en el tiempo y su inversa es integrable, entonces tenemos una forma de hacer nuestro coalescente independiente del tamaño poblacional. Veamos un ejemplo. El crecimiento exponencial de una población (por ejemplo, las poblaciones bacterianas al comienzo de la etapa de multiplicación) está dado por una función del tiempo de tipo \(N_t=N_0 e^{gt}\), cuando el tiempo va hacia adelante. Ahora, en nuestro caso el tiempo va hacia atrás (en la generación \(0\), \(N(0)\) es la población ya crecida al nivel actual y en tiempo \(t\) hacia atrás, \(N(t)\) es mucho menor en tamaño), por lo que el exponente debe ser negativo

\[\begin{equation} N(t)=N(0) e^{-gt} \tag{3.61} \end{equation}\]

Ahora, si sustituimos esta función del tamaño poblacional en (3.60) e integramos tenemos que

\[\begin{equation} \tau = \int_0^t \frac{N(0)}{N(t)} dt = \int_0^t \frac{N(0)}{N(0) e^{-gt}} dt = \int_0^t e^{gt} dt = \frac{1}{g}e^{gt} \bigg\rvert_{t=0}^t = \frac{1}{g} (e^{gt}-1) \tag{3.62} \end{equation}\]

Despejando \(t\) de la ecuación (3.62), tenemos que

\[\begin{equation} t = \frac{\ln{(1+g\tau)}}{g} \tag{3.63} \end{equation}\]

Ahora, para terminar alcanza con generar un modelo coalescente con tamaño fijo igual al inicial \(N(0)\) y luego re-escalar los tiempos de acuerdo la ecuación (3.63).

PARA RECORDAR

• En organismos diploides, en poblaciones de N individuos, la probabilidad de coalescer de dos alelos en la generación anterior es

\[\begin{equation*} \mathbb{Pr}(\text{coalescer})=\frac{k(k-1)}{4N} \end{equation*}\]

• Como los eventos de coalescencia en cada generación son independientes de la previa, el tiempo a la coalescencia (\(u_k\)) tiene distribución geométrica, usualmente aproximada por una distribución exponencial con tasa inversa a la probabilidad de coalescer por generación, es decir

\[\begin{equation*} \mathbb{E}(u_k)=\frac{4N}{k(k-1)} \end{equation*}\]

• Como además en cada evento de coalescencia \(k\) se reduce en uno, los tiempos hacia atrás serán cada vez más largos.
• El tamaño poblacional juega un papel muy importante en los tiempos de coalescencia (está en el numerador de la esperanza), por lo que si el mismo varía a lo largo del tiempo entonces no se cumple uno de los supuestos fundamentales del coalescente. Sin embargo, en los casos en que el tamaño poblacional es una función del tiempo cuya inversa sea integrable, es posible aplicar una transformación del tiempo tal que se puede trabajar en esta escala temporal ficticia con el coalescente sin modificar.

3.9 Conclusión

En este capítulo, exploramos cómo la introducción de una limitación realista al modelo de Hardy-Weinberg (específicamente, el tamaño poblacional finito) lleva a esperar cambios en las frecuencias alélicas a lo largo del tiempo, simplemente por el muestreo azaroso de gametos. Este cambio en las frecuencias alélicas es en efecto un proceso evolutivo, y recibe comunmente el nombre de deriva genética. Lo que es más, vimos cómo el marco conceptual que nos dió el modelo de Hardy-Weinberg nos permite construir un nuevo modelo (el de Wright-Fisher), el cual nos permite estudiar este proceso evolutivo. También vimos que en un ensemble de poblaciones de tamaño finito, la tendencia observada es una disminución progresiva de la heterocigosidad total respecto a lo esperado bajo equilibrio. Esto ocurre porque se termina rompiendo el régimen de apareamiento aleatorio, un fenómeno en el que ahondaremos en más detalle en capítulos posteriores. A medida que pasa el tiempo en las poblaciones, la deriva lleva al aumento de la representación de alguno de los alelos en cada población, hasta que eventualmente algún alelo se fija en cada subpoblación. El modelo del coalescente nos brinda una herramienta para comprender cómo se da el proceso de aumento progresivo de copias alélicas en una población. Por último es importante resaltar que si bien procesos netamente aleatorios (y por lo tanto, neutrales desde el punto de vista evolutivo) pueden modificar las frecuencias alélicas, es esperable que en las poblaciones naturales también jueguen un papel importante los procesos sistemáticos (o selectivos). Estos serán próximo objeto de estudio en el siguiente capítulo. Modelos de mayor complejidad matemática, como la aproximación de difusión, nos permiten integrar los procesos estocásticos y los selectivos. Este es un buen ejemplo de como la integración de distintas elaboraciones teóricas no sólo se puede llevar a cabo a nivel conceptual, sino también matemático, lo cual permite elaborar predicciones que interpelen y enriquezcan las elaboraciones teóricas originales.

3.10 Actividades

3.10.1 Control de lectura

1. ¿Qué es la deriva genética? ¿Cómo afecta a la evolución de las poblaciones?
2. La influencia del azar en la evolución de las frecuencias alélicas de una población se ve estrechamente ligada al tamaño de la población. Utilice algunas de las ecuaciones presentadas en este capítulo para explicar esta dependencia.
3. ¿Qué es el coeficiente de fijación? Describa cómo varía el mismo según el modelo de Wright-Fisher conforme transcurren las generaciones.
4. En poblaciones de tamaño se espera un aumento de la homocigosidad por efecto del azar, aumentando la frecuencia de algunos alelos a expensas de otros (que a largo plazo van desapareciendo). Según el modelo coalescente, ¿cuánto tiempo es de esperar para que todos los alelos presentes en una población sean réplicas de un mismo alelo ancestral?
5. ¿Qué es el tamaño poblacional efectivo (\(N_e\)), y qué utilidad tiene en el marco de la aplicación del modelo de Wright-Fisher? Nombre al menos una situación biológica en la que se posea una ecuación para obtener \(N_e\).

3.10.2 ¿Verdadero o falso?

1. En una población de tamaño finito se espera un decrecimiento lineal de la heterocigosidad a medida que se suceden las generaciones. Esto se debe a que por efecto del muestreo aleatorio es de esperar a largo plazo que alguno de los alelos aumente su número, disminuyendo la frecuencia del resto (y por lo tanto la heterocigosidad).
2. Dos poblaciones pueden tener un mismo número de individuos y, sin embargo, el ritmo de la deriva genética puede ser bastante distinto en ambas.
3. Utilizando el modelo de Wright-Fisher podemos predecir de forma exacta la evolución de las frecuencias alélicas en una población.
4. Los tiempos de coalescencia no son iguales durante el proceso que lleva de una muestra de \(k\) alelos a su alelo ancestral.
5. Las ecuaciones de Kolmogorov nos permiten modelar cambios tanto hacia atrás (Kolmogorov Backward Equation) como hacia adelante (Kolmogorov Forward Equation), modelando en conjunto los efectos estocásticos y direccionales en la evolución de una población.

Solución

1. Falso. La frase es parcialmente cierta: sí se espera un decrecimiento de la heterocigosidad, y la explicación dada es razonable. No obstante, como se vió en el capítulo cuando se presentó el coeficiente de fijación, la heterocigosidad en la población decrece de forma aproximadamente exponencial (no de forma lineal, como se menciona).
2. Verdadero. El punto clave en la afirmación es que el ritmo de la deriva genética dependera del tamaño poblacional efectivo (\(N_e\)), y no del tamaño censal (número de individuos). Un ejemplo claro que podría ser el de dos poblaciones de ganado de igual tamaño, una de ellas con igual número de machos y hembras y la otra compuesta casi en su totalidad por hembras. ¿Es de esperar que la deriva genética tenga igual ritmo en ambas poblaciones? No, ya que la diversidad genética aportada generación a generación en la población que cuenta con un único individuo macho es sustancialmente menor. Esto se verá reflejado en el número poblacional efectivo, el cual podemos utilizar para ajustar el número censal a los modelos teóricos que trabajan el efecto de la deriva genética.
3. Falso. Las trayectorias de una población de tamaño finito no pueden ser determinadas con precisión, justamente por la naturaleza estocástica del proceso. No obstante, un conjunto de poblaciones (ensemble) si tendrá características que son predecibles desde un punto de vista estadístico: no podremos asegurar qué acontecerá en una población particular, pero sí qué tendencias esperamos ver en un conjunto de poblaciones de igual característica.
4. Veradero. Según el modelo del coalescente, se espera que una muestra de \(k\) alelos haya provenido \(4N\) generaciones de un único alelo ancestral. No obstante, \(2N\) generaciones es el tiempo estimado de coalescencia de los últimos dos alelos, lo cual deja claro que el proceso de coalescencia no es homogéneo en el tiempo. Si se lo piensa, esto tiene bastante sentido: si tenemos en cuenta por ejemplo cien alelos, es claro que resultará más fácil que suceda el evento de coalescencia que cuando se consideran cincuenta, diez o los últimos dos alelos ancestrales.
5. Falso. Sí es cierto que las ecuaciones de Kolmogorov buscan modelar en conjunto los efectos estocásticos y direccionales en la evolución de una población. Sus nombres, sin embargo, no describen la capacidad de hacer predicciones hacia el pasado (como si se tratara de una especie de modelo del coalescente) o el futuro, si no que refieren a cómo se derivan matemáticamente las ecuaciones: en la Kolmogorov Backward Equation se recrea el proceso “mirando hacia atrás” en el tiempo y partiendo de la primera generación, intentando razonar y trabajar con las probabilidades de los sucesos que llevan al estado actual del sistema. En la Kolmogorov Forward Equation se trabaja partiendo del estado actual dei sistema, e intentando razonar los cambios que pueden acontecer si “se avanza” una generación en el tiempo.

3.10.3 Ejercicios

Ejercicio 3.1

En una población con \(N=20\) individuos diploides, el alelo \(A_1\) presenta 6 copias en una generación dada.

a. ¿Cuál es la probabilidad de que el alelo duplique su cantidad de copias en la siguiente generación?

b. El alelo \(A_2\) presenta la mitad de copias en la generación. ¿Tiene la mitad de probabilidad de duplicar su número que la que tiene el alelo \(A_1\)?

Solución

a. La probabilidad de pasar de un número \(i\) de copias a un número \(j\) de copias en la siguiente generación está dada por

\[ T_{ij} = {2N \choose j}p^jq^{2N-j} \]

(recordemos que \({n \choose k}=\frac{n!}{k!(n-k)!}\)).

Tenemos \(2N=40\) alelos en la población, Para el alelo \(A_1\) tenemos \(p=\frac{6}{40} \Rightarrow q = \frac{34}{40}\), por lo que la probabilidad de pasar de \(i=6\) a \(j=12\) copias alélicas corresponde a

\[ T_{6,12} = \frac{40!}{12! \cdot (40-12)!} \cdot (\frac{6}{40})^{12} \cdot (\frac{34}{40})^{28} \approx 0,00766 \]

b. En el caso del alelo \(A_2\), tenemos por razonamiento análogo una probabilidad de pasar de \(i=3\) copias a \(j=6\) copias en la próxima generación de

\[ T_{3,6} = \frac{40!}{6! \cdot (40-6)!} \cdot (\frac{3}{40})^{6} \cdot (\frac{37}{40})^{34} \approx 0,0482 \]

Como se puede apreciar, el alelo \(A_2\) tiene claramente mayores probabilidades de dulpicar su número que el alelo \(A_1\).

Ejercicio 3.2

Una población de ratones tiene fluctuaciones en su tamaño poblacional. La población crece sin mayores problemas hasta alcanzar un tamaño aproximado de \(N=2000\); llegado este punto una pobación de gatos se pone manos a la obra, disminuyendo a la población hasta \(N = 50\) aproximadamente. Los ratones que logran pasar disimulados son los encargados de reestablecer a la población de ratones, cerrando el ciclo de la población. Asuma que cada ciclo involucra a tres generaciones. ¿Cual es el coeficiente de fijación para un locus bi-alélico, luego de que pasen 30 generaciones de ratones?

Solución

Notemos que en cada ciclo el tamaño poblacional efectivo corresponde a

\[ \frac{1}{N_e} = \frac{1}{2} \cdot (\frac{1}{2000} + \frac{1}{50}) \Rightarrow N_e = \frac{2}{(\frac{1}{2000} + \frac{1}{50})} \]

La cantidad de generaciones considerada equivale a 15 de estos ciclos.

Tenemos a su vez que el coeficiente de fijación a tiempo \(t\) equivale a

\[ F_t = 1 - (1-\frac{1}{2N_e})^t \]

por lo que al tiempo pedido tenemos \(F_{15}=1-(1-\frac{1}{2 \cdot (\frac{2}{(\frac{1}{2000} + \frac{1}{50})})})^{15} \Rightarrow F_{15} \approx 0,0742\).

Ejercicio 3.3

Una población de organismos diploides de tamaño \(N\) desconocido se estructuró geográficamente en cinco subpoblaciones de igual tamaño. En las mismas se segrega un locus con dos alelos (\(A_1\) y \(A_2\) , de frecuencias \(p_i\) y \(q_i\) respectivamente en la subpoblación \(i\)). Se estima que el evento de estructuración geográfica ocurrió al rededor de 3000 años atrás. Se genotipan 50 individuos al azaar de cada población, observándose el siguiente conteo de individuos:

Genotipo	Subpoblación.1	Subpoblación.2	Subpoblación.3	Subpoblación.4	Subpoblación.5
\(A_1A_1\)	2	16	20	26	36
\(A_1A_2\)	16	26	22	19	13
\(A_2A_2\)	32	8	8	5	1

Estime el tamaño de la población inicial, asumiendo i) que las subpoblaciones mantuvieron un tamaño aproximadamente constante a lo largo del tiempo, ii) que el tiempo generacional de la especie es de 30 años aproximadamente, iii) que las subpoblaciones cumplen todas las suposiciones para asumir que se encuentran en equilibrio de Hardy-Weinberg (salvo, naturalmente, la suposición de tamaño infinito).

Solución

La varianza que se espera observar en el ensemble poblacional para la frecuencia de un alelo (elegimos arbitrariamente el alelo \(A_1\)) luego de \(t\) generaciones está dada por

\[ \sigma^2_t(p) = t \cdot \frac{pq}{2N_e} \]

Notemos que podemos calcular la varianza observada para la frecuencia alélica \(p\) en el ensemble de subpoblaciones a partir de los datos de genotipado. Para ello debemos primero calcular las frecuencias alélicas \(p_i\) para cada subpoblación.

Así, por ejemplo, tenemos \(p_1 = f_1(A_1A1) + \frac{1}{2}f_1(A_1A_2) = (\frac{2}{50}) + \frac{1}{2} \cdot (\frac{16}{50}) = 0,2\). Por analogía, se tiene que \(p_2 = 0,58;\ p_3 = 0,62;\ p_4 = 0,71;\ p_5 = 0,85\). Dado que se asume que las poblaciones tienen aproximadamente el mismo tamaño, el promedio de frecuencias alélicas equivale a \(\bar{p} = \frac{1}{n}\sum_{i=1}^{i=n}p_i = \frac{0,2 + 0,58 + 0,62 + 0,71 + 0,85}{5} = 0,592\). Por lo tanto, la varianza observada es de

\[ \sigma^2_t(p) = \frac{1}{n}\sum_{i=1}^{i=n}(p_i-\bar{p})^2 \]

\[ \sigma^2_t(p) = \frac{(0,2-0,592)^2 + (0,58-0,592)^2 + (0,62-0,592)^2 + (0,71-0,592)^2 + (0,85-0,592)^2}{5} \]

\[ \sigma^2_t(p) = 0,047016 \]

Retomando nuestra primera ecuación, y teniendo en cuenta que pasaron \(t = \frac{3000}{30} = 100\) generaciones (dado que se estima un tiempo generacional de al rededor de 30 años), tenemos

\[ 0,047016 = 100 \cdot \frac{0,592 \cdot (1-0,592)}{2N_e} \]

en donde se utilizó la estimación de \(\bar{p}\) antes realizada.

De aquí podemos obtener un estimado del tamaño poblacional efectivo de las subpoblaciones observadas

\[ 0,047016 = 100 \cdot \frac{0,592 \cdot (1-0,592)}{2N_e} \Longrightarrow \frac{1}{N_e} = \frac{2 \cdot 0,047016}{100 \cdot 0,592 \cdot (1 - 0,592)} \]

\[ N_e = \frac{100 \cdot 0,592 \cdot (1 - 0,592)}{2 \cdot 0,047016} \]

\[ N_e \approx 257 \]

Por lo tanto, podemos estimar que el tamaño poblacional efectivo de la población inicial se encontraba en el orden de los 1285 individuos.

Ejercicio 3.4

Una población compuesta por 250 individuos diploides de la especie Peluca mustensis se encuentra segregando un locus bi-alélico (alelos \(A_1\) y \(A_2\) ; frecuencias alélicas denotadas por \(p\) y \(q\) , respectivamente).

Un genotipado de la población arroja los siguientes conteos:

\[ \begin{cases} \text{Genotipo }A_1A_1: 102\text{ individuos} \\ \text{Genotipo }A_1A_2: 96\text{ individuos} \\ \text{Genotipo }A_2A_2: 52\text{ individuos} \end{cases} \]

Determine si la población se encuentra segregando el locus acorde a lo esperado bajo equilibrio de Hardy-Weinberg. De no ser así, estime el valor del coeficiente de fijación (\(F\)).

Solución

Se puede estimar las frecuencias alélicas \(p\) y \(q\) a partir de los conteos genotípicos presentados.

Tenemos que

\[ \begin{cases} p = f(A_1A_1) + (\frac{1}{2})f(A_1A_2) = \frac{102}{250} + (\frac{1}{2})(\frac{96}{250}) = 0,6 \\ q = 1-p \Rightarrow q = 0,4 \end{cases} \]

Para estas frecuencia alélicas se esperan las siguientes frecuencias genotípicas (y conteos en una población de \(N = 250\) individuos):

\(\text{Genotipo}\)	\(\text{Frecuencia esperada}\)	\(\text{Conteo esperado }(N = 250)\)
\(A_1A_1\)	\(0,36\ (0.6^2)\)	\(90\ (0,36 \cdot 250)\)
\(A_1A_2\)	\(0,48\ (2\cdot0,6\cdot0,4)\)	\(120\ (0,48 \cdot 250)\)
\(A_2A_2\)	\(0,16\ (0,4^2)\)	\(40\ (0,16 \cdot 250)\)

Realizando un test de \(\chi^2\) con los conteos obtenidos, podemos establecer si las desviaciones observadas son estadísticamente significativas (en cuyo caso queda refutada la hipótesis nula de segregación en equilibrio de Hardy-Weinberg).

Recordando que \(\chi^2 = \sum_{i=1}^{i=n} \frac{(\text{obs.} - \text{esp.})^2}{\text{esp.}}\) , tenemos entonces \(\chi^2 = \frac{(102-90)^2}{90} + \frac{(96-120)^2}{120} + \frac{(52-40)^2}{40} = 10\). Considerando 1 grado de libertad, tal desviación respecto de los valores esperados se espera observar con una probabilidad \(<0.01\) según la distribución de \(\chi^2\) . Por lo tanto, se rechaza la hipótesis nula, según la cual el locus se encuentra segregando acorde a las esperado bajo equilibrio de Hardy-Weinberg. Podemos estimar el coeficiente de fijación a partir de la desviación observada en la frecuencia de heterocigotas, considerando que \(H_{obs} = 2pq(1-F) \Rightarrow F = 1 - \frac{H_{obs}}{2pq}\). Reemplazando con los valores correspondientes, tenemos \(F = 1 - \frac{96/250}{2 \cdot 0,6 \cdot 0,4} = 0.2\), siendo esta nuestra estimación para el coeficiente de fijación.

Ejercicio 2.2

Como ya se ha planteado en este capítulo, existen varias situaciones donde las asunciones del modelo Wright-Fisher no se cumplen. La noción de tamaño poblacional efectivo (\(N_e\)) resulta sumamente útil en algunos de estos casos: en lugar de derivar un modelo teórico alternativo, se compara el comportamiento observado en el caso de estudio con el de una población ideal que sí cumple con las asunciones del modelo (y posee este tamaño poblacional).

a. Demuestre que el tamaño poblacional efectivo de una población dioica (con dos sexos), con posible desbalance en la proporción de sexos, equivale a \(N_e=\frac{4N_mN_h}{N_m + N_h}\).

[Pista: bajo el modelo de Wright-Fisher la probabilidad de que dos alelos sean idénticos por ascendencia no tiene en cuenta la procedencia del alelo (es decir, si el alelo fue aportado a la generación por un macho o una hembra). En una población de organismos diploides dioicos esto debe tenerse en cuenta, ya que todos los organismos de la generación están formados por un gameto masculino y uno femenino.]

b. ¿Cuál es el \(N_e\) esperado para un locus asociado al cromosoma \(X\)?

c. ¿Cuál es el \(N_e\) esperado para un locus mitocondrial? Tenga en cuenta que las mitocondrias son heredadas de forma exclusiva por línea materna.

Solución

a. En una población ideal la probabilidad de que dos alelos tomados al azar en una población sean idénticos por ascendencia es de \(\frac{1}{2N}\); por lo tanto, en una población de tamaño poblacional efectivo \(N_e\) que se comporte acorde al modelo de Wright-Fisher esta probabilidad es de \(\frac{1}{2N_e}\). Vayamos ahora al caso de una población diploide dioica, compuesta por \(N_m\) machos y \(N_h\) hembras (o los sexos análogos según el sistema de definición de sexos de la especie).

¿Cual es la probabilidad de que dos alelos tomados al azar sean idénticos por ascendencia? Notemos que en este caso los organismos de cada generación no se forman tomando completamente al azar dos gametos de la generación anterior: por definición, cada organismo se conforma muestreando al azar un gameto aportado por un macho y uno aportado por una hembra. Por lo tanto, dos alelos tomados al azar de una generación pueden ser idénticos por ascendencia según dos eventos disjuntos: i) se muestrearon dos alelos aportados por un mismo macho de la generación anterior, o ii) se muestrearon dos alelos aportados por una misma hembra de la generación anterior. Por cómo están conformados los organismos (un alelo aportado por cada sexo), la probabilidad de muestrear dos alelos aportados por un organismo del mismo sexo en la generación anterior es de \(\frac{1}{2} \cdot \frac{1}{2} = (\frac{1}{4})\) . En este punto, la probabilidad de que el alelo muestreado sea el mismo en cada caso se obtiene con un razonamiento análogo al planteado cuando se desarrolló el modelo teórico: la probabilidad de que se trate del mismo alelo es o bien \(\frac{1}{2N_m}\) (si los alelos fueron aportados por un macho), o bien \(\frac{1}{2N_h}\) (si fueron aportados por una hembra). Estos son eventos disjuntos, por lo que las probabilidades deben ser sumadas para contemplar todos los casos de interés. -Dado que buscamos encontrar el tamaño poblacional efectivo \(N_e\) tal que lo observado en la población se ajuste a lo esperado idealmente bajo el modelo de Wright-Fisher, tenemos que esta probabilidad y la del modelo teórico deben ser iguales cuando se asigna este tamaño poblacional:

\[ \frac{1}{2N_e} = (\frac{1}{4}) \cdot \frac{1}{2N_m} + (\frac{1}{4}) \cdot \frac{1}{2N_h} \]

\[ \frac{1}{2 N_e} = \frac{N_h + N_m}{4 \cdot 2 \cdot N_m \cdot N_h} \]

\[ \frac{1}{N_e} = \frac{N_h + N_m}{4 N_m N_h} \Rightarrow \therefore N_e = \frac{4N_mN_h}{N_m + N_h} \]

b. Se puede aproximar el problema siguendo una lógica similar a la planteada para el caso anterior. Debe tenerse en cuenta, no obstante, que en este caso los dos sexos aportan de alelos de forma desigual en la población: \(\frac{1}{3}\) de los alelos son aportados por machos, y \(\frac{2}{3}\) de los alelos son aportados por las hembras. La probabilidad de muestrear en la población dos alelos provenientes de un macho es por lo tanto \((\frac{1}{3}) \cdot (\frac{1}{3}) = \frac{1}{9}\); la probabilidad de que a su vez se trate del mismo alelo en este caso es de \(\frac{1}{N_m}\) (dado que los machos solo aportan \(N_m\) alelos). Análogamente, la probabilidad de muestrear dos alelos aportados por una hembra es de \((\frac{2}{3}) \cdot (\frac{2}{3}) = (\frac{4}{9})\); que se trate del mismo alelo es un evento de probabilidad \(\frac{1}{2N_h}\) (dado que las hembras aportan \(2N_h\) alelos).

Por lo tanto, tenemos en este caso

\[ \frac{1}{2N_e} = (\frac{1}{9}) \cdot \frac{1}{N_m} + (\frac{4}{9}) \cdot \frac{1}{2N_h} \]

\[ \frac{1}{2 \cdot N_e} = \frac{2 N_h + 4N_m}{9 \cdot 2 \cdot N_m \cdot N_h} \]

\[ \frac{1}{N_e} = \frac{2 N_h + 4N_m}{9 \cdot N_m \cdot N_h} \Rightarrow \therefore N_e = \frac{9N_mN_h}{4N_m + 2N_h} \]

Nótese que la ecuación refleja la disparidad que tiene el número de individuos de cada sexo para los locus ligados al cromosoma \(X\): una población de \(N = 10\) con \(N_m = 9\) y \(N_h = 1\) se comportará acorde a lo esperado para un tamaño poblacional de \(N_e = \frac{81}{38} \approx 2\), mientra que una población con \(N_m = 1\) y \(N_h = 9\) se comportará como una población de tamaño \(N_e = \frac{81}{22} \approx 4\) , cerca del doble de tamaño.

c. Dado que todo locus mitocondrial es heredado por línea materna, la probabilidad de que dos alelos sean idénticos por ascendencia es de \(\frac{1}{N_h}\). Si asumimos paradidad en el número de sexos (i.e. \(N_h = \frac{N}{2}\)), tenemos que

\[ \frac{1}{2N_e} = \frac{1}{N_h} = \frac{1}{(N/2)} = \frac{2}{N} \]

\[ \frac{1}{N_e} = \frac{4}{N}\Rightarrow \therefore N_e = \frac{N}{4} \]

Por lo tanto, un locus mitocondrial segrega acorde a lo esperado por el modelo de Wright-Fisher para un locus diploide en una población de tamaño cuatro veces menor a la población considerada.

Ejercicio 3.6

[Inspirado en una acotación de “Applied Population Genetics”, de Rodney J. Dyer (disponible en https://dyerlab.github.io/applied_population_genetics/index.html).] Los organismos del orden de insectos Hymenoptera (e.g. abejas, avispas u hormigas, entre otros) presentan un sistema de ploidía mixto: las hembras son diploides, mientras que los machos son haploides.

Considere una població de abejas, compuesta por 10000 machos y una hembra. En un momento dado se observa para un locus segregando en la población una heterocigosidad \(H_0\) de 0,476. ¿Cuál es la heterocigosidad esperada luego de 25 generaciones? Asuma, por simplicidad, que todos los machos pueden reproducirse con la abeja reina.

Solución

Notemos que el esquema de ploidías planteado para himenopteros es prácticamente idéntico al planteado para locus ligados al cromosoma \(X\) en humanos (uno de los sexos es diploide para el locus considerado, mientras que el otro es haploide). Por lo tanto, se espera que el locus segregue acorde a las expectativas de un locus diploide que se comporte según el modelo de Wright-Fisher con el siguiente tamaño poblacional efectivo (ver Ejercicio 3.5, donde se deriva la fórmula para \(N_e\) en estos casos):

\[ N_e = \frac{9N_mN_h}{4N_m + 2N_h} \]

\[ N_e = \frac{9 \cdot 10000 \cdot 1}{(4 \cdot 10000) + (2 \cdot 1)} \Rightarrow N_e \approx 2,250 \]

(increíble, ¿no?).

Sabemos a su vez que \(H_t \approx H_0 \cdot e^{\frac{-t}{2N_e}}\), por lo que se espera observar luego de 20 generaciones, en promedio, la siguiente heterocigosidad:

\[ H_t \approx 0,476 \cdot e^{\frac{-20}{2 \cdot 2,25}} \approx 0,00872 \]

Esto equivale a una reducción de la heterocigosidad a menos del \(2\%\) del valor inicial. Mantener en mente que estos cálculos solo tienen en cuenta el efecto esperado de la deriva genética sobre la frecuencia esperada de heterocigotas (además de la simplificación sobre el modo de reproducción de la especie). Por lo tanto, el cálculo no necesariamente refleja la variabilidad genética observada en poblaciones reales, donde también es esperable juegue un rol la acción de otras fuerzas evolutivas.

Ejercicio 3.7

Considerando el coeficiente de fijación \(F\), se tiene que la expectativa para la frecuencia de heterocigotas para un locus bi-alélico (alelos \(A_1\) y \(A_2\) con frecuencias \(p\) y \(q\), respectivamente) en una población de tamaño finito corresponde a \(H=2p q(1-F)\). Demuestre que las frecuencias esperadas para los genotipos homocigotas.

Solución

Recordemos que las frecuencias alélicas se vinculan a las frecuencias genotípicas según

\[ \begin{cases} p = f(A_1A_1) + \frac{1}{2}f(A_1A_2) \\ q = f(A_2A_2) + \frac{1}{2}f(A_2A_2) \end{cases} \]

Por lo tanto, tenemos que \(f(A_1A_1)=p-\frac{1}{2}f(A_1A_2)\) y \(f(A_2A_2)=q-\frac{1}{2}f(A_1A_2)\) . Dado que \(f(A_1A_2)=2pq(1-F)\) , tenemos entonces

\[ f(A_1A_1) = p - 2(\frac{1}{2})pq(1-F) \]

\[ f(A_1A_1) = p - p(1-p)(1-F) \]

\[ f(A_1A_1) = p -(p-pF-p^2+p^2F) \]

\[ f(A_1A_1) = p-p+pF+p^2-p^2F \]

\[ f(A_1A_1) = p^2(1-F) + pF \]

Análogamente, tenemos

\[ f(A_2A_2) = q - 2\frac{1}{2}pq(1-F) \]

\[ f(A_2A_2) = q - (1-q) q(1-F) \]

\[ f(A_2A_2) = q - (q-qF-q^2+q^2F) \]

\[ f(A_2A_2) = q -q + qF+q^2-q^2F \]

\[ f(A_2A_2) = q^2 (1-F) + qF \]

Vemos entonces que todas las frecuencias genotípicas son corregidas por un factor de corrección de \((1-F)\) respecto a lo esperado bajo equilibrio de Hardy-Weinberg, pero en el caso de los genotipos homocigotas se suma a su vez un factor de \(pF\) o \(qF\) (según el genotipo), correspondiente al aumento esperado en la frecuencia de homocigotas.

Ejercicio 3.8

Como se mencionó en este capítulo, el tiempo medio transcurrido hasta la fijación o pérdida de un alelo está dado por la ecuación

\[ \bar{t} = -4N[p \cdot ln(p) + (1-p) \cdot ln(1-p)] \]

donde \(N\) es el tamaño poblacional y \(p\) la frecuencia del alelo considerado.

La gráfica de ésta función sugiere un máximo en \(p=\frac{1}{2}\). Demuestre que esto es cierto.

Solución

Notemos que el máximo para la función se da cuando su derivada primera respecto a \(p\) equivale a cero. Tenemos entonces

\[ \frac{\delta \bar{t}}{\delta p} = 0 \Rightarrow \frac{\delta [-4N[p \cdot ln(p) + (1-p) \cdot ln(1-p)]]}{\delta p} =0 \]

Dado que \(-4N\) es consante respecto a \(p\), esto equivale a considerar

\[ \frac{\delta [p \cdot ln(p) + (1-p) \cdot ln(1-p)]}{\delta p} = \frac{\delta[p \cdot ln(p)]}{\delta p} + \frac{\delta [(1-p) \cdot ln(1-p)]}{\delta p} = 0\]

El primero de estos términos equivale a \(\frac{\delta p}{\delta p} \cdot ln(p) + p \cdot \frac{\delta ln(p)}{\delta p}\) ; recordando que \(\frac{\delta ln(f(x))}{\delta x} = \frac{\delta f(x)}{\delta x} \cdot \frac{1}{f(x)}\) (lo cual utilizaremos también al desarrollar el segundo término), tenemos que

\[\frac{\delta p \cdot ln(p)}{\delta p} = ln (p) + p \cdot \frac{1}{p} = ln(p) + 1\] de forma similar, tenemos

\[ \frac{\delta [(1-p) \cdot ln (1-p)]}{\delta p} = \frac{\delta [(1-p) ]}{\delta p} \cdot ln (1-p) + (1-p) \cdot \frac{\delta ln(1-p)}{\delta p} = -1 \cdot ln(1-p) + (1-p)\cdot -1\frac{1}{(1-p)} \]

por lo que

\[ \frac{\delta [(1-p) \cdot ln (1-p)]}{\delta p} = -ln(1-p) -1 \]

Combinando ambos resultados, tenemos

\[ \frac{\delta [p \cdot ln(p) + (1-p) \cdot ln(1-p)]}{\delta p} = ln(p) + 1 -ln(1-p) -1 = 0 \]

\[ ln(p) - ln(1-p) = 0 \Rightarrow ln(p) = ln (1-p) \]

\[ p = 1-p \Rightarrow 2p =1 \therefore p = \frac{1}{2} \]

con lo que queda demostrado que el máximo valor para \(\bar{t}\) ocurre cuando \(p=\frac{1}{2}\) .

---

Bibliografía

Charlesworth, Brian, Russel Lande, and Montgomery Slatkin. 1982. “A Neo-Darwinian Commentary on Macro Evolution.” Evolution 36 (3): 474–98.

Denny, Mark, and Steven Gaines. 2000. Chance in Biology: Using Probability to Explore Nature. Princeton University Press.

Felsenstein, Joseph. 2004. Inferring Phylogenies. Sinauer Associates, Inc.

Grandi, M. Florencia, Larissa R. de Oliveira, Silvana L. Dans, and Enrique A. Crespo. 2012. “A Hunted Population in Recovery: Effective Population Size for South American Sea Lions from Patagonia.” Animal Biology 62 (4): 433–50. https://doi.org/https://doi.org/10.1163/157075612X642941.

Hamilton, Matthew B. 2009. Population Genetics. Wiley-Blackwell.

Hartl, Daniel L, and Andrew G Clark. 2007. Principles of Population Genetics. 4th. ed. Sinauer.

Kimura, M. 1962. “On the probability of fixation of mutant genes in a population.” Genetics 47 (June): 713–19.

Kimura, M., and T. Ohta. 1969. “The Average Number of Generations until Fixation of a Mutant Gene in a Finite Population.” Genetics 61 (3): 763–71.

Kingman, JFC. 1982a. “On the Genealogy of Large Populations.” Journal of Applied Probability 19A: 27–43.

———. 1982b. “The Coalescent.” Stochastic Processes and Their Applications 13: 235–48.

Rosenberg, N. A., and M. Nordborg. 2002. “Genealogical trees, coalescent theory and the analysis of genetic polymorphisms.” Nat Rev Genet 3 (5): 380–90.

Tagliani-Ribeiro, A., M. Oliveira, A. K. Sassi, M. R. Rodrigues, M. Zagonel-Oliveira, G. Steinman, U. Matte, N. J. Fagundes, and L. Schuler-Faccini. 2011. “Twin Town in South Brazil: a Nazi’s experiment or a genetic founder effect?” PLoS One 6 (6): e20328.

Tajima, F. 1983. “Evolutionary Relationship of DNA Sequences in Finite Populations.” Genetics 105 (2): 437–60.

Walsh, Bruce, and Michael Lynch. 2018. Evolution and Selection of Quantitative Traits. Oxford University Press.

Wright, Sewall. 1922. “Coefficients of inbreeding and relationship.” American Naturalist 56: 330–38.

---

32. Gregor Mendel (20 de julio 1822 - 6 de enero de 1884) fue un meteorólogo, biólogo y matemático, nacido en Heizendorf bei Odrau, Imperio Austro-Húngaro (hoy República Checa). Considerado el padre de la “genética moderna”, realizó diversos experimentos con plantas que lo llevaron a postular algunas “leyes”, decenas de años antes de conocerse las bases moleculares de la herencia.↩︎

33. Obviamente, habríamos llegado a lo mismo sabiendo que \(p_{azul}+p_{roja}=1 \therefore p_{roja}=1-p_{azul}=1-\frac{1}{2}=\frac{1}{2}\).↩︎

34. Recordemos que \(\prod_a^b\) simboliza a la productoria de \(a\) a \(b\). Esta operación es análoga a la sumatoria, pero en lugar de calcularse la suma de los números entre \(a\) y \(b\), se considera el producto de estos números. A modo de ejemplo, \(\prod_1^5 = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5\).↩︎

35. Sewall Green Wright (21 de diciembre, 1889 - 3 marzo, 1988), fue un genetista que realizó notables aportes sobre los efectos de la selección y la deriva, así como el análisis de pequeñas poblaciones y el efecto de la consanguinidad . Junto a Ronald A. Fisher y JBS Haldane establecieron la fundación matemática de la genética de poblaciones y de la teoría evolutiva.↩︎

36. Sir Ronald Aylmer Fisher (17 de febrero 1890 - 29 de julio 1962) fue un matemático, estadístico y biológo evolutivo inglés. A partir de los datos colectados en la Estación Experimental de Rothamsted desarrollo las bases estadísticas para el diseño de experimentos, desarrollo también el análisis de varianza y fue unos de los tres pioneros (junto a Sewall Wright y John Burdon Sanderson Haldane) que participaron de la fundación de la teoría en genética de poblaciones, el neo-darwinismo y la síntesis moderna de la evolución.↩︎

37. Jacob Bernoulli (6 de enero 1655 - 16 de agosto 1705) fue un matemático Suizo que realizó diversos descubrimientos importante y uno de promotores tempranos del cálculo integral. Miembro de las academias reales de París y Berlín, la distribución lleva su nombre en homenaje a sus contribuciones.↩︎

38. Notar que se utiliza el símbolo \(G\) para denotar al conjunto de genotipos homocigotos, como en la sección Tres o más alelos del capítulo anterior.↩︎

39. La persona interesada en el modelado e implicancias de la relación entre mutación y deriva genética puede referirse a la bibliografía de referencia, donde suele tratarse dicho tema. A lo largo de este capítulo se deja este aspecto de lado, a efectos de simplificar el análisis y hacer foco en el fenómeno de la deriva genética.↩︎

40. Esta operación matemática puede resultar arbitraria. ¿Por qué haríamos esto? ¿Existe algún razonamiento biológico que de sustento a la maniobra? Notemos que \((1 - F_t)\) es la probabilidad de que dos alelos no sean idénticos por ascendencia en el tiempo \(t\). Por lo tanto, la utilización de esta maniobra matemática simplifica los cálculos, pero además puede ser vista como un intento de resolver el problema planteandoló desde una óptica biológica “complementaria”. Si resolvemos qué sucede con la probabilidad de que dos alelos no sean idénticos por ascendencia, automáticamente resolvemos qué sucede con la probabildad de que si lo sean, por ser estos eventos disjuntos. La relación entre \(F\) y desviación de la heterocigosidad esperada es analizada más adelante en este capítulo.↩︎

41. Notemos que las probabilidades de transición entre estados no cambian con el paso del tiempo; formalmente decimos que se trata de una cadena de Markov homogénea o estacionaria en el tiempo. En el siguiente párrafo se ahonda en el concepto de cadena de Markov.↩︎

42. Andrey Andreyevich Markov (14 de junio 1856 – 20 de julio 1922) fue un matemático ruso, ampliamente conocido por sus trabajos en procesos estocásticos.↩︎

43. El/la lector/a puede referirse al Apéndice correspondiente a álgebra matricial para más información sobre productos matriciales↩︎

44. Debido al matemático soviético Andrey Nikolaevich Kolmogorov (25 April 1903 - 20 October 1987). Si bien la ecuación hacia atrás (Kolmogorov Backward Equation) fue un aporte completamente novedoso, la ecuación hacia adelante ya era conocida para los físicos como la ecuación de Fokker-Planck.↩︎

45. Recordemos que \(\sum_{i=1}^{i=n}i = \frac{n(n+1)}{2}\); si reemplazamos con \(n=k-1\) llegamos al resultado mencionado.↩︎