Capítulo 8 El modelo genético básico

En la última parte de nuestro curso nos enfocaremos en la Genética Cuantitativa, es decir, la genética de características que en principio son cuantificables. En general, a nivel agronómico, la mayor parte de las características que deseamos mejorar son de este tipo y por eso la importancia en nuestro curso. Ejemplos de las mismas que han experimentado un “avance” sostenido durante el siglo XX, avance mayormente determinado por la selección artificial, lo constituyen la producción de leche en bovinos, el tamaño de “pollos parrilleros”, la concentración de proteína y grasa en la leche, la producción de la mayor parte de los cultivares y casi todas las características que han mostrado cierta respuesta a la selección.

A diferencia de los modelos que hemos utilizado en la Parte II, en general el modelo de un locus con dos alelos no alcanzará para explicar la variación cuantitativa observada, y deberemos construir modelos más generales, con menos detalle al nivel de locus, pero con mucha mayor capacidad de explicar los aportes de las distintas componentes que afectan la expresión de una característica. En general, vamos a trabajar asumiendo que el fenotipo observado de una característica se encuentra explicado por los aportes de la genética del individuo y su ambiente, así como por la interacción de la genética y el ambiente. Más aún, pasaremos de modelos centrados en el individuo, para los que era necesario conocer la configuración genética y ambiental completa, a pensar en los individuos como integrantes de poblaciones, que tienen una distribución aleatoria particular, y por lo tanto nos enfocaremos en hacer predicciones sobre los mismos y su descendencia. Como notarás rápidamente, esta última parte del curso recurrirá a un tratamiento estadístico de la mayor parte de los problemas, y por lo tanto es necesario tener frescos los conceptos de distribuciones, esperanzas, varianzas, momentos, correlación y regresión, entre otros. Si bien existen diferentes materiales que explican mejor o complementan lo escrito por nosotros, gran parte de lo que trabajaremos en esta última parte del curso está basado en el libro de Falconer y Mackay (Douglas S. Falconer and Mackay 1996) (o en la vieja versión en castellano (Douglas S. Falconer 1983)), que sigue siendo una referencia hoy en día. Un excelente complemento se encuentra en el libro de Lynch y Walsh (Michael Lynch and Walsh 1998), aunque el nivel de profundidad es bastante mayor.

Todos somos capaces de observar a diario que más allá de la similitud que presentan determinados organismos cuando los comparamos con otros muy diferentes (e.g., de otra especie), la misma es bastante parcial, y reconocemos fácilmente que ningún ser vivo es exactamente igual a otro ser vivo. Esto nos lleva a intentar entender la base de la similitud y de las diferencias entre organismos. Al mismo tiempo que (en general) somos capaces de distinguir claramente entre hermanos/as, también reconocemos que cada uno/a se parece más a un progenitor que a otro; lo que es más, en general se parecen más a alguno de sus progenitores que al resto de las personas del barrio. Además, desde los experimentos de Gregor Mendel, hemos venido confirmando la base genética de muchas características, y aún somos capaces de predecir razonablemente bien cómo será la descendencia de determinada pareja de progenitores. Sin duda esto es posible para características discretas gobernadas por un locus (o a lo sumo muy pocos loci): si se tiene la información referente a los distintos alelos existentes, esta tarea es un ejercicio bastante sencillo. Sin embargo, cuando las características presentan variación contínua (por ejemplo, pesos, alturas, producción de leche, volumen, etc.) el sencillo modelo mendeliano básico ya no puede dar cuenta de las diferencias observadas y necesitamos construir un modelo que tenga en cuenta tanto los aspectos genéticos como los efectos ambientales que afectan la expresión de la característica estudiada.

En el presente capítulo vamos a elaborar un modelo que nos permita interpretar la variabilidad fenotípica (es decir, lo observable) a la luz de los componentes genéticos y ambientales que la afectan. Para ello, primero introduciremos el tema de los tipos de variación, continua y discreta, así como el hecho de que la suma de diferentes (muchas) variables aleatorias produce una variación casi-continua (lo que se conoce como el teorema del límite central). Esto a su vez nos permitirá vincular el modelo mendeliano de herencia con los enfoques biométricos de la misma, lo que fue un hito en la construcción de la síntesis Darwiniana, permitiendo resolver varias contradicciones de ambos enfoques previos. Más aún, esto será la base del modelo infinitesimal, que supone que las características continuas pueden consistir de la suma infinitesimal de los aportes de un número infinito de loci. Si bien totalmente incorrecto a la luz de nuestro conocimiento (el tamaño del genoma es finito), este enfoque permite construir modelos sencillos pero de gran poder predictivo y para la comprensión de los fenómenos subyacentes.

A partir de nuestro modelo genético básico, que asume que el fenotipo de cualquier individuo es la suma de los efectos genéticos y ambientales en el mismo, más la interacción entre ambos tipos de efectos, iremos disgregando tanto los efectos genético como los ambientales en componentes que nos permitan entender sus interrelaciones. Veremos que podemos descomponer los efectos genéticos en i) efectos de carácter aditivo (i.e., que se puede sumar directamente el efecto de cada alelo presente en el individuo), ii) los desvíos de la aditividad de la combinación particular de alelos que tiene cada genotipo, que llamaremos desvío de dominancia, y finalmente iii) los desvíos de interacción de los efectos entre diferentes loci, que llamaremos efectos epistáticos. Además, para los efectos aditivos y de dominancia, analizaremos en detalle el modelo de un gen de efecto mayor, donde una característica está básicamente gobernada por un solo gen con dos alelos. Finalmente, extenderemos nuestros análisis al nivel de las poblaciones, buscando entender la importancia relativa de las distintas componentes a partir de las varianzas que generan las mismas.

OBJETIVOS DEL CAPÍTULO

\(\square\) Introducir el marco conceptual de la genética cuantiativa.

\(\square\) Presentar el modelo matemático con el que trabajaremos en capítulos posteriores: el modelo genético básico.

\(\square\) Discutir resultados obtenidos al aplicar el modelo al caso de un locus con dos alelos.

\(\square\) Introducir los conceptos de efecto medio, valor reproductivo y desvío de dominancia.

\(\square\) Tener una primera aproximación a un problema complejo: analizar la interaccioń entre genotipo y ambiente.

\(\square\) Descomponer la varianza genética para poder analizar el aporte relativo de las fuentes que generan dicha variación.

8.1 Variación continua y discreta

Hasta el momento hemos basado todo el desarrollo del curso casi exclusivamente en razonamientos obtenidos a partir de un locus o de un par de loci con dos alelos. En organismos haploides, suponiendo que el efecto de cada alelo sea constante en un determinado momento en el tiempo (i.e., que no dependa de otros factores), apenas se pueden tener dos genotipos distintos, y poco cambia la situación el que los organismos sean diploides (donde aparecen tres genotipos posibles). Cuando el tipo de característica que analizamos es categórica, por ejemplo el color verde o amarillo de los guisantes de Mendel (Pisum sativum), todo los resultados entran en alguna de las categorías permitidas o definidas, y entonces mientras el número de categorías sea menor o igual al número de genotipos tenemos alguna esperanza de vincular el genotipo con el fenotipo. Es decir, si las categorías son “verde” y “amarillo”, es porque asumimos que las pequeñas variaciones de color son irrelevantes para nosotros o sencillamente no existen (cosa que parece totalmente improbable) y solo tenemos que asociar algún (o algunos) genotipos con un color y el resto con el otro. Claramente, en un locus diploide con dos alelos podemos encontrar como máximo tres genotipos, por lo que podría codificarse un nuevo color de guisantes tan extraño como el “tan” (sí, es un color), o un color intermedio entre el verde y el amarillo; las diferencias entre estas alternativas están en la base bioquímica del color, pero no existe en nuestro modelo una imposibilidad matemática para codificar estos genotipos. Sin embargo, cuando la paleta de colores de nuestros guisantes hipotéticos es un poco más amplia (e.g., 14 colores), comienza a existir una imposibilidad para describirla directamente con un mapeo unívoco de genotipos a colores. Dicho de otra forma, cada genotipo debería estar asociado a más de un color, lo que implica involucrar otros tipos de factores, ya sean ambientales o genéticos; resulta claro que en último caso, estos factores genéticos se encontrarían fuera del locus estudiado. Pese a ello, seguimos frente a un tipo de variación categórica, ya que nuestra paleta de colores tiene un número finito de colores, y no tendría sentido en este contexto hablar de matemático la distancia entre esos colores.

Claramente esto podemos “arreglarlo” invocando otros loci, o sencillamente colocando más alelos en nuestro locus original; si suponemos además que cada combinación de dos alelos produce un color diferente, entonces con \(k\) alelos podemos formar \(n=k(k+1)/2\) genotipos diploides distintos (incluyendo los homocigotos). Por ejemplo, con \(k=5\) alelos podemos formar \(n=5(5+1)/2=15\) genotipos diferentes, los cuales nos permitirían codificar esos 14 colores, sobrando incluso la capacidad de acomodar uno nuevo. Todo esto es apenas una disgresión acerca de las posibilidades matemáticas de nuestros modelos, pero obviamente la base bioquímica y molecular de la herencia del color será la que mande, y nuestro modelo deberá ser capaz de representar esa realidad.

Otro tipo de variables de interés agronómico y biológico suelen producir resultados que son contables pero que, ahora sí, tiene sentido plantear y analizar las distancias entre las observaciones involucradas. Por ejemplo, el número de granos de maíz en una mazorca es en principio cuantificable, y si una mazorca produce 483 granos y otra 497, puede calcularse la diferencia como \(497-483=14\) granos. Claramente, no podía realizar esta operación con los colores, al menos como los definimos previamente en categorías⁷⁹. A las características que tienen este tipo de variación se les llama a veces merísticas. Poseen una distribución discreta, en contraposición a continua; son además del tipo de variables cuyo resultado se obtiene de contar el número de elementos que hay en ellas y que los mismos (los elementos) siguen un ordenamiento natural, donde la “distancia” entre elementos tiene sentido. Como vimos más arriba, en principio alcanzaría con \(k=\frac{-1+\sqrt{1+8n}}{2}\) (el resultado de resolver la ecuación \(n=k(k+1)/2\)) alelos en un locus para codificar todas las \(n\) categorías posibles de una característica discreta como el color. Sin embargo, esto tiene poco sentido en variables discretas donde cada combinación (genotipo) debería acomodarse en el ordenamiento discreto posible. Por ejemplo, para acomodar la posibilidad de tener entre 1 y 528 granos por mazorca alcanzaría en un locus diploide con 32 alelos, pero sus combinaciones deberían de alguna manera tener un ordenamiento lógico (a nivel bioquímico) que se traduzca en conteos del 1 al 528.

Una alternativa más razonable parece ser invocar más loci y asumir, en principio, que los efectos de los alelos son aditivos (i.e., se pueden sumar), tanto dentro de cada locus como entre loci. En la Figura 8.1 podemos ver el resultado de una simulación particular de este modelo, para un solo locus (izquierda arriba), así como para 5, 10 y 50 loci en un gen de organismos diploide, con dos alelos en cada loci y frecuencias de \(p=q=\frac{1}{2}\) en cada uno. Para cada situación se simularon los valores de \(100.000\) individuos, suponiendo además que cada copia de uno de los dos alelos suma una unidad (1) a la característica, mientras que el otro alelo no suma nada (0).

Claramente, con 1 locus solo hay 3 genotipos posibles, es decir 0, 1 o 2 copias del alelo que suma una unidad, y por lo tanto los valores posibles son 0, 1 y 2. Con 5 loci tenemos mucha más variación posible. Primero, los límites se darán cuando se consideren 0 copias del alelo que suma (i.e, valor total 0) para el valor mínimo, y como valor máximo para el caso donde en los 5 loci se encuentren en homocigosis las copias que suma (i.e., valor total de \(5 \times2 = 10\) unidades). Pero por otro lado, comenzamos a apreciar un fenómeno interesante: la distribución de los valores no es uniforme, y los valores centrales tienen mayor cantidad de datos (individuos que tienen ese valor genotípico), al tiempo que a medida que se consideran los extremos del rango de valores posibles las barras disminuyen de tamaño (i.e., hay menos individuos que presentan estos valores).

La situación se ve aún más clara cuando tenemos 10 loci. Con la misma cuenta que antes para 5, tenemos que los límites de valores serán 0 cuando el individuo no tenga ningún alelo que aporte valor, a un máximo de 20 (2 copias en los 10 loci). Además, la tendencia sobre la forma de la distribución instalada en la gráfica de 5 loci se ve plenamente confirmada en la gráfica de 10 loci, con la masa concentrada en los valores centrales y disminuyendo hacia los extremos. En la última gráfica, la correspondiente a 50 loci se aprecia otro fenómeno interesante: si bien los límites son ahora de 0 y de 100, ya no apreciamos que ninguna barra se encuentra cerca de esos valores, al menos con \(100.000\) individuos simulados. De hecho, es fácil calcular la probabilidad de cualquiera de los dos eventos extremos en las colas. Por ejemplo, para que el valor de un individuo sea 100 es necesario que los 50 loci sean homocigotos para el alelo que aporta una unidad (y por lo tanto aportan 2 unidades por locus). Asumiendo que los loci se encuentran en equilibrio de Hardy-Weinberg con una probabilidad \(p=q=\frac{1}{2}\), como hemos usado en la Figura 8.1, la probabilidad en un locus de que sea homocigoto para el alelo que aporta una unidad es \(\left(\frac{1}{2}\right)^2=\frac{1}{4}\). Asumiendo que todos los loci son independientes, la probabilidad de que en todos se dé etsa situación es el producto de cada una de las probabilidades, o lo que es lo mismo \(\left(\frac{1}{4}\right)^{50} \approx 7,89\times 10^{-31} \approx 0\). En términos prácticos, ya que apenas hemos muestreado solo 100 mil individuos, resulta claro que es muy remota la posibilidad de observar un individuo con estas características; siendo más exactos, esperamos ver \(\approx 7,89\times 10^{-31} \cdot 100.000 \approx 7,89\times 10^{-26}\) individuos. La otra cosa interesante acerca de esta distribución es que a medida de que aumentamos el número de loci en consideración, también aumenta el número de categorías de valores (barras en el gráfico) y rápidamente el gráfico empieza a insinuar que una línea continua podería ser trazada sin gran pérdida de precisión.

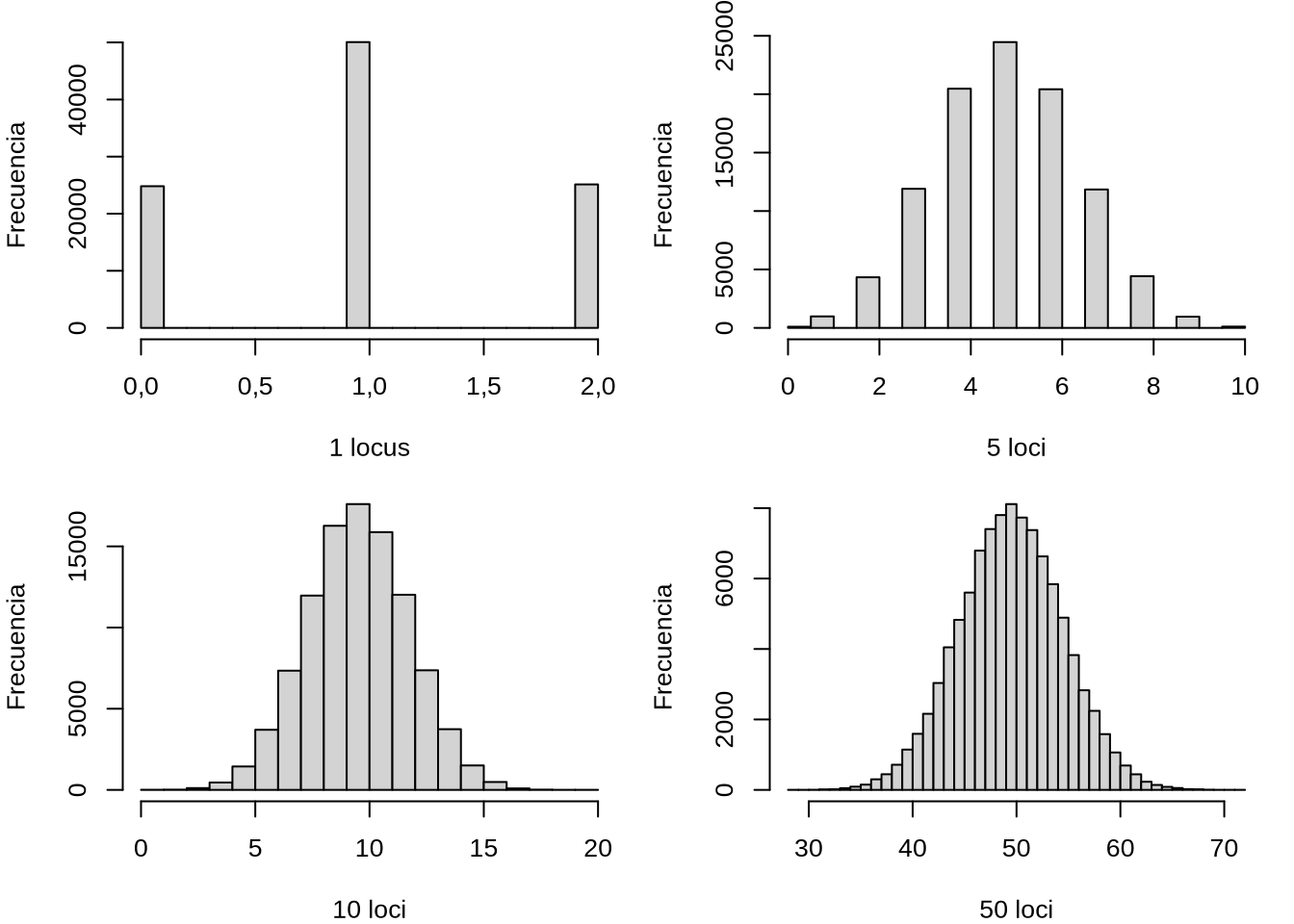
Figura 8.1: Distribución de valores al sumar los efectos de diferente número de loci, De arriba izquierda a abajo derecha, 1 locus, 5 loci, 10 loci y 50 loci. En todos los casos se muestrearon 100.000 individuos en los que cada uno de los loci fueron muestreados independientemente, bajo equilibrio de Hardy-Weinberg y frecuencia de \(p=q=\frac{1}{2}\) y con valores 0, 1, 2 para los tres genotipos.

Más aún, si recuerdas tus cursos de estadística notarás que la forma en la gráfica de 50 loci se asemeja bastante al de una distribución normal. Esto no nos debería sorprender para nada si recordamos el enunciado del teorema del límite central: la suma de variables aleatorias independientes e idénticamente distribuidas tiende a la distribución normal a medida que el número de variables sumadas se incrementa. Es importante tomarse el tiempo necesario para refrescar este concepto, ya que resultará central para este y el resto de los capítulos que conforman el libro.

El fenómeno que describimos anteriormente es mucho más relevante de lo que imaginamos. Durante el comienzo del siglo XX se desarrolló un intenso debate entre la escuela Mendeliana (que enfocaba el problema de la herencia en los términos en los que Mendel había definido el problema de los guisantes) y la escuela biométrica (mucho más enfocada en lo continuo de la variabilidad), ambos manteniendo posiciones irreconciliables sobre los mecanismos de la herencia, que en ese momento eran desconocidos⁸⁰ . Sin embargo, la posibilidad de aproximarse a distribuciones continuas simplemente a partir de la suma de variables discretas genera un puente conceptual entre las dos visiones. Más aún, si a esta variabilidad casi-continua le solapamos el efecto de la variabilidad ambiental, dada la “discretitud” (permítasenos acuñar este término) de las escalas “reglas” con las que usualmente medimos, entonces estamos frente a una situación donde resulta mucho más difícil distinguir si se trata de una variable discreta o continua. Aportes sustantivos en este sentido fueron los realizados por George Udny Yule⁸¹ (Yule 1902) y Wilhelm Johannsen (Johannsen 1903), que fueron fundamentales para los posteriores trabajos que llevaron a la “ley” de Hardy-Weinberg (Castle 1903; Hardy 1908; Weinberg 1908) y que contribuyeron a reconciliar ambas posiciones en lo que luego terminaría siendo la síntesis neo-Darwinista.

Muchas de las características en genética cuantitativa pueden describirse por alguno de los dos tipos de variables que vimos más arriba, discretas y continuas. Algunas otras características, sin embargo, tienen una distribución donde es posible tomar uno solo de unos pocos valores posibles y que los mismos tienen un ordenamiento natural, o que se trata de características del tipo presencia-ausencia. Por ejemplo, en el caso de enfermedades o patologías con cierta base genética, ciertas veces la causa es multifactorial y su base genética es poligénica, es decir, influenciada por muchos genes. En esos casos, también es posible pensar que existe una característica subyacente no observable, que es continua y que al sobrepasar un determinado valor de umbral, entonces la enfermedad se manifiesta. Esta forma de pensar las características y modelarlas, los modelos umbral (Sewall Wright 1934a), puede tener una base molecular y funcional real o puede ser sencillamente un truco adecuado para modelarla, pero el hecho es que suele ser una buena alternativa en mejoramiento genético para varias características (Daniel Gianola 1982).

PARA RECORDAR

• El Teorema del límite central propone que la suma de muchas y diferentes variables aleatorias producen una variación casi contínua.

• El Modelo infinitesimal supone que las características continuas pueden consistir de la suma infinitesimal de los aportes de un número infinito de loci.

• Cuando nos enfrentamos a una variación de tipo categórica (es decir con un número finito y contable de las mismas), donde a su vez asumimos que cada combinación de dos alelos producirá una categoría distinta, con \(k\) alelos podemos formar \(n=k(k+1)/2\) genotipos diploides diferentes (incluyendo los homocigotos).

• Los modelos Umbral se construyen a partir de la suposición de que existe una característica subyacente no observable, que es continua y que al sobrepasar un determinado valor cierta característica se menifiesta.

8.2 El modelo genético básico

En general, para la mayoría de las características que poseen una componente genética en su expresión estamos limitados en un principio a observar su manifestación fenotípica, sin poder acceder a identificar directamente el genotipo de cada individuo. Esto es así, por ejemplo, en las características productivas de interés económico en ganado como el peso en distintos momentos de su vida, la producción de leche, grasa y proteína, pero también en humanos (la altura, el peso, la presión sanguínea) o en plantas. Claramente, lo que observamos puede tener un componente genético, pero también existe en esas observaciones un “ruido” superpuesto. En general, este ruido es imposible de eliminar en este nivel de análisis, y “contamina” nuestras estimaciones sobre el efecto de genes y alelos. Es decir, aún si una característica cuantitativa se encontrara \(100\%\) determinada por los efectos genéticos, las mediciones que realizamos de la misma tienen, de forma ineluctable, un error de medición (como toda medida). Esto nos lleva a considerar que nuestros modelos de lo que observamos deberían incluir, al menos, estos dos factores: el genotipo y los errores de medición. Más en general, el ambiente tiene una influencia importante o determinante en la mayor parte de las características cuantitativas de interés. Si bien todos reconocemos que la altura de los padres es de alguna manera heredable, también todos sabemos que la altura de las poblaciones humanas ha ido aumentando a medida de que el ambiente (alimentación, deportes, hábitos, salud) han ido cambiando, en particular durante el siglo XX. Más directamente vinculado a la producción, todos sabemos que la producción de leche por vaca ha aumentado dramáticamente durante la segunda mitad del siglo XX, en gran parte por el mejoramiento genético, pero sin embargo, aún la misma vaca incorrectamente alimentada apenas producirá una fracción de todo su potencial genético. De hecho, como nosotros en este curso estamos mayormente interesados en la genética, podemos considerar que los errores de medición son a nuestros efectos parte del ambiente. Eso nos lleva a una primera aproximación, algo rústica, para el modelado de los fenotipos. Conisderaremos el fenotipo de cada individuo, al que identificamos con la letra \(P\) (por su nombre en inglés, “phenotype” y para diferenciarlo claramente de la \(F\) que hemos usado para el índice de fijación). El fenotipo es en nuestro modelo la suma de los efectos genéticos (que notamos con \(G\)) y los efectos ambientales (que notamos con \(E\), del inglés “environment”). Tenemos entonces,

\[ \begin{split} P=G+E \end{split} \tag{8.1} \]

A decir verdad, para que quedase más claro el significado de esta ecuación deberíamos escribirla como \(P_i=G_i+E_i\), a efectos de explicitar que se trata de una ecuación correspondiente al individuo \(i\). Sin embargo, como usaremos subíndices para indicar otras cosas, omitiremos el subíndice referente al individuo. Pese a eso, debe quedar claro que las ecuaciones corresponden a un individuo.

El genotipo de un individuo es el arreglo particular de alelos en los distintos loci, ya sea en todos ellos o, al menos, en los relevantes para el estudio realizado. Dependiendo del nivel de sofisticación de nuestro tratamiento necesitaremos conocer también las fases de los mismos, es decir qué alelos de cada loci se encuentran localizados con qué alelos de los otros loci en el mismo cromosoma (heredado por vía materna o paterna). Esto es relevante para poder identificar los haplotipos presentes, aunque generalmente nosotros no vamos a considerar este nivel de análisis. En la Figura 8.2 podemos ver una representación esquemática de una característica que está gobernada (al menos) por dos loci, con al menos dos alelos en cada uno de ellos.

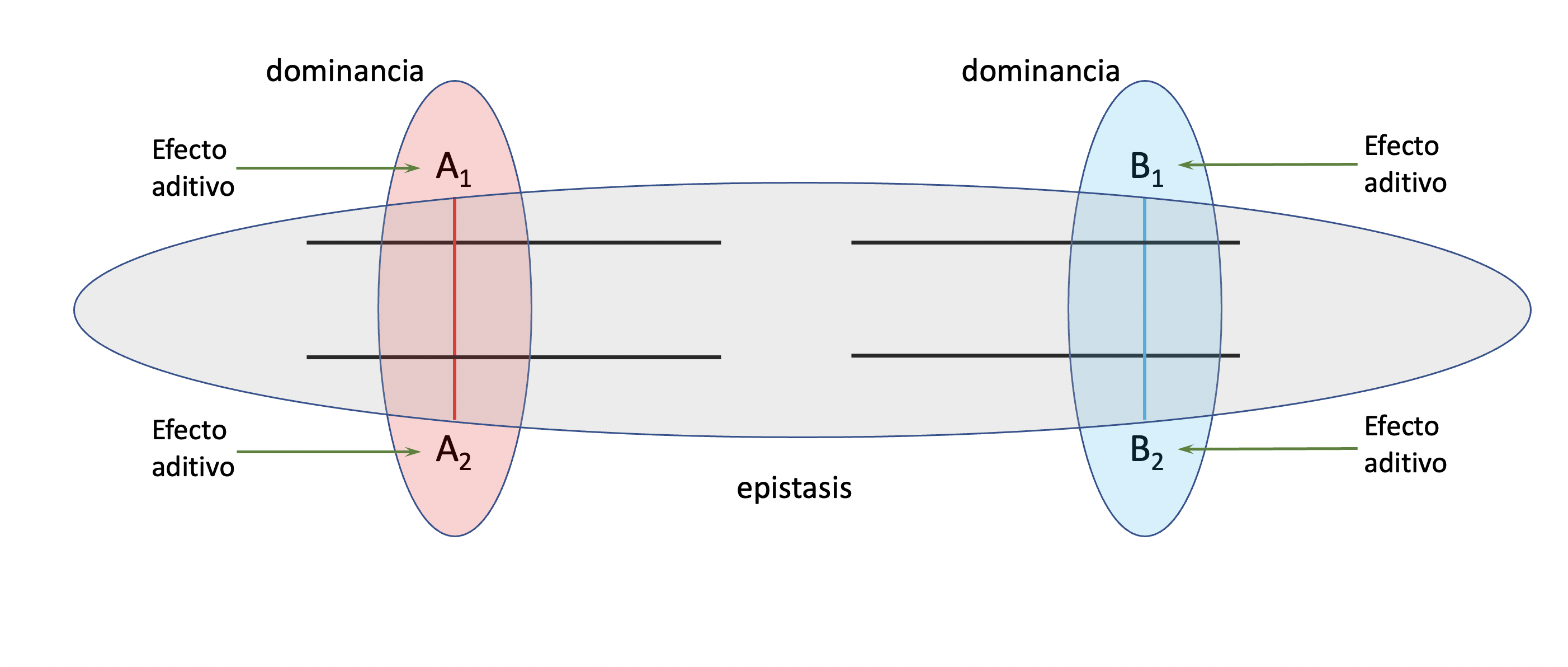
Figura 8.2: Representación esquemática de los efectos genéticos en el modelo genético básico. En dos o más loci con dos o más alelos en cada uno, tenemos los efectos aditivos de cada alelo por separado, que simplemente suman el efecto de cada uno presente (sin importar su combinación), los efectos de dominancia que son los desvíos intra-locus de la aditividad (marcados acá con los óvalos de color rosado y celeste) y finalmente los efectos de epistasis, que son las desviaciones de interacción correspondientes a las diferentes combinaciones inter-loci (el óvalo gris).

Por un lado tenemos el efecto que cada alelo confiere a la característica, independiente de la combinación en que se encuentre, tanto dentro de su locus como considerando lo que hay en otros loci. Llamamos a esto efectos aditivos, ya que como no dependen de combinaciones simplemente podemos sumar el aporte de cada uno de ellos para tener la contribución de todos al valor genotípico y fenotípico. Por ejemplo, para conocer el valor aditivo \(A\) del individuo que aparece representado en la figura alcanza con sumar los efectos de los 2 alelos presentes en cada loci, es decir \(A=A_1+A_2+B_1+B_2\). Notar que los subíndices se refieren a los alelos presentes, y pueden ir en cada locus desde el 1 al número de alelos presentes en el mismo. Siempre sumaremos los efectos de dos alelos por locus, porque siempre hay dos alelos en un locus diploide (pueden ser el mismo, y en ese caso lo sumamos dos veces) y por lo tanto, si definimos \(i=1:2\) el recorrido por los alelos de cada locus y \(n\) el número de loci, entonces tenemos

\[ \begin{split} A=\sum_{i=1,j=1}^{i=2,j=n}A_{i,j} \end{split} \tag{8.2} \]

Pero, como vimos previamente en el capítulo de Selección Natural, el fitness de un individuo heterocigoto no necesariamente tiene que ser el punto medio entre los genotipos homocigotas, por lo que no alcanza con conocer estos dos valores, en general, para poder representar los 3 genotipos. Una forma matemática de acomodar esto es expresando los desvíos de cada genotipo respecto a su valor aditivo (es decir, a la suma de los dos alelos que lo componen) y le llamamos a esto efecto de dominancia, o desvío de dominancia. En el caso de que los valores de todos los genotipos (3 en el caso de dos alelos, \(k(k+1)/2\) en general) sean exactamente iguales a la suma de los alelos que lo conforman, entonces el efecto de dominancia será cero y decimos que el locus tiene un comportamiento aditivo. Muchas son las posibles causas bioquímicas/moleculares que pueden subyacer al efecto de dominancia. Un ejemplo ilustrativo y fácil de comprender es la no-linealidad de la actividad enzimática respecto al número de copias del alelo; dicho de otra forma, dos copias del mismo alelo “ventajoso” no generan el doble de actividad enzimática (e.g., porque la misma muestra saturación), por lo que no existe una relación lineal entre número de copias de ese alelo y el valor genotípico/fenotípico. Puesto en términos matemáticos, como la dominancia es un efecto intra-locus que depende de la combinación específica de alelos en cada uno de los loci, si llamamos \(l\) a la combinación específica que tiene nuestro individuo en cada locus, podemos escribir el efecto total de dominancia como

\[ \begin{split} D=\sum_{j=1}^{n}D_{l,j} \end{split} \tag{8.3} \]

Por otro lado, como se ve en la Figura 8.2, también pueden existir desvíos de los valores de determinadas combinaciones respecto a los efectos aditivos y también a los efectos de los desvíos de dominancia, ya que ninguno de ellos ha considerado las combinaciones de alelos entre loci. A estos desvíos le llamamos epistáticos, y se corresponden a interacciones alélicas inter-génicas. Las causas más usuales a nivel molecular para estos efectos son la pleiotropía y el ligamiento. Estas interacciones pueden ser de muchos tipos, por ejemplo entre dos loci tenemos interacciones de efectos aditivos en un locus con los efectos aditivos del otro, \(I_{AA}\), de los aditivos con los de dominancia, \(I_{AD}\) y de los de dominancia con los de dominancia, \(I_{DD}\). A medida de que aumentamos el número de loci crecen las combinaciones y a fines prácticos agrupamos todos en el término \(I\), es decir

\[ \begin{split} I=I_{AA}+I_{AD}+I_{DD}+I_{AAA}+I_{AAD}+... \end{split} \tag{8.4} \]

Por lo general solo se tienen en cuenta las interacciones entre dos componentes ya que las superiores suelen tener poco efecto en el valor global y en términos prácticos implica estimar una gran cantidad de componentes, lo que los datos no suelen garantizar.

Veamos ahora un ejemplo de dos loci que se comportan en forma aditiva. En el locus \(A\) tenemos dos alelos, con valores \(A_1=2\), \(A_2=-2\), mientras que para el segundo locus, sus alelos aportan \(B_1=1\) y \(B_2=-1\). En el cuadro siguiente tenemos todas las 9 combinaciones posibles de los genotipos en los dos loci y los valores correspondientes, que surgen de sumar los efectos de los alelos presentes en cada uno:

	\(A_1A_1\)	\(A_1A_2\)	\(A_2A_2\)
\({B_1B_1}\)	\(6\)	\(2\)	\(-2\)	\(2\)
\({B_1B_2}\)	\(4\)	\(0\)	\(-4\)	\(0\)
\({B_2B_2}\)	\(2\)	\(-2\)	\(-6\)	\(-2\)
\(\textbf{Promedio}\)	\(4\)	\(0\)	\(-4\)

Como el efecto de ambos genes es aditivo, tanto a nivel de filas como de columnas, el pasaje de una celda a la consiguiente es constante (diferentes constantes en filas que en columnas) y el valor del cambio es igual a la diferencia de valor del alelo que cambia. Por ejemplo, si miramos la primera fila, el pasaje de \(A_1A_1\) a \(A_1A_2\) significa perder una copia de \(A_1\) con valor \(2\) y ganar una de \(A_2\) con valor \(-2\), es decir, el cambio es de \(-2-2=-4\), que es lo que observamos, ya que pasamos de un valor de \(6\) a uno de \(2\) y por lo tanto \(\Delta=2-6=-4\). El mismo valor vamos a obtener en cualquier movida de una celda a su contigua a la derecha, sin importar la fila, al tiempo que si movemos de derecha a izquierda su valor será el opuesto (\(4\)) en este caso. Para las columnas ocurre lo mismo, pero ahora el valor de \(\Delta=-2\) si nos desplazamos a la contigua inferior, mientras que \(\Delta=2\) si nos desplazamos a la contigua superior.

Veamos ahora qué ocurre cuando aparece el efecto de dominancia en uno de los locus. En el cuadro siguiente los efectos aditivos son idénticos que en el cuadro anterior, pero ahora aparece un efecto de dominancia en el locus \(A\). Mientras que si nos movemos verticalmente, es decir cambiamos en el número de copias de los alelos \(B_1\) y \(B_2\), las distancias entre celdas contiguas se mantienen, es decir hay aditividad, si nos movemos en sentido horizontal la situación cambia. No solo cambia respecto al cuadro anterior, sino que tambien cambia dependiendo de en que columna me pare. Por ejemplo, la distancia entre cualquier celda de la primer columna (que corresponde al genotipo \(A_1A_1\)) a la contigua de la segunda columna (que corresponde al genotipo \(A_1A_2\)) es de \(\Delta=-3\) unidades, mientras que de la segunda a la tercera columna (que corresponde al genotipo \(A_2A_2\)) el cambio es de \(\Delta=-5\) unidades. Claramente el promedio no coincide en ningún caso con el valor del genotipo de \(B\) correspondiente a esa fila, como sí ocurría en el cuadro de arriba (aditividad en los dos loci).

	\(A_1A_1\)	\(A_1A_2\)	\(A_2A_2\)
\({B_1B_1}\)	\(6\)	\(3\)	\(-2\)	\(2,333\)
\({B_1B_2}\)	\(4\)	\(1\)	\(-4\)	\(1\)
\({B_2B_2}\)	\(2\)	\(-1\)	\(-6\)	\(-1,667\)
	\(4\)	\(1\)	\(-4\)

Finalmente, en el cuadro siguiente le hemos agregado al cuadro de efectos aditivos un efecto de interacción aditivo x aditivo, sencillamente como el producto de los valores del efecto aditivo de los dos loci para cada par de genotipos (las funciones de interacción pueden ser infinitas, esta es una sola, elegida por sencilla para representar el fenómeno). El primer valor de cada celda corresponde al efecto aditivo y el segundo al efecto de epistasis del tipo \(I_{AA}\). Además de haberse alterado los valores de casi todas las celdas, el cambio entre celdas contiguas experimenta ahora algunos valores leves y otros abruptos, en los dos sentidos. Por ejemplo, pasar de \(A_1A_1/B_1B_1\) a \(A_1A2/B_1B_1\) significa solo \(\Delta=14-2=12\) unidades, mientras que de \(A_1A_1/B_2B_2\) a \(A_1A_2/B_2B_2\) el cambio correspondiente es de \(\Delta=-6-(-2)=-4\) unidades. Claramente, los efectos epistáticos pueden cambiar totalmente la configuración de los genotipos respecto a la aditividad o a la dominancia.

	\(A_1A_1\)	\(A_1A_2\)	\(A_2A_2\)
\({B_1B_1}\)	\(6+8=14\)	\(2+0=2\)	\(-2-8=-10\)	\(2\)
\({B_1B_2}\)	\(4-0=4\)	\(0+0\)	\(-4-0=-4\)	\(0\)
\({B_2B_2}\)	\(2-8=-6\)	\(-2+0=-2\)	\(-6+8=2\)	\(-2\)
	\(4\)	\(0\)	\(-4\)

Teniendo en cuenta todo lo anterior, podemos ahora escribir nuestro modelo genético de una forma algo más complicada, pero menos rústica, describiendo mejor los componentes del genotipo y sus diversas interacciones. Si notamos con \(A\) los efectos aditivos, con \(D\) los desvíos de dominancia y con \(I\) los efectos epistáticos, entonces podemos describir el fenotipo de cada individuo como

\[ \begin{split} P=G+E=A+D+I+E \end{split} \tag{8.5} \]

Claramente, esto asume que la relación entre lo genético y lo ambiental es aditiva, lo que no necesariamente es así y por lo tanto debemos entrar en el campo de las interacciones entre ambos componentes, como veremos en más detalle en sección Interacción Genotipo x Ambiente. Dicho de otra forma, en términos matemáticos, no alcanza con sumar los efectos de genotipo y ambiente para describir de la mejor forma posible el comportamiento diferencial de los genotipos en los ambientes y es necesario incorporar un parámetro adicional que describa esa diferencia de comportamientos en los distintos ambientes. Se trata de una interacción, y vamos a usar también la letra \(I\) como en el caso de epistasis, pero ahora con un subíndice que refiera específicamente a la clase de interacción genotipo-ambiente, por lo que el modelo de la ecuación (8.5) quedará ahora

\[ \begin{split} P=G+E+I_{G\times E}=A+D+I+E+I_{G\times E} \end{split} \tag{8.6} \]

que será una de las maneras más explícitas de expresar el fenotipo de un individuo que usaremos en el curso.

• Definiremos al fenotipo (\(P\)) de un individuo como la suma de los efectos genéticos (\(G\)), los ambientales (\(E\)) y la interacción entre los mismos (\(I_{G\times E}\)).

• El genotipo del individuo, definido como el arreglo particular de alelos en los distintos loci, consistirá de la suma de los efectos aditivos (\(A\)), de dominancia (\(D\)) y epistáticos (\(I\)).

• Los efectos aditivos corresponden al efecto que cada alelo confiere a la característica, independiente de la combinación en que se encuentre, tanto dentro de su locus como considerando lo que hay en otros loci. Tomando como referencia un locus diploide, entonces:

\[ \begin{split} A=\sum_{i=1,j=1}^{i=2,j=n}A_{i,j} \end{split} \]

• El efecto o desvío de dominancia expresa el desvío de cada fenotipo respecto a su valor aditivo. La dominancia es un efecto intra-locus que depende de la combinación específica de alelos en cada uno de los loci. Si llamamos \(l\) a la combinación específica que tiene nuestro individuo en cada locus, podemos escribir el efecto total de dominancia como:

\[ \begin{split} D=\sum_{j=1}^{n}D_{l,j} \end{split} \]

• Los efectos o desvíos epistáticos se corresponden a interacciones alélicas inter-génicas, es decir, entre distintos loci. Las causas más usuales a nivel molecular para estos efectos son la pleiotropía y el ligamiento. Este efecto corresponde a la suma de todas las interaciones entre los loci y podemos resumirlo mediante el término \(I\):

\[ \begin{split} I=I_{AA}+I_{AD}+I_{DD}+I_{AAA}+I_{AAD}+... \end{split} \]

8.3 Modelo genético básico: un locus con dos alelos

Como hemos mencionado antes, en general, la mayor parte de las características de interés para la genética cuantitativa son de herencia poligénica, es decir, controlada por el efecto de alelos en varios (muchos) genes. Esto, sumado a la imposibilidad de conocer para cada uno de esos genes sus estados alélicos, además de los efectos de cada alelo, ha llevado a la genética cuantitativa del siglo XX a desarrollarse basada en una aproximación estadística simple y potente, llamada el modelo infinitesimal. La misma traslada el problema de conocer el efecto de cada gen y de cada alelo a un problema de distribuciones estadísticas, que asumiendo un número de loci razonablemente grande y una pequeña contribución de cada loci, nos permite invocar el teorema del límite central, como ya vimos antes también. Una porción importante de esta Parte III del libro estará basada en dicho modelo, por lo que será de gran relevancia para nosotros.

Por el contrario, los genes de efecto mayor, aquellos genes en que algunas o todas las variantes (alelos) marcan una diferencia importante en el fenotipo, son relativamente escasos en la genética cuantitativa, aunque a veces determinantes en diferencias importante en producción, o entre razas de la misma especie. En una revisión reciente, D. Wright (2015) identifica varios de ellos en especies animales domésticas. Por ejemplo, en el perro el largo de patas estaría gobernado en gran medida por el gen \(FGF4\), mientras que el tamaño corporal estaría determinado por el gen \(IGF1\). En ganado vacuno el crecimiento muscular estaría determinado en gran medida por el gen \(MSTN\), el (mal) olor en la leche por el gen \(FMO3\), mientras que la producción de leche estaría influenciada por el gen \(DGAT1\) y la composición influenciada por las variantes en el gen \(ABCG1\). En ovinos, la tasa de ovulación incrementada y la tasa de melliceros estaría influenciada por el gen \(BMP15\), mientras que el conocido gen del efecto Booroola estaría determinado por las variantes en el gen \(BMPR1B\). En caballo, mientras tanto, el tipo de paso estaría determinado por el gen \(DMRT3\). Finalmente, en cerdos, la hipertermia maligna viene dada por variantes en el gen \(RYR1\), el contenido de glicógeno en músculo por el gen \(PRKAG3\), el tamaño de las orejas por el gen \(PPARD\), la muscularidad y la grasa dorsal influenciados por el gen \(IGF2\), mientras que la terneza de la carne estaría gobernado por el gen \(CAST\).

Veamos, a partir de un ejemplo ficticio, como actúa un gen de efecto mayor y hasta dónde podemos llegar con el análisis del mismo. La Figura 8.3 muestra el comportamiento fenotípico de un gen en un organismo diploide, con dos alelos, \(A_1\) y \(A_2\), con frecuencias \(p=0,6\) y \(q=0,4\), respectivamente, en una característica como peso al año en una raza vacuna. Supongamos que se trata de una característica en que conocemos la base molecular de la misma y que tenemos un test genético para determinar a que genotipo corresponde cada animal (por ejemplo, a partir de un chip de genotipado o a partir de un ensayo de PCR). El genotipo \(A_1A_1\) produce animales con un peso de \(180\) Kg, el genotipo \(A_2A_2\) produce animales de \(120\) Kg de peso, mientras que el heterocigoto produce animales de \(160\) Kg de peso, cada uno de ellos marcado en la Figura 8.3 como una línea rayada vertical del color correspondiente al genotipo. Sin embargo, como existe variabilidad ambiental, definida como variabilidad no-genética, los animales de cada genotipo se distribuirán alrededor del valor correspondiente en forma aleatoria. En este caso asumimos que la variabilidad ambiental no depende del genotipo, es decir que es igual para todos los animales, algo que discutiremos más adelante, y por lo tanto, como de acuerdo a la ecuación (8.1) el fenotipo es igual a \(G+E\), si \(G\) es un valor fijo para cada genotipo (\(G_{11}\), \(G_{12}\) y \(G_{22}\)), entonces los fenotipos correspondientes a cada genotipo seguirán una distribución aleatoria con media en su correspondiente valor genotípico y varianza igual a la varianza ambiental (que llamaremos \(\sigma_E^2\)). Es decir,

\[P_{11}=G_{11}+N(0,\sigma_E^2)=N(G_{11},\sigma_E^2)\] \[P_{12}=G_{12}+N(0,\sigma_E^2)=N(G_{12},\sigma_E^2)\] \[ \begin{split} P_{22}=G_{22}+N(0,\sigma_E^2)=N(G_{22},\sigma_E^2) \end{split} \tag{8.7} \]

Esto se aprecia claramente en la figura como las curvas gaussianas de diferentes colores, centradas en los correspondientes valores genotípicos.

En nuestro caso particular, hemos asumido además que la población se encuentra en equilibrio de Hardy-Weinberg, por lo que las frecuencias de cada genotipo serán

\[\text{fr}(A_1A_1)=p^2=0,6^2=0,36\] \[\text{fr}(A_1A_2)=2pq=2 \times 0,6 \times 0,4=0,48\] \[\text{fr}(A_2A_2)=q^2=0,4^2=0,16\]

lo que se aprecia claramente por el área de cada curva en la figura. Si juntamos las tres curvas, es decir unimos las sub-poblaciones con distinto genotipo, entonces tenemos toda la población, representada por la curva negra. La media de la población general se encuentra representada por una línea continua de color negro, a la derecha de la línea rayada violeta que corresponde al genotipo heterocigoto. Finalmente, esta figura también muestra un aspecto interesante, que suele confundir a muchos cuando trabajamos con modelos lineales, por ejemplo. Pese a que las distribuciones de valores de los individuos pertenecientes a cada genotipo es normal y con la misma varianza, la distribución resultante de combinar los individuos de todos los genotipos no es normal. Esto no suele representar ningún problema cuando el modelo es infinitesimal porque no existe un número pequeño de clases, como en nuestro caso de la Figura (8.1) y como cada clase está formada por diferentes combinaciones (suma) de contribuciones infinitesimales, entonces la distribución es aproximadamente normal en esos casos. En estadística, el supuesto de normalidad en modelos lineales (en ANOVA, por ejemplo) se refiere a la distribución de los residuos (es decir, luego de descontados los efectos del modelo), no de los datos originales.

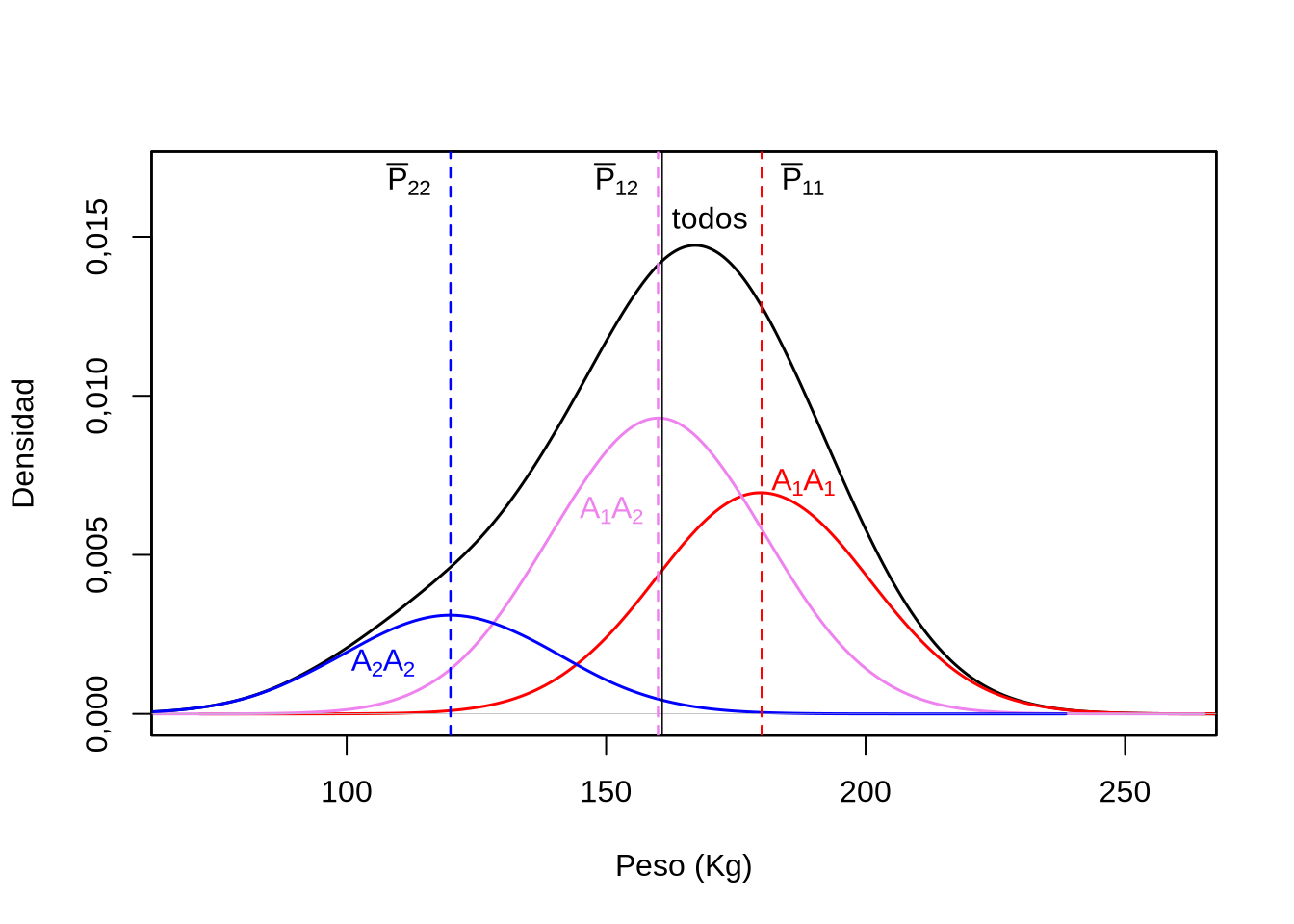
Figura 8.3: Distribución de pesos en una población compuesta de tres genotipos para un gen de efecto mayor, con dos alelos. La frecuencia del alelo \(A_1\) es \(p=0,6\) y la población se encuentra en equilibrio Hardy-Weinberg. Los pesos promedio de los tres genotipos son \(\bar{P}_{22}=120\) Kg, \(\bar{P}_{12}=160\) Kg y \(\bar{P}_{11}=180\) Kg, mientras que el efecto aleatorio del ambiente se muestrea de una distribución \(N(\mu=0,\sigma^2=400 \text{ Kg}^2)\). Casi pegado a la línea rayada violeta, puede verse en una línea vertical continua de color negro la media de la población general, es decir la media fenotípica de la población.

En la Figura 8.3 hemos colocado una línea vertical en el valor correspondiente a cada uno de los genotipos, pero hasta ahora no hemos mencionado de dónde salieron esos valores. Es decir, el test genético lo único que es capaz de decirme son los genotipos de cada animal al que le realizamos el ensayo, pero no puede decirme cuánto vale ese genotipo. ¿De dónde sale entonces esa información? Si consideramos que los valores de los genotipos son independientes de otro tipo de información genómica y que la distribución de valores fenotípicos alrededor de cada valor genotípico es la misma, una distribución normal producto de la variabilidad ambiental, entonces las medias de los fenotipos de cada clase se corresponderá con el consiguiente valor genotípico. Es ddecir, si se cumplen nuestros supuestos, entonces, usando los resultados de la ecuación (8.7), tenemos que

\[\bar{P}_{11}=\mathbb{E}(P_{11})=\mathbb{E}[G_{11}+N(0,\sigma_E^2)]=\mathbb{E}[N(G_{11},\sigma_E^2)]= G_{11}\] \[\bar{P}_{12}=\mathbb{E}(P_{12})=\mathbb{E}[G_{12}+N(0,\sigma_E^2)]=\mathbb{E}[N(G_{12},\sigma_E^2)]= G_{12}\] \[ \begin{split} \bar{P}_{22}=\mathbb{E}(P_{22})=\mathbb{E}[G_{22}+N(0,\sigma_E^2)]=\mathbb{E}[N(G_{22},\sigma_E^2)]= G_{22} \end{split} \tag{8.8} \]

Dicho de otra forma, si se conocemosn los pesos de cada animal y su genotipo, es posible separamosr a los animales por genotipo y calculamosr el promedio depara cada grupo,. Se obteniendo entoncese así el valor esperado para ese genotipo, que se asumimos se corresponde sin error al “verdadero” valor del mismo⁸². Pasamos entonces, ahora, de manejarnos conasí de una distribución de valores fenotípicos a un conjunto de 3 valores genotípicos. Antes de comenzar a trabajar con estos valores genotípicos, veamos si podemos reducir el número de parámetros de 3 a 2, de forma tal de simplificar nuestras ecuaciones futuras. De todas las transformaciones imaginables, posiblemente la más utilizada en los textos de genética cuantitativa es la que aparece representada en la Figura 8.4.

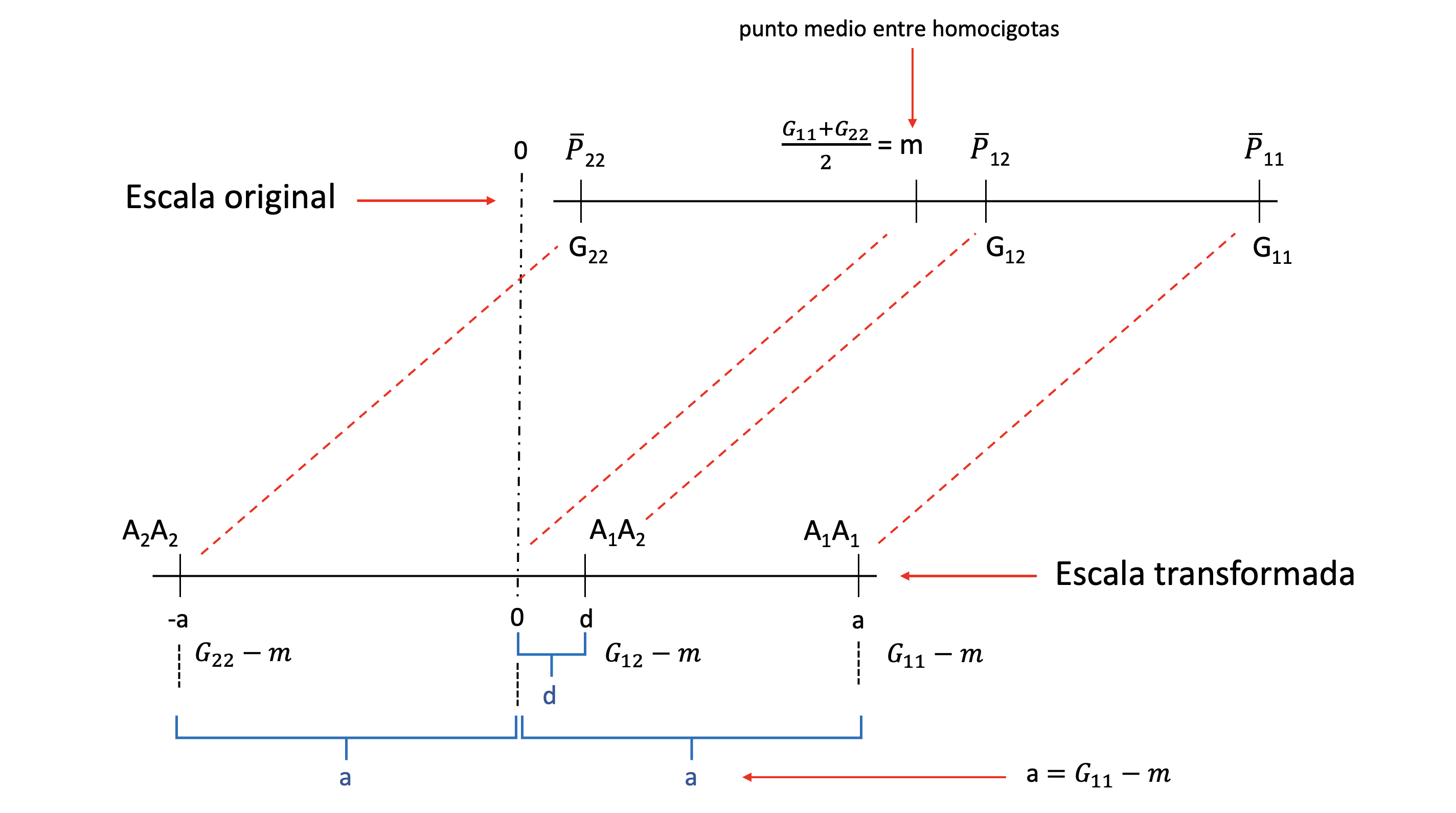
Figura 8.4: Transformación de escalas entre las mediciones originales, en la escala original (arriba) de la característica y la correspondiente transformación lineal para ubicar los genotipos extremos simétricamente al cero, en la escala transformada (abajo). El punto medio entre los homocigotos en la escala original es \(m=\frac{G_{11}+G_{22}}{2}\), que si se lo restamos a cada uno de los genotipos originales nos da la correspondiente ubicación en la escala transformada. El cambio de notación de los genotipos en la escala superior a la inferior, con los alelos específicos es para resaltar el pasaje al modelo conceptual.

En la parte superior de la misma vemos representados los valores de los tres genotipos (\(G_{11}\), \(G_{12}\), \(G_{22}\)), o lo que es lo mismo las medias de las clases fenotípicas (\(\bar{P}_{11}\), \(\bar{P}_{12}\), \(\bar{P}_{22}\)) en la escala original, es decir, la escala en la que se tomó la medida. En nuestro caso, con los valores de la Figura 8.3, \(G_{11}=180\) Kg, \(G_{12}=160\) Kg y \(G_{22}=120\) Kg. También sobre la misma escala, podemos ahora identificar el punto medio entre los homocigotas, que llamaremos \(m\) y cuyo valor está dado por

\[ \begin{split} m=\frac{G_{11}+G_{22}}{2} \end{split} \tag{8.9} \]

Es importante notar que \(m\), el punto medio entre los homocigotas, no es en general igual a la media de la población, que es un concepto totalmente diferente. Mientras que \(m\) solo depende de los valores de \(G_{11}\) y \(G_{22}\) (en forma aritmética es el promedio de estos dos valores, mientras que geométricamente es el punto medio del segmento que los une), la media de la población \(\mathbb{E}(P)=\bar{P}\) depende de los 3 valores genotípicos y de sus frecuencias. Si ahora, a cada uno de los valores genotípicos le restamos el valor del punto medio, tenemos ahora que en la escala transformada que aparece en la parte inferior de la figura, los valores correspondientes a cada uno de los genotipo homociogotas estarán dados por

\[A_1A_1=G_{11}-m=G_{11}-\frac{G_{11}+G_{22}}{2}=\frac{2G_{11}-G_{11}-G_{22}}{2}=\frac{G_{11}-G_{22}}{2}\] \[ \begin{split} A_2A_2=G_{22}-m=G_{22}-\frac{G_{11}+G_{22}}{2}=\frac{2G_{22}-G_{11}-G_{22}}{2}=\frac{G_{22}-G_{11}}{2} \end{split} \tag{8.10} \]

Si ahora definimos \(a=\frac{G_{11}-G_{22}}{2}\), usando los resultados de la ecuación anterior, el valor genotípico en la nueva escala para los homocigotas será

\[ \begin{split} A_1A_1=\frac{G_{11}-G_{22}}{2}=a\\ A_2A_2=\frac{G_{22}-G_{11}}{2}=-a \end{split} \tag{8.11} \]

El último resultado sale de multiplicar \(a\) por \(-1\), es decir \(-1 \times a=-a=-1 \times \frac{G_{11}-G_{22}}{2}=\frac{G_{22}-G_{11}}{2}\). Como para definir los valores de dos genotipos (\(G_{11}\) y \(G_{22}\)) usamos un solo parámetro (\(a\), ya que en la caso de \(G_{22}\) es solamente su opuesto), entonces hemos conseguido la reducción del número de parámetros que deseábamos. Si ahora, además, le llamamos \(d\) a la diferencia \(G_{12}-m\), tenemos entonces finalmente que los valores de los tres genotipos estarán dados por

\[A_1A_1=\frac{G_{11}-G_{22}}{2}=a\] \[A_1A_2=\frac{2G_{12}-G_{11}-G_{22}}{2}=d\] \[ \begin{split} A_2A_2=\frac{G_{22}-G_{11}}{2}=-a \end{split} \tag{8.12} \]

como aparece representado en la escala transformada (inferior) de la Figura 8.4. De más está decir que se trata de una transformación lineal que conserva las distancias originales entre puntos y que la posibilidad de reducir un parámetro es a costa de expresar los valores como desvío de un punto medio (\(m\)), con ningún otro significado importante que permitirnos una manipulación algebraica más sencilla.

Ejemplo 8.1

En un estudio sobre el efecto de los genes de la miostatina y la \(\mu\)-calpaína sobre características de la carcasa, Bennett y colaboradores (Bennett et al. 2019) eligen el marcador (SNP) rs110065568 para el gen de la miostatina (en el cromosoma BTA2), que se trata de una sustitución de Fenilalanina (F) por Leucina (L) en la posición del aminoácido 94 (F94L). El gen de la miostatina es el responsable principal del fenotipo doble musculado común a varias razas de ganado, como el toro de la raza Belgian Blue que aparece en la Figura 8.5 y aún a diferentes especies de interés doméstico.

Figura 8.5: Toro de la raza Belgian Blue mostrando su impresionante musculatura (de wikipedia, autor: Mastiff, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons).

En el cuadro siguiente se aprecian los promedios de mediciones para dos características que obtuvieron los autores del trabajo, de acuerdo al genotipo de los animales (\(G_{FF}\) homocigotos para Fenilalanina, \(G_{LL}\) para Leucina y \(G_{FL}\) heterocigotos)

Característica	\(G_{FF}\)	\(G_{FL}\)	\(G_{LL}\)
Peso al nacimiento (kg)	\(40,7\)	\(41,4\)	\(43,3\)
Área del ojo del bife (cm\(^2\))	\(89\)	\(93\)	\(103\)

Asumiendo que estos valores son los promedios de un gran número de animales y que por lo tanto el promedio de los efectos ambientales es cero, transformar los valores genotípicos de las características a la escala en la que el cero es el punto medio entre los homocigotos.

Para la primera característica, peso al nacimiento, el punto medio entre los homocigotas los calculamos como

\[ \begin{split} m=\frac{G_{LL}+G_{FF}}{2}=\frac{43,3+40,7}{2}=42 \text{ Kg} \end{split} \]

Por lo tanto, los valores de los genotipos expresados en esta escala transformada serían

\[A_{LL}=G_{LL}-m=(43,3-42)\text{ Kg}=1,3 \text{ Kg}=a\] \[A_{FL}=G_{FL}-m=(41,4-42) \text{ Kg}=-0,6\text{ Kg}=d\] \[A_{FF}=G_{FF}-m=(40,7-42)\text{ Kg}=-1,3\text{ Kg}=-a\]

Con la misma idea, para la segunda característica tenemos

\[ \begin{split} m=\frac{G_{LL}+G_{FF}}{2}=\frac{103+89}{2}=96 \text{ cm}^2 \end{split} \]

y los genotipos transformados

\[A_{LL}=G_{LL}-m=(103-96) \text{ cm}^2=7 \text{ cm}^2=a\] \[A_{FL}=G_{FL}-m=(93-96) \text{ cm}^2=-3 \text{ cm}^2=d\] \[A_{FF}=G_{FF}-m=(89-96) \text{ cm}^2=-7 \text{ cm}^2=-a\]

Media de la población

A partir del cambio de escala que realizamos previmamente, los valores genotípicos quedarán expresados como desvíos del punto medio (\(m\)) entre los homocigotas. En general, dicho punto no coincide con la media de la población ya que el mismo se desplazará de acuerdo a la importancia de \(d\) en relación a \(a\) y de las frecuencias de los alelos.⁸³ Para calcular la media procedemos como de costumbre, multiplicando el valor de cada categoría por su frecuencia relativa. Asumiendo que los genotipos están en equilibrio de Hardy-Weinberg, las frecuencias de los 3 genotipos (\(A_1A_1\), \(A_1A_2\) y \(A_2A_2\)) serán \(p^2\), \(2pq\) y \(q^2\), mientras que los valores genotípicos correspondientes (en la escala transformada) serán \(a\), \(d\) y \(-a\). Poniendo todo junto en un cuadro, lo anterior queda resumido de la siguiente manera:

\(\textbf{Genotipo}\)	\(\textbf{Frecuencia}\)	\(\textbf{Valor genotípico}\)	\(\textbf{Producto}\)
\({A_1A_1}\)	\(p^2\)	\(a\)	\(p^2a\)
\({A_1A_2}\)	\(2pq\)	\(d\)	\(2pqd\)
\({A_2A_2}\)	\(q^2\)	\(-a\)	\(-q^2a\)
\(\textbf{Suma}\)			\(M=a(p-q)+2pqd\)

El resultado final, \(M=a(p-q)+2pqd\), vienederiva de sumar todos los términos de la última columna y simplificar, es decir

\[ \begin{split} M=p^2a+2pqd-q^2a=a(p^2-q^2)+2pqd=a(p+q)(p-q)+2pqd \ \therefore \end{split} \]

\[ \begin{split} M=a(p-q)+2pqd \end{split} \tag{8.13} \]

En el caso particular de un locus con dos alelos, la restricción de que \(p+q=1 \Leftrightarrow q=1-p\) nos permite ir un poco más lejos y expresar la media solo en función de \(a\),\(d\) y \(p\), de la siguiente manera

\[ \begin{split} M=a(p-q)+2pqd=a[p-(1-p)]+2dp(1-p)=a(2p-1)+2d(p-p^2) \end{split} \tag{8.14} \]

En la Figura 8.6 podemos apreciar cómo varía la media genotípica de la población en función de la frecuencia de alelo \(A_1\) (\(p\)) y del desvío del punto medio del heterocigota (\(d\)).

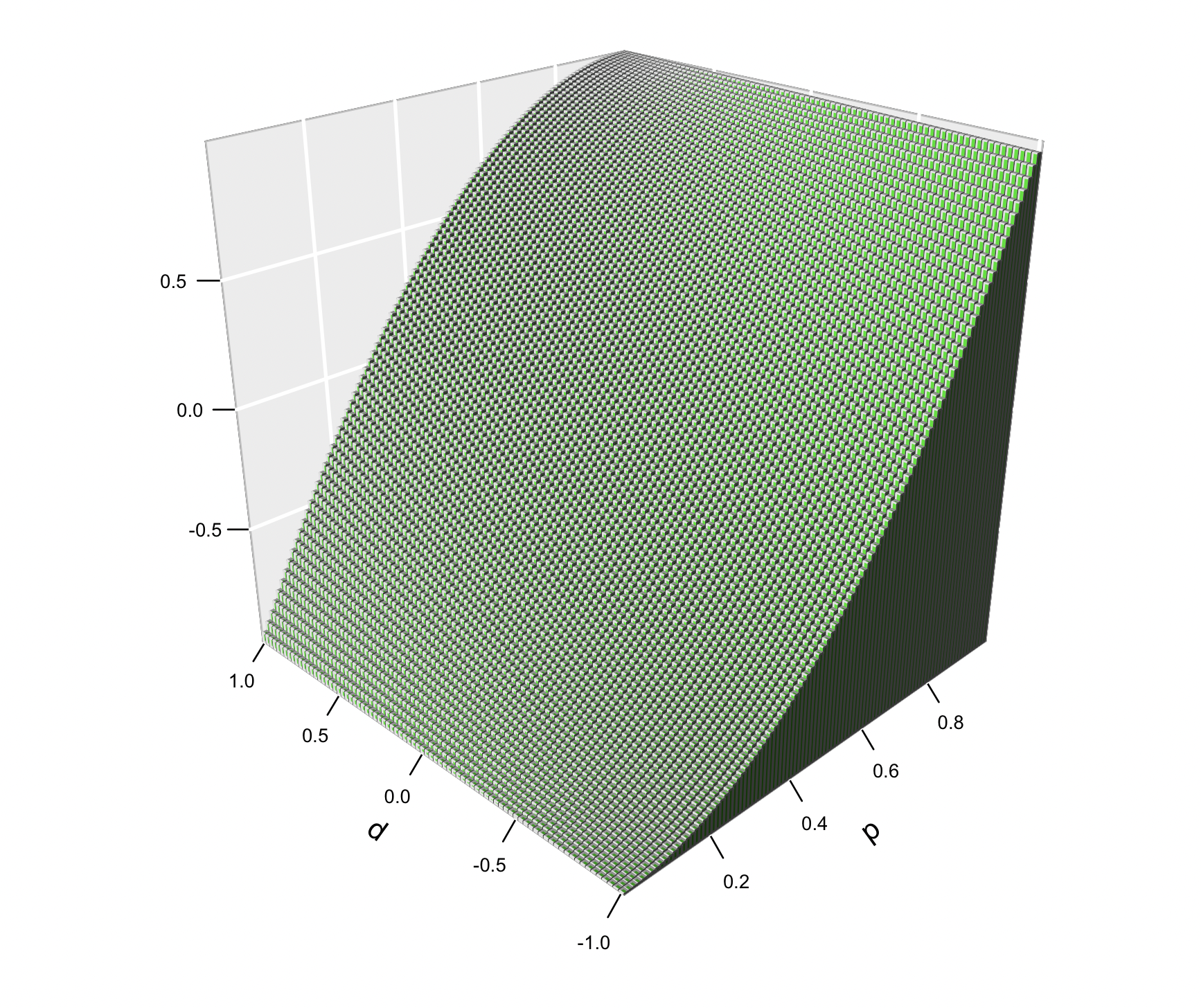
Figura 8.6: Media genotípica de la población como función de la frecuencia del alelo \(A_1\) (\(p\)) y del valor de dominancia \(d\). El valor de \(a\) fue fijado en 1 y por lo tanto \(-1 \leqslant d \leqslant 1\), asumiendo que no hay subdominancia ni sobredominancia. Se observa claramente que mientras la media crece siempre con el valor de \(p\) (ya que \(p^2\) es la frecuencia del homocigota con valor positivo, \(a\)), como \(d\) puede variar en un sentido u otro alrededor del cero, su valor aumentará o decrecerá la media respecto a la situación de ausencia de dominancia, cambiando también la forma (concavidad) de la curva.

Para hacer el gráfico independiente del valor de \(a\) (porque en general no podemos interpretar gráficos en 4 dimensiones) fijamos éste en 1 yparámetro en \(a = 1\), por lo tantoque \(-1 \leqslant d \leqslant 1\), asumiendo que no hay subdominancia ni sobredominancia. Claramente, a medida de que aumenta el valor de \(p\) siempre aumenta la media de la población, lo que debería resultar obvio ya que la frecuencia del homocigota con valor positivo (\(a\)) es \(p^2\), es decirlo cual implica que crece con \(p\), (y por lo tanto, la frecuencia del otro homocigota, (que tiene valor \(-a\),) decrece con \(p\)). Por otro lado, también es posible observar que la media de la población decrece a medida de que \(d\) va de \(+a\) (\(1\)) a \(-a\) (\(-1\)). Sin embargo, la interacción entre \(p\) y \(d\) no es lineal, ya que en la ecuación (8.14) hay un término que involucra su producto. De hecho, podemos entender la ecuación (8.14) como el aporte de dos componentes a la media, el correspondiente al aporte de \(a\), que es (\(a(p-q)\)), y el aporte correspondiente al desvío del heterocigota (por dominancia), que es de \(2d(p-p^2)=2pqd\), que no es más que el desvío \(d\) multiplicado por la frecuencia de heterocigotas (\(2d(p-p^2)=2pqd\)). Pero como hemos visto repetidas veces, \(2pq\) es máximo cuando \(p=q=\frac{1}{2}\), en cuyo caso \(2pq=2 \cdot (\frac{1}{2}) \cdot (\frac{1}{2})=\frac{1}{2}\), y en ese caso el aporte será \(2pqd=\frac{d}{2}\). A medida de que las frecuencias de \(p\) o de \(q\) se acerquen a cero, entonces habrá cada vez menos heterocigotas, y por lo tanto \(2pqd \to 0\). En los casos extremos, cuando \(p=1\), entonces \(M=a(p-q)+2pqd=a (1-0)+2 \cdot 1 \cdot 0 \cdot d=a\) y en el caso opuesto, cuando \(q=1\), entonces tenemos \(M=a(p-q)+2pqd=a \cdot (0-1)+ 2 \cdot 0 \cdot 1 \cdot d=-a\), lo que es obvio ya que en cada uno de estos casos solo hay un genotipo.

En general, si asumimos que no hay subdominancia ni sobredominancia, es decir (i.e., el valor genotípico del heterocigota se encuentra entre el de los dos homocigotas,) la amplitud total de la variación genotípica es \(a-(-a)=a+a=2a\).

En esta sección nos hemos manejado con un locus de un organismo diploide que cuenta solo con dos alelos. Sin embargo, si asumimos que no existe interacción entre loci, es decir, los efectos epistáticos no existen o son despreciables a los fines de nuestro interés (una simplificación), entonces es posible generalizar el resultado de la ecuación (8.14) a todos los loci involucrados en la característica de interés. El supuesto anterior implica que el efecto de todos los loci en conjunto es aditivo, o d. Dicho de otra forma, asumimos que los efectos de cada locus se suman para obtener el efecto total. Si ahora llamconsideramos \(a=\sum_i a_i\), es decir, la diferencia entre los homocigotos fijados para todos los alelos positivos y el cero (en la escala transformada, con el cero el punto medio de cada uno de ellos), entonces la ecuación (8.14) se transforma en

\[ \begin{split} M=\sum_i a_i(p_i-q_i)+2\sum_i p_iq_id_i \end{split} \tag{8.15} \]

que es la generalización de la ecuación (8.14) asumiendo aditividad entre loci.

Ejemplo 8.2

En el mismo estudio de Bennett et al. (2019), los autores encuentran que en una de las razas evaluadas la frecuencia del alelo \(L\) (F94LaL) es de \(20,7\%\). Calcular las medias de la población para las dos características analizadas en el Ejemplo 8.1.

Si \(p=0,207 \Rightarrow q=1-p=1-0,207=0,793\), con los valores de la primer característica (peso al nacimiento) \(a=1,3\) y \(d=-0,6\) y usando la ecuación (8.13), tenemos

\[ \begin{split} M=a(p-q)+2pqd=1,3(0,207-0,793)+2\times 0,207 \times 0,793 \times(-0,6)=-0,9588 \end{split} \]

respecto al punto medio entre los homocigotos, que era \(m=42 \text{ Kg}\), por lo que sumando ambos tenemos la media expresada en la escala original, es decir

\[ \begin{split} 42+(-0,9588)=42-0,9588=41,0412 \text{ Kg} \end{split} \]

Aplicando idéntico razonamiento para la segunda característica, pero ahora con los valores de \(a=7\) y \(d=-3\), tenemos

\[ \begin{split} M=a(p-q)+2pqd=7(0,207-0,793)+2\times 0,207 \times 0,793 \times(-3)=-5,0869 \text{ cm}^2 \end{split} \]

respecto al punto medio entre los homocigotos (\(m=96 \text{ cm}^2\)), por lo que sumando ambos nos queda

\[ \begin{split} 96+(-5,0869)=96-5,0869=90,9131 \text{ cm}^2 \end{split} \]

como el valor de la media para la segunda característica, expresada en la escala original.

• Los genes de efecto mayor son aquellos en que algunas o todas las variantes (alelos) marcan una diferencia importante en el fenotipo, son relativamente escasos en la genética cuantitativa.

• Si consideramos que los valores de los genotipos son independientes de otro tipo de información genómica y que la distribución de valores fenotípicos alrededor de cada valor genotípico es la misma (una distribución normal producto de la variabilidad ambiental), entonces las medias de los fenotipos de cada clase se corresponderá con el consiguiente valor genotípico.

• Podemos transformar de escala los valores genotípicos, ubicándolos en torno a cero (la media de los homocigotas en la escala orginal), para trabajar con un parámetro menos en nuestros cálculos.

• Los valores de los tres genotipos transformados serán:

\[A_1A_1=\frac{G_{11}-G_{22}}{2}=a\] \[A_1A_2=\frac{2G_{12}-G_{11}-G_{22}}{2}=d\] \[A_2A_2=\frac{G_{22}-G_{11}}{2}=-a\]

• Usando los valores transformados, podremos entonces calcular la media de la población como:

\[ \begin{split} M=a(p-q)+2pqd \end{split} \]

8.4 Efecto medio

Hasta ahora hemos discutido la separación de lo genético y lo ambiental, asumiendo que el genotipo es lo relevante desde el punto de vista genético, ya que lo que identifica a los individuos desde ese punto de vista es no solo la suma de los valores de los alelos presentes sino también el aporte de las combinaciones específicas, tanto intra-locus como inter-loci . Sin embargo, cuando nos interesa entender la capacidad de transmitir un determinado valor genético de un individuo a sus descendientes, entonces debemos enfocarnos en los mecanismos de herencia y en la forma en que los individuos transmiten información a sus descendientes. En los organismos diploides con dos sexos, cada individuo transmite a su descendencia solamente la mitad de la información que este tendrá para cada posición del genoma autosomal (esto no es cierto para los cromosomas sexuales, por ejemplo, ni para los genomas de organelos como la mitocondria), viniendo la otra mitad del otro padre (o madre). Dicho de otra forma, los padres/madres transmiten a sus hijos uno de los dos alelos que cada uno de ellos posee en cada loci del genoma. Como nunca transmiten el par de alelos que cada padre/madre posee, entonces nunca transmiten genotipos y por lo tanto mal podrían transmitir su correspondiente valor.

En este sentido, es necesario entender cuál es el impacto en el cambio de valor medio de una población que proporciona un alelo cuando es introducido en la misma. Supongamos que tenemos una población que tiene dos alelos, \(A_1\) y \(A_2\), con frecuencias \(p\) y \(q\), tanto en machos como en hembras. Supongamos ahora que elegimos como reproductor macho uno o más animales que son homocigotos para el alelo \(A_1\), es decir es \(A_1A_1\). Eso nos asegura que los gametos producidos por los machos serán \(A_1\) (el mismo razonamiento vale si intercambiamos el rol de los sexos). Esos gametos se unirán a los gametos producidos por la hembras, que como son sacados al azar de la población estarán en frecuencias \(p\) el alelo \(A_1\) y \(q=1-p\) el alelo \(A_2\). Si ponemos está información en un cuadro, donde la frecuencia del macho aparece en la primera fila y las frecuencias de los gametos en las hembras en las columnas, tenemos el siguiente resumen de la situación:

	\(\bf{A_1}\)	\(\text{fr}(A_1)=p\)	\(\bf{A_2}\)	\(\text{fr}(A_2)=q\)
\(\bf{A_1}\), \(\text{fr}(A_1)=1\)	\(A_1A_1\)	\(p\)	\(A_1A_2\)	\(q\)

Es decir, como el macho produce gametos \(A_1\) con frecuencia igual a uno, los únicos genotipos posibles serán \(A_1A_1\) y \(A_1A_2\), con frecuencias respectivas \(1 \times p=p\) y \(1 \times q=q\). Como los valores de los genotipos \(A_1A_1\) y \(A_1A_2\) son, respectivamente, \(a\) y \(d\), entonces multiplicando cada valor por su frecuencia obtenemos la media de valores genotípicos de la población luego de haber asegurado que uno de los alelos de los individuos es \(A_1\) y el otro está tomado al azar, es decir

\[ \begin{split} M_1=a \times p+d \times q=pa+dq \end{split} \tag{8.16} \]

Como vimos antes, el valor genotípico de la población antes del apareamiento con el animal \(A_1A_1\) era

\[M_0=a \times p^2+d \times 2pq+(-a) \times q^2=a[p^2-q^2]+2pqd\ \therefore\] \[ \begin{split} M_0=a[(p+q)(p-q)]+2pqd=a(p-q)+2pqd \end{split} \tag{8.17} \]

La diferencia, por lo tanto, atribuible a la introducción de alelo \(A_1\) como uno presente en todos los genotipos es

\[M_1-M_0=pa+dq-[a(p-q)+2pqd]=pa+qd-pa+qa-2pqd \Leftrightarrow\] \[ \begin{split} q[d+a-2pd]=q[a+d(1-2p)]=q[a+d(p+q-2p)]=q[a+d(q-p)] \end{split} \tag{8.18} \]

Si definimos \(\alpha=a+d(q-p)\), tenemos entonces que el efecto medio del alelo \(A_1\), que llamaremos \(\alpha_1\), es

\[ \begin{split} \alpha_1=q\alpha \end{split} \tag{8.19} \]

De la misma manera, para estudiar el efecto de asegurar la presencia del otro alelo en todos los genotipos de los descendientes (de la población original), podemos hacer el mismo cuadro que antes, pero ahora el o los machos serán homocigotos para el alelo \(A_2\), es decir serán \(A_2A_2\), mientras que los gametos de las hembras serán nuevamente extraídos al azar de la población (con frecuencias \(p\) y \(q\)). Poniendo todo junto, tenemos el siguiente cuadro:

	\(A_1\)	\(\text{fr}(A_1)=p\)	\(A_2\)	\(\text{fr}(A_2)=q\)
\(A_2\), \(\text{fr}(A_2)=1\)	\(A_1A_2\)	\(p\)	\(A_1A_2\)	\(q\)

En este caso, la media de la nueva población estará dada por

\[ \begin{split} M_1=d \times p-a \times q=dp-aq \end{split} \tag{8.20} \]

La diferencia, por lo tanto, atribuible a la introducción de alelo \(A_2\) como uno presente en todos los genotipos es

\[M_1-M_0=dp-qa-[a(p-q)+2pqd]=dp-qa-pa+qa-2pqd \Leftrightarrow\] \[ \begin{split} \Leftrightarrow -p[a-d+2qd]=-p[a+d(2q-1)]=-p[a+d(2q-p-q)]=-p[a+d(q-p)] \end{split} \tag{8.21} \]

y usando la definición previa de \(\alpha=a+d(q-p)\), entonces el cambio de valor genotípico en la población producto de asegurar la presencia del alelo \(A_2\) en los genotipos será

\[ \begin{split} \alpha_2=-p[a+d(q-p)]=-p\alpha \end{split} \tag{8.22} \]

que es el efecto medio del alelo \(A_2\).

Resumiendo, podemos juntar ambos cuadros y tenemos el cambio en la media genotípica de la población correspondiente a cada alelo:

Gameto	\(A_1A_1\)	\(A_1A_2\)	\(A_2A_2\)	Valor medio	Media poblacional	Efecto medio del gen
\(\bf{A_1}\)	\(p\)	\(q\)		\(pa+qd\)	\([a(p-q)+2pqd]\)	\(q[a+d(q-p)]\)
\(\bf{A_2}\)		\(p\)	\(q\)	\(pd-qa\)	\([a(p-q)+2pqd]\)	\(-p[a+d(q-p)]\)

Otra forma de entender lo que implican estos cambios es a través del concepto de efecto medio de sustitución de alelos, que se puede aplicar cuando tenemos dos alelos en un gen. Supongamos que podemos reemplazar al azar alelos \(A_2\) de la población de individuos, sustituyéndolos con alelos \(A_1\). Los genotipos afectados serán los \(A_1A_2\), cuya mitad son alelos \(A_2\) y que tienen frecuencia \(2pq\), porque su frecuencia de cambios será \(pq\) y los \(A_2A_2\), con frecuencia \(q^2\). Asumiendo que cambiamos un solo alelo por genotipo, los cambios serán del genotipo \(A_1A_2\) al \(A_2A_2\) y del \(A_2A_2\) al \(A_1A_2\). Poniendo todo junto tenemos

\[\frac{pq(a-d)+q^2[d-(-a)]}{q^2+pq}=\frac{pq(a-d)+q^2(d+a)}{q(p+q)}=\frac{pq(a-d)+q^2(d+a)}{q}=\] \[ \begin{split} \frac{q[p(a-d)+q(d+a)]}{q}= p(a-d)+q(d+a)=pa-pd+qd+qa=a(p+q)+d(q-p)=a+d(q-p)=\alpha \end{split} \tag{8.23} \]

como lo definimos previamente.

De hecho, usando la notación \(A_1A_1\), \(A_1A_2\) y \(A_2A_2\) para los valores de los correspondientes genotipos, la primera fracción en (8.23) se puede escribir como

\[\alpha=\frac{pq(A_1A_1-A_1A_2)+q^2(A_1A_2-A_2A_2)}{q^2+pq}=\frac{q[p(A_1A_1-A_1A_2)+q(A_1A_2-A_2A_2)]}{q}=\] \[ \begin{split} p(A_1A_1-A_1A_2)+q(A_1A_2-A_2A_2) \end{split} \tag{8.24} \]

que es una forma más conceptual de ver el significado del efecto de sustitución alélica. Otra forma de apreciar esto mismo es aún más conceptual e implica ver el efecto de \(\alpha\) al sustituir un alelo por el otro como la diferencia entre los efectos medios de los alelos que se intercambian (es decir, \(\alpha_1\)y \(\alpha_2\)). Utilizando las ecuaciones (8.19) y (8.22), entonces \(\alpha\) sería

\[ \begin{split} \alpha_1 - \alpha_2=q \alpha - [-p \alpha]=q \alpha + p \alpha = \alpha (p+q) = \alpha \end{split} \tag{8.25} \]

que es lo que queríamos mostrar.

Ejemplo 8.3

Usando los datos previos del estudio de Bennett et al. (2019), calcular el efecto medio de los alelos \(L\) y \(F\) para la característica peso al nacimiento, así como el efecto de sustitución correspondiente.

Tenemos varias formas de llegar a lo mismo, pero una de ellas es primero estimar el efecto de sustitución (\(\alpha\)) y luego usarlo para calcular \(\alpha_1\) y \(\alpha_2\).De acuerdo a la definición \(\alpha=a+d(q-p)\). Como ya tenemos todos los valores se trata solo de sustituirlos

\[ \begin{split} \alpha=a+d(q-p)=1,3+(-0,6)(0,793-0,207)=1,3-0,6(0,586)=0.9484 \text{ Kg} \end{split} \]

Luego, usando los resultados de las ecuaciones (8.19) y (8.22), tenemos

\[ \begin{split} \alpha_1=q\alpha=0,793 \times 0.9484 \text{ Kg}=0,7521\text{ Kg} \alpha_2=-p\alpha=-0,207 \times 0.9484 \text{ Kg}=-0,1963\text{ Kg} \end{split} \]

Obviamente, como verificación trivial, \(\alpha=\alpha_1-\alpha_2=[0,7521-(-0,1963)] \text{ Kg}= 0,9484 \text{ Kg}=\alpha\).

---

-En una población que posee dos alelos \(A_1\) y \(A_2\), el efecto medio del alelo \(A_1\), que llamaremos \(\alpha_1\), es \(\alpha_1=q\alpha\). Como contraparte, el efecto medio del alelo \(A_2\), que llamaremos \(\alpha_2\), es \(\alpha_2=-p[a+d(q-p)]=-p\alpha\).

• El efecto medio de la sustitución de un alelo por otro (cuando tenemos dos alelos en un gen) será \(\alpha_1 - \alpha_2=q \alpha - [-p \alpha]=q \alpha + p \alpha = \alpha (p+q)\), es decir \(\alpha\).

8.5 Valor reproductivo (o valor de cría)

Como vimos antes, en organismos diploides con el modo de reproducción sexual, los mismos transmiten a su descendencia la mitad de sus alelos. Este proceso es aleatorio en el sentido de que la combinación particular de alelos que va en cada gameto está determinada por el azar, ya que además de los procesos de recombinación a nivel de cada cromosoma, la combinación de cromosomas que va a cada gameto es también al azar (en el sentido de que puede ir la copia “paterna” o “materna” que tiene el organismo que se reproduce, no en qué número de cromosomas van). Más aún, como vimos más arriba, los organismos diploides de reproducción sexual pasan a los descendientes solamente alelos, no genotipos, por lo que fue necesario definir el efecto medio de un alelo precisamente como el efecto teórico de introducir dicho alelo de forma obligatoria en todos los genotipos de la nueva generación.

En genética animal, por ejemplo, una posibilidad de conocer el valor reproductivo (también llamado valor de cría o EBV -estimated breeding value- según sus siglas en inglés) de un individuo determinado sería realizar en la práctica el experimento conceptual que nos permitió definir el concepto de efecto medio de un alelo, es decir, aparear a nuestro candidato con una muestra lo más amplia y representativa posible de la población. Los hijos de nuestro candidato se distribuirán en forma aleatoria en torno a un valor medio particular que en general no coincidirá con la media de la población. El desvío de la media de los hijos de nuestro candidato respecto a la media de la población será un estimador de la mitad del valor cría (o del valor reproductivo) del candidato. Será la mitad porque el candidato le aporta a sus hijos solo la mitad de sus alelos, la otra mitad viniendo al azar del otro progenitor. Es de destacar que cuanto más descendientes se evalúen más cerca estaremos del verdadero valor de cría del candidato (que se alcanzaría perfectamente si el mismo se aparease con un número infinito de individuos de la población) y por esto el término estimador (que como todo estimador posee una incertidumbre asociada, algo que veremos más adelante).

Como el valor reproductivo se trata del efecto que cada alelo aporta al individuo, en nuestro modelo se trata de efectos aditivos y debemos sumarlos. En el caso de un locus con dos alelos las posibilidades se reducen al cuadro siguiente:

Genotipo	Valor alelo 1	Valor alelo 2	Valor reproductivo
\(\bf{A_1A_1}\)	\(\alpha_1 = q \alpha\)	\(\alpha_1 = q \alpha\)	\(2 \alpha_1 = 2 q \alpha\)
\(\bf{A_1A_2}\)	\(\alpha_1 = q \alpha\)	\(\alpha_ 2 = -p \alpha\)	\(\alpha_1+ \alpha_2 =(q-p) \alpha\)
\(\bf{A_2A_2}\)	\(\alpha_2=-p \alpha\)	\(\alpha_2= -p \alpha\)	\(2 \alpha_2 = -2p \alpha\)

Por ejemplo, el genotipo \(A_1A_1\) está formado por dos alelos \(A_1\), que cada uno aporta un valor de \(\alpha_1=q \alpha\), por lo que el valor de cría de los individuos con este genotipo es de \(2\alpha_1=2q \alpha\). En el caso de un individuo con genotipo \(A_1A_2\) el mismo tendrá un alelo de cada tipo, por lo que su valor de cría será \(\alpha_1+\alpha_2=q \alpha +(-p\alpha)=(q-p) \alpha\). Finalmente, en el caso de un individuo con genotipo \(A_2A_2\), el mismo tendrá dos alelos \(A_2\) y por lo tanto su valor de cría será \(2\alpha_2=-2p\alpha\).

En general, el valor de cría se expresa como desvío de la media de la población, y como esta depende de las frecuencias de los alelos, entonces los valores de cría (igual que el efecto medio de cada alelo) son específicos a una población de referencia. El valor reproductivo medio de la población viene dado por la multiplicación de los valores reproductivos de cada genotipo por su frecuencia correspondiente, es decir

\[ \begin{split} \bar{A}=p^2(2q\alpha)+2pq[(q-p)\alpha]+q^2(-2p\alpha)=2\alpha(p^2q+pq^2-p^2q-pq^2)=0 \end{split} \tag{8.26} \]

Es decir, el valor de cría promedio de una población, en un modelo de un locus con dos alelos es cero, lo que no sorprende ya que realizamos todas las cuentas a partir de desvíos de la media de la población.

En el caso del valor de cría, al tratarse de la suma de los efectos aditivos de los alelos, el concepto es inmediatamente generalizable, tanto a un número indeterminado de loci como a un número de alelos igual o mayor a 2 en cada uno de esos loci. En cada locus un individuo puede tener solo dos alelos, por más que existan mayor cantidad de alelos posibles para ese locus, por lo que si utilizamos los números 1 y 2 para referirnos a los dos lugares en cada locus que pueden ser ocupados por alelos y utilizamos la letra \(k\) para los \(n\) loci que influencian la característica de interés, entonces tenemos

\[ \begin{split} A=\sum_{k=1}^n \alpha_{k,1} + \sum_{k=1}^n \alpha_{k,2} = \sum_{j=1,k=1}^{j=2,k=n} \alpha_{k,j} \end{split} \tag{8.27} \]

Es decir, en la ecuación (8.27) estamos sumando los aportes de cada locus, que son a su vez de dos alelos, que pueden ser iguales o distintos entre ellos, entre un número variable de alelos en cada locus. La Figura 8.7 muestra una representación gráfica del significado de la ecuación (8.27). En la misma se observan 3 cromosomas (representados por diferentes colores) que albergan un total de 6 loci (identificados por letras de la A a la E) que contribuyen a una característica cuantitativa. El valor de cría será la suma de los efectos medios de los alelos presentes en cada uno de los loci, es decir

\[A=\sum_{j=1,k=1}^{j=2,k=6} \alpha_{k,j}=(\alpha_{A1}+\alpha_{A3})+(\alpha_{B5}+\alpha_{B2})+(\alpha_{C8}+\alpha_{C4})+(\alpha_{D7}+\alpha_{D2})+\] \[(\alpha_{E1}+\alpha_{E1})+(\alpha_{F9}+\alpha_{F2})\]

donde los distintos \(\alpha\) son los efectos medios de los alelos correspondientes.

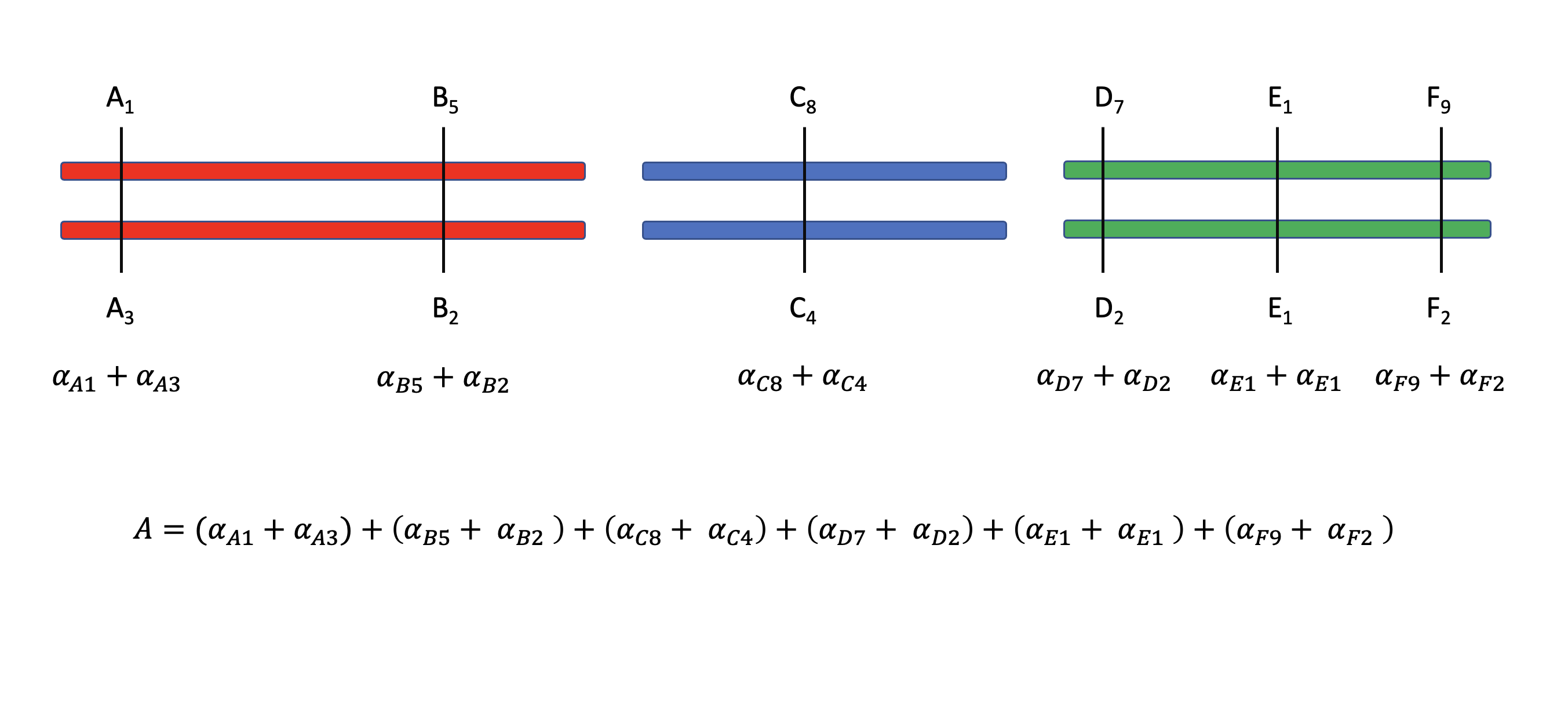
Figura 8.7: Valor de cría (o reproductivo) de un individuo diploide. Tres cromosomas, marcados por colores diferentes, presentan un total de 6 loci (nombrados A-E) que contribuyen al valor genotípico y fenotípico de una característica. El valor de cría está completamente determinado por la suma de los aportes individuales de todos los alelos presentes en los 6 loci. Cada loci tiene un número distinto de alelos, pero para cada uno de ellos siempre habrá dos alelos en particular, identificados por los números en el subíndice.

Si bien hemos dado dos definiciones diferentes del valor de cría, una de base teórica basada en el efecto medio de los alelos y otra más práctica, basada en la descendencia del candidato, ambas son estrictamente equivalentes cuando no existen efectos epistáticos, ya que si existe desequilibrio de ligamiento los alelos de diferentes loci van a ir juntos en relaciones distintas al producto de sus frecuencias y por lo tanto determinadas combinaciones (efectos epistáticos) serán más o menos frecuentes.

Ejemplo 8.4

En el trabajo de Bennett et al. (2019), los autores describen, además del gen de la miostatina, el aporte de los diplotipos (un par determinado de haplotipos) CC-CC, CC-NN y NN-NN en el gen de la \(\mu\)-calpaína. Para este gen se utilizaron dos marcadores (SNP), el CAPN1_316 (BTA29; rs17872000) y el CAPN1_4751 (BTA29;rs17872050). El marcador CAPN1_316 segrega los alelos C y G, mientras que CAPN1_4751 segrega los alelos C y T. Un haplotipo común es el CC (o sea, una C en el CAPN1_316 junto con una C en el CAPN1_4751), por lo que el resto se consideraron en conjunto como NN (es decir, alelos no-C en los dos marcadores).

En un estudio de simulación (hipotético) sobre datos del estudio de Bennett et al. (2019), se llega a la conclusión de que con frecuencias del alelo \(L\) de \(p_{MSTN}=0,20\), el efecto de sustitución en dicha población es de \(\alpha_{MSTN}=6,6 \text{ cm}^2\) para área del ojo del bife, mientras que para el diplotipo \(CC\), con frecuencia de \(p_{CAPN1}=0,45\), el efecto de sustitución en dicha población es de \(\alpha_{CAPN1}=0,3 \text{ cm}^2\). Calcular los valores de cría de los 9 genotipos posibles (3 genotipos de MSTN x 3 diplotipos de CAPN1).

Primero, usando la información de los efectos de sustitución y de las frecuencias para cada gen, calculamos los efectos medios de los alelos (los haplotipos pueden considerarse alelos). Es decir, para la miostatina (MSTN), tenemos

\[\alpha_{MSTNaL}=q(\alpha_{MSTN})=(1-0,20)6,6\text{ cm}^2=0,8\times 6,6\text{ cm}^2=5,28\text{ cm}^2\] \[\alpha_{MSTNaF}=-p(\alpha_{MSTN})=-0,20\times 6,6\text{ cm}^2=-1,32\text{ cm}^2\]

Para el gen de la \(\mu\)-caspaína (CAPN1), tenemos, de la misma forma

\[\alpha_{CAPN1aCC}=q\alpha_{CAPN1}=(1-0,45)0,3\text{ cm}^2=0,55\times0,3\text{ cm}^2=0,165\text{ cm}^2\] \[\alpha_{CAPN1aNN}=-p\alpha_{CAPN1}=-0,45\times 0,3\text{ cm}^2=-0,135\text{ cm}^2\]

Poniendo todo junto en el cuadro, recordando que los efectos aditivos de los alelos presentes se suman, tenemos (expresados en cm\(^2\))

	\({CC-CC}\)	\({CC-NN}\)	\({NN-NN}\)
\(LL\)	\(2.5,28+2.0,165=10,89\)	\(2.5,28+0,165-0,135=10,59\)	\(2.5,28-2.0,135=10,29\)
\(LF\)	\(5,28-1,32+2.0,165=4,29\)	\(5,28-1,32+0,165-0,135=3,99\)	\(5,28-1,32-2.0,135=3,69\)
\(FF\)	\(-2.1,32+2.0,165=-2,31\)	\(-2.1,32+0,165-0,135=-2,61\)	\(-2.1,32-2.0,135=-2,91\)

Derivación de los efectos medios por mínimos cuadrados

Una forma alternativa de derivar los efectos de sustitución es a partir del método de mínimos cuadrados, buscando los valores de los parámetros \(\alpha1\) y \(\alpha2\) de tal manera que minimicen las distancias entre los genotipos y la recta que pasa por los valores reproductivos. Esto podemos hacerlo tanto en la escala transformada (con el cero igual al punto medio entre los homocigotas) o como desvíos de la media \(M\). De hecho, es posible la transformación entre ambas escalas de forma muy sencilla, como veremos en la siguiente sección. Por lo tanto, haremos la derivación en la escala transformada y al final, cambiaremos de escala para verificar que es el mismo resultado obtenido previamente como desvíos de la media poblacional.

Si, siguiendo la notación de John H. Gillespie (2004), llamamos \(Q(\alpha1,\alpha2)\) a la función que establece la distancia de los genotipos a la recta de valores reproductivos, entonces

\[ \begin{split} Q(\alpha1,\alpha2)=p^2(a-2\alpha_1)^2+2pq(d-\alpha_1-\alpha_2)^2+q^2(-a-2\alpha_2)^2 \end{split} \tag{8.28} \]

Para encontrar los valores de los parámetros \(\alpha_1\) y \(\alpha_2\) que minimicen esta función debemos derivar e igualar a cero. Como la derivada de una suma es la suma de las derivadas, usando la regla de la cadena y teniendo en cuenta que cuando derivamos respecto a \(\alpha_1\), \(\alpha_2\) pasa a ser tratada como una constante (y viceversa), entonces

\[\frac{\partial Q}{\partial \alpha_1}=-4[p^2(a-2\alpha_1)+pq(d-\alpha_1-\alpha_2)]=0\] \[ \begin{split} \frac{\partial Q}{\partial \alpha_2}=-4[pq(d-\alpha_1-\alpha_2)]+q^2(-a-2\alpha_2)]=0 \end{split} \tag{8.29} \]

Operando con la primera ecuación de (8.29), tenemos

\[ \begin{split} -4[p^2(a-2\alpha_1)+pq(d-\alpha_1-\alpha_2)]=-4p[p(a-2\alpha_1)+q(d-\alpha_1-\alpha_2)] \end{split} \]

y dividiendo entre \(-4p\), usando además el hecho de que \(p\alpha_1+q\alpha_2=0\) ya que es el efecto aditivo medio, tenemos

\[p(a-2\alpha_1)+q(d-\alpha_1-\alpha_2)=pa-2p\alpha_1+qd-q\alpha_1-q\alpha_2 =\] \[pa-p\alpha_1-p\alpha_1+qd-q\alpha_1-q\alpha_2=pa-(p\alpha_1+q\alpha_2)-\alpha_1(p+q)+qd=\] \[ \begin{split} pa+qd-\alpha_1 \end{split} \tag{8.30} \]

e igualando a cero el resultado de la ecuación (8.30) tenemos que

\[ \begin{split} pa+qd-\alpha_1=0 \Leftrightarrow \alpha_1=pa+qd \end{split} \tag{8.31} \]

De manera análoga, operando con la segunda ecuación de (8.29), dividiendo entre \(-4q\), tenemos

\[p(d-\alpha_1-\alpha_2)]+q(-a-2\alpha_2)]=pd-p\alpha_1-p\alpha_2-qa-2q\alpha_2=\] \[ \begin{split} pd-(p\alpha_1+q\alpha_2)-\alpha_2(p+q)-qa=pd-qa-\alpha_2 \end{split} \tag{8.32} \]

e igualando a cero el resultado de la ecuación (8.32) tenemos que

\[ \begin{split} pd-qa-\alpha_2=0 \Leftrightarrow \alpha_2=pd-qa \end{split} \tag{8.33} \]

Para verificar que el resultado obtenido en la escala transformada es idéntico al obtenido previamente como desvío de la media poblacional, teniendo en cuenta que la media de la población es \(M=a(p-q)+2pqd\), tenemos entonces

\[\alpha_1=p(a-M)+q(d-M)=pa+qd-pM-qM=\] \[=pa+qd-M(p+q)=pa+qd-M=pa+qd-[a(p-q)+2pqd]\ \therefore\] \[\alpha_1=pa+qd-pa+qa-2pqd=q[a+d-2pd]=q[a+d(1-2p)]\ \therefore\] \[ \begin{split} \alpha_1=q[a+d(1-p-p)]= q[a+d((1-p)-p)]=q[a+d(q-p)] \end{split} \tag{8.34} \]

que es el mismo resultado que habíamos obtenido previamente, o usando la definición original de \(\alpha=a+d(q-p)\), \(\alpha_1=q\alpha\).

De la misma manera, para \(\alpha_2\) en la escala como desvío de la media poblacional, tenemos

\[\alpha_2=p(d-M)-q(a-M)=pd-qa-M=pd-qa-[a(p-q)+2pqd]=\] \[=pd-qa-pa+qa-2pqd=-p[a+d(2q-1)]=-p[a+d(q+q-1)]\ \therefore\] \[ \begin{split} \alpha_2=-p[a+d(q-(1-q))]=-p[a+d(q-p)] \end{split} \tag{8.35} \]

que es el mismo resultado obtenido previamente, o \(\alpha_2=-p\alpha\), mostrando la consistencia de las dos aproximaciones.

• El valor de cría es un estimador del mérito genético de un animal. El mismo se expresa como desvío de la media de la población, y como esta depende de las frecuencias de los alelos, entonces los mismos son específicos a una población de referencia.

• Dado que en cada locus un individuo puede únicamente tener dos alelos (que denominaremos \(1\) y \(2\) haciendo referencia al lugar del locus que ocupan), y usando la letra \(k\) para los \(n\) loci que influencian la característica de interés:

\[ \begin{split} A=\sum_{k=1}^n \alpha_{k,1} + \sum_{k=1}^n \alpha_{k,2} = \sum_{j=1,k=1}^{j=2,k=n} \alpha_{k,j} \end{split} \]

-El valor de cría será la suma de los efectos medios de los alelos presentes en cada uno de los loci.

8.6 Desvío de dominancia

En la sección anterior avanzamos en la comprensión de uno de los componentes del genotipo, el que tiene que ver con los valores aditivos de los alelos que lo constituyen. Pero como hemos discutido previamente, en general la expresión de los alelos presentes en un locus trasciende el valor de cada uno en particular. La razón de esto es fácil de imaginar en la biología subyacente al problema. Por un lado, no necesariamente las dos copias presentes en un locus determinado tienen por que transcribirse/traducirse (por ejemplo, en determinadas regiones de cromosomas como el X). Por el otro, la cinética de las reacciones, en el caso de que se trate de un locus que produce un sustrato enzimático, no suele ser simplemente aditiva ya que el comportamiento es varias veces sigmoidal. Todas estas razones nos llevan a pensar que, en general, debemos considerar en forma matemática el desvío correspondiente a la interacción entre alelos dentro del locus como una posibilidad bastante razonable.

De acuerdo a nuestro modelo genético para el caso de un solo locus, como no consideramos los efectos epistáticos ya que no hay otro locus con el cual interactuar, entonces \(G=A+D*I=A+D\) y por lo tanto,

\[ \begin{split} G=A+D \Leftrightarrow D=G-A \end{split} \tag{8.36} \]

Es decir, de acuerdo a nuestro modelo, la interacción entre alelos del mismos locus lo modelamos como un desvío de los valores genotípicos respecto a los valores de cría (o valores aditivos). En la sección precedente expresamos los valores reproductivos como desvíos de la media de la población, por lo que si queremos mantener la consistencia de nuestras derivaciones del desvío de dominancia debemos entonces expresarlo de la misma forma. Para eso vamos a expresar primero los valores genotípicos como desvíos de la media de la población, lo que resulta inmediato al restar \(M=a(p-q)+2pqd\) a cada uno de los tres valores genotípicos en la escala transformada (\(a\), \(d\) y \(-a\)). Operando, si denotamos con \(\gamma\) a los desvíos genotípicos respecto a la media poblacional, es decir, \(\gamma_{ij}=G_{ij}-M=G_{ij}-[a(p-q)+2pqd]\), tenemos entonces

\[\gamma_{11}=a-[a(p-q)+2pqd]=a(1-p+q)-2pqd=a(q+q)-2pqd=2qa-2pqd\ \therefore\] \[\gamma_{11}=2q(a-pd)\] \[\gamma_{12}=d-[a(p-q)+2pqd]=a(q-p)+d(1-2pq)\] \[\gamma_{22}=-a-[a(p-q)+2pqd]=-a(1-q+p)-2pqd=-a(p+p)-2pqd\ \therefore\] \[ \begin{split} \gamma_{22}=-2p(a+qd) \end{split} \tag{8.36} \]

Pero de acuerdo a nuestra definición \(\alpha=a+d(q-p) \Leftrightarrow a=\alpha -d(q-p)\), por lo que sustituyendo en la ecuación (8.36) tenemos para los homocigotas las siguientes expresiones

\[\gamma_{11}=2q(a-pd)=2q[\alpha -d(q-p)-pd]=2q(\alpha-qd+pd-pd)\ \therefore\] \[\gamma_{11}=2q(\alpha-qd)\] \[\gamma_{22}=-2p(a+qd)=-2p[\alpha -d(q-p)+qd]=-2p(\alpha-qd+pd+qd)\ \therefore\] \[ \begin{split} \gamma_{22}=-2p(\alpha+pd) \end{split} \tag{8.37} \]

Para los heterocigotas el principio es el mismo, aunque la derivación nos lleva un poquito más de trabajo para finalmente arribar a una expresión sencilla

\[\gamma_{12}=a(q-p)+d(1-2pq)=[\alpha-d(q-p)](q-p)+d(1-2pq)=\] \[=\alpha(q-p)-d(q-p)^2+d-2pqd=\alpha(q-p)-d(q^2-2pq+p^2)+d-2pqd=\] \[\alpha(q-p)-d(q^2+p^2)+2pqd+d-2pqd=\alpha(q-p)+d[1-(p^2+q^2)]=\] \[=\alpha(q-p)+d(2pq)\ \therefore\] \[ \begin{split} \gamma_{12}=\alpha(q-p)+2pqd \end{split} \tag{8.38} \]

Una forma sencilla de entender el procedimiento que hemos utilizado es organizar toda la información en un cuadro como el siguiente:

	\(\bf{A_1A_1}\)	\(\bf{A_1A_2}\)	\(\bf{A_2A_2}\)
\(\textbf{Frecuencia H-W}\)	\(p^2\)	\(2pq\)	\(q^2\)
\(\textbf{Valor genotípico}\)	\(a\)	\(d\)	\(-a\)
\(\textbf{Genotípico como desvío de M}\)	\(2q(\alpha-qd)\)	\((q-p)\alpha+2pqd\)	\(-2p(\alpha+pd)\)
\(\textbf{Valor Reproductivo (de cría)}\)	\(2q \alpha\)	\((q-p)\alpha\)	\(-2p \alpha\)
\(\textbf{Desvío de dominancia}\)	\(-2q^2d\)	\(2pqd\)	\(-2p^2d\)

En un locus con dos alelos tenemos 3 genotipos posibles, que si además le incorporamos la restricción de que las frecuencias se encuentren en equilibrio de Hardy-Weinberg, estarán en las clásicas proporciones \(p^2\), \(2pq\) y \(q^2\) (para una frecuencia \(p\) del alelo \(A_1\)). Los valores, como ya hemos visto, en la escala transformada son \(a\), \(d\) y \(-a\). A partir de las ecuaciones (8.36) a (8.38), los valores genotípicos como desvíos de la media \(M\) son los que aparecen en la tercera línea del cuadro. Si ahora le restamos a esos valores genotípicos los correspondientes valores reproductivos que aparecen en la cuarta línea (y que dedujimos en la sección precedente), tenemos ahora los desvíos de dominancia que aparecen en la última línea. Por ejemplo, para el genotipo \(A_1A_1\), su valor como desvío de la media de la población (como vimos en la ecuación (8.37)) es \(\gamma_{11}=2q(\alpha-qd)=2q\alpha-2q^2d\), por lo que si ahora le restamos su valor reproductivo \(A_{11}=2q\alpha\), tenemos el valor \(-2q^2\). Lo mismo se aplica para los otros genotipos, por lo que resumiendo tenemos

\[\delta_{11}=\gamma_{11}-A_{11}=2q\alpha-2q^2d-2q\alpha=-2q^2d\] \[\delta_{12}=\gamma_{12}-A_{12}=(q-p)\alpha+2pqd-(q-p)\alpha=2pqd\] \[ \begin{split} \delta_{22}=\gamma_{22}-A_{22}=-2p\alpha-2p^2d-(-2p\alpha)=-2p^2d \\ \end{split} \tag{8.39} \]

Es importante notar que al igual que los valores reproductivos, los desvíos de dominancia también dependen de las frecuencias de los alelos, así como de los valores de \(a\) y \(d\), por lo que son específicos de cada población. Una forma gráfica de entender la relación entre los valores genotípicos, los valores reproductivos y los desvíos de dominancia se aprecia en la Figura 8.8. En la misma, podemos ver los tres genotipos representados por los círculos negros y sus correspondientes valores en la escala transformada (\(a\), \(d\) y \(-a\)) en el eje de las ordenadas a la izquierda. Si hacemos la regresión de los valores genotípicos en el número de copias del alelo \(A_1\), por ejemplo usando la técnica de mínimos cuadrados, entonces obtenemos la línea roja a trazos que vemos en la figura. El cambio en las ordenadas de esta línea con un cambio de una unidad en el número de copias de \(A_1\) es la pendiente de dicha recta y se corresponde con nuestra definición del efecto de sustitución y es por lo tanto de \(\alpha\). La recta no queda equidistante de los puntos negros porque cada punto tiene una “inercia” diferente, dada por la frecuencia del correspondiente genotipo: en el caso de la Figura 8.8, \(q^2=\left(\frac{1}{4}\right)^2=\frac{1}{16}\) pesa mucho menos que \(p^2=\left(\frac{3}{4}\right)^2=\frac{9}{16}\) y por lo tanto la diferencia de distancias de los puntos negros a la recta. Ahora, si observamos el valor de los tres puntos rojos que están sobre la recta en la escala de la derecha, que es la escala como desvíos de la media poblacional \(M=a(p-q)+2pqd\), entonces tenemos los valores reproductivos que se corresponden con cada genotipo. Por lo tanto, la distancia entre los puntos rojos y los puntos negros, es decir la ordenada de los puntos negros (genotipos) menos la de los correspondientes puntos rojos (valores reproductivos) son los desvíos de dominancia. Notar que en la ecuación (8.39) todos los desvíos de dominancia depende exclusivamente de la frecuencia alélicas (\(p\) o \(q=1-p\)) y del valor del desvío del genotipo heterocigota respecto del punto medio entre los homocigotas (o lo que es lo mismo, del apartarmiento de este genotipo del cero en la escala transformada), por lo que cuando el mismo sea cero (\(d=0\)) los valores genotípicos serán idénticos a los valores reproductivos.

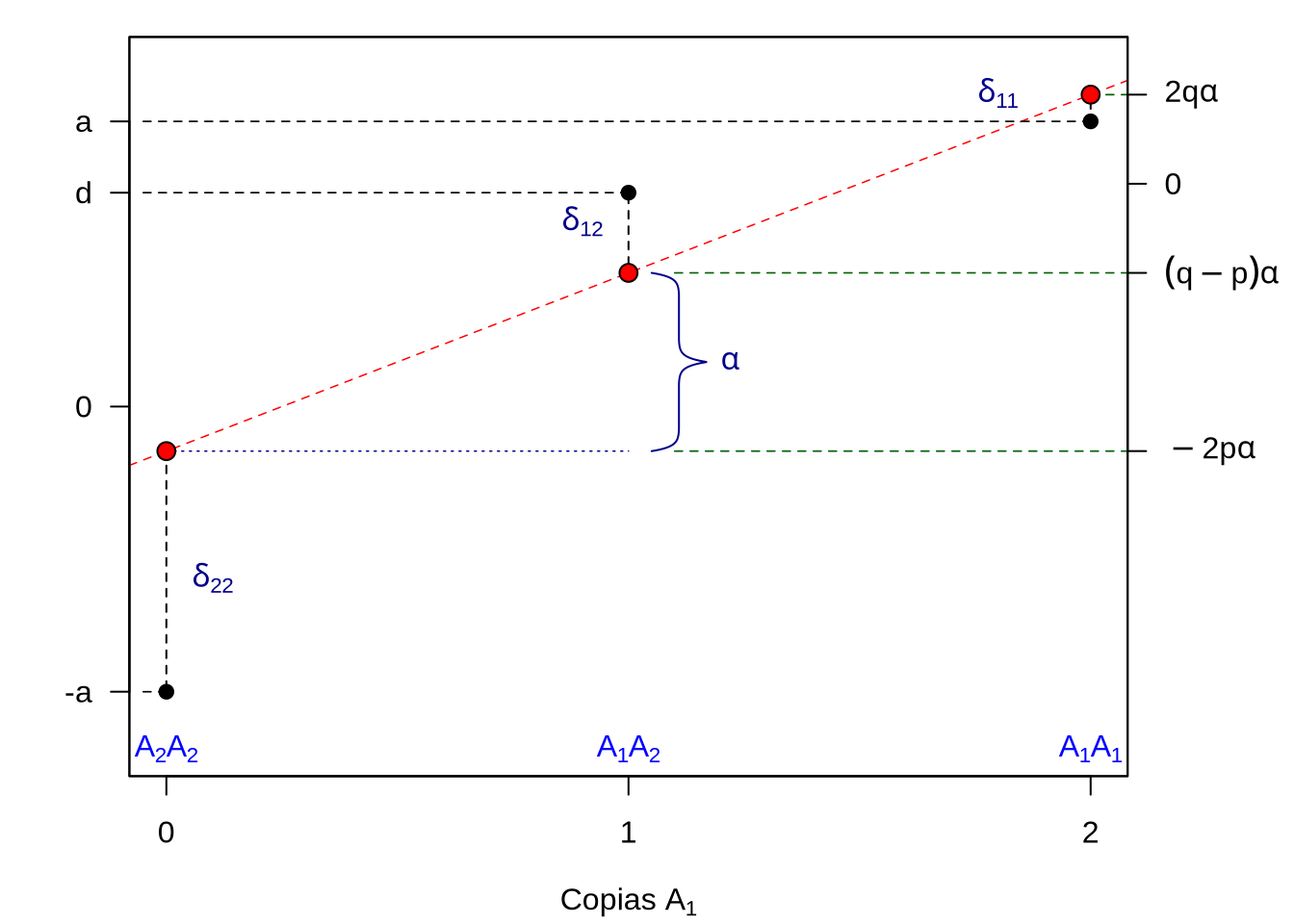
Figura 8.8: Representación gráfica de los valores genotípicos, círculos negros, valores de cría (o reproductivos), círculos rojos y la desviación entre ambos valores correspondiente al desvío de dominancia. La línea roja a trazos representa la recta de regresión de los valores genotípicos en el número de copias del alelo \(A_1\). La pendientes de dicha recta es \(\alpha\) (el efecto de sustitución) y los valores de las ordenadas de dicha recta para los puntos en las abscisas 0, 1 y 2 se corresponden con los valores de cría de los genotipos con dichos número de copias del alelo \(A_1\). Mientras que el eje de la izquierda refiere a los valores de los genotipos en la escala transformada, los valores del eje a la derecha se corresponden a desvíos de la media \(M=a(p-q)+2pqd\). Los valores usados para la representación fueron \(d=\frac{3}{4}a\) y \(p=\frac{3}{4}\). Figura de elaboración propia sobre idea en Douglas S. Falconer (1983).

Para ilustrar el efecto del cambio en el desvío de dominancia con la frecuencia del alelo \(A_1\) y del desvío del heterocigoto respecto al punto medio de los homocigotos en la Figura 8.9 ilustramos diferentes combinaciones de estos parámetros. En la misma figura, los círculos azules representan los valores genotípicos, mientras que las líneas rojas a trazos representan las regresiones de los mismos en el número de copias del alelo \(A_1\) (lo que nos da los valores de cría, o aditivos, de cada genotipo). En la línea superior de la figura se ven los gráficos cuando el desvío del heterocigoto respecto del punto medio es cero (\(d=0\)), es decir que el comportamiento de los genotipos es totalmente aditivo (alcanza con conocer el número de copias de \(A_1\) en cada uno de ellos y la pendiente \(\alpha\) para predecir con exactitud su valor genotípico), por eso los puntos están sobre la recta siempre. En la fila del medio apreciamos la situación con dominancia parcial (\(d=0,75a\)), donde el genotipo \(A_1A_2\) está mucho más cerca en valor del \(A_1A_1\) que del \(A_2A_2\) y por eso está por encima de la recta de regresión. A su vez, al movernos de izquierda a derecha aumenta la frecuencia del alelo \(A_1\) (de \(p=0,50\), \(p=0,75\) a \(p=0,90\)), por lo que la importancia del genotipo \(A_1A_1\) (frecuencia \(p^2\)) en la determinación de la pendiente crece, en particular respecto al \(A_2A_2\). Por esta razón, a medida de que nos vamos hacia la derecha en los gráficos la pendiente parece mucho más determinada por los valores de \(A_1A_1\) y \(A_1A_2\) que por los de \(A_2A_2\) y mientras que la distancia de \(A_1A_1\) a la recta decrece, la de \(A_2A_2\) aumenta. Este efecto se ve aún más magnificado cuando tenemos efecto de sobredominancia, como en la última fila de la figura (\(d=1,75a\)), donde a altas frecuencia del alelo \(A_1\) llega a invertirse el signo de la pendiente, casi ignorando el aporte del genotipo \(A_2A_2\) en la regresión ya que su proporción es ínfima (\(q^2=(1-p)^2=(1-0,90)^2=0,10^2=0,01=1\%\)). Claramente, cuanto más cerca se encuentre la recta de regresión de los puntos, mejor explican los efectos aditivos los valores genotípicos.

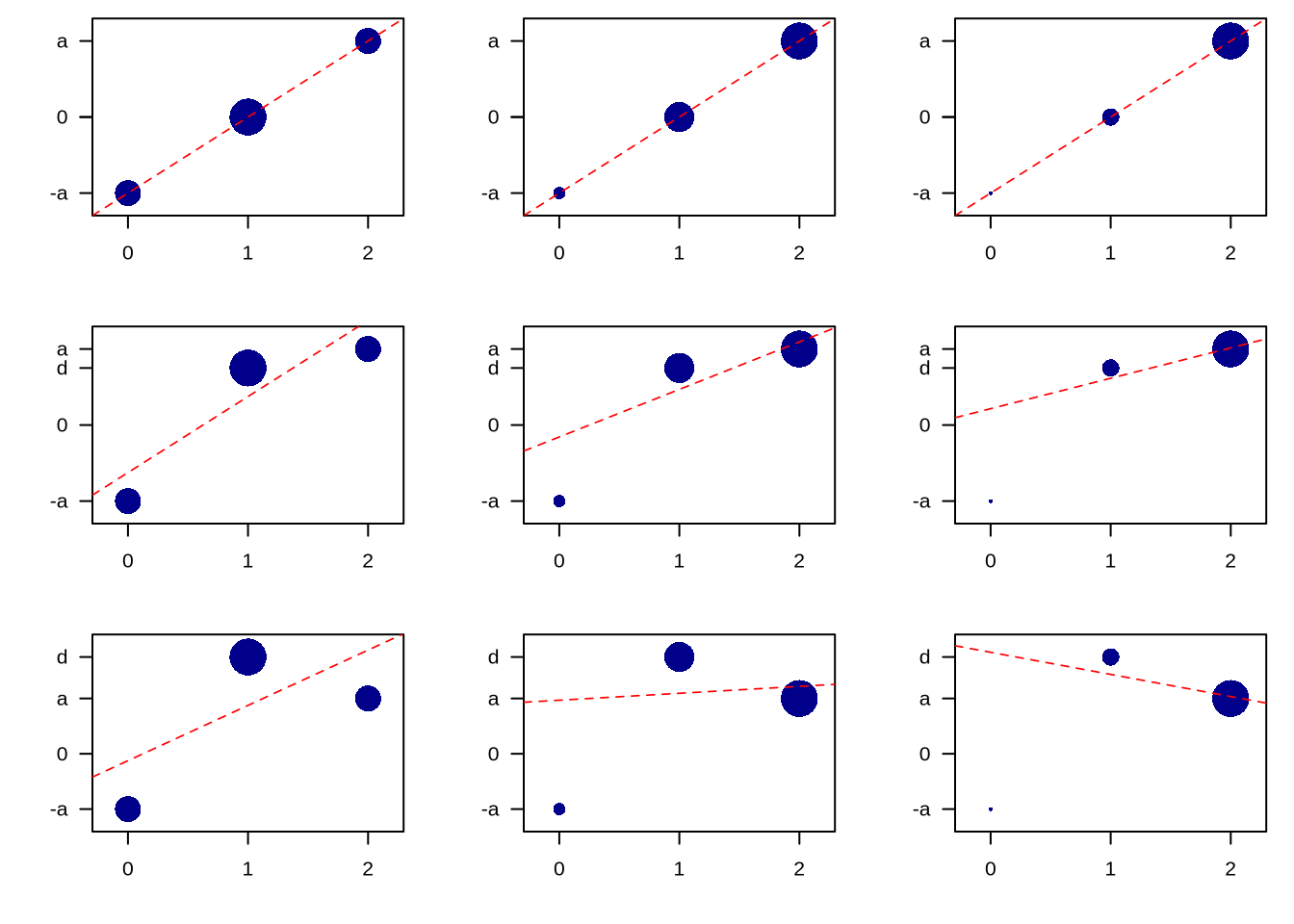
Figura 8.9: Representación gráfica de los valores genotípicos (círculos azules) y la correspondiente recta de regresión de los valores genotípicos en el número de copias del alelo \(A_1\) (cuya pendiente es \(\alpha\)) para diferentes combinaciones de frecuencias del alelo \(A_1\) (de izquierda a derecha, \(p=0,50\), \(p=0,75\) y \(p=0,90\)) y de el desvío del heterocigoto respecto al punto medio de los homocigotos (de arriba a abajo, \(d=0\), \(d=0,75a\) y \(d=1,75a\)). Las áreas de cada círculo son proporcionales a la frecuencia de cada genotipo (dentro de cada gráfico). Figura de elaboración propia sobre idea en Michael Lynch and Walsh (1998).

En el caso del valor de cría, vimos previamente en la ecuación (8.26) que el valor medio de la población era igual a cero. Veamos ahora que ocurre con el desvío de dominancia promedio. Nuevamente, multiplicando los valores de desvío de cada genotipo por las frecuencias correspondientes y sumando tenemos

\[ \begin{split} \bar{\delta}=p^2(-2q^2d)+2pq(2pqd)+q^2(-2p^2)d=2p^2q^2d(-1+2-1)=2p^2q^2d \times 0=0 \end{split} \tag{8.40} \]

por lo que también el valor promedio del desvío de dominancia en nuestra población será cero. Esto no nos debería sorprender ya que por construcción, es decir, por propiedades del ajuste por mínimos cuadrados el desvío promedio de la recta es cero. Finalmente, un punto importante a entender es que también por construcción, bajo apareamientos al azar (es decir, equilibrio de Hardy-Weinberg) los valores reproductivos son ortogonales a los valores de desvío dominante. Dicho de otra forma, no existe correlación entre unos valores y los otros. Para demostrar hacemos la suma de los productos cruzados, multiplicado cada uno por su frecuencia correspondiente, es decir

\[p^2[(2q\alpha)(-2q^2d)]+2pq[(q-p)\alpha(2pqd)]+q^2[(-2p\alpha)(-2p^2d)]=\] \[ \begin{split} =4p^2q^2d\alpha[-q+(q-p)+p]=4p^2q^2d\alpha [0]=0 \end{split} \tag{8.41} \]

o dicho de otra forma, no existe correlación entre los valores de cría de los genotipos y los desvíos de dominancia, que es lo que queríamos demostrar.

Ejemplo 8.5

Asumiendo que los genotipos se encuentran en equilibrio de Hardy-Weinberg, calcular el desvío de dominancia para los tres genotipos del gen de la miostatina, para la característica área del ojo del bife, con los datos del estudio de Bennett et al. (2019) que aparecen en el Ejemplo 8.1 y recordando que la frecuencia del alelo \(L\) era \(p=0,207 \Rightarrow q=1-p=0,793\).

Usando los resultado del Ejemplo 8.1, tenemos que los genotipos en la escala transformada eran

\[A_{LL}=G_{LL}-m=(103-96) \text{ cm}^2=7 \text{ cm}^2=a\] \[A_{FL}=G_{FL}-m=(93-96) \text{ cm}^2=-3 \text{ cm}^2=d\] \[A_{FF}=G_{FF}-m=(89-96) \text{ cm}^2=-7 \text{ cm}^2=-a\]

Ahora, a partir de la ecuación (8.39), tenemos

\[\delta_{LL}=-2q^2d=-2 \times 0,793^2 (-3 \text{ cm}^2)=3,773 \text{ cm}^2\] \[\delta_{FL}=2pqd=2 \times 0,207 \times 0,793 (-3 \text{ cm}^2)=-0,985 \text{ cm}^2\] \[\delta_{FF}=-2p^2d=-2 \times 0,207^2 (-3 \text{ cm}^2)=0,257 \text{ cm}^2\]

Claramente, como la frecuencia del genotipo \(LL\) es menor que la del \(FF\), entonces la incidencia en la regresión (valores de cría) es menor para \(LL\) y por lo tanto su desvío de dominancia debe ser mucho mayor.

---

• Podemos modelar la interacción entre alelos del mismos locus como un desvío de los valores genotípicos respecto a los valores de cría (o valores aditivos). Por lo tanto si \(d=0\), los valores genotípicos serán iguales a los valores reproductivos.

• Los desvíos de dominancia correspondientes a los genotipos \(A_1A_1\), \(A_1A_2\) y \(A_2A_2\) serán \(-2q^2d\), \(2pqd\) y \(-2p^2d\) respectivamente.

• Al igual que los valores reproductivos, los desvíos de dominancia también dependen de las frecuencias de los alelos, así como de los valores de \(a\) y \(d\), por lo que son específicos de cada población.

• Por construcción y bajo apareamiento al azar, no existe correlación entre los valores de cría de los genotipos y los desvíos de dominancia.

8.7 Interacción Genotipo x Ambiente

Como discutimos en la propuesta original del modelo genético básico, consideramos el fenotipo de un individuo como la resultante de los aportes de su genética y del ambiente en que expresa la característica. Sin embargo, vimos que considerar exclusivamente estas dos fuentes de variabilidad a partir de la suma de los aportes de cada una podía ser extremadamente limitado para describir las observaciones fenotípicas. De hecho, el mismo genotipo suele tener un comportamiento fuertemente dependiente del ambiente en que se expresa y los distintos genotipos son diferentes también en como responden a estos cambios de ambiente.

La Figura 8.10 muestra un ejemplo de falta de interacción y de una importante interacción GxE en ganado lechero.

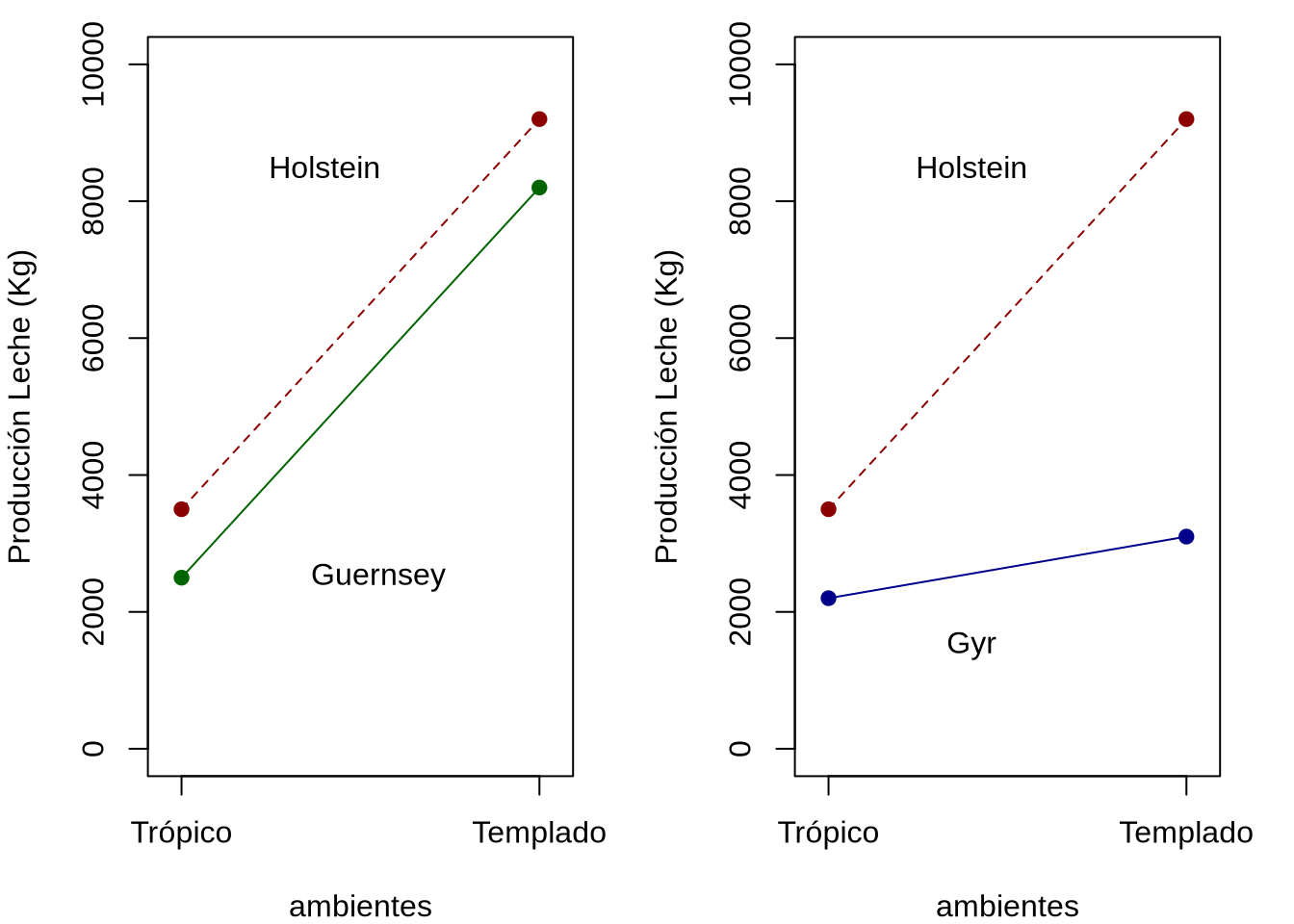
Figura 8.10: Interacción GxE en ganado lechero. En la gráfica de la izquierda, dos razas típicamente lecheras (Guernsey y Holstein) expresan su producción en el trópico y en un clima templado y si bien en ambas la producción cambia enormemente con el ambiente, las distancias entre razas se mantienen, es decir la líneas son paralelas y no existe interacción GxE. En la gráfica de la derecha, ahora comparando Holstein contra una raza cebuína (Gyr), si bien ambas razas experimentan un decrecimiento en la producción en el trópico respecto a condiciones ambientales más moderadas, mientras que en Holstein el decrecimiento es enorme, en Gyr el cambio es sumamente menor.

Las razas lecheras tradicionales, como Holstein, Jersey, Guernsey, etc. producirán leche en grandes cantidades si cuentan con comida ad libitum en climas templados y mejor aún en climas fríos. En la gráfica de la izquierda vemos la comparación de dos razas lecheras en dos ambientes contrastantes, el trópico y un clima templado. Claramente, ambas razas sufren del estress térmico asociado a la producción en el trópico y su producción es sustancialmente menor que en clima templado, pero las diferencias entre razas en los dos ambientes se mantienen y por lo tanto las líneas son paralelas, por lo que no existe interacción genotipo-ambiente. Por otro lado, la raza cebuina Gyr, aún con comida ad libitum producirá bastante menos leche aún en óptimas condiciones climáticas ya que posee menor capacidad genética para producirla. En la gráfica de la derecha vemos la comparación de Gyr y Holstein en los mismos dos ambientes contrastantes. Cuando comparamos la producción de ambas razas en el trópico, donde la temperatura puede ser agobiante, la enorme diferencia que podemos observar en climas templado se ve completamente reducida en el trópico. Claramente, ambas razas producen menos en el trópico que en climas templados, pero mientras que en el trópico la producción de la vaca Holstein caerá enormemente, el animal Gyr continuará produciendo leche en forma razonable en proporción a su máxima capacidad genética.

En general, los animales (al menos los de interés productivo) tienen cierta capacidad de modular estos efectos “eligiendo” el ambiente, en la medida de sus posibilidades. Ninguna vaca Holando se va a quedar a pleno rayo de sol, en un día típico de verano, al mediodía, en Salto, pudiendo resguardarse en el montecito que tiene el potrero. Las plantas, por el contrario, tienen limitada capacidad de desplazamiento (por no decir incapacidad), por lo que en general sufrirán todas las consecuencias del ambiente y por lo tanto el componente de interacción genotipo-ambiente se verá en toda su expresión. Dada la complejidad del tratamiento de este tema, le dedicaremos todo el capítulo final (Normas de reacción e interacción Genotipo x Ambiente) al mismo.

8.8 La varianza en el modelo genético básico

Hasta el momento hemos trabajado en este capítulo considerando lo que le ocurre a cada individuo en particular y hemos visto cómo podemos modelar su fenotipo, es decir, la observación o medición directa de una característica en el individuo. Sin embargo, como también hemos discutido en forma abundante, los individuos pertenecen a poblaciones y los distintos fenotipos de los integrantes de las mismas están sujetos a distintos factores estocásticos, tanto en lo que hace a la genética de los mismos, como a los ambientes. Con esto en mente, resulta muy claro que no alcanza con las medias de cada uno de los componentes para describir la importancia relativa de las distintas fuentes de variabilidad y debemos recurrir a otros descriptores de las mismas.

En general, con distribuciones que se comportan en forma razonable, la varianza (el segundo momento centrado de una distribución) es un buen indicador de la dispersión y variabilidad de las observaciones. Más aún, para conocer la importancia relativa de las distintas fuentes de variabilidad y su importancia estadística, por ejemplo la genética en relación a la ambiental, la forma usual de hacerlo es comparando las varianzas, una aproximación que introdujo Ronald Fisher con su análisis de varianza. Si recordamos nuestro modelo genético básico, en una de sus formas más simplificadas establecía que el fenotipo de un individuo era la suma de los efectos del genotipo y del ambiente en el mismo, más un componente referido a la interacción genotipo ambiente, es decir \(P=G+E+I_{GxE}\). Como cada individuo de nuestra población podemos considerarlo como una extracción al azar de los factores genéticos y ambientales, entonces los fenotipos serán un también una extracción al azar de una distribución aleatoria. Por lo tanto, aplicando la regla para el cálculo de la varianza de una suma de variables aleatorias, tenemos que

\[ \begin{split} V_P=\mathbb{V}(G+E+I_{GxE})=V_G+V_E+V_{GxE}+2 {Cov}_{GE} \end{split} \tag{8.42} \]

Es decir, la varianza fenotípica (la varianza de lo que observamos) es la suma de la varianza genética, la varianza ambiental, la varianza de la interacción genotipo-ambiente (\(V_{GxE}\)), más dos veces la covarianza entre genotipo y ambiente. La varianza de interacción es la correspondiente a ese término del modelo genético básico, como lo discutimos previamente y parece ser bastante ubicua en la biología de animales y plantas al menos. Ya vimos previamente que cuando el cambio de ambientes implicaba diferentes pendientes en dos genotipos era necesario agregar este término de interacción, que se trata de sumar valores a combinaciones específicas de genotipos y ambientes, por lo que este “número” tendrá una varianza. En el caso de la covarianza entre genotipo y ambiente la misma se refiere al hecho de que muchas veces los “ambientes” no se distribuyen al azar respecto a los genotipos. Un ejemplo usual de esto es cuando a determinados animales de “elite” se le asignan mejores recursos (alimentación, alojamiento, tratamiento, etc.) que al resto de los animales. En general no es posible desentrañar esta covarianza por lo que de existir puede afectar las estimaciones de ambos componentes, genéticos y ambientales.

Como vimos en la introducción del modelo genético básico, la componente genética del mismo (\(G\)) puede descomponerse en los aportes de los efectos aditivos, los efectos de dominancia y los efectos epistáticos, es decir \(G=A+D+I\), por lo que sustituyendo en la ecuación (8.43), tenemos que la varianza fenotípica se puede descomponer de la siguiente manera

\[ \begin{split} V_P=\mathbb{V}(G+E+I_{GxE})=(V_A+V_D+V_I)+V_E+V_{GxE}+2 {Cov}_{GE} \end{split} \tag{8.43} \]

que es una de las maneras de descomponerla que más usaremos en el curso (tanto la varianza de efectos epistáticos, como la varianza ambiental se pueden descomponer aún más, pero el uso de estas divisiones será muy pautado).

Componentes genéticos de la varianza: un locus con dos alelos

En el caso de la varianza genética, cuando reducimos nuestro modelo al caso de un locus con dos alelos, podemos continuar el análisis que realizamos previamente para deducir el valor reproductivo y los desvíos de dominancia. Comencemos entonces por la varianza aditiva. Como los valores reproductivos ya están medidos como desvíos de la media de la población, entonces la varianza es solamente la suma de los productos de las frecuencias por el cuadrado del valor reproductivo de cada genotipo. Si organizamos la información de los valores reproductivos y las frecuencias de cada genotipo en un cuadro, así como los cuadrados de los valores reproductivos y el producto de las frecuencias por los cuadrados, tenemos la siguiente información:

Genotipo	Frecuencia	Valor reproductivo	Cuadrado	Producto
\(\bf{A_1A_1}\)	\(p^2\)	\(2q \alpha\)	\(4q^2 \alpha^2\)	\(4p^2q^2 \alpha^2\)
\(\bf{A_1A_2}\)	\(2pq\)	\((q-p) \alpha\)	\((1-4pq) \alpha^2\)	\((2pq-8p^2q^2) \alpha^2\)
\(\bf{A_2A_2}\)	\(q^2\)	\(-2p \alpha\)	\(4p^2 \alpha^2\)	\(4p^2q^2 \alpha^2\)
\(\textbf{Suma}\)				\(2pq \alpha^2\)

Los cuadrados de los valores reproductivos de los genotipos \(A_1A_1\) y \(A_2A_2\) son triviales de obtener, mientras que el del valor reproductivo del heterocigota es bastante sencillo si tenemos en cuenta que \(p^2+2pq+q^2=1 \Leftrightarrow p^2+q^2=1-2pq\), por lo que

\[ \begin{split} [(q-p) \alpha]^2=(q-p)^2 \alpha^2=(p^2+q^2-2pq) \alpha^2=(1-2pq-2pq) \alpha^2=(1-4pq) \alpha^2 \end{split} \]

La suma de los valores de la última columna es la varianza aditiva de la característica explicada por nuestro locus. Para obtenerla hacemos

\[ \begin{split} V_A=4p^2q^2 \alpha^2+(2pq-8p^2q^2) \alpha^2+4p^2q^2 \alpha^2=2pq\alpha^2[2pq+1-4pq+2pq]=\\ =2pq\alpha^2(1) \therefore V_A=2pq\alpha^2\\ \end{split} \tag{8.44} \]

Para determinar la varianza de dominancia podemos aplicar el mismo procedimiento, ya que también se trata de desvíos de la media de la población. Organizando la información en un cuadro tenemos:

Genotipo	Frecuencia	Desvío dominancia	Cuadrado	Producto
\(A_1A_1\)	\(p^2\)	\(-2q^2d\)	\(4q^4d^2\)	\(4p^2q^4d^2\)
\(A_1A_2\)	\(2pq\)	\(2pqd\)	\(4p^2q^2d^2\)	\(8p^3q^3d^2\)
\(A_2A_2\)	\(q^2\)	\(-2p^2d\)	\(4p^4d^2\)	\(4p^4q^2d^2\)
\(\textbf{Suma}\)				\((2pqd)^2\)

Esta vez los cuadrados de los valores de desvíos de dominancia son todos triviales, por lo que si pasamos a sumar los productos por las correspondientes frecuencias, en la última columna, tenemos

\[V_D=4p^2q^4d^2+8p^3q^3d^2+4p^4q^2d^2=4p^2q^2d^2[q^2+2pq+p^2]=4p^2q^2d^2(1)=4p^2q^2d^2\ \therefore\] \[ \begin{split} V_D=(2pqd)^2 \end{split} \tag{8.45} \]

Si ignoramos la varianza de los efectos epistáticos, cosa que podemos hacer en este caso ya que al tratarse de una característica explicada por un solo locus, entonces

\[ \begin{split} V_G=V_A+V_D \end{split} \tag{8.46} \]

y por lo tanto, haciendo uso de las ecuaciones (8.44) y (8.45), poniendo todo junto, tenemos una expresión para la varianza genética en el caso de características gobernadas por un gen de efecto mayor y la misma es

\[ \begin{split} V_G=2pq\alpha^2+(2pqd)^2=2pq[a+d(q-p)]^2+(2pqd)^2 \end{split} \tag{8.47} \]

En la Figura 8.11 se ilustra la partición de la varianza genética en sus componentes aditivo y de dominancia, de acuerdo a la frecuencia del alelo \(A_1\) (\(p\)) y del desvío del heterocigota respecto del punto medio entre los homocigotas (\(d\)). A la izquierda, \(d=0,5a\), es decir el heterocigota se encuentra a medio camino entre lo que le correspondería si el locus fuese aditivo y el valor del homocigota \(A_1A_1\). Se aprecia claramente que con ese apartamiento de la aditividad la varianza de dominancia es relativamente pequeña respecto a la aditiva y por lo tanto la proporción de la varianza de dominancia en el total de la varianza genética es pequeña. Por otro lado, con \(d=0,95a\), es decir que la dominancia de \(A_1\) es casi total, la varianza de dominancia ya no es pequeña y puede llegar a ser una proporción importante del total de varianza genética cuando la frecuencia del alelo \(A_1\) es elevada (notar que para \(p > 0,75 \Rightarrow V_D>V_A\)).

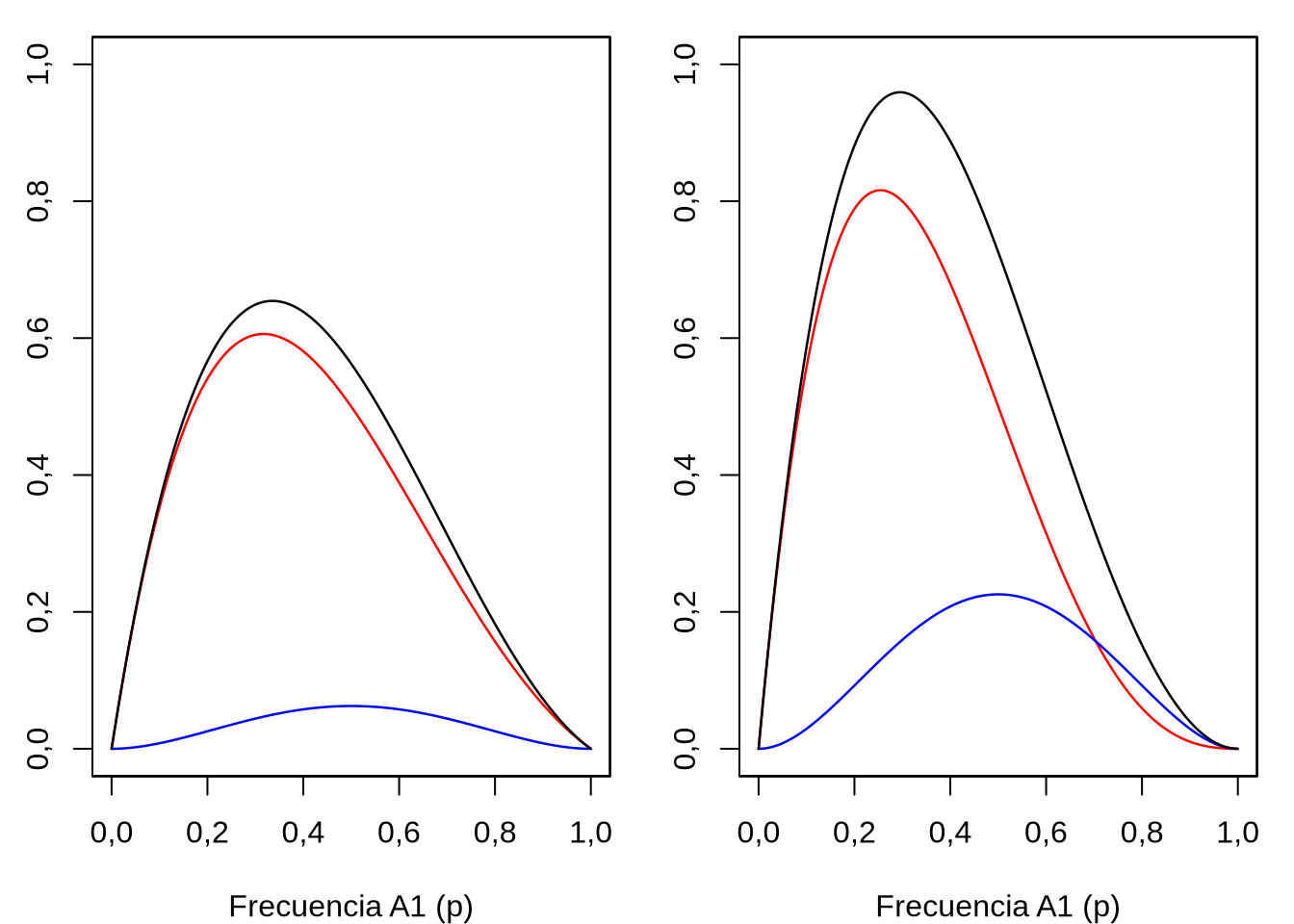
Figura 8.11: Partición de la varianza genética de acuerdo a la frecuencia del alelo \(A_1\) (\(p\)) en dos situaciones del desvío de dominancia (desvío del heterocigota, \(d=0,50a\) a la izquierda, \(d=0,95a\) a la derecha). En rojo se representa la varianza de efectos aditivos, en azul la varianza del desvío de dominancia y en negro la varianza genética total.

Ejemplo 8.6

Calcular la varianza genética aditiva, de dominancia y varianza genética total si el fenotipo de la característica área del ojo del bife en la raza Limousin (Figura 8.12) estuviese genéticamente determinada exclusivamente por los alelos \(L\) y \(F\) del marcador \(F94L\) del gen de la miostatina, con frecuencias y valores genotípicos como en el [Ejercicio 8.1]. Discutir la importancia relativa de la varianza aditiva y de la de dominancia.

Figura 8.12: Toro de la raza Limousin, originaria de la región con dicho nombre en el centro de Francia, con vacas de la raza pastando detrás (de wikipedia, autor: Velela, figura de dominio público).

De acuerdo a los datos del Ejercicio 8.1, \(a=7 \text{ cm}^2\) y \(d=-3 \text{ cm}^2\), mientras que \(p=0,207\). Utilizando las ecuaciones (8.44), (8.45) y (8.46), tenemos que

\[V_A=2pq[a+d(q-p)]^2=2\times 0,207 \times 0,793 \times [7-3(0,586)]^2=9,0213 \text{ cm}^4\] \[V_D=(2pqd)^2=[2\times 0,207 \times 0,793 \times -3]^2=0,9700 \text{ cm}^4\] \[V_G=V_A+V_D=(9,0213+0,9700) \text{ cm}^2=9,9913 \text{ cm}^4\]

La proporción de la varianza genética total debida la varianza aditiva es \(V_{A\%}=\frac{9,0213}{9,9913}=0,9029=90,29\%\) y por lo \(V_{D\%}=100\%-90,29\%=9,71\%\).

---

• Podemos descomponer el modelo genético básico en términos de varianza de la siguiente manera: \(V_P={V}(G+E+I_{GxE})=(V_A+V_D+V_I)+V_E+V_{GxE}+2{Cov}_{GE}\).

• En el caso de características gobernadas por un gen de efecto mayor podemos expresar la varianza genética como: \(V_G=2pq\alpha^2+(2pqd)^2=2pq[a+d(q-p)]^2+(2pqd)^2\)

La varianza ambiental

La varianza ambiental es, por definición, la varianza de todos los efectos que no sean genéticos. De otra forma, en el “ambiente” englobamos todo aquello que no podemos modelar como genético. Sin duda se trata de una definición de ambiente apenas operativa, es decir, por conveniencia y que nada tiene que ver con las definiciones de ambiente más aceptadas en otras disciplinas científicas. Por ejemplo, como usualmente no podemos incorporar explícitamente los errores de medición (ya que no los conocemos, porque suelen ser aleatorios), esto pasa a formar parte de la variación no-genética, y nuestra única posibilidad de acomodarla en el modelo genético básico es que forme parte de los “efectos del ambiente”.

Esta forma de considerar la partición de efectos y varianzas, si entendemos el significado e interpretación de la misma, no tiene más consecuencias que el sobre-uso de un término para referirnos de manera genérica a todo lo que no es genético, que es el foco de nuestro curso. De hecho, nada nos impide de escribir todos los términos de efectos y varianzas ambientales que se nos ocurra o nos guste en nuestro modelo sin que ninguna de las conclusiones se vea alterada, en la medida de que los mismos no afecten de manera novedosa lo genético. Por ejemplo, si una característica se ve afectada por la temperatura y yo registro en forma consistente la misma, nada me impide incluirla en forma explícita en mis modelos.

En otras partes del curso procederemos a descomponer la varianza ambiental de diferentes formas, de acuerdo a las necesidades o conveniencias de cada tema o enfoque. Por ejemplo, en medidas que se repiten en la vida de un organismo es posible descomponer la varianza ambiental en temporal y permanente, la primera referida a los cambios que atañen a una sola observación, la segunda a aquellos que afectan todas las mediciones del organismo. Es decir,

\[ \begin{split} V_E=V_{Ep}+V_{Et} \end{split} \]

Por ejemplo, un árbol frutal puede ver afectado su crecimiento en edad temprana y esto afectará todos sus futuros registros productivos, por lo que con nuestro criterio operativo, se tratará de un efecto ambiental permanente. Además, cada año el árbol experimentará variaciones ambientales que cambiarán su producción de año en año y por lo tanto se trata de efectos ambientales temporales. Lo mismo puede ocurrir con el crecimiento de un cordero que es gestado como mellizo y que es criado por su madre también como mellizo, lo que afectará definitivamente su crecimiento; por lo tanto, este sería un efecto ambiental permanente. Ambiental porque no es genético, aunque la preponderancia de animales melliceros tenga una base genética, la misma no hace al crecimiento del cordero. Luego, este efecto “ambiental” afectará los registros productivos de lana todos los años, más allá de que otros efectos ambientales temporales también los afecten (y por eso los registros de cada año son diferentes).

En otros casos consideraremos la partición de la varianza ambiental en componentes que nos ayuden con el tratamiento estadístico de los datos a los fines específicos. Por ejemplo, en diseños experimentales con grupos de parientes con una estructura determinada, un tema que veremos en el capítulo Parentesco y Semejanza entre Parientes, aparecen ciertos componentes de covariación que pueden atribuirse a efectos ambientales compartidos. Por ejemplo, en un diseño experimental de hermanos enteros en especies multíparas (cerdos, perros, etc.), los animales de la misma camada comparten un ambiente que será mucho más “parecido” que el ambiente compartido entre animales de distintas camadas. Por eso, a este efecto ambiental se le llama del ambiente común (\(E_c\)) y la varianza la representamos como \(V_{Ec}\).

En general, no necesitamos asumir una distribución particular para la varianza ambiental y la misma se debería ajustar a la distribución de los residuos luego de ajustados los efectos principales del modelo, ya que hemos asumido que “ambiental” implica todo lo no-genético. A pesar de esto, para características continuas o casi-continuas, con distribución simétrica y densidad (probabilidad) importante en el centro de la distribución se suele asumir una distribución normal con media cero.

La varianza de la interacción

Como vimos antes, los efectos epistáticos son aquellos producto de la interacción entre dos o más loci. Como hasta ahora hemos ido construyendo el modelo genético capa por capa, es decir, primero los efectos aditivos explicando el máximo posible de la varianza (con la restricción de aditividad), sobre estos estimamos los efectos de dominancia como desvíos del comportamiento aditivo dentro de cada locus y luego recién estamos por estimar los efectos epistáticos, los mismos serán desvíos, tanto del comportamiento aditivo dentro de cada locus como de la suma de los mismos y de los efectos de dominancia correspondientes a los genotipos en los diferentes loci. Claramente, podemos a su vez ir construyendo la estimación de estos efectos usando un diferentes número de loci, empezando por las interacciones entre todos los pares de loci, pasando luego a interacciones entre tríos de loci y así sucesivamente. A cada capa que vamos agregando quedará menos varianza por explicar, por lo que no suelen considerarse las interacciones de más de a dos loci por vez.

Por otro lado, dentro las posibles interacciones entre dos loci podemos distinguir tres tipos: 1) interacciones entre los efectos aditivos en cada loci, 2) las interacciones entre efectos aditivos en un locus y los efectos de dominancia en el otro locus, y 3) las interacciones entre efectos de dominancia en ambos loci. Poniendo todo esto junto y asumiendo que despreciamos los efectos de orden 3 y mayores, tenemos que la varianza de los efectos epistáticos puede escribirse como

\[ \begin{split} V_I=V_{AA}+V_{AD}+V_{DD}+... \approx V_{AA}+V_{AD}+V_{DD} \end{split} \tag{8.48} \]

En general, resulta bastante complejo de estimar por separado los distintos componentes de la varianza epistática, que ya de por sí es complicada de estimar en la mayor parte de los diseños experimentales tradicionales, al menos en el caso del modelo infinitesimal. Cuando en el próximo capítulo desarrollemos la covarianza entre parientes, veremos que algunas relaciones de parentesco incluyen estos efectos y que en teoría podemos llegar a estimar sus efectos con determinadas combinaciones de estructuras de parentesco.

-En general, utilizamos el término varianza ambiental para describir de manera genérica todo aquello que no este englobado en lo genético.

• Podemos descomponer la varianza ambiental en permanente (\(V_{Ep}\)) y temporal (\(V_{Et}\)), dependiendo si los fenómenos afectan al organismo en un registro o si lo afectarán durante toda su vida.

-Respecto a los efectos epistáticos, podemos distinguir tres tipos de variaciones entre 2 loci: interacciones entre los efectos aditivos en cada loci, interacciones entre efectos aditivos en un locus y los efectos de dominancia en el otro locus, e interacciones entre efectos de dominancia en ambos loci.

8.9 Conclusión

La relación entre el genotipo de un individuo y su fenotipo no es lineal. Podemos pensar en el caso de organismos de reproducción clonal para pensar esto: aún cuando todos posean el mismo genotipo (si despreciamos los efectos mutacionales), resulta claro que existirán variaciones fenotípicas entre los mismos. El estudio de la variación fenotípica y la capacidad de transmisión de caracteres de interés de una generación a otra se vuelve entonces complejo, ya que muchos factores tendrían que ser tomados en cuenta; aspirar a adoptar una aproximación de modelado explícita (como hicimos hasta ahora en este libro, teniendo en cuenta las frecuencias alélicas en la población, desequilibrio de ligamiento, tasa mutacional, etc.) se vuelve inviable. ¿Cómo podemos aproximarnos a esta problemática? En este capítulo introducimos una forma de plantear este problema que utilizaremos de ahora en más: realizaremos una aproximación estadística, observando las desviaciones respecto a la media de generación a generación, así como la cantidad de variación existente. Para ello introdujimos un modelo (el Modelo genético básico) que tiene en cuenta las principales clases de variación que deben ser contempladas cuando se plantea el estudio de la herencia de caracteres fenotípicos complejos. En los siguientes capítulos de esta parte del libro nos volcaremos a emplear este modelo para explorar qué tanto se heredan estos caracteres de generación a generación, y en qué medida podemos hacer un estudio sistemático respecto a la influencia que podemos tener sobre los mismos (i.e., ejercer un proceso de selección artificial de caracteres de interés, objetivo primario del mejoramiento genético).

8.10 Actividades

8.10.1 Control de lectura

1. Una de las formas más explícitas de expresar el fenotipo de un individuo nombradas en este capítulo es la ecuación \(P=G+E+I_{G\times E}=A+D+I+E+I_{G\times E}\). ¿A qué se refiere cada uno de los términos de la misma?

2. ¿De qué manera se modifica el modelo descrito en el punto anterior si queremos evaluar sus componentes a nivel poblacional?

3. ¿Qué es el efecto medio de un alelo? ¿Qué relación tiene con el efecto de sustitución?

4. ¿Qué es el valor de cría de un individuo? ¿Cómo se vincula este concepto con el de efecto medio de un alelo?

5. ¿De qué manera afecta al fenotipo el ambiente?

8.10.2 ¿Verdadero o falso?

1. En un organismo diploide, se dan interacciones entre los alelos de un locus. Esto genera en el fenotipo una desviación que es conocida como efecto de epistasis (término acuñado de la genética clásica).
2. El cambio en la media genotípica de una población donde las frecuencias alélicas varían se verá afectada por la existencia de dominancia.
3. Una población de ranas se encuentra compuesta por individuos \(RR\), \(Rr\) y \(rr\). Cada uno de estos genotipos corresponden a un locus que codifica el largo de la cola y los valores de largo asociados son \(RR=0,2\text{ mm}\), \(Rr=0,4\text{ mm}\) y \(rr=0,1\text{ mm}\) por lo que la característica presenta sobredominancia.
4. Cada gen hará un aporte particular al fenotipo, dependiendo de lo que codifique (e.g., alguna proteína o ARN con una función particular), lo cual se ve reflejado en lo que se denomina efecto medio. Esta medida es, por lo tanto, característica y constante para cada gen en un organismo dado.
5. El valor de cría de un individuo es dependiente de la población en la cual se encuentre.

Soluciones

1. Falso. El apartamiento en el fenotipo de un organismo heterocigota para un locus dado se denomina desvío de dominancia (concepto similar al parámetro \(h\) visto en capítulos de la segunda sección de este libro). El efecto de epistasis refiere al apartamiento del fenotipo respecto a lo esperado para el conjunto de genes, y está dada por la interacción que pueden tener estos productos génicos (entre sí o por su co-ocurrencia, además de las consecuencias de dichas interacciones). [Voy a pulir esto último después]

2. Verdadero. Como se muestra en la Figura 8.6 [poner texto para que haga link], el cambio en la media genotípica de una población depende de las frecuencias alélicas, pero la forma en la cual se da el cambio depende a su vez del desvío de dominancia (\(d\)).

3. Verdadero. El valor intermedio entre los genotipos homocigotas es de \(\frac{0,2+0,1}{0,2} = \frac{0,3}{0,2} = 1,5 \text{ mm}\). Notemos que los individuos heterocigotas poseen un largo de cola mayor (\(0,25 \text{ mm}\)). En efecto, poseen largos de cola mayor a cualquiera de los heterocigotas; esto indica un modo de acción génica de sobredominancia (como vimos en el capítulo Selección natural).

4. Falso. El efecto medio de un alelo es dependiente de la población en la que se encuentra, ya que depende de su frecuencia en la población (ver subsección Efecto medio). Por lo tanto, este valor no puede ser característico de un alelo (si lo fuera, no variaría).

5. Verdadero. El valor de cría (aditivo) es la suma de los efectos medios de los alelos presentes en cada uno de los loci del individuo que aportan a una característica dada. Por lo tanto, al ser el efecto medio dependiente de las frecuencias alélicas en la población, el valor de cría también será dependiente de las mismas.

Ejercicios

Ejercicio 8.1

Un locus bi-alélico que afecta a un carácter poligénico de interés se encuentra segregando en una población (alelos \(A_1\) y \(A_2\)). Mediante herramientas de secuenciación se logra estimar las frecuencias alélicas del mismo.

a. La media poblacional (en escala transformada) para la medida de interés en una población con frecuencias \(p = 0,56\) y \(q = 0,44\) es de \(0,59\). ¿Cuál es el modo de acción génica para el locus considerado? Tenga en cuenta que los genotipos homocigotas tienen un valor genotípico estimado de magnitud \(|0,42|\)

b. ¿Cómo cambió el valor de cría para los genotipos en esa población si la frecuencia del alelo \(A_1\) aumenta un 20%?

Solución

a. La media poblacional en escala transformada corresponde a \(M = a(p-q) + 2pqd\). El valor genotípico de los homocigotas es a su vez equivalente en magnitud a \(a\), por lo que podemos obtener \(d\) operando algebraicamente:

\[M = a(p-q) + 2pqd \Rightarrow\] \[2pqd = M - a(p-q)\] \[d = \frac{M - a(p-q)}{2pq}\] \[d = \frac{0,59 - 0,42 * (0,56 - 0,44)}{2 \cdot 0,56 \cdot 0,44}\] \[d \approx 1,095\]

Por lo tanto, el modo de acción génica es de sobredominancia.

b. El valor de cría de los posibles genotipos se calcula según

\[ \begin{cases} \text{EBV}(A_1A_1) = 2q \alpha \\ \text{EBV}(A_1A_2) = (q-p) \alpha \\ \text{EBV}(A_2A_2) = -2p \alpha \end{cases} \]

donde \(\alpha = a + d(q-p)\)

En el primer momento (antes del cambio de frecuencias alélicas) tenemos

\[ \begin{cases} \text{EBV}(A_1A_1) = 2 \cdot 0,44 \cdot [0,42 + 1,095 \cdot (0,44 - 0,56)] \approx 0,254 \\ \text{EBV}(A_1A_2) = (q-p) \alpha = (0,44 - 0,56) \cdot [0,42 + 1,095 \cdot (0,44 - 0,56)] \approx -0,0346 \\ \text{EBV}(A_2A_2) = -2p \alpha = -2 \cdot 0,56 \cdot [0,42 + 1,095 \cdot (0,44 - 0,56)] \approx -0,323 \end{cases} \]

Notemos que \(p\) aumenta a \(p’ = 0,56 + 0,20 \cdot 0,56 = 0,672\) (\(q = 1 -p \Rightarrow q’ = 1-0,672 = 0,328\)). Con estos datos podemos calcular los valores estimados de valor de cría para los genotipos nuevamente

\[ \begin{cases} \text{EBV}(A_1A_1) = 2 \cdot 0,328 \cdot [0,42 + 1,095 \cdot (0,328 - 0,672)] \approx 0,0284 \\ \text{EBV}(A_1A_2) = (q-p) \alpha = (0,328 - 0,672) \cdot [0,42 + 1,095 \cdot (0,328 - 0,672)] = -0,0149 \\ \text{EBV}(A_2A_2) = -2p \alpha = -2 \cdot 0,372 \cdot [0,42 + 1,095 \cdot (0,328 - 0,372)] \approx -0,277 \end{cases} \]

Ejercicio 8.2

El dingo (Canis dingo), es un canino salvaje australiano que pese a sus características predatorias contra animales domésticos, ha sido clasificado por la UICN (Unión Internacional para la Conservación de la Naturaleza) como vulnerable (i.e., presenta una alta probabilidad de pasar a ser una especie en peligro de extinción). Los dingos, al igual que los lobos pero a diferencia de los perros, se reproducen una única vez por año, obteniendo camadas de 5 cachorros en promedio según reporta la literatura. Una estrategia de conservación para aumentar el número de animales de esta especie consiste en aumentar el número de cachorros por camada. Con este fin, una investigación ha descubierto que existe un solo locus con dos alelos que controla esta característica (\(D\) y \(d\)). A su vez, se ha determinado que una población de referencia en el sur de Australia (que se encuentra en equilibrio de Hardy-Weinberg) tiene los siguientes números de dingos hembra por genotipo: \(DD=18\), \(Dd=24\) y \(dd=8\). Luego de un monitoreo extensivo, detectaron que el genotipo \(DD\) tenía camadas de 8 cachorros, el genotipo \(Dd\) de 6 y \(dd\) de apenas 2 cachorros por camada.

a. Bajo este esquema de apareamiento, ¿cuántos cachorros nacen en promedio por año? b. El equipo de conservación de la especie propone introducir sólo machos \(DD\) a la población y evitar que otros machos se apareen con las hembras. Si fueran exitosos, ¿cuántos cachorros nacerían por año?¿Cuál es el efecto del alelo \(D\)? c. Si por el contrario ahora las hembras se aparearan únicamente con machos \(dd\), ¿cuántos cachorros nacerían por año?¿Cuál es el efecto del alelo \(d\)?

Solución

a. Para saber en promedio cuantos cachorros nacen en esta población basta con hacer un promedio ponderado de cuantos cachorros nacen por madre:

\[\frac {18*8 + 24*6 + 8*2}{50}=6.08\]

Lo mismo obtendremos si utilizamos los valores de los genotipos en la escala transformada y luego les sumamos \(m\) tal que:

\[m=\frac{8+2}{2}=5\] \[a=8-5=3\] \[-a=2-5=-3\] \[d=6-5=1\]

Y sabiendo que \(p= \frac{18 + 12}{50} = 0,6\) por lo tanto \(q=1-p = 0,4\), \(M=a(p-q)+2pqd = 3(0,6 - 0,4) + 2*0,6*0,4*1 = 1,08\), por lo que la media en la escala original sería \(1,08+5 =6,08\).

b. En el paso anterior determinamos que \(p=0,6\) y por lo tanto \(q= 0,4\) (i.e., la frecuencia de \(D=0,6\) y la de \(q=0,4\)).

Podemos entonces generar un cuadro que nos ayude a visualizar el apareamiento de esta población con los machos \(DD\).

		Frec. nuevos machos
		\(D=1\)
\(\text{Frec. población}\)	\(D=0,6\)	\(DD=0,6\)
	\(d=0,4\)	\(Dd=0,4\)

Como se puede observar, al introducir machos homocigotos \(DD\), la nueva generación no contará con individuos \(dd\). A su vez, la nueva media poblacional será de \(0,6*8 + 0,4*6 = 7,2\) cachorros por camada. Por lo tanto, el efecto medio del alelo \(D\) será de \(7,2-6,08=1,12\), ya que corresponde al efecto producido por la introducción del alelo a la población.

c. Al igual que en el caso anterior podemos determinar las nuevas frecuencias a partir de una tabla:

		Frec. nuevos machos
		\(d=1\)
\(\text{Frec. población}\)	\(D=0,6\)	\(Dd=0,6\)
	\(d=0,4\)	\(dd=0,4\)

La nueva de esta media población sería entonces \(0,6*6 + 0,4*2 = 4,4\) y el efecto medio del alelo \(d\) sería \(4,4-6,08=-1,68\).

Ejercicio 8.3

a. Comprobar los resultados de efecto medio de los alelos del ejercicio anterior usando el concepto de efecto de sustitución y su relación con el efecto medio de cada alelo.

b. Calcular el valor de cría de un macho con genotipo \(Dd\).

Solución

a. En principio, podemos calcular el efecto de sustitución (\(\alpha\)) según REF: \(\alpha=a+d(q-p)=3+1(0,4-0,6)=2,8\)

A partir del mismo, podemos entonces calcular el efecto medio de cada gen tal que:

El efecto medio del alelo \(D\) que llamaremos \(\alpha_1\) será \(\alpha_1=q\alpha = 0,4*2,8=1,12\). Mientras que el efecto medio de \(d\) que llamaremos \(\alpha_2\) será \(\alpha_2=-p\alpha=-0,6*2,8=-1,68\) comprobando entonces los resultados obtenidos previamente.

b. El valor de cría será igual a la suma de los efectos medios de los alelos que componen el genotipo, tal que:

\[VC_{Dd}=\alpha_1 + \alpha_2 = 1,12 -1,68 = -0,56\]

Ejercicio 8.4

a. En una población salvaje de perros salchicha, hace 20 años se determinó que existe un locus con dos alelos (con valores \(F=10\text{ cm}\) y \(f= 4\text{ cm}\)), que determina el largo de la cola de estos animales. Se ha determinado a su vez que el valor del fenotipo \(Ff\) en escala transformada es \(0\), y al genotipar esta población salvaje se determina que \(17\) perros poseen genotipo \(FF\), \(102\text{ } Ff\) y \(153\text{ } ff\). Se asume que esta característica no se ve afectada por el ambiente.

Responda:

1. ¿Cuánto mide la cola de los perros de cada genotipo presente en la población?

2. ¿Cuál es el promedio de largo de cola para estos perros?

3. Basados en esta información, ¿qué efectos genéticos afectan esta característica?

b. Este año, un nuevo estudio descubrió que existe otro locus con efecto en la característica. Este locus también posee dos alelos, sus valores son \(M=2 \text{ cm}\) y \(m= -3 \text{ cm}\), y se ha determinado que el valor del fenotipo \(Mm\) en escala transformada es de \(3\text{ cm}\). No existe interacción entre los alelos de los loci que influyen en el largo de la cola. Debido a este nuevo descubrimiento, se realizó un nuevo genotipado de los individuos de la población (descubriendo que se había visto muy reducida debido al aumento de las aves rapaces) y se encontró la siguiente distribución de individuos por genotipo:

	FF	Ff	ff
\(\text{MM}\)	\(2\)	\(6\)	\(6\)
\(\text{Mm}\)	\(8\)	\(9\)	\(8\)
\(\text{mm}\)	\(5\)	\(5\)	\(1\)

1. ¿Cuánto mide la cola de los perros de cada genotipo presente en la población sabiendo que la característica está controlada por los dos loci?

2. ¿Cuál es el promedio de largo de cola para estos perros sabiendo que la característica está controlada por los dos loci?

3. Basados en esta nueva información, ¿se modificaron los efectos genéticos que afectan esta característica?

Solución

a.

1. En primer lugar se asume que la característica no está afectada por el ambiente, lo que determinará que sólo los componentes genéticos afectan la misma. Dado que la característica se encuentra determinada por los alelos de un sólo locus, también podemos descartar la influencia de la epistasis en la expresión de la misma. A su vez, al transformar los valores se determina que el genotipo \(Ff\) posee valor \(0 \text{ cm}\); esto implica que el valor del mismo coincide con el valor promedio de los genotipos homocigotas (i.e., no existe dominancia de un alelo sobre el otro). Esto nos determina que el largo de la cola es una característica de carácter totalmente aditivo, por lo que basta sumar el valor o “aporte” de cada uno de los alelos para determinar el valor del fenotipo.

Por lo tanto, tenemos que:

\[FF = 10 + 10 = 20 \text{ cm}\] \[Ff = 10 + 4 = 14 \text{ cm}\] \[Ff = 4 + 4 = 8 \text{ cm}\]

2. La media del largo de la cola para cada genotipo será igual a la frecuencia del mismo multiplicado por su valor. En este caso podemos desarrollar dos alternativas: realizar este cálculo de forma explícita, o recurrir a la ecuación

\[ M= a(p-q) + 2pqd \]

que se encuentra expresada en términos de la escala transformada. Comenzaremos por esta última aproximación.

En primer lugar podemos comprobar que esta población se encuentra en equilibrio Hardy-Weinberg

\[\text{Frec F } (p) = (17 + 102/2)/(17 + 102 + 153) = 0,25\] \[\text{Frec f } (q) = 1- p = 1- 0,25 = 0,75\]

\[\text{Frec FF }= p^2 = 0,0625 \Rightarrow n_{esperado} = 0,0625 * 272 = 17 \text{ individuos}\] \[\text{Frec Ff }= 2pq = 0,375 \Rightarrow n_{esperado} = 0,375* 272 = 102 \text{ individuos}\] \[\text{Frec ff }= q^2 = 0,5625 \Rightarrow n_{esperado} = 0,5625 * 272 = 153 \text{ individuos}\]

Corroboramos por tanto que nos encontramos en equilibrio de Hardy-Weinberg.

Expresamos los genotipos como desvíos del punto \(m\):

\[ m = \frac{20 + 8}{2} = 14 \text{ cm} \]

Resultado que podíamos intuir debido a que coincide con el valor del genotipo heterocigota dada a la ausencia de dominancia.

Pasamos a calcular \(a\)

\[a = 20 - 14 = 6 \text{ cm}\] \[-a = 8 - 14 = -6 \text{ cm}\]

Por lo que podemos aplicar la ecuación 8.13 para expresar la media en función del punto m:

\[M= a(p-q) + 2pqd\] \[M = 6 (0,25 - 0,75) + 2*0,25*0,75*0\] \[M = -3 \text{ cm}\]

Para determinar la media en escala original basta con sumarle el valor del punto m, por lo que el largo promedio de patas en la población es de \(14-3 = 11 \text{ cm}\).

La segunda alternativa consiste en simplemente multiplicar la frecuencia de cada genotipo por su valor:

\[\text{frec (FF) } = 17/272= 0,0625\] \[\text{frec (Ff) } = 102/272= 0,375\] \[\text{frec (ff) } = 153/272= 0,5625\] \[0,0625*20 + 0,375*14 + 0,5625*8 = 11 \text{ cm}\]

3. Cómo discutimos en la parte a) del ejercicio, al tratarse de una característica determinada por los alelos de un sólo locus podemos descartar la existencia de epistasis (interacción entre alelos de diferentes loci). A su vez, como el valor del genotipo heterocigota coincide con el promedio de los homocigotas, podemos determinar que no hay efecto de dominancia. Por lo tanto, el único efecto que afecta esta característica es el aditivo.

b.

1. Al ahora existir dos loci que determinan la característica existirán más genotipos posibles y mayor número de interacciones. En primer lugar, podemos descartar los efectos epistáticos debido a que no existe interacción entre los alelos de los loci. Posteriormente podemos hallar el valor aditivo de cada genotipo calculando la suma del valor de los alelos que lo componen (como en el caso anterior). Por último, deberemos tener en cuenta el efecto de dominancia que existe entre los alelos de este nuevo locus, por lo que a los genotipos que presenten heterocigosis \(Mm\) deberemos sumarles el valor de la dominancia (\(+3\text{ cm}\)).

En la siguiente tabla se resume el largo de patas por genotipo calculado con estas consideraciones:

	FF	Ff	ff
\(\text{MM}\)	\(24\)	\(18\)	\(12\)
\(\text{Mm}\)	\(22\)	\(16\)	\(10\)
\(\text{mm}\)	\(14\)	\(8\)	\(2\)

2. Podemos calcular el largo de patas promedio ponderando la frecuencia de cada genotipo por su valor.

Tenemos así

\[ \text{frec(FFMM)}*24 + \text{frec(FFMm)}*22 + \cdots + \text{frec(ffmm)}*2 = 14,8 \text{ cm} \]

3. Si, los efectos genéticos que afectan a la característica se modificaron. Ahora, además de tener en cuenta los efectos aditivos debemos considerar la dominancia que presenta \(M\) sobre \(m\) en el nuevo locus.

Ejercicio 8.5

Campbell, McGrath, and Paaby (2018)

Un grupo de investigación se dedica a estudiar la capacidad de resistencia de una cepa de S. cerevisiae frente a diferentes productos de la destilación (una característica poligénica de alta relevancia para la industria). De particular interés es la capacidad de metabolización del ácido acético, por lo cual el grupo trama un experimento para medir la tasa de metabolización en dos cepas para las que se sabe las frecuencias alélicas en algunos locus.

Es importante resaltar que, en las condiciones experimentales usadas por el grupo, la población de S. cerevisiae se compone únicamente de células haploides que se reproducen de forma asexual.

a. Mediante una serie de experimentos se obtiene una población compuesta por individuos donde se han fijado alelos de alto rendimiento en los loci codificantes para proteínas de la vía metabólica (en las condiciones especificadas anteriormente) la varianza fenotípica es de \(V_P \approx 1,2 \times 10^{-3} \ g \cdot {hora}^{-1}\) (lo que se estima es la cantidad de masa de ácido acético metabolizada por hora). Teniendo en cuenta que la varianza asociada al error de medición se estima en \(V_E \ approx 1,0 \times 10^{-4} \ g \cdot {seg}^{-1}\), ¿qué componentes genéticos aportan a la variabilidad de la característica fenotípica en la población? Nota: por simplicidad no tener en cuenta los efectos de interacción genotipo-ambiente.

b. Teniendo en cuenta que el ciclo de vida de la levadura (Saccharomyces cerevisiae) alterna entre dos fases (una haploide y la otra diploide) discuta si se puede utilizar el mismo abordaje en cualquier condición de estudio

Solución

a. Notemos que en organismos haploides, por definición, no puede existir la varianza de efecto de dominancia, en tanto cada organismo hereda un solo alelo para cada locus. A su vez, los investigadores trabajan sobre una población donde se han fijado diferentes alelos involucrados directamente en la vía metabólica que produce el fenotipo; esto implica que no existirá varianza aditiva. Esto implica que la varianza fenotípica, según el modelo básico, queda reducida a

\[ V_P = V_G + V_E + V_{G \times E} = (V_I) + V_E + V_{G \times E} \]

Lo que es más, si no tenemos en cuenta los efectos de interacción genotipo-ambiente, tenemos que

\[ V_P = V_I + V_E \]

Es decir, los únicos factores que aportan a la varianza fenotípica son la varianza de interacción (epistasis) y la varianza asociada al ambiente (la cual, en una visión simplista, equivale al error de medición).

Tenemos así que, en este caso

\[ 1,2 \times 10^{-3} \ g \cdot {hora}^{-1} = V_I + 1,0 \times 10^{-4} \ g \cdot {seg}^{-1} \]

de lo que se deduce que la varianza asociada a la epistasis es de

\[ \begin{split} V_I \approx (1,2 \times 10^{-3} - 1,0 \times 10^{-4}) \ g \cdot {hora}^{-1} \\ V_I \approx 1,1 \times 10^{-4} \ g \cdot {hora}^{-1} \end{split} \]

Se puede estimar así el componente de varianza asociado a la epistasis, que es el fenómeno que más contribuye a la variación fenotípica observada en el modelo.

b. Notemos que durante las fases diploides ya no podremos descartar los efectos de desvío de dominancia atribuibles a la interacción intra-locus en las cepas estudiadas. A su vez, si bien en principio no existirá varianza aditiva (ya que en los loci que se consideran hay alelos fijados), a medida que se generen variantes por efecto de la mutación este componente genético debe también ser tenido en cuenta. Teniendo en cuenta lo anterior, notamos que según el modelo genético básico

\[ V_P = V_G + V_E + V_{G \times E} = (V_A + V_D + V_I) + V_E + V_{G \times E} \]

Aún desestimando la interacción genotipo-ambiente, se tienen tres componentes que aportan a la varianza sin posibilidad de discernir el aporte relativo (i.e., \(V_A\), \(V_D\) y \(V_I\)).

Por lo tanto, el abordaje experimental realizado no es directamente extrapolable a las condiciones en las que S. cerevisiae alterne entre una fase haploide y una diploide.

---

Bibliografía

Bennett, G. L., R. G. Tait, S. D. Shackelford, T. L. Wheeler, D. A. King, E. Casas, and T. P. L. Smith. 2019. “Enhanced estimates of carcass and meat quality effects for polymorphisms in myostatin and µ-calpain genes.” J Anim Sci 97 (2): 569–77.

Campbell, Richard F., Patrick T. McGrath, and Annalise B. Paaby. 2018. “Analysis of Epistasis in Natural Traits Using Model Organisms.” Trends in Genetics 34 (11): 883–98. https://doi.org/10.1016/j.tig.2018.08.002.

Castle, W. E. 1903. “The laws of Galton and Mendel and some laws governing race improvement.” Proceedings of the American Academy of Arts and Sciences 35 (8): 233–42.

———. 1983. Introducción a La Genética Cuantitativa. CIA. Editorial Continental, S.A. de C.V.

Falconer, Douglas S, and Trudy FC Mackay. 1996. Quantitative Genetics. Benjamin-Cummings Pub Co.

Gianola, Daniel. 1982. “Theory and Analysis of Threshold Characters.” Journal of Animal Science 54 (5): 1079–96.

Gillespie, John H. 2004. Population Genetics. A Concise Guide. The Johns Hopkins University Press.

Hardy, G. H. 1908. “MENDELIAN PROPORTIONS IN A MIXED POPULATION.” Science 28 (706): 49–50.

Johannsen, Wilhelm L. 1903. Über Erblichkeit in Populationen Und in Reinen Linien : Ein Beitrag Zur Beleuchtung Schwebender Selektionsfragen. Fischer (Jena).

Lynch, Michael, and Bruce Walsh. 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates (Oxford University Press).

Weinberg, W. 1908. “Über den Nachweis der Vererbung beim Menschen.” Jahreshefte Des Vereins für Vaterländische Naturkunde in Württemberg. 64: 369–82.

Wright, D. 2015. “The Genetic Architecture of Domestication in Animals.” Bioinform Biol Insights 9 (Suppl 4): 11–20.

———. 1934a. “AN ANALYSIS OF VARIABILITY IN NUMBER OF DIGITS IN AN INBRED STRAIN OF GUINEA PIGS.” Genetics 19 (6): 506–36.

Yule, George Udny. 1902. “MENDEL’s LAWS AND THEIR PROBABLE RELATIONS TO INTRA-RACIAL HEREDITY.” New Phytologist 1: 193–207, 222–38.

---

79. Los colores pueden llevarse a vectores numéricos que permiten una aproximación más cuantitativa a los mismos, permitiendo distinguir entre los infinitos matices que existen entre los mismos (¡los inuit cuentan con cincuenta palabras para los tonos de blanco!). Ejemplos de esta aproximación a los colores son formas de cuantificación como los modelos de color aditivo RGB y CYMK. De todas formas, resulta claro que entrar en este grado de detalle y análisis cuantitativo no tendría sentido para analizar la herencia de colores planteada en el esquema mendeliano clásico.↩︎

80. …↩︎

81. George Udny Yule (18 de febrero 1871 – 26 junio 1951) fue un estadístico escocés, alumno de Karl Pearson y conocido por la distribución que lleva su nombre, además de por sus trabajos fundacionales en bioestadística.↩︎

82. Obviamente que toda estimación tiene error, pero el concepto de “verdadero” es parte de la base filosófica del problema, ya que para la escuela estadística bayesiana lo único real y “verdadero” son los datos, no el valor de un parámetro ficticio, que depende del modelo que estemos usando↩︎

83. Recordar que la media no equivale al promedio de valores presentes en la población, ya que para obtener el valor medio debemos ponderar por la frecuencia de cada uno de los valores que observamos. La persona interesada en ahondar en este tema puede referirse al apéndice matemático de este libro.↩︎