Capítulo 11 Selección Artificial I

Alcanza con observar las diferentes formas de los organismos vivientes para comprender, a la luz de la teoría de la evolución, el rol que la selección natural ha jugado en la adaptación de los organismos al ambiente. En lo que llevamos avanzado del presente material, hemos intentado ponderar el rol de las distintas fuerzas aleatorias y determinísticas en la evolución de los organismos. En el capítulo dedicado a la Selección Natural estudiamos, a través de modelos muy simples y estilizados cómo la selección natural puede cambiar las frecuencias de los alelos en un locus o apenas en un par de loci. Claramente, la selección natural llamó la atención de Charles Darwin⁸⁸ de tal manera que la experiencia como naturalista a bordo durante la expedición del “Beagle” le permitió formular las bases de teoría evolutiva a partir de la selección natural. Sin embargo, la comprensión del mecanismo subyacente fue en gran parte a través de la observación del proceso de selección artificial que realizaban y realizan los mejoradores de diferentes razas de animales domésticos o de producción (y de los colombófilos).

En efecto, alcanza con observar la variedad de razas de perros para entender que la fuerte presión de selección por desarrollar determinadas características puede tener una respuesta concomitante en relativamente pocas generaciones. De hecho, la mayor parte de las razas de perros que conocemos en la actualidad surgieron a mitad del siglo XIX, en plena revolución industrial. Pese a tratarse de animales de la misma especie, resulta difícil imaginarse el apareamiento de un Gran Danés con un Chihuahua (en realidad artificialmente es posible lograr crías de una hembra de Gran Danés con un macho Chihuahua, al revés es imposible la gestación). Todos los cambios y la diversidad observada desde el ancestro lobo domesticado se han obtenido como resultado de ese esfuerzo por modelar esta especie de acuerdo a nuestros gustos, costumbres y necesidades.

Lo mismo es posible de observar en cada especie que tiene alguna importancia económica o cultural en nuestra vida diaria. En las diferentes razas bovinas vemos animales completamente especializados en la producción de leche, mientras que otros se especializan en la producción de carne. Las diferencias morfológicas son notables, pero aún más lo son en las características de interés productivo. El tamaño de los pollos parrilleros en los EEUU creció más de 4 veces desde 1957 a 1991 (Havenstein et al. (1994)), en gran parte debido a la selección especializada para carne o producción de huevos.

En el presente capítulo vamos a comenzar a estudiar la selección artificial para características métricas. Para ello usaremos un escenario sencillo, esencialmente basado en lo que se conoce como selección por truncamiento, en el que solo los individuos que sobrepasen un valor umbral de la característica (asumiendo que los mejores se corresponden a valores altos, al revés si los mejores son los valores bajos) son considerados como reproductores y progenitores de la siguiente generación.

OBJETIVOS DEL CAPÍTULO

\(\square\) Definir el concepto de diferencial de selección direccional, buscando comprender la relación entre la media poblacional en un momento dado y la obtenida luego de seleccionar una fracción de individuos.

\(\square\) Introducir la ecuación del criador, que nos permite explorar la conexión entre estas medias fenotípicas y la heredabilidad de la característica seleccionada.

\(\square\) Introducir el concepto de intensidad de selección, discutiendo cómo se relaciona con la proporción de individuos seleccionados.

\(\square\) Obtener otra perspectiva del diferencial de selección direccional a través de la identidad de Robertson-Price.

11.1 Factores de corrección

El interés en mejoramiento genético suele estar puesto en elegir los “mejores” individuos para que se reproduzcan y usualmente dependemos de la información fenotípica para poder realizar la selección de los “mejores” individuos. Podríamos imaginar que para un característica fácil de medir, como lo son el peso de vellón sucio o limpio, la producción de leche diaria, el peso a los 18 meses en bovinos de carne o muchas otras, alcanza con medir y elegir a los individuos que poseen los valores “mejores” en la característica. Sin embargo, como se puede deducir de nuestro modelo genético básico, si bien el fenotipo es lo único con lo que contamos usualmente, no es de por sí una excelente referencia sobre el valor reproductivo de los individuos. Claramente, los efectos genéticos no-aditivos y el ambiente tienen una influencia usualmente importante en la manifestación fenotípica de la característica. Desafortunadamente, en general nos resulta imposible conocer los efectos de dominancia y epistasis, así como los efectos ambientales que han influido en la vida del individuo, por lo que en ese sentido no podemos reducir la incertidumbre.

Sin embargo, existen una serie de efectos que se manifiestan siempre de la misma manera y que por lo tanto afectan los registros fenotípicos en forma sistemática. En mamíferos, por ejemplo, existen en general importantes diferencias en la expresión de características métricas asociadas al tamaño de los individuos. Si volvemos a mirar con atención la Figura 10.1 del capítulo Parámetros Genéticos: Heredabilidad y Repetibilidad veremos que antes de deducir la relación entre alturas de padres e hijos, Galton (1886), multiplica la altura de las mujeres por el coeficiente \(1,08\) a fin de que las mismas sean comparables. Es decir, Galton reconoce algo que todos observamos diariamente: que existen diferencias sistemáticas en las alturas de hombres y mujeres, siendo estas últimas más bajas. Eso no quiere decir que todas las mujeres sean más bajas que todos los hombres, ni que determinada mujer sea más baja que determinado hombre. Simplemente establece una relación entre la media de un grupo y la media del otro grupo. Claramente esto se aplica a muchas otras características, tanto en seres humanos como en otras especies. En algunas características un sexo poseerá registros promedialmente superiores al otro y en otras será a la inversa.

En este punto podríamos plantearnos si tiene algo de sentido lo que estamos discutiendo. Al ser características con distribuciones aleatorias (por todos los efectos que tienen esas distribuciones, genéticos y ambientales), es altamente probable que cualquier factor que utilicemos para separar los individuos (por ejemplo el color de pelo, color de ojos, etc) genere diferencias, algunas de ellas estadísticamente significativas. ¿Qué hace entonces particular a los factores que estamos discutiendo en esta sección? Lo particular de los factores que estamos analizando es precisamente su caracter sistemático. Es decir, no importa si analizamos la diferencia de peso de vellón entre machos y hembras en Salto, Paysandú, Rio Negro o en Tacuarembó (utilizando siempre un gran número de individuos para reducir la incertidumbre en las estimaciones), la diferencia observada en las medias de ambos sexos será similar en todos ellos. No importa si analizamos esas diferencias este año, el año pasado o tres años hacia atrás, las diferencias entre sexos serán similares.

Otras diferencias sistemáticas no están relacionadas al sexo de los individuos. Por ejemplo, hasta la cuarta o quinta lactancia las vacas producirán en cada lactancia un poco más que en la anterior; esto se debe al crecimiento que experimenta la vaca con el paso del tiempo y se trata de diferencias que son sistemáticas. Lo mismo ocurrirá con el peso de los borregos, que se verá afectado por el sexo del animal, por el hecho de haber transcurrido la gestación como mellizo o trillizo y aún por haber sido criado en los primeros meses como único, mellizo o trillizo; se trata en todos los casos de diferencias sistemáticas entre las clases consideradas y que por lo tanto se repetirán en signo y magnitud durante un intervalo de tiempo razonable (no sería razonable suponer que esas mismas diferencias se observaran hace dos siglos, por ejemplo, aunque sí el signo de las mismas).

Un punto importante es el qué hace al caracter genético o ambiental de los efectos y su consideración como efectos ambientales sistemáticos. Claramente, el sexo está determinado genéticamente, por lo que resulta llamativo que lo incluyamos en el mismo lugar que otros efectos ambientales. En cierta forma, lo mismo podría pensarse para la calidad de mellizos, que en ovinos está parcialmente controlada por los alelos presentes en el gen de Fecundidad “Booroola” (FecB). El punto aquí es que para nuestros objetivos, mejorar la característica métrica de interés, tanto el sexo como la calidad mellicera son genéticamente irrelevantes. Para reproducir la especie necesitaremos individuos de ambos sexos y si no consideramos las correlaciones entre características (algo que veremos en el próximo capítulo) el hecho de que sean mellizos o no es irrelevante para nuestro mejoramiento en el peso de cada borrego. Lo mismo, las diferencias entre producción de diferentes lactancias en la vaca tiene un correlato con la curva de crecimiento de los animales, la que se encuentra determinada en gran parte a nivel genético. Sin embargo, no tendría sentido para nosotros elegir todas las vacas que serán reproductoras entre las de quinta lactancia; debemos poder corregir por esas diferencias sistemáticas (esperables).

Esto nos lleva directamente a la pregunta fundamental ¿Por qué son tan importantes para nosotros las diferencias sistemáticas? La respuesta es relativamente sencilla: porque podemos corregir fácilmente por estas diferencias (ya que son siempre del mismo signo y magnitud), tratando en forma más justa a los diferentes candidatos a la selección. Tradicionalmente se aplicaron factores de corrección como forma de corregir por esas diferencias sistemáticas, calculándose los mismos previamente y luego ajustando los datos antes de procesarlos en la evaluación. Afortunadamente, desde hace tiempo, los modelos lineales mixtos usados en las evaluaciones permiten “corregir” directamente por los efectos sistemáticos, estimando sus efectos al mismo tiempo que los efectos genéticos y otros efectos (como el del grupo contemporáneo), por lo que no es ya más necesaria la pre-corrección. Sin embargo, a fines didácticos, el cálculo de los mismos sigue siendo interesante porque muestra más de cerca los problemas de comparar cosas que tienen diferentes bases y las formas de corregir por esas diferencias que no son relevantes a nuestros fines, por lo que incluimos esta sección.

¿Como funcionan los factores de corrección? El funcionamiento de los mismos es sencillo, pero cuenta con dos fases completamente diferentes:

1. Cálculo de los factores de corrección (que se hace en forma regular, cada determinado tiempo) a partir de la mayor cantidad posible de registros de la “misma” gran población.

2. Aplicación del factor de corrección correspondiente a cada registro que se pretenda utilizar en una evaluación genética.

Factores de corrección aditivos

Hasta aquí hemos venido discutiendo en términos generales acerca de los efectos sistemáticos, mencionando que al tratarse de diferencias con el mismo signo y magnitud por un plazo razonable de tiempo, resultaba sencillo corregir por ellas. Sin embargo, no mencionamos hasta ahora el cómo corregirlas. Lo primero a tener en cuenta a la hora de corregir por diferencias sistemáticas entre determinadas clases es entender las diferencias en las distribuciones de las clases (o niveles) del factor en consideración para la característica de interés. Para esto, un histograma o un gráfico de densidad de la distribución suele ser extremadamente útil, acompañado de los estadísticos resumen usuales (media, mediana, varianza, cuantiles).

En la Figura 11.1 se representa una situación clásica para una característica métrica de interés. Por lo que se aprecia en la figura, los dos sexos presentan una distribución diferente ya que las medias de ambas distribuciones se encuentran desplazadas una respecto a la otra. En este caso, por otra parte, las dos distribuciones tienen aproximadamente la misma varianza, por lo que la forma de hacerlas coincidir parece obvia: o desplazamos la distribución de machos a la izquierda hasta que coincida con la de hembras, o desplazamos la de hembras hasta que coincida con la de machos. En la figura nos hemos decidido por esta última opción, en forma totalmente arbitraria. Para ello calcularemos un factor de corrección aditivo para cada clase (o nivel) del factor, en este caso sexo. Para que el método sea general a más de dos niveles o clases, vamos a definir siempre una clase como la clase de referencia, clase cuyos registros ajustados permanecerán idénticos a pesar del ajuste. En el caso de la figura, elegimos la categoría de los machos como clase de referencia. Si llamamos \(\bar y_r\) a la media de la clase de referencia, entonces los factores para la clase \(i\) se calcula como

\[ \begin{split} c_i=\bar y_r - \bar y_i \end{split} \tag{11.1} \]

En el caso de la clase de referencia, \(\bar y_i=\bar y_r\), por lo que la ecuación anterior nos deja con

\[ \begin{split} c_{i=r}=\bar y_r - \bar y_i=\bar y_r - \bar y_r=0 \end{split} \tag{11.2} \]

Es decir, para calcular los distintos factores de corrección aditivos alcanza con restarle a la media de la clases de referencia las medias de cada una de las clases.

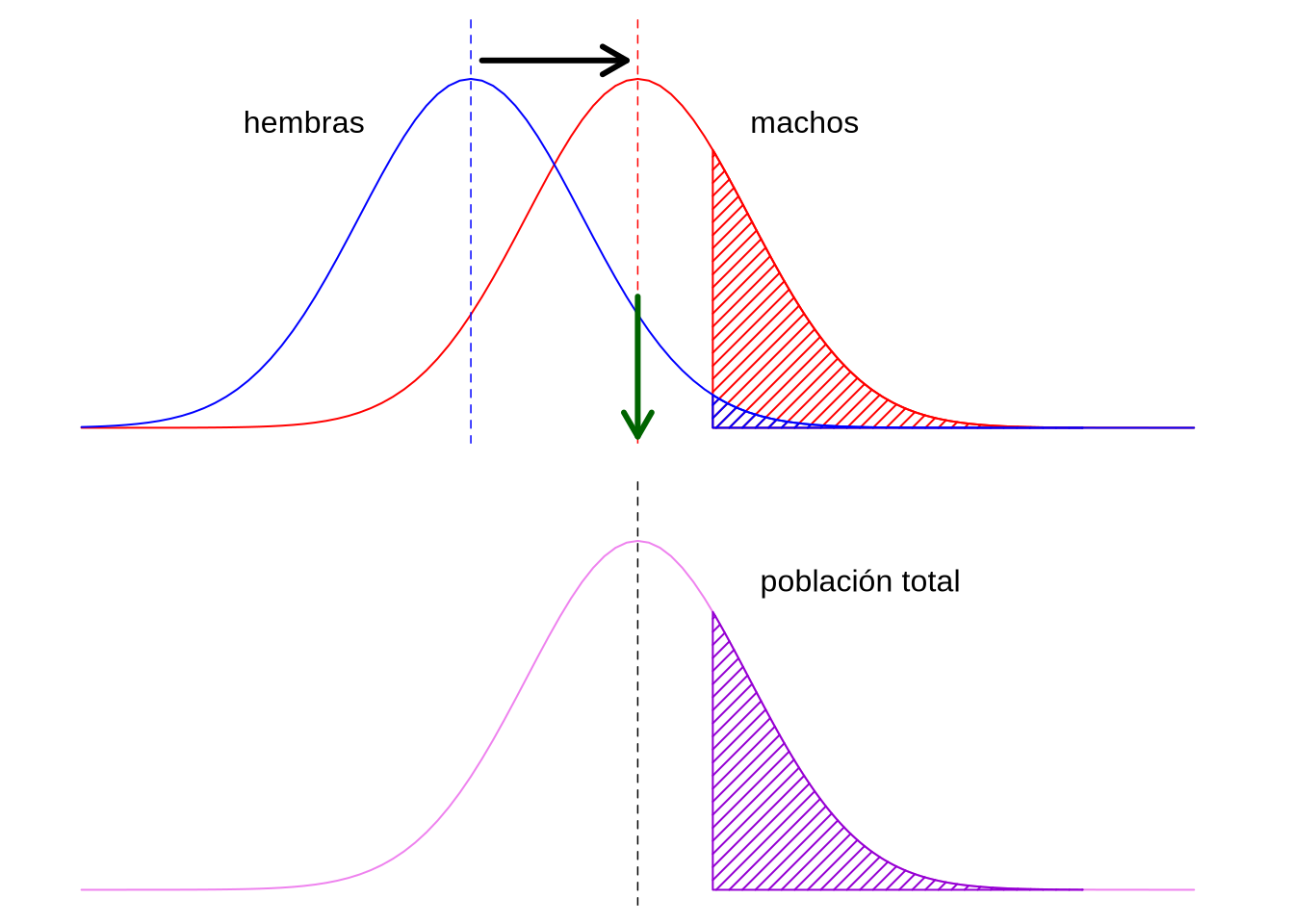
Figura 11.1: Factor de corrección aditivo. La característica de interés tiene una distribución diferente en hembras y machos ya que si bien su varianza es igual, las medias para ambos sexos son diferentes. Si definimos un umbral de selección determinado, si no corregimos por esta diferencia casi ninguna hembra resultaría seleccionada (la pequeña porción rayada en azul en la parte superior de la figura). Como la diferencia entre las distribuciones es apenas en la media, alcanza con desplazar la media de hembras hasta alcanzar la media de machos (podríamos haber hecho lo contrario), categoría que usaremos como referencia. Esto produce que las dos distribuciones ahora coincidan (parte inferior de la figura) y que el umbral de selección brinde las mismas posibilidades de ser elegidos a machos y hembras.

El paso final, luego de haber calculado los distintos factores de corrección será aplicarlos sobre los distintos registros. Para eso alcanza con sumar al registro fenotípico el valor del factor de corrección correspondiente a la clase a la que pertenece el registro. Es decir, si un registro fenotípico \(j\) pertenece a la clase \(i\), su valor ajustado será

\[ \begin{split} y_{j}=y_{i,j}+c_i \end{split} \tag{11.3} \]

Notar que esta notación desapareció el subíndice \(i\) luego de la corrección ya que todas las clases serán comparables en pie de igualdad luego de ajustadas.

Ejemplo 11.1

Supongamos que tenemos un grupo de vacas lecheras, y queremos seleccionar como reproductora a la que produce mayor volumen de leche por lactancia.

Como información sabemos que, a nivel poblacional para producción de leche, distintas subclases de lactancia presentan diferente media e igual varianza:

Lactancia (no.)	Media leche 305d \((\text{litros})\)	Varianza leche 305d \((\text{litros}^2)\)
\(1\)	\(3897\)	\(1,3\times 10^6\)
\(2\)	\(4481\)	\(1,3\times 10^6\)
\(3\)	\(4740\)	\(1,3\times 10^6\)

¿Cuál de las siguientes vacas seleccionaríamos? Calculae la producción de leche corregida para cada vaca, planteado como subclase de referencia a la lactancia 2.

Vaca	Nº Lactancia	Leche 305d \((\text{litros})\)
\(I801\)	\(1\)	\(4000\)
\(J805\)	\(1\)	\(3500\)
\(K709\)	\(2\)	\(4900\)
\(L713\)	\(2\)	\(6000\)
\(M607\)	\(3\)	\(5600\)

Lo primero que tenemos que hacer es calcular los factores de corrección para cada clase (número de lactancia), lo que hacemos eligiendo una clase de referencia, restándole luego a la media de dicha clase la media de cada clase, es decir (si elegimos la segunda lactancia como referencia)

\[ \begin{split} \mathbf{a_1}= \bar y_r - \bar y_1= 4481 − 3897 = 584\\ \mathbf{a_2}= \bar y_r - \bar y_2= 4481 − 4481 = 0 \\ \mathbf{a_3}= \bar y_r - \bar y_3= 4481 − 4740 = −259\\ \end{split} \]

A partir de estos factores de corrección (poblacionales) debemos corregir cada registro individual, sumándole el factor de corrección que le corresponda. Por lo tanto, para cada una de las 5 vacas, la producción corregida será igual a:

\[y_{I801}^*= y_{I801} + a_1= 4000 + 584 = 4584 \text{ litros}\] \[y_{J805}^*= y_{J805} + a_1= 3500 + 584 = 4084 \text{ litros}\] \[y_{K709}^*= y_{K709} + a_2= 4900 + 0 = 4900 \text{ litros}\] \[y_{L713}^*= y_{L713} + a_2= 6000 + 0 = 6000 \text{ litros}\] \[y_{M607}^*= y_{M607} + a_3= 5600 + (-259) = 5341 \text{ litros}\]

Seleccionaríamos a la vaca L713, la cual presenta la mayor producción de leche corregida.

Factores de corrección multiplicativos

Como discutimos antes, los factores de corrección aditivos se pueden aplicar cuando las diferencias en las distribuciones de los fenotipos de las clases son exclusivamente en las medias de cada una de ellas. En esos casos alcanza con sumar un valor (el factor de corrección aditivo) a cada uno de los registros de la clase para que todos los registros queden expresados en términos equivalentes respecto al factor en consideración. Sin embargo, en muchos casos no solo las medias difieren sino que también lo hacen las dispersiones de cada clase. Un ejemplo típico es el de la producción de leche por lactancia. Mientras que en las primeras lactancias la producción es promedialmente menor que en las segundas lactancias, la variación también es menor en las primeras respecto a las segundas. Esto se extiende a su vez a las terceras lactancias, como puede verse en el ejemplo de la Figura 11.2, en la parte superior de la misma. Si utilizáramos un umbral de selección sin corregir, casi ninguna vaca de segunda lactancia sería elegida y ninguna de las vacas en primera lactancia lo sería. Más aún, si aplicásemos un factor de corrección aditivo tomando como referencia la 3era lactancia, solamente desplazaríamos las curvas de 1era y 2da lactancia hacia la derecha, pero al quedar con menor variación que la curva de 3era tampoco estaríamos siendo justos con las vacas en 1era o 2da lactancia (que se elegirían en menor proporción que las de 3era). Por lo tanto, hace falta aplicar alguna corrección que al mismo tiempo que desplace las medias para hacerlas coincidir con la media de 3era lactancia, también expanda las varianzas de las distribuciones. Nuevamente, si llamamos \(\bar y_r\) a la media de la clase de referencia, ahora el factor de corrección para la clase \(i\) estará dado por

\[ \begin{split} c_i=\frac{\bar y_r} {\bar y_i} \end{split} \tag{11.4} \]

En el caso de la clase de referencia, \(\bar y_i=\bar y_r\), por lo que la ecuación anterior nos deja con

\[ \begin{split} c_{i=r}=\frac{\bar y_r}{\bar y_i}=\frac{\bar y_r}{\bar y_r}=1 \end{split} \tag{11.5} \]

o lo que es lo mismo, un factor multiplicativo de \(c_r=1\) para la clase de referencia.

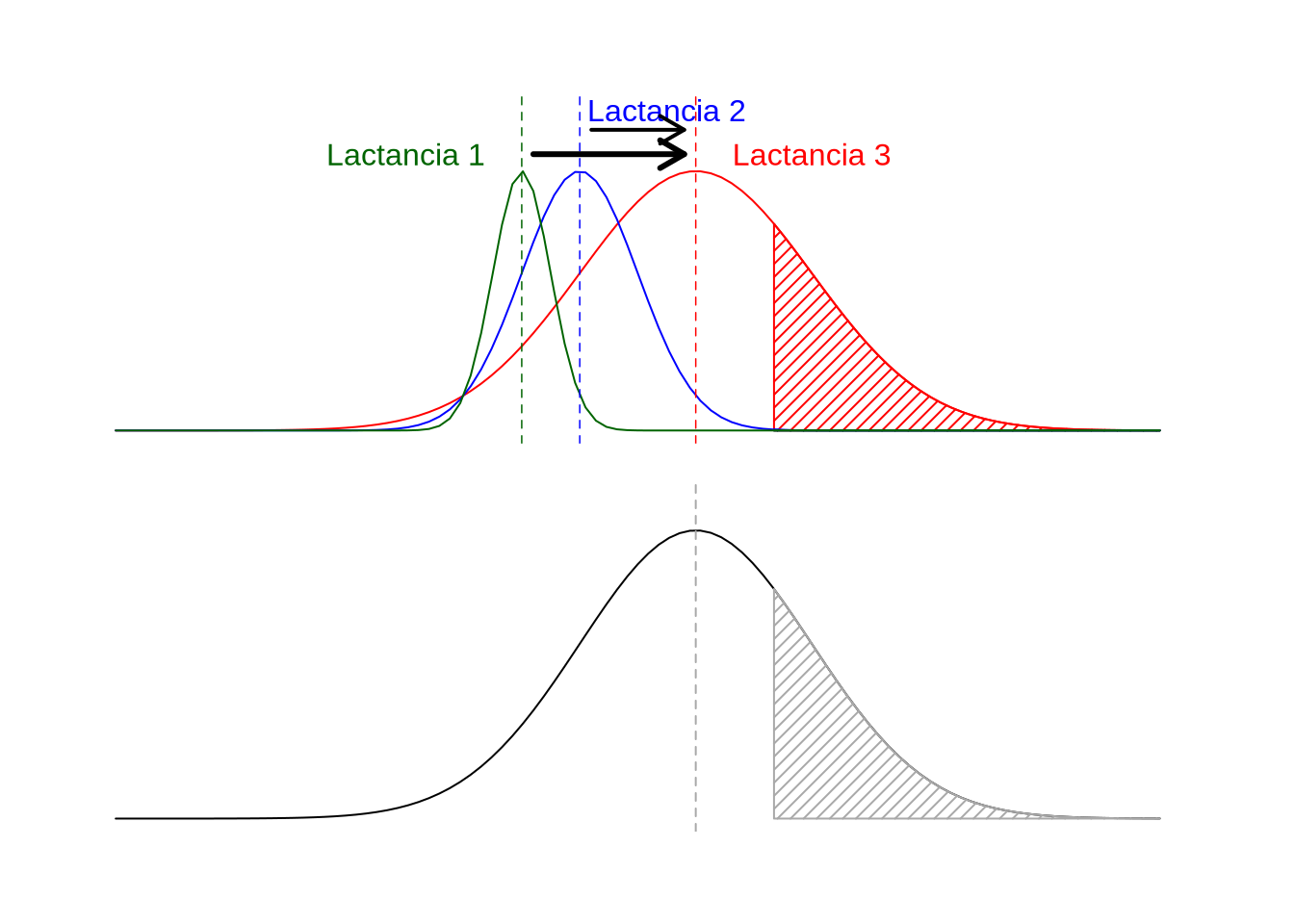
Figura 11.2: Factor de corrección multiplicativo La característica de interés, producción de leche a 305 días, posee una distribución diferente en cada lactancia (1era, 2da y 3era) y así como crece las medias de la característica también lo hacen las varianzas. Si definimos un umbral de selección determinado, si no corregimos por esta diferencia casi ninguna hembra segunda y ninguna de primera lactancia resultaría seleccionada (la pequeña porción rayada en azul en la parte superior de la figura y la no existente rayada en verde). Como la diferencia entre las distribuciones es en ambos parámetros (medias y varianzas), ambos en el mismo sentido, es posible que si definimos la 3era lactancia como categoría de referencia, al multiplicar los registros de las otras dos categorías por su correspondiente factor de corrección multiplicativo estemos corrigiendo ambos parámetros, como se ve en la figura de abajo.

Nuevamente, el paso final, luego de haber calculado los distintos factores de corrección será aplicarlos sobre los distintos registros. Para eso alcanza con multiplicar el valor del registro fenotípico por el valor del factor de corrección correspondiente a la clase a la que pertenece el registro. Es decir, si un registro fenotípico \(j\) pertenece a la clase \(i\), su valor ajustado será

\[ \begin{split} y_{j}=y_{i,j} \cdot c_i \end{split} \tag{11.6} \]

Igual que para el factor de corrección aditivo, observar que en esta notación desapareció el subíndice \(i\) luego de la corrección ya que todas las clases serán comparables en pie de igualdad luego de ajustadas.

Ejemplo 11.2

Supongamos que tenemos un grupo de terneros, y queremos seleccionar al de mayor peso al destete.

Como información sabemos que, a nivel poblacional para peso al destete, distintas subclases de edad de la madre presentan diferente media y diferente varianza (creciente con la edad de la madre):

Edad de la madre \((años)\)	Media peso al destete \((\text{kg})\)
\(3\)	\(157\)
\(4\)	\(166\)
\(5\)	\(169\)

¿Cuál de los siguientes terneros seleccionaríamos? Calculae el peso al destete corregido para cada ternero, planteado como subclase de referencia a la edad de la madre de 4 años.

Ternero	Edad de la madre \((\text{años})\)	Peso al destete \((\text{kg})\)
\(P101\)	\(3\)	\(132\)
\(Q108\)	\(3\)	\(145\)
\(R114\)	\(4\)	\(140\)
\(T123\)	\(5\)	\(150\)

Lo primero que debemos hacer es nuevamente calcular los factores de corrección, en este caso multiplicativos. Para ello vamos a dividir la media de la clase de referencia entre el valor de la media de cada clase de edad de la madre, es decir

\[ \begin{split} m_3=\frac{{\bar y_r}}{{\bar y_3}}=\frac{{166}}{{157}}= 1,06 \end{split} \]

\[ \begin{split} m_4=\frac{{\bar y_r}}{{\bar y_4}}=\frac{{166}}{{166}}= 1,0 \end{split} \]

\[ \begin{split} m_5=\frac{{\bar y_r}}{{\bar y_5}}=\frac{{166}}{{169}}= 0,98 \end{split} \]

Luego, para tener los registros corregidos por el efecto de la edad de la madre alcanza con multiplicar el valor de cada registro por su correspondiente factor de corrección, es decir

\[y_{P101}^*= y_{P101} \times m_3= 132 \times 1,06 = 140 \text{ kg}\] \[y_{Q108}^*= y_{Q108} \times m_3= 145 \times 1,06 = 154 \text{ kg}\] \[y_{R114}^*= y_{R114} \times m_4= 140 \times 1 = 140 \text{ kg}\] \[y_{T132}^*= y_{T132} \times m_5= 150 \times 0,98 = 147 \text{ kg}\]

Seleccionaríamos al ternero Q108, el cual presenta el mayor peso al destete corregido.

---

Un detalle práctico final a la hora de observar las diferencias entre factores aditivos y multiplicativos es la que tiene que ver con la relación que existe en el elemento neutro de las operaciones de adición y multiplicación y los correspondientes valores de las clases de referencia para factores de corrección aditivos y multiplicativos, respectivamente. Llamamos clase de referencia a aquella a la que íbamos a referir todos los registros y que asumíamos como que no cambiaba luego de ajustados los registros. Es decir, luego de aplicar la operación correspondiente al tipo de corrección, los registros quedaban intactos. En la adición, el único elemento que sumado a otro deje sin cambiar el valor de este último es el cero, neutro de la suma. Por lo tanto, el factor de corrección aditivo correspondiente a la clase de referencia debe ser cero. De la misma manera, el único elemento que al multiplicar a un número por este deja sin cambio al último es el uno, el neutro de la multiplicación. Por lo tanto, el factor de corrección multiplicativo correspondiente a la clase de referencia debe ser uno. Esto tan sencillo puede ser una ayuda importante si poseemos una tabla de factores de corrección pero no sabemos si se trata de factores de corrección aditivos o multiplicativos.

Factores de corrección lineales

En algunos casos existe un gran número de categorías posibles o aún infinitas, por lo que calcular un factor de corrección aditivo para cada una de ellas resulta impráctico o aún imposible. Ejemplo de esto podría ser la necesidad de corregir pesos de acuerdo al crecimiento del animal. Por ejemplo, si definimos una característica peso al destete (a los 205 días), lo ideal sería pesar a todos los animales exactamente cuando cumplen 205 días. Sin embargo, en la práctica resulta impracticable esta idea ya que los animales suelen parir en un período extendido de tiempos y deberíamos estar pesando todos los días. La resultante de esto es que algunos animales serán pesados exactamente cuando tienen 205 días, pero unos cuantos lo serán con menos días y otros varios con más de 205 días. ¿Cómo corregimos entonces por estas diferencias en el número de días?

Si asumimos que en intervalos cortos de tiempo, por ejemplo hasta un par de semanas después de los 205 días, el comportamiento de la evolución del peso con los días se corresponde a un crecimiento lineal, entonces podríamos ajustar una recta (por mínimos cuadrados, por ejemplo) de los pesos como función de los días desde el nacimiento, si tuviésemos esos varios datos para cada animal. La pendiente de esta recta será la ganancia diaria, que llamaremos \(b_{PE}\) por ejemplo en Kg/día, que es el elemento central en la corrección lineal que vamos a aplicar. En caso de no tener esa posibilidad, si tenemos el peso al nacimiento (\(P_N\)), además del peso a la edad cercana a los 205 días (\(P_d\)), por ejemplo a los \(d\) días, podemos estimar esa pendiente de ganancia diaria como

\[ \begin{split} b_{PE}=\frac{(P_d-P_N)}{d} \end{split} \tag{11.7} \]

Si llamamos \(b_{PE}\) a la pendiente de regresión del peso en la edad (cualquiera sea el método para obtenerla) para el animal en particular que queremos corregir, es decir a la ganancia diaria esperada para ese animal, entonces un registro de peso \(P_d\) obtenido a los \(d\) días se corregirá a 205 días de acuerdo a la siguiente ecuación

\[ \begin{split} P_{205}=P_N + b_{PE} \cdot 205 \end{split} \tag{11.8} \]

Dicho de otra forma, el registro corregido a 205 días será igual al peso al nacimiento sumado a la ganancia diaria esperada multiplicada por los 205 días establecidos como referencia. En el caso de que \(d=205\), entonces \(b_{PE}=\frac{(P_d-P_N)}{205}\), por lo que al sustituir en la ecuación (11.8) tenemos

\[ \begin{split} P_{205}=P_N + b_{PE} \cdot 205=P_N+\frac{(P_{d}-P_N)}{205} \cdot 205=P_N+P_d-P_N=P_d \end{split} \]

PARA RECORDAR

• Existen una serie de efectos o factores que se manifiestan siempre de la misma manera y que por lo tanto afectan los registros fenotípicos en forma sistemática, es por ello que tenemos la posibilidad de corregir por estas diferencias con el fin de hacer sus medidas comparables.

• El funcionamiento de los factores de corrección consta de dos fases:

1. Cálculo de los factores de corrección a partir de la mayor cantidad posible de registros de la “misma” gran población.
2. Aplicación del factor de corrección correspondiente a cada registro que se pretenda utilizar en una evaluación genética.

• Los factores de corrección aditivos los utilizamos cuando las distribuciones de las características a corregir presentan diferente media pero tienen aproximadamente la misma varianza. Para aplicarlos se calcula un factor de corrección para cada clase del factor donde se define siempre una clase de referencia cuyos registros ajustados permanecerán idénticos a pesar del ajuste. Llamamos \(\bar y_r\) a la media de la clase de referencia, entonces los factores para la clase \(i\) se calculan como \(c_i=\bar y_r - \bar y_i\).

• En el caso de la clase de referencia de los factores aditivos, \(\bar y_i=\bar y_r\), por lo tanto: \(c_{i=r}=\bar y_r - \bar y_i=\bar y_r - \bar y_r=0\). En el caso de los registros del resto de las clases, teniendo un registro fenotípico j que pertenece a la clase i , su valor ajustado será \(y_{j}=y_{i,j}+c_i\).

• En los casos en los que no sólo las medias difieren sino que también lo hacen las dispersiones de las clases, debemos recurrir a factores de corrección multiplicativos. Si denominamos \(\bar y_r\) a la media de la clase de referencia, el factor de corrección para la clase \(i\) será \(c_i=\frac{\bar y_r} {\bar y_i}\).

• Para la clase de referencia de los factores multiplicativos, \(\bar y_i=\bar y_r\), por lo que: \(c_{i=r}=\frac{\bar y_r}{\bar y_i}=\frac{\bar y_r}{\bar y_r}=1\). En el caso de los registros del resto de las clases, teniendo un registro fenotípico j que pertenece a la clase i , su valor ajustado será \(y_{j}=y_{i,j} \cdot c_i\).

• Los factores de corrección lineales son aquellos a los que recurrimos cuando el número de categorías a corregir es tal que se convierte en impráctico o imposible la determinación de un factor para cada una de ellas.

• Tomando como ejemplo la ganancia de peso de terneros, podríamos ajustar una recta de los pesos como función de los días desde el nacimiento (si tuviésemos varios datos para cada animal). En caso de no contar con varios registros, podremos realizar una estimación utilizando el peso al nacimiento \(P_N\) y un peso cercano a los 205 días (\(P_d\);como ejemplo), con \(d\) días podremos determinar: \(b_{PE}=\frac{(P_d-P_N)}{d}\).

• Siendo \(b_{PE}\) la pendiente de la recta de la regresión del peso en la edad para el animal que queremos corregir, la misma representará la ganancia media diaria esperada y será el elemento central en la corrección lineal que vamos a aplicar. Entonces, un registro de peso \(P_d\) obtenido a los \(d\) días se corregirá a 205 días de acuerdo a \(P_{205}=P_N + b_{PE} \cdot 205\).

11.2 La respuesta a la selección y su predicción

Cualquiera que haya salido al campo puede fácilmente reconocer las diferencias entre las razas de ganado bovino, por ejemplo entre vacas lecheras y vacas destinadas a la producción de carne. No solo son claramente observables las diferencias en color (en nuestro país las razas más abundantes en ganado de carne son la Hereford y Aberdeen Angus, mientras que en leche es Holando), sino también en el tamaño y en el desarrollo morfológico del animal. Aún para aquellos que nunca salieron al campo, resultan obvias las diferencias entre razas de perros, tamaños, colores, formas de la cabeza, etc. Tanto en ganado bovino como en cánidos domésticos, las diferencias que observamos no fueron producto de la evolución actuando libremente sino que mayormente fueron guiadas por el ser humano y moldeadas de acuerdo a sus intereses. Vista la diversidad y el poco tiempo (en términos evolutivos) en el que la humanidad realizó la selección artificial, resulta bastante llamativo el éxito obtenido.

Las bases de la selección artificial tradicional son muy sencillas y razonables: si una característica se hereda, entonces eligiendo en cada generación a los “mejores” individuos como reproductores (padres de la siguiente generación) es de esperar que la característica vaya “mejorando”. Este razonamiento ha estado con nosotros desde el inicio de la domesticación, tanto en plantas, animales, como en microbiología (mejores fermentos, etc.). Por ejemplo, si obtener mayor cantidad de lana por oveja parece una buena idea, entonces también lo parece elegir (seleccionar) a los mejores animales (aquellos con más lana) como reproductores y progenitores de la próxima generación. En principio alcanza con repetir este proceso tantas veces como sea necesario para llegar a nuestro objetivo.

Veamos cómo opera esta idea concretamente. Supongamos que tenemos una característica fenotípica de nuestro interés y que deseamos individuos con valores altos de la misma, es decir, cuanto más a la derecha de la media mejor. Para ser objetivos, definimos un determinado valor umbral, que indica que individuos son aceptables para reproducirse y seleccionamos a los que superen dicho umbral. Una representación de esto puede verse en la parte superior de la Figura 11.3, donde el área rayada en rojo denota los individuos seleccionados en la generación parental. La diferencia entre la media de los individuos seleccionados \(\mathrm{\bar x_S}\) y la media de la población \(\mathrm{\bar x_0}\) será igual al diferencial de selección, es decir \(\mathrm{S=\bar x_S-\bar x_0}\). Aunque puede parecer trivial, es un error frecuente confundir el valor umbral a partir del cual vamos a elegir los individuos que serán reproductores con la media de la característica para los reproductores seleccionados; en el caso de que estemos seleccionando para valores altos de la característica, el valor umbral es el mínimo de la misma para que los individuos sean considerados como reproductores, por lo que la media será en general mayor que el umbral (en el peor de los casos será igual).

Diferencial de selección (\(S\)) es la diferencia entre la media de los individuos seleccionados como progenitores de la siguiente generación respecto a la media de la población contemporánea. En selección por truncamiento (selección masal), la media de los animales seleccionados debe tener una valor más favorable (más alto si estamos seleccionado para valores altos) que el umbral de selección. El diferencial de selección, al tratarse de una resta de medias de la característica, tendrá las mismas unidades que la característica.

Umbral de selección es un valor fijo a partir del cual elegimos a los individuos que serán reproductores de la siguiente generación, es decir, aquellos individuos que tengan una fenotipo igual o más favorable que el valor umbral.

Como ya vimos en el capítulo Parámetros Genéticos: Heredabilidad y Repetibilidad, no todas las diferencias que obervamos en los padres respecto a la media será observada en la progenie, un fenómeno que ya había sido observado por Francis Galton y descrito como regresión hacia la mediocridad. También vimos previamente que la pendiente de la regresión del fenotipo de los hijos en el promedio del fenotipo de los padres es igual a la heredabilidad (\(\mathrm{h^2}\)). Más aún, como adelanto de este capítulo vimos en la sección Heredabilidad lograda que la pendiente de la recta que relacionaba la respuesta a la selección \(\mathrm{R}\) en función del diferencial de selección \(\mathrm{S}\) era \(\mathrm{\frac{R}{S}=h^2}\). Dado de que la regresión lineal del valor fenotípico de los hijos en el promedio de los padres (seleccionados) es una función lineal, entonces la media de la regresión es igual a la regresión de la media. Dicho de otra manera, si usamos el coeficiente de regresión para, a partir del valor fenotípico de los padres seleccionados, obtener el valor fenotípico predicho de los hijos y luego le hacemos la media a ese valor, sería lo mismo que predecir la media de la generación de hijos (\(\mathrm{\bar x_1}\)) usando el coeficiente de regresión (\(\mathrm{b_{O\bar P}=h^2}\)) sobre la media de los padres seleccionados (\(\mathrm{\bar x_0}\)). Como el coeficiente de esta regresión lo habíamos obtenido de datos centrados, tanto en la variable dependiente como en la independiente (no tiene intercepto), la predicción debemos hacerla en los mismos términos. Es decir, en términos matemáticos, la predicción será a partir de \(\mathrm{\bar x_S - \bar x_0=S}\).

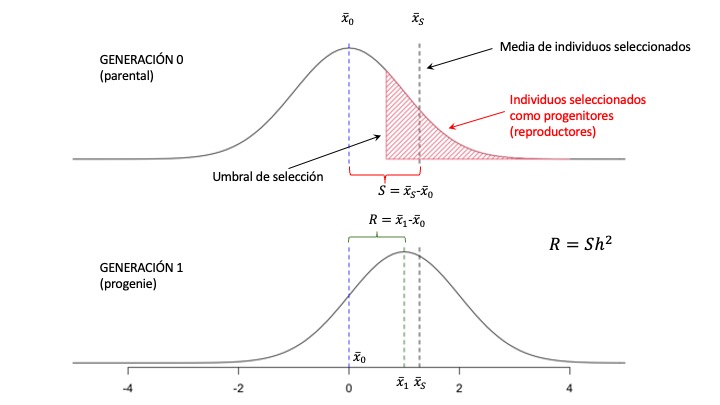
Figura 11.3: Respuesta a la selección. En la parte superior aparece la distribución valores fenotípicos centrados de un característica cuantitativa en la generación parental. Si realizamos selección masal, luego de definido un valor umbral, los individuos que superen (en este caso) dicho valor son elegidos para reproducirse (área rayada en rojo). Claramente, la media de la característica debe ser (en este caso) mayor al valor umbral. La diferencia entre la media de los seleccionado y la media de su generación es el diferencial de selección \(\mathrm{S=\bar x_S-\bar x_0}\). La descendencia de los animales seleccionados constituirán la siguiente generación (distribución de abajo). La respuesta a la selección será la diferencia de medias entre la población en la generación 1 y en la generación 0, es decir \(\mathrm{R=\bar x_1 - \bar x_0}\). La relación entre la respuesta y lo elegido como reproductores es igual a la heredabilidad de la característica, es decir \(\mathrm{\frac{R}{S}=h^2}\) y por lo tanto \(\mathrm{R=S\ h^2}\), que se conoce como la ecuación del criador.

Como muestra la Figura 11.3, la media de la nueva generación será \(\mathrm{\bar x_1}\) y por lo tanto, la respuesta a la selección será la diferencia entre la media de la generación de los progenitores y la media de los descendientes, es decir \(\mathrm{R=\bar x_1-\bar x_0}\). Por lo tanto, usando como criterio de predicción de la media de la generación de los hijos (\(\mathrm{\bar x_1}\)) respecto a la media de la generación parental (\(\mathrm{\bar x_0}\)) el desvío de la media de los animales seleccionados respecto a la media de su generación (\(\mathrm{S=\bar x_S - \bar x_0}\)), tenemos

\[\mathrm{(\bar x_1 - \bar x_0)=R=(\bar x_S - \bar x_0) b_{O\bar P}= (\bar x_S - \bar x_0) h^2}\ \therefore\]

\[ \begin{split} \mathrm{R=S\ h^2} \end{split} \tag{11.9} \]

que es uno de los resultados más importantes de la genética cuantitativa. La ecuación (11.9) es central para el mejoramiento genético y es conocida como la ecuación del criador. El mensaje de la misma es muy claro: cuando la heredabilidad es alta, la respuesta a la selección basada en el fenotipo individual será muy eficiente y la media de la nueva generación será cercana a la media de los animales seleccionados como reproductores. Por otro lado, cuando la heredabilidad es muy baja, la respuesta a la selección será pobre y la media de la nueva generación será casi igual a la de la generación anterior. Desafortunadamente, como lo plantea Houchmandzadeh (2014), el alcance de la linealidad implícita en la ecuación del criador se encuentra restringida al caso en que tanto en los genotipos como los factores ambientales tienen distribución normal. Pese a esto, dado que para muchas características de interés agronómico parece ser un supuesto razonable, seguiremos con esta forma particular de la relación entre diferencial de selección y respuesta.

Otra cosa que seguramente te llamó la atención es el hecho de que pese a que la distribución de los individuos seleccionados como progenitores (el área rayada en rojo en la Figura 11.3) no es una distribución normal, ni siquiera simétrica, hemos dibujado para los descendientes de estos nuevamente una distribución normal.

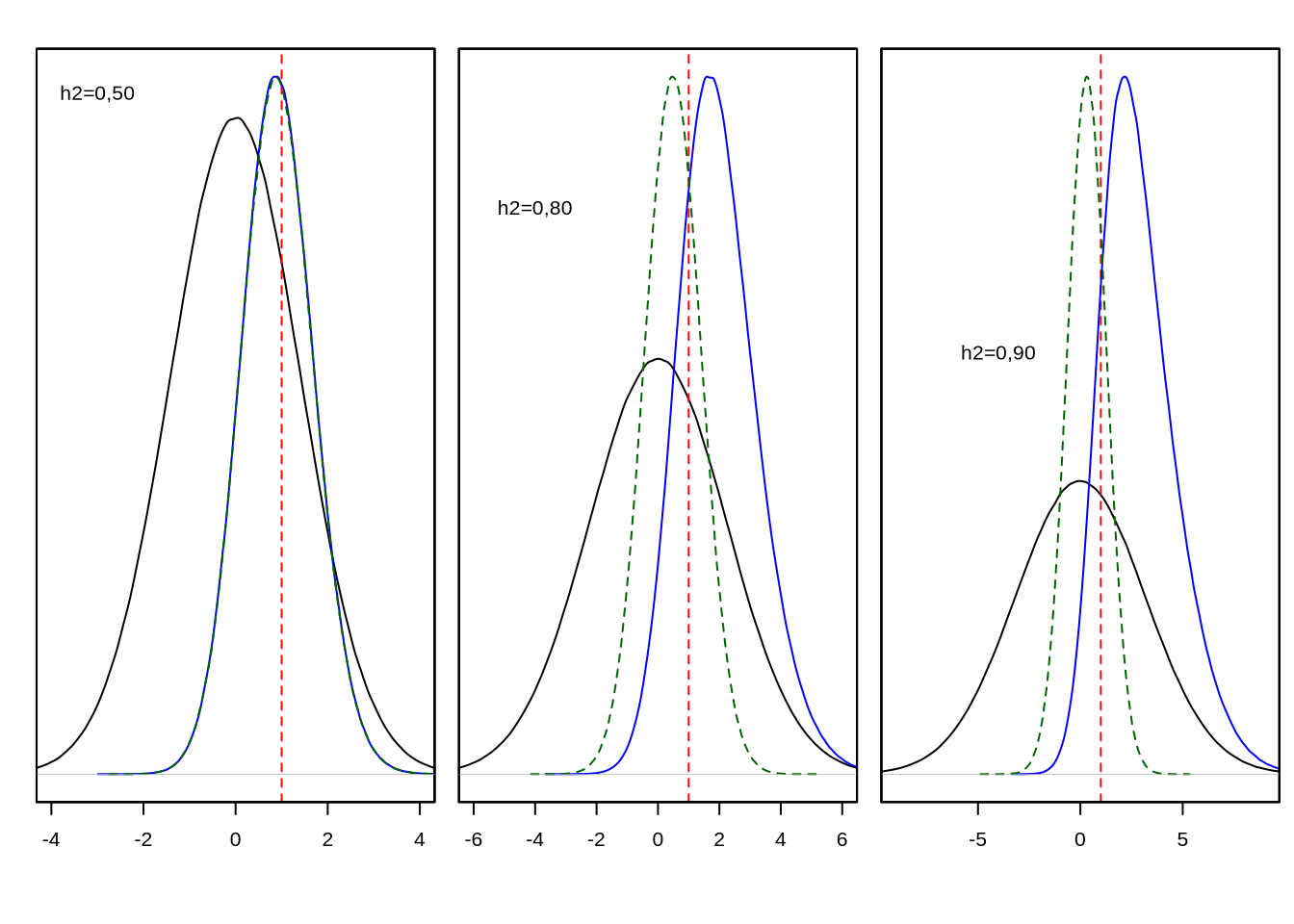
Figura 11.4: Distribución fenotípica de la población (en negro), de los fenotipos seleccionados como reproductores (área rayada en rojo) y de los genotipos seleccionados (azul), así como de los efectos ambientales (verde) en los individuos seleccionados. De izquierda a derecha, heredabilidades de \(h^2=0,50\), \(h^2=0,80\) y \(h^2=0,90\). Se aprecia claramente que pese a que la selección es por truncamiento en los fenotipos, los genotipos de los individuos seleccionados se distribuyen en casi todo el continuo de valores y con una distribución aproximadamente normal a heredabilidades no demasiado altas.

Por ejemplo, la densidad de los individuos que están cerca del valor umbral es mucho mayor que la densidad de los individuos que están hacia valores extremos a la derecha en la distribución. Entonces, la pregunta sería ¿por qué razón los descendientes tendrían pese a esto una distribución aproximadamente normal? La razón es intuitiva: como genotipo y ambiente son independientes (y a su vez los componentes genéticos son ortogonales entre sí), los individuos que están cerca del umbral (límite inferior de los seleccionados) pueden provenir de muchas combinaciones de genotipos y ambientes. Por ejemplo, muy buen genotipo y ambiente mediocre, relativamente buen genotipo y ambiente, o excelente ambiente y mediocre genotipo. En cambio, a medida de que nos desplazamos hacia la derecha en los fenotipos seleccionados, ambos factores, genéticos y ambientales deben ser muy buenos para que su suma sea excelente. Esto nos deja con una distribución de genotipos seleccionados (y en particular los valores aditivos) que tiene una distribución mucho más simétrica que la zona roja rayada, como se puede apreciar en la Figura 11.4. En la misma, se grafican para tres valores de heredabilidad diferentes las distribuciones de los efectos genotípicos y ambientales de los animales seleccionados. Claramente, pese a que realizamos selección por truncamiento, tanto los efectos de los genotipos como los ambientales tienen una distribución continua y aproximadamente normal. Además, para generar los descendientes de esta distribución los apareamientos serán al azar y en este caso lo único relevante son los valores aditivos, que tienen una distribución bastante razonable y a la que se le sumarán el resto de los efectos aleatorios (dominancia, epistasis y ambiente), por lo que no es difícil imaginar que el resultado será aproximadamente normal.

Como en la ecuación del criador la respuesta a la selección es directamente proporcional al diferencial de selección y a la heredabilidad, incrementos en cualquiera de las dos llevan a incrementar la respuesta a la selección. Sin embargo el significado de ambas es conceptualmente distinto. Por un lado, mientras que el diferencial de selección se refiere a una decisión que podemos adoptar casi a nuestra voluntad en una población reducida (rodeo, majada, etc.), la heredabilidad se trata de un parámetro genético poblacional que requiere de mucho esfuerzo para ser modificado en el sentido deseado. Como vimos previamente, la heredabilidad es igual a la proporción de la varianza fenotípica que corresponde a los efectos aditivos, es decir, a la varianza aditiva. Por lo tanto, la única forma de incrementarla, dada la arquitectura genética de una característica, es reducir la varianza ambiental. En muchas características esto es posible a nivel del predio, con manejo más controlados, mejores registros que permitan de alguna manera “corregir” por diferencias, etc., pero en general suele ser algo complicado y costoso.

Por otro lado, el diferencial de selección es una función de la varianza de la característica y de la proporción de individuos que decidamos quedarnos como reproductores. Cuanto más varianza fenotípica tenga la característica en la población en la que estoy haciendo la selección, mayor podrá ser el diferencial de selección a la misma proporción de individuos seleccionados. En general, la idea es mover la media lo más hacia el extremo deseado que sea posible, pero en casi cualquier distribución razonable eso suele implicar cada vez menos individuos que cumplen con los criterios de inclusión (que superen el umbral, por ejemplo).

En la Figura 11.5 se puede apreciar la relación existente entre el diferencial de selección y la varianza de la distribución a partir de un valor de umbral prefijado.

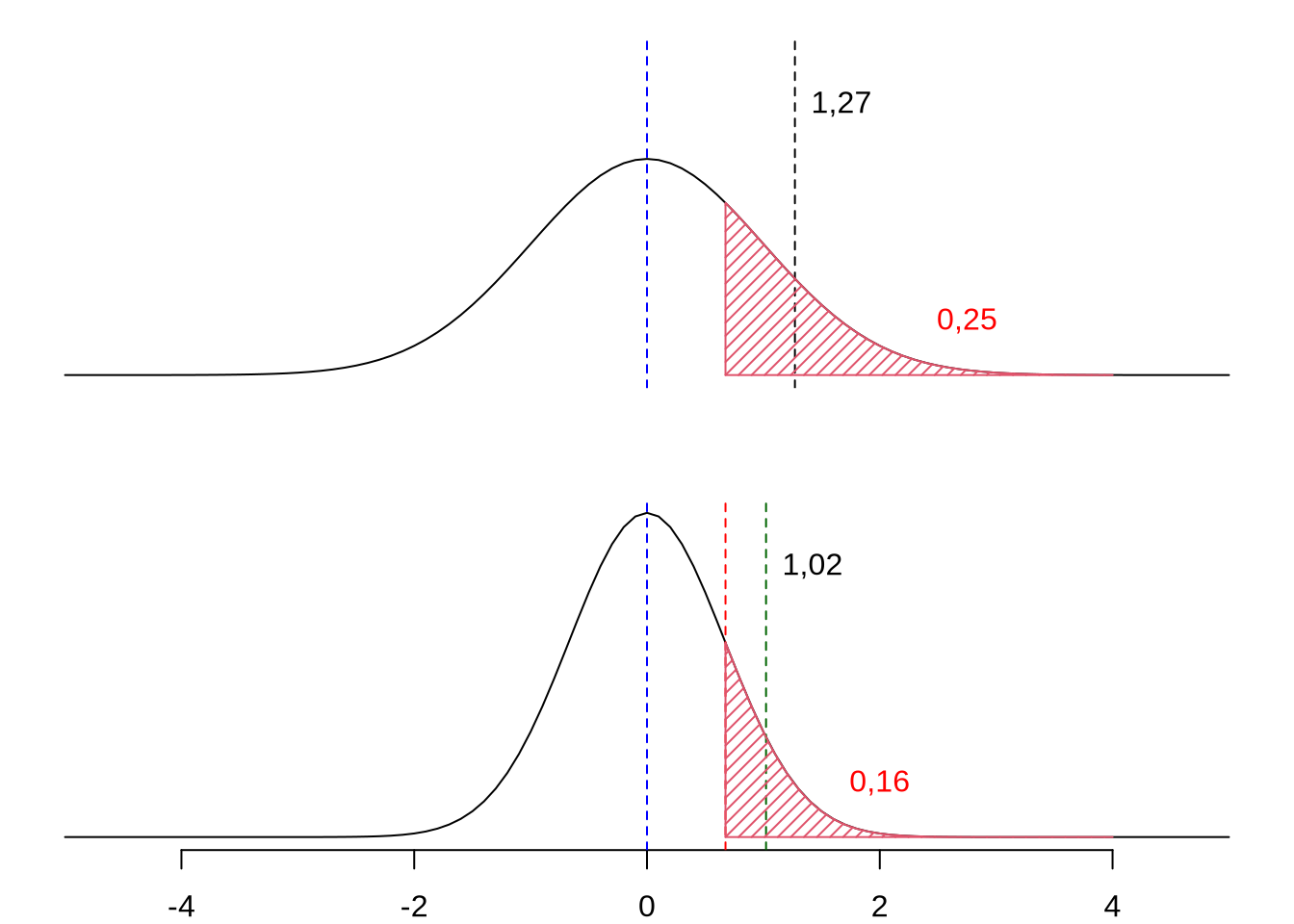
Figura 11.5: La relación entre el diferencial de selección y la varianza fenotípica de la característica. En la parte superior se ilustra la distribución fenotípica de una característica respecto a la media de la misma (es decir, con media de cero) y con desvío estándar de \(1\) unidad de la característica. Si decidimos hacer selección por truncamiento, eligiendo arbitrariamente un umbral \(\mathrm{u=0,6745}\) (el percentil \(75\) de la distribución normal estándar), los individuos que pasen ese valor serán consideramos como reproductores. En este caso, \(25\%\) de los individuos cumplen esa condición y la media de los individuos seleccionados es de \(\mathrm{\bar x_S=1,27}\), por lo que el diferencial de selección será \(\mathrm{S=\bar x_S-\bar x_0=1,27-0=1,27}\). En la parte inferior, la población (para la misma característica) tiene un desvío de \(2/3\), inferior al de la población en la parte superior; esto implica que ahora solo el \(16\%\) de los individuos serán seleccionados como reproductores. Además, el diferencial de selección será ahora de \(\mathrm{S=\bar x_S-\bar x_0=1,02-0=1,02}\), inferior al de la población de la gráfica superior, pese a que el valor de umbral es el mismo en ambos casos.

En la parte superior de la figura podemos apreciar la gráfica de una característica con distribución normal que por comodidad hemos centrado restándole el valor de la media, por lo que ahora la media será cero y con desvío estándar igual a \(1\) unidad de la característica (por ejemplo kg en peso de vellón, micras en diámetro, etc.). Si definimos un umbral de selección, por ejemplo de \(\mathrm{u=0,6745}\), todos los individuos que superen ese valor en su fenotipo serán considerados como reproductores, es decir, progenitores de la siguiente generación. Con ese umbral, en la distribución normal estándar (media igual a cero y desvío estándar igual a 1) quedan \(25\%\) de individuos en el área seleccionada (rayada en rojo) y la media de la característica para esos individuos es de \(\mathrm{\bar x_S=1,27}\). Como la media de la característica para toda la población en nuestro caso es de \(\mathrm{\bar x_0=0}\) (porque la centramos), entonces el diferencial de selección será de \(\mathrm{S=\bar x_S-\bar x_0=1,27-0=1,27}\) unidades de la característica. Por otra parte, en la parte inferior de la figura se representa la situación para la misma característica pero en una población cuyo desvío estándar fenotípico es de \(2/3\) (menor a \(1\) que era el valor de la distribución en la parte superior). Ahora, utilizando el mismo umbral de selección que utilizamos en la población de arriba, es decir \(\mathrm{u=0,6745}\), ahora tendremos solamente el \(16\%\) de los individuos como reproductores en el área rayada en rojo y el valor de la media para los mismos será \(\mathrm{\bar x_S=1,02}\), por lo que el diferencial de selección será ahora de \(\mathrm{S=\bar x_S-\bar x_0=1,02-0=1,02}\) unidades de la característica.

En conclusión, pese a que en ambos casos el valor de umbral de selección utilizado es el mismo, en el primer caso la varianza mayor hace que una proporción mayor de los individuos cumpla con el criterio de selección y además, en el caso de la distribución normal, que el diferencial de selección sea mayor.

11.2.0.1 Ejemplo 11.3

En la la Figura 11.6 se presentan diferentes situaciones de proporción de selección representadas gráficamente, suponiendo características de distribución normal. Determinar para cada una de ellas la correspondiente intensidad de selección

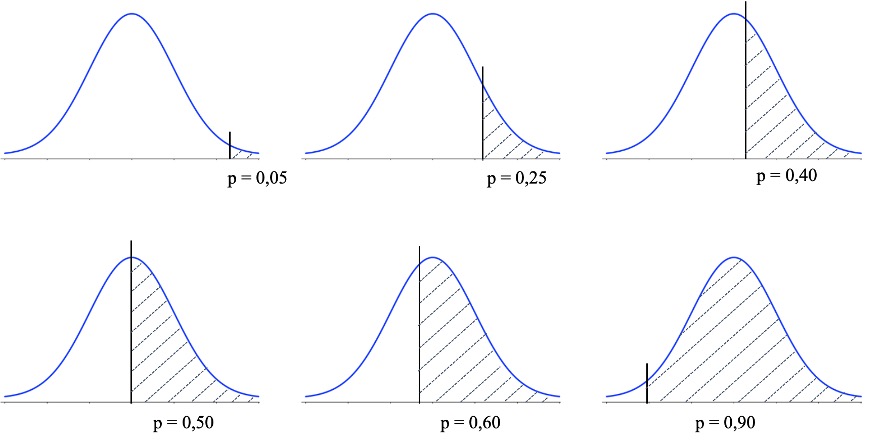
Figura 11.6: Proporción de selección representada gráficamente, suponiendo características de distribución normal

Asumiendo normalidad, podemos usar la relación \(i=\frac{z}{p}\), donde \(p\) es la proporción de animales seleccionados. A partir de esta relación podemos generar una tabla como la siguiente, con la proporción de animales seleccionados (aquí expresada en %) y la consiguiente intensidad de selección \(i\):

Proporción %	\(i\)
1	2,6652
2	2,4209
3	2,2681
4	2,1543
5	2,0627
6	1,9854
7	1,9181
8	1,8583
9	1,8043
10	1,7550
15	1,5544
20	1,3998
25	1,2711
30	1,1590
35	1,0583
40	0,9659
50	0,7979
60	0,6439
70	0,4967
80	0,3500
90	0,1950
100	0,0000

Por lo tanto, el primer gráfico de la línea superior corresponde a seleccionar el \(5\%\) de los mejores animales y de acuerdo a nuestra tabla eso equivale a una intensidad de selección de \(i=2,0627\). De la misma forma, para \(p=0,25\) (es decir, \(25\%\)) la intensidad será de \(i=1,2711\), para \(p=0,40\) de \(i=0,9659\), para \(p=0,50\) de \(i=0,7979\), para \(p=0,60\) de \(i=0,6439\), para \(p=0,80\) de \(i=0,3500\) y finalmente \(p=0,90\) será de \(i=0,1950\).

PARA RECORDAR

• Cuando estamos trabajando en seleccionar animales a partir de un umbral, es muy importante no confundir el umbral a partir del cuál los animales son seleccionan con la media de los seleccionados.

• El diferencial de selección (\(S\)) es la diferencia entre la media de los individuos seleccionados como progenitores de la siguiente generación respecto a la media de la población contemporánea; al tratarse de una resta de medias de la característica, tendrá las mismas unidades que la característica.

• El umbral de selección es un valor fijo a partir del cuál elegimos a los individuos que serán reproductores de la siguiente generación, es decir, aquellos individuos que tengan una fenotipo igual o más favorable que el valor umbral.

• Recordando la ecuación del criador (\(R=S h^2\)), cuando la heredabilidad es alta, la respuesta a la selección basada en el fenotipo individual será muy eficiente y la media de la nueva generación será cercana a la media de los animales seleccionados como reproductores. Por otro lado, cuando la heredabilidad es muy baja, la respuesta a la selección será pobre y la media de la nueva generación será casi igual a la de la generación anterior.

• Como en la ecuación del criador la respuesta a la selección es directamente proporcional al diferencial de selección y a la heredabilidad, incrementos en cualquiera de las dos llevan a incrementar la respuesta a la selección. El significado de ambas es conceptualmente distinto: mientras que el diferencial de selección se refiere a una decisión que podemos adoptar casi a nuestra voluntad en una población reducida, la heredabilidad se trata de un parámetro genético poblacional que requiere de mucho esfuerzo para ser modificado en el sentido deseado.

11.3 Diferencial de selección e intensidad de selección

Como vimos más arriba (Figura 11.5), el diferencial de selección para un determinado umbral de selección es una función de la varianza de la característica. Esto nos deja con una medida de la presión de selección que es dependiente de los parámetros de la distribución fenotípica de la población de interés. Es decir, el significado de un determinado umbral de selección es completamente dependiente de la distribución fenotípica de la característica en la población en la que se piensa aplicar.

Por otra parte, cuando queremos comparar la presión de selección en dos característica diferentes, el diferencial de selección deja de tener sentido: ¿cómo podría comparar la presión de selección en peso sucio de vellón (PVS, en \(kg\)) con la presión de selección en diámetro de fibras (DF, \(\mu m\))? ¿Es acaso más importante un esfuerzo de 100 gramos en PVS que \(2 \mu m\) en DF? Claramente, resulta imposible de comparar cuando ambas características tienen distintas unidades. Aún teniendo las mismas unidades, si se trata de características distintas es esperable que las distribuciones sean diferentes y por lo tanto el diferencial de selección sea incomparable en términos del esfuerzo de selección o presión de selección que implican.

Todo lo anterior sugiere que para poder comparar la presión de selección de una manera razonable es necesario estandarizar de alguna forma el diferencial de selección. Como vimos antes, una de las dificultades para comparar esta presión usando el diferencial de selección era la dependencia de este último en la varianza de la característica: a un determinado valor del diferencial de selección, cuanto menor era la varianza de la característica mayor era el esfuerzo que implicaba ya que debía quedarme con menos individuos como reproductores (pese a que el diferencial de selección podía ser menor en valor absoluto). Esto nos sugiere que a una presión de selección determinada hay una relación inversa entre el diferencial de selección y la dispersión de la distribución. Por otro lado, el desvío estándar de una característica posee las mismas unidades que la característica. Por lo tanto, dividiendo el diferencial de selección entre el desvío estándar fenotípico de la misma estamos corrigiendo los dos problemas en forma simultánea, es decir

\[ \begin{split} {i=\frac{S}{\sigma_P}} \end{split} \tag{11.10} \]

La intensidad de selección es una medida de la presión de selección que es independiente de las unidades de la característica y que es igual al diferencial de selección estandarizado, es decir, el diferencial de selección divido entre el desvío estándar fenotípico de la característica.

Claramente, tanto el diferencial de selección como el desvío estándar fenotípico tienen las unidades de la características, por lo que al dividir ambas cantidades el resultado es adimensional (es decir, no tiene unidades). Por otra parte, cuanto mayor la varianza de una característica, mayor es su desvío estándar (que es la raíz cuadrada de la varianza) y dado un valor fijo de umbral una mayor parte de la población superará ese umbral (aumentando el diferencial de selección). Sin embargo, ese efecto se ve contrarrestado en la intensidad de selección ya que el diferencial de selección se divide entre el desvío estándar fenotípico, lo que compensa exactamente el incremento del diferencial de selección.

Normalmente, en especies de mamíferos domésticos de interés productivo (bovinos, ovinos, equinos, caprinos, porcinos, etc.) es posible mantener una presión de selección mucho más alta en machos que en hembras. Esto se debe a que las hembras deben hacerse cargo de la preñez, quedando “bloqueadas” durante todo ese período a los fines de nuevos eventos reproductivos. Es decir, una vez preñada la hembra deberá continuar con la gestación hasta que nazcan las crías y recién a partir de ese momento (en general algo después) estará disponible para volver a ser gestante. En cambio, para los machos la preñez de la hembra no significa ninguna restricción a su capacidad de fecundar los gametos de otras hembras. Claramente, el factor limitante de la parte reproductiva de la mayor parte de los sistemas de producción animal es la capacidad de alojar a las hembras gestantes, ya que los machos, luego de la fecundación, dejan de tener importancia para el nacimiento de las crías. Estas diferencias nos llevan a que un macho pueda aparearse con muchas hembras y por lo tanto necesitaremos muchos menos machos que hembras.

En términos de la proporción de animales seleccionados, lo anterior puede expresarse de la siguiente manera. Usualmente, la proporción de hembras que debo retener es la relación entre el número de hembras que tengo en la categoría de entrada a la población (rodeo, majada, piara, etc.) y el número de las mismas que generé como reemplazos. El número de hembras que tengo en la categoría de entrada es función de la estructura de edades de la población y de la capacidad de animales que tiene el establecimiento, mientras que el número de reemplazos generados es función del número de hembras reproductivas en la población y de la eficiencia reproductiva de las mismas. Por otro lado, la proporción de machos retenidos como reproductores (en el caso de que los mismos salgan del establecimiento) suele obtenerse sobre un base mucho más sencilla: el número de machos requeridos es una función del número de hembras que un solo macho puede fecundar por estación de cría, mientras que el número de reemplazos generados es (en general) el mismo que el de hembras generadas.

Todo lo anterior nos lleva a la necesidad de poder manejar de forma integrada las diferencias en intensidad de selección que corresponde a machos y hembras. Como el aporte genético a la nueva generación vendrá la mitad por el lado de machos y la mitad por el lado de hembras, la intensidad de selección a nivel de la población será el promedio de la intensidad de selección en machos y en hembras.

\[ \begin{split} {i=\frac{i_M+i_H}{2}} \end{split} \tag{11.11} \]

En el caso de que en ambos sexos la varianza fuese diferente, la ecuación anterior implica

\[ \begin{split} {i=\frac{i_M+i_H}{2}=\frac{\frac{S_M}{\sigma_{P_M}}+\frac{S_H}{\sigma_{P_H}}}{2}=\frac{1}{2}\left[\frac{S_M}{\sigma_{P_M}}+\frac{S_H}{\sigma_{P_H}}\right]} \end{split} \tag{11.12} \]

es decir, cada diferencial de selección es dividido entre su correspondiente desvío estándar fenotípico y luego ambos promediados.

Por otro parte, si la característica tiene el mismo desvío estándar en machos que en hembras, es decir \({\sigma_{P_M}=\sigma_{P_H}=\sigma_P}\), entonces sustituyendo la definición de la ecuación (11.10) en la ecuación (11.11) tenemos ahora

\[ \begin{split} {i=\frac{i_M+i_H}{2}=\frac{\frac{S_M}{\sigma_P}+\frac{S_H}{\sigma_P}}{2}=\frac{\frac{S_M+S_H}{\sigma_P}}{2}=\frac{S_M+S_H}{2\sigma_P}=\frac{\frac{S_M+S_H}{2}}{\sigma_P}=\frac{\bar S}{\sigma_P}} \end{split} \tag{11.13} \]

PARA RECORDAR

• Cuando queremos comparar la presión de selección en dos característica diferentes, el diferencial de selección deja de tener sentido, por lo que debemos recurrir a una variable adimensional que llamaremos intensidad de selección.

• La intensidad de selección es una medida de la presión de selección que es independiente de las unidades de la característica y que es igual al diferencial de selección estandarizado, es decir, el diferencial de selección divido entre el desvío estándar fenotípico de la característica (\({i=\frac{S}{\sigma_P}}\)).

• En general y en el tipo de animales productivos que trabajamos la presión de selección es mayor en machos que en hembras

• La intensidad de selección a nivel de la población será el promedio de la intensidad de selección en machos y en hembras (\({i=\frac{i_M+i_H}{2}}\)). En el caso de que en ambos sexos la varianza fuese diferente, la ecuación anterior implica \({i=\frac{i_M+i_H}{2}=\frac{\frac{S_M}{\sigma_{P_M}}+\frac{S_H}{\sigma_{P_H}}}{2}=\frac{1}{2}\left[\frac{S_M}{\sigma_{P_M}}+\frac{S_H}{\sigma_{P_H}}\right]}\).

11.4 Intensidad de selección y proporción seleccionada

La definición de intensidad de selección que hemos dado, es decir, el diferencial de selección estandarizado, nos deja con una medida de presión de selección que es sencilla de obtener si conocemos tanto el diferencial de selección como el desvío fenotípico de la característica. Sin embargo, en muchos casos no podemos darnos el lujo de determinar un valor dado de umbral para la característica ya que podría comprometer la sostenibilidad del sistema o implicar una presión de selección mucho menor que la posible y deseable. Por ejemplo, si fijamos un umbral tan alto que restrinja el número de hembras por debajo de las necesarias para generar reemplazos de la primera categoría en el rodeo, entoces comenzarermos un proceso de reducción en el tamaño del mismo, a menos que compensemos de otra forma. Esto nos lleva a la posibilidad de que el determinante para la presión de selección posible sea la proporción de individuos que debo quedarme como reproductores.

En general, para distribuciones arbitrarias esto implicaría obtener la media de los individuos que quedan en la proporción seleccionada, lo que puede resultar algo complejo de derivar. Para distribuciones conocidas una alternativa adecuada a los tiempos es recurrir a algún software que permita hacer los cálculos basados en las distribuciones o aún realizar simulaciones (R Core Team (2021)) y obtener una buena estimación de esta media y del desvío estándar de la característica. Claramente, esto implica conocer la distribución, así como un estimado razonable de sus parámetros. Afortunadamente, la mayor parte de las características productivas siguen una distribución normal, con media \(\mu\) y varianza \(\sigma_P^2\), es decir \(N(\mu,\sigma^2)\). El diferencial de selección es igual a la media de los seleccionados menos la media de la población, por lo que al restarle la media de la población a los todos los datos los mismos quedan centrados en cero (ya que si \(\mu=x_0\), entonces la nueva media al restarle \(x_0\) será \(\mu=x_0-x_0=0\)). Esta operación solo desplaza la distribución centrándola en \(\mu=0\), es decir, cada valor será un desvío de la media, pero no cambia su varianza. Sin embargo, en la definición de intensidad de selección que vimos, \({\mathrm i=\frac{\mathrm S}{\sigma_P}}\). Ahora, si a esta distribución centrada en cero la dividimos entre el desvío estándar fenotípico, es decir \(\sigma_P\), tenemos que los datos tienen ahora distribución \(N(0,1)\).

Dicho de otra forma, haciendo las operaciones clásicas que haríamos para obtener la intensidad de selección a partir del diferencial de selección, lo que estamos haciendo es obtener el apartamiento para la media de los individuos seleccionados en una distribución normal estandarizada, es decir \(N(0,1)\). Esto que puede parecer trivial es de suma importancia ya que la distribución normal estandarizada nos permite obtener varios resultados importantes sin tener que hacer cuentas específicas para cada combinación de \(x_0\) y \(\sigma_P^2\).

Como muestra la Figura 11.7, en una distribución normal estandarizada la media de los individuos seleccionados es exactamente la intensidad de selección. Es decir, para estandarizar una distribución normal \(N(x_0, \sigma_P^2)\) primero le restamos \(x_0\) a todas las observaciones y luego dividimos esto entre el desvío estándar de la distribución (\(\sigma_P\)). La primera operación deja la media de los individuos seleccionados exactamente igual al diferencial de selección ya que \(\mathrm{x_S-x_0=S}\), mientras que la segunda transforma el diferencial de selección en la intensidad de selección ya que \({\frac{\mathrm S}{\sigma_P}=\mathrm i}\). Ahora, basados en las propiedades de la distribución normal estándar, la media de la región seleccionada es igual a la altura del punto de truncamiento dividido entre el área bajo la curva a partir del límite de truncamiento y hasta \(+\infty\).

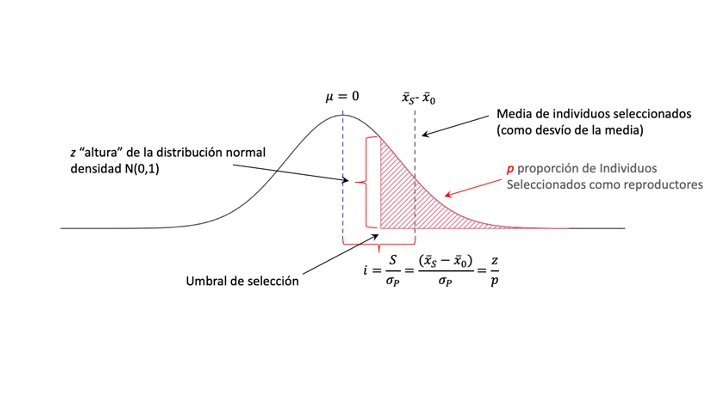
Figura 11.7: La intensidad de selección en una distribución normal estandarizada. Al haber estandarizado la distribución fenotípica, es decir, restado a los valores la media original y luego dividido entre el desvío estándar, ahora la media de los individuos seleccionados será directamente \(\mathrm{i}\), ya que \({\frac{\mathrm{(\bar x_s - \bar x_0)}}{\sigma_P}=\frac{\mathrm S}{\sigma_P}=\mathrm i}\). Esto nos permite explotar la relación existente en la distribución normal de la media de la región seleccionada como la relación entre la altura en el punto de truncamiento \(\mathrm{z}\) (que es la densidad de la normal \(N(0,1)\) en ese punto) y la proporción seleccionada \(\mathrm{p}\) (que es el área bajo la curva entre el punto de truncamiento y \(+\infty\)), es decir \(\mathrm{i=\frac{z}{p}}\).

El resultado obtenido, \(\mathrm{i=z/p}\), es muy importante porque nos dice que a una proporción determinada de individuos seleccionados en una característica con distribución normal, cualquiera sea esta, le corresponde siempre la misma intensidad de selección. Además, como esta intensidad de selección es siempre la misma para una proporción dada es posible construir una tabla, como la que sigue, con los pares de valores a la precisión deseada. Más aún, es trivial calcular el valor exacto para cualquier proporción en la mayoría de las hojas de cálculo o en software estadístico como R Core Team (2021).

Intensidad de selección en función de la proporción de individuos seleccionados como reproductores en una característica con distribución normal

Proporción seleccionada (%)	Intensidad		Proporción seleccionada (%)	Intensidad
100	0		50	0,7979
99	0,0269		49	0,8139
98	0,0494		48	0,8301
97	0,0701		47	0,8464
96	0,0898		46	0,8629
95	0,1086		45	0,8796
94	0,1267		44	0,8964
93	0,1444		43	0,9135
92	0,1616		42	0,9307
91	0,1785		41	0,9482
90	0,195		40	0,9659
89	0,2113		39	0,9838
88	0,2273		38	1,002
87	0,2432		37	1,0205
86	0,2588		36	1,0392
85	0,2743		35	1,0583
84	0,2897		34	1,0777
83	0,3049		33	1,0974
82	0,32		32	1,1175
81	0,335		31	1,138
80	0,35		30	1,159
79	0,3648		29	1,1804
78	0,3796		28	1,2022
77	0,3943		27	1,2246
76	0,409		26	1,2476
75	0,4237		25	1,2711
74	0,4383		24	1,2953
73	0,4529		23	1,3202
72	0,4675		22	1,3459
71	0,4821		21	1,3724
70	0,4967		20	1,3998
69	0,5113		19	1,4282
68	0,5259		18	1,4578
67	0,5405		17	1,4886
66	0,5552		16	1,5207
65	0,5698		15	1,5544
64	0,5846		14	1,5898
63	0,5993		13	1,6273
62	0,6141		12	1,667
61	0,629		11	1,7094
60	0,6439		10	1,755
59	0,6589		9	1,8043
58	0,674		8	1,8583
57	0,6891		7	1,9181
56	0,7043		6	1,9854
55	0,7196		5	2,0627
54	0,7351		4	2,1543
53	0,7506		3	2,2681
52	0,7662		2	2,4209
51	0,782		1	2,6652

En la Figura 11.8 se muestra la curva de intensidad de selección en función de la proporción de individuos seleccionados. A la izquierda se grafica esta relación para todo el intervalo posible de proporciones (es decir entre cero y uno), expresado como porcentaje y en la misma se aprecia el carácter aproximadamente sigmoidal de la relación. Claramente, a medida de que nos vamos acercando hacia el cero la pendiente se hace más empinada. Por esta razón, a la izquierda se grafica solamente la región entre \(0\%\) y \(10\%\), una zona que es usual en machos de mamíferos domésticos. Por ejemplo, si seleccionamos el \(2\%\) de los machos como reproductores, tendremos entonces (de acuerdo a la gráfica) aproximadamente una intensidad de selección igual a \(2,4\); como referencia, el valor “exacto” usando la expresión “dnorm(qnorm(0.98))/0.02” en R Core Team (2021) es de \(2,420907\).

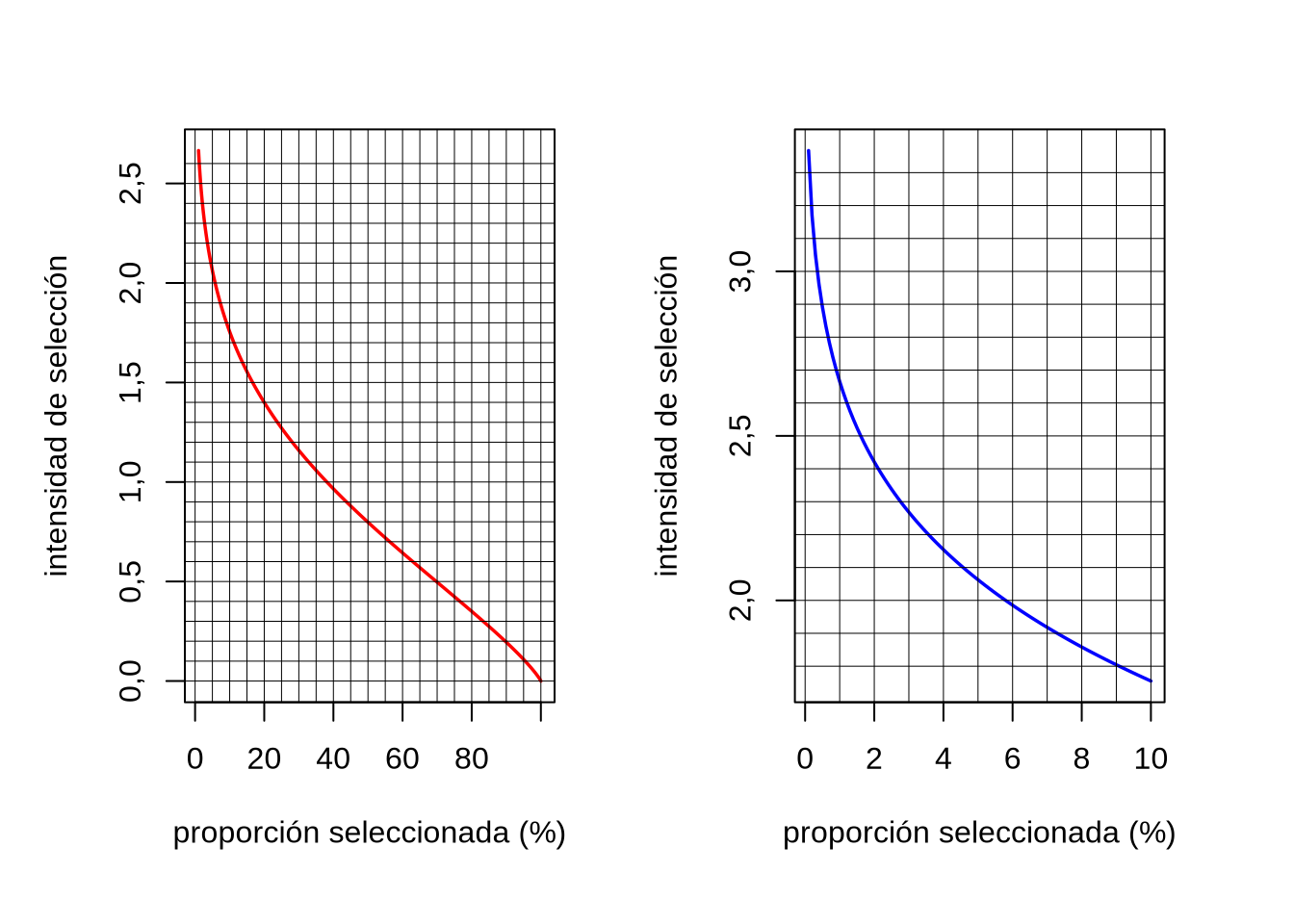
Figura 11.8: Intensidad de selección en función de la proporción de individuos seleccionados como reproductores en una característica con distribución normal. Mientras que la gráfica de la derecha representa todo el intervalo posible de selección, la de la derecha representa la región de más intensidad de selección, típica de machos en la mayor parte de las especies de mamíferos domésticos.

Un tema relativamente menor en la práctica, pero relevante en algunos casos es el del tamaño poblacional y su efecto en el cálculo de la intensidad de selección. La obtención de la intensidad de selección a partir de las propiedades de la distribución normal asume precisamente eso, una distribución normal de la característica. En particular, con muy pocos individuos, el efecto de seleccionar una determinada proporción nunca será continuo, como sí lo asume la distribución normal. Por ejemplo, si de 10 individuos voy a seleccionar solo 1, la proporción de elegidos es \(p=1/10=0,1\). Por otro lado, si tengo que elegir 100 individuos de una población que tiene 1.000 individuos, también la proporción será de \(p=100/1.000=0,100\). Sin embargo, mientras que la “resolución” de este último caso es de \(1/1000\) (si hubiese tenido que elegir 1 individuo más la proporción sería de \(p=101/1.000=0,101\)), en el primer caso la “resolución” es de \(1/10\) (si hubiese elegido un individuo más sería \(p=2/10=0,2\)). Claramente, el tamaño de los pasos en la discontinuidad es de \(1/n\). Para corregir este efecto, Bulmer (1980) propone una “corrección” de la proporción a utilizar en la distribución normal (que llamaremos \(\mathrm{p^*}\)) y que para seleccionar \(k\) individuos entre \(n\) individuos disponibles es igual a

\[ \begin{split} {p^* = \frac{\left(k+\frac{1}{2}\right)}{\left(n+\frac{k}{2n}\right)}} \end{split} \tag{11.14} \]

En la Figura 11.9 se puede apreciar el efecto del número total de individuos de la población en la corrección necesaria para la proporción de individuos seleccionados. Cada una de las curvas de colores representa una proporción diferente de individuos seleccionados, desde \(10\%\) (curva en rojo) hasta \(20\%\) (curva en azul). Mientras que a partir de los 100 individuos las diferencias entre la proporción realmente seleccionada (\(\mathrm{p}\)) y el equivalente efectivo de proporción (\(\mathrm{p^*}\)) a considerar para calcular la intensidad de selección es insignificante, a valores bajos del número de individuos (\(\mathrm{n}\)) puede ser bastante importante. Por ejemplo, para \(\mathrm{k=1}\) y \(\mathrm{n=10}\), mientras que \(\mathrm{p=0,10}\), \(\mathrm{p^* \approx 0.1492}\). Sin embargo, para la misma proporción en \(\mathrm{n=100}\) individuos (por lo tanto \(\mathrm{k=10}\)), tenemos que \(\mathrm{p^* \approx 0.1049}\). El comportamiento asintótico se puede apreciar claramente en la figura ya que a medida de que aumenta el \(\mathrm{n}\) las curvas de colores tienden a las líneas punteadas que les “corresponden”, es decir \(\mathrm{\lim_{n \to \infty}p^*=p}\).

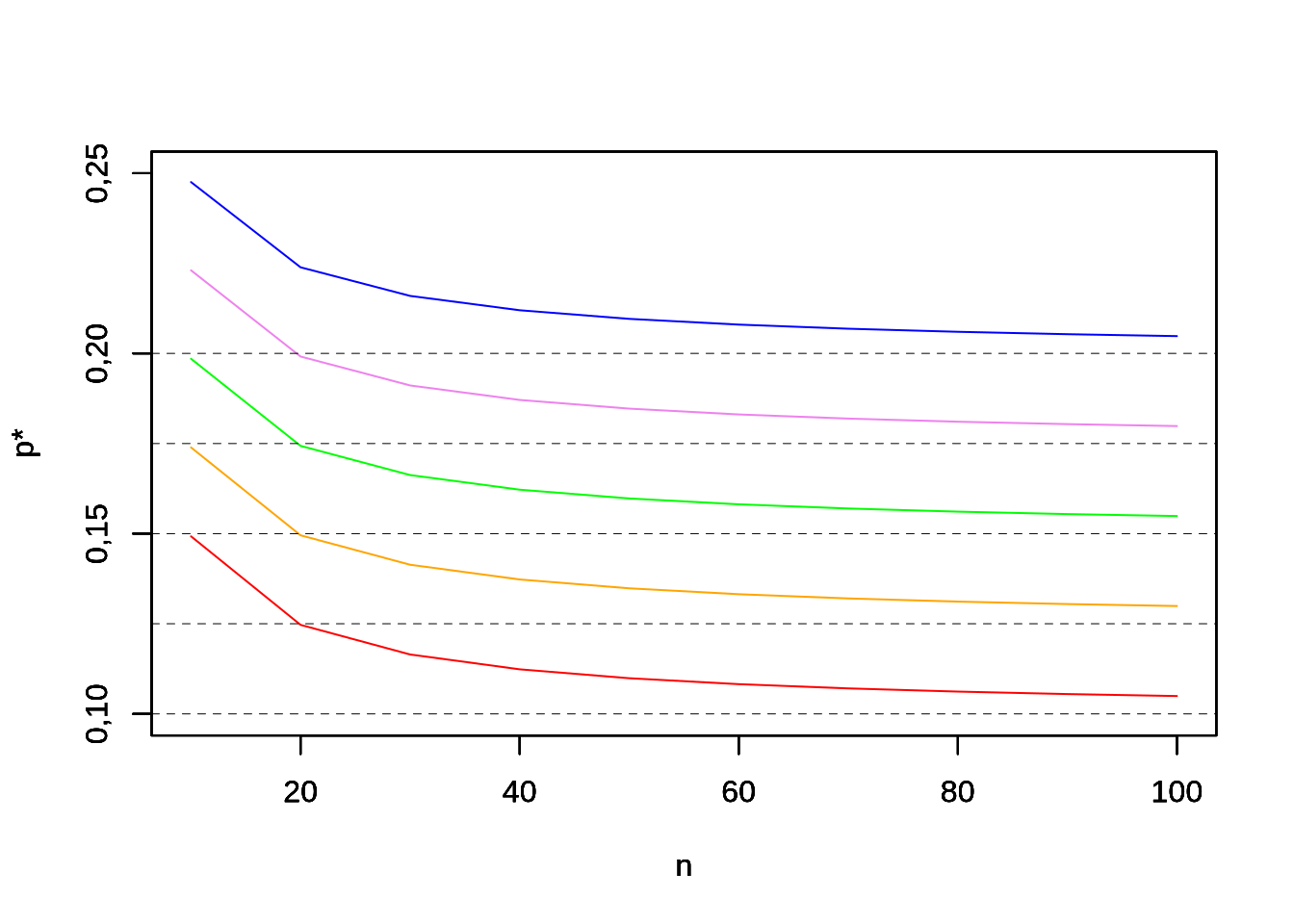
Figura 11.9: Ajuste de la proporción de individuos seleccionados para un número bajo de individuos. De abajo hacia arriba, las curvas representan proporciones reales de \(0,100\), \(0,125\), \(0,150\), \(0,175\) y \(0,200\), como lo indican las líneas a trazos correspondientes. A medida de que el número total de individuos crece la diferencia entre la proporción real \(p\) (línea a trazos) y la proporción ajustada \(p^*\) (curvas de color) tiende a cero.

Hasta ahora hemos solo considerado el caso de la selección contra determinados individuos (aquellos que quedan por debajo del umbral), pero no necesariamente este tipo de selección es óptimo a largo plazo. Si la presión de selección es muy alta, en la medida de que elegimos los “mejores individuos” basados en nuestra característica de interés, estamos reduciendo en forma sustancial la variabilidad genética disponible, lo que puede atentar contra el futuro genético a mediano o largo plazo. Una alternativa más general es utilizar una función continua (por ejemplo) de nuestra característica de interés para determinar la probabilidad de que el individuo quede entre los reproductores. Esto es lo mismo que establecer el fitness del individuo como función de la característica. Con esto en mente, ahora existe una probabilidad de permanecer como reproductor para cada valor fenotípico estandarizado y que será el “peso” que tendrá cada fenotipo en el cálculo de \(\mathrm{i}\). Es decir, la intensidad de selección será la media ponderada (por la función fitness) de los fenotipos estandarizados.

¿De dónde sale la relación \(i=\frac{z}{p}\)?

Una de las relaciones más usadas para conocer la intensidad de selección en mejoramiento genético animal es la que establece \(i=\frac{z}{p}\), es decir, en selección por truncamiento, la intensidad es la relación de la ordenada de una distribución \(\sim N(0,1)\) en el punto de truncamiento, dividido la proporción de animales seleccionados. ¿Pero de dónde sale esta relación?
Para entenderla, recordemos que la intensidad de selección era igual al diferencial de selección dividido entre el desvío estándar fenotípico, lo que nos referirá a una distribución \(\sim N(0,1)\) y por lo tanto la intensidad de selección será la media de la fracción seleccionada a partir del punto de truncamiento. En el caso de la distribución normal, la Función de Densidad Acumulada es⁸⁹

\[ \begin{split} \Phi_{\mu,\sigma^2}(x)= \frac{1}{\sigma \sqrt{2 \pi}} \int^x_{-\infty} e^{- \frac{(u-\mu)^2}{2 \sigma^2}} du = 1- \frac{1}{\sigma \sqrt{2 \pi}} \int^{x}_{-\infty} e^{\frac{(u-\mu)^2}{2 \sigma^2}} du \end{split} \]

por lo que la proporción \(p\) de individuos seleccionados a partir de un valor \(X_u\) en una \(\sim N(0,1)\) será

\[ \begin{split} p = \frac{1}{\sqrt{2 \pi}} \int^{\infty }_{X_u} e^{- \frac{u^2}{2}} du = 1- \frac{1}{\sqrt{2 \pi}} \int^{X_u}_{-\infty} e^{- \frac{u^2}{2}} du = 1 - \Phi_{0,1}(X_u) \end{split} \]

Pero la media es la integral en el intervalo de interés del producto de \(x\) por la densidad, que ahora será la densidad original de la normal, pero dividida por la integral de la misma en el intervalo (la proporción de individuos con los que nos quedamos), para que integre a 1. Calculemos la primitiva del numerador

\[\frac{1}{\sqrt{2 \pi}} \int x e^{- \frac{x^2}{2}} dx. \text{ Ahora, si}\ u=-\frac{x^2}{2} \Rightarrow \frac{du}{dx}=-x \therefore dx= - \frac{1}{x} du\] \[\frac{1}{\sqrt{2 \pi}} \int x e^{- \frac{x^2}{2}} dx = - \frac{1}{\sqrt{2 \pi}} \int x e^{u} \frac{du}{x} = - \frac{1}{\sqrt{2 \pi}} \int e^{u} du =\] \[- \frac{e^u}{\sqrt{2 \pi}} = - \frac{e^{\frac{x^2}{2}}}{\sqrt{2 \pi}}\]

Ahora, de acuerdo a la definición que dimos recién, si dividimos este último resultado (evaluado en el intervalo de interés) entre la proporción de individuos, obtenemos

\[ \begin{split} i= \frac{\frac{1}{\sqrt{2 \pi}} \int^{\infty }_{X_u} u e^{- \frac{u^2}{2}} du}{\frac{1}{\sqrt{2 \pi}} \int^{\infty }_{X_u} e^{- \frac{u^2}{2}} du} = \frac{-\dfrac{ {e}^{-\frac{u^2}{2}}}{\sqrt{2\pi}} \Big|_{u=X_u}^{\infty}}{\dfrac{\operatorname{erf}\left(\frac{u}{\sqrt{2}}\right)}{2} \Big|_{u=X_u}^{\infty}} = \frac{\dfrac{ {e}^{-\frac{X_u^2}{2}}}{\sqrt{2\pi}}}{\dfrac{\operatorname{erf}\left(\frac{u}{\sqrt{2}}\right)}{2} \Big|_{u=X_u}^{\infty}} = \frac{z}{p} \end{split} \]

En las ecuaciones anteriores \(erf(z)=\frac{2}{\sqrt{\pi}}\int_0^z e^{-t^{2}} dt\) es la función de error (o función de error de Gauss).

Resumiendo, la intensidad de selección es la ordenada de la función de densidad \(\sim N(0,1)\) en el punto de truncamiento, dividida entre la proporción de la distribución que es mayor a ese punto de truncamiento (la proporción de individuos seleccionados).

La relación entre diferentes formas de calcular la intensidad de selección

Vimos más arriba dos formas diferentes de calcular la intensidad de selección, \(i=\frac{S}{\sigma_P}\) y \(i=\frac{z}{p}\). La pregunta que nos hacemos entonces es si estas definiciones son exactamente equivalentes. Recordemos que desde el punto de vista conceptual, la intensidad de selección es la media de los individuos seleccionados, pero expresada en relación al desvío estándar, o sea, independiente de las unidades con que se mide la característica. Ahora, la primera de las dos ecuaciones claramente se ajusta a esta definición en palabras, que no asume ninguna forma de la distribución de valores de la característica, al menos en forma explícita. En cambio, la segunda ecuación invoca explícitamente una distribución \(\sim N(0,1)\).

La definición de intensidad de selección como el diferencial de selección estandarizado es simple y precisa, pero requiere del conocimiento del diferencial de selección, lo que requiere usualmente del conocimiento de las medias de la población y de los individuos seleccionados, además del desvío estándar fenotípico de la característica en la población. En cambio, la definición de la intensidad de selección como la relación \(i=z/p\) es apenas una definición operacional que se cumple bajo el supuesto de normalidad. Por el contrario, lo único que es necesario conocer es la proporción de animales que se seleccionarán, lo que usualmente resulta trivial de calcular para estructuras poblacionales típicas de la producción animal. En resumen, el uso de una u otra dependerá de la información disponible y de que se cumpla o no el supuesto de normalidad para la característica de interés.

11.4.0.1 Ejemplo 11.4

En la siguiente figura se presentan diferentes situaciones de diferencial e intensidad de selección representados gráficamente, suponiendo características de distribución normal:

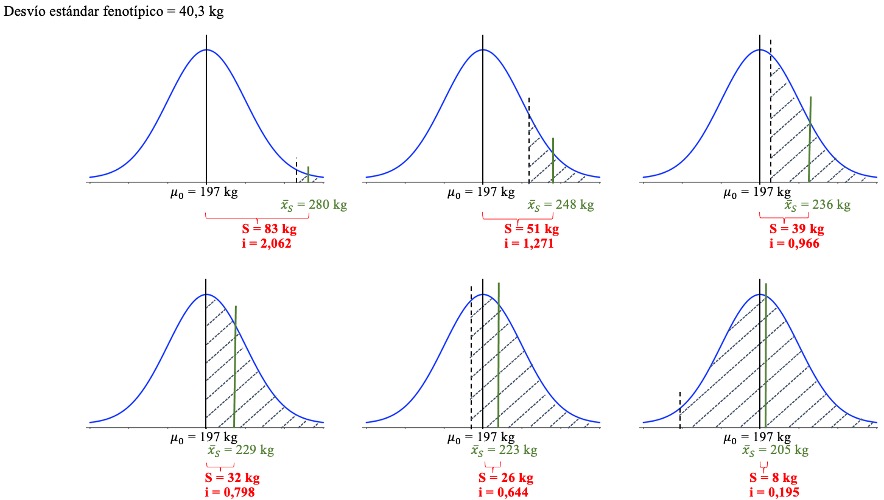
Figura 11.10: Diferencial e intensidad de selección representados gráficamente, suponiendo características de distribución normal

PARA RECORDAR

• En muchos casos no podemos darnos el lujo de determinar un valor dado de umbral para la característica ya que podría comprometer la sostenibilidad del sistema o implicar una presión de selección mucho menor que la posible y deseable. Esto nos lleva a la posibilidad de que el determinante para la presión de selección posible sea la proporción de individuos que debo quedarme como reproductores.

• La proporción \(i=z/p\) nos indica que a una proporción determinada de individuos seleccionados en una característica con distribución normal, cualquiera sea esta, le corresponde siempre la misma intensidad de selección. Además, como esta intensidad de selección es siempre la misma para una proporción dada es posible construir una tabla con los pares de valores a la precisión deseada.

• Si la presión de selección es muy alta, en la medida de que elegimos los “mejores individuos” basados en nuestra característica de interés, estamos reduciendo en forma sustancial la variabilidad genética disponible, lo que puede atentar contra el futuro genético a mediano o largo plazo. Una alternativa más general es utilizar una función continua de nuestra característica de interés para determinar la probabilidad de que el individuo quede entre los reproductores. Esto es lo mismo que establecer el fitness del individuo como función de la característica.

• Respecto a las dos formas diferentes de calcular la intensidad de selección que mencionamos (\(i=S/\sigma P\) y \(i=z/p\)), el uso de una u otra dependerá de la información disponible y de que se cumpla o no el supuesto de normalidad para la característica de interés.

11.5 Intervalo generacional

En general, el progreso genético medido en términos de generaciones nos permite desarrollar los conceptos principales sobre los mecanismos y procesos que intervienen en el mejoramiento genético o en el estudio de las variaciones en las frecuencias génicas. Sin embargo, su utilidad resulta reducida cuando tenemos que pensar su significado en los términos a los que estamos acostumbrados a referenciarnos los seres humanos. Por ejemplo, un productor rural debe pagar los impuestos todos los años, un productor ganadero debe entorar todos los años y un productor lechero idealmente debe elegir dosis de semen cada año para las vacas en producción. Es decir, solemos manejarnos con nuestro marco de referencia temporal a la hora de decidir y eso requiere que podamos expresar el progreso genético en dicho marco. Más aún, como veremos más adelante, diferentes estrategias de selección suelen implicar diferentes intervalos de tiempo para observar el progreso genético, por lo que debemos poder “ajustar” nuestros resultados para tener en consideración estos efectos.

El ciclo de vida de diferentes organismos implica que cuando una generación alcanza la madurez para reproducirse, la anterior ya desapareció o al menos no se encuentra más en su fase reproductiva. Ejemplo de esto serían las plantas anuales, especies de peces anuales y varios otros organismos. En estos casos, pasar del progreso generacional al anual es muy sencillo: alcanza con dividir el progreso genético generacional (es decir, expresado en las unidades de la característica que avanzamos por generación) entre el intervalo (en años) entre dos generaciones (años/generación), es decir

\[ \begin{split} {R_a=\frac{R}{IG}} \end{split} \tag{11.15} \]

Las unidades de \(\mathrm{R_a}\) serán entonces las de la característica pero por año (o sea, divididas entre año). En el caso de plantas anuales, el intervalo de tiempo entre generaciones será igual a 1 año, por lo que los valores de \(\mathrm{R_a}\) y \(\mathrm{R}\) serán iguales, aunque expresados en distintas unidades. En animales, un ejemplo de especies anuales son las Cynolebias, peces que pertenecen a la familia Rivulidae y al orden Ciprinodontiformes. Estos peces habitan en charcos o bañados y su distribución incluye Argentina, Brasil, Paraguay y Uruguay. El ciclo de vida de estos organismos comienza como huevos que son puestos por la generación parental en primavera, los que son enterrados en el fondo barroso. Al llegar el verano el calor hace que los charcos se sequen y los adultos mueran, mientras que los huevos continúan incubándose en el suelo. Con las primeras lluvias de Abril y Mayo los peces nacen y se desarrollan rápidamente hasta la primavera, donde ya maduros sexualmente comenzarán una nueva puesta.

Hasta acá resulta inmediata la relación entre progreso genético generacional y progreso genético anual ya el intervalo generacional es trivial de calcular, por lo que también la aplicación de la ecuación (11.15) es trivial. Sin embargo, en poblaciones en las que las generaciones se superponen resulta mucho menos intuitivo cuál es el intervalo generacional ya que en cada momento del tiempo hay individuos de diferentes generaciones reproduciéndose. Esto nos lleva a la necesidad de tener una definición operativa del intervalo generacional.

Llamamos intervalo generacional a la edad promedio de los padres cuando nacen sus hijos. Acá es importante tener en cuenta que promedio se refiere tanto al promedio entre los dos sexos, como al promedio dentro de cada progenitor (ya que cada progenitor puede tener más de un hijo en distintos momentos).

Esto nos deja con una definición muy clara pero que en general no será trivial de calcular, excepto en situaciones bastante estilizadas o simplificadas. Lo primero que se deriva de nuestra definición es que el intervalo generacional será el promedio de los intervalos generacionales de ambos sexos, es decir

\[ \begin{split} {IG=\frac{IG_{m}+IG_{h}}{2}=\frac{IG_{m}}{2}+\frac{IG_{h}}{2}} \end{split} \tag{11.16} \]

Si bien el número de machos no es, por lo general, igual al de hembras, los aportes genéticos de ambos sexos son similares (desde el punto de vista del genoma nuclear) ya que los hijos reciben la mitad de sus genomas de cada progenitor. Por otra parte, el promedio de la edades a las que nacen los hijos deberá tener en cuenta el aporte relativo en cada categoría de edad. Por ejemplo, en seres humanos, es posible encontrar madres que tuvieron descendencia a los 55 años de edad, pero claramente son casos bastante excepcionales y este aporte es proporcionalmente mucho menor que el de las madres de 25 años de edad. Por lo tanto, para cada sexo, si \(j\) representa una edad determinada, la edad promedio será

\[{IG_m=\frac{1}{n_m}\sum_j n_{j_{m}}\cdot j}\] \[ \begin{split} {IG_h=\frac{1}{n_h}\sum_j n_{j_{h}}\cdot j} \end{split} \tag{11.17} \]

con

\[{\sum_j n_{j_{m}}=n_m}\] \[ \begin{split} {\sum_j n_{j_{h}}=n_h} \end{split} \tag{11.18} \]

el número total de machos y hembras, respectivamente. Es decir, el intervalo generacional será el promedio de edades de los padres al nacer los hijos, ponderado el promedio por la proporción de hijos en cada una de las edades.

Ejemplo 11.5

Un rodeo vacuno que produce sus propios reemplazos posee las siguientes cantidades de machos y hembras en las distintas categorías de edades (en años, al nacimiento de los hijos)

Edad en años (al nacimiento de los hijos)	Hembras	Machos
\(3\)	\(250\)	\(15\)
\(4\)	\(220\)	\(10\)
\(5\)	\(200\)	\(5\)
\(6\)	\(170\)	\(-\)
\(7\)	\(160\)	\(-\)
\(\textbf{TOTAL}\)	\(1000\)	\(30\)

Calcular el intervalo generacional de machos, el de hembras y el intervalo generacional promedio.

En machos hay solo 3 categorías de edad, por lo que el intervalo generacional de machos sería, aplicando las ecuaciones (11.17) y (11.18), tenemos que

\[ \begin{split} {n_m=\sum_j n_{j_{m}}=15+10+5=30}\\ \end{split} \]

y

\[ \begin{split} {IG_m=\frac{1}{n_m}\sum_j n_{j_{m}}\cdot j=\frac{3 \times 15+4 \times 10 + 5 \times 5}{30}=\frac{110}{30}=3,6667} \text{ años} \end{split} \]

En hembras, usando el mismo razonamiento y las mismas ecuaciones, tenemos

\[ \begin{split} {n_h=\sum_j n_{j_{h}}=250+220+200+170+160=1000}\\ \end{split} \]

y

\[ \begin{split} {IG_h=\frac{1}{n_h}\sum_j n_{j_{h}}\cdot j=\frac{3 \times 250+4 \times 220 + 5 \times 200+ 6 \times 170 + 7 \times 160}{1000}=\frac{4770}{1000}=4,77} \text{ años} \end{split} \]

Por lo tanto, ahora aplicando la ecuación (11.16), tenemos que el intervalo generacional del rodeo será igual a

\[ \begin{split} {IG=\frac{IG_{m}+IG_{h}}{2}=\frac{3,6667+4,77}{2}=\frac{8,4367}{2} \sim 4,22} \text{ años} \end{split} \]

---

Es importante destacar que la estructura de edades en el rodeo, majada o población que nos importa es la de los individuos activos en términos reproductivos (y que sean exitosos, es decir que generan descendencia). En general, para que una estructura de edades sea estable en una población es necesario que se cumplan algunas cosas. Por ejemplo, si consideramos a todos los individuos de una población cerrada a los ingresos, cada categoría de edad debe tener el mismo número o menos de individuos que la edad que la antecede, ya que de lo contrario los individuos aparecerían mágicamente o no se trataría de una estructura de edades estabilizada. La estructura de edades de los individuos que se reproducen sí puede ser arbitraria, con más individuos reproductivos en edades más avanzadas, por ejemplo, si impedimos que los más jóvenes se reproduzcan o aún si los más jóvenes tienen menor éxito reproductivo que los mayores (y lo tenemos en cuenta en el modelo). Por lo general, para simplificar, usaremos ejemplos y ejercicios que muestran el número total de individuos en cada categoría de edad, asumiendo que refugamos a los individuos que no se reproducen o que directamente no están (por muerte, por ejemplo).

PARA RECORDAR

• En el caso de el ciclo de vida de algunos organismos, cuando una generación alcanza la madurez para reproducirse, la anterior ya desapareció o al menos no se encuentra más en su fase reproductiva. En estos casos, pasar del progreso generacional al anual es muy sencillo: alcanza con dividir el progreso genético generacional entre el intervalo (en años) entre dos generaciones (años/generación), es decir \({R_a=\frac{R}{IG}}\).

• En poblaciones en las que las generaciones se superponen resulta mucho menos intuitivo cuál es el intervalo generacional ya que en cada momento del tiempo hay individuos de diferentes generaciones reproduciéndose.

• Llamamos intervalo generacional a la edad promedio de los padres cuando nacen sus hijos. Es importante tener en cuenta que promedio se refiere tanto al promedio entre los dos sexos, como al promedio dentro de cada progenitor (ya que cada progenitor puede tener más de un hijo en distintos momentos).

• El intervalo generacional poblacional lo calcularemos como el intervalo generacional promedio entre los sexos: \({IG=\frac{IG_{m}+IG_{h}}{2}=\frac{IG_{m}}{2}+\frac{IG_{h}}{2}}\). Por su parte, para calcular el IG de cada sexo, si \(j\) representa una edad determinada, la edad promedio será \({IG_m=\frac{1}{n_m}\sum_j n_{j_{m}}\cdot j}\); \({IG_h=\frac{1}{n_h}\sum_j n_{j_{h}}\cdot j}\); con \({\sum_j n_{j_{m}}=n_m}\) y \({\sum_j n_{j_{h}}=n_h}\).

• Debemos siempre recordar que la estructura de edades en el rodeo, majada o población que nos importa es la de los individuos activos en términos reproductivos (y que sean exitosos, es decir que generan descendencia).

11.6 Medidas de la respuesta

En este capítulo hemos manejado hasta ahora el progreso genético ocurrido en el transcurso de una generación y su relación con el diferencial de selección y la heredabilidad. Claramente, cuando presentamos la ecuación del criador como forma de estimar la Heredabilidad lograda, es decir \(\hat h^2=\frac{R}{S}\), necesitamos tener buenas medidas de la respuesta a la selección y de diferencial de selección.

El diferencial de selección teórico es simplemente la diferencia entre la media de la población seleccionada y la media de la población de referencia, es decir \(S=\mu_S-\mu_0\), por lo que su medición no presenta, en principio mayores dificultades. Alcanza con medir los individuos en ambos grupos, la población seleccionada y la población en general (o al menos un estimado razonable de esta última) y calcular la diferencia. Sin embargo, ese diferencial de selección teórico funcionaba en nuestras derivaciones si asumíamos que todos los padres seleccionados dejaban el mismo número de descendientes. En los casos en los que existen diferencias notorias en la descendencia que dejaron los padres seleccionados es necesario obtener una mejor estimación del diferencial de selección efectivo, lo que puede obtenerse ponderando la medida fenotípica de cada progenitor por el número de descendientes que aportaron a la nueva generación. Esto tiene en cuenta no solo el efecto de la fertilidad de los reproductores sino la viabilidad de los descendientes. Por ejemplo, si existen diferencias en la fertilidad o viabilidad asociadas a fenotipos más extremos, pese a que nuestro esfuerzo en la selección artificial es hacia los mismos, el efecto de la selección natural contrarrestará, de alguna manera, este esfuerzo. Un ejemplo de esto podría ser en la producción lechera, donde los fenotipos más productores (extremos) suelen tener peores resultados reproductivos (vinculado esto a la partición energética de base genética).

Por otra parte, como ya vimos en la sección dedicada a la Heredabilidad lograda, el resultado del progreso genético observado en cada generación sucesiva puede ser diferente de los otros, esencialmente debido a los efectos del azar en la respuesta, sumados a las variaciones aleatorias de los efectos del diferencial de selección efectivo (por diferencias en el número de progenies dejadas debido al azar). Esto nos lleva a la necesidad de buscar algo de estabilidad, lo que podemos hacer a partir del promedio de varias generaciones, o del ajuste de una regresión de la respuesta acumulada en el diferencial de selección acumulado (como vimos previamente). Sin embargo, en estas estimaciones estamos pasando por alto un factor que puede ser determinante: la evolución del “ambiente”. La mejora en la producción puede y suele venir de la genética, del “ambiente”, o de ambos (y de sus interacciones). Cuando miramos la respuesta a la selección como solo de origen genético nos estamos olvidando de la posible existencia de mejoras en las condiciones de producción (alimentación, alojamiento, salud, manejo, etc.), por lo que estaríamos sobrestimando la respuesta. Como \(\hat h^2=\frac{R}{S}\), una sobrestimación del numerador nos lleva a una sobrestimación de la heredabilidad también. Una alternativa para esto es el uso de datos en una población similar pero en la que no se realizó selección en el mismo período de tiempo. Eso nos permitiría tener un testigo y usar además esa información para descontarla del progreso obtenido en la población bajo selección.

11.7 Progreso genético generacional y anual

Como vimos previamente en la ecuación (11.15), el progreso genético anual es simplemente el resultado de dividir el progreso genético que se observa en una generación entre el intervalo de tiempo que le toma a una generación sustituir a la siguiente (en términos reproductivos), es decir, el intervalo generacional. En las ecuaciones (11.17) y (11.18) encontramos una forma de calcular el intervalo generacional cuando las generaciones se solapaban, mientras que previamente habíamos obtenido distintas formulaciones para el progreso genético generacional (por ejemplo, en la ecuación del criador \(\mathrm{R=S\ h^2}\), ecuación (11.9)).

Por lo tanto, poniendo todo junto, tenemos una primera expresión algo más explícita del progreso genético anual

\[ \begin{split} \mathrm{R_a=\frac{R}{IG}=\frac{S\ h^2}{IG}} \end{split} \tag{11.19} \]

En ciertos casos, como vimos antes, es difícil obtener el diferencial de selección ya que implica conocer tanto la media de la población como la media de los individuos seleccionados. Sin embargo, para características fenotípicas con distribución normal, la intensidad de selección es mucho más fácil de obtener a partir de la proporción de individuos seleccionados. Recordando además que la relación entre diferencial de selección e intensidad de selección es \(i={\frac{S}{\sigma_P}}\therefore {S=}i \cdot {\sigma_P}\), sustituyendo en la ecuación (11.19) tenemos ahora

\[ \begin{split} {R_a=\frac{S\ h^2}{IG}=\frac{\mathit{i}\ \sigma_P\ h^2}{IG}} \end{split} \tag{11.20} \]

Ahora, como la intensidad de selección de la población es igual al promedio de machos y hembras y el intervalo generacional de la población también es igual al promedio de dicho intervalo en machos y hembras, poniendo todo junto tenemos que la ecuación (11.20) se transforma en

\[ \begin{split} \mathrm{R_a}=\frac{\mathrm{\left(\frac{\mathit{i_m}+\mathit{i_h}}{2}\right)\ h^2}\ \sigma_P}{\mathrm{\left[\frac{IG_m+IG_h}{2}\right]}} \end{split} \tag{11.21} \]

A su vez, \(\mathrm{h}=\frac{\sigma_A}{\sigma_P}\), entonces, sustituyendo en el numerador de la ecuación (11.20) tenemos

\[\mathrm{R=i\ h^2}\ \sigma_P=\mathrm{i\ h\ h}\ \sigma_P=\mathrm{i\ h}\ \frac{\sigma_A}{\sigma_P} \sigma_P\ \therefore\] \[ \begin{split} \mathrm{R=i\ h}\ \sigma_A \end{split} \tag{11.22} \]

lo que nos deja con el siguiente equivalente de la ecuación (11.21)

\[ \begin{split} \mathrm{R_a}=\frac{\mathrm{\left(\frac{\mathit{i_m}+\mathit{i_h}}{2}\right)\ h}\ \sigma_A}{\mathrm{\left[\frac{IG_m+IG_h}{2}\right]}} \end{split} \tag{11.23} \]

Recordando que \(h\) era la precisión en el caso de selección individual basada en el fenotipo y que también era la correlación entre el valor de cría y la fuente de información, \(\mathrm{r_{AC}}\) (en este caso el fenotipo del individuo), entonces, podemos generalizar la ecuación (11.22) a

\[ \begin{split} \mathrm{R=i\ r_{AC}}\ \sigma_A \end{split} \tag{11.24} \]

o llevar la ecuación (11.23) a una de sus formas más explícitas que usaremos en este capítulo

\[ \begin{split} \mathrm{R_a}=\frac{\mathrm{\left(\frac{\mathit{i_m}+\mathit{i_h}}{2}\right)\ r_{AC}}\ \sigma_A}{\mathrm{\left[\frac{IG_m+IG_h}{2}\right]}} \end{split} \tag{11.25} \]

PARA RECORDAR

• En los casos en los que existen diferencias notorias en la descendencia que dejaron los padres seleccionados es necesario obtener una mejor estimación del diferencial de selección efectivo, lo que puede obtenerse ponderando la medida fenotípica de cada progenitor por el número de descendientes que aportaron a la nueva generación.

• Por ejemplo, si existen diferencias en la fertilidad o viabilidad asociadas a fenotipos más extremos, pese a que nuestro esfuerzo en la selección artificial es hacia los mismos, el efecto de la selección natural contrarrestará, de alguna manera, este esfuerzo.

• Cuando miramos la respuesta a la selección como solo de origen genético nos estamos olvidando de la posible existencia de mejoras en las condiciones de producción, por lo que estaríamos sobrestimando la respuesta. Una alternativa para esto es el uso de datos en una población similar pero en la que no se realizó selección en el mismo período de tiempo.

• Podemos expresar la respuesta anual (\(R_a\)) a la selección cómo: \(\mathrm{R_a}=\frac{\mathrm{\left(\frac{\mathit{i_m}+\mathit{i_h}}{2}\right)\ r_{AC}}\ \sigma_A}{\mathrm{\left[\frac{IG_m+IG_h}{2}\right]}}\)

11.8 Cambio en las frecuencias alélicas bajo selección artificial

Hasta ahora hemos visto el proceso de selección de diferentes maneras, pero sin conectarlas entre sí. Mientras que en el capítulo sobre Selección Natural analizamos diferentes formas de selección y sus implicancias en el cambio de frecuencias alélicas, en este capítulo vimos el proceso de selección desde la perspectiva del cambio en la distribución de los valores fenotípicos resultantes. Es momento pués de combinar las dos aproximaciones para intentar entender los cambios en las frecuencias alélicas que ocurren como resultante del proceso de selección basado en la información fenotípica disponible.

Abundemos un poco en lo anterior antes de avanzar en los cálculos. Mientras que en el capítulo sobre Selección Natural trabajamos sobre el fitness específico de cada genotipo en un locus determinado, en combinación con las frecuencias respectivas, en el presente capítulo supusimos que la característica de interés puede estar gobernada por uno o más loci y que no contamos con la información correspondiente (ni siquiera asumimos saber cuántos loci gobiernan la característica). Este hecho nos llevó a tener que trabajar con la información que contamos, básicamente la distribución fenotípica de la característica y el conocimiento sobre los parámetros genéticos más relevantes, en particular las varianzas fenotípicas y aditivas o la heredabilidad. Mientras que el primer enfoque nos permite derivaciones más profundas sobre el cambio de las frecuencias alélicas, excepto a partir de información genómica y en situaciones muy particulares, su aplicación no resulta para nada práctica o realizable. En cambio, la segunda aproximación (condicional a que se cumplan los supuestos) es totalmente practicable y ha sido la base del mejoramiento genético animal durante mucho tiempo y en particular durante la segunda mitad del siglo XX.

Veamos entonces ahora cómo podemos conectar las dos aproximaciones. Para ello vamos a suponer al comienzo una situación muy estilizada, de una característica que es gobernada mayormente por un locus con dos alelos, donde además el modo de acción es de dominancia completa del alelos \(A_1\). La situación se ilustra en la Figura 11.11. Como nos encontramos en una situación de dominancia total de uno de los dos alelos (el \(A_1\)), entonces los genotipos \(A_1A_1\) y \(A_1A_2\) serán indistiguibles desde el punto de vista de los fenotipos para la característica, pero ambos serán diferentes del genotipo \(A_2A_2\). Por lo tanto, desde el punto de vista de los genotipos, nuestra población la podemos descomponer en dos distribuciones, las que poseen al menos un alelo \(A_1\) (en rojo en la figura) y las que no tienen ningún alelo \(A_1\). De acuerdo al modelo genético básico, en la escala fenotípica (genotípica) transformada, los genotipos homocigotos \(A_1A_1\) y \(A_2A_2\) tenían valores respectivos de \(a\) y \(-a\), por lo que la diferencia entre ellos es de \(a-(-a)=a+a=2a\). Obviamente, el genotipo \(A_1A_2\) pertenece a la misma clase fenotípica que el \(A_1A_1\), por lo que compartirá distribución de valores con este. En nuestro caso, asumiremos adicionalmente que no existe interacción genotipo ambiente y que la varianza residual es igual en ambas clases fenotípicas (y centrada en cero), por lo que la amplitud de las distribuciones respecto a la media es similar para ambas clases, como se muestra en la Figura 11.11.

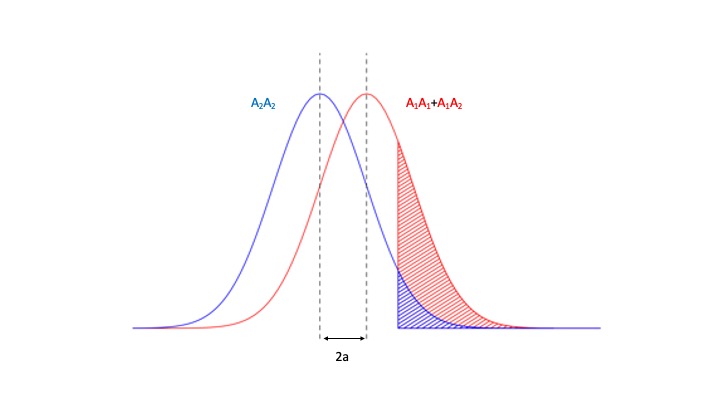
Figura 11.11: Cambio en las frecuencias alélicas como producto de la selección por umbral. En este caso asumimos que el alelo \(A_1\) es completamente dominante, por lo que existen solo dos fenotipos para este locus, lo que se ve enmascarado por los efectos ambientales y del resto de los loci dando la distribución continua para la característica. La diferencia entre las medias de los genotipos \(A_1A_1+A_1A_2\) y \(A_2A_2\) será igual a \(a-(-a)=2a\). En la figura se representa la situación en que \(q^2=\frac{1}{2}\).

Claramente, si fijamos un umbral de selección (como hemos hecho en este capítulo), la proporción de individuos seleccionados de la distribución \(A_1A_1/A_1A_2\) es mayor que la de los individuos \(A_2A_2\). Este es el caso particular en que \(q^2=\frac{1}{2}\), por lo que hay la misma proporción en las dos clases fenotípicas, pero lo mismo se aplicaría a cualquier frecuencia si consideramos la relación entre las frecuencias de las dos clases antes de la selección y en los individuos seleccionados. Eso es así debido a que la distribución de la clase \(A_2A_2\) está más a la izquierda respecto al umbral y por lo tanto solo los valores más extremos respecto a la media de la clase alcanzan el umbral.

En principio, no tenemos una forma de conocer la frecuencia del alelo \(A_2\) entre los seleccionados, pero podemos recurrir al concepto de regresión que hemos utilizado antes para determinar esta frecuencia a partir de la diferencia de la media de los individuos seleccionados. Esta media era, por definición, el diferencial de selección \(S\), por lo que la nueva frecuencia del alelo \(A_2\) será igual a

\[ \begin{split} q_1=q+b_{qP}S \end{split} \tag{11.26} \]

Es decir, la nueva frecuencia será igual a la frecuencia anterior \(q\), más la regresión de la frecuencia en el diferencial de selección. Para determinar el coeficiente de selección vamos a necesitar calcular la covarianza entre las frecuencias de los alelos (\(q\)) en los genotipos y los valores fenotípicos. Para ello vamos a emplear la siguiente tabla

Genotipo	Frecuencia	Alelo \(q\)	\(G=P\)
\(A_1A_1\)	\(p^2\)	\(0\)	\(a\)
\(A_1A_2\)	\(2pq\)	\(\frac{1}{2}\)	\(d\)
\(A_2A_2\)	\(q^2\)	\(1\)	\(-a\)

En ella tenemos las frecuencias de cada genotipo (asumiendo equilibrio de Hardy-Weinberg), la frecuencia del alelo \(q\) en cada genotipo (no hay ninguno en \(A_1A_1\), hay uno de dos en \(A_1A_2\) y hay dos de dos en \(A_2A_2\)), así como el valor genotípico (observar que los heterocigotas se especifican como \(d\), por lo que no estamos asumiendo ningún modo particular de relación entre alelos). La covarianza podemos calcularla como el producto cruzado de la proporción de alelos \(q\) en cada genotipo con el valor genotípico, ponderado por la frecuencia de cada genotipo. En la definición que hemos usado de covarianza hacíamos este producto cruzado de los desvíos respecto a las medias respectivas, pero más práctico en este caso resulta hacer los productos de las columnas 2, 3 y 4 de la tabla y a eso restarle el producto de las medias de la frecuencia alélica por la media fenotípica (genotípica). Del capítulo El Modelo Genético Básico, recordarás que la media era \(M=a(p-q)+2pqd\) (ecuación (8.13)). Por lo tanto, la covarianza será

\[ \begin{split} Cov_{qP}=[a \times 0 \times p^2+d \times \frac{1}{2} 2pq -a \times 1 \times q^2]-qM=pqd-q^2a-qM \end{split} \tag{11.27} \]

Sustituyendo el valor de \(M\) en la ecuación anterior, recordando que \(1-2q=[p+q]-2q=p-q\), tenemos entonces que

\[Cov_{qP}=pqd-q^2a-q[a(p-q)+2pqd]=pqd-q^2a-pqa+q^2a-2pq^2d=pq[a+d(1-2q)]=pq[a+d(q-p)]\ \therefore\] \[ \begin{split} Cov_{qP}=-pq \alpha \end{split} \tag{11.28} \]

con \(\alpha=a+d(q-p)\) el efecto de sustitución alélica (ecuación (8.19)). Por lo tanto, usando este resultado para la covarianza, con la varianza fenotípica igual \(\sigma_P^2\), el coeficiente de regresión será simplemente

\[ \begin{split} b_{qP}=-\frac{pq\alpha}{\sigma^2_P} \end{split} \tag{11.29} \]

Por otra parte, teniendo en cuenta que el diferencial de selección podemos escribirlo como el producto entre la intensidad de selección y el desvío estándar fenotípico, es decir \(S=i\sigma_P\), tenemos por lo tanto que la ecuación (11.26) la podemos escribir ahora como

\[ \begin{split} q_1=q+b_{qP}i \sigma_P=q-\frac{pq\alpha}{\sigma^2_P}i \sigma_P \end{split} \tag{11.30} \]

y por lo tanto, el cambio de frecuencia \(\Delta q\) esperable en una generación producto de la selección será igual a

\[ \begin{split} \Delta q=q_1-q=[q-\frac{pq\alpha}{\sigma^2_P}i \sigma_P]-q=-ipq\frac{\alpha}{\sigma_P} \end{split} \tag{11.31} \]

La interpretación de esta ecuación es bastante sencilla: el cambio en la frecuencia del alelo \(A_2\) será negativo ya que estamos seleccionando en contra del mismo. La intensidad del cambio será directamente proporcional a la intensidad de selección \(i\), al producto de las frecuencias de los alelos (\(pq\)) y al efecto de sustitución alélica estandarizado entre el desvío fenotípico de la característica.

La pregunta que nos hacemos ahora es cómo se relaciona esto con los cambios de frecuencia esperados bajo selección que vimos en capítulos previos (en especial en el capítulo Selección Natural). Para ello vamos a realizar una pequeña disgresión para recordar como derivábamos el cambio de frecuencia en una generación bajo selección.

Por ejemplo, en el caso de que el modo de acción génica fuese de dominancia completa, con un coeficiente de selección \(s\) contra el recesivo, teníamos la siguiente tabla

Genotipo	\(A_1A_1\)	\(A_1A_2\)	\(A_2A_2\)
$ ext{Frecuencia inicial}$	\(p^2\)	\(2pq\)	\(q^2\)	\(1\)
\(\text{Fitness}\)	\(1\)	\(1\)	\(1-s\)
\(\text{Contribución}\)	\(p^2\)	\(2pq\)	\(q^2(1-s)\)	\(1-sq^2\)

Por lo tanto, la frecuencia en la siguiente generación (es decir, después de la selección) sería

\[ \begin{split} q_1=\frac{q^2(1-s)+pq}{1-sq^2} \end{split} \tag{11.32} \]

y el cambio de frecuencia, por lo tanto

\[\Delta q=q_1-q=\frac{q^2(1-s)+pq}{1-sq^2}-\frac{q(1-sq^2)}{1-sq^2}=\frac{q^2(1-s)+(1-q)q-q(1-sq^2)}{1-sq^2}=\] \[=\frac{q^2-sq^2+q-q^2-q+sq^3}{1-sq^2}=\frac{-sq^2+sq^3}{1-sq^2}\ \therefore\]

\[ \begin{split} \Delta q=-\frac{sq^2(1-q)}{1-sq^2} \end{split} \tag{11.33} \]

En el caso

Genotipos	\(A_1A_1\)	\(A_1A_2\)	\(A_2A_2\)
\(\text{Frecuencia inicial}\)	\(p^2\)	\(2pq\)	\(q^2\)	\(1\)
\(\text{Fitness}\)	\(1\)	\(1-rac{1}{2}s\)	\(1-s\)
\(\text{Contribución}\)	\(p^2\)	\(2pq-pqs\)	\(q^2(1-s)\)	\(1-sq\)

El nuevo total de frecuencias (para relativizar) el resultado de cada alelo será \[ \begin{split} p^2+2pq-pqs+q^2(1-s)=1-pqs-q^2s=1-s[pq+q^2]=1-s[q(p+1)]=1-sq \end{split} \tag{11.34} \]

La nueva frecuencia del alelo \(A_2\), \(q_1\), será por lo tanto

\[q_1=\frac{pq-\frac{1}{2}pqs+q^2(1-s)}{1-sq}=\frac{q-q^2-\frac{1}{2}s[q-q^2]+q^2-q^2s)}{1-sq}=\] \[=\frac{q-\frac{1}{2}s[q-q^2]-q^2s)}{1-sq}=\frac{q[1-\frac{1}{2}s(1-q)-qs]}{1-sq}=\] \[=\frac{q[1-\frac{1}{2}s+\frac{1}{2}qs-qs]}{1-sq}=\frac{q[1-\frac{1}{2}s-\frac{1}{2}qs]}{1-sq}=\] \[ \begin{split} =\frac{q[1-\frac{1}{2}s-\frac{1}{2}qs]}{1-sq} \end{split} \tag{11.35} \]

y entonces, el cambio de frecuencia correspondiente será igual a

\[\Delta q=q_1-q=\frac{q[1-\frac{1}{2}s-\frac{1}{2}qs]}{1-sq}-q=\frac{q[1-\frac{1}{2}s-\frac{1}{2}qs]-q[1-sq]}{1-sq}=\] \[ \begin{split} =\frac{q-\frac{1}{2}qs-\frac{1}{2}q^2s-q+sq^2}{1-sq}=\frac{-\frac{1}{2}qs+\frac{1}{2}q^2s}{1-sq}=-\frac{\frac{1}{2}sq(1-q)}{1-sq} \end{split} \tag{11.36} \]

En general, cuando las frecuencias del alelo recesivo son bajas, podemos considerar una buena aproximación el hecho de que el denominador será cercano a \(1\) (en ambos casos, sin dominancia y sobre todo con dominancia completa), lo que nos deja solo con el numerador de las correspondientes fórmulas.

La idea ahora es entonces igualar los resultados obtenidos para el cambio de frecuencia en los distintos modos génicos en una generación de selección con el resultado obtenido a partir del diferencial (intensidad) de selección.

Cuando no hay dominancia, como vimos más arriba, el cambio de frecuencia en el alelo \(A_2\), asumiendo bajas frecuencias de este alelo, podemos aproximarlo a

\[ \begin{split} \Delta q=-\frac{\frac{1}{2}sq(1-q)}{1-sq^2} \sim \frac{1}{2}sq(1-q) \end{split} \tag{11.37} \]

En este caso, por otra parte, \(d=0\) y \(\alpha=a+d(q-p)=a\), por lo que sustituyendo ese valor de \(\alpha\) en la ecuación (11.31) e igualando al resultado de la ecuación (11.37), tenemos

\[ \begin{split} ipq\frac{a}{\sigma_P} \sim \frac{1}{2}sq(1-q) \end{split} \tag{11.38} \]

Por otra parte, si la dominancia es completa, entonces \(d=a\) y entonces \(\alpha=a+a(q-p)=a(p+q)+a(q-p)=2qa\), por lo que

\[ \begin{split} ipq\frac{2qa}{\sigma_P} \sim sq^2(1-q) \end{split} \tag{11.39} \]

En general, ambas ecuaciones, (11.39) y (11.38), se reducen a

\[ \begin{split} s=i\frac{2a}{\sigma_P} \end{split} \tag{11.40} \]

Por ejemplo, la ecuación (11.38), asumiendo que la aproximación es exacta, se reduce mediante

\[ \begin{split} ipq\frac{a}{\sigma_P} = \frac{1}{2}sq(1-q) \Leftrightarrow 2ipq \frac{a}{\sigma_P}=spq \\ \Leftrightarrow s=i \frac{2a}{\sigma_P} \end{split} \]

mientras que la ecuación (11.39) se reduce mediante

\[ipq\frac{2qa}{\sigma_P} = sq^2(1-q) \Leftrightarrow ip\frac{2a}{\sigma_P} = s(1-q) \Leftrightarrow\] \[i (1-q)\frac{2a}{\sigma_P} = s(1-q) \Leftrightarrow i \frac{2a}{\sigma_P} = s\]

Es decir, la ecuación (11.38) nos dice que hemos encontrado una relación directa entre las dos formas de expresar la selección que venimos trabajando. El coeficiente de selección que hemos usado para encontrar las frecuencias de los genotipos y el cambio de la frecuencia del alelo \(A_2\) es igual a la intensidad de selección multiplicada por el factor \(\frac{2a}{\sigma_P}\), que no es otra cosa que la diferencia entre los genotipos (fenotipos) de los homocigotas, estandarizados entre el desvío estándar fenotípico de la característica.

Una otra forma interesante de ver este resultado es haciendo uso de la relación \(i=\frac{S}{\sigma_P}\) y de la ecuación del criador. A partir de la ecuación (11.38), utilizando la relación entre intensidad de selección y diferencial de selección podemos hacer

\[ \begin{split} s=i\frac{2a}{\sigma_P}=\frac{S}{\sigma_P}\frac{2a}{\sigma_P}=S\frac{2a}{\sigma_P^2} \Leftrightarrow S=s\frac{\sigma_P^2}{2a} \end{split} \tag{11.41} \]

Sustituyendo este resultado en la ecuación del criador, tenemos

\[R=h^2 S=h^2 s\frac{\sigma_P^2}{2a} = \frac{\sigma_A^2}{\sigma_P^2} s\frac{\sigma_P^2}{2a}\ \therefore\]

\[ \begin{split} R=\sigma^2_A \frac{s}{2a} \end{split} \tag{11.42} \]

El resultado de la ecuación (11.42) tiene dos formas interesantes de verse. La primera tiene una relación directa con El teorema fundamental de la selección natural que vimos en el capítulo de Selección Natural. Si recuerdas, la idea del mismo era que existía una relación directa entre la tasa de cambio en la aptitud (fitness) debida a la selección natural en una característica y la varianza genética aditiva de la misma. La ecuación (11.42) establece que el progreso genético es directamente proporcional a la varianza genética aditiva de la característica. Si no hay varianza genética, sin importar la magnitud del coeficiente de selección, no existirá progreso genético. Esto nos lleva directamente a reflexionar sobre la posibilidad de utilizar la clonación para propagar el mejoramiento genético, una idea que pareció extenderse a partir de la clonación de la oveja “Dolly”. Si clonásemos al mejor animal existente (un concepto algo absurdo) y lo utilizáramos para reemplazar todo el stock, todos los animales sería idénticos, por lo que no existiría varianza genética aditiva y por lo tanto nos anularíamos la posibilidad de mejorar la característica (al menos hasta que aparezcan nuevas mutaciones que introduzcan varianza y que sean en el sentido correcto).

La segunda forma interesente de ver este resultado es si sustituimos en la ecuación (11.42) la varianza genética aditiva por su valor esperado en el modelo de un locus con dos alelos, ecuación (8.44), \(V_A=\sigma^2_A=2pq\alpha^2\)

\[ \begin{split} R=\sigma^2_A \frac{s}{2a}=\frac{2pq\alpha^2}{2a}s\ \therefore\ R=\frac{pq\alpha^2}{a}s \end{split} \tag{11.43} \]

De acuerdo con esta última ecuación, a valores determinados del coeficiente de selección y del efecto de sustitución (que depende del modo de acción génica y de las frecuencias alélicas), la respuesta a la selección será máxima cuando el producto \(pq\) sea máximo, cosa que como ya vimos ocurre cuando \(p=q=\frac{1}{2}\). Es decir, el progreso genético será máximo a frecuencias intermedias y luego irá disminuyendo a medida de que la frecuencia del alelo que seleccionamos en contra decrece.

PARA RECORDAR

• Si tomamos como ejemplo que la proporción de individuos seleccionados \(A_1A_1/A_1A_2\) de una distribución es mayor que la de los individuos \(A_2A_2\). Este es el caso particular en que \(q^2=1/2\), por lo que hay la misma proporción en las dos clases fenotípicas, pero lo mismo se aplicaría a cualquier frecuencia si consideramos la relación entre las frecuen- cias de las dos clases antes de la selección y en los individuos seleccionados. Eso es así debido a que la distribución de la clase \(A_2A_2\) está más a la izquierda respecto al umbral y por lo tanto solo los valores más extremos respecto a la media de la clase alcanzan el umbral.

• La nueva frecuencia del alelo \(A_2\) será \(q_1=q+b_{qP}S\). Es decir, la nueva frecuencia será igual a la frecuencia anterior \(q\), más la regresión de la frecuencia en el diferencial de selección.

• El cambio de frecuencia \(\Delta q\) esperable en una generación producto de la selección será igual a\(\Delta q=-ipq\frac{\alpha}{\sigma_P}\). Dónde el cambio en la frecuencia del alelo \(A_2\) será negativo ya que estamos seleccionando en contra del mismo. La intensidad del cambio será directamente proporcional a la intensidad de selección \(i\), al producto de las frecuencias de los alelos (\(pq\)) y al efecto de sustitución alélica estandarizado entre el desvío fenotípico de la característica.

• Cuando no hay dominancia, el cambio de frecuencia en el alelo \(A_2\), asumiendo bajas frecuencias de este alelo, podemos aproximarlo a \(\Delta q=-\frac{\frac{1}{2}sq(1-q)}{1-sq^2} \sim \frac{1}{2}sq(1-q)\)

• Por otra parte, si la dominancia es completa, entonces \(ipq\frac{2qa}{\sigma_P} \sim sq^2(1-q)\)

• Podemos reducir ambas ecuaciones a \(s=i\frac{2a}{\sigma_P}\), que no es otra cosa que la intensidad multiplicada por un factor que representa la diferencia entre los genotipos (fenotipos) de los homocigotas, estandarizados entre el desvío estándar fenotípico de la característica.

• A valores determinados del coeficiente de selección y del efecto de sustitución (que depende del modo de acción génica y de las frecuencias alélicas), la respuesta a la selección será máxima cuando el producto \(pq\) sea máximo (\(p=q=1/2\)). Es decir, el progreso genético será máximo a frecuencias intermedias y luego irá disminuyendo a medida de que la frecuencia del alelo que seleccionamos en contra decrece: \(R=\sigma^2_A \frac{s}{2a}=\frac{2pq\alpha^2}{2a}s \therefore R=\frac{pq\alpha^2}{a}s\)

11.9 El diferencial de selección direccional y la identidad de Robertson-Price

Una perspectiva integradora del diferencial de selección direccional viene de la llamada identidad de Robertson-Price (Robertson (1966); Price (1970); Price (1972)). En esta sección usaremos la notación de Michael Lynch and Walsh (1998), así como el razonamiento empleado, con \(z\) representando el fenotipo de una característica de interés para el fitness. Hacemos énfasis en direccional, ya que es el tipo de selección que hemos manejado esencialmente en este capítulo (seleccionamos los individuos que se encontraban hacia un extremo de la distribución). Como vimos previamente, el diferencial de selección es igual a la diferencia de los individuos seleccionados (pero antes de la reproducción) y la media de la población en general, es decir

\[ \begin{split} S=\mu_s - \mu \end{split} \tag{11.44} \]

Por simplicidad asumamos que las diferencias entre los individuos solo conciernen a la probabilidad de llegar a la madurez, por lo que la función de fitness \(W(z)\) es la probabilidad de que los individuos con fenotipo \(z\) alcancen la edad reproductiva. En particular, no asumimos acá ninguna forma particular de \(W(z)\), por lo que esta podría ser una función discontinua, como en selección por truncamiento, o una continua, como en la selección gaussiana (Houchmandzadeh (2014)). Si llamamos \(p(z)\) a la función de densidad correspondiente al fenotipo \(z\) antes de la selección, entonces la densidad después de la selección será

\[ \begin{split} p_s(z)=\frac{W(z)\ p(z)}{\int W(z)\ p(z)\ dz} \end{split} \tag{11.45} \]

La lógica del numerador de la ecuación (11.45) es sencilla, si pensamos que \(W(z)\) es la ponderación del éxito de cada fenotipo \(z\), multiplicado en el numerador por la densidad correspondiente a ese fenotipo. Notar que el denominador ya no integra necesariamente a \(1\) y por lo tanto es el factor de escalado de la nueva densidad. Por otra parte, \(\int W(z)\ p(z)\ dz=\bar W\), el fitness medio individual. Si ahora llamamos a \(w(z)=\frac{W(z)}{\bar W}\) el fitness relativo del fenotipo \(z\), entonces la ecuación (11.45) se transforma en

\[p_s(z)=\frac{W(z)\ p(z)}{\int W(z)\ p(z)\ dz}=\frac{W(z)\ p(z)}{\bar W}=\frac{W(z)}{\bar W} p(z)\ \therefore\] \[ \begin{split} p_s(z)=w(z)\ p(z) \end{split} \tag{11.46} \]

El fenotipo medio después de la selección estará dado por

\[ \begin{split} \mu_s=\int z\ p_s(z)\ dz=\int z\ w(z)\ p(z)\ dz= {E}[z\ w(z)] \end{split} \tag{11.47} \]

que es la esperanza del producto del fenotipo por su fitness relativo. Por otra parte, el fitness medio relativo en la población estará dado por

\[ \begin{split} \bar w=\int w(z)\ p(z)\ dz=\frac{1}{\bar W} \int W(z)\ p(z)\ dz=\frac{\bar W}{\bar W}=1 \end{split} \tag{11.48} \]

El resultado de la ecuación (11.48) nos muestra que el fitness medio relativo de una población siempre será igual a \(1\). Al mismo tiempo, la esperanza de la media de la población antes de la selección será igual a

\[ \begin{split} \mu= {E}(z) \cdot {E}(w)= {E}(z) \cdot 1 \end{split} \tag{11.49} \]

Uniendo este último resultado con la ecuación (11.47) y sustituyendo ambos en la ecuación (11.44), tenemos

\[ \begin{split} S=\mu_s - \mu= {E}[z\ w(z)] - {E}(z) \cdot {E}(w) ={\sigma}[z,w(z)] \end{split} \tag{11.50} \]

con \({\sigma}[z,w(z)]\) representando la covarianza entre el fenotipo y el fitness relativo.

Bajo el supuesto de linealidad en la respuesta del promedio de los padres hacia su descendencia, como asumimos en otras partes, el cambio generacional en función del diferencial de selección direccional será

\[ \begin{split} R=\Delta \mu=\mu_o - \mu= \beta (\mu_s-\mu)=\beta S=h^2\ S \end{split} \tag{11.51} \]

la última igualdad (asumiendo que el coeficiente de regresión lineal es \(\beta=h^2\)) correspondiendo a la ecuación del criador, que vimos antes. Uniendo esto último con la ecuación (11.50), tenemos que (utilizando la notación de \(z\) para el fenotipo) podemos escribir el progreso genético generacional como

\[R=h^2\ S=\frac{\sigma_A^2}{\sigma_z^2}S=\frac{\sigma_A^2}{\sigma_z^2} {\sigma}[z,w(z)]\ \therefore\]

\[ \begin{split} R=\sigma_A^2 \frac{ {\sigma}[z,w(z)]}{\sigma_z^2}=\sigma_A^2 b_{w(z),z} \end{split} \tag{11.52} \]

donde \(b_{w(z),z}\) representa el coeficiente de regresión del fitness relativo en el fenotipo. La forma de la ecuación (11.52) tiene una estrecha relación con la ecuación (11.42) donde estudiamos el cambio de frecuencias bajo selección y nuevamente resalta la relación existente entre la respuesta a la selección y la varianza aditiva de la característica.

PARA RECORDAR

• Si asumimos que las diferencias entre los individuos solo conciernen a la probabilidad de llegar a la madurez, por lo que la función de fitness \(W(z)\) es la probabilidad de que los individuos con fenotipo \(z\) alcancen la edad reproductiva. En particular, no asumiendo ninguna forma particular de \(W(z)\), por lo que esta podría ser una función discontinua, como en selección por truncamiento, o una continua, como en la selección gaussiana. Si llamamos \(p(z)\) a la función de densidad correspondiente al fenotipo \(z\) antes de la selección, entonces la densidad después de la selección será: \(p_s(z)=\frac{W(z)\ p(z)}{\int W(z)\ p(z)\ dz}\).

• El fitness medio relativo de una población siempre será igual a 1. Al mismo tiempo, la esperanza de la media de la población antes de la selección será igual \(E(z)\cdot1\), con el diferencial de selección siendo igual a \({\sigma}[z,w(z)]\) representando la covarianza entre el fenotipo y el fitness relativo.

• Utilizando la notación de \(z\) para el fenotipo podemos escribir el progreso genético generacional como \(R=h^2\ S=\sigma_A^2 b_{w(z),z}\) donde \(b_{w(z),z}\) representa el coeficiente de regresión del fitness relativo en el fenotipo.

11.10 Conclusión

Hasta este momento hemos estado aproximándonos al estudio de caracteres fenotípicos influídos por múltiples genes. Hemos dejado de lado, sin embargo, qué acontece cuando fuerzas externas influyen sobre las frecuencias de los alelos referentes a dichos loci. Cuando esta influencia es ejercida por la acción de un ser humano, se habla generalmente de selección artificial. En este capítulos nos volcamos a estudiar cómo responden caractes fenotípicos de interés a la selección artificial.

De alguna forma retomamos conceptos que desarrollamos en la segunda parte de este libro, pero con un cambio fundamental, dado por nuestro objeto de estudio. Sabemos que el cambio fenotípico se debe al cambio en las frecuencias alélicas de múltiples loci, pero intentar desarrollar un modelo explícito para este fenómeno sería imposible; para hacerlo tendríamos que tener en cuenta la posibilidad de cambio en múltiples frecuencias a la vez, y modelar todas las interacciones y motivos de desvío subyacentes. Como alternativa, decidimos tomar una aproximación desde la estadística, analizando media, varianza y covarianza del caracter fenotípico de interés. Al desarrollar desde esta perspectiva llegamos a algunos resultados fundamentales de la genética cuantiativa, como puede ser la ecuación del criador, la cual justamente relaciona la respuesta a la selección con la intensidad de la misma y la heredabilidad del caracter (un concepto central que desarrollamos en el capítulo anterior).

En los dos siguientes capítulos ampliaremos nuestra perspectiva, teniendo como base la siguiente cuestión: ¿cómo afecta la selección en un caracter fenotípico a otros caracteres, y cómo podemos tener esto en cuenta al momento de ejercer la selección artificial?

11.11 Actividades

11.11.1 Control de lectura

1. ¿Qué papel juega la heredabilidad de una característica durante el proceso de selección artificial? Desarrolle conceptualmente y realice un planteo matemático explícito que sintetice los conceptos presentados.
2. ¿Qué tipos de factores de corrección existen? Mencione en qué casos se aplica cada uno.
3. ¿Qué relación existe entre el diferencial de selección y la varianza fenotípica de una característica? ¿Por qué es importante tener esto en cuenta al comparar presiones de selección?
4. ¿Qué relación existe entre la proporción de animales seleccionados y la intensidad de selección? ¿Brindan la misma información estas medidas?
5. ¿Cómo se evalúa a nivel práctico la respuesta de una característica a la selección artificial?

11.11.2 ¿Verdadero o falso?

1. Existen diferencias biológicas subyacentes que llevan a la necesidad de emplear factores de corrección al momento de comparar una característica en diferentes clases de estudio (e.g., sexos). Estos factores son universales para dicha característica.
2. Generalmente, se cuestiona por qué en la selección por truncación la distribución de la característica fenotípica seleccionada en los progenitores no se mantiene igual en la descendencia. Esta discrepancia se debe a la influencia del ambiente en la obtención de los fenotipos.
3. Un aumento en el intervalo generacional conlleva un incremento en la respuesta a la selección anual.
4. En una población animal comercial de tamaño estable los machos contribuyen en mayor medida al progreso genético que las hembras.
5. Si la heredabilidad de una característica es baja, es posible realizar selección compensando esta falta de varianza genético aditiva con factores ambientales.

Soluciones

1. Falso. Los factores de corrección son idiosincráticos, dependiendo de la población considerada. Por ejemplo, podemos considerar que no será lo mismo corregir un factor de altura en poblaciones asiáticas que en poblaciones africanas. A su vez, es de esperar que estos factores de corrección también varíen con el tiempo.
2. Verdadero. Es importante resaltar la influencia del ambiente en la distribución de valores que toma la característica fenotípica de nuestro interés. Aún cuando su genotipo no posea gran potencial, los individuos pueden verse beneficiados por un ambiente que fomente a la característica estudiada (lo mismo puede ocurrir en sentido opuesto, perjudicando a individuos de alto potencial genético). No obstante, sólo el genotipo es heredado de una generación a la siguiente (i.e., los ambientes no son heredables). Esto implica que, aún cuando se haya establecido un régimen de selección artificial en base a los fenotipos, no seremos capaces de asegurar que la genética de los individuos seleccionados lleve necesariamente a obtener una progenie que correlacione perfectamente a nivel fenotípico.
3. Falso. Notemos que la respuesta de selección anual es una medida de respuesta estandarizada (i.e., en un intervalo definido de tiempo). Recordemos que el intervalo generacional (\(\text{IG}\)) es el promedio de la edad de sus progenitores cuando nacen los descendientes que los reemplazarán. A la vez, el \(\text{IG}\) es el denominador del cálculo del progreso genético anual; de esto queda claro que un aumento en el \(\text{IG}\) conlleva necesariamente una reducción de esta medida. Conceptualmente, esto es coherente con el hecho de que cuanta mayor edad poseen los progenitores al generar la progenie de reemplazo, mayor será el tiempo necesario para observar el resultado del proceso selectivo llevado a cabo.
4. Verdadero. La presión de selección que se puede hacer en los machos es mucho mayor, en tanto se requiere un menor número por generación para mantener el tamaño poblacional estable. En el caso de las hembras, por el contrario, los tiempos de gestación suelen llevar a tener que ejercer una presión selectiva comparativamente menor (de lo contrario se elegiría un número absurdamente chico de progenitoras).
5. Falso. La selección (ya sea natural o artificial) es un proceso que requiere como condición necesaria la herencia.

Ejercicios

Ejercicio 11.1

Un grupo de criadores se dispone a seleccionar perros de la raza basset hound con el fin de aumentar el largo de sus orejas. Para ello llevan a cabo un proceso de selección por truncación, eligiendo perros de cada camada. Cuentan con 150 perros en total, los cuales presentan una media de largo de oreja que sigue una distribución normal \(N(\mu = 32,5 \text{ cm},\ \sigma = 1\).

Asumiendo que por cada perro seleccionado se puede obtener como máximo cuatro perros, ¿cuál es el valor máximo para media de largo de oreja que se puede seleccionar manteniendo constante el número de perros en cada camada?

Solución

Recordemos que la intensidad de selección \(i\) se comporta tal que

\[i = \frac{S}{\sigma_p} = \frac{\bar{x}_S - \bar{x}_0}{\sigma_P} = \frac{z}{p}\]

donde \(S\) es el diferencial de selección (como desvío de la media; \(\bar{x}_S - \bar{x}_0\)), \(\sigma_P\) es la desviación fenotípica, \(z\) es la “altura” de la distribución normal de densidad \(N(0,1)\) y \(p\) es la proporción de individuos seleccionados como productores. La distribución de largos de orejas es una distribución normal con desviación \(\sigma_P = 1\), por lo que a efectos prácticos podremos trabajar con esta fórmula, teniendo en cuenta que reemplazamos la media por \(\mu’ = X - \mu\) a efectos de tener en cuenta una distribución normal estándar \(N(0,1)\).

Si se puede seleccionar a lo sumo \(\frac{1}{4}\) de los individuos de cada camada (a efectos de mantener constante el número de la misma), esto equivale a decir \(\frac{z}{p} = 0,25\). Por lo tanto, tenemos que en el caso extremo se da

\[i = \frac{\bar{x}_S - \bar{x}_0}{\sigma_P} = 0,25\] \[\bar{x}_S - \bar{x}_0 = 0,25 \cdot \sigma_P = 0,25 \cdot 1\] \[\bar{x}_S = \bar{x}_0 + 0,25 \Rightarrow\] \[\bar{x_S} = 32,5 + 0,25 = 32,75 \text{ cm}\]

Es decir, con los datos planteados se deduce que si se seleccionan individuos con una media de selección que supere los \(32,75 \text{ cm}\), resultaría inviable mantener el tamaño de camada constante.

Ejercicio 11.2

(Adaptado de J. Felsenstein 2019)

Consideremos un caracter fenotípico cuyo valor numérico está controlado por dos loci, sin varianza ambiental. Si los valores especificados por los genotipos de estos loci bialélicos son

	\(\text{BB}\)	\(\text{Bb}\)	\(\text{bb}\)
\(\text{AA}\)	\(6\)	\(7\)	\(8\)
\(\text{Aa}\)	\(7\)	\(8\)	\(9\)
\(\text{aa}\)	\(8\)	\(9\)	\(10\)

y las proporciones de las frecuencias génicas en ambos casos son \(50:50\) (tal que \(p_A = 0,5\) y \(p_B = 0,5\))

a. ¿Cuál será el valor medio para este fenotipo?

b. ¿Cuál será su varianza? ¿Y su desviación estándar?

c. ¿Son estos loci individualmente aditivos para sus efectos alélicos? ¿Muestran algún tipo de interacción (epistasis)?

d. En vista del punto anterior, ¿cuál será la heredabilidad del caracter?

e. Si realizamos selección artificial quedándonos sólo con los individuos que poseen un valor fenotípico mayor o igual a \(8\), ¿cuál será la respuesta de selección en la primera generación obtenida?

Solución

a. El valor medio para el caracter fenotípico será la media ponderada de los valores fenotípicos según su respectiva frecuencia genotípica. A efectos de calcular estas últimas, asumiremos que los loci se encuentran segregando bajo equilibrio de Hardy-Weinberg y en equilibrio de ligamiento. Dado que las frecuencias génicas son \(p_A = 0.5\) y \(p_B = 0.5\), las frecuencias genotípicas serán

\[ \begin{cases} f(AABB) = (p_A^2) \cdot (p_B^2) = 0,5^4 \\ f(AaBB) = (2 \cdot p_A p_a) \cdot (p_B^2) = 2 \cdot 0,5^4 \\ f(aaBB) = (p_a^2) \cdot (p_B^2) = 0,5^4 \\ f(AABb) = (p_A^2) \cdot (2 \cdot p_B p_b) = 2 \cdot 0,5^4 \\ f(AaBb) = (2 \cdot p_A p_a) \cdot (2 \cdot p_B p_b) = 4 \cdot 0,5^4 \\ f(aaBb) = (p_a^2) \cdot (2 \cdot p_Bp_b) = 2 \cdot 0,5^4 \\ f(AAbb) = (p_A^2) \cdot (p_b^2) = 0,5^4 \\ f(Aabb) = (2 \cdot p_A p_a) \cdot (p_b^2) = 2 \cdot 0,5^4 \\ f(aabb) = (p_a^2) \cdot (p_b^2) = 0,5^4 \end{cases} \]

con lo que el valor medio (que llamaremos \(\bar{x}\)) estará dado por

\[\bar{x} = (0,5^4 \cdot 6) + (2 \cdot 0,5^4 \cdot 7) + (0,5^4 \cdot 8) + ( 2 \cdot 0,5^4 \cdot 7) + (4 \cdot 0,5^4 \cdot 8) + (2 \cdot 0,5^4 \cdot 9) + (0,5^4 \cdot 8) + (2 \cdot 0,5^4 \cdot 9) + (0,5^4 \cdot 10)\] \[\bar{x} = 7,5\]

b. Calcularemos la varianza según

\[\sigma^2_x = \sum p_i \cdot (x_i - \bar{x})^2\]

donde \(x_i\) es el valor fenotípico para el \(i\)-ésimo genotipo y \(p_i\) su frecuencia (i.e. debemos ponderar al momento de calcular la varianza). Tenemos así

\[\sigma^2_x = [0,5^4] \cdot (6 - 7,5)^2 + [2 \cdot 0,5^4] \cdot (7 - 7,5)^2 + [0,5^4] \cdot (8 - 7,5)^2 + \] \[[2 \cdot 0,5^4] \cdot (7 - 7,5)^2 + [4 \cdot 0,5^4] \cdot (8 - 7,5)^2 + [2 \cdot 0,5^4] \cdot (9 - 7,5)^2 + \] \[[0,5^4] \cdot (8 - 7,5)^2 + [2 \cdot 0,5^4] \cdot (9 - 7,5)^2 + [(0,5^4] \cdot (10 - 7,5)^2\] \[\sigma^2_x \approx 1,9375 \Rightarrow \sigma_x = \sqrt{\sigma^2_x} \approx \sqrt{1,9375} \approx 1,3919\]

c. Observemos que en todos los casos el cambio de un alelo por otro genera un cambio en el valor fenotípico del respectivo genotipo de \(1\). Esto es una señal clara de aditividad: si existieran efectos epistáticos deberíamos observar desviaciones debido a las interacciones entre loci. A su vez es también señal de que no existen efectos de dominancia (de lo contrario, los fenotipos heterocigotas no serían equidistantes de los homocigotas). En resumen, la variación fenotípica parece estar determinada, en su componente genético, sólo por la componente aditiva.

d. Dado que toda la variación genética está dada por el componente aditivo, tenemos que en este caso \(h^2 = 1\).

e. Para calcular la respuesta de selección podemos aplicar la ecuación del criador (\(R = h^2 S\), donde \(S = \bar{x}_s - \bar{x}_0\) es el diferencial de selección). Podemos calcular la media fenotípica para los genotipos seleccionados (i.e., \(\bar{x}_S\)) de forma análoga a lo realizado en la primera parte del ejercicio. Solo debemos tener en cuenta que las frecuencias genotípicas cambiarán por un factor común en todos los casos, ya que cambió la composición de la población (ya que descartamos individuos). La frecuencia total de los individuos seleccionados en la población original es de \(f(aaBB) +f(AaBb) + f(aaBb) + f(AAbb) + f(Aabb) + f(aabb) = 0,5^4 + 4 \cdot0,5^4 + 2 \cdot 0,5^4 + 0,5^4 + 2 \cdot 0,5^4 + 0,5^4 = 0,6785\). Podemos realizar un ajuste de las proporciones genotípicas en la nueva población con una regla de tres (o lo que es igual, aplicando un factor de \(\frac{1}{0,6785}\). Las nuevas frecuencias serán de

\[ \begin{cases} f’(aaBB) = f(aaBB) \cdot \frac{1}{0,6785} \\ f’(AaBb) = f(AaBb) \cdot \frac{1}{0,6785} \\ f’(aaBb) = f(aaBb) \cdot \frac{1}{0,6785} \\ f’(AAbb) = f(AAbb) \cdot \frac{1}{0,6785} \\ f’(Aabb) = f(Aabb) \cdot \frac{1}{0,6785} \\ f’(aabb) = f(aabb) \cdot \frac{1}{0,6785} \end{cases} \]

De esto sale que la media de los individuos seleccionados es de

\[\bar{x}_s = (0,5^4 \cdot \frac{1}{0,6785} \cdot 8 ) + (4 \cdot 0,5^4 \frac{1}{0,6785} \cdot 8) + \] \[(2 \cdot 0,5^4 \frac{1}{0,6785} \cdot 9) + (0,5^4 \cdot \frac{1}{0,6785} \cdot 8) + \] \[(2 \cdot 0,5^4 \cdot \frac{1}{0,6785} \cdot 9) + (0,5^4 \cdot \frac{1}{0,6785} \cdot 10)\]

\[\bar{x}_s \approx 8,6588\]

Por lo tanto, \(R \approx 1 \cdot (8,6588 - 7,5) = 1,1588\).

Ejercicio 11.3

En un rodeo de bovinos, se tiene como objetivo disminuir el peso adulto (\(h^2=0,45\)). En este rodeo, el porcentaje de destete logrado es del 75% y el desvío fenotípico de la característica es de 30 kg. La estructura del mismo se presenta a continuación:

\(\text{Edad al parto}\)	\(\text{Hembras}\)	\(\text{Machos}\)
\(3\)	\(210\)	\(10\)
\(4\)	\(190\)	\(8\)
\(5\)	\(120\)	\(6\)
\(6\)	\(60\)
\(7\)	\(20\)
\(\text{TOTAL}\)	\(600\)	\(24\)

¿Cuál es el progreso genético logrado al cabo de una generación?

Solución

En primer lugar, determinaremos la proporción de animales seleccionados:

\(600*0,75= 450\) animales nacidos de los cuales \(225\) serán hembras y \(225\) machos

Luego determinaremos la proporción de animales seleccionados de cada sexo:

\[p_h=\frac{210}{225}\approx 0,93= 93\%\] \[p_m=\frac{10}{225}\approx 0,04 = 4\%\]

A partir de la table de intensidades podremos determinar que estas proporciones de animales seleccionados implican una intensidad de selección de \(0,1444\) en las hembras y de \(2,1543\) en los machos. Por lo tanto, la intensidad de selección poblacional es de \(\frac{0,1444+2,1543}{2}=1,14935\).

Si recordamos que \(i=\frac{S}{\sigma_P}\) entonces \(S=i* \sigma_P\). Entonces el diferencial de selección será \(S=1,14935*30=34,48\) por lo que podremos calcular el progreso genético mediante la ecuación del criador tal que \(PG=0,45*34,48\approx 15,52 kg\).

Ejercicio 11.4

Un equipo de trabajo se encuentra trabajando en el mejoramiento de dos características fenotípicas que poseen valores de heredabilidad muy dispares (\(h^2_1 = 0,121\) y \(h^2_1 = 0,932\)). Si pretenden obtener una misma respuesta de selección para los mismos, ¿cuántas veces mayor será el diferencial de selección \(S_2\) respecto al \(S_1\)?

Solución

Emplearemos la ecuación del criador (\(R = h^2 S\)). Si \(R_1 = R_2\), esto implica que

\[h^2_1 S_1 = h^2_2 S_2 \Rightarrow\] \[\frac{h^2_1}{h^2_2} = \frac{S_2}{S_1}\] \[\frac{0,932}{0,121} = \frac{S_2}{S_1}\] \[\frac{S_2}{S_1} = 7,7\]

Vemos que el diferencial de selección debe ser casi \(8\) veces mayor. En efecto, debe compensar exactamente en la misma proporción la diferencia entre las heredabilidades (ya que ambos términos se encuentran multiplicando en la ecuación del criador).

Ejercicio 11.5

El objetivo de un criador de ovinos es la disminución del diámetro de la fibra, y para ello se propone realizar selección en los carneros a usar. En este sentido, anualmente se logran señalar \(150\) machos de los cuales el productor planea seleccionar con los \(8\) mejores para utilizar como carneros. La media de la población en cuanto a diámetro de fibra es de \(28,4 \mu\) y el registro de cada uno de los machos seleccionados fue de \(18, 22, 17, 21, 20, 19, 20, 21 \mu\). A su vez, se ha estimado que la heredabilidad de la característica es de 0,48.

a. ¿Cuánto progreso genético se logra al cabo de una generación? b. Si en lugar de seleccionar \(8\) machos se seleccionarán \(5\), ¿qué progreso genético se lograría?

Solución

a. En primer lugar deberemos calcular la media de los machos seleccionados:

\[\bar{x}=\frac{18+22+17+21+20+19+20+21}{8}=19,75\]

A partir de la misma podremos calcular el diferencial de seleccón de los machos y el poblacional para el que deberemos tener en cuenta que no se está haciendo selección en las hembras:

\[S_m=19,75-28,45=-8,7\] \[S_p=\frac{-8,7+0}{2}=-4,35\]

Por último, podremos calcular el progreso genético:

\[PG=h^2*S=0,48*-4,35=-2,088\]

Es decir que cada generación es posible disminuir en algo más de \(2 \mu\) el grosor de la fibra.

b. En el caso que se seleccionaran \(5\) machos en lugar de \(8\), deberemos repetir el mismo procedimiento:

\[\bar{x}=\frac{18+17+20+19+20}{5}=18,8\] \[S_m=18,8-28,45=-9,65\] \[S_p=\frac{-9,65+0}{2}=-4,825\] \[PG=h^2*S=0,48*-4,825=-2,316\]

---

Bibliografía

Bulmer, Michael George. 1980. The Mathematical Theory of Quantitative Genetics. Clarendon Press.

Felsenstein, J. 2019. Theoretical Evolutionary Genetics. University of Washington. https://felsenst.github.io/pgbook/pgbook.html.

Galton, Francis. 1886. “Regression Towards Mediocrity in Hereditary Stature.” Journal of the Anthropological Institute 15: 246–63.

Havenstein, G. B., P. R. Ferket, S. E. Scheideler, and B. T. Larson. 1994. “Growth, livability, and feed conversion of 1957 vs 1991 broilers when fed "typical" 1957 and 1991 broiler diets.” Poult Sci 73 (12): 1785–94.

Houchmandzadeh, B. 2014. “An Alternative to the Breeder’s and Lande’s Equations.” G3 (Bethesda) 4 (1): 97–108.

Lynch, Michael, and Bruce Walsh. 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates (Oxford University Press).

Price, G. R. 1970. “Selection and covariance.” Nature 227 (5257): 520–21.

———. 1972. “Extension of covariance selection mathematics.” Ann Hum Genet 35 (4): 485–90.

R Core Team. 2021. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

———. 1966. “A Mathematical Model of the Culling Process in Dairy Cattle.” Animal Production 8: 95–108.

---

88. Charles Darwin (12 febrero 1809 – 19 abril 1882) fue un naturalista inglés, fundador de la teoría de la selección natural. En el segundo viaje del HMS-Beagle, con el objetivo primario de cartografiar la costa sudamericana, Darwin viajó como naturalista, recogiendo observaciones geológicas y diferentes especímenes biológicos. Su obra más famosa, “On the Origin of Species”, fue publicada por primera vez en 1859.↩︎

89. La igualdad se sostiene debido a que se cumple que \(\Phi(x) = 1-\Phi(-x)\), hecho que la persona interesada puede consultar en libros de texto que traten estadística básica.↩︎