Capítulo 10 Parámetros genéticos: heredabilidad y repetibilidad

En el mejoramiento genético, tanto animal como vegetal, el objetivo central suele ser cambiar la frecuencia de los alelos relevantes de tal forma de modificar los valores aditivos en la dirección deseada (selección) y por lo tanto el fenotipo, o buscar estrategias para incrementar las combinaciones de alelos favorables (cruzamientos). En la determinación de la mejor estrategia, tanto la elección de una u otra, como de la combinación de las mismas, resulta fundamental entender la arquitectura genética de la característica a mejorar. Entendemos por arquitectura genética de una característica tanto los componentes que la afectan (número de genes, número de alelos en esos genes, distribución espacial de los mismos) como su interrelación y su regulación.

Desafortunadamente, en general esto no se trata más que de una expresión de deseo ya que los estudios requeridos para comprender a cabalidad dicha arquitectura suelen ser imposibles excepto para características determinadas por muy pocos genes. Sin embargo, pese a estas limitaciones, resulta fundamental comprender cómo se comporta la característica desde el punto de vista genético. ¿Tiene alguna base genética la característica? ¿Se parecen los progenitores a sus hijos más de lo que se parecen a la progenie de otros progenitores? ¿Existe variación genética importante en la población? ¿Qué rol juega el ambiente en la característica? Como veremos en capítulos siguientes, la heredabilidad de una característica es un parámetro central a la hora de seleccionar los individuos que serán los progenitores de la siguiente generación, así como para definir la mejor estrategia de mejoramiento.

Por otra parte, ciertas características parecen repetirse en los individuos, alguna en forma espacial (es decir en distintas partes del individuo) y otras en forma temporal. Por ejemplo, los árboles frutales tenderán a reproducir anualmente su producción de frutos (medida como diferencia respecto a la media de su población), tanto en número como en peso. Los ovinos producirán todos los años vellones y si comparamos las diferencias del peso del mismo respecto a la media de los animales contemporáneos, estos desvíos de la media (hacia arriba y hacia abajo) tenderán a repetirse en cada zafra. En vacas lecheras, la producción total de cada lactancia, medida como desvío de la media del grupo contemporáneo y corregida por diferencias sistemáticas entre lactancias, también tenderá a repetirse. Esto no quiere decir que las diferencias sean exactamente las mismas, ya que el ambiente no afectará a todos los animales de la misma forma en distintos años. Tampoco todas las características tienen la misma repetibilidad.

Para entender mejor cómo juegan los distintos componentes de nuestro modelo genético en la arquitectura de una característica, de lo heredable de la misma y de su repetibilidad (en caso de que la misma se exprese varias veces en la vida del individuo) es que vamos a volver al modelo genético básico y utilizar distintas herramientas estadísticas, tanto para entender estos parámetros genéticos, como para predecir el valor de cría de los individuos o la producción más probable en una próxima medición en el mismo individuo.

OBJETIVOS DEL CAPÍTULO

\(\square\) Definir el concepto de heredabilidad y discutir su relevancia en la selección de individuos.

\(\square\) Comprender las diferencias entre la heredabilidad en sentido amplio y sentido estricto.

\(\square\) Analizar peculiaridades de la heredabilidad en diferentes contextos.

\(\square\) Indagar en agunos aspectos evolutivos de la heredabilidad.

\(\square\) Analizar cómo es posible estimar la heredabilidad en la era genómica.

\(\square\) Comprender métodos estadísticos y computacionales utilizados para estimar la heredabilidad.

\(\square\) Definir el concepto de repetibilidad y comprender su uso como herramienta.

10.1 Heredabilidad

Intuitivamente, cuando hablamos de heredabilidad de una característica tendemos a pensar en el parecido entre progenitores y progenie. Sin embargo, el parecido entre progenitores y progenie puede tener causas genética como no genéticas. Por ejemplo, es muy conocido el problema (en realidad casi todos son problemas en esa área) de determinar la heredabilidad de una característica como el coeficiente intelectual (en seres humanos): si bien parece existir cierta base genética en las diferencias observadas entre individuos al realizar las pruebas, es indudable el rol que juega el ambiente donde crecieron y se educaron los individuos; padres que han alcanzado un importante nivel educativo suelen invertir más en la educación y estimulación de sus hijos que aquellos padres que cuentan con menos posibilidades. Esto hace que los padres tiendan a parecerse a sus hijos en los logros académicos, más allá de la posible existencia de una base genética en la característica.

Otras características tienen una base totalmente genética, pero sin embargo las diferencias que podemos observar entre padres e hijos no siempre se deben a la genética. Por ejemplo, el número de patas en los mamíferos terrestres es de cuatro (tetrápodos), un número determinado por el genoma y su regulación, así como la disposición de los miembros. La aparición de animales de tres patas o de inviduos con la disposición y orientación diferentes de los mismos por causas ambientales en el desarrollo embrionario (drogas, por ejemplo la Talidomida) no cambiarán el determinismo genético de la misma, pese a introducir variaciones, por lo que debemos definir estrictamente a qué nos referimos con heredabilidad de una característica.

La heredabilidad como relación de varianzas

Como vimos previamente, podemos descomponer las causas biológicas de los fenotipos que observamos en distintas componentes, tanto genéticas como ambientales. En general, para la mayoría de las características cuantitativas, dado el fenotipo observado en los progenitores esperamos que en alguna medida su progenie se les parezca, aunque difícilmente el parecido sea total. Ya en el año 1886, sir Francis Galton⁸⁶ había reportado este hecho, curioso para la época (Galton 1886). El estudio de Galton involucraba las alturas de 205 parejas de padre y madre, así como las de 930 hijos de las mismas, todos en edad adulta (y multiplicando las alturas de las mujeres por el factor de corrección \(1,08\), para que fuesen comparables). A partir de graficar la altura promedio de los padres (en las abscisas) y las de los hijos (en las ordenadas), Galton observaba que los puntos caían dentro de una elipse, cuyo eje mayor sería la recta de regresión (en términos modernos) y que la pendiente de esta recta era menor a \(1\). Es decir, respecto a la altura, en promedio los hijos se desviaban de la media poblacional menos que el promedio de sus padres, como se puede apreciar en la Figura 10.1, en la relación \(1 \to \frac{2}{3}\). A este fenómeno Galton lo llamó “regresión hacia la mediocridad” y el mismo fue una de las fuentes de discrepancia durante años entre biométricos y mendelianos (si en cada generación los valores más alejados tienden hacia el promedio, en pocas generaciones todos los individuos estarán muy cerca del promedio, desapareciendo la variabilidad). Como ya vimos parcialmente antes y como dejaremos en claro ahora, la perspectiva biométrica y la mendeliana son claramente compatibles y la explicación de este fenómeno es relativamente sencilla: no todas la diferencias que observamos en los padres tienen base genética y por lo tanto no es esperable que dichas diferencias aparezcan totalmente incambiadas en los hijos.

Nuestro modelo genético establecía que el fenotipo era la suma de los efectos genéticos y ambientales, así como sus interacciones. En forma simplificada nuestro modelo era \(P=A+D+I+E\). Si un individuo posee un valor fenotípico elevado respecto al promedio de la población, en altura por ejemplo, desde el punto de vista matemático cualquier combinación de estos efectos podría producir este efecto. Sin embargo, en general, los individuos más altos de la población serán aquellos en los que tanto los componentes genéticos como los ambientales se alineen para arriba, es decir que tanto los genéticos son positivos, como los ambientales son positivos respecto de la media. Como ya vimos antes, los padres no transmiten a sus hijos sus propias combinaciones de alelos, que son las bases de la dominancia y de la epistasis. Tampoco transmiten en ambiente, ya que es algo externo a ellos. Por lo tanto, el único componente transmisible de padres a hijos sería el componente de los efectos genéticos aditivos.

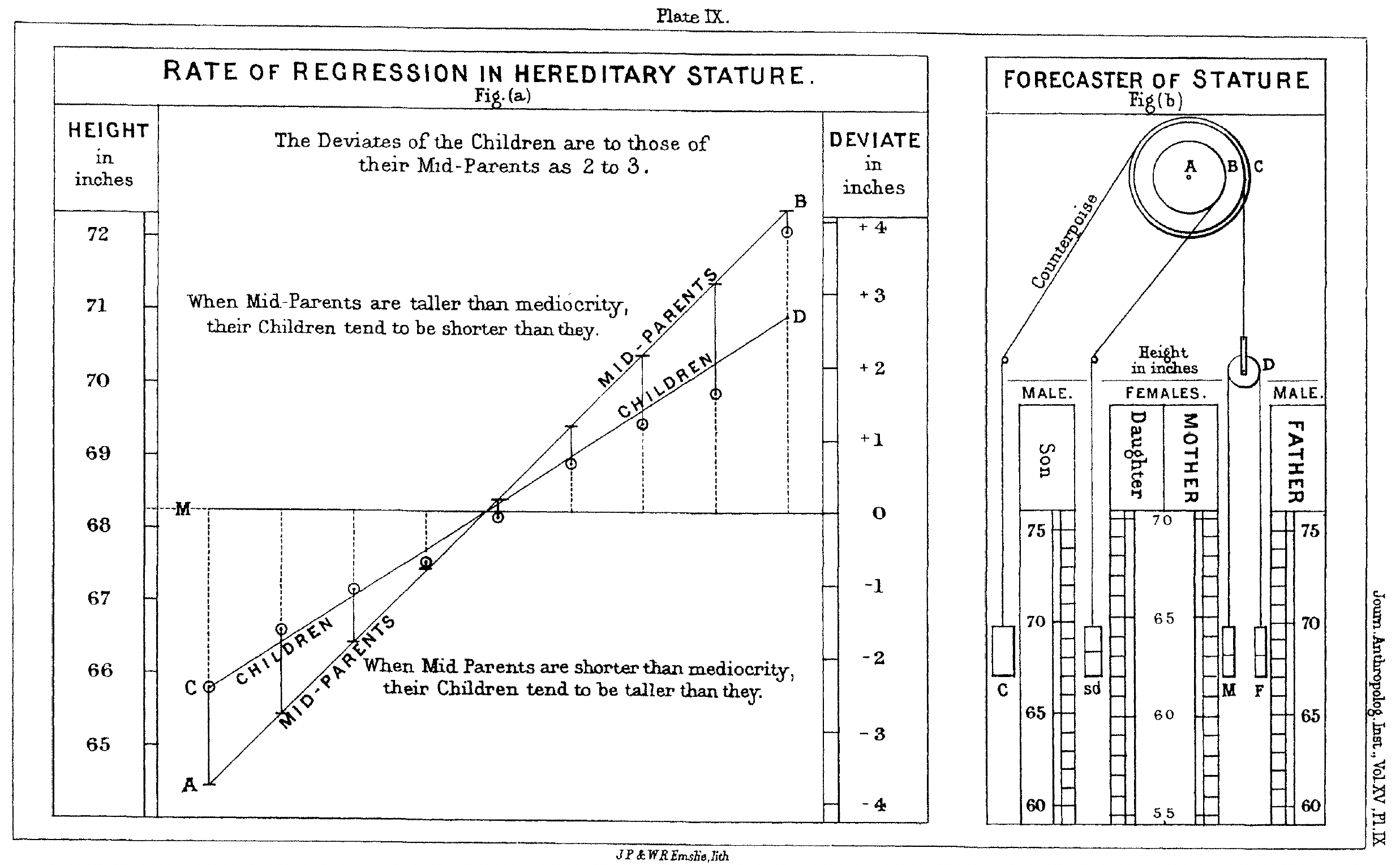
Figura 10.1: Captura de imagen de la figura original (“Plate IX”) en el artículo de Galton (1886). A la izquierda (“Fig. (a)”) se aprecia la forma en que dedujo la relación \(1 \to \frac{2}{3}\) para las desviaciones de altura de padres e hijos, ya que los segmentos de recta correspondientes a los hijos tienen aproximadamente \(\frac{2}{3}\) del largo correspondiente al de sus progenitores. Notar que la forma del gráfico de regresión difiere respecto a cómo lo graficaríamos en la actualidad, ya que tanto abscisas como ordenadas se refieren a la medida en los padres (por esa razón el ajuste de la recta de padres es perfecto). La escala de la derecha es en términos absolutos, mientras que la escala a la izquierda del gráfico marca los puntos como desvío de la media. A la derecha (“Fig. (b)”) aparece el diagrama de una máquina para pronosticar la altura de los hijos (e hijas) a partir de la altura de los padres, donde se aprecia la diferencia en las escalas de los dos sexos. (Trabajo de dominio público en casi todos los países al haber pasado más 70 años de la muerte del autor).

El resto de los efectos esperamos que se comporten de forma aleatoria con media cero y por lo tanto no aportarán más altura a los hijos que el promedio de los efectos aditivos de sus padres, que era menor a su vez que el promedio fenotípico. Esto explica perfectamente lo observado por Galton de que los hijos de padres altos suelen estar también sobre el promedio, pero menos que el promedio de sus padres. Idéntico razonamiento se aplica a los padres bajos, pero en este caso sus hijos serán menos bajos que el promedio de sus padres, acercándose también al promedio general.

Ahora que nos resulta más clara la base conceptual de lo que esperar de la transmisión de una característica cuantitativa, veamos lo que ocurre con la variación. Vimos antes, en el capítulo El Modelo Genético Básico, la forma en que podíamos pasar de trabajar con los datos indivivuales a la descripción del modelo en forma de varianzas, es decir

\[ \begin{split} \mathrm{V_P}=\mathrm{V_G+V_E}=\mathrm{V_A+V_D+V_I+V_E} \end{split} \tag{10.1} \]

Ahora, si queremos entender el papel que juega la única fuente de variación heredable, es decir la de los efectos genéticos aditivos, resulta natural expresar esta como la proporción de la variabilidad total correspondiente a los efectos aditivos. Por lo tanto, llamamos heredabilidad a la relación

\[ \begin{split} h^2=\frac{\mathrm{V_A}}{\mathrm{V_P}}=\frac{\mathrm{V_A}}{\mathrm{V_A+V_D+V_I+V_E}} \end{split} \tag{10.2} \]

Notar que el símbolo \(h^2\) representa la heredabilidad, no el cuadrado de la misma. Esto se debe a que originalmente se definió el símbolo \(h\) como el coeficiente en el método de “path analysis” del artículo S. Wright (1921) y que por lo tanto su cuadrado (\(h^2\)) representa la proporción heredable de la variabilidad. Otra cosa fundamental a tener en cuenta, que a esta altura debería resultar obvia, cuando hablamos de la heredabilidad de una característica se trata de un parámetro poblacional. Esto se refiere, por un lado, a que los individuos NO TIENEN una heredabilidad específica a cada uno de ellos (ya que se trata de una relación de varianzas, ambas determinadas en la misma población). Pero por otro lado, también se refiere a que la heredabilidad de una característica corresponde a la determinación de la misma en una población dada y en un momento dado.

Para entender esto último alcanza con analizar la definición en la ecuación (10.2). Por un lado, la varianza aditiva puede variar de población en población; bajo fuerte selección es esperable que la misma disminuya en la población a lo largo del tiempo ya que si en forma continua elegimos animales “mejores”, irán disminuyendo su frecuencia en la población alelos y genotipos (fuentes de varianza aditiva). Por otro lado, mucho más importante aún es la variabilidad que podemos observar en el denominador. De acuerdo a nuestro modelo genético \(P=G+E\) y despreciando las interacciones \(\mathrm{V_P=V_G+V_E}\). Más aún, habíamos acordado que en este modelo todas las variaciones no explicadas por lo genético las considerábamos como variaciones ambientales, entre ellas los errores de medición. Por ejemplo, si estamos considerando la heredabilidad de la característica producción de leche a 305 días en un determinado rodeo de gran tamaño y las mediciones de producción las realizamos con un equipamiento con gran error aleatorio, entonces la varianza “ambiental” será mayor y todo el denominador será mayor que si lo realizamos con un equipo más preciso. Como la varianza aditiva permanece incambiada, en el primer caso nuestra estimación de la heredabilidad de la característica será menor que en el segundo, exclusivamente debido a la forma de medir la característica.

Una representación gráfica de la heredabilidad como cociente de varianzas se observa en la Figura 10.2.

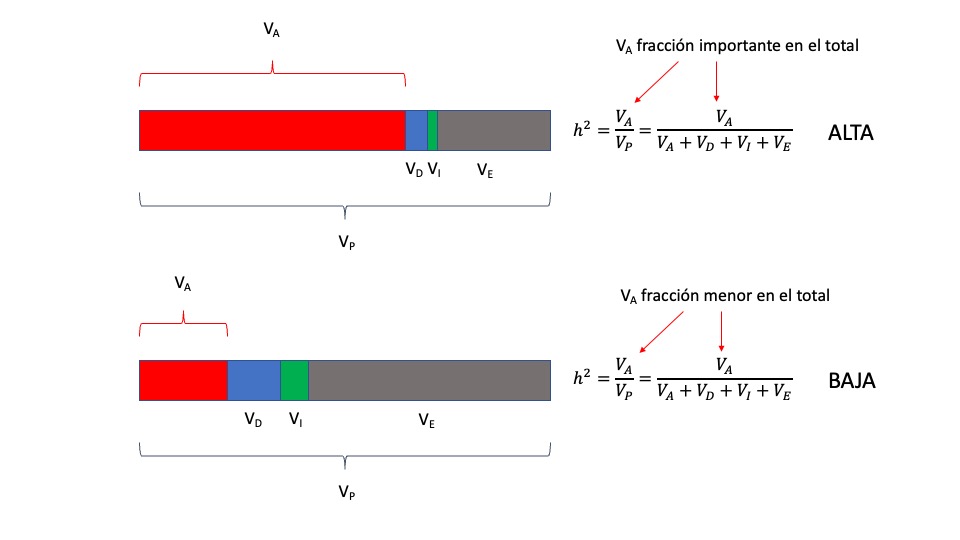
Figura 10.2: Representación gráfica de la heredabilidad como relación de varianzas. En la situación de arriba la varianza aditiva (en rojo) representa una fracción importante de la varianza fenotípica, es decir de la varianza total (\(V_P=V_A+V_D+V_I+V_E\)), por lo que la heredabilidad de la característica será alta. En la situación de abajo, la varianza aditiva (en rojo) es bastante pequeña en relación al total y por lo tanto la heredabilidad de la característica será baja.

En la misma, los distintos componentes de la varianza se representan como barras de colores, rojo para la varianza aditiva, azul para la de dominancia, verde para la de epistasis y gris para la varianza ambiental (incluyendo en esta todas las fuentes no-genéticas). De acuerdo a nuestro modelo, la varianza fenotípica es igual a la suma de todas estas fuentes de variación, es decir \(\mathrm{V_P=V_A+V_D+V_I+V_E}\). En la situación ilustrada en la parte superior, la varianza aditiva es el componente más importante de toda la varianza y por lo tanto la relación \(\frac{ {V_A}}{ {V_A+V_D+V_I+V_E}}\) será alta, o lo que es lo mismo, la heredabilidad de la característica será alta. En la situación de abajo, por otra parte, la varianza aditiva es relativamente pequeña en el total y por lo tanto \(\frac{ {V_A}}{ {V_A+V_D+V_I+V_E}}\) será pequeña, lo que es decir que la heredabilidad será pequeña.

Claramente, como la heredabilidad la definimos acá como un cociente entre dos varianzas, la aditiva y la total (fenotípica), la heredabilidad estará entre 0 y 1, es decir \(0 \leqslant h^2 \leqslant 1\). El límite inferior de \(h^2\) se alcanza solamente en la situación en que la característica de interés no posee varianza aditiva (\({V_A=0}\)), mientras que el límite superior se alcanza en el caso hipotético donde la única fuente de varianza es la aditiva (\({V_P=V_A}\)). En general, para la mayor parte de las características de interés agronómico existe algo de varianza aditiva y por lo tanto la heredabilidad es mayor a cero, mientras que el límite superior es casi imposible de alcanzar aun cuando toda la varianza teórica fuese aditiva ya que las mediciones conllevan error siempre. Notar que como la heredabilidad es una relación de varianzas de la misma característica, siempre tendremos las mismas unidades en el numerador que en el denominador y por lo tanto las mismas desaparecerán de la heredabilidad, por lo que se trata de una parámetro genético adimensional (no tiene dimensiones).

Ejemplo 10.1

En un estudio previo Ejemplo 9.4 para determinar los componentes genéticos de la varianza en diámetro de fibras en ovejas verdes llegamos a que nuestro mejor estimador de la varianza aditiva era \(\hat \sigma^{2}_A =1,80\ \mu\text{m}^2\), mientras que para la varianza de dominancia era \(\hat \sigma^{2}_D=1,40\ \mu\text{m}^2\). Asumiendo que para la característica la varianza de epistasis es prácticamente cero y que la varianza ambiental es de \(\hat \sigma^{2}_E =0,80\ \mu\text{m}^2\), obtener una estimación puntual de la heredabilidad.

De acuerdo a nuestra definición en la ecuación (10.2), la heredabilidad es igual a

\[ \begin{split} h^2=\frac{ {V_A}}{ {V_P}}=\frac{ {V_A}}{ {V_A+V_D+V_I+V_E}} \end{split} \]

por lo que sustituyendo las varianzas por nuestros estimadores de las mismas tenemos

\[ \begin{split} h^2=\frac{\hat \sigma^{2}_A}{\hat \sigma^{2}_A+\hat \sigma^{2}_D+\hat \sigma^{2}_I+\hat \sigma^{2}_E}=\frac{1,80}{1,80+1,40+0+0,80}=0,45 \end{split} \]

Por lo tanto, nuestro estimador puntual de la heredabilidad de la característica diámetro de fibras en esta majada de ovejas verdes es \(h^2=0,45\), un valor intermedio.

PARA RECORDAR

• El único componente transmisible del fenotipo de padres a hijos es el aditivo, el resto de los efectos esperamos que se comporten de forma aleatoria con media cero.

• La heredabilidad, expresada como relación entre varianzas puede definirse como: \(h^2=\frac{ {V_A}}{ {V_P}}=\frac{ {V_A}}{ {V_A+V_D+V_I+V_E}}\)

• La heredabilidad de una característica es un parámetro poblacional, por lo que los individuos no tienen una heredabilidad específica para cada uno.

• La heredabilidad de una característica corresponde a la determinación de la misma en una población dada y en un momento dado.

• Al estar definida como un cociente entre varianzas (la aditiva y la fenotípica), la heredabilidad estará entre 0 y 1, es decir \(0 \leqslant h^2 \leqslant 1\). A su vez, al no tener unidades, se trata de un parámetro genético adimensional.

La heredabilidad como regresión

En la sección anterior vimos nuestra primera definición matemática de la heredabilidad de una característica y esta era la proporción de la varianza total atribuible a los efectos aditivos, es decir \(h^2= {V_A/V_P}\). Sin embargo, ya en el trabajo de Galton (1886) se encuentra implícito el concepto de predicción a partir de los datos fenotípicos (ver Figura 10.1, “Fig(b)” a la derecha). En el caso planteado por Galton (1886), la idea era predecir el fenotipo de los hijos a partir del fenotipo de los padres, pero nosotros podemos plantearnos algo un poco más diferente y posiblemente más interesante: predecir el valor de cría de los individuos a partir de su propio fenotipo. Planteado de otra manera, sabemos que en general no podemos determinar directamente el valor de cría de un individuo ya que no es algo que observemos directamente. Sin embargo, el fenotipo aporta información clave para predecir el valor de cría. Entonces, ¿cómo podemos usar esta información?

Regresión del valor de cría en el fenotipo individual

Seguramente recordarás de los cursos previos de estadística que en el caso de que exista una asociación lineal entre dos variables podemos usar esta relación para inferir los parámetros de una ecuación de predicción. En particular, cuando centramos las dos variables (es decir, les restamos sus correspondientes medias), la recta de regresión debe pasar por la intersección de los ejes, el punto \((0,0)\) y por lo tanto el valor del intercepto (el valor de las ordenadas cuando la abscisa es cero) es \(0\) también. Esto nos deja con un solo parámetro para estimar que es la pendiente de la recta de regresión. En nuestro caso estamos interesados en predecir el valor de cría de los individuos a partir de sus fenotipos, por lo que la pendiente de la recta de regresión (\(b_{AP}\)) me permitirá la mejor predicción posible del valor de cría a partir de un valor fenotípico dado.

La situación se ilustra en la Figura 10.3. Supongamos que de alguna manera obtuvimos el verdadero valor de cría de un conjunto de animales, así como sus valores fenotípicos, para una característica determinada. Cada punto azul representa un individuo. En el eje de las abscisas tenemos los valores fenotípicos y en el eje de las ordenadas los correspondientes valores de cría (es decir, genéticos aditivos). A primera vista parece claro que existe una relación entre las dos variables, posiblemente lineal, ya que la densidad de puntos en los cuadrantes inferior derecho y superior izquierdo es mucho más baja que en los otros dos cuadrantes.

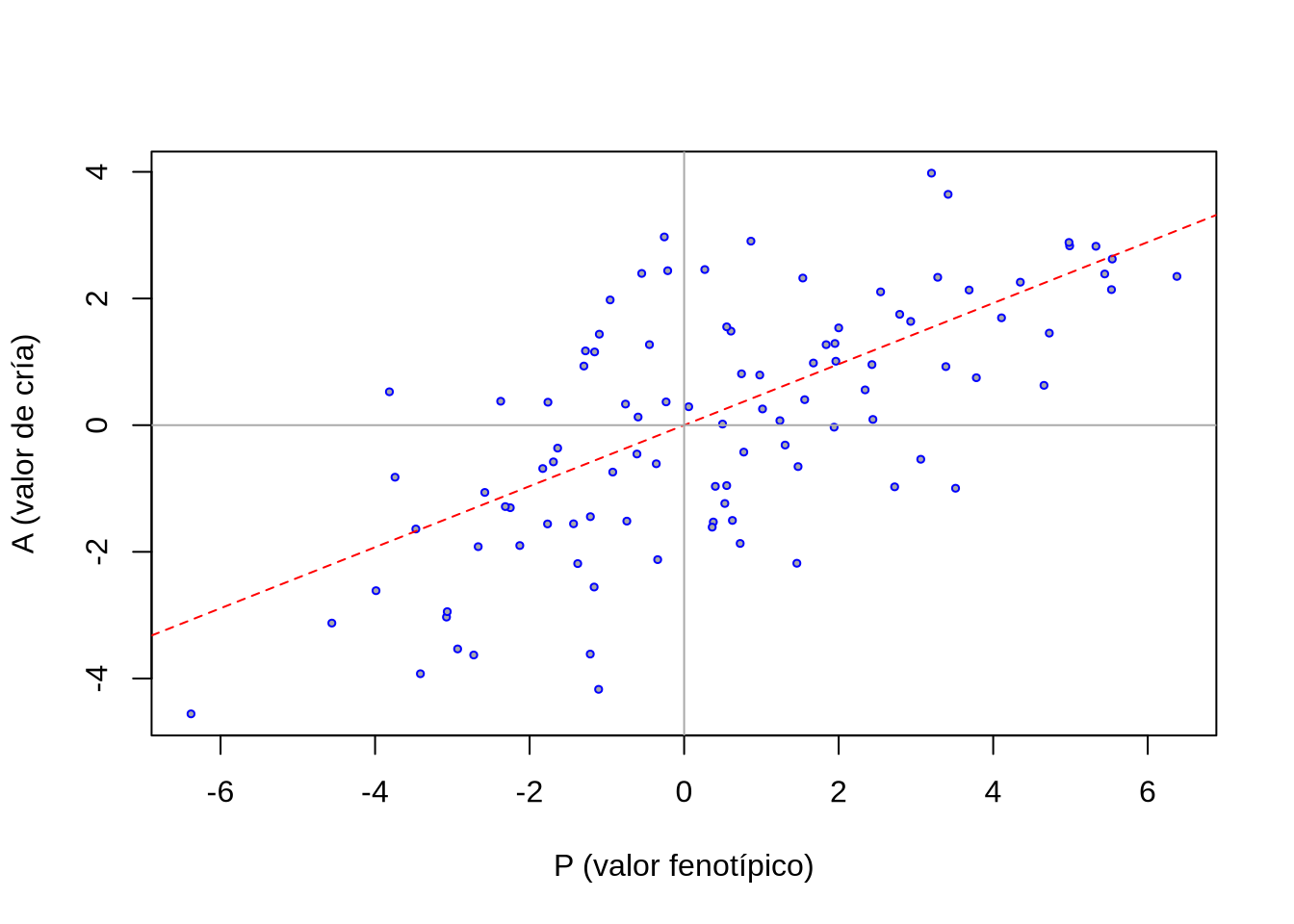
Figura 10.3: Regresión de los valores de cría en los valores fenotípicos (centrados). La pendiente de la regresión por el cero es \(b_{AP}=\frac{ {V_A}}{ {V_P}}=h^2\).

Veamos ahora qué ocurre si “ajustamos” una recta de regresión por mínimos cuadrados. De acuerdo a lo que has visto en cursos previos, el estimador por mínimos cuadrados de la pendiente entre \(X\) e \(Y\) es igual a \(b_{XY}=\frac{ {Cov(X,Y)}}{ {Var(X)}}\), por lo que en nuestro caso tenemos

\[ \begin{split} b_{AP}=\frac{ {Cov(A,P)}}{ {V_P}}=\frac{ {Cov(A,A+D+I+E)}}{ {V_P}} \therefore \\ b_{AP}=\frac{ {Cov(A,A)}+ {Cov(A,D)}+ {Cov(A,I)}+ {Cov(A,E)}}{ {V_P}} \end{split} \tag{10.3} \]

Sin embargo, como ya vimos antes, por construcción la covarianza entre el valor aditivo y de dominancia es cero, al igual que el que corresponde a aditivo y de epistasis (porque ambos se construyen como desvíos de lo explicado por el efecto anterior). Además, también hemos supuesto que en general lo ambiental no se correlaciona con lo genético, por lo que también la covarianza entre lo aditivo y lo ambiental será cero. Poniendo todo junto, como excepto la covarianza entre aditivo y aditivo el resto de los términos del numerador son cero y dado que la covarianza de una variable consigo misma es igual a la varianza, tenemos ahora que

\[ \begin{split} b_{AP}=\frac{ {Cov(A,A)}}{ {V_P}}=\frac{ {V_A}}{ {V_P}}=h^2 \end{split} \tag{10.4} \]

Es decir, el valor de la pendiente de la recta de regresión entre el valor aditivo y el valor fenotípico es igual a la heredabilidad. En la Figura 10.4 podemos apreciar como funciona nuestra “máquina de predicción” (en lugar de los pesos y poleas de la máquina de Galton): para un nuevo individuo, entramos su valor fenotípico (como desvío de la media) en las abscisas y subimos (o bajamos) verticalmente hasta encontrar la recta de regresión, momento en que nos movemos horizontalmente hasta el corte con el eje de las ordenadas (el eje vertical); el punto de corte en las ordenadas será el valor de cría predicho para nuestro individuo.

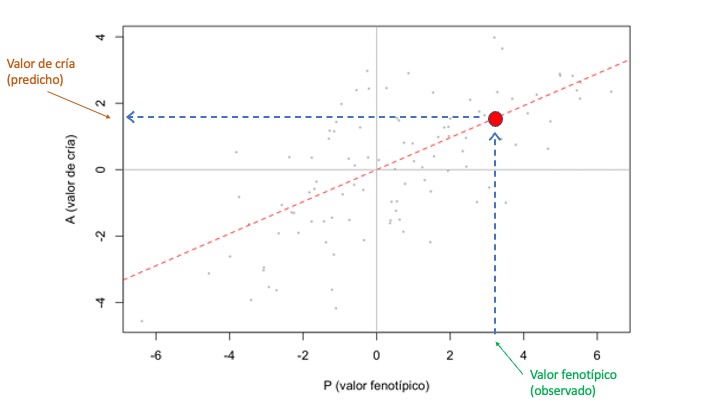
Figura 10.4: Predicción del valor de cría de un individuo a partir de su propio fenotipo. A partir de los pares de datos valor de cría y fenotipo (puntos grises) estimamos una recta de regresión cuya pendiente es la heredabilidad (\(b_{AP}= {V_A/V_P}=h^2\)). A partir de esta recta podemos predecir el valor de cría de nuevos individuos teniendo el valor fenotípico de los mismos. En la figura, entramos el valor fenotípico en el eje de las abscisas y luego “subimos” por la línea azul a trazos hasta el corte con la recta (roja a trazos) y en ese punto vamos hacia el eje de las ordenadas por la línea azul horizontal: el valor de corte en las ordenadas será el valor de cría de nuestro individuo.

En principio, hemos encontrado una herramienta fantástica. Luego de haber “calibrado” nuestra máquina con algunos pares de datos valor de cría y valor fenotípico, alcanza con tener el valor fenotípico de los individuos a los que les queremos predecir el valor de cría y nuestra “máquina” lo hará de inmediato por nosotros. En particular, el valor de cría estimado para el individuo \(i\) será

\[ \begin{split} {\hat A_i=(P_i-\bar P)}\ b_{AP}= {(P_i-\bar P)}\ h^2 \end{split} \tag{10.5} \]

Sin embargo, en general, nuestra máquina de predicción no será perfecta, como ocurre con la mayoría de las máquinas de predicción. El problema es fácil de apreciar en la Figura 10.4. Mientras que para cualquier valor fenotípico existe una distribución de valores de cría que le corresponden (puntos grises con la misma abscisa), la máquina siempre me devolverá un solo valor: el de la ordenada del punto de corte de la abscisa con la recta de predicción. Dicho de otra manera, las distancias entre los puntos “grises” y la recta representan los errores de predicción que cometemos usando la recta como mejor predictor. La pregunta que sigue es ¿cómo se relacionan los errores que cometemos con la heredabilidad?

Claramente, para cada punto (individuo) el error \(\mathrm{e_i=A_i-\hat A_i=A_i-(P_i-\bar P)}\ h^2\) será posiblemente diferente, por lo que estamos hablando de una distribución de errores. En el caso de dos variables aleatorias ligadas por una relación lineal y con distribución normal ambas (como es generalmente nuestro caso), una forma usual de medir el grado de asociación entre ellas, o la precisión de la predicción (lo que es equivalente), es el coeficiente de correlación de Pearson (por Karl Pearson ⁸⁷). Seguramente recordarás que para dos variables \(X\) e \(Y\), dicho coeficiente se definía como \(r_{XY}=\frac{ {Cov(X,Y)}}{\sqrt{ {V_X V_Y}}}\), por lo que en nuestro caso, el coeficiente de correlación entre el valor de cría y el valor fenotípico será

\[ \begin{split} r_{AP}=\frac{ {Cov(A,P)}}{\sqrt{ {V_A}}\sqrt{ {V_P}}}=\frac{ {V_A}}{\sqrt{ {V_A}}\sqrt{ {V_P}}}=\frac{\sqrt{ {V_A}}\sqrt{ {V_A}}}{\sqrt{ {V_A}}\sqrt{ {V_P}}}=\sqrt{\frac{ {V_A}}{ {V_P}}}=\sqrt{h^2}=h \end{split} \tag{10.6} \]

Es decir, en este caso particular de predecir el valor de cría a partir del valor fenotípico del individuo, la precisión es la raíz cuadrada de la heredabilidad (\(\sqrt{h^2}=h\)). Cuanto más alta sea la heredabilidad, mayor será por lo tanto la precisión de la predicción. De hecho, un estadístico usado normalmente para comparar el ajuste de modelos es el coeficiente de determinación \(R^2\), que en modelos de como el nuestro es el cuadrado del coeficiente de correlación de Pearson y por lo tanto (con datos infinitos) \(R^2=h^2\). La relación entre la heredabilidad y la precisión de la predicción del valor de cría a partir del fenotipo del individuo se observa claramente en la Figura 10.5.

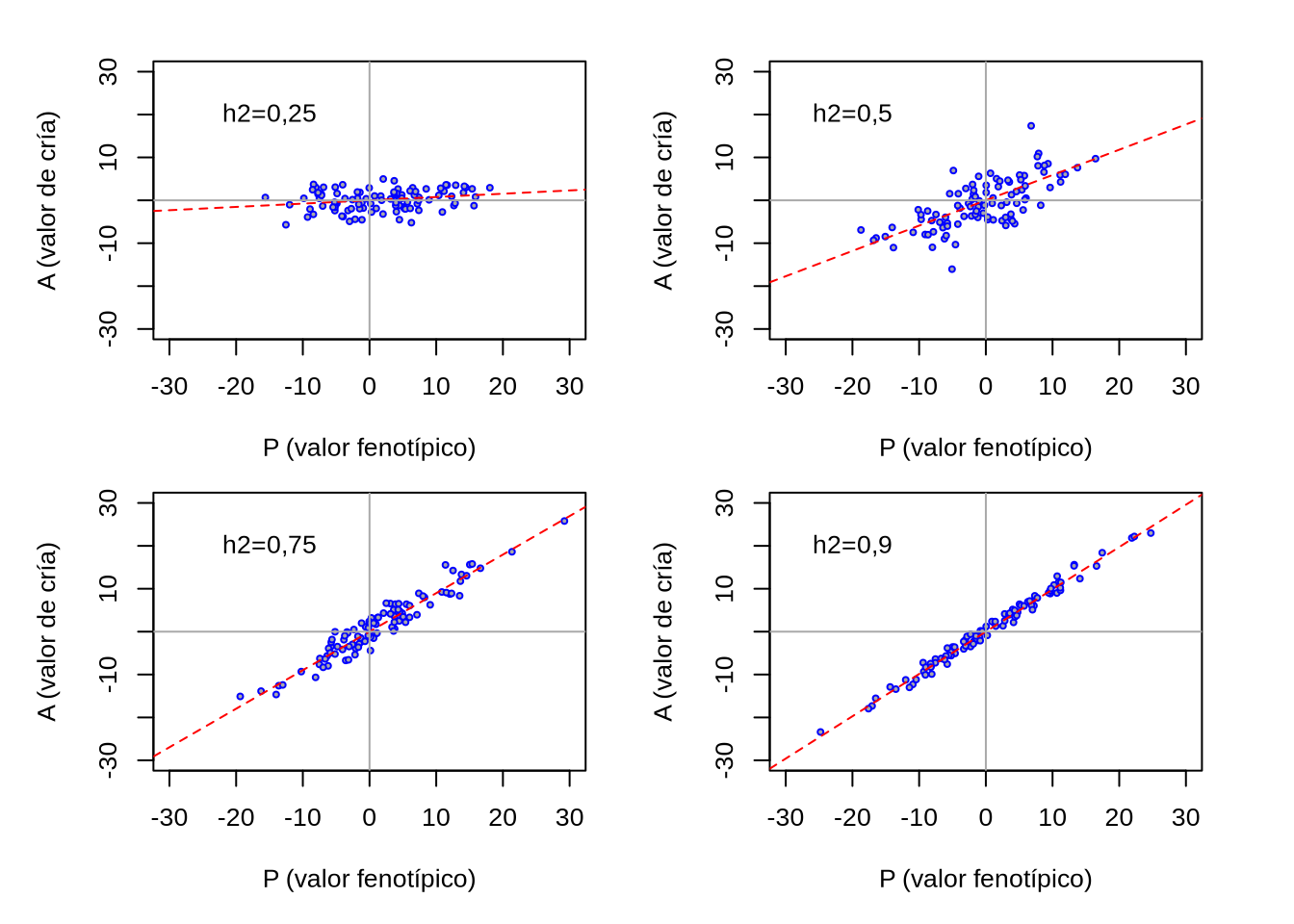
Figura 10.5: Relación entre la heredabilidad y la precisión de la predicción. La pendiente de la regresión es \(b_{AP}=\frac{ {V_A}}{ {V_P}}=h^2\), mientras que la precisión es \(r_{AP}=\frac{ {V_A}}{ {\sqrt{V_P V_A}}}=h\). A medida de que aumenta la pendiente (es decir la heredabilidad), los puntos se distribuyen más cerca de la línea de regresión, o lo que es lo mismo, aumenta la precisión.

A medida de que aumenta la heredabilidad de la característica, que es igual a la pendiente,los puntos se van “acercando” a la recta, lo que es equivalente a decir que disminuye el error (\(\mathrm{e_i=A_i-\bar A_i}\)) y por lo tanto aumenta la precisión.

En general, la relación entre el coeficiente de regresión y el de correlación está dada por

\[ \begin{split} r_{XY}=\frac{\sigma_{XY}}{\sigma_X \sigma_Y} \Leftrightarrow r_{XY} \frac{\sigma_Y}{\sigma_X}=\frac{\sigma_Y}{\sigma_X} \frac{\sigma_{XY}}{\sigma_X \sigma_Y}=\frac{\sigma_Y}{\sigma_Y} \frac{\sigma_{XY}}{\sigma_X \sigma_X}=\frac{\sigma_{XY}}{\sigma_X^2}=b_{XY} \therefore \\ b_{XY}=r_{XY} \frac{\sigma_Y}{\sigma_X} \end{split} \tag{10.7} \]

por lo que en nuestro caso, como verificación de nuestros resultados previos, sustituyendo en la ecuación (10.7) \(A\) por \(Y\) y \(P\) por \(X\), tenemos

\[ \begin{split} h^2=b_{AP}=r_{AP} \frac{\sigma_A}{\sigma_P}=h \cdot h=h^2 \end{split} \tag{10.7} \]

Ejemplo 10.2

Dada las estimación de la heredabilidad obtenida en el Ejemplo 10.1 para el diámetro de fibras (DF) en las ovejas verdes (\(h_{DF}^2=,45\)) y sabiendo que la media de diámetro en la población de referencia es de \(17,2 \mu\text{m}\), estimar el valor de cría para dicha característica de los carneros con los siguientes fenotipos:

Carnero	\(\hat A\) Diámetro (\(\mu \text{m}\))	\(\hat A\) Peso del vellón sucio (kg)
Elmas Astado	\(16,8\)	\(7,635\)
Peloduro	\(19,3\)	\(9,457\)
Ram Bullero	\(17,2\)	\(6,356\)
Capicubo	\(16,1\)	\(7,574\)
Keto Maste	\(14,7\)	\(11,574\)

Conociendo que la heredabilidad de Peso del Vellón Sucio (PVS) en esta majada es de \(h_{PVS}^2=0,36\) y la media fenotípica es de \(7,345\) Kg, estimar los valores de cría de los carneros. Calcular las precisiones de las estimaciones de valor de cría para ambas características.

De acuerdo a la ecuación (10.5)

\[ \begin{split} {\hat A_i}= {(P_i-\bar P)}\ h^2 \end{split} \]

por lo que podemos transformar los valores en el cuadro anterior a

Carnero	\(\hat A\) Diámetro (\(\mu \text{m}\))	\(\hat A\) Peso del vellón sucio (kg)
Elmas Astado	\((16,8-17,2) 0,45=-0,180\)	\((7,635-7,345) 0,36=0,10440\)
Peloduro	\((19,3-17,2) 0,45=0,945\)	\((9,457-7,345) 0,36=0,76032\)
Ram Bullero	\((17,2-17,2) 0,45=0,000\)	\((6,356-7,345) 0,36=-0,35604\)
Capicubo	\((16,1-17,2) 0,45=-0,495\)	\((7,574-7,345) 0,36=0,08244\)
Keto Maste	\((14,7-17,2) 0,45=-1,125\)	\((11,574-7,345) 0,36=1,52244\)

Como vimos previamente, de acuerdo a la ecuación (10.6), la precisión de las estimaciones a partir del fenotipo individual vienen dadas por

\[ \begin{split} r_{AP}=h=\sqrt{h^2} \end{split} \]

por lo que \(r_{DF}=\sqrt{h^2_{DF}}=\sqrt{0,45} \approx 0,671\), mientras que para PVL será \(r_{PVL}=\sqrt{h^2_{PVL}}=\sqrt{0,36} = 0,60\).

Regresión del valor fenotípico de los hijos sobre el fenotipo de un progenitor

Más arriba veíamos la importancia de considerar la heredabilidad como la pendiente de regresión entre el valor de cría de los individuos y su fenotipo ya que de esta forma podíamos predecir el valor de cría de nuevos individuos. Sin embargo, el verdadero valor de cría de los individuos es usualmente desconocido, de ahí la trascendencia de poder predecirlo, por lo que para estimar esta pendiente es necesario hacerlo de otra forma. Es decir, para predecir los valores de cría precisamos de una pendiente cuya estimación precisa de valores de cría (además de los fenotípicos), por lo que de alguna manera no hay salida por ese lado.

Sin embargo, la regresión de los valores fenotípicos entre progenie y progenitores tiene también una relación directa con la heredabilidad, como veremos aquí. Para empezar por lo más sencillo vamos a estudiar la regresión entre los valores fenotípicos de una progenie en uno de sus progenitores. Esto es, vamos a formar parejas de datos de un progenitor (padre o madre) y uno de los descendientes. Para simplificar más las cosas, vamos a asumir que la varianza fenotípica de la característica es igual en ambos sexos, así como sus medias, aunque luego vamos a relajar alguno de estos supuestos.

Llamemos \(x_1\) y \(x_2\) a los progenitores y \(y\) a su progenie. Si \(V_P\) es la varianza fenotípica en los padres, la regresión del fenotipo de un hijo en el fenotipo de un progenitor, por ejemplo \(x_1\), la podemos escribir como

\[ \begin{split} {b_{HP}=\frac{Cov_{HP}}{V_P}=\frac{Cov(y,x_1)}{V_P}} \end{split} \tag{10.8} \]

El denominador de la ecuación es fácilmente estimable en forma directa a partir de las observaciones fenotípicas de los padres, por ejemplo, con el estimador usual de la varianza (\(\hat \sigma_P^2=\frac{1}{n-1}\sum_n (x_i-\bar x)^2\)) y es interpretable directamente en términos de nuestro modelo genético básico. Sin embargo, el numerador (que también podemos estimar directamente de los datos como \(\hat \sigma_P^2=\frac{1}{n-1}\sum_n (x_i-\bar x)(y_i-\bar y)\)) no nos dice directamente su significado en el modelo genético básico. Para obtener dicho significado debemos expresar los fenotipos de progenie y progenitor en términos del modelo genético básico, es decir

\[ \begin{split} {Cov_{HP}=Cov(y,x_1)=Cov(A_y+D_y+I_y+E_y,A_{x_1}+D_{x_1}+I_{x_1}+E_{x_1})} \end{split} \tag{10.9} \]

Pero \(y\) es hijo de \(x_1\) y \(x_2\), por lo que su valor de cría esperado será la suma de la mitad de cría del valor de cada uno de los progenitores. Por lo tanto, podemos escribir el resultado de la ecuación (10.9) como

\[ \begin{split} {Cov(\left(\frac{A_{x_1}+A_{x_2}}{2}\right)+D_y+I_y+E_y,A_{x_1}+D_{x_1}+I_{x_1}+E_{x_1})} \end{split} \tag{10.10} \]

Pero, como vimos previamente, los efectos de dominancia no covarían entre padres e hijos (al menos bajo apareamientos aleatorios), mientras que no es usual que los efectos ambientales en las dos generaciones covaríen, por lo que también los asumiremos iguales a cero. La relación progenitor-progenie incluye efectos epistáticos ya que hay combinaciones de los alelos del padre que pueden “viajar juntas” (\(\mathrm{\frac{1}{4}V_{AA}}\),\(\mathrm{\frac{1}{8}V_{AAA}}\), etc.), pero como hacemos usualmente, en general podemos despreciar estas interacciones. Esto nos deja con la siguiente relación

\[ \begin{split} {Cov(\left(\frac{A_{x_1}+A_{x_2}}{2}\right),A_{x_1})=} {\frac{1}{2}[Cov(A_{x_1},A_{x_1})+Cov(A_{x_2},A_{x_1})]=\frac{1}{2}Cov(A_{x_1},A_{x_1})} \end{split} \tag{10.11} \]

La última igualdad en (10.11) es debida a que bajo apareamientos aleatorios la covarianza entre valores aditivos de los progenitores es cero, es decir, mejores padres no se aparean preferentemente con mejores o peores madres. A su vez, \(\mathrm{Cov(A_{x_1},A_{x_1})=V_A}\), ya que \(x_1\) es un individuo tomado al azar de una población con varianza genética \(\mathrm{V_A}\), por lo tanto

\[ \begin{split} {Cov_{HP}=\frac{1}{2}Cov(A_{x_1},A_{x_1})=\frac{1}{2}V_A} \end{split} \tag{10.12} \]

Tenemos ahora una expresión interpretable en términos del modelo genético básico de la covarianza entre un progenitor y su progenie, que es además el numerador del estimador del coeficiente de regresión del valor fenotípico de la progenie en el de uno de sus progenitores. Volviendo a la ecuación (10.8), si colocamos este resultado de la covarianza fenotípica entre padres e hijos tenemos que

\[ \begin{split} {b_{HP}=\frac{Cov_{HP}}{V_P}=\frac{\frac{1}{2}V_A}{V_P}=\frac{1}{2}\frac{V_A}{V_P}=\frac{1}{2} h^2} \end{split} \tag{10.13} \]

Por lo tanto, la pendiente de la regresión de los valores fenotípicos de una progenie en uno de sus progenitores igual a un medio de la heredabilidad, por lo que al multiplicar dicho coeficiente de regresión por 2 tenemos un estimador insesgado de la heredabilidad, es decir

\[ \begin{split} {b_{HP}=\frac{1}{2} h^2 \Leftrightarrow h^2=2\ b_{HP}} \end{split} \tag{10.14} \]

La importancia de la ecuación (10.14) es obvia. A partir de valores fenotípicos de padres e hijos podemos estimar la heredabilidad de una característica, que como vimos previamente es a su vez la pendiente de la regresión de los valores de cría individuales en sus correspondientes valores fenotípicos. Esto nos permite salir de la encrucijada desde la que partimos y ahora sí (teniendo un estimado de la heredabilidad) podemos utilizar todo el poder predictor de los valores de cría que tienen los fenotipos.

Veamos ahora algunos aspectos prácticos de esta regresión fenotípica. Por un lado, hemos trabajado con un solo hijo por progenitor, pero es fácil de demostrar que hubiese sido lo mismo trabajar con el promedio de varios hijos (en principio, un número determinado e igual para todos los padres). Es decir, mientras que las parejas se formen al azar, la covarianza entre valor de cría de un progenitor y el promedio de \(N\) de sus progenies se podrá descomponer como

\[{Cov_{\bar HP}=\frac{1}{N}[\frac{1}{2}Cov(A_{x_1},A_{x_1})+\frac{1}{2}Cov(A_{x_1},A_{x_1})+...+\frac{1}{2}Cov(A_{x_1},A_{x_1})+\frac{1}{N}[\frac{1}{2}Cov(A_{x_?},A_{x_1})+}\] \[ \begin{split} \frac{1}{2}Cov(A_{x_?},A_{x_1})+...+\frac{1}{2}Cov(A_{x_?},A_{x_1}) \end{split} \tag{10.15} \]

con \(\mathrm{A_{x_?}}\) representando el valor de cría de todos los individuos que no son \(x_1\). Pero como ya vimos, al ser formadas al azar las parejas, la correlación entre valores de cría de \(x_1\) con el resto de los \(x_?\) será cero y por lo tanto todo el segundo término de la derecha en (10.15) es cero. Esto nos deja con

\[{Cov_{\bar HP}=\frac{1}{N}[\frac{1}{2}Cov(A_{x_1},A_{x_1})+\frac{1}{2}Cov(A_{x_1},A_{x_1})+...+\frac{1}{2}Cov(A_{x_1},A_{x_1})]=\frac{1}{2}\frac{1}{N}[N\ Cov(A_{x_1},A_{x_1})]}\ \therefore\] \[ \begin{split} {Cov_{\bar HP}=\frac{1}{2} V_A} \end{split} \tag{10.15} \]

Por otro lado, asumimos que la varianza fenotípica de la característica era la misma en los dos sexos, algo que no siempre ocurre en la características de interés económico. Esto nos deja con dos posibilidades al menos: a) estimar la heredabilidad de la característica para cada sexo, y b) corregir los registros de alguna manera para compensar por estas diferencias. Más aún, algunas características solo se expresan en solamente uno de los dos sexos, por ejemplo la producción de leche. En ese caso resulta obvia la regresión dentro de sexo, por ejemplo, vacas lecheras hijas de otras vacas lecheras. En el caso de la regresión de hijos e hijas en madres también debe considerarse la existencia de un componente de varianza materna (\({V_M}\)), cuyo aporte será \(\frac{1}{2} {V_M}\) y que puede no ser despreciable, especialmente en aquellas características como el crecimiento en bovinos donde el aporte de la madre es fundamental. En estos casos la no consideración de este componente sesgará hacia arriba el estimado de la heredabilidad ya que el numerador incluye elementos que no corresponden a la varianza aditiva.

Ejemplo 10.3

Diferentes estudios concluyen que la mejor raza de perros para el cuidado de las ovejas verdes es el Perro de montaña de los Pirineos (Figura 10.6), un perro de gran tamaño, rústico y suficientemente tranquilo como para no alterar el comportamiento de las ovejas. Sin embargo, dado el gran tamaño de las ovejas verdes, es necesario seleccionar perros de gran altura, por lo que fue encargado un estudio sobre la heredabilidad de esta característica entre los criaderos de la zona. Se seleccionaron 10 perros (machos) que habían sido criados en la mismas condiciones de alimentación y cuidados y para cada uno de ellos se eligió al azar un hijo (macho). Todos los animales se midieron a edad adulta (3 años).

Figura 10.6: Perro de montaña de los Pirineos, también conocido como Gran Pirineo, Chien des Pyrénées, Chien de Montagne des Pyrénées, Gigante de los Pirineos, Gran Pirineu, Gos de Muntanya dels Pirineus, Patou, entre otros. Un perro pastor de gran tamaño, con una altura a la cruz de entre 65 y 80 cm (foto de Wikipedia, HeartSpoon, CC BY-SA 3.0 via Wikimedia Commons).

En el cuadro siguiente se presentan las alturas de padres e hijos. A partir de estos datos estimar la heredabilidad de la característica altura a la cruz.

Padre	Altura..cm.	Altura.hijo..cm.
Euler	\(76\)	\(70\)
Leonardo	\(72\)	\(77\)
Galileo	\(67\)	\(73\)
Poisson	\(75\)	\(74\)
Galois	\(80\)	\(75\)
Maxwell	\(63\)	\(62\)
Newton	\(62\)	\(70\)
Bernoulli	\(69\)	\(70\)
Gauss	\(75\)	\(72\)
Fermi	\(74\)	\(75\)

De acuerdo a lo que vimos previamente, la pendiente de la regresión lineal de progenie en progenitor es igual a la mitad de la heredabilidad (Figura 10.7), por lo que un buen estimador de esta última es \(\mathrm{\hat h^2=2\ b_{HP}}\). El estimador OLS de la pendiente es

\[ \begin{split} {b_{HP}=\frac{Cov_{HP}}{V_P}=\frac{\sum_{n=1}^N (x_i-\bar x)(y_i-\bar y)}{\sum_{n=1}^N (x_i-\bar x)^2}} \end{split} \]

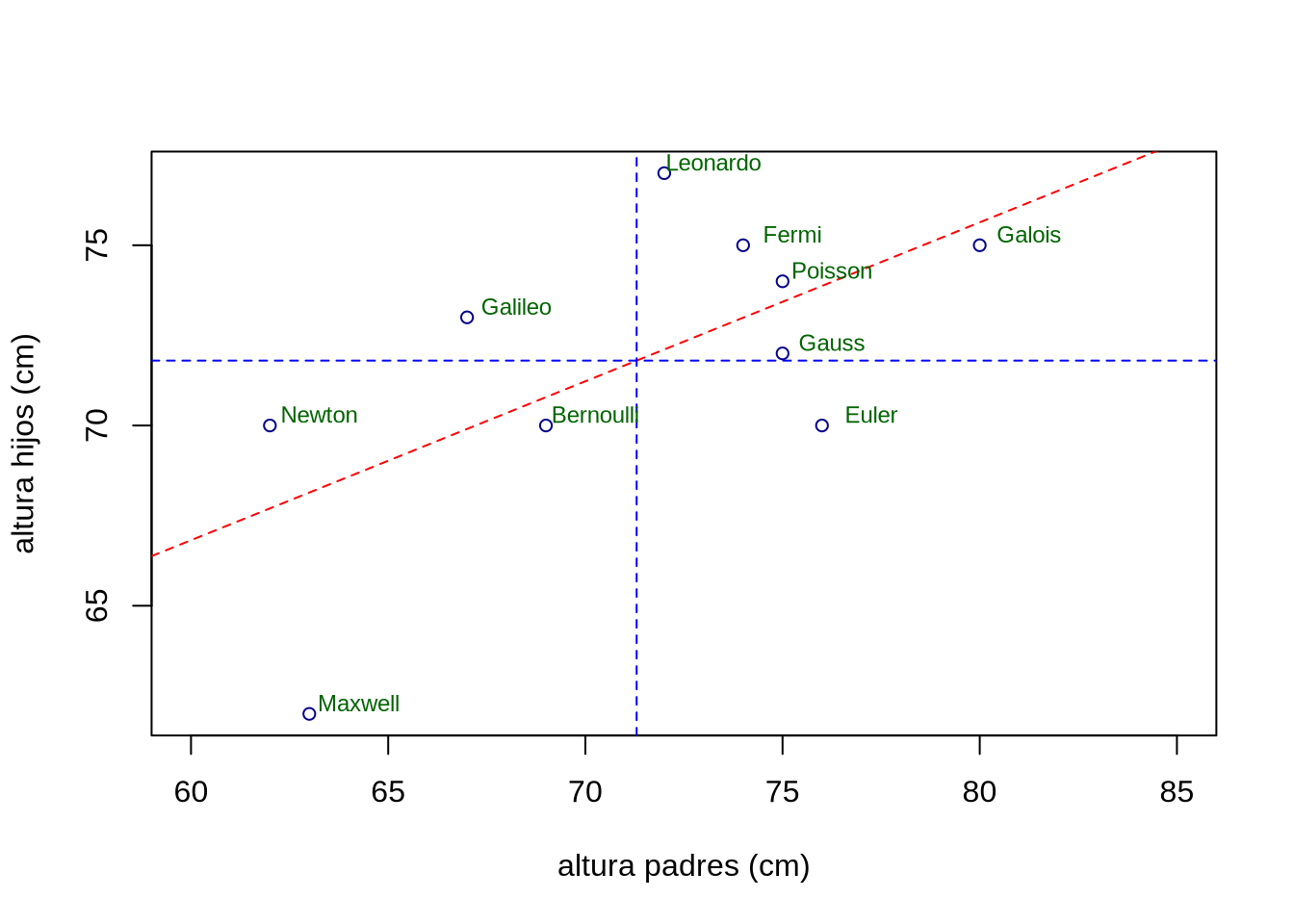
Figura 10.7: Regresión de los hijos en los padres para la altura a la cruz. Las medias fenotípicas de padres e hijos se corresponden con las líneas azules a trazos, mientras que la recta de regresión se marca en rojo.

La media de los padres es \(\bar x=71,3 \text{ cm}\), mientras que la media de hijos es \(\bar y=71,8 \text{ cm}\). Restando a los valores originales la correspondiente media, haciendo el cuadrado de los desvíos en padres y el producto cruzado de los desvíos, tenemos el siguiente cuadro

Padre	\((x_i-\bar x)\)	\((x_i-\bar x)^2\)	\((y_i-\bar y)\)	\((x_i-\bar x)(y_i-\bar y)\)
Euler	\(4,7\)	\(22,09\)	\(-1,39\)	\(-6,53\)
Leonardo	\(0,7\)	\(0,49\)	\(5,03\)	\(3,52\)
Galileo	\(-4,3\)	\(18,49\)	\(1,14\)	\(-4,89\)
Poisson	\(3,7\)	\(13,69\)	\(2,06\)	\(7,61\)
Galois	\(8,7\)	\(75,69\)	\(3,28\)	\(28,55\)
Maxwell	\(-8,3\)	\(68,89\)	\(-10,07\)	\(83,55\)
Newton	\(-9,3\)	\(86,49\)	\(-1,82\)	\(16,96\)
Bernoulli	\(-2,3\)	\(5,29\)	\(-1,31\)	\(3,02\)
Gauss	\(3,7\)	\(13,69\)	\(0,20\)	\(0,73\)
Fermi	\(2,7\)	\(7,29\)	\(2,89\)	\(7,79\)
\(\textbf{SUMA}\)
	\(0,0\)	\(312,1\)	\(0,0\)	\(140,3\)

Por lo tanto, usando estos valores en la ecuación del estimador OLS de la pendiente obtenemos

\[ \begin{split} {b_{HP}=\frac{\sum_{n=1}^N (x_i-\bar x)(y_i-\bar y)}{\sum_{n=1}^N (x_i-\bar x)^2}}=\frac{140,3 \text{ cm}^2}{312,1 \text{ cm}^2}=0,44954 \end{split} \]

Como \(\mathrm{\hat h^2=2\ b_{HP}}\), entonces \(\mathrm{\hat h^2}=2 \times 0,44954 \approx 0,899\). Como referencia, el proyecto Framingham Heart Study, sobre una cohorte de más de 5.000 pacientes (humanos) con distintas mediciones en padres e hijos arrojó una estimación de la heredabilidad de la altura (HT, por height) de \(h_{HT}^2=0,84 \pm 0,01\) (Byars et al. (2010)), por lo que no parece tan descabellado el valor obtenido en nuestra “prospección” ficticia en perros.

Regresión del valor fenotípico de los hijos sobre el fenotipo de ambos progenitores

En características que se expresan en ambos sexos, es posible pensar la regresión del fenotipo de los hijos (o su promedio) en el promedio del fenotipo de ambos progenitores. Esta alternativa a la regresión en uno de los progenitores tiene la ventaja de que contempla posibles sesgos en la elección de las parejas (por ejemplo, cuando individuos altos buscan parejas altas, o cuando apareamos toros grandes con vacas grandes y vacas chicas con toros chicos). Claramente, además de que la característica debe expresarse en ambos sexos, las medidas deben poder promediarse. Esto plantea un problema cuando existen diferencias notorias en la distribución de la característica entre sexos. Por ejemplo, en muchas características productivas como peso de vellón, ganancias diarias de peso, peso a determinada edad, etc. las diferencias entre sexos son notorias, tanto en medias, como en algunos casos la varianza de la característica. Una posibilidad es considerar los fenotipos como desvíos del grupo contemporáneo del mismo sexo. Otra alternativa es aplicar algún tipo de factores de corrección que ponga las dos distribuciones en plano de igualdad. Más general, podrían incluirse todos los factores a corregir necesarios en un modelo lineal y de esta forma obtener una estimación corregida simultaneamente para todos ellos.

La pendiente de la regresión del fenotipo de hijos (o su promedio, todas las parejas con el mismo número de hijos) en el promedio de los dos padres estará dada por

\[ \begin{split} {b_{H \bar P}=\frac{Cov_{H \bar P}}{V_{\bar P}}} \end{split} \tag{10.16} \]

Precisamos ahora entender a qué equivale la covarianza fenotípica entre hijos (o su promedio dentro de padres) y el promedio del fenotipo de los padres. Si \(x_1\) y \(x_2\) son los padres, mientras que \(y\) es un hijo de la pareja (o el promedio de los mismos), entonces

\[{Cov_{H\bar P}=Cov(\bar y,\frac{x_1+x_2}{2})=Cov(\bar y,\frac{x_1}{2})+Cov(\bar y,\frac{x_2}{2})=}\] \[{=\frac{1}{2}Cov(\bar y,x_1)+\frac{1}{2}Cov(\bar y,x_2)=Cov_{HP}}\ \therefore\] \[ \begin{split} {Cov_{H\bar P}=\frac{1}{2}V_A} \end{split} \tag{10.17} \]

Por otro lado, asumiendo que la varianza fenotípica en ambos sexos es igual, la varianza del promedio fenotípico de los padres será igual a

\[{V_{\bar P}=Var(\frac{x_1+x_2}{2})=Var(\frac{1}{2}(x_1+x_2))=\frac{1}{4}[Var(x_1)+Var(x_2)]=}\] \[ \begin{split} {=\frac{1}{4}[2\ Var(x)]=\frac{1}{4}[2\ V_P]=\frac{1}{2}V_P} \end{split} \tag{10.18} \]

Por lo tanto, sustituyendo los resultados de las ecuaciones (10.17) y (10.18) en (10.16), tenemos

\[ \begin{split} \mathrm{b_{H \bar P}=\frac{\frac{1}{2}V_A}{\frac{1}{2}V_P}=\frac{V_A}{V_P}=h^2} \end{split} \tag{10.19} \]

Por lo tanto, teniendo en cuenta este resultado, la pendiente de la regresión del fenotipo de los hijos en el promedio del fenotipo de los padres es igual a la heredabilidad, o en términos matemáticos \(\mathrm{b_{H \bar P}=\hat h^2}\).

Precisión en las estimaciones de heredabilidad: varianza del estimador

Previamente demostramos que la regresión de los valores genéticos aditivos en los fenotípicos es igual a la heredabilidad. También vimos que regresiones de los fenotipos de la progenie en fenotipos de los progenitores son funciones lineales simples de la heredabilidad. En particular, la pendiente de las rectas de regresión son las que acarrean significado respecto a la heredabilidad y por lo tanto conocer las distribución del estimador resulta fundamental para entender cómo varía y establecer límites para la inferencia. Es decir, si conocemos las propiedades distribucionales del estimador y en particular el primer y segundo momento (media y varianza), podemos establecer un intervalo de confianza para nuestras estimaciones de la pendiente y por lo tanto de la heredabilidad. En general, no tiene mucho sentido conocer un valor puntual de estimación de heredabilidad si no conocemos alguna medida de incertidumbre de este estimado que nos permita afirmarnos en su relevancia para nuestras proyecciones ulteriores. Claramente, no es lo mismo decir que un estimado de heredabilidad es de \(h^2=0,45 \pm 0,05\) (desvíos estándar) que \(h^2=0,45 \pm 0,20\): mientras en el segundo caso (considerando una distribución aproximadamente normal) con probabilidad cercana la \(95\%\) el “verdadero valor” de la heredabilidad podría estar entre \(0,05 < h^2 < 0,85\), en el primero el intervalo se reduce a \(0,35 < h^2 < 0,55\).

Una excelente introducción a este tema se encuentra en el libro Wooldrigde (2013), del que tomaremos prestada la notación inicial. Para encontrar estos momentos en el estimador de mínimos cuadrados ordinarios, partimos del modelo lineal corriente, es decir

\[ \begin{split} y_i=\beta_0+\beta_1\ x_i+e_i \end{split} \tag{10.20} \]

con \(e_i \sim N(0,\sigma_e^2)\). Antes de poder derivar la varianza del estimador de \(\beta_1\) (la pendiente de la recta), es decir \(\hat \beta_1\), vamos a demostrar un par de resultados accesorios. En primer lugar, vamos a demostrar que \(\sum_{i=1}^n(x_i-\bar x)(y_i-\bar y)=\sum_{i=1}^n (x_i-\bar x) y_i\), un resultado que puede parecer a primera vista contra-intuitivo. Sin embargo, si operamos con el lado izquierdo de la igualdad, tenemos

\[\sum_{i=1}^n(x_i-\bar x)(y_i-\bar y)=\sum_{i=1}^n x_i y_i-\bar x y_i +\bar x \bar y - x_i \bar y=\] \[\sum_{i=1}^n x_i y_i-\bar x y_i + \sum_{i=1}^n \bar x \bar y - x_i \bar y=\sum_{i=1}^n x_i y_i-\bar x y_i + n\bar x \bar y -\sum_{i=1}^n x_i \bar y=\] \[\sum_{i=1}^n x_i y_i-\bar x y_i + n\bar x \bar y - \bar y \sum_{i=1}^n x_i =\sum_{i=1}^n x_i y_i-\bar x y_i + n\bar x \bar y - \bar y (n \bar x)=\] \[\sum_{i=1}^n x_i y_i-\bar x y_i=\sum_{i=1}^n (x_i-\bar x) y_i\ \therefore\] \[ \begin{split} \sum_{i=1}^n(x_i-\bar x)(y_i-\bar y)=\sum_{i=1}^n (x_i-\bar x) y_i \end{split} \tag{10.21} \]

que es lo que queríamos demostrar. Pensándolo un poco mejor, no debería resultarnos extraño ni contraintuitivo ya que \(y_i-\bar y\) es lo mismo que desplazar los datos de la variable dependiente una cantidad fija, lo que alterará el intercepto, pero no la pendiente de la recta. A partir de esto, si aplicamos la igualdad de la ecuación (10.21) en el numerador de la definición clásica del estimador OLS (por “ordinary least squares”, o mínimos cuadrados ordinarios), tenemos que

\[ \begin{split} \hat \beta_1=\frac{\sum_{i=1}^n (x_i - \bar x)(y_i - \bar y)}{\sum_{i=1}^n (x_i - \bar x)^2}=\frac{\sum_{i=1}^n (x_i - \bar x)y_i}{\sum_{i=1}^n (x_i - \bar x)^2} \end{split} \tag{10.22} \]

Si por conveniencia usamos la notación siguiente:

\[ \begin{split} {STC_x}=\sum_{i=1}^n (x-\bar x)^2 \end{split} \tag{10.23} \]

entonces, sustituyendo \(y_i\) por \(\beta_0+\beta_1\ x_i+e_i\) (el lado derecho de la ecuación (10.20)), el estimador OLS de la pendiente de la recta puede escribirse como

\[ \begin{split} \hat \beta_1=\frac{\sum_{i=1}^n (x_i - \bar x)y_i}{STC_X}=\frac{\sum_{i=1}^n (x_i - \bar x)(\beta_0+\beta_1\ x_i+e_i)}{STC_X} \end{split} \tag{10.24} \]

Trabajemos ahora con el numerador de (10.24). Operando, tenemos

\[ \begin{split} \sum_{i=1}^n (x_i - \bar x)(\beta_0+\beta_1\ x_i+e_i)=\beta_0\ \sum_{i=1}^n (x_i - \bar x) + \beta_1\ \sum_{i=1}^n (x_i - \bar x) x_i + \sum_{i=1}^n (x_i - \bar x) e_i \end{split} \tag{10.25} \]

El resultado de la ecuación (10.25) puede parecer complejo, pero como \(\sum_{i=1}^n (x_i - \bar x)=(\sum_{i=1}^n x_i) -n \bar x=n \bar x-n \bar x=0\), entonces el primer término del lado derecho de la ecuación (10.25) es cero. Utilizando el resultado de la ecuación (10.21) y la definición de (10.23), el segundo término es igual a

\[ \begin{split} \beta_1\ \sum_{i=1}^n (x_i - \bar x) x_i=\beta_1\ \sum_{i=1}^n (x_i - \bar x)(x_i - \bar x)=\beta_1\ \sum_{i=1}^n (x_i - \bar x)^2=\beta_1 STC_X \end{split} \tag{10.26} \]

Si usamos la siguiente definición para simplificar la notación

\[ \begin{split} d_i=x_i-\bar x \end{split} \tag{10.27} \]

El numerador de la ecuación (10.24) queda

\[ \begin{split} \beta_1 STC_X + \sum_{i=1}^n d_i e_i \end{split} \tag{10.28} \]

por lo que sustituyendo esto por el numerador de la ecuación (10.24), tenemos ahora que

\[ \begin{split} \hat \beta_1=\frac{\beta_1 STC_X + \sum_{i=1}^n d_i e_i}{STC_X}=\beta_1+(1/STC_X)\sum_{i=1}^n d_i e_i \end{split} \tag{10.29} \]

que es nuestro segundo resultado previo. El resultado de la ecuación (10.29) nos indica que nuestro estimador de la pendiente de regresión será igual al “verdadero valor de la pendiente” (\(\beta_1\)), más un término aleatorio que es una combinación lineal de los errores. De hecho, esto nos permite demostrar fácilmente que condicional a la muestra (\(x_1,x_2,x_3...,x_n\)), \(\hat \beta_1\) es un estimador insesgado en OLS de \(\beta_1\):

\[{E(\hat \beta_1)}= {E(\beta_1+(1/STC_X)\sum_{i=1}^n d_i e_i)}=\beta_1+ {E((1/STC_X)\sum_{i=1}^n d_i e_i)}=\] \[ \begin{split} \beta_1+(1/STC_X)\sum_{i=1}^n {E(d_i e_i)}=\beta_1+(1/STC_X)\sum_{i=1}^n d_i {E(e_i)}=\beta_1+(1/STC_X)\sum_{i=1}^n d_i\ \cdot 0\ \therefore \\ {E(\hat \beta_1)}=\beta_1 \end{split} \tag{10.30} \]

También se puede demostrar que \(\hat \beta_0\) es un estimador insesgado de \(\beta_0\), pero eso carece de importancia para nosotros ya que por un lado el intercepto no tiene significación genética relevante en este contexto y por otro lado, en algunas regresiones al centrar la variable dependiente y la independiente, la recta debe pasar por el punto \((0,0)\) (el origen del sistema cartesiano de ejes).

Veamos ahora si podemos derivar una expresión para la varianza del estimador de la pendiente, es decir \(\hat \beta_1\). Si partimos de la ecuación (10.29)

\[ \begin{split} \hat \beta_1=\beta_1+(1/STC_X)\sum_{i=1}^n d_i e_i \end{split} \]

y teniendo en cuenta que \(\beta_1\) es constante (el “vardadero valor” de la pendiente), mientras que condicional en los valores \(x_i\), \(STC_X\) y \(d_i\) también lo son, entonces

\[ \begin{split} {Var}(\hat \beta_1)= {Var}(\beta_1+(1/STC_X)\sum_{i=1}^n d_i e_i)=(1/STC_X)^2 {Var}(\sum_{i=1}^n d_i e_i) \end{split} \tag{10.31} \]

Además, considerando que los \(e_i\) son realizaciones independientes de una variable aleatoria (o sea, la misma distribución, con varianza \(\sigma_e^2\)), entonces la varianza de la suma es igual a la suma de las varianzas y por lo tanto

\[{Var}(\hat \beta_1)=(1/STC_X)^2 \sum_{i=1}^n (d_i^2 {Var}(e_i))=(1/STC_X)^2 \sum_{i=1}^n (d_i^2 \sigma_e^2)=\] \[\sigma_e^2(1/STC_X)^2 \sum_{i=1}^n d_i^2=\sigma_e^2 (1/STC_X)^2 STC_X\ \therefore\] \[ \begin{split} {Var}(\hat \beta_1)=\frac{\sigma_e^2}{STC_X} \end{split} \tag{10.32} \]

Este último es un resultado fundamental para nosotros ya que venimos trabajando la heredabilidad como una regresión y por lo tanto necesitamos tener un estimador del error en nuestras estimaciones de heredabilidad.

---

Es momento de volver a la genética cuantitativa. Por comodidad, para simplificar la notación, a partir de acá definimos \(b \equiv \hat \beta_1\), es decir que llamaremos \(b\) a nuestro estimador de la pendiente. Más aún, ahora \(X\) e \(Y\) representan dos variables aleatorias, por ejemplo fenotipo de progenitores y fenotipos de progenie, y por lo tanto con varianzas \(\sigma_X^2\) y \(\sigma_Y^2\).

En primer lugar, dadas \(N\) observaciones, un estimador de la varianza en \(X\) a partir de las mismas es

\[ \begin{split} \hat \sigma_X^2=\frac{1}{N-2}\sum_{i=1}^n (x-\bar x)^2 \Leftrightarrow STC_X=\sigma_X^2 (N-2) \end{split} \tag{10.33} \]

Como vimos en la ecuación (10.32), utilizando la nueva notación, en OLS la varianza del estimador de la pendiente es

\[ \begin{split} {Var(b)}=\sigma_b^2=\frac{\sigma_e^2}{ {STC_X}} \end{split} \tag{10.34} \]

Por otro lado, en general es desconocida la varianza del error (el numerador de (10.34)), pero de acuerdo a nuestro modelo lineal

\[y_i=b\ x_i+e_i \Leftrightarrow e_i=y_i-b\ x_i\ \therefore\] \[{Var(e)}=\hat \sigma_e^2= {Var(y_i-b\ x_i)}=\sigma_Y^2- {Var(b\ x_i)}\ \therefore\] \[ \begin{split} \hat \sigma_e^2=\sigma_Y^2-b^2\sigma_X^2 \end{split} \tag{10.35} \]

Sustituyendo los resultados de las ecuaciones (10.33) y (10.35), condicional en el valor de \(b\), en la ecuación (10.34), tenemos

\[\sigma_b^2=\frac{\hat \sigma_e^2}{ {STC_X}}=\frac{\sigma_Y^2-b^2\sigma_X^2}{\sigma_X^2 (N-2)}\ \therefore\] \[ \begin{split} \sigma_b^2=\frac{1}{N-2}\left[\frac{\sigma_Y^2}{\sigma_X^2}-\frac{b^2 \sigma_X^2}{\sigma_X^2} \right] \end{split} \tag{10.36} \]

Finalmente, operando sobre (10.36), llegamos a una forma de la varianza del estimador de la pendiente de regresión que se presta para trabajarlo y sacar conclusiones.

\[ \begin{split} \sigma_b^2=\frac{1}{N-2}\left[\frac{\sigma_Y^2}{\sigma_X^2}-b^2\right] \end{split} \tag{10.37} \]

Un tema donde la ecuación (10.37) puede ser de relevancia es a la hora de diseñar experimentos para la estimación de la heredabilidad, buscando optimizar la combinación de progrenitores y progenie dadas determinadas capacidades experimentales (entendido esto como la varianza mínima del estimador). En ese sentido, Douglas S. Falconer (1983) plantea que asumiendo que \(b\) es por lo general pequeño, \(b^2\) lo es mucho más y por lo tanto, asumiendo además que \(N\) es grande, una aproximación razonable de la varianza del estimador sería

\[ \begin{split} \sigma_b^2 \approx \frac{1}{N}\frac{\sigma_Y^2}{\sigma_X^2} \end{split} \tag{10.37} \]

Para ser más específicos, supongamos que vamos a estimar la heredabilidad de una característica a partir de la regresión de \(n \geqslant1\) hijos para alguna combinación de \(k=1,2\) padres (por ejemplo, la media de \(n\) hijos para cada media de \(k\) padres) y que tenemos \(N\) pares de esas medidas. El total de de inviduos medidos será \(Nn\) progenies más \(kN\) progenitores (\(k=1\) si se mide uno solo, o \(k=2\) si se miden los dos), por lo que los totales de individuos medidos serán \(T=N(n+k)\). Por ejemplo, cuando se trata de la regresión de un hijo en uno de sus padres (asumiendo que las varianzas fenotípicas son iguales en ambos sexos), la varianza de los progenitores (\(\sigma_X^2\)) es igual a la varianza fenotípica \(\mathrm{V_P}\).

Por otro lado, (\(\sigma_Y^2\)) es igual a la varianza de las medias de familias de \(n\) individuos. Como demostraremos más adelante La reducción en la varianza fenotípica con varias medidas, la varianza de la media familiar es igual a

\[ \begin{split} \sigma_Y^2=\frac{1+(n-1)t}{n} {V_P} \end{split} \tag{10.38} \]

donde \(t\) es el coeficiente de correlación intraclase \(t=r_{A_{1}A_{2}}h^2\), es decir el parentesco aditivo entre miembros de la familia (\(r_{A_{1}A_{2}}\)) multiplicado por la heredabilidad. Ahora, sustituyendo \(\sigma_Y^2\) en la ecuación (10.37), tenemos

\[ \begin{split} \sigma_b^2 \approx \frac{1}{N}\frac{\frac{1+(n-1)t}{n} {V_P}}{ {V_P}}=\frac{1+(n-1)t}{nN} \end{split} \tag{10.39} \]

Más generalmente, en el caso del promedio de los dos progenitores, \(\sigma_X^2=\frac{ {V_P}}{k}\), con \(k=2\), por lo que de acuerdo a Douglas S. Falconer and Mackay (1996), la varianza del estimador será

\[ \begin{split} \sigma_b^2 \approx \frac{1}{N}\frac{\frac{1+(n-1)t}{n} {V_P}}{\frac{ {V_P}}{k}}=\frac{k[1+(n-1)t]}{Nn} \end{split} \tag{10.40} \]

En general \(t=r_{A_{1}A_{2}}h^2\) no se conoce de antemano ya que no conocemos la heredabilidad y \(t\) es función de la misma. Si pretendemos usar la varianza del estimador para planificar un experimento de forma óptima, variando el número y tamaños de las familias, habrá que suponer diferentes valores de la heredabilidad y ver qué ocurre bajo los diferentes supuestos.

PARA RECORDAR

• El valor de la pendiente de la recta de regresión del valor de cría (valor aditivo) en el fenotipo individual es igual a la heredabilidad (\(h^2\)) puesto que:

\(b_{AP}=\frac{ {Cov(A,P)}}{ {V_P}}= \frac{ {Cov(A,A)}+ {Cov(A,D)}+ {Cov(A,I)}+ {Cov(A,E)}}{ {V_P}}=\frac{ {Cov(A,A)}}{ {V_P}}=\frac{ {V_A}}{ {V_P}}=h^2\)

• Cuando predecimos el valor de cría a partir del valor fenotípico del individuo, la precisión es la raíz cuadrada de la heredabilidad (\(\sqrt{h^2}=h\)).

• Podemos describir la regresión del fenotipo de un hijo en el fenotipo de un progenitor como: \({b_{HP}=\frac{Cov_{HP}}{V_P}=\frac{Cov(y,x_1)}{V_P}}\) donde \(x_1\) y \(x_2\) a los progenitores y \(y\) a su progenie.

• Si además sabemos que la covarianza entre hijos y padres es: \({Cov_{HP}=\frac{1}{2}Cov(A_{x_1},A_{x_1})=\frac{1}{2}V_A}\) entonces \({b_{HP}=\frac{Cov_{HP}}{V_P}=\frac{\frac{1}{2}V_A}{V_P}=\frac{1}{2}\frac{V_A}{V_P}=\frac{1}{2} h^2}\) Por lo tanto, la pendiente de la regresión de los valores fenotípicos de una progenie en uno de sus progenitores igual a un medio de la heredabilidad.

• Para realizar la regresión del fenotipo de los hijos en el promedio del fenotipo de ambos progenitores, la característica de interés debe expresarse en ambos sexos además de que las medidas deben ser promediables. La pendiente de la regresión será: \(\mathrm{b_{H \bar P}=\frac{Cov_{H \bar P}}{V_{\bar P}}=\frac{\frac{1}{2}V_A}{\frac{1}{2}V_P}=\frac{V_A}{V_P}=h^2}\) por lo tanto la pendiente de la regresión del fenotipo de los hijos en el promedio del fenotipo de los padres es igual a la heredabilidad.

• La varianza del estimador de la pendiente de la regresión es: \({Var(b)}=\sigma_b^2=\frac{\sigma_e^2}{ {STC_X}}\)

10.2 Heredabilidad en sentido amplio y sentido estricto

En especies animales la clonación no es una realidad extendida, ni en la producción ni en el mejoramiento, pero en vegetales o en procariotas sí lo es. Los clones son individuos idénticos desde el punto de vista genético (al menos si ignoramos la epigenética) y por lo tanto comparten tanto los efectos aditivos de todos sus alelos como las interacciones entre los mismos, dentro de locus (efectos de dominancia) y entre loci (epistasis).

Supongamos que de una planta extraemos muchos clones y los mismos crecen en diferentes partes de un campo. Como todos tienen la misma base genética, las diferencias que podamos observar en las características se corresponden a diferencias en el ambiente. Por otra parte, si colocamos diferentes individuos de la especie (elegidos al azar, por ejemplo) en un ambiente extremadamente homogéneo, de laboratorio, prácticamente toda la varianza fenotípica será de origen genético ya que no existe varianza ambiental. Esto nos lleva a la posibilidad de definir un nuevo parámetro genético que tenga en cuenta la determinación genética de la característica. Llamamos heredabilidad en sentido amplio o coeficiente de determinación genética (y la notamos como \(H^2\)) a la proporción de la varianza fenotípica que se corresponde a los efectos genéticos, es decir

\[ \begin{split} {H^2}=\frac{ {V_G}}{ {V_P}}=\frac{ {V_A+V_D+V_I}}{ {V_A+V_D+V_I+V_E}} \end{split} \tag{10.41} \]

Como las varianzas son siempre mayores o iguales a cero, entonces \(\mathrm{H^2 \geqslant h^2}\). Es decir

\[{H^2=\frac{V_A+V_D+V_I}{V_A+V_D+V_I+V_E}=\frac{V_A}{V_A+V_D+V_I+V_E}+\frac{V_D+V_I}{V_A+V_D+V_I+V_E}}\ \therefore \] \[ \begin{split} {H^2=h^2+\frac{V_D+V_I}{V_A+V_D+V_I+V_E}} \end{split} \tag{10.42} \]

y como \(\mathrm{\frac{V_D+V_I}{V_A+V_D+V_I+V_E} \geqslant 0}\), entonces \(\mathrm{H^2 \geqslant h^2}\). Esto tiene mucho sentido intuitivo, ya que en el concepto de heredabilidad en sentido amplio tenemos en cuenta no solo los efectos aditivos de los alelos sino también los de sus combinaciones. En animales (incluido el ser humano) los gemelos monocigóticos son un buen ejemplo de individuos que comparten toda la genética ya que despreciando nuevamente la epigenética son idénticos desde el punto de vista genético.

Pero los gemelos no solo comparten la genética. Claramente, tanto los gemelos monocigóticos como los dicigóticos (también conocidos como mellizos) comparten ambiente en mucho mayor medida que el resto de los hermanos. Esto nos sugiere que comparando gemelos monocigóticos con dicigóticos y con otros hermanos enteros podríamos llegar a estimar la proporción de varianzas de interacción genética (dominancia y epistasis en conjunto). Desafortunadamente, existen algunas otras complicaciones metodológicas adicionales, así como la dificultad en encontrar suficiente número de casos, por lo que se trata de una técnica con alcance bastante limitado en animales.

En plantas resulta muy sencillo ver su utilidad, así como la forma de estimarla. Supongamos que, sin pérdida de generalidad, una característica de nuestro interés se encuentra determinada por 3 loci, sin ligamiento, con dos alelos en cada uno. Supongamos que llamamos a los dos alelos alternativos para los loci \(A\), \(B\) y \(C\), \(A_1\) y \(A_2\), \(B_1\) y \(B_2\), \(C_1\) y \(C_2\) respectivamente. En vegetales es relativamente sencillo obtener líneas puras (“inbred lines”, en inglés) sin comprometer demasiado la viabilidad de las mismas. Supongamos que para la característica de nuestro interés tenemos dos líneas puras que son contrastantes para los alelos de los loci con influencia en la característica. Es decir, llamaremos \(\mathbf{P_1}\) línea pura que tiene la configuración \(A_1A_1/B_1B_1/C_1C_1\) y \(\mathbf{P_2}\) a la línea con configuración genómica \(A_2A_2/B_2B_2/C_2C_2\). Claramente, el cruzamiento de ambas líneas será \(\mathbf{P_1} \times \mathbf{P_2}=\mathbf{F_1}\), cuyos individuos tendrán una configuración genómica idéntica en los loci de interés, es decir \(A_1A_2/B_1B_2/C_1C_2\).

Como en la \(\mathbf{F_1}\) todos los individuos son idénticos desde el punto de vista genético (al menos para los loci que tienen influencia en la característica), no existirá varianza de origen genético y toda la varianza fenotípica se puede adscribir a la varianza ambiental. Dicho de otra forma, como \(\mathrm{V_G=0}\), entonces \(\mathrm{V_P=V_G+V_E=0+V_E \therefore V_P=V_E}\). Por lo tanto, ya tenemos una estimación de la varianza ambiental. Ahora, si cruzamos entre sí a la \(\mathbf{F_1}\) tenemos \(\mathbf{F_1 \times F_1=F_2}\). Como asumimos que los loci no se encontraban ligados, entonces en cada uno de ellos alcanzaremos en una sola generación el equilibrio de Hardy-Weinberg con las proporciones \(\mathbf{1:2:1}\) (por ejemplo, de \(A_1A_1\), \(A_1A_2\) y \(A_2A_2\)). A su vez, los tres genotipos de cada uno de los 3 loci se combinarán al azar (porque al no estar ligados asumimos que se distribuyen en forma independiente desde el punto de vista estadístico), por lo que en la \(\mathbf{F_2}\) tendremos toda la varianza genética además de la ambiental. Si llamamos \(\mathbf{V_{P_{F1}}}\) a la varianza fenotípica observada en la \(\mathbf{F_1}\) y \(\mathbf{V_{P_{F2}}}\) a la varianza fenotípica observada en la \(\mathbf{F_2}\), entonces

\[ \begin{split} {V_E=V_{P_{F1}}}\\ {V_{P_{F2}}=V_G+V_E=V_G+V_{P_{F1}} \Leftrightarrow V_G=V_{P_{F2}}-V_{P_{F1}}} \end{split} \tag{10.43} \]

Por lo tanto, combinando los resultados de la ecuación (10.43) con la definición de heredabilidad en sentido amplio de la ecuación (10.41), tenemos que

\[ \begin{split} {\hat H^2=\frac{V_G}{V_P}=\frac{V_{P_{F2}}-V_{P_{F1}}}{V_{P_{F2}}}} \end{split} \tag{10.44} \]

sería nuestro estimador del coeficiente de determinación genética o heredabilidad en sentido amplio. En la práctica, las estimaciones de heredabilidad en plantas suelen ser más complicadas, ya que casi siempre el fenotipo correspondiente a un genotipo es alguna suerte de media. Además, las evaluaciones se realizan normalmente en múltiples ambientes y durante muchos años, involucrando en muchos casos diseños no-balanceados, por lo que se requieren métodos de estimación más complejos, algunos de los cuales comparten la metodología BLUP/BLUE de uso corriente en animales (ver por ejemplo Schmidt et al. (2019)).

Ejemplo 10.4

En un experimento para determinar la heredabilidad en sentido amplio del rendimiento en materia seca del maíz se cruzaron dos líneas puras contrastantes para rendimiento. En la \(\mathbf{F_1}\) se observó una varianza fenotípica de \(\mathrm{200\ dt^2 ha^{−2}}\), mientras que en la \(\mathbf{F_2}\) la varianza fenotípica observada fue de \(\mathrm{1200\ dt^2 ha^{−2}}\). Asumiendo que la característica se encuentra determinada por loci independientes, obtener un estimado de la heredabilidad en sentido amplio para la característica rendimiento de materia seca.

Usando la fórmula de la ecuación (10.44), un estimador de la heredabilidad lograda sería

\[ \begin{split} {\hat H^2=\frac{V_{P_{F2}}-V_{P_{F1}}}{V_{P_{F2}}}} \end{split} \]

por lo que sustituyendo los valores correspondientes tenemos

\[ \begin{split} {\hat H^2=\frac{[1200-200]\ dt^2 ha^{−2}}{1200\ dt^2 ha^{−2}}=\frac{1000}{1200}=0,833} \end{split} \]

PARA RECORDAR

• Llamamos heredabilidad en sentido amplio o coeficiente de determinación genética (y la notamos como \(H^2\)) a la proporción de la varianza fenotípica que se corresponde a los efectos genéticos: \({H^2}=\frac{ {V_G}}{ {V_P}}=\frac{ {V_A+V_D+V_I}}{ {V_A+V_D+V_I+V_E}}\)

• Dado que \(\mathrm{H^2=h^2+\frac{V_D+V_I}{V_A+V_D+V_I+V_E}}\) y que \(\mathrm{\frac{V_D+V_I}{V_A+V_D+V_I+V_E} \geqslant 0}\), entonces \(\mathrm{H^2 \geqslant h^2}\).

• El estimador de la heredabilidad en sentido amplio será: \({\hat H^2=\frac{V_G}{V_P}=\frac{V_{P_{F2}}-V_{P_{F1}}}{V_{P_{F2}}}}\)

10.3 Heredabilidad lograda

Una perspectiva diferente de la heredabilidad, estrechamente ligada a la selección direccional es la que se conoce como heredabilidad lograda o heredabilidad realizada. Si para una característica determinada, que supongamos tiene distribución normal con media \(\mu_0\), seleccionamos una proporción determinada de los mejores animales como progenitores de la siguiente generación, este grupo de animales seleccionados tendrá una media \(\mu_S\) diferente a la de la población. Por ejemplo, si mayores valores de la característica son favorables, es decir cuanto más a la derecha en la distribución mejor el valor, entonces los animales seleccionados tendrán una media \(\mu_S>\mu_0\). A la diferencia entre la media de los individuos seleccionados y la media de la población de la que estos forman parte le llamamos diferencial de selección y lo notamos con la letra \(S\), es decir \(S=\mu_S-\mu_0\).

En general, como el fenotipo está compuesto de aportes genéticos y ambientales, como vimos en el modelo genético básico, asumiendo que el ambiente en padres e hijos no se encuentra correlacionado, no toda la diferencia de los padres respecto a la media de su generación se transmitirá a los hijos. De hecho, lo único transmisible en esas condiciones son los efectos aditivos, por lo que la respuesta a la selección \(R\), será menor que la diferencia en la generación parental. Formalmente, la respuesta a la selección es \(R=\mu_1-\mu_0\), es decir la diferencia entre la media de la población luego de la selección respecto a antes de la selección. En la Figura 10.8 podemos observar una representación de esta situación. En el eje de las abscisas tenemos el diferencial de selección, obviamente en la generación parental, mientras que en el eje de las ordenadas observamos la respuesta a la selección \(R\). Claramente, la respuesta es menor que el diferencial, es decir \(R \leqslant S\). Si \(R=S\), entonces toda la diferencia en padres se observaría en hijos y el ángulo \(\alpha\) entre el eje de las abscisas y la recta con pendiente \(R/S\) sería de \(45^{\circ}\) ya que ambos catetos del triángulo rectángulo son iguales (\(R\) y \(S\)). Cuanto más pequeño es \(\alpha\) (más acostada está la recta roja), más pequeña es la respuesta \(R\) en proporción a \(S\), es decir menor es \(R/S\). Esto nos indica claramente que existe una asociación directa entre el ángulo \(\alpha\) y la relación \(R/S\).

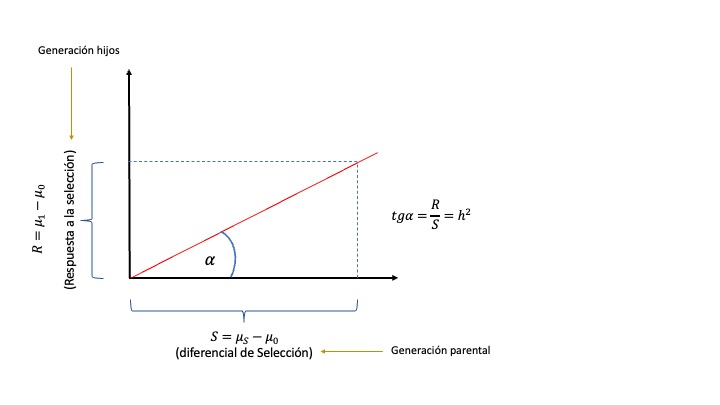
Figura 10.8: Representación gráfica de la heredabilidad lograda (o realizada). En el eje de las abscisas se marca el diferencial de selección (\(S=\mu_S-\mu_0\)) en la generación parental (la diferencia entre la media de los animales seleccionados y la media de la generación) mientras que en las ordenadas aparece la respuesta a la selección (\(R=\mu_1-\mu_0\)), es decir la diferencia entre la media de la nueva generación (\(\mu_1\)) y la generación anterior (\(\mu_0\)). La pendiente de la recta es igual a la tangente del ángulo que forma con la horizontal, es decir la relación \(tg \alpha=R/S=h^2\). Notar que el eje de las abscisas representa una diferencia en la generación parental, mientras que el de las ordenadas representa una diferencia en la generación de los hijos.

Pero como vimos más arriba, la relación \(R/S\) es la heredabilidad de la característica. Por lo tanto, como la pendiente de la recta con ángulo \(\alpha\) es igual a la tangente de dicho ángulo, es decir \(tg \alpha\), entonces

\[ \begin{split} {tg \alpha=\frac{\text{cateto opuesto}}{\text{cateto adyacente}}=\frac{R}{S}=\frac{\mu_1-\mu_0}{\mu_S-\mu_0}=h^2} \end{split} \tag{10.45} \]

Como de esta forma la heredabilidad queda definida como la relación entre la mejora lograda (\(R\)) y la mejora pretendida (\(S\)), a esta forma de estimarla se le conoce como heredabilidad lograda. En general, las variaciones ambientales entre diferentes generaciones pueden introducir cambios relativamente importantes en las estimaciones de generación en generación. Más aún, las estimaciones sucesivas pueden seguir cierta tendencia que se aparte de una recta, por ejemplo a causa de una disminución sostenida de la varianza aditiva debida al proceso de selección. Por esta razón se suele repetir el proceso durante varias generaciones. Esto puede llevar a la necesidad de tiempos enormes si el intervalo generacional de la especie es grande, como ocurre en general en muchas especies de animales grandes.

En un artículo muy interesante, Hill (1972) discute diferentes alternativas para estimar la heredabilidad a partir del concepto de heredabilidad lograda. Uno de los métodos más simples es el propuesto por Douglas S. Falconer (1960), que consiste en la regresión de la respuesta acumulada en el diferencial de selección acumulado. La idea es bien sencilla y la representamos en la Figura 10.9: en cada generación de selección vamos a obtener un diferencial de selección y una respuesta a la selección, por lo que vamos acumulando las dos variables (sumando cada nuevo valor al acumulado anterior) durante el número de generaciones que deseamos. Si bien las variaciones entre generaciones son notorias en la figura (pendientes de los segmentos de recta de color negro, entre puntos), la tendencia lineal general (considerando todos los puntos) es claramente estable y consistente.

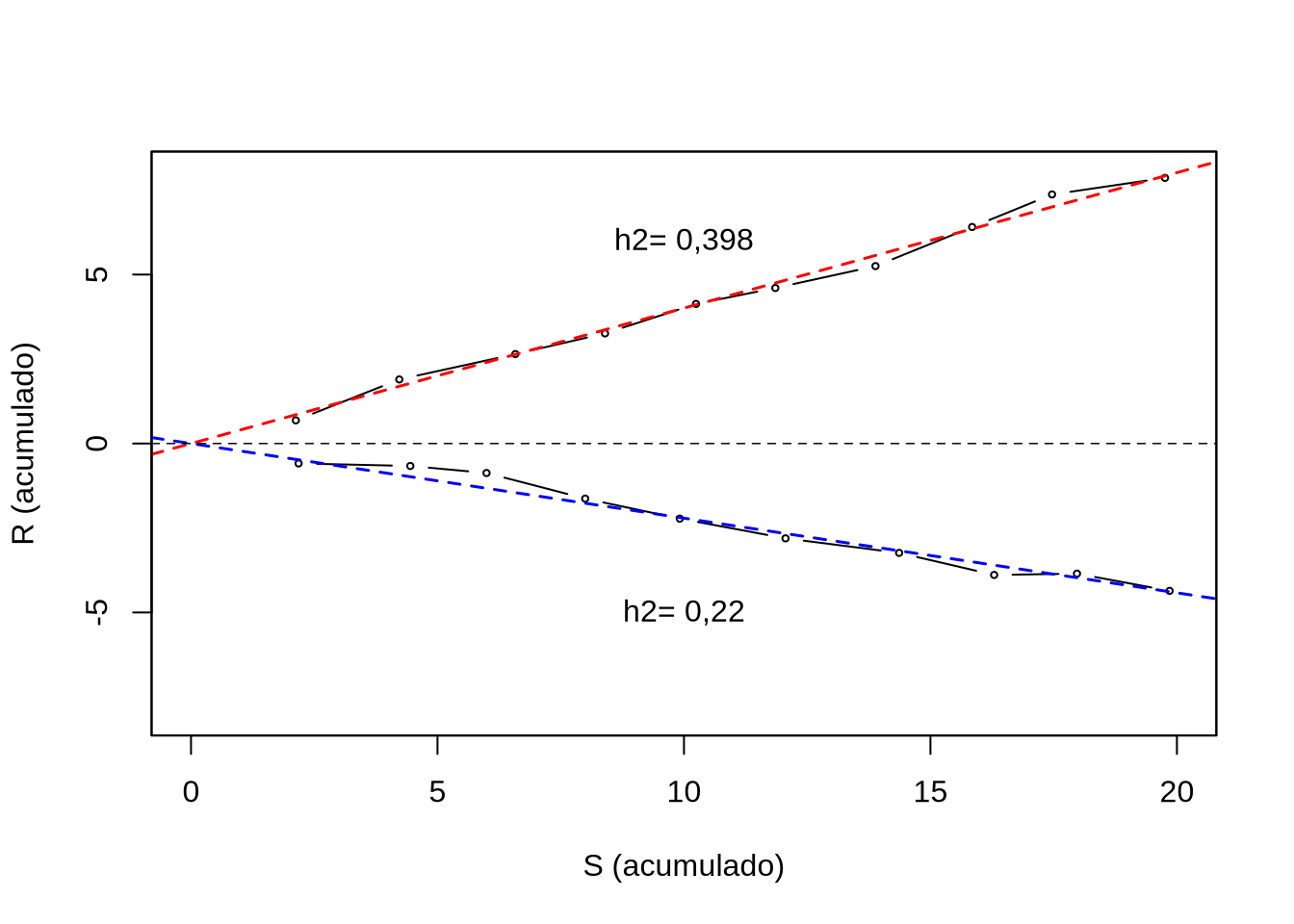
Figura 10.9: Estimación de la heredabilidad lograda a partir del diferencial de selección acumulado y de la correspondiente respuesta a la selección. A cada generación agregamos un nuevo punto como el diferencial de selección agregado al anterior (en las abscisas) y lo mismo para la respuesta a la selección (en las ordenadas). Se realiza selección simultánea en sentidos opuestos. Conectando los puntos (negros) tenemos las líneas quebradas (en negro), que representan la variación entre generaciones de la relación \(R/S\). Con el conjunto de puntos se puede hacer un ajuste por mínimos cuadrados (incrementando la característica, línea roja a trazos, decrementando la característica, línea azul a trazos) o directamente calcular la relación \(\mathrm{\hat h^2=tg \alpha=\frac{R_{acum}}{S_{acum}}}\). A fin de poder representar la divergencia en el gráfico, para la línea descendente se gráfica el valor opuesto del diferencial de selección (o sea, \(-S\)).

Un fenómeno interesante que ocurre en ciertas características y poblaciones es la asimetría en la respuesta a la selección cuando hacemos selección en direcciones opuestas. Una representación gráfica de este fenómeno se puede ver en la Figura 10.9 donde la selección apuntando a disminuir el valor de la característica (línea de regresión azul) tiene diferente valor absoluto de la pendiente (por un tema de representación gráfica, para la línea descendiente graficamos la respuesta en función de \(-S\)). Douglas S. Falconer (1983) presenta un ejemplo extraído de un trabajo propio presentado en 1954 en el que realizó selección divergente para el peso a las 6 semanas durante 21 (descendente) y 28 (ascendente) generaciones. Los estimados de heredabilidad que obtuvo fueron de \(\hat h_A^2=0,175 \pm 0,0161\) para la línea ascendente, mientras que fue \(\hat h_D^2=0,518 \pm 0,0231\) para la descendente. Es decir en el caso del peso a las 6 semanas en ratones la respuesta a la selección para disminuir el peso fue mucho más efectiva que para aumentarlo.

Esto plantea alguna interrogantes y nos sugiere precaución a la hora de interpretar estos resultados. En primer lugar, suponemos que se trata de la misma característica desde el punto de vista genético la que movemos hacia arriba o hacia abajo. En ese caso, surge a primera vista una contradicción con la definición de heredabilidad como relación entre la varianza aditiva y la fenotípica ya que, al menos al comienzo del experimento, las mismas son iguales sin importar la dirección de selección. Una alternativa es considerar el promedio de las dos heredabilidades obtenidas, como una forma de suavizar las diferencias, pero sin demasiado soporte teórico. Otra alternativa es considerar la heredabilidad lograda en el sentido de nuestro interés. Por ejemplo, si queremos disminuir el peso al nacimiento de los terneros, aunque sea interesante conocer el estimado de la heredabilidad de aumentar el peso al nacimiento, mucho más útil sería el estimado de disminuir el peso. Aún en el caso de estudiar el comportamiento bajo selección en una dirección suele ser importante incluir una línea de control, es decir animales que no experimentan selección direccional a fin de controlar que no existan otros factores ambientales (como la dieta) que interfieran en los resultados.

Si bien el fenómeno de la asimetría en la respuesta a la selección se ha observado regularmente, las causas de la asimetría no son del todo claras. Douglas S. Falconer (1983) postula las siguientes:

1. Diferencial de selección que difiera entre las líneas ascendente y descendente por diferentes razones, entre ellas la coincidencia del sentido de selección natural y artificial, fertilidad incrementada en una dirección y el cambio de la varianza con la media que permitiría mayor diferencial a mayor varianza.

2. La “asimetría genética” producto de la distribución de los efectos de dominancia en un sentido (por ejemplo, hacia arriba) por los que a frecuencias intermedias de los alelos llevaría a respuestas mayores en el sentido en que los alelos tienden a ser recesivos.

3. La selección para los heterocigotas, cuando la selección en una dirección favorece a los heterocigotas en muchos loci o en pocos de gran efecto, a medida que nos acercamos a la frecuencia de equilibrio la respuesta es cada vez más lenta, mientras que alejándonos en dirección opuesta del “óptimo” avanzamos muhco más rápido hacia la fijación de alelos.

4. La depresión endogámica (algo que veremos en profundidad en otros capítulos), ya que la mayor parte de las poblaciones experimentales son pequeñas. Si existe depresión endogámica en la característica, la misma disminuirá la respuesta en un sentido y la incrementará en el otro.

5. Los efectos maternos. En algunas características como el peso de los ratones a las 6 semanas existen dos componentes, uno atribuible al ratón (el crecimiento desde el destete) y el otro casi totalmente materno (el peso al destete). Mientras que de acuerdo a Falconer no existieron diferencias en la heredabilidad de crecimiento, las diferencias se atribuyeron al peso al destete, lo que nos lleva a que la asimetría en peso a las 6 semanas refleja la asimetría en la “habilidad materna”.

Si bien este método de estimar la varianza de una característica no es usual en poblaciones animales de interés comercial, el mismo sigue siendo válido para explorar la arquitectura genética de varias características y sigue siendo motivo de investigación metodológica (ver por ejemplo Lstibůrek et al. (2018)).

Finalmente, como anticipación a lo que veremos en próximos capítulos, si manipulamos la definición de heredabilidad lograda tenemos que

\[ {\frac{R}{S}=h^2 \Leftrightarrow R=S\ h^2} \]

que se conoce como la ecuación del criador y es una de las piedras fundamentales del mejoramiento genético.

Ejemplo 10.5

Para estudiar la posibilidad de mejorar la producción de lana verde natural se condujo un estudio sobre la población original, separándola en mitades, una mitad bajo las condiciones normales de crecimiento y reproducción, la otra sujeta a selección direccional para aumentar la producción de lana. El cuadro siguiente contiene los resultados del experimento mantenido durante 7 generaciones parentales, en el cual se seleccionaron los animales reproductores basados en el peso sucio del segundo vellón (corrigiendo previamente por diferencias entre sexos). La pendiente de la regresión de acumulados para la línea control fue de cero.

\(\textbf{Generación parental}\)	\(\textbf{Diferencial selección}\) (\(S\), g)	\(\textbf{Respuesta a la selección}\) (\(R\), g)
\(0\)	\(715\)	\(475\)
\(1\)	\(770\)	\(485\)
\(2\)	\(745\)	\(410\)
\(3\)	\(815\)	\(405\)
\(4\)	\(790\)	\(375\)
\(5\)	\(766\)	\(395\)
\(6\)	\(825\)	\(325\)
\(\textbf{TOTAL}\)	\(5426\)	\(2870\)

Graficar la respuesta a la selección acumulada, el diferencial de selección acumulado, calcular la pendiente de la línea de regresión y graficarla. ¿Cuánto vale la heredabilidad estimada para esta característica? ¿Qué podría representar que el intercepto sea distinto de cero? ¿Es razonable el supuesto de linealidad de los acumulados? ¿Qué podría estar indicando la forma de la curva de datos reales?

Para resolverlo primero calculamos los acumulados, básicamente sumando todos los datos correspondientes hasta cada punto, lo que nos deja con el siguiente cuadro

\(\textbf{Gener.}\)	\(\textbf{Dif. sel. acum. }(\sum_{i=0} S_i\), g)	\(\textbf{Respuesta acum. }(\sum_{i=0} R_i\), g)
\(0\)	\(715\)	\(475\)
\(1\)	\(1485\)	\(960\)
\(2\)	\(2230\)	\(1370\)
\(3\)	\(3045\)	\(1775\)
\(4\)	\(3835\)	\(2150\)
\(5\)	\(4601\)	\(2545\)
\(6\)	\(5426\)	\(2870\)

La pendiente de la recta la calculamos a partir de los datos acumulados como

\[ \begin{split} {b=\frac{Cov(S_{acum},R_{acum})}{Var(S_{acum})}=\frac{1455487\text{ g}^2}{2873509\text{ g}^2}=0,50652} \end{split} \]

La gráfica de los resultados aparece en la Figura 10.10. Como la pendiente de la recta de regresión es nuestro estimado de heredabilidad, entonces tenemos que \(\mathrm{\hat h^2=b=0,50652}\). Claramente, en la gráfica siguiente se aprecia que el intercepto es distinto de cero. Asumiendo que la pendiente de regresión de la línea control fue de cero (como dice la letra), entonces no es de esperar que existan variaciones sistemáticas en el peso de vellón que no se deban a la selección, por lo que en principio descartaríamos ese factor. Al mirar el ajuste de la recta de regresión a los puntos podemos notar un leve pero consistente apartamiento hacia abajo de los puntos en los extremos. Eso pone en duda la linealidad de la curva y puede explicar el intercepto distinto de cero. Más aún, la forma de la curva real parece comenzar una tendencia hacia la horizontal a medida de que pasan las generaciones, es decir una reducción sostenida en la respuesta a la selección, lo que podría indicar problemas futuros para seguir por este camino (algo que discutiremos más adelante, en próximos capítulos).

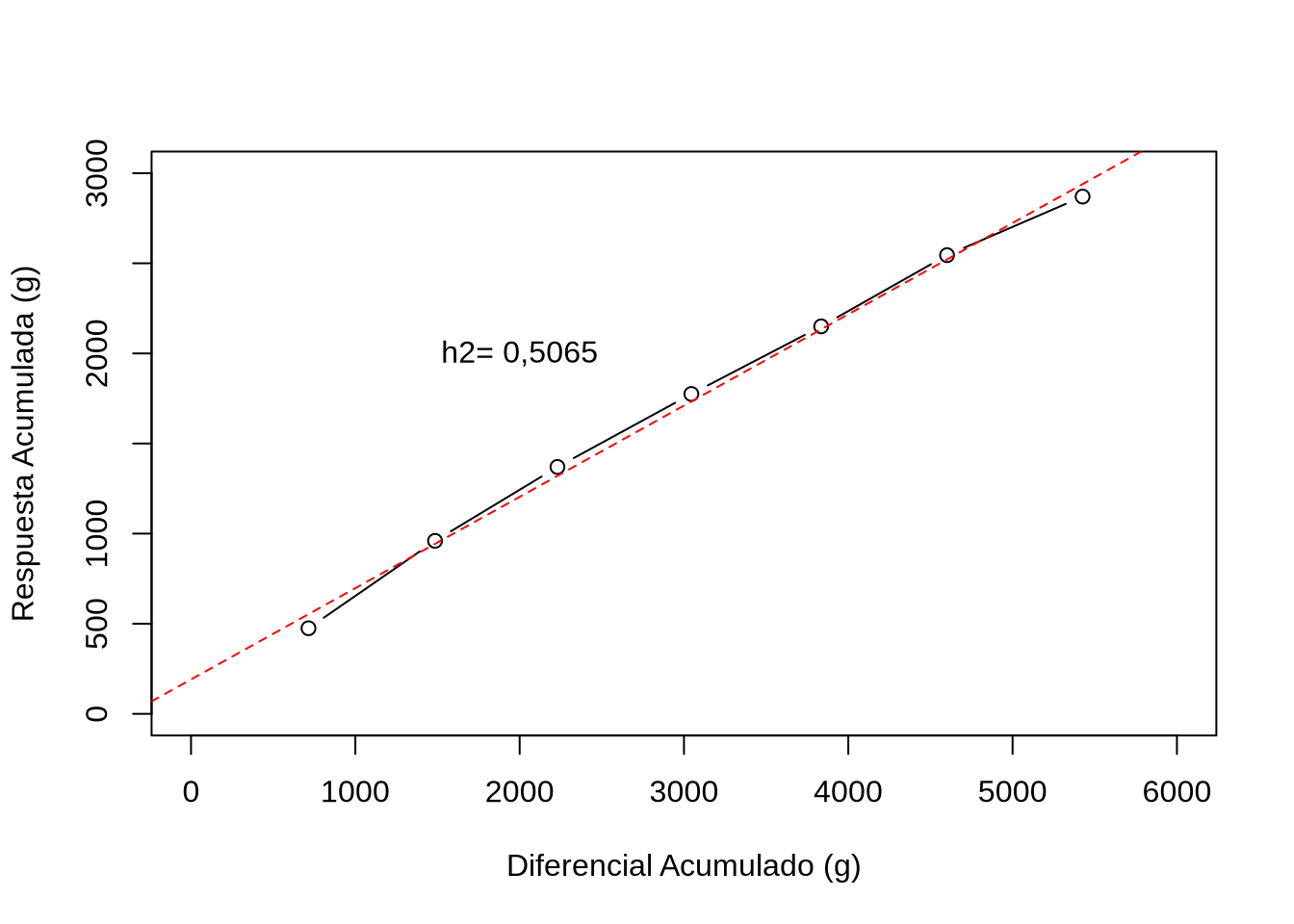
Figura 10.10: Estimación de la heredabilidad del peso de vellón (verde) sucio en ovejas verdes a través de la heredabilidad lograda. La línea roja a trazos representa la recta de regresión obtenida por mínimos cuadrados ordinarios.

PARA RECORDAR

• Llamaremos diferencial de selección (\(S\)) a la diferencia entre la media de los individuos seleccionados y la media de la población de la que estos forman parte, es decir \(S=\mu_S-\mu_0\).

• Llamaremos respuesta a la selección (\(R\)) a la diferencia entre la media de la población luego de la selección respecto a antes de la selección, es decir \(R=\mu_1-\mu_0\).

• La heredabilidad lograda queda definida como la relación entre la mejora lograda (\(R\)) y la mejora pretendida (\(S\)). Alternativamente, podemos pensar en la misma como la regresión de la respuesta acumulada en el diferencial de selección acumulado.

• Manipulando esta última definición llegamos a que \(R= S h^2\) conocida como la ecuación del criador.

10.4 Heredabilidad en poblaciones agronómicas/lab. vs poblaciones naturales

Las estimaciones de heredabilidad son fundamentales, tanto para los programas de mejoramiento genético en plantas y animales, así como para el estudio de la evolución a corto y mediano de características cuantitativas en poblaciones naturales.

Las condiciones para las estimaciones de heredabilidad deben condecirse con el uso pretendido de la misma. Sin duda, en condiciones de laboratorio o aún a campo, pero con condiciones ambientales sumamente controladas producirán por lo general estimados más altos que en condiciones naturales o sin ambientes controlados. La razón de esto es sencilla, ya que el denominador de la heredabilidad es la varianza fenotípica, uno de cuyos componentes es la varianza ambiental; en la medida de que la varianza ambiental es menor, menor será el denominador y por lo tanto mayor el cociente \(\mathrm{h^2=\frac{V_A}{V_P}}\). Sin embargo, pretender basar un programa de mejora de una raza que mayormente presenta condiciones de expresión de la característica en ambientes sumamente variables a partir de las estimaciones realizadas en condiciones controladas es la receta ideal para el fracaso, o al menos para obtener logros mucho menores de los planificados. Sin embargo, para intentar entender la arquitectura genética de la característica o para imaginar el potencial evolutivo a corto y mediano plazo de una característica, posiblemente sea mejor idea obtener estimaciones en condiciones de laboratorio o muy controladas.

Por estas razones, los métodos y condiciones de estimación de la heredabilidad deben poder representar el uso pretendido. Además, bajo condiciones de selección moderada a fuerte, tanto la varianza genética como la fenotípica es posible que cambien, lo que implica cambios en los estimados de la heredabilidad. Esto lleva a la necesidad de estimar los parámetros genéticos en forma regular, particularmente en los programas de mejoramiento genético de especies o razas con bajo número de participantes en las evaluaciones, dada la inestabilidad que introduce el bajo número de animales y registros.

En las subsecciones siguientes veremos algunos ejemplos locales en animales domésticos y plantas, pero un recurso interesante es la base de datos \({H^2DB}\), donde podemos escoger la especie de nuestro interés o el tipo de característica y obtener distintas estimaciones, la fuente de las mismas, así como diferentes gráficos que representan los resultados.

Estimaciones de heredabilidad en animales domésticos

La estimación de la heredabilidad de una característica suele ser fundamental a la hora de diseñar un programa de mejoramiento genético, o aún de entender la capacidad de evolucionar en una dirección de la misma. Por esta razón, una parte importante del trabajo de los genetistas y mejoradores suele ser la estimación de la heredabilidad en las condiciones lo más parecidas posible a las condiciones en las que se va a utilizar la estimación. Dicho de otra forma, no tiene mucho sentido obtener una estimación de la heredabilidad en condiciones de laboratorio para luego diseñar un programa de mejoramiento a campo. Resulta obvio que las estimaciones de laboratorio serán más precisas y seguramente más altas que las realizadas a campo, pero como el programa de mejoramiento involucra condiciones menos controladas los resultados obtenidos del programa de mejora no tendrán mucho que ver con nuestras expectativas. El contenido de esta sección no pretende ser una revisión de valores de heredabilidad de algunas características sino simplemente un motivador de las discusión de diferentes características de este parámetro genético tan importante.

Las estimaciones de heredabilidad en animales domésticos se pueden obtener de diferentes formas. Por un lado, como vimos en el capítulo Parentesco y Semejanza entre Parientes, a partir de diferentes diseños experimentales es posible realizar estimaciones de la varianza aditiva, mientras que la varianza fenotípica se puede estimar directamente a partir de los datos, por lo que el cociente de ambos nos da una estimación de la heredabilidad (\(h^2= {V_A/V_P}\)). Cada uno de estos diseños tiene sus ventajas y desventajas, pero algo común a todos ellos es que usualmente implican tener un gran número de animales controlados bajo condiciones similares. Por ejemplo, si pensamos en un diseño de medios hermanos, por cada padre que incluimos en el diseño debemos mantener varios hijos o hijas posteriormente. Como, a su vez, debemos incluir varios padres para obtener estimaciones razonables y que la muestra de machos sea representativa de los animales en la población, el número de animales a mantener en el experimento es necesariamente alto. Más aún, como vimos previamente, existen tensiones entre las propiedades deseables de los estimadores que se pueden obtener en los distintos diseños experimentales para estimar la varianza aditiva. En el caso de medios hermanos teníamos que la covarianza era igual a \(\frac{1}{4} {V_A}\), por lo que era necesario multiplicar por 4 para tener un estimador insesgado, lo que inflaba el error de la estimación en la misma proporción y subsecuentemente la estimación de la heredabilidad. Por otra parte, el estimador que surgía de usar una estructura de hermanos enteros era producto de multiplicar la covarianza entre hermanos enteros por 2, pero con la consecuencia de estar incluyendo en este estimador también una parte de la varianza de dominancia y aún la del ambiente común. Es decir, nuestro estimador de la heredabilidad a partir del diseño de hermanos enteros será

\[ \begin{split} \hat{h}^2=\frac{ {2\ Cov_{P_{HE}}}}{ {V_P}}=\frac{\sigma^{2}_A+\frac{1}{2}\ \sigma^{2}_D +2\ \sigma^{2}_{EC}}{ {V_P}}=\frac{\sigma^{2}_A}{ {V_P}}+\frac{\frac{1}{2}\ \sigma^{2}_D +2\ \sigma^{2}_{EC}}{ {V_P}}=h^2+\frac{\frac{1}{2}\ \sigma^{2}_D +2\ \sigma^{2}_{EC}}{ {V_P}} \end{split} \]

lo que claramente sesga el estimador hacia arriba pues el término \(\frac{\frac{1}{2}\ \sigma^{2}_D +2\ \sigma^{2}_{EC}}{ {V_P}}\) es en general mayor a cero (es una relación de varianzas, por lo que al menos no debería ser negativo).

En vista de estas dificultades para la estimación a través de experimentos, como veremos más adelante en el curso y seguramente profundizarás en cursos siguientes, la forma corriente de hacerlo es mediante modelos estadísticos más elaborados que pemiten incluir toda la información disponible de la estructura de parentesco entre todos los animales (los modelos mixtos lineales o aún los modelos mixtos lineales generalizables). Esta información se encuentra usualmente codificada en la matriz de parentesco, como vimos en el capítulo previo y por lo tanto puedo realizar las estimaciones a partir de todos los animales que tengan registros y sus parientes aún sin registros. De esta forma, el número de observaciones que puedo incorporar a la estimación de la heredabilidad se incrementa notoriamente (por ejemplo, todos los animales en una evaluación) y por lo tanto se incrementa también la precisión de la estimación. Además, bajo ciertas condiciones, los estimadores obtenidos cumplen con varias de las propiedades deseables de los estimadores.

En el cuadro siguiente se pueden apreciar estimaciones de heredabilidad para distintas características, en diferentes especies y razas dentro de las mismas, todas a partir de registros obtenidos en Uruguay. Por un lado, es fácil de apreciar que mientras que algunas características presentan heredabilidades bajas, como el intervalo destete-concepción en cerdos, o como el intervalo interpartos en bovinos de leche (raza Holando en este caso), otras características poseen heredabilidades muy altas, como el diámetro de fibras en ovejas de la raza Merino Australiano. Claramente, las características que tienen una base genética compleja (donde lo aditivo no es tan importante), un ambiente extremadamente variable o interacciones entre genotipo y ambiente llevarán a menores estimaciones de la heredabilidad. Esto, a veces se confunde con el concepto de que baja heredabilidad es sinónimo de casi inexistencia de varianza aditiva (ya que es el numerador de la heredabilidad), pero esto es totalmente erróneo, como ya discutimos previamente. A la misma varianza aditiva de una característica, reducir el resto de los componentes de varianza, controlando el “ambiente” por ejemplo, llevará a un incremento concomitante en la heredabilidad. Dicho de otra forma, la baja heredabilidad de una característica está muchas veces asociada a la forma en que se registran los datos fenotípicos de la misma o a la definición imprecisa de lo que queremos medir (por ejemplo, en características reproductivas, difíciles de medir).

Por otro lado, aún en la misma característica y muy bien definida, como por ejemplo diámetro de fibras en ovinos, las estimaciones de heredabilidad pueden presentar diferencias muy importantes. Por ejemplo, se aprecia en el cuadro las diferencias entre la estimaciones para esta característica en las razas Corriedale (\(h^2=0,43\pm0,08\)) y Merino Australiano (\(h^2=0,82\pm ?\)). Si bien las razas podrían presentar diferencias notorias como las vistas, producto de diferentes bases genéticas en la característica (algo improbable) o de diferencias en la varianza genética existente (producto de la selección, por ejemplo), la causa que aparece como más probable acá tiene que ver con las condiciones en las que se realizaron las mediciones y el número de animales usados. Por otro lado, el trabajo de Ciappesoni et al. (2011) no reporta la incertidumbre de las estimaciones, por lo que resulta difícil comparar las distribuciones de las mismas. Esto resalta la importancia de las estimaciones de incertidumbre, ya que un valor puntual sin tener referencia de la distribución (dispersión, por ejemplo) no nos permite trabajar en forma confiable: no es lo mismo una heredabilidad de \(h^2=0,500\pm0,025\) (desvío estándar) que \(h^2=0,500\pm0,250\); en el primer caso (asumiendo una distribución normal) el valor posible del parámetro con un \(95\%\) de confianza será aproximadamente \(0,450 \leqslant h^2 \leqslant 0,550\), mientras que en el segundo será \(0,000 \leqslant h^2 \leqslant 1,000\) (es decir, casi no informativo).

(#tab:datosh2_html)(#tab:datosh2_html)Heredabilidades para diferentes características en especies de animales domésticos, así como las correspondientes estimaciones de incertidumbre (“EE”=error estándar,“SD”=desvío estándar).

Raza	Característica	Año	h2	Incertidumbre	Tipo	Cita
Cerdos
Población multiracial	Número de lechones nacidos vivos	2015	0,13	0,06	EE	1
	Peso vivo del lechón al nacimiento		0,31	0,08		1
	Número de lechones destetados		0,14	0,06		1
	Peso vivo del lechón al destete		0,17	0,02		1
	Sobrevivencia durante la lactancia		0,10	0,01		1
	Intervalo destete-concepción		0,08	0,03		1
Ovinos
Corriedale	Peso de vellón limpio	2016	0,42	0,09	SD	2
	Diámetro de fibra		0,43	0,08		2
	Presencia / Ausencia fibras meduladas		0,37	0,10		2
	Presencia / Ausencia fibras Kemp		0,63	0,09		2
	Presencia / Ausencia fibras pigmentadas		0,35	0,08		2
	HPG1 (ln)	2008	0,15			3
	HPG2 (ln)		0,28			3
Merino Australiano	Resistencia a PGI en corderos (medida como HPG)	2012	0,25	0,03	SD	4
	Resistencia a PGI en ovejas periparturientas (medida como HPG)		0,08	0,03		4
	Peso de vellón limpio en borregos	2011	0,39			5
	Diámetro de fibra en borregos		0,67			5
	Peso de cuerpo en borregos		0,62			5
	Peso de vellón limpio en ovejas		0,38			5
	Diámetro de fibra en ovejas		0,82			5
	Peso de cuerpo en ovejas		0,58			5
Bovinos de leche
Holando	Intervalo interparto	2012	0,07			6
	Producción de leche		0,3			6
	Días abiertos	2016	0,05			7
	Producción de leche		0,23			7
	Producción de grasa		0,21			7
	Producción de proteína		0,21			7

Cita: \(^1\) Bell et al. (2015), \(^2\) Sánchez et al. (2016), \(^3\) Castells Montes (2008), \(^4\) Goldberg, Ciappesoni, and Aguilar (2012), \(^5\) Ciappesoni et al. (2011), \(^6\) Frioni (2012), \(^7\) Frioni (2016).

En algunos casos las características a mejorar son un poco más complejas y difíciles de especificar. En el cuadro siguiente aparecen algunas estimaciones de heredabilidad en caballos de competencia, en particular en competencias de resistencia (750 Km en 15 días de competencia) en nuestro país. En primer lugar, en el caso de carreras de este tipo, si bien la ubicación en el ranking y el tiempo total empleado parecen tener una parte importante de su base genética en común, no necesariamente la misma es total. Más aún, ambas características tienen distribuciones completamente diferentes, por lo que los modelos bajo los que se estima la heredabilidad no tienen por que ser necesariamente equivalentes. Por esta razón es usual ensayar diferentes modelos y reportar los estimados para cada uno de ellos. En el cuadro siguiente, dado de que López-Correa (2013) reportan varios resultados diferentes para diferentes modelos, nosotros aprovechamos esto para mostrar que en algunos casos las estimaciones son consistentes entre modelos (lo que aparece en el cuadro es el intervalo de las medias de los distintos modelos).

Variable	Especie/raza	\(h^2\)	Autor
\(\textbf{Competencias de resistencia (750 km/15días)}\)
Ranking	Caballos/Criollo	\(0,156(0,051–0,273)\)	\(^1\)
Tiempo final	Caballos/Criollo	\(0,10-0,13\)	\(^2\)
Ranking	Caballos/Criollo	\(0,07-0,10\)	\(^2\)

\(^1\) (López-Correa et al. 2018) \(^2\) (López-Correa 2013) (intervalo de medias en los distintos modelos ensayados).

En otros casos las características a mejorar se encuentran “mal medidas” (en el sentido de poca precisión) o no hay forma razonable de medir directamente lo que deseamos mejorar. Usualmente es el caso de las características reproductivas, donde el conjunto de los procesos que llevan a la preñez o al nacimiento de la cría resultan imposibles de separar a nivel de establecimientos comerciales, lo que nos lleva a usar variables poco informativas (cría nacida, por ejemplo). Más aún, en condiciones de predios comerciales, en muchos casos se superpone el problema de la ausencia de algunos registros importantes, por lo que las variables son aún menos informativas. Por ejemplo, teniendo en cuenta los problemas anteriores, para estimar parámetros genéticos de variables reproductivas (endpoints) en la raza Aberdeen Angus, H. Naya, Peñagaricano, and Urioste (2017) ensayaron diferentes modelos, incluyendo modelos lineales (gaussianos), de Poisson, probit (umbral), de Poisson censurados y gaussianos censurados. Los criterios tradicionales para rasgos de fertilidad incluyen el éxito del parto (CS), un rasgo binario codificado con 1 para el éxito y 0 para el fracaso, y uno algo más descriptivo, días al parto (CD), representado como el número de días desde el comienzo de la temporada de partos de un rodeo hasta la fecha de parto de la vaca. Mientras que CD es más descriptivo que CS, el mismo no permite una forma directa de representar la información de las vacas fallidas (que no tuvieron ternero). Existen diferentes alternativas para tratar este problema, alguna de las cuales incluyen añadir un ciclo estral a la variable (CD+21d), asumiendo que estas vacas estarían preñadas en el siguiente celo si se permitiese, tratar estos registros como información faltante (CD_NA) o considerar la CD como censurada a la derecha y modelizarla en consecuencia. Otra alternativa propuesta por H. Naya, Peñagaricano, and Urioste (2017) es la de modelar el número total de celos fallidos hasta la concepción (FE), como una nueva variable de respuesta no censurada de interés. La idea es de expresar en número de ciclos estrales (21 días) el tiempo en el que una vaca no está preñada, a pesar de estar en la temporada de cría; ventajas de esta variable incluyen de que es cuantitativa, con el número de eventos relevantes (ciclos estrales, no días) y que permite conectar de forma continua los años en caso de haber fallado todas las oportunidades en uno.

En el cuadro siguiente se puede ver un resumen de las estimaciones de heredabilidad obtenidas por estos autores para los diferentes “endpoints” considerados, usando diferentes modelos de acuerdo al tipo de variable.

Nombre	Modelo	Variable	\(h^2\)
\(\text{FE.L}\)	\(\text{Linear}\)	\(\text{FE}\)	\(0,052 (0,041–0,063)\)
\(\text{FE.P}\)	\(\text{Poisson}\)	\(\text{FE}\)	\(0,253 (0,221–0,284)\)
\(\text{CS.L}\)	\(\text{Linear}\)	\(\text{CS}\)	\(0,037 (0,031–0,042)\)
\(\text{CS.Pr}\)	\(\text{Probit}\)	\(\text{CS}\)	\(0,237 (0,195–0,277)\)
\(\text{CD21.L}\)	\(\text{Linear}\)	\(\text{CD+21d}\)	\(0,062 (0,050–0,074)\)
\(\text{CD21.P}\)	\(\text{Poisson}\)	\(\text{CD+21d}\)	\(0,282 (0,272–0,293)\)
\(\text{CDNA.L}\)	\(\text{Linear}\)	\(\text{CD\_NA}\)	\(0,067 (0,053–0,084)\)
\(\text{CDNA.P}\)	\(\text{Poisson}\)	\(\text{CD\_NA}\)	\(0,292 (0,281–0,304)\)
\(\text{CD.CG}\)	\(\text{CenGaussian}\)	\(\text{CD}\)	\(0,076 (0,062–0,090)\)
\(\text{CD.CP}\)	\(\text{CenPoisson}\)	\(\text{CD}\)	\(0,254 (0,244–0,264)\)

Claramente, en ningún caso las heredabilidades estimadas son altas o muy altas, manteniéndose siempre en el rango de bajas. Sin embargo, hay diferencias importantes entre trabajar una característica con heredabilidad del entorno de \(h^2=0,05\), que de \(h^2=0,25\). Por un lado, los modelos no-lineales mostraron sistemáticamente estimaciones más altas de heredabilidad en todos los casos que los modelos lineales (\(h^2 < 0,08\) para los modelos lineales; \(h^2 > 0,23\) para los modelos no lineales). Por otro lado, mientras que en el caso de los modelos relacionados con FE y el CS, los modelos no lineales superaron a sus homólogos lineales en el ajuste, en el caso de los modelos derivados del CD, las versiones lineales mostraron un mejor ajuste que las homólogas no lineales. Más allá de esto, la interpretabilidad del modelo es una cuestión fundamental y en el caso de los modelos no-lineales la misma suele verse comprometida. Finalmente, este estudio también muestra (algo que discutiremos en otros capítulos) que la correlación genética entre los “endpoints” considerados fue alta, pero lejos de ser igual a 1, lo que habla de que diferentes arquitecturas genéticas trabajarían sobre los diferentes “endpoints”.

Estimaciones de heredabilidad en plantas

Como ya vimos, en plantas los métodos de estimación pueden ser diferentes que en animales, particularmente por la posibilidad de estimar en forma relativamente la heredabilidad en sentido amplio y a su vez explotar el valor de la misma a partir de la clonación.

En el cuadro siguiente vemos algunos ejemplos de estimaciones de heredabilidad para dos especies de interés comercial, el Eucalyptus, especie de interés para la producción forestal y el arándano, una especie frutal.

(#tab:datosh2p_html)(#tab:datosh2p_html)Heredabilidades para diferentes características en especies de plantas de interés comercial , así como las correspondientes estimaciones de incertidumbre (“EE”=error estándar,“SD”=desvío estándar).

Especie	Experimento	Característica	Año	h2	Incertidumbre	Cita
Eucalyptus
Eucalyptus	E. grandis x E. urophyla	Diametro a la altura del pecho	2019	0,41	0,15
		Altura		0,09	0,13
		Volumen		0,46	0,14
		Celulosa		0,32	0,11
		Hemicelulosa		0,33	0,09
		Lignina insoluble		0,58	0,12	1
		Lignina soluble		0,87	0,13
		Lignina total		0,57	0,12
		Densidad madera		0,7	0,16
		angulo microfibra		0,11	0,11
		Largo fibra		0,36	0,2
		Ancho fibra		0,08	0,08
Arándanos
Arandanos	Arandanos (tetraploide)	Rendimiento	2018	0,45
		Peso fruto		0,58
		Firmeza fruto		0,35
		Diametro fruto		0,25		2
		PH		0,36
		solidos solubles		0,33
		Densidad brotes		0,16

\(^1\) Marco de Lima et al. (2019) \(^2\) Cellon et al. (2018)

Estimaciones de heredabilidad en condiciones naturales

Los métodos de estimación de la heredabilidad que hemos visto hasta ahora, tanto por análisis de la varianza como por regresión implican estructuras de parentesco conocidas y determinadas. En muchos casos esto puede significar un impedimento importante a la hora de obtener estimados de heredabilidad en condiciones naturales. Por un lado, la determinación de parentesco puede resultar difícil o aún imposible en especies donde no resulta fácil identificar las relaciones progenitor-progenie, tanto debido a que durante la estación de cría una hembra se puede aparear con diferentes machos o que en vegetales la polinización es al azar y la dispersión de semillas elevada u otras razones similares. Por otro lado, conseguir implementar un diseño experimental con determinadas estructuras de parentesco en condiciones naturales suele ser imposible, lo que nos llevará a usar las pocas observaciones que cumplan con los criterios de parentesco. Por lo tanto, las estimaciones de heredabilidad en estas condiciones suelen incluir pocos individuos y un trabajo de observación considerable.

Pese a la dificultad de generar experimentos, como veremos en Métodos más avanzados de estimación, existen alternativas para usar la información de todos los individuos si conocemos o podemos estimar el parentesco entre los mismos. En la mayor parte de las especies de aves, por ejemplo, los huevos del nido pertenecen todos a la misma pareja de padres, por lo que se trata de hermanos enteros. En caso de características que se pueden medir en individuos juveniles (antes de abandonar el nido), resulta muchas veces posible utilizar este diseño de hermanos enteros que nos brinda la naturaleza para estimar a través de un modelo de ANOVA la varianza genética de la característica y de allí la heredabilidad.

En mucho casos, sin embargo, no es posible aprovecharse de la historia de vida de la especie para poder explotar determinadas relaciones de parentesco. Hasta hace poco eso constituía una importante limitante aún para especies en las que la medición del fenotipo era razonablemente posible. Sin embargo, la aparición de los métodos de identificación de parentesco a partir del ADN, en particular los métodos de genotipado y secuenciado han permitido analizar un grupo de individuos escogidos al azar, utilizando las mismas herramientas de estimación a través de métodos por Máxima Verosimilitud o métodos bayesianos (ver Métodos más avanzados de estimación).

10.5 Heredabilidad y filogenética

Como a esta altura debería quedar claro, existe una clara conexión entre la genética de poblaciones y la genética cuantitativa, una relación que se ve mucho más clara cuando ambas se consideran en un contexto evolutivo. En la “ciencia moderna”, con investigadores cada día más enfrascados en sus respectivas especialidades (a su vez cada día más específicas) resulta muchas veces difícil escapar a las limitaciones propias y hacer conexiones con desarrollos de otras áreas del conocimiento. Sin embargo, cada tanto tiempo aparecen investigadores con curiosidad más amplia que su propio foco y que logran arrimar estos desarrollos externos a su área. Un caso de estos lo constituye el aporte de M. Lynch (1991), que aplicó con creatividad los desarrollos observados en la genética cuantitativa animal para comprender mejor la evolución de los caracteres cuantitativos a escala evolutiva.

La evolución de los organismos se suele representar en forma de árboles filogenéticos donde un clado ancestral se deriva en dos clados diferentes, que pueden continuar evolucionando sin dar lugar a nuevos clados o nuevamente particionarse y así sucesivamente. Esto genera una estructura que se puede representar en forma de árbol y que por lo tanto se conocen como árboles filogenéticos. Un problema típico para estudiar los caracteres cuantitativos en evolución es que uno de los supuestos tradicionales que se hacen en estadística para la mayor parte de las pruebas es que las observaciones son independientes e igualmente distribuidas. Claramente, como las especies derivan de ancestros comunes, que para cualquier característica de interés tenían determinados valores, entonces cada par de especies tiene un largo diferente de ramas hasta llegar a ese ancestro en común entre ellas (ese ancestro puede ser diferente para cada par de especies). Eso implica que han evolucionado en conjunto el tiempo desde el origen de la vida hasta el ancestro en común a ambas, o dicho de otra manera, la divergencia entre esas dos especies solo ocurre a partir del último ancestro en común. Por lo tanto, una medida intuitiva de la similaridad genética de dos especies dado que conocemos un árbol filogenético que las representa sería la proporción del largo de ramas compartido entre las dos especies dividido el largo de ramas total desde el origen (raíz del árbol) hasta las puntas (nuestras especies). Si tenemos \(n\) especies, podemos acomodar la similaridad filogenética de cada par en una matriz cuadrada de \(\mathrm{n \times n}\), simétrica. Si los largos totales de ramas desde el origen a las puntas (especies) son iguales, entonces la diagonal estará constituida por valores de \(1\). En caso de que no sean iguales los valores de la diagonal pueden reflejar esta relación entre “el tiempo compartido consigo mismo” y la similaridad genética haciendo que el valor de la diagonal sea distinto de \(1\).

La similaridad entre la matriz que representa la similaridad filogenética y la matriz de parentesco entre especies es evidente. En principio, desde el punto de vista matemático, el diagrama de flechas que usamos para representar el pedigree y el árbol filogenético con raíz son ambos grafos dirigidos acíclicos (DAG por sus iniciales en inglés). Los grafos son estructuras matemáticas que tienen vértices (o nodos), que se conectan entre sí a través de aristas. Cuando las aristas son dirigidas, es decir apuntan desde un vértice a otro, esto representa una dirección, jerarquía o lo que corresponda, entre los vértices. Por otra parte, acíclico significa que no se forman ciclos en la misma dirección, es decir que siguiendo las flechas de un vértice al siguiente nunca podemos volver al vértice inicial.

En el caso de los árboles filogenéticos con raíz (la raíz representa el origen de todas las especies que participan del árbol), los vértices representan especies o taxa, vivientes o ancestrales y las flechas representan las especies derivadas de una anestral, obviamente apuntando en la dirección desde la ancestral a la descendiente. En el caso de un pedigree, como ya vimos, los vértices son individuos y las flechas apuntan de un progenitor a su progenie. La similitud es obvia también a este nivel. En el caso de los árboles filogenéticos los largos de las aristas (ramas) suelen representar el tiempo evolutivo (por ejemplo, como función del número de sustituciones nucleotídicas) y por lo tanto ser variables. En el caso de los pedigrees, la aristas representan el pasaje de información de un padre a su hijo, que es siempre la mitad de su genoma, por lo tanto la proporción \(\frac{1}{2}\) es igual para todas las aristas. En el caso de un árbol filogenético dicotómico (los más usuales, digamos), cada nodo (vértice) interno genera dos descendientes y es descendiente de otro vétices (excepto la raíz), mientras que en el caso de un pedigree cada nodo es descendiente de como máximo 2 vértices (sus padres, los dos si el pedigree está completo, algo imposible en la práctica ya que la recursión sería infinita) pero puede emitir cualquier número de flechas (apuntando a ese número de hijos).

Esta similaridad entre pedigrees y árboles filogenéticos fue la que llevó a M. Lynch (1991) a sugerir que la misma aproximación de modelos mixtos lineales que usaban los genetistas cuantitativos en el área del mejoramiento genético animal se podía usar en el contexto filogenético. Ya que en el contexto del mejoramiento genético se conocían como modelos mixtos, la aproximación filogenética pasó a ser conocida como PMM (por “Phylogenetic Mixed Model”). A partir de esto, usando un enfoque por Máxima Verosimilitud y las ecuaciones de BLUP/BLUE, era posible estimar la varianza que correspondía a la filogenia (el “equivalente” del parentesco) y la que correspondía al ambiente, es decir todo lo no explicado por la filogenia.

Una diferencia práctica importante entre filogenias y pedigrees es que estos últimos suelen incluir miles y aún millones de individuos y datos y que además los nodos internos son conocidos y aún suelen tener datos. En el caso de las filogenias casi nada de esto es cierto: no se conocen los nodos internos (por lo que obviamente no tienen datos), tampoco la topología y los largos de ramas, que deben estimarse y las especies suelen ser del orden de las decenas o centenas como máximo. Teniendo todo esto en cuenta, H. Naya et al. (2006) propusieron el enfoque bayesiano para resolver estos problemas, lo que dio origen al BPMM (“Bayesian PMM), que luego Hadfield (2010) implementó de forma eficiente.

A pesar de las similitudes entre pedigrees y filogenias, que nos permitirían estimar una heredabilidad filogenética de la característica, la varianza explicada por la filogenia no es de origen exclusivamente genético aditivo y ni siquiera genético ya que las especies derivadas suelen compartir ambiente con sus correspondientes especies ancestrales. Esto “oscurece” la interpretación de esa heredabilidad filogenética, pero no deja de ser un método extremadamente interesante para el análisis de caracteres cuantitativos en la evolución.

10.6 Heredabilidad en la era genómica

El advenimiento de la genómica ha tenido un profundo impacto en las estimaciones de heredabilidad. Por un lado, en el caso de la poblaciones silvestres ha permitido obviar las dificultades de tener que realizar experimentos específicos con diseños controlados para poder llegar a estimados de la misma. La posibilidad de genotipar o aún de secuenciar individuos al azar en la población permite obtener la matriz de Parentesco genómico, lo que unido a Métodos más avanzados de estimación nos permite a partir de los fenotipos de los individuos seleccionados obtener una estimación razonable. Claramente, eso evita un trabajo de campo importante en el caso de animales difíciles de manejar, por ejemplo con la identificación de las parejas reproductivas y sus respectivas crías, el desbalance en el número de descendientes, el número menor de animales a incluir, etc., todo lo cual reduce la calidad de las estimaciones. En la actualidad existen chips de genotipado para muchas especies, aunque la oferta es escasa para las especies no-domésticas o no de uso en experimentación. Sin embargo, como vimos antes, la secuenciación genómica es una alternativa que se puede considerar libre-de-hipótesis en el sentido de que no introduzco un sesgo al buscar solo la información conocida o aún seleccionada (como es en el caso de los chips). Dados los relativamente altos costos de secuenciación para muchas especies eucarióticas, existen varias alternativas como el Low-Pass Whole Genome Sequencing (LP-WGS) donde se reduce en forma aleatoria la cobertura del genoma, o el Genotype By Sequencing (GBS) donde se secuencia específicamente el producto de cortes por enzimas de restricción.

Por otra parte, la llegada de la genómica ha permitido definir y medir nuevos fenotipos moleculares. Por ejemplo, tanto con chips de expresión como a través de la secuenciación de transcritos (RNAseq) es posible determinar el nivel de expresión (transcripción) de diferentes genes en diferentes condiciones; es lo que se conoce como transcriptómica. En muchos casos, en genes codificantes, las diferencias entre alelos que producen diferencias en el fenotipo se deben al nivel de expresión de las proteínas que estos producen. Si asumimos que el nivel de expresión de los transcritos (que es ARNm) se correlaciona muy fuertemente con el nivel de proteína (es decir, después de la traducción), entonces la transcriptómica sería un proxy (una variable que se aproxima a la que desearíamos medir) al nivel de expresión de las proteínas, algo mucho más fácil y barato de medir que estas últimas y que puede hacerse en forma masiva (todos los genes a la vez). Como en muchos casos se conocen genes que están directamente relacionados con diferencias en el fenotipo, podemos estar interesados en conocer la heredabilidad de la expresión de los mismos. Es importante destacar que si bien podemos conocer todo el genoma de cada individuo eso no implica que podamos conocer o modelar razonablemente (al menos hoy) la regulación de la expresión génica, por lo que nuestros nuevos fenotipos moleculares no se diferencian tanto de los clásicos fenotipos a los que estamos acostumbrados. Como los loci de expresión cuantitativa se conocen en general como QTL (por sus siglas en inglés), las variantes genómicas que producen una alteración en el nivel de expresión de los transcritos se como como eQTL (“expression Quantitative Trait Loci”).

En otro sentido, técnicas estándar para medir fenotipos clásicos pueden transformarse en fuente inagotable de nuevos fenotipos cuando exploramos los datos brutos generados por el equipamiento y los combinamos con fenotipos clásicos usando herramientas de aprendizaje automático. Por ejemplo, para la determinación del porcentaje de proteína y grasa en leche se utilizan en forma rutinaria espectrómetros de infrarrojos medios (MIRS o FTIR, por “Fourier Transform Infra Red”). Estos equipos obtienen un espectro de infrarrojos en, por ejemplo, 935 puntos de longitud de onda diferente. Es decir, el resultado de “medir” cada muestra de leche es un conjunto de 935 mediciones a longitudes de onda diferentes, que luego, usando una calibración previa del aparato con estándares conocidos y una ecuación que usa la información de algunos de esos 935 puntos, genera el resultado (predice) el porcentaje de proteína y grasa de la muestra. Sin embargo, usando esa misma información de los 935 puntos, si tenemos miles de muestras medidas y los fenotipos correspondientes para otra variable de nuestro interés, podemos buscar un modelo de predicción de la misma usando la información del espectrómetro. Por ejemplo, actualmente la medición de emisiones de metano en bovinos suele ser compleja y costosa, por lo que se reduce a unos pocos animales en condiciones experimentales. Sin embargo, si de esos pocos animales también obtenemos al mismo tiempo los espectros infrarrojos, podemos intentar desarrollar una ecuación de predicción que nos permita predecir la emisión de metano a partir de las muestras de leche. Se trata de una predicción, es decir, no es una medición específica del analito (metano en este caso), pero en la medida de que la precisión de la ecuación de predicción sea lo suficientemente alta podría ser una excelente herramienta para la reducción de las emisiones. Obviamente, cualquier otro fenotipo de nuestro interés y que en principio posea alguna relación con el espectro infrarrojo de la leche podría estudiarse en lugar del metano.

Finalmente, el acceso a los datos genómicos nos permite obtener una mucho mejor medida del parentesco entre dos individuos, ya que no es más necesario depender del parentesco estadístico esperado (ver Parentesco genómico) y esto nos permite mejorar las estimaciones de heredabilidad. Una excelente revisión sobre la heredabilidad en el contexto de la genómica se encuentra en Visscher, Hill, and Wray (2008), así como abudantes referencias.

10.7 Métodos más avanzados de estimación

Hasta aquí hemos visto la estimación de la heredabilidad a través de estructuras de parentesco conocidas, tanto en el caso de estimarla como relación varianzas recurriendo a diferentes forma del análisis de varianza (ANOVA), como en el caso de regresiones entre progenitores y progenies. Por otro lado, una alternativa que no depende de estructuras de parentesco determinadas es a través de la hererabilidad lograda, pero como ya vimos antes dicho método requiere usualmente de largos períodos de tiempo y un buen número de individuos para obtener resultados estables y con cierta precisión.

En la práctica, la mayor parte de las razas bovinas y ovinas de interés comercial que poseen una estructura de criadores suficientemente grande y estable participan de un sistema de evaluaciones genéticas a partir de los registros fenotípicos que aportan todos los participantes, así como los registros genealógicos que llevan las asociaciones y que permiten el armado de la matriz de parentesco aditivo de los animales. A partir de estos registros, si se conocen las varianzas aditivas y fenotípicas (o las residuales) es posible estimar los valores de cría de los distintos individuos a partir de las ecuaciones BLUE/BLUP de modelos mixtos lineales desarrolladas por Charles Roy Henderson y que veremos en detalle en otro capítulo. Sin embargo, desafortunadamente para nosotros, lo que queremos estimar en este capítulo es justamente la heredabilidad de la característica, que como vimos es igual a \(\mathrm{\frac{V_A}{V_P}}\), por lo que estamos de alguna forma en el mismo lugar del que partimos.

Afortunadamente, existen dos enfoque conceptualmente distintos pero estrechamente relacionados para obtener los estimados de varianzas aditivas y fenotípicas a partir de las ecuaciones BLUE/BLUP. Conceptualmente distintos en lo que hace a la escuela estadística por detrás: el más tradicional basado filosóficamente en la escuela “frecuentista” y su aproximación por máxima verosimilitud (ML), el más moderno (pero cuya escuela es más antigua) basado en el enfoque estadístico “bayesiano” y su aproximación práctica basada en métodos Monte Carlo. Estrechamente vinculados en el hecho de que la estimación es básicamente iterativa, en el enfoque por ML avanzando sucesivamente hacia un óptimo (el máximo de la función de verosimilitud), en el bayesiano muestreando desde la distribución a posteriori de los parámetros de interés (en nuestro caso las varianzas aditiva y residual).

En el método usado para la estimación por máxima verosimilitud (usualmente REML, máxima verosimilitud restringida), una vez que el algoritmo alcanza el criterio de convergencia, además de un estimador puntual para cada una de la varianzas es posible obtener un estimador de la varianza de los estimadores (o sea, un estimador de la varianza de los estimadores de varianza), por lo que bajo ciertos supuestos (entre ellos normalidad asintótica) es posible calcular un intervalo de confianza.

En el enfoque bayesiano, la alternativa más sencilla y que funciona muy bien para una gran cantidad de características es el muestreo de Gibbs (“Gibbs sampling”), donde asumiendo determinadas distribuciones a priori como conjugadas de la distribución de los datos es posible obtener distribuciones a posteriori de la misma familia y por lo tanto muestrear de las mismas en forma eficiente. En cada ciclo del muestreador (iteraciones) los parámetros se van “muestreando” en forma sucesiva (algunos se pueden muestrear en bloque) condicional a los resultados obtenidos previamente para los otros parámetros. El resultado de este proceso, a partir de que se alcanza la convergencia, es una cadena de Markov muestreando de la distribución a posteriori de cada parámetro. Esto nos permite realizar inferencia directamente sobre las muestras obtenidas, pudiendo extraer estadísticos resumen (media, mediana, cuantiles, desvío estándar, etc.) pero a su vez analizar la distribución gráficamente para comprender mejor el proceso de muestreo y el alcance de la información brindada por los datos respecto a la información brindada a priori. Un excelente material para entender el enfoque bayesiano en los modelos mixtos lineales en genética animal se encuentra en el libro Sorensen and Gianola (2002), mientras que un excelente libro general para entender los modelos lineales en genética cuantitativa es Mrode (2014).

10.8 Repetibilidad

Ciertas características fenotípicas se repiten en cada individuo, así sea en el tiempo o en el espacio. Por ejemplo, en animales podemos pesar el vellón de cada oveja todos los años, en vacas lecheras la producción de leche en cada lactancia, pero también podemos contar el número de setas en los segmentos abdominales de moscas de la especie Drosophila (Douglas S. Falconer (1983)) y por lo tanto se trataría de una repetición en el espacio en lugar del tiempo. En plantas que repiten anualmente su producción, cualquier característica que se puede medir en los distintos ciclos claramente entra dentro de esta categoría, como el número de frutos en árboles, el peso total de los frutos y cualquier otra que siga este patrón. Es decir, existen características que tendemos a considerar como la misma, expresada varias veces en la vida del individuo.

Así como consideramos la heredabilidad como el parámetro genético central para entender el proceso de transferencia de información de padres a hijos, ahora nos enfocaremos en definir y entender un parámetro genético que hace a la repetibilidad de la característica de interés. Consideremos la repetición en el tiempo de una característica ya que nos resulta mucho más intuitiva. Veamos entonces qué componentes de la varianza fenotípica se corresponden con efectos que se repiten “inmutables” durante la vida del animal. Claramente, más allá de los posibles cambios epigenéticos (que despreciaremos), el genotipo de un animal no cambiará durante su vida y por lo tanto ni los efectos aditivos de los genes, ni los efectos de dominancia o epistáticos (al menos asumiendo que no hay cambios importantes en las medias poblacionales en el período en consideración). Esto nos deja con el ambiente como posibilidad a considerar en las causas de las variaciones entre medidas.

Sin duda, en la mayor parte de las características fenotípicas de interés el ambiente juega un rol importante en su desarrollo. Por ejemplo, un árbol frutal producirá diferente número de frutos o peso total de los mismos en un año “bueno” que en un año “malo”. Lo mismo, una oveja producirá diferente cantidad de lana en diferentes años, producto de las variaciones entre años en factores como la alimentación y el bienestar, entre otros. Por lo tanto, nos resulta claro que las variaciones ambientales afectarán el fenotipo entre medidas en el mismo animal, pero la pregunta que nos surge es si toda la influencia ambiental que afecta a los animales varía de medición en medición. Antes de seguir, debemos de tener en cuenta que en el contexto de nuestro modelo genético básico le llamamos ambiental a todo lo que no es genético.

Volvamos a la discusión de si toda la influencia del ambiente hará variar el fenotipo de año en año. Por ejemplo, un árbol que crece en malas condiciones difícilmente llegará a desarrollar todo su potencial genético y la producción en el mismo se verá afectada durante toda la vida del árbol. Lo mismo para un cordero que crece en malas condiciones o aún para una vaquillona que sufre la pérdida definitiva de un cuarto de la ubre al comenzar su primera lactancia. En todos los casos se trata de factores ambientales de acuerdo a nuestra consideración de ambiental como lo no-genético, pero claramente estos efectos afectarán la producción de toda la vida del individuo. Sin embargo, como vimos antes, algunos factores cambian de año en año el fenotipo del animal en medidas repetidas, por lo que podemos descomponer los efectos ambientales en dos tipos: a) efectos ambientales permanentes y b) efectos ambientales temporarios.

Llamamos efectos ambientales permanentes a aquellos efectos en los que las diferencias no son atribuibles a la genética, pero que van a afectar todos los registros fenotípicos de una característica que se repite durante la vida del individuo.

Por otro lado, llamamos efectos ambientales temporarios a aquellos efectos de origen no-genético que afectan en forma particular cada una de las mediciones repetidas de la misma característica.

La repetibilidad como cociente de varianzas

De acuerdo a estas definiciones podemos partir los efectos ambientales en dos componentes, uno que se manifestará de la misma manera durante toda la vida del animal y otro que variará de observación en observación, por lo que, considerando que no hay covariación entre ambos efectos, tenemos

\[{E={E_{perm}}+{E_{temp}}\ \therefore}\] \[ \begin{split} {V_E=V_{E_{perm}}+V_{E_{temp}}} \end{split} \tag{10.46} \]

Ahora, si colocamos esta división de la varianza de los efectos ambientales en nuestro modelo genético básico, es decir si sustituimos \(\mathrm{V_E}\) por \(\mathrm{V_{E_{perm}}+V_{E_{temp}}}\), tenemos que

\[ \begin{split} {V_P=V_G+V_E=V_G+V_{E_{perm}}+V_{E_{temp}}} \end{split} \tag{10.47} \]

Por lo tanto, la fracción de la varianza fenotípica correspondiente a los efectos que se repiten entre diferentes mediciones en la vida del individuo le llamamos \({\rho}\) y la misma será

\[ \begin{split} \rho=\mathrm{\frac{V_G+V_{E_{perm}}}{V_P}=\frac{V_A+V_D+V_I+V_{E_{perm}}}{V_P}} \end{split} \tag{10.48} \]

En diferentes textos es usual usar \(R\) para la repetibilidad, o aún \(r\) (Douglas S. Falconer (1983)), pero ambos símbolos se prestan a confusión, el primero con la respuesta a la selección (o progreso genético), el segundo con cualquier coeficiente de correlación (aunque, como veremos más adelante, la repetibilidad también se puede definir como correlación), por lo que nos hemos decidido por usar \(\rho\) (la letra griega “rho” o “ro”) para simbolizarla.

La repetibilidad como coeficiente de correlación intraclase

Como vimos previamente en el caso de la heredabilidad, a veces es posible definir los parámetros genéticos de diferentes formas. En el caso de la heredabilidad vimos que además de como cociente de varianzas podíamos definirlo como el coeficiente de regresión lineal, tanto del valor de cría en el fenotipo individual, como de funciones sencillas de la regresión fenotípica entre progenitores y progenie. En el caso de la repetibilidad es posiblemente aún más intuitiva otra forma matemática de definirla.

Si una característica se repite exactamente con el mismo valor una segunda vez, entonces la correlación entre pares de medidas en el individuo, es decir varios individuos medidos dos veces, será de \(1\). Si los valores de la segunda medida son completamente al azar respecto a la primera, entonces la correlación entre ambas medidas será de cero. Claramente, la correlación entre medidas nos indica de alguna forma cuán repetible es la característica. Como se trata de la correlación entre medidas de la misma clase, al coeficiente de correlación de Pearson de este tipo se le llama coeficiente de correlación intraclase y lo simbolizaremos con \(\mathrm{t}\).

Si recordamos que el coeficiente de correlación de Pearson es igual al cociente entre la covarianza y el producto de los desvíos entre las dos variables aleatorias, entonces para el caso de dos medidas fenotípicas en el mismo individuo tenemos que

\[{t=\frac{Cov_{P_{1}P_{2}}}{\sqrt{V_{P_{1}}V_{P_{2}}}}=}\] \[ \begin{split} {\frac{Cov(A_1+D_1+I_1+E_{perm_{1}}+E_{temp_{1}},A_2+D_2+I_2+E_{perm_{2}}+E_{temp_{2}})}{\sqrt{V_{P_{1}}V_{P_{2}}}}} \end{split} \tag{10.49} \]

Pero por definición, como se trata de dos mediciones en el mismo individuo, los efectos genéticos serán los mismos en ambas mediciones, así como los del ambiente permanente. Por lo tanto

\[ \begin{split} {A_1=A_2=A;\ D_1=D_2=D;\ I_1=I_2=I;\ E_{perm_{1}}=E_{perm_{2}}=E_{perm}} \end{split} \tag{10.50} \]

Ahora, utilizando los resultados de (10.50) en (10.49) tenemos

\[ \begin{split} {t=\frac{Cov(A+D+I+E_{perm},A+D+I+E_{perm})}{\sqrt{V_{P_{1}}V_{P_{2}}}}} \end{split} \tag{10.51} \]

Como ya vimos previamente, por construcción no tenemos covarianza entre efectos aditivos y de dominancia o epistasis, ni entre estos últimos y por lo tanto, cuando no existe covarianza genético-ambiental la ecuación (10.51) se transforma en

\[ \begin{split} {t=\frac{V_A+V_D+V_I+V_{E_{perm}}}{\sqrt{V_{P_{1}}V_{P_{2}}}}} \end{split} \tag{10.52} \]

Claramente se trata de otra forma de definir la repetibilidad de una característica, esta vez como la correlación entre medidas repetidas del mismo individuo. Más aún, si la varianza ambiental temporal es igual en las distintas mediciones, es decir, en particular \(V_{E_{temp_{1}}}=V_{E_{temp_{2}}}=V_{E_{temp}}\), entonces

\[ \begin{split} {V_{P_{1}}=V_G+V_{E_{perm}}+V_{E_{temp_{1}}}=V_G+V_{E_{perm}}+V_{E_{temp_{2}}}=V_G+V_{E_{perm}}+V_{E_{temp_{1}}}=V_P} \end{split} \tag{10.53} \]

y por lo tanto \(\sqrt{V_{P_{1}}V_{P_{2}}}=\sqrt{V_{P}V_{P}}=\sqrt{V_{P}^2}=V_P\) y sustintuyendo en el denominador de (10.52) tenemos que

\[ \begin{split} {t=\frac{V_A+V_D+V_I+V_{E_{perm}}}{\sqrt{V_{P_{1}}V_{P_{2}}}}=\frac{V_A+V_D+V_I+V_{E_{perm}}}{V_P}=\rho} \end{split} \tag{10.54} \]

Por lo tanto, en el caso de que las varianzas fenotípicas sean iguales en las distintas mediciones consideradas, las dos definiciones de repetibilidad, como cociente de varianzas y como coeficiente de correlación intraclase coinciden.

La relación entre la heredabilidad y la repetibilidad

A esta altura es lógico preguntarnos cuál es la importancia práctica de la repetibilidad. Para eso, en primer lugar veamos cuál es la relación entre la repetibilidad, la heredabilidad en sentido amplio y la heredabilidad en sentido estricto.

Si escribimos en forma explícita los distintos componentes del numerador de la repetibilidad, recordando \(\mathrm{V_A+V_D+V_I=V_G}\) tenemos que

\[ \begin{split} {\rho=\frac{V_A+V_D+V_I+V_{E_{perm}}}{V_P}=\frac{V_A+V_D+V_I}{V_P}+\frac{V_{E_{perm}}}{V_P}=H^2+\frac{V_{E_{perm}}}{V_P}} \end{split} \tag{10.55} \]

Como las varianzas son positivas, entonces \(\mathrm{\frac{V_{E_{perm}}}{V_P} \geqslant 0}\) y por lo tanto, de acuerdo a la ecuación (10.55) la repetibilidad es igual a la heredabilidad en sentido amplio más un número positivo (estrictamente, entre \(0\) y \(1\), ya que \(\mathrm{V_{E_{perm}} \leqslant \mathrm{V_P}}\)). Por lo tanto \(\rho \geqslant \mathrm{H^2}\).

Con igual razonamiento, recordando que \(\mathrm{h^2=\frac{V_A}{V_P}}\), tenemos que

\[ \begin{split} \rho=\mathrm{\frac{V_A+V_D+V_I+V_{E_{perm}}}{V_P}=\frac{V_A}{V_P}+\frac{V_D+V_I+V_{E_{perm}}}{V_P}=h^2+\frac{V_D+V_I+V_{E_{perm}}}{V_P}} \end{split} \tag{10.56} \]

Nuevamente, como las varianzas son positivas, tenemos ahora que \(\rho \geqslant \mathrm{h^2}\). Más aún, como \(\rho=\mathrm{H^2+\frac{V_{E_{perm}}}{V_P}=h^2+\frac{V_D+V_I+V_{E_{perm}}}{V_P}}\) y \(\mathrm{\frac{V_D+V_I+V_{E_{perm}}}{V_P} \geqslant \frac{V_{E_{perm}}}{V_P}}\), entonces \(\mathrm{H^2}\) debe ser mayor a \(\mathrm{h^2}\), cosa que no hace más que verificar lo que ya sabíamos. Esto nos permite establecer firmemente la siguiente la relación entre los tres parámetros genéticos

\[ \begin{split} \rho \geqslant \mathrm{H^2 \geqslant h^2} \end{split} \tag{10.57} \]

Estas relaciones son matemáticamente correctas si se cumplen los supuestos de los que partimos. Sin embargo, las estimaciones de repetibilidad pueden no establecer un límite superior a la heredabilidad si se da alguna de las siguiente condiciones (Dohm (2002)):

• 1. los rasgos medidos no son idénticos desde el punto de vista genético
• 2. los efectos ambientales comunes se oponen a los efectos genéticos directos
• 3. los entornos temporales de cada rasgo están correlacionados negativamente
• 4. existe una interacción significativa entre el genotipo y el ambiente
• 5. los rasgos están influidos por los efectos maternos.

En ese caso, además de no necesariamente cumplirse la relación \(\rho \geqslant \mathrm{H^2 \geqslant h^2}\), los estimados de los parámetros pueden ser incorrectos bajo los supuestos que los realizamos. Un ejemplo hipotético de c) podría ser una característica en la que el éxito en la expresión en el ciclo \(n\) implicase un gasto energético tal que el ciclo \(n+1\) se ve comprometido seriamente. Por ejemplo, en algunas especies de tiburones el costo energético de la reproducción es suficientemente alto como para que el ciclo natural sea de dos años pese a que la gestación es del orden del año. Si obligásmeos a estas especies a reproducirse artificialmente todos los años y efectuásemos mediciones sobre las crías, posiblemente algunas características se correlacionarían negativamente entre mediciones ya que el exceso de habilidad en una gestación sería un detrimento serio para la siguiente.

Cada parámetro describe una proporción distinta de la variabilidad fenotípica que explicada por diferentes efectos genéticos y ambientales y por lo tanto tiene sentido aplicarlos en distintos contextos. Como vimos previamente, la heredabilidad en sentido estricto nos permite realizar una predicción del valor de cría de cada individuo a partir de su fenotipo y por lo tanto tiene más sentido su utilización en el contexto del mejoramiento genético en aquellas especies y características donde los efectos aditivos dominan la expresión fenotípica. En general, en mejoramiento genético animal la heredabilidad en sentido estricto es el parámetro genético central para la toma de decisiones (tanto de estrategia como a la hora de seleccionar individuos). En cambio, en mejoramiento genético vegetal, dependiendo de la especie puede tener mucho más sentido el uso de la heredabilidad en sentido amplio. Más aún, en especies que no tienen reproducción clonal y que repiten su producción a lo largo de la vida es mucha veces más fácil obtener un estimado de la repetibilidad que de la heredabilidad. Como vimos antes, para las estimas de heredabilidad es necesario recurrir a diseños experimentales con determinadas estructuras de parentesco conocidas o al menos conocer las relaciones de parentesco entre individuos y utilizar métodos iterativos y las ecuaciones BLUE/BLUP. En cambio, para estimar la repetibilidad alcanza con un par de mediciones por individuo y a través de estos datos calcular el coeficiente de correlación intraclase \(\mathrm{t}\), que como hemos visto es igual a la repetibilidad.

Esto nos deja con un método de obtener una cota superior para la heredabilidad, tanto en sentido amplio como estricto ya que ambas deben ser menores a \(\rho\) (ecuación (10.57)). Si el valor de repetibilidad obtenido es alto, la heredabilidad puede ser alta, media o baja (es decir, cualquier valor entre \(0\) y \(\rho\)), lo que no clarifica demasiado pero nos da esperanza y ciertas pistas si hacemos suposiciones adicionales. Por ejemplo, si por otros estudios sabemos que se trata de una característica cuya arquitectura genética es mayormente aditiva (es decir, los efectos de dominancia y espistasis son menores) y que en general los efectos del ambiente permanente son relativamente menores (por un control estricto del ambiente durante la fase de crecimiento, por ejemplo), entonces \(\mathrm{h^2} \approx \rho\) y como estamos en el caso de alta repetibilidad, entonces la heredabilidad también será alta. Por el otro lado, si la repetibilidad es baja, entonces necesariamente la heredabilidad será baja ya que la esta última no puede superar a la primera.

La reducción en la varianza fenotípica con varias medidas

Un concepto general que está por detrás del uso de la repetibilidad como herramienta de predicción (algo que veremos pronto) es la reducción en la varianza fenotípica producto de promediar varias observaciones de la misma característica en el mismo individuo. La idea subyacente es muy sencilla: los componentes permanentes (genéticos y ambientales) son los mismos en todas las medidas repetidas, mientras que los efectos ambientales temporales son desvíos aleatorios respecto a una media de cero; cuantas más medidas promediemos en el individuo más cerca la media de los efectos ambientales temporales será de cero y menor será la varianza de la media de los efectos temporales. Veamos cómo funciona esta idea desde el punto de vista matemático.

En general, para aquellos caracteres que se repiten a lo largo de la vida del animal, ya sea a lo largo del tiempo (lo más usual en el contexto del mejoramiento genético animal) o aún de la anatomía del mismo, vimos que podemos descomponer nuestro modelo genético básico de tal forma de separar ahora los efectos ambientales en aquellos que son permanentes en la vida del animal, de aquellos que son temporarios:

\[ \begin{split} {P=A+D+I+E_{perm}+E_{temp}} \end{split} \tag{10.58} \]

En términos de varianzas, asumiendo como de costumbre que las covarianzas entre componentes son iguales a cero, tenemos entonces:

\[ \begin{split} {V_P=V_A+V_D+V_I+V_{E_{perm}}+V_{E_{temp}}} \end{split} \tag{10.59} \]

Veamos ahora qué ocurre con la varianza fenotípica del promedio de \(n\) medidas en cada animal. Para aquellos componentes que son idénticos durante la vida del animal, por definición los permanentes, la varianza del promedio de n medidas en cada animal es simplemente el correspondiente componente de la varianza (ya que no hay una reducción de la varianza por tratarse para cada animal de un valor fijo, no aleatorio). En cambio, para los efectos temporales que si son aleatorios dentro de animal (cada año, por ejemplo, el clima afecta en forma diferente la producción de cada animal), la varianza del promedio es ahora \(\frac{VE_{temp}}{n}\). Esto nos lleva a que

\[ \begin{split} {V_{\bar P_{n}}=V_A+V_D+V_I+V_{E_{perm}}+\frac{V_{E_{temp}}}{n}} \end{split} \tag{10.60} \]

Si comparamos la varianza fenotípica de \(n\) medidas por individuo con la varianza fenotipíca de la población, tenemos

\[{\frac{V_{\bar P_{n}}}{V_P}=\frac{V_A+V_D+V_I+V_{E_{perm}}+\frac{V_{E_{temp}}}{n}}{V_P}}\] \[ \begin{split} {\frac{V_{\bar P_{n}}}{V_P}=\frac{V_A+V_D+V_I+V_{E_{perm}}}{V_P}+\frac{\frac{V_{E_{temp}}}{n}}{V_P}} \end{split} \tag{10.61} \]

\[ \begin{split} {\frac{V_{\bar P_{n}}}{V_P}=\frac{V_A+V_D+V_I+V_{E_{perm}}}{V_P}+\frac{1}{n} \frac{V_{E_{temp}}}{VP}} \end{split} \tag{10.62} \]

Pero

\[ \begin{split} {\frac{V_A+V_D+V_I+V_{E_{perm}}}{V_P}=\rho} \end{split} \tag{10.63} \] y

\[{\frac{V_{E_{temp}}}{V_P}=\frac{V_P-(V_A+V_D+V_I+V_{E_{perm}})}{V_P}}\] \[ \begin{split} {\frac{V_{E_{temp}}}{V_P}=\frac{V_P}{V_P}-\frac{VA+VD+VI+V_{E_{perm}}}{V_P}=1-\rho} \end{split} \tag{10.64} \]

Sustituyendo en (10.62) el primer término de la derecha por el resultado de (10.63) y colocando en el segundo el resultado de (10.64), tenemos

\[ \begin{split} {\frac{V_{\bar P_{n}}}{V_P}=\rho+\frac{1}{n} (1-\rho)=\frac{n\rho+1-\rho}{n}=\frac{1+(n-1)\rho}{n}} \end{split} \tag{10.65} \]

Ahora, si en lugar de verlo como la reducción de la varianza producto de las \(n\) medidas individuales, lo miramos de la forma inversa, es decir como la ganancia en precisión, tenemos una relación que veremos en gran parte de las ecuaciones para la estimación de los valores de cría y sus correspondientes precisiones en aquellos casos en que tengamos alguna forma de medidas repetidas (o correlación intraclase más generalmente).

\[ \begin{split} {\frac{V_P}{V_{\bar P_{n}}}=\frac{n}{1+(n-1)\rho}}\\ \end{split} \tag{10.66} \]

Como en los parámetros genéticos que hemos visto el numerador representa la varianza fenotípica, una reducción de la misma producto de promediar diferentes medidas repetidas tiene como efecto aumentar la precisión de estos a la hora de utilizarlos como predictores (del valor de cría o de la producción más probable). El efecto de la reducción de la varianza producto de promediar diferente número de observaciones se puede apreciar en la Figura 10.11. Claramente, cuantas más medidas promediamos mayor será la reducción en la varianza fenotípica del promedio, lo que nos llevaría a pensar que es una buena idea esperar a tener muchas mediciones. Sin embargo, cuando las repeticiones son temporales y no espaciales, cada repetición implica esperar un nuevo ciclo entero, por lo general anual. ¿Qué sentido puede tener esperar a tener 6, 7 u 8 mediciones de peso de vellón para elegir un animal como reproductor si la vida misma del animal es de este orden de duración? De hecho, la reducción de la varianza es cada vez menor y la asíntota de la misma será igual a

\[ \begin{split} {\lim_{n \to \infty}\frac{V_{\bar P_{n}}}{V_P}=\lim_{n \to \infty} \rho+\frac{1}{n} (1-\rho)=\rho} \end{split} \tag{10.67} \]

Más aún, para repetibilidades relativamente altas vemos la curva se vuelve asintótica relativamente rápido. Dicho de otra manera, cuando las repetibilidades son altas ganamos muy poco al añadir nuevas mediciones. Por ejemplo, con una repetibilidad de \(\rho=0,75\) tres observaciones ya están suficientemente cerca de la asíntota como para tener que pensar si justifica obtener nuevas mediciones. En la práctica, la consideración debe incluir los costos y las complejidades asociadas a esperar nuevas mediciones y una o dos observaciones suelen ser suficientes, como verás en próximos cursos. Cuando las repetibilidades son más bajas, por ejemplo \(\rho < 0,30\), claramente el promediado de varias observaciones representa una ganancia fundamental en precisión, por lo que se suele esperar por dos o tres mediciones, raramente cuatro.

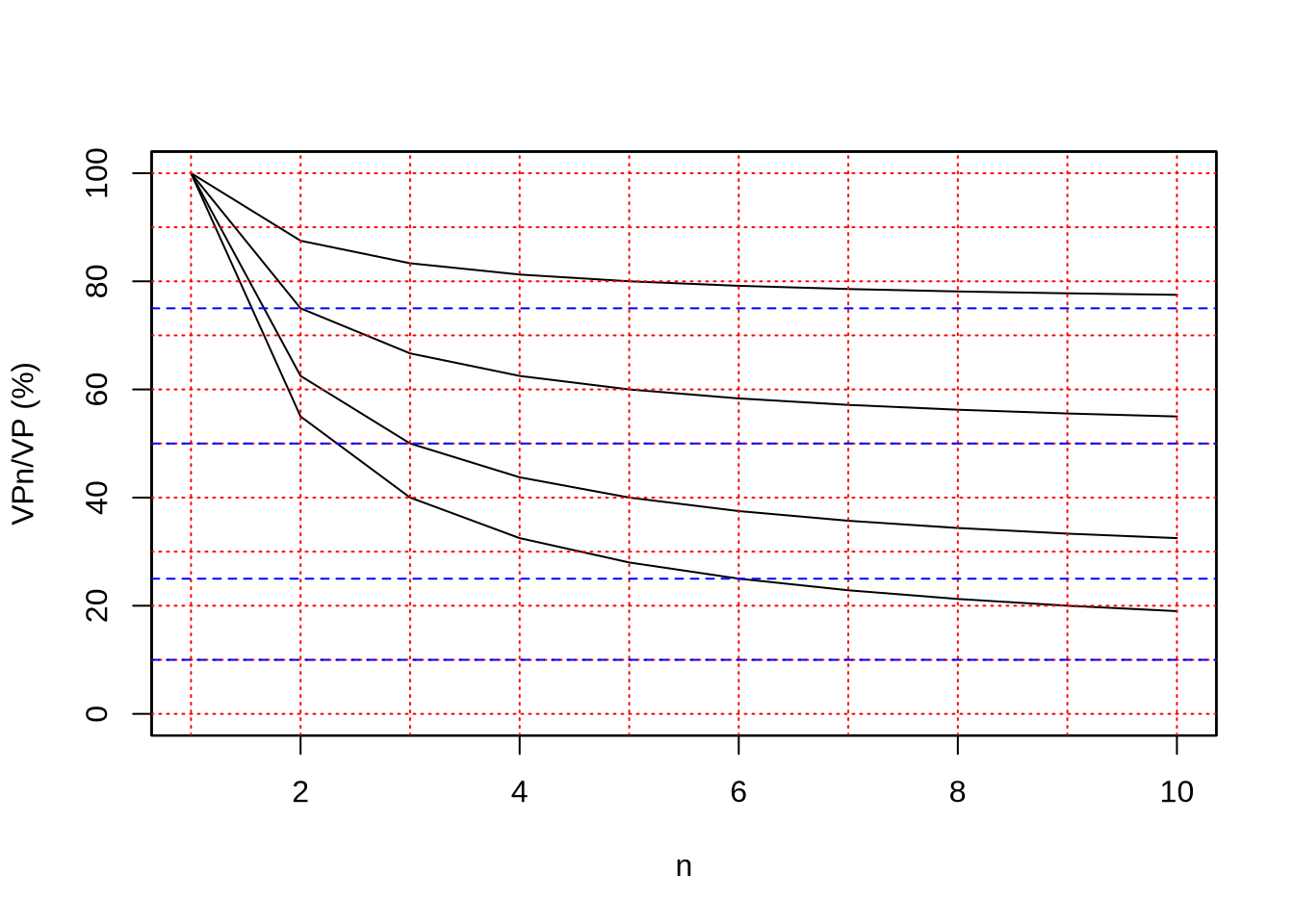
Figura 10.11: Reducción en la varianza fenotípica producto de promediar \(n\) observaciones. En las abscisas aparece en número de observaciones fenotípica promediadas mientra que en las ordenadas aparece la relación \(\mathrm{\frac{V_{P_{n}}}{V_P}=\frac{1+r(n-1)}{n}}\) (como porcentaje). Se ilustra el comportamiento de la relación para distintos valores de repetibilidad. Mientras que a valores altos de la repetibilidad tenemos poca reducción de la varianza y por lo tanto poca ventaja de incorporar más observaciones, a valores bajos de la repetibilidad (por ejemplo, \(r=0,10\)) la reducción es sustancial hasta cerca de 4 medidas. Las líneas azules a trazos representan las asíntotas correspondientes a las distintas repetibilidades.

PARA RECORDAR

• Al realizar una estimación de la heredabilidad debemos tener en cuenta que los métodos y condiciones de estimación de la misma deben poder representar el uso pretendido. El denominador de la heredabilidad es la varianza fenotípica, uno de cuyos componentes es la varianza ambiental: en la medida de que la varianza ambiental es menor, menor será el denominador y por lo tanto mayor el cociente por lo que estimaciones en ambientes más controlados tenderán a estimar mayores heredabilidades. Teniendo esto en cuenta, no parecería recomendable utilizar estimaciones realizadas en laboratorios para diseñar un programa de mejora a campo.

• Nuestro estimador de la heredabilidad a partir del diseño de hermanos enteros será:
  \(\hat{h}^2=h^2+\frac{\frac{1}{2}\ \sigma^{2}_D +2\ \sigma^{2}_{EC}}{ {V_P}}\) lo que sesga el estimador hacia arriba dado que el término \(\frac{\frac{1}{2}\ \sigma^{2}_D +2\ \sigma^{2}_{EC}}{ {V_P}}\) es en general mayor a cero.

• Las características que tienen una base genética compleja (donde lo aditivo no es tan importante), un ambiente extremadamente variable o interacciones entre genotipo y ambiente llevarán a menores estimaciones de la heredabilidad.

• Es importante tener en cuenta que una baja heredabilidad no es reflejo de una baja varianza aditiva, la baja heredabilidad de una característica está muchas veces asociada a la forma en que se registran los datos fenotípicos de la misma o a la definición imprecisa de lo que queremos medir.

• Las estimaciones de heredabilidad a campo suelen incluir pocos individuos y un trabajo de observación considerable debido a los requisitos que sabemos conlleva esta estimación.

• La aparición de los métodos de identificación de parentesco a partir del ADN, en particular los métodos de genotipado y secuenciado han permitido analizar un grupo de individuos escogidos al azar, utilizando las mismas herramientas de estimación a través de métodos por Máxima Verosimilitud o métodos bayesianos.

• Los árboles filogenéticos constituyen estructuras donde un clado ancestral se deriva en dos clados diferentes, que pueden con- tinuar evolucionando sin dar lugar a nuevos clados o nuevamente particionarse y así sucesivamente.

• Alternativas más avanzadas en la determinación de las varianzas aditivas y fenotípicas pueden ser la aproximación por máxima verosimilitud (ML; a través del método REML usualmente) perteneciente a la escuela frecuentista o el método Monte Carlo (muestreo de Gibbs) que sigue el enfoque estadístico bayesiano.

• Recordando que en el contexto de nuestro modelo genético básico le llamamos ambiental a todo lo que no es genético podemos descomponer los efectos ambientales en dos tipos:

1. efectos ambientales permanentes serán aquellos efectos en los que las diferencias no son atribuibles a la genética, pero que van a afectar todos los registros fenotípicos de una característica que se repite durante la vida del individuo.
2. efectos ambientales temporarios serán aquellos efectos de origen no-genético que afectan en forma particular cada una de las mediciones repetidas de la misma característica.

• Al igual que con la heredabilidad, podemos expresar la repetibilidad (que representaremos con la letra \(\rho\)) como un coeficiente de varianzas tal que: \({\rho=\frac{V_G+V_{E_{perm}}}{V_P}=\frac{V_A+V_D+V_I+V_{E_{perm}}}{V_P}}\)

10.9 La repetibilidad como herramienta en la predicción

En muchos casos, para producciones que se repiten a lo largo de la vida del individuo resulta interesante conocer de antemano que se puede esperar en un nuevo ciclo productivo del mismo. Por ejemplo, en el caso del peso de vellón en lanares, o de la producción de leche en razas lecheras, la producción de frutos en árboles, etc. Como ya vimos antes, en estos casos es interesante plantearse una regresión lineal como predictor de los nuevos valores, basados en los valores anteriores obtenidos para cada animal.

En el caso de que poseamos o usemos un solo registro previo, entonces resulta claro que si la varianza fenotípica del previo y del que vamos a predecir es la misma, entonces el coeficiente de la regresión será igual a

\[ \begin{split} {b_{P_{2}P_{1}}=\frac{Cov_{P_{1}P_{2}}}{V_{P_{1}}}=\frac{Cov_{P_{1}P_{2}}}{\sqrt{V_{P_{1}}V_{P_{2}}}}=\rho} \end{split} \tag{10.68} \]

Por lo tanto, considerando que la regresión la hicimos con valores que son desvíos de la media poblacional, la predicción de un nuevo registro (\({x_2}\)) a partir del registro anterior ($ {x_1}$), a la que llamamos producción más probable y denotamos como \(\mathrm{PMP}\) sería

\[ \begin{split} \mathrm{PMP(x_2)=\bar x+(x_1-\bar x)\rho} \end{split} \tag{10.69} \]

Es decir, se trata de un simple predictor lineal de la próxima producción basado en el desvío del presente registro respecto a la media poblacional, \(\mathrm{(x_1-\bar x)}\). En la práctica, dadas las diferencias sistemáticas que suelen existir entre sexos, por ejemplo, se suelen corregir los registros previamente por esas diferencias sistemáticas. Además, como es posible que existan diferencias de tratamientos entre años o grupos de manejo, entonces es posible realizar las comparaciones respecto a la media del grupo contemporáneo en lugar de la media general.

De acuerdo a lo que vimos antes y al concepto mismo de repetibilidad, cuando disponemos de más registros previos de la misma característica en la vida de un individuo más nos acercamos al verdadero valor de los efectos permanentes y por lo tanto se incrementa la información acerca de las predicciones futuras. Esto nos lleva a considerar la alternativa de desarrollar la regresión no en el último registro (o alguno en particular), sino en el promedio de los mismos. Supongamos que tenemos entonces \(n\) registros de la misma característica en cada individuo y queremos desarrollar un predictor lineal con los mismos para el próximo registro (o sea, el registro \(n+1\)).

Por definición, el coeficiente de regresión para los registros (como desvíos de la media) será

\[ \begin{split} {b_{P_{n+1}P_{\bar n}}=\frac{Cov_{P_{\bar n}P_{n+1}}}{V_{P_{\bar n}}}} \end{split} \tag{10.70} \]

Pero como vimos antes, en la ecuación (10.66) por ejemplo, la varianza del promedio de \(n\) medidas fenotípicas en el mismo individuo es

\[ \begin{split} {\frac{V_P}{V_{\bar P_{n}}}=\frac{n}{1+(n-1)\rho} \therefore} {V_{\bar P_{n}}=\left[\frac{1+(n-1)\rho}{n}\right] V_P} \end{split} \tag{10.71} \]

A su vez, como la covarianza entre la media de \(n\) efectos temporarios y el próximo efecto temporario es cero, la covarianza del promedio de \(n\) medidas fenotípicas con una nueva medida es

\[ \begin{split} {Cov_{P_{\bar n}P_{n+1}}=Cov(A+D+I+E_{perm}+\bar E_{temp},A+D+I+E_{perm}+E_{temp_{n+1}})=}\\ {V_A+V_D+V_I+V_{E_{perm}}=\rho\ V_P } \end{split} \tag{10.72} \]

La última línea de la ecuación anterior surge de que \(\rho=\mathrm{\frac{V_A+V_D+V_I+V_{E_{perm}}}{V_P} \Leftrightarrow V_A+V_D+V_I+V_{E_{perm}}}=\rho\ \mathrm{V_P}\) Sustituyendo el resultado de la ecuación (10.72) en el numerador de la ecuación (10.70) y el resultado de la ecuación (10.71) por el denominador de (10.70), tenemos ahora que

\[ \begin{split} {b_{P_{n+1}P_{\bar n}}=\frac{\rho\ V_P}{\left[\frac{1+(n-1)\rho}{n}\right] V_P}=\frac{n\rho}{1+(n-1)\rho}} \end{split} \tag{10.73} \]

Por lo tanto, en el caso de utilizar el promedio de \(n\) medidas de la misma característica como predictor de la producción más probable en el próximo registro, el coeficiente regresión será el de la ecuación (10.73) y la producción más probable para el registro \(n+1\) será

\[ \begin{split} {PMP(x_{n+1})=\bar x+ (x_{n+1}-\bar x)\left[\frac{n\rho}{1+(n-1)\rho}\right]} \end{split} \tag{10.74} \]

De hecho, podemos escribir el factor que multiplica al desvío del próximo registro como

\[ \begin{split} {\frac{n\rho}{1+(n-1)\rho}=\rho \frac{n}{1+(n-1)\rho}=\rho \left[\frac{n}{1+(n-1)t}\right]} \end{split} \tag{10.75} \]

con \(\mathrm{t}\) el coeficiente de correlación intraclase. En este caso particular \(\mathrm{t}=\rho\), pero vimos antes y lo veremos con más detalle luego que en otros casos \(\mathrm{t=r_{A_{1}A_{2}}h^2}\) (cuando discutimos la varianza del estimador de la heredabilidad por regresión).

Claramente, la ecuación (10.69) es un caso particular de la ecuación (10.74), cuando \(n=1\), es decir cuando la predicción está basada en un solo registro, ya que si \(n=1\) entonces

\[{PMP(x_{n+1})=\bar x+ (x_{n+1}-\bar x)\left[\frac{n\rho}{1+(n-1)\rho}\right]=\bar x+(x_2-\bar x)\left[\frac{(1) \rho}{1+(1-1)\rho}\right]=}\] \[{\bar x+ (x_2-\bar x)\left[\frac{\rho}{1+0}\right]=\bar x+ (x_2-\bar x)\rho=PMP(x_2)}\]

Hasta ahora vimos cómo el incremento en el número de registros nos permite incrementar la precisión en la predicción de una nueva producción. Sin embargo, el mismo criterio se aplica a la predicción del valor de cría a partir de una regresión. Como vimos en la sección La heredabilidad como regresión, el coeficiente de regresión que usábamos para predecir el valor de cría de un animal a partir de un registro fenotípico individual era la heredabilidad, es decir

\[ \begin{split} {\hat A_i=h^2(x_i-\bar x)} \end{split} \tag{10.76} \]

Esto venía de la ecuación (10.3), la que ahora, si consideramos que poseemos la información de \(n\) medidas en el indivuo y usamos su promedio se transforma en

\[ \begin{split} {b_{A\bar P}}=\frac{ {Cov(A,\bar P)}}{ {V_{\bar P}}}=\frac{ {Cov(A,A+D+I+E_{perm}+\bar E_{temp})}}{ {V_{\bar P}}}= {\frac{V_A}{V_{\bar P}}} \end{split} \tag{10.77} \]

Pero como vimos en la ecuación (10.71), \({V_{\bar P_{n}}=\left[\frac{1+(n-1)\rho}{n}\right] V_P}\), por lo que sustituyendo esto en el denominador de la ecuación (10.77) tenemos ahora

\[ \begin{split} {b_{A\bar P_{n}}}= {\frac{V_A}{V_{\bar P}}=\frac{V_A}{\left[\frac{1+(n-1)\rho}{n}\right] V_P}=\frac{V_A}{V_P}\left[\frac{n}{1+(n-1)\rho}\right]=h^2 \left[\frac{n}{1+(n-1)\rho}\right]} \end{split} \tag{10.71} \]

Por lo tanto, con este coeficiente de regresión, el predictor del valor de cría de un individuo a partir del promedio de \(n\) registros fenotípicos en el mismo será

\[ \begin{split} {\hat A_i=h^2 \left[\frac{n}{1+(n-1)\rho}\right] (x_i-\bar x)} \end{split} \tag{10.78} \]

y la precisión de la estimación, \(r_{AC}\), estará dada ahora por

\[ \begin{split} {r_{AC}=h \sqrt{\frac{n}{1+(n-1)\rho}}} \end{split} \tag{10.79} \]

en lugar de \(h\), que era cuando teníamos un solo registro. Obviamente, sustituyendo \(n=1\) en la ecuación (10.73), es decir un solo registro, obtenemos el mismo resultado \(\mathrm{r_{AC}=h}\).

PARA RECORDAR

• El concepto de repetibilidad se desprende del interés de conocer de antemano (para producciones que se repiten a lo largo de la vida del individuo) qué se puede esperar en un nuevo ciclo productivo del mismo.

• La predicción de un nuevo registro (\(x_2\)) a partir del registro anterior (\(x_1\)), a la que llamamos producción más probable (PMP) sería: \({PMP(x_2)=\bar x+(x_1-\bar x)\rho}\) que se trata de un predictor lineal de la próxima producción basado en el desvío del presente registro respecto a la media poblacional (\({(x_1-\bar x)}\)) o al grupo contemporáneo.

• Cuando tenemos más de un registro, podemos calcular la PMP para el registro \(n+1\): \({PMP(x_{n+1})=\bar x+ (x_{n+1}-\bar x)\left[\frac{n}{1+(n-1)t}\right]}\) siendo \(t\) el coeficiente de correlación intraclase.

• El predictor del valor de cría de un individuo a partir del promedio de \(n\) registros fenotípicos en el mismo será: \({\hat A_i=h^2 \left[\frac{n}{1+(n-1)\rho}\right] (x_i-\bar x)}\) y la precisión de la estimación, \(r_{AC}\), estará dada ahora por \({r_{AC}=h \sqrt{\frac{n}{1+(n-1)\rho}}}\)

10.10 Evolucionabilidad

Un tema importante en términos evolutivos es la capacidad de evolucionar de una característica y que por lo tanto ha adoptado el extraño término de evolucionabilidad en castellano (como traducción de “evolvability”). En principio, resulta tentador pensar en la heredabilidad de una característica como su potencial de evolucionar, particularmente a partir de la ecuación del criador \({R=h^2S}\). En un artículo de gran profundidad conceptual, Houle (1992) plantea que la heredabilidad no es una buena medida de la capacidad de evolucionar de una característica. En lugar de proponer estandarizar la varianza aditiva entre la varianza fenotípica, propone en su lugar la estandarización a partir de la media de la característica usando el coeficiente de variación aditivo, es decir el desvío aditivo dividido la media de la característica \({CV_A= \frac{\sigma_A}{\bar x}}\).

De esta manera, de acuerdo con Houle (1992), características que presentan sistemáticamente baja heredabilidad, como las directamente asociadas al fitness (por ejemplo, las reproductivas), tendrian una gran evolucionabilidad, mayor a las morfológicas (que tienen usualmente heredabilidad alta) cuando se realiza la estandarización por la media. Sin embargo, utilizar un coeficiente de variación solo tiene sentido para características en las que la media tiene un sentido biológico intrínseco y además la respuesta a la selección natural o artificial es una función de \({h\ \sigma_A}\), por lo que no solo depende de la varianza aditiva sino también de la heredabilidad.

En resumen, si bien la heredabilidad no es una buena medida de la capacidad de evolucionar de una característica, la alternativa planteada por Houle (1992) también presenta problemas importantes y su campo de aplicación es restringido.

PARA RECORDAR

• La capacidad de evolucionar de una característica y ha tomado el término de evolucionabilidad y se ha planteado que la heredabilidad no es una buena medida de la misma. En su lugar se ha propuesto la estandarización a partir de la media de la característica usando el coeficiente de variación aditivo, es decir el desvío aditivo dividido la media de la característica \({CV_A= \frac{\sigma_A}{\bar x}}\).

10.11 Conclusión

En este capítulo presentamos un concepto de suma importancia para la teoría de genética cuantitiva y el mejoramiento genético: la heredabilidad. Como vimos en los capítulos anteriores no siempre resulta fácil estimar los componentes de la varianza fenotípica en la realidad, ya que algunos de ellos requerirían de condiciones demasiado costosas o incluso inmedibles en la actualidad (podemos pensar en los componentes epistáticos o algunos casos respecto a la variabilidad ambiental). Afortunadamente, la heredabilidad es una medida que teniendo en cuenta la componente genético aditiva y la varianza fenotípica total nos permite tener una cuantificación de la similitud entre parientes para un caracter de interés. La selección (ya sea natural o artificial) sólo puede operar sobre componentes hereditarios, por lo que resulta claro que para poder realizar un análisis racional del proceso de selección artificial es necesario poseer una medida que nos permita estimar en qué medida los valores fenotípicos observados en una generación se ven reproducidos en la siguiente; todo esfuerzo de selección será vano si la variabilidad fenotípica observada no se explica por un componente hereditario. Por lo tanto, ahora sí nos encontramos prontos para utilizar los conocimientos teóricos y prácticos desarrollados en este capítulo, combinado con nuestro conocimiento de los procesos selectivos, para llevar nuestra atención al proceso de selección artificial.

10.12 Actividades

10.12.1 Control de lectura

1. Defina el concepto de heredabilidad, describiendo el mismo matemática y conceptualmente.
2. A partir de la observación de fenotipos es posible predecir la heredabilidad de un carácter de interés. ¿Cómo se logra esto? Tenga en cuenta los posibles errores del método descrito.
3. Defina el concepto de repetibilidad, describiendo el mismo matemática y conceptualmente.
4. ¿Cuál es la diferencia conceptual entre repetibilidad y heredabilidad? ¿Estos parámetros son referentes a un individuo o una población?
5. Es posible hacer una regresión de los valores fenotípicos de una progenie (o un conjunto de progenies) en i) los valores fenotípicos de un progenitor, o ii) del promedio de los progenitores. ¿Qué información se puede obtener en cada uno de estos procedimientos?

10.12.2 ¿Veradero o falso?

1. Todos los componentes genéticos del fenotipo son heredables de padres a hijos.
2. La heredabilidad de una característica se define como \(h = \sqrt{\frac{V_A}{V_P}}\) (o lo que es equivalente, \(h^2 = \frac{V_A}{V_P}\)).
3. La estimación de la heredabilidad a partir de caracteres fenotípicos por métodos de regresión es dependiente de qué carácter se desea estudiar.
4. La repetibilidad de una característica será siempre mayor o igual a la heredabilidad de la misma.
5. La producción más probable (PMP) de una población nos posibilita predecir un nuevo registro de una característica basándonos en un registro previo de la misma.

Soluciones

1. Falso. Según el modelo genético básico podemos descomponer la variabilidad fenotípica en un componente de efectos genéticos aditivos, de dominancia y ambiental. Los primeros dos son componentes que refieren a la genética de los individuos, pero sólo el primero es heredable (en tanto los genotipos de un progenitor no son heredables por su progenie).

2. Falso. El símbolo utilizado para denotar a la heredabilidad es \(h^2\), pero no se trata de una cantidad elevada al cuadrado. Matemáticamente, la heredabilidad se define como \(h^2 = \frac{V_A}{V_P}\) (y no la raíz de esta fracción).

3. Verdadero. Esto se ve claramente al tener en cuenta que el coeficiente de Pearson para una recta de regresión entre heredabilidad y carácter fenotípico posee una magnitud de \(h\) (proporcional a la heredabilidad, \(h^2\)). Esto implica que la estimación de heredabilidad poseerá un error de estimación que depende de la heredabilidad del carácter estudiado.

4. Verdadero. Teniendo en cuenta la definición en términos de varianza de ambos parámetros (y recordando que no existen las varianzas negativas) podemos notar que la repetibilidad es mayor a la heredabilidad en una magnitud \(\frac{V_D + V_I + V_{Ep}}{VP}\). Es decir, a lo sumo la repetibilidad puede ser igual a la heredabilidad de una característica, pero nunca menor a esta.

5. Falso. Si bien la PMP nos permite predecir un registro de una característica basándonos en registros anteriores, es importante recordar que este no es un parámetro poblacional, sino que se calcula para cada individuo de una población.

10.12.3 Ejercicios

Ejercicio 10.1

(Inspirado en J. Felsenstein 2019)

Una población de tamanduás (T. tetradactyla) posee un largo promedio de lengua de \(63,2 \text{ cm}\), con una varianza de \(8,4 \text{ cm}^2\). La correlación padre-hijo es de \(0,43\).

a. ¿Cuál es la heredabilidad del caracter fenotípico “largo de lengua”?

b. Si elegimos machos que tengan lenguas de exactamente \(70 \text{ cm}\) y los apareamos con hembras tomadas al azar, cuál es el valor medio más probable para el largo de lengua de la descendencia? Nota: asuma que la varianza genotípica es de \(6,7 \text{ cm}\) aproximadamente.

Solución

a. Recordemos que la correlación padre-hijo equivale a \(\frac{1}{2} h^2\), por lo que \(0,43 = \frac{1}{2} h^2 \Rightarrow h^2 = 0,43 \cdot 2 = 0,86\).

b. El valor medio más probable (equivalente al concepto de \(\text{PMP}\) presentado en el capítulo) viene dado por

\[\text{PMP} = \bar{x} + (x_1 - \bar{x})\rho\]

donde \(\bar{x}\) es la media poblacional para el caracter fenotípico de interés, \(x_1\) es la media de la población seleccionada respecto a dicho promedio y \(\rho\) es la repetibilidad.

Tengamos en cuenta que \(\rho = \frac{V_G}{VP} = \frac{6,7}{8,4}\). Tenemos entonces

\[\text{PMP} = 63,2 + (70 - 63,2) \cdot (\frac{6,7}{8,4})\]

\[\text{PMP} \approx 68,62 \text{cm}\]

Ejercicio 10.2

Un conjunto de investigadores se encontraban investigando parámetros genéticos relacionados a la resistencia de la fibra de cáñamo (Cannabis sativa) con fines industriales. Sin embargo, víctimas de su propio desorden, obtuvieron resultados pero no recuerdan a qué corresponden cada uno. En un cuaderno de laboratorio encontraron que un parámetro estimado era de \(0,562\) y otro de \(0,734\).

Otro grupo de investigación, más ordenado, estimó para esa población que la covarianza padre-hijo es de \(0,142\).

a. ¿Cuál de los valores encontrados por el grupo de investigación corresponde a la heredabilidad y cuál a la repetibilidad?

b. ¿Cuál es la estimación para la varianza fenotípica para la característica “resistencia de la fibra” en esta población?

Solución

a. Como podemos recordar, la repetibilidad es el límite superior de la heredabilidad, es decir, en un caso extremos ambas serían iguales si \(\frac{V_D + V_I + V_{Ep}}{VP} = 0\). Por lo tanto, la estimación de 0,562 corresponde a la heredabilidad y la de 0,734 a la repetibilidad de la característica.

b. Para lograr una estimación de la varianza fenotípica de la característica, podremos valernos de dos datos: la heredabilidad y la covarianza que existe entre padres e hijos para la misma.

Recordemos que \(h^2 = \frac{V_A}{V_P}\) y que \(COV_{PH}= \frac{1}{2}V_A\) por lo que:

\[V_A=COV_{PH}*2 = 0,142*2 = 0,284\] \[V_P=\frac{V_A}{h^2} = \frac{0,284}{0,562} \approx 0,505\]

Ejercicio 10.3

(Tomado de Hartl 2020)

Demostrar que en una población en equilibrio de Hardy-Weinberg:

a. La heredabilidad en sentido estricto de una característica determinada completamente por un alelo autosomal recesivo con frecuencia \(q\) equivale a \(2q/(1+q)\), lo cual implica que \(h^2 \approx 0\) para \(q \approx 0\). (Pista: si \(V_E = 0\), entonces \(V_G = V_A + V_D\))

b. La heredabilidad de una característica determinada por un solo alelo autosomal dominante con frecuencia \(q\) equivale a \(2(1-q)/(2-q)\), lo cual implica que \(h^2 \approx 1\) para \(q \approx 0\)

Solución

a. Para un alelo recesivo \(d = a\), y por lo tanto \(\alpha = a + (q -p) d = 2qa\). Por lo tanto, \(V_A = 2pq \alpha^2 = 8pq^3a^2\) y \(V_D = 4p^2q^2a^2\). Luego, notemos que \(h^2 = \frac{V_A}{V_A + V_D}\), expresión que queda reducida a \(2q/(1+q)\), como se quería demostrar.

b. En este caso tenemos que \(d = -a\). Por lo tanto, \(V_A = 8p^3qa^2\) y \(V_D = (2pqd)^2 = 4p^2q^2a^2\). Por lo tanto, la expresión \(h^2 = \frac{V_A}{V_A + V_D}\) se reduce a \(2(1-q)(2-q)\).

Ejercicio 10.4

El peso adulto de las ratas de laboratorio es un carácter de gran importancia debido a que puede afectar los resultados experimentales. En este sentido, se han estimado los siguientes valores de cría para los individuos Ratín (\(VC=-5,12\)), Ratón (\(VC=12,16\)) y Ratún (\(VC=-1,28\)) pertenecientes a una población cuya media es 24 g. Los registros fenotípicos utilizados para estas estimaciones fueron de 16, 43 y 22 g respectivamente. ¿Cuál es la heredabilidad de la característica?

Solución

Recordemos que \(VC= (x_i - \bar{x}) h^2\) por lo que \(h^2= \frac{VC}{(x_i - \bar{x})}\), entonces podremos comprobar que:

\[h^2= \frac{-5,12}{(16 - 24)}=0,64\] \[h^2= \frac{12,16}{(43 - 24)}=0,64\] \[h^2= \frac{-1,28}{(22 - 24)}=0,64\]

Ejercicio 10.5

Un productor de porcinos se ha propuesto refugar dos cerdas que actualmente se encuentran en producción por falta de espacio en las parideras. Su criterio será basarse en el tamaño de camada que logra destetar cada cerda y refugar los animales que tengan las camadas más pequeñas al momento del destete. A su vez, se ha logrado estimar para la población que la varianza genética es de 1.2 individuos\(^2\), la varianza genética no aditiva es de 0.4 individuos\(^2\), la varianza ambiental permanente es de 2.1 individuos\(^2\) y la la varianza ambiental total es de 4.4 individuos\(^2\). La media de esta población es de 9.9 lechones destetados. Por otra parte las candidatas a ser refugadas son:

• Cerda 0837: 3 partos con camadas de 13, 9 y 8 lechones destetados

• Cerda 3759: 5 partos con camadas de 8, 5, 14, 0 y 9 lechones destetados

• Cerda 0193: 5 partos con camadas de 2, 9, 11, 8 y 8 lechones destetados

• Cerda 4132: 2 partos con camadas de 10 y 8 lechones destetados

• Cerda 2845: 1 parto con 11 lechones destetados

Con esta información,

a. ¿Qué cerdas refugaría? b. ¿Cuál sería una estimación de la heredabilidad de la característica?

Solución

a. Para poder evaluar a estos animales como productores y realizar una elección de refugo, debemos evaluarlos en cuanto a su producción. Para ellos calcularemos la producción más probable (PMP) según la ecuación REF tal que:

\({PMP}= \mu + \frac{nR}{1 + (n-1)R}(\bar x_{i} - 𝜇)\)

Pero previamente deberemos calcular la repetibilidad:

\[\rho=\frac{\mathrm{\sigma_G^2 + \sigma_{EP}^2 }}{\mathrm{\sigma_P^2}}=\frac{1.2 + 2.1}{6.6}=0,50\]

Ahora podemos calcular la PMP de cada cerda y tomar la decisión de refugo:

Cerda 0837:

\[\text{PMP}= 9,9 + \frac{3 \cdot 0,5}{1 + (3 - 1) \cdot 0,5} \cdot (10 - 9.9) = 10 \text{ lechones destetados}\]

Cerda 3759:

\[\text{PMP}= 9,9 + \frac{5 \cdot 0,5}{1 + (5 - 1) \cdot 0,5} \cdot (7.2 - 9.9) = 7.7 \text{ lechones destetados}\]

Cerda 0193:

\[{PMP}= 9,9 + \frac{5 \cdot 0,5}{1 + (5 - 1) \cdot 0,5} \cdot (7.6 - 9.9) = 8 \text{ lechones destetados}\]

Cerda 4132:

\[{PMP}= 9,9 + \frac{2 \cdot 0,5}{1 + (2 - 1) \cdot 0,5} \cdot (9.0 - 9.9) = 9.3 \text{ lechones destetados}\]

Cerda 2845: 1 parto con 11 lechones destetados

\[{PMP}= \mu + R (\bar x_{i} - \mu)= 9,9 +0,5 \cdot (11 - 9,9) = 10,5 \text{ lechones destetados}\]

Entonces, las cerdas a ser refugadas serán la 3759 y 0193, debido a que sus PMP son las menores.

b. Como sabemos la heredabilidad (\(h^2\)) puede calcularse como:

\[h^2=\frac{\mathrm{\sigma_A^2}}{\mathrm{\sigma_P^2}}\]

Entonces, utilizando la información de esta población podemos despejar la varianza aditiva (\(𝜎_A^2\)) ya que la varianza genética total es la suma de la varianza genética aditiva y no aditiva. A su vez, la varianza fenotípica, es la suma de la varianza genética total y varianza ambiental total, por lo tanto:

\[h^2=\frac{\mathrm{1,2-0,4}}{\mathrm{1,2+4,4}} \approx 0,14\]

---

Bibliografía

Bell, Washington, Jorge I. Urioste, Nelson Barlocco, Antonio Vadell, and Raquel Pérez Clariget. 2015. “Genetic and Environmental Factors Affecting Reproductive Traits in Sows in an Outdoor Production System.” Livestock Science 182: 101–7. https://doi.org/https://doi.org/10.1016/j.livsci.2015.10.025.

Byars, S. G., D. Ewbank, D. R. Govindaraju, and S. C. Stearns. 2010. “Colloquium papers: Natural selection in a contemporary human population.” Proc Natl Acad Sci U S A 107 Suppl 1 (January): 1787–92.

Castells Montes, Daniel. 2008. “EVALUACIÓn DE RESISTENCIA GENÉTICA DE OVINOS CORRIEDALE a LOS NEMATODOS GASTROINTESTINALES EN URUGUAY: Heredabilidad y Correlaciones Genéticas Entre El Recuento de Huevos de Nematodos y Caracterı́sticas Productivas EVALUACIÓn DE RESISTENCIA GENÉTICA DE OVINOS CORRIEDALE a LOS NEMATODOS GASTROINTESTINALES EN URUGUAY: Heredabilidad y Correlaciones Genéticas Entre El Recuento de Huevos de Nematodos y Caracterı́sticas Productivas.” Master’s thesis, Facultad de Agronomı́a - Universidad de la República.

Cellon, C., R. R. Amadeu, J. W. Olmstead, M. R. Mattia, L. F. V. Ferrao, and P. R. Munoz. 2018. “Estimation of Genetic Parameters and Prediction of Breeding Values in an Autotetraploid Blueberry Breeding Population with Extensive Pedigree Data.” Euphytica 214 (87).

Ciappesoni, Gabriel, Ignacio De Barbieri, Diego Gimeno, and Fabio Montossi. 2011. “Parámetros Genéticos Para ı́Ndices de Selección de La Raza Merino Australiano.” Revista Argentina de Producción Animal.

Dohm, M. R. 2002. “Repeatability Estimates Do Not Always Set an Upper Limit to Heritability.” Functional Ecology 16: 273–80.

———. 1960. Introduction to Quantitative Genetics. Oliver & Boyd, Edinburgh.

———. 1983. Introducción a La Genética Cuantitativa. CIA. Editorial Continental, S.A. de C.V.

Falconer, Douglas S, and Trudy FC Mackay. 1996. Quantitative Genetics. Benjamin-Cummings Pub Co.

Felsenstein, J. 2019. Theoretical Evolutionary Genetics. University of Washington. https://felsenst.github.io/pgbook/pgbook.html.

Frioni, Nicolás. 2012. “Estimación de Heredabilidad Del Intervalo Entre Partos y Su Correlación Genética Con Producción de Leche En Ganado Holando Uruguayo.” Facultad de Agronomı́a - Universidad de la República.

———. 2016. “Estimación de Parámetros Genéticos En Caracterı́sticas Reproductivas y Productivas Para La Raza Holando En Uruguay.” Master’s thesis, Facultad de Agronomı́a - Universidad de la República.

Galton, Francis. 1886. “Regression Towards Mediocrity in Hereditary Stature.” Journal of the Anthropological Institute 15: 246–63.

Goldberg, Virginia, Gabriel Ciappesoni, and Ignacio Aguilar. 2012. “Genetic Parameters for Nematode Resistance in Periparturient Ewes and Post-Weaning Lambs in Uruguayan Merino Sheep.” Livestock Science 147 (1): 181–87. https://doi.org/https://doi.org/10.1016/j.livsci.2012.05.003.

Hadfield, Jarrod D. 2010. “MCMC Methods for Multi-Response Generalized Linear Mixed Models: The MCMCglmm R Package.” Journal of Statistical Software 33 (2): 1–22. https://www.jstatsoft.org/v33/i02/.

Hartl, Daniel L. 2020. A Primer of Population Genetics and Genomics. 4th ed. London, England: Oxford University Press.

Hill, W. G. 1972. “Estimation of realised heritabilities from selection experiments. I. Divergent selection.” Biometrics 28 (3): 747–65.

Houle, D. 1992. “Comparing evolvability and variability of quantitative traits.” Genetics 130 (1): 195–204.

López-Correa, Rodrigo D. 2013. “Variabilidad Genética Del Desempeño de Caballos Criollos En Pruebas de Resistencia.” Master’s thesis, Facultad de Agronomı́a - Universidad de la República.

López-Correa, Rodrigo D, Francisco Peñagaricano, Gabriel Rovere, and Jorge Ignacio Urioste. 2018. “Genetic Parameter Estimation for Long Endurance Trials in the Uruguayan Criollo Horse.” Journal of Animal Breeding 135 (3): 186–93.

Lstibůrek, M., V. Bittner, G. R. Hodge, J. Picek, and T. F. C. Mackay. 2018. “Estimating Realized Heritability in Panmictic Populations.” Genetics 208 (1): 89–95.

Lynch, M. 1991. “METHODS FOR THE ANALYSIS OF COMPARATIVE DATA IN EVOLUTIONARY BIOLOGY.” Evolution 45 (5): 1065–80.

Marco de Lima, B., E. P. Cappa, O. B. Silva-Junior, C. Garcia, S. D. Mansfield, and D. Grattapaglia. 2019. “Quantitative genetic parameters for growth and wood properties in Eucalyptus "urograndis" hybrid using near-infrared phenotyping and genome-wide SNP-based relationships.” PLoS One 14 (6): e0218747.

Mrode, Raphael. 2014. Linear Models for the Prediction of Animal Breeding Values. 3rd ed. CABI.

Naya, H., D. Gianola, H. Romero, J. I. Urioste, and H. Musto. 2006. “Inferring parameters shaping amino acid usage in prokaryotic genomes via Bayesian MCMC methods.” Mol Biol Evol 23 (1): 203–11.

Naya, H., F. Peñagaricano, and J. I. Urioste. 2017. “Modelling female fertility traits in beef cattle using linear and non-linear models.” J Anim Breed Genet 134 (3): 202–12.

Sánchez, A. L., J. I. Urioste, F. Peñagaricano, K. Neimaur, I. Sienra, H. Naya, and R. Kremer. 2016. “Genetic parameters of objectionable fibers and of their associations with fleece traits in Corriedale sheep1.” Journal of Animal Science 94 (1): 13–20. https://doi.org/10.2527/jas.2015-9619.

Schmidt, P., J. Hartung, J. Rath, and H.-P. Piepho. 2019. “Estimating Broad-Sense Heritability with Unbalanced Data from Agricultural Cultivar Trials.” Crop Science 59: 525–36.

Sorensen, Daniel, and Daniel Gianola. 2002. Likelihood, Bayesian, and MCMC Methods in Quantitative Genetics. Springer-Verlag.

Visscher, P. M., W. G. Hill, and N. R. Wray. 2008. “Heritability in the genomics era–concepts and misconceptions.” Nat Rev Genet 9 (4): 255–66.

Wooldrigde, Jeffrey M. 2013. Introductory Econometrics: A Modern Approach. 5th. ed. South-Western, Cengage Learning.

———. 1921. “Systems of Mating. I. the Biometric Relations between Parent and Offspring.” Genetics 6 (2): 111–23.

---

86. Sir Francis Galton (16 febrero 1822 – 17 enero 1911) fue un científico y “polymath” inglés de la era victoriana. Entre otras área del conocimiento abundó en estadística, sociología, sicología, antropología, metereología y geografía. Además, propuso las técnicas de análisis de correlación y regresión que serían fundamentales para el desarrollo temprano de la genética.↩︎

87. Karl Pearson (27 marzo 1857 – 27 abril 1936) fue un matemático y estadístico inglés, fundador de la estadística matemática, propulsor del darwinismo social, la eugenesis y aún del “racismo científico”. Curador y biógrafo oficial de Sir Francis Galton, sus aportes a la bioestadística fueron fundamentales para el desarrollo de las ciencias biológicas en general y de la genética en particular.↩︎