Capítulo 7 Genética de poblaciones microbianas

En general, todos tenemos una visión muy antropocéntrica de la vida y por lo tanto nos cuesta muchas veces tomar real magnitud de la variabilidad existente entre lo que vemos, mucho más en lo que no vemos. El conocimiento de la existencia de vida microscópica tiene varios siglos, pero no fue hasta la aparición del microscopio que comenzamos a apreciar su importancia y empezar a sospechar de su diversidad. Más aún, no fue hasta los trabajos de Louis Pasteur⁶⁴ que se apreció la relevancia de los mismos, tanto en la enfermedad como en los procesos biotecnológicos usuales en nuestra alimentación. A partir de ese momento fue claro que la diversidad de organismos microscópicos era enorme y que su importancia para la vida del planeta también lo era. No es, sin embargo, hasta los trabajos de Carl Woese⁶⁵, entrando en el último cuarto del siglo XX, que se aprecia que dentro de esos organismos la diversidad surgía a nivel basal en el árbol de la vida y que dos de los tres dominios de la vida (archaea y bacteria) eran de organismos microscópicos a los que juntos denominamos procariotas (porque no poseen un núcleo altamente organizado, como los eucariotas).

Estos organismos, los procariotas, poseen una diversidad de estilos de vida enorme y los podemos encontrar en los ambientes que nos imaginemos, desde las fuentes termales oceánicas con temperaturas cercanas a los \(100^{\circ}\)C, hasta en la Antártida, desde nuestra piel hasta nuestros intestinos, en el rumen, en la rizósfera, en las aguas ácidas del drenaje de las minas, en el océano y en casi todos los ambientes conocidos en los que exista vida. Pequeños y con gran capacidad de multiplicación, comparten algunas características importantes entre ellos pero se diferencian en otras importantes, por ejemplo entre archaeas y bacterias a nivel de la maquinaria y procesos moleculares. Sin embargo, para el cometido del presente capítulo, alcanza con agruparlos en el término procariotas y ya los distinguiremos cuando sea necesario.

OBJETIVOS DEL CAPÍTULO

\(\square\) Describir las particularidades genéticas de los procariotas, comparandolos con los eucariotas diploides que hemos utilizado como modelo en el desarrollo de modelos matemáticos y conceptuales en capítulos anteriores. Examineramos modelos aleatorios alternativos al modelo de Wright-Fisher presentado en capítulos anteriores, interconectando los modelos obtenidos.

\(\square\) Comprender la dinámica de las poblaciones microbianas y los factores que contribuyen a su crecimiento rápido, analizando los límites de este crecimiento a partir de modelos matemáticos explícitos.

\(\square\) Explorar el papel de la selección en organismos monoploides y su influencia en la dinámica poblacional. Discutiremos también el rol del estudio de organismos procariotas en el debate entre las teorías seleccionistas y neutralistas de la evolución molecular.

\(\square\) Discutir cómo los avances tecnológicos en genómica contribuyen a la comprensión de la dinámica poblacional en procariotas. \(\square\) Abordar el tema de la resistencia a los antimicrobianos en el contexto de la genética de poblaciones de microorganismos.

7.1 Genómica y mecanismos de herencia en procariotas

Hasta ahora nos hemos manejado con las ideas y conceptos fundamentales acerca de los mecanismos de herencia que se corresponden con organismos diploides y poliploides, esencialmente en eucariotas casi sin mención a los procariotas. Si bien en lo que respecta a los mecanismos conceptuales de duplicación de la información existen pocas diferencias que sean relevantes para nuestro enfoque del curso, las diferencias a otros niveles son sustantivas y tienen profundas implicancias en los distintos procesos evolutivos que ocurren en las poblaciones. Hasta hace relativamente poco se consideraba que los procariotas eran constitutivamente haploides, de alguna forma vinculándolo al hecho de un núcleo relativamente desorganizado (respecto a eucariotas), pero de un tiempo a esta parte se viene acumulando evidencia que apunta a que la poliploidía se trataría de un fenómeno bastante extendido también en procariotas (Soppa 2014). Ejemplos notables son la bacteria Deinococcus radiodurans, altamente tolerante a las radiaciones y que posee entre 4 y 10 copias de su genoma (dependiendo, entre otras cosas, de la velocidad de crecimiento), o la arquea Haloferax volcanii que es capaz de usar las copias extras de su genoma como fuente de almacenamiento de fosfato. Pese a los variados contra-ejemplos, la norma sigue siendo por el momento que la mayor parte de los procariotas son haploides (o monoploides, un término posiblemente más adecuado). Por lo tanto, en este capítulo le dedicaremos una atención importante a este tema y a cómo ésta característica afecta a la dinámica evolutiva de las poblaciones procariotas.

Otra diferencia notable entre procariotas y eucariotas es la existencia de circularidad en los cromosomas de los primeros. Mientras que en los eucariotas los cromosomas son lineales (lo cual implica un gran problema respecto a la conservación de sus extremos), en el caso de los procariotas la mayor parte de las especies poseen cromosomas circulares, sin bordes libres. En eucariotas los riesgos y dificultades que implica la existencia de bordes libres en los cromosomas (e.g., para la replicación del ADN) se han resuelto a través de la aparición de telómeros, y es generalmente aceptado que la longitud de éstos se relaciona estrechamente con la edad celular. Por otro lado, la circularidad existente en cromosomas procariotas presenta también sus desafíos, en particular en lo que respecta a la separación de las dos copias resultantes de la replicación del genoma. De hecho, existen abundantes ejemplos de procariotas que poseen cromosomas lineales, y diversos eventos de linealidad-circularidad parecen haber ocurrido en diversos puntos de la filogenia de procariotas (Moldovan 2019).

Ambos puntos mencionados anteriormente, la existencia de genomas haploides en procariotas y la circularidad de los mismos, presentan un desafío importante al momento de aplicar los conceptos y modelos de recombinación y el desequilibrio de ligamiento tratados en capítulos anteriores. Mientras que la existencia de una sola copia del genoma en las células presenta la obvia restricción de que resulta imposible recombinar con la otra copia genómica (porque no existe), es importante tener en cuenta que los procariotas sin embargo acceden a otros mecanismos que posibilitan la recombinación genética dentro de la especie, o aún la incorporación de material genético de otras especies (fenómeno conocido como transferencia horizontal). Los mecanismos clásicos de intercambio genético de las bacterias incluyen la transducción, la transformación y la conjugación. En el primero de estos mecanismos un bacteriófago⁶⁶ se adsorbe sobre la superficie bacteriana para inyectar su material genético en la célula. Dependiendo de si se trata de un fago virulento o moderado, el programa genético puede derivar en un ciclo lítico donde se producirán múltiples copias del mismo y la concomitante lisis celular, o el fago puede integrar su ADN en el genoma bacteriano, transformándose en un profago, hasta que en algún momento se produzca la inducción del mismo (i.e., la activación del fago); a través de este proceso el fago puede arrastrar material genético adicional de unas bacterias a otras.

El segundo mecanismo es la transformación, donde luego de entrar en un estado particular conocido como competencia, las células bacterianas son capaces de captar ADN libre de doble cadena e incoroporarlo en su genoma. En las bacterias Gram-positivas la bacteria no discrimina entre ADN homólogo y heterólogo, aunque la incorporación depende de la similaridad de secuencias, mientras que en el caso de las Gram-negativas la bacteria reconoce la diferencia y en general solo incorporará material de la misma especie o de especies estrechamente relacionadas. El tercer mecanismo, la congujación, podríamos decir que es lo más cercano al intercambio de material genético vía sexo en bacterias. En este mecanismo existen bacterias (denominadas \(F^+\)) que poseen un plásmido conjugativo, que lleva a la formación de vios pili⁶⁷ en la superficie que le permiten hacer contacto con bacterias que carecen de dicho plásmido (\(F^-\)). Luego de ese contacto, la despolimerización en la base de los pelos lleva a que las bacterias se acerquen y exista un contacto estrecho, formándose un puente citoplasmático por donde se transfiere el material genético del plásmido. La transferencia de ADN desde una célula \(F^+\) a una \(F^-\) es un proceso especial de replicación asimétrica por círculo rodante, donde una de las dos cadenas parentales del plásmido F pasa a la célula receptora, replicándose en ella, mientras que la otra cadena parental se queda en el donador, sirviendo a su vez como molde para la síntesis de una nueva cadena complementaria; este hecho explica además por qué las células \(F^+\) siguen siendo \(F^+\) después de la conjugación. De hecho, se ha observado que el proceso suele ocurrir en agregados de bacterias donde en lugar de formarse parejas específicas se dan intercambios entre varias a la vez (Achtman 1975). ¡No parece ser tan mala la vida de las bacterias, después de todo!.

El otro problema con la forma en que vimos el desequilibrio de ligamiento es que a medida de que nos alejábamos de una posición dentro de un mismo cromosoma (i.e., a medida de que aumentaba la distancia física entre dos loci), se esperaba que el desequilibrio se fuese atenuando en los cromosomas lineales. Más aún, vimos a partir de algunas estimaciones que la distancia genética por \(cM\) es del orden de \(1,25\ text{Mb}\), o al revés \(\approx 0,8\ \text{Mb/cM}\) en bovinos, mientras que estimaciones más precisas para el genoma humano son del orden de \(0,75\ \text{Mb/cM}\). En procariotas, si bien la variabilidad del tamaño del genoma es enorme, desde alguna centenas de \(Kb\) hasta más de \(10\ \text {Mb}\), la misma es mucho menor en órdenes de magnitud que la existente en eucariotas. Un genoma bacteriano promedio se encuentra en el orden de los \(4\ \text{Mb}\) (e.g., Escherichia coli, el caballito de batalla de la microbiología). Con los números de recombinación en los genomas bovino y humano no existiría mucho espacio para el equilibrio de ligamiento en procariotas, ya que \(4\ \text{Mb}\) divididos entre \(0,75\ \text{Mb/cM}\) nos da aproximadamente \(5,33\ \text{cM}\). Peor aún, eso sería entre loci ubicados en los extremos de un cromosoma lineal, pero como se aprecia en la Figura 7.1, en un cromosoma circular la máxima distancia entre dos puntos para un cromosoma de largo \(L\) es igual a \(L/2\): si nos pasamos de ese punto en el círculo, lo que aumentamos por un lado disminuye por el otro y como en lo que hace a distancia física lo relevante es la menor de las distancias consideradas, esta será siempre \(\leqslant L/2\). Es decir, en un cromosoma de tamaño \(4\ \text{Mb}\) esto implicaría, con las tasa de recombinación de humano, un máximo de \(\approx 2,7\ \text{cM}\) entre los loci a mayor distancia.

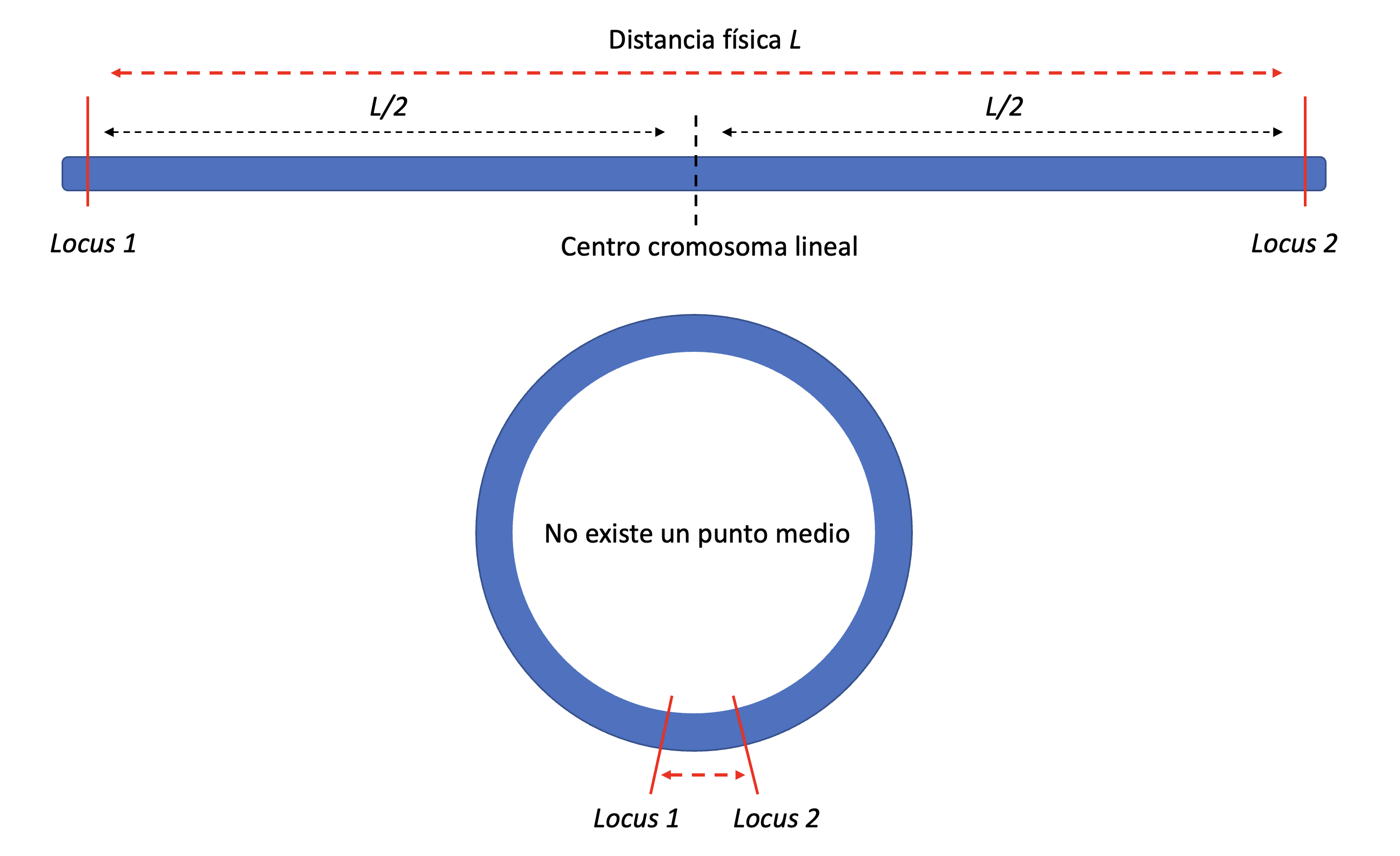
Figura 7.1: Distancia física y sus implicancias para la recombinación de cromosomas lineales y circulares. Mientras que en el cromosoma lineal la mayor distancia física ocurre entre loci que se encuentran el los extremos (y es equivalente, por lo tanto, al largo del cromosoma \(L\)), en los cromosomas circulares la distancia máxima es \(L/2\), ya que en los mismos una distancia \(L\) implica una vuelta al punto de partida.

Obviamente que estos cálculos no aplican al caso de los procariotas. Por un lado, porque los mecanismos de recombinación son completamente diferentes. En procariotas un evento de recombinación requiere de dos puntos de intercambio, el inicio y fin, por lo que se asemeja al mecanismo de conversión génica que hemos discutido previamente. Por el otro, porque las tasas calculadas para bovinos y humano en un evento de recombinación de material genético de la misma célula no son comparables con un proceso que requiere la llegada de material genético externo a la célula. Este material externo será en general producto de células cercanas y, dado que las bacterias se dividen por fisión, es de esperar que las mismas sean descendientes de la misma célula ancestral que originó a la receptora poco tiempo antes (ya veremos que la dinámica de las poblaciones bacterianas suele ser vertiginosa). Esto implica que el material con el que se va producir la recombinación es idéntico (o a lo sumo casi idéntico) que el del organismo receptor, por lo que será imposible distinguir los efectos de la recombinación. En conjunto estos fenómenos generan el efecto de casi-clonalidad que es posible apreciar en muchas poblaciones bacterianas, pudiendo llevar a subestimar la tasa de recombinación de las mismas. Dicho de otra forma, si nuestro muestreo de bacterias está formado por los integrantes de una colonia que desciende de una sola bacteria inicial, será casi imposible observar variabilidad genética. Esto se debe a que la misma depende de las mutaciones que hayan arribado, y solo aquellas que hayan ocurrido cerca de la fundación de la colonia producirán un número de representantes suficiente para ser observadas en el muestreo.

Una diferencia importante entre eucariotas y procariotas es lo que hace a la organización interna de los cromosomas y la arquitectura de los genes. Mientras que en eucariotas los genes están generalmente organizados en una estructura de exones separados por intrones, además de poseer secuencias reguladoras que pueden encontrarse a miles de pares de bases, en el caso de los procariotas la arquitectura de los genes es extremadamente sencilla, por lo general solo una secuencia codificantes continua, con regulación en la región inmediata upstream (antes del inicio de la codificante). Por un lado esto le da una ventaja evolutiva a los eucariotas en la posibilidad de reorganizar las proteínas para cumplir nuevas funciones a través del exon shuffling u otros mecanismos del tipo, además de ofrecer formas mucho más complejas de regulación⁶⁸. Por el otro lado, implica un alto costo en secuencias no-codificantes que deben duplicarse, lo que es una importante desventaja también. De hecho, la escasa longitud del ADN en las secuencias codificantes de procariotas permite que la selección positiva opere para favorecer una organización de orden superior como lo son los operones, un conjunto de genes vinculados a través de una vía metabólica o de un proceso particular que se encuentran co-regulados y normalmente muy cerca físicamente (lo que permite además, que en caso de exportarse como ADN para recombinación vayan todas las piezas importantes juntas). Además, la presión por reducir el ADN que no es directamente codificante ha llevado a los procariotas a reducir las regiones intergénicas en forma sustancial. Mientras que en eucariotas como los mamíferos la proporción de ADN no-codificante es mayor al \(95\%\), en procariotas es usualmente del orden de \(10-15\%\) y a veces menos.

De alguna manera relacionado con todo lo anterior, si bien las posibilidades de recombinación aparecen como más complejas y con menos garantías intrínsecas, la estructura y organización de los genomas procariotas es muchísimo más flexible que la de eucariotas, al tiempo que los tamaños poblacionales suelen ser gigantescos. Esto permite que la evolución opere a una velocidad importante incluso bajo presiones selectivas bajas. La flexibilidad de la organización de los genomas procariotas se hace patente al observar la distribución del material genético en los mismos. La mayor parte de los procariotas (conocidos) poseen uno o dos cromosomas circulares que contienen casi la totalidad del material genético de las células y que definen la especie. Sin embargo, en procariotas en general y en algunos eucariotas unicelulares (e.g., la levadura Saccharomyces cerevisiae (Chan et al. 2013)) existen elementos genéticos de carácter móvil denominados plásmidos. En general, los mismos son de pequeño tamaño comparado a los cromosomas estables del organismo correspondiente, y en los mismos la mayor parte del material genético no es indispensable para la vida en “condiciones normales” de la célula. Una parte importante de los mismos se transfiere mediante conjugación, un mecanismo altamente eficiente, y por lo tanto se transforman en uno de los mecanismos de mayor impacto para el intercambio de material genético y base para la evolución rápida de adaptación en microorganismos (Aminov 2011).

PARA RECORDAR

• Una diferencia genética importante entre eucariotas y procariotas es que mientras que en los primeros gran parte de los genomas son diploides o poliploides, en los segundos la mayor parte son monoploides (haploides), aunque con excepciones importantes en ambos grupos.
• Mientras que en los eucariotas los cromosomas son lineales, lo que implica un gran problema respecto a la conservación de los extremos, en el caso de los procariotas la mayor parte de las especie poseen cromosomas circulares, sin bordes libres por lo tanto.
• Los mecanismos clásicos de intercambio genético de las bacterias incluyen la transducción, la transformación y la conjugación.
• En la transducción un bacteriófago se adsorbe sobre la superficie bacteriana para inyectar su material genético en la célula. Dependiendo de si se trata de un fago virulento o moderado, el programa genético puede derivar en un ciclo lítico donde se producirán múltiples copias del mismo y luego se producirá la lisis celular o el fago puede integrar su ADN en el genoma bacteriano, transformándose en un profago. En este proceso el fago puede arrastrar material genético adicional de unas bacterias a otras.
• En la transformación, luego de entrar en un estado particular conocido como competencia, las células bacterianas son capaces de captar ADN libre de doble cadena e incoroporarlo en su genoma. En las bacterias Gram-positivas la bacteria no discrimina entre ADN homólogo y heterólogo, aunque la incorporación depende de la similaridad de secuencias, mientras que en el caso de las Gram-negativas la bacteria reconoce la diferencia y en general solo incorporá material de la misma especie o de especies estrechamente relacionadas.
• En la congujación, existen bacterias (\(F^+\)) que poseen un plásmido conjugativo, que lleva a la formación de varios pili en la superficie que le permiten hacer contacto con bacterias con ausencia de ese plásmido (\(F^-\)). Luego de ese contacto, la despolimerización en la base de los pelos lleva a que las bacterias se acerquen y hagan conatcto íntimo, formándose un puente citoplasmático por donde se transfiere el material genético del plásmido.
• Una diferencia importante entre eucariotas y procariotas es en lo que hace a la organización interna de los cromosomas y la arquitectura de los genes. Mientras que en eucariotas los genes están generalmente organizados en una estructura de exones separados por intrones, además de poseer secuencias reguladoras que pueden encontrarse a miles de pares de bases, en el caso de los procariotas la arquitectura de los genes es extremadamente sencilla, por lo general solo una secuencia codificantes continua, con regulación en la región inmediata upstream.

7.2 Dinámica de las poblaciones bacterianas

Hasta ahora, en este libro nos hemos manejado con tamaños poblacionales constantes o, en limitados casos, mencionado qué consecuencias genera la variación en el tamaño poblacional en determinados contextos, pero sin dar mayor cuenta de la dinámica de las poblaciones. La justificación mayor a esto es que los supuestos asumidos cuadran razonablemente bien con la dinámica de muchas poblaciones eucariotas (incluidas las de interés económico), al menos a la escala considerada en procesos de mejoramiento genético. Sin embargo, las bacterias y otros organismos unicelulares poseen una capacidad de replicación muy alta, lo cual les permite tener dinámicas muy variables e incluso explosivas. Claramente, es mucho más sencillo duplicar una célula que un organismo multicelular, formado por muchísimas células y donde los eventos de multiplicación deben seguir un orden determinado. Existen bacterias de lenta duplicación y otras de duplicación rápida. Por ejemplo, el caballito de batalla de los laboratorios de microbiología experimental, la bacteria Escherichia coli, tiene capacidad de duplicarse cada 20 minutos en condiciones ideales, mientras que en otras, como Mycobacterium tuberculosis, el tiempo de duplicación es de 12 a 16 horas. Algunas bacterias replican aún más rápido que E. coli. Por ejemplo, la bacteria halófila (con preferencia por medios salinos) Vibrio natriegens tiene capacidad de duplicarse en menos de 10 minutos. Estos números pueden no parecernos demasiado impresionantes, pero luego de unas breves cuentas estamos seguros de que se apreciará su magnitud. Si bien los modelos de dinámica poblacional que veremos en este capítulo no son exclusivos de microorganismos, en los mismos se puede apreciar en toda su magnitud el fenómeno y por lo tanto conforman un excelente caso para su estudio y aplicación.

El modelo exponencial

Una bacteria típica pesa en el orden de \(1\times10^{-12}\ \text{g}\), o de otra forma, se precisa un billón (\(1\times10^{12}\), un millón de millones) de bacterias para que pesen un gramo. Supongamos que a tiempo cero tenemos una bacteria, por ejemplo E. coli, que se duplicará en condiciones óptimas y sin restricciones de nutrientes, espacio o cualquier otra limitante. Al cabo de 20 minutos tendremos dos bacterias, que al cabo de otros 20 minutos se duplicaran para dar lugar a 4 bacterias. Al llegar a la hora, es decir luego de 3 ciclos de duplicaciones, tendremos \(2^3=8\) bacterias. Claramente, este número continúa siendo insignificante. En dos horas habrá 6 ciclos de duplicación, por lo que tendremos apenas \(2^6=64\) bacterias, y al cabo de 3 horas (9 ciclos) apenas \(2^9=512\). La primera impresión es que a este ritmo va a ser difícil llegar algún día no a un billón, sino incluso a un millón de bacterias. Para calcular cuánto tiempo (en generaciones, \(t\)) nos va a llevar llegar hasta nuestro primer millón podemos hacer una cuenta sencilla:

\[ \begin{split} 2^t=1 \times 10^6 \Leftrightarrow \ln{(2^t)}=\ln{(1 \times 10^6)} \Leftrightarrow t=\frac{\ln{(1 \times 10^6)}}{\ln{(2)}} \approx 19,94 \text{ generaciones} \end{split} \]

Si tenemos 3 generaciones por hora, \(19,94/3 \approx 6,65\) horas. Sin duda sorprendente, ya que al cabo de 3 horas teníamos apenas \(512\) bacterias y poco más de otras 3 horas llegamos al millón de bacterias. A esta altura no nos resultaría llamativo imaginarnos que no queda tan lejos llegar a un billón. Si hacemos la misma cuenta que antes, pero ahora con \(1 \times 10^{12}\) bacterias, llegamos a que son necesarias \(t=\frac{\ln{(1 \times 10^{12})}}{\ln{(2)}} \approx 39,86\) generaciones, que es equivalente a \(39,86/3 \approx 13,3\) horas. Es decir, en poco más de 13 horas llegamos a un gramo de bacterias, sin duda una proeza considerando de que partimos de una bacteria, pero nada para asustarse. En función de esto, veamos si podemos calcular la masa de bacterias al cabo de un día. Un día tiene 24 horas y hay 3 duplicaciones por hora, por lo que al cabo de un día habrá 72 ciclos de duplicaciones. Por lo tanto, el número de bacterias será \(2^{72}=4,722 \times 10^{21}\). Si multiplicamos este número por la masa de una bacteria y lo dividimos entre los gramos que hay en una tonelada, tenemos que la masa al cabo de un día será ¡\(\frac{(4,722 \times 10^{21} \text{ bacterias/día}) \times (1 \times 10^{-12} \text{ g/bacteria})}{1 \times 10^6 \text{ g/tonelada}}=4722,4\) toneladas por día!⁶⁹ Si tenemos en cuenta que un contenedor de 20 pies admite una carga de \(21,92\) toneladas, si fuésemos a exportar la producción de bacterias de un día requeriría de \(4722,4/21,92 \approx 215\) de estos contenedores. De hecho, el HMM Algeciras, el mayor barco porta-contenedores del mundo carga 23.964 contenedores de 20 pies y alcanzaría con menos de 27 horas para completarlo. ¡Verdaderamente impresionante!

Los cálculos que realizamos previamente claramente no son razonables a la luz de nuestra experiencia o aún de extender las cuentas previas un poquito más: en 99 generaciones este proceso generaría una masa de bacterias que es mayor a la biomasa total existente en la tierra (del orden de \(550 \times 10^9\) toneladas de carbono unido orgánicamente), un total sinsentido. ¿Dónde está el problema entonces? Obviamente, las condiciones que asumimos nosotros no son razonables en la vida real. La primera y más obvia es la necesidad de mantener las condiciones para que los nutrientes no sean una limitación al crecimiento y duplicación; a esto se suman otras varias limitaciones, como las relacionadas a la competencia e interacción entre los organismos (imaginemos el problema técnico de hacerles llegar el alimento a las primeras bacterias a medida de que la masa y el volumen del cultivo crece), que sin duda llevan a quedar lejos del óptimo de crecimiento a medida de que este se produce. De alguna manera, debemos buscar modelos más realistas, que nos permitan entender la dinámica de las poblaciones bacterianas

En general, las poblaciones bacterianas como las de casi cualquier otro organismo, experimentan durante su vida un proceso que se repite una y otra vez, lo cual nos permite generar modelos para entender la dinámica de las mismas. La base de entender la dinámica de una población consiste en comprender cómo cambia el número de individuos a medida de que pasa el tiempo. Normalmente, el estado de una población depende del número de individuos en estados previos de la misma, particularmente en el estado anterior inmediato. Para modelar esa dependencia existen dos alternativas respecto a la forma en que consideramos el tiempo: discreto y continuo.

En la Figura 7.2 podemos ver una conceptualización sencilla del ciclo de vida simple de una población bacteriana en un modelo de tiempo discreto. En este caso decimos “simple” ya que no estamos considerando en el mismo otros mecanismos/estados (e.g., esporulación). Tiempo discreto se refiere a que manejamos el mismo como si fuese una variable discreta, por ejemplo generaciones no-solapantes. En este caso, la mayor parte del problema suele concentrarse en entender cómo será el número de individuos en la generación siguiente, \(n(t+1)\), si en la generación \(t\) existen \(n(t)\) individuos. El círculo de la figura representa que se trata de un ciclo, el ciclo de vida, que se repetirá una y otra vez en la población.

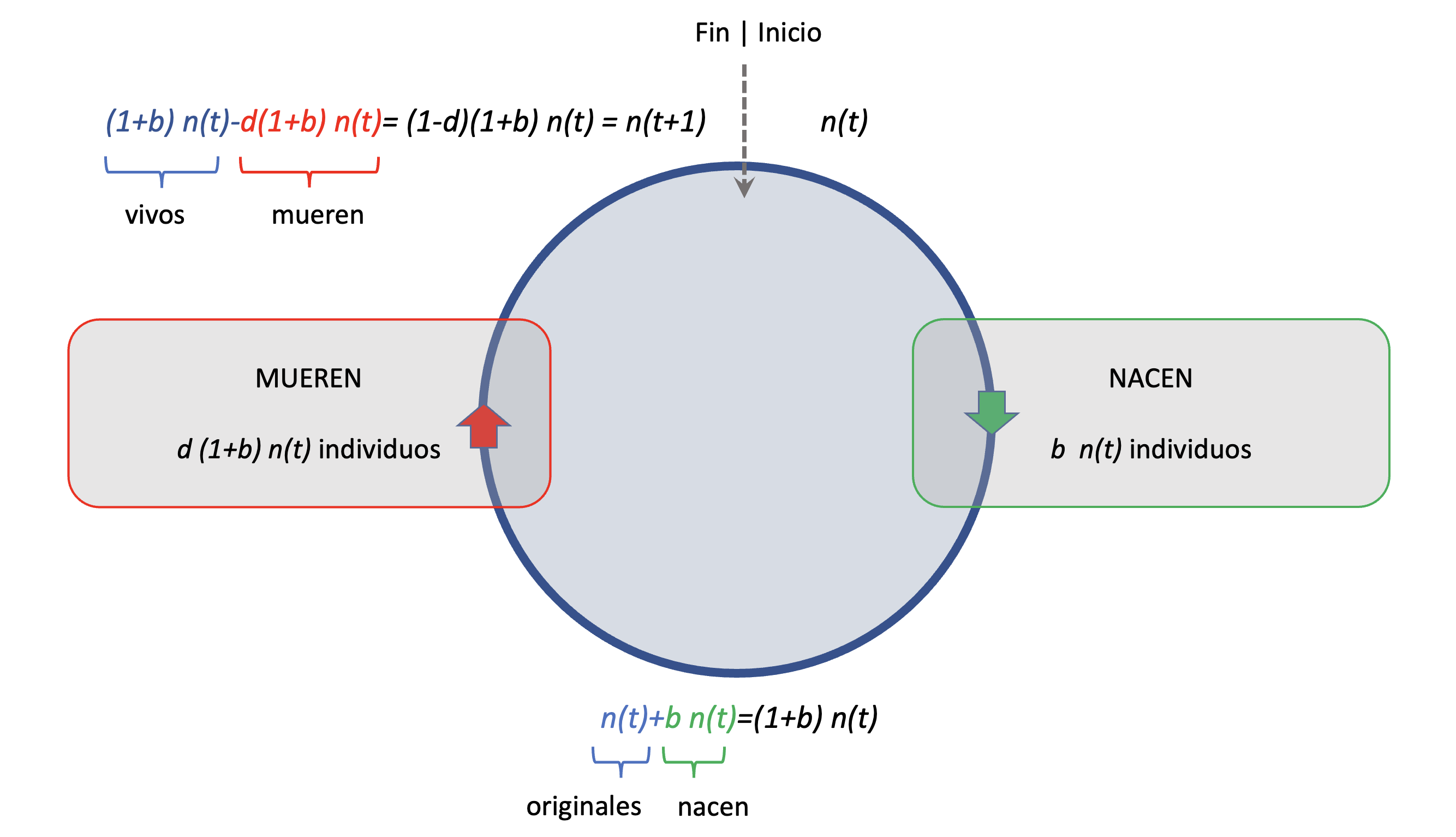
Figura 7.2: Modelo discreto del ciclo de vida simple de una bacteria. El ciclo gira en sentido horario, comenzando en la parte superior con \(n(t)\) individuos. Luego de un evento (flecha verde) en que cada individuo deja un número \(b\) de individuos adicionales, el número de individuos que llega a la parte inferior del círculo es \(n(t)+b\cdot n(t)=(1+b)\cdot n(t)\). El siguiente evento (flecha roja) es la muerte, donde una proporción \(d\) de los individuos se muere, resultando en \(b\cdot (1-d)\cdot n(t)\) individuos muertos, que si los restamos de los vivos me permite llegar al final del ciclo con \(n(t+1)=(1+b)\cdot n(t)-d\ (1+b)\cdot n(t)=(1-d) \cdot (1+b) \cdot n(t)\) individuos.

Partiendo de la parte superior del círculo, el recorrido lo haremos en sentido horario e iremos agregando primas (\('\)) para caracterizar la población luego de cada evento. Arrancamos con \(n(t)\) individuos, y en la primera fase del círculo los individuos (bacterias, por ejemplo) se reproducirán a una tasa \(b\) (por “births”, nacimientos en inglés), agregando a la población \(b\ n(t)\) individuos. Como antes había \(n(t)\), si sumamos los recién nacidos tenemos ahora \(n'(t)=n(t)+b\ n(t)=(1+b)\ n(t)\) individuos en la población. El siguiente evento será la muerte, que si ocurre a una tasa \(d\) (por “deaths”, muertes en inglés) entonces removerá \(d\ n'(t)=d\ (1+b)\ n(t)\) individuos. Como antes teníamos \(n'(t)=(1+b)\ n(t)\) individuos, si le restamos estos últimos nos quedaremos con \(n''(t)=n'(t)\ -\ d\ n'(t)=(1+b)\ n(t)-d\ (1+b)\ n(t)=(1-d)(1+b)\ n(t)\). Pero \(n''(t)\) marca el final del ciclo, por lo que se trata también del inicio del ciclo próximo (ya que no hay eventos entre fin e inicio), es decir \(n(t+1)\). Por lo tanto, hemos arribado a la siguiente relación de recurrencia para el número de individuos en la población

\[ \begin{split} n(t+1)=(1-d) \cdot (1+b) \cdot n(t) \end{split} \tag{7.1} \]

Si definimos \(R=(1-d) \cdot (1+b)\) como el factor reproductivo, entonces la ecuación de recursión (7.1) se simplifica a

\[ \begin{split} n(t+1)=R \cdot n(t) \end{split} \tag{7.2} \]

El factor reproductivo es el número de individuos sobreviviente por progenitor (un abuso de lenguaje en nuestro caso, ya que las bacterias se reproducen por fisión). Haciendo la expansión de los componentes del factor reproductivo tenemos

\[ \begin{split} R=(1-d)(1+b)=1+b-d-bd \end{split} \tag{7.3} \]

La interpretación de la ecuación (7.3) es sencilla. El \(1\) es el factor que representa los organismos originales, ya que al multiplicar por este número nos da \(1 \times n(t)=n(t)\). El \(b\) representa la fracción de organismos original que nacen en ese ciclo, mientras que \(d\) representa la fracción de los que mueren. Finalmente, el término \(bd\) representa la proporción de los que nacen en el ciclo que también mueren en ese ciclo.

Normalmente, para la mejor interpretación de la dinámica de la población nos interesa ver el cambio del número de individuos entre dos generaciones, es decir \(\Delta n\). Para ello nos basta con restar \(n(t)\) a \(n(t+1)\), es decir, usando la ecuación (7.2), si le restamos \(n(t)\) tenemos

\[ \begin{split} \Delta n=n(t+1)\ -\ n(t)=R\ n(t)\ -\ n(t)=n(t)\ (R-1) \end{split} \tag{7.4} \]

Al número \((R-1)=b-d-bd=r\) es el cambio per cápita en el número de individuos de una generación a la siguiente, y tiene una interpretación obvia en función de los componentes que lo definen, las tasas de nacimientos y muertes por generación.

Una forma alternativa de analizar la dinámica de las poblaciones es a partir de los modelos continuos. Ahora, a diferencia del caso de los modelos discretos, como el intervalo de tiempo considerado es infinitesimal, no tiene importancia el orden en los componentes del ciclo y además nunca van a ocurrir dos eventos en el mismo instante infinitesimal (en nuestro caso nacimiento y muerte, del que daba cuenta el término \(-bd\)). Para derivar la ecuación del modelo continuo podemos partir de la correspondiente ecuación del modelo discreto e ir reduciendo el intervalo de tiempo para pasar al límite. En particular, si consideramos un intervalo de tiempo arbitrariamente pequeño \(\Delta t\) (que podríamos ver como una fracción de la generación), entonces el número de individuos nacidos en ese intervalo de tiempo será \(b \cdot \Delta t\), mientras que el número de muertes será \(d \cdot \Delta t\). Por lo tanto, a partir de la definición de derivada tenemos

\[\frac{dn}{dt}=\lim_{\Delta t \to 0}\ \frac{[n(t+1)-n(t)]}{\Delta t}=\lim_{\Delta t \to 0}\ \frac{[(1- d \cdot \Delta t)(1+ b \cdot \Delta t) \cdot n(t)-n(t)]}{\Delta t}\ \therefore\] \[ \begin{split} \frac{dn}{dt}=\lim_{\Delta t \to 0}\ \frac{[1- d \cdot \Delta t+ b \cdot \Delta t-bd(\Delta t)^2-1] \cdot n(t)}{\Delta t}=\lim_{\Delta t \to 0}\ [b-d-bd \cdot \Delta t]\ n(t) \end{split} \tag{7.5} \]

En el límite, cuando \(\Delta t \to 0\), \(-bd \cdot \Delta t \to 0\), por lo que (dejando implícito que \(n\) es función de t) la ecuación (7.5) queda finalmente como

\[ \begin{split} \frac{dn}{dt}=(b-d) \cdot n = r_c\ n \end{split} \tag{7.6} \]

con \(r_c=b-d\) la tasa neta de crecimiento para el modelo continuo (de ahí la \(c\) como subscrito). Como la ecuación (7.6) involucra una variable \(n\) que es función de otra \(t\), pero también aparecen derivadas de la función, entonces se trata de una ecuación diferencial, que como solo involucra la derivada primera es de primer orden y su solución es sencilla

\[\frac{dn}{dt}=r_c n \Rightarrow \frac{dn}{n}=r_c \cdot dt\] \[\int_{n(0)}^{n(t)} \frac{1}{n} \cdot dn=r_c\ \int_{0}^{t} dt\] \[\ln{n}\big\rvert^{n(t)}_{n(0)}=r_c \cdot t \big\rvert^t_0\] \[\ln (n(t)) - \ln (n(0)) = r_c \cdot t\] \[e^{[\ln (n(t)) - \ln (n(0))]}=e^{r_c \cdot t}\] \[\frac{n(t)}{n(0)}=e^{r_c\ t} \therefore\]

\[ \begin{split} n(t)=n(0) \cdot e^{r_c\ t} \end{split} \tag{7.7} \]

La ecuación (7.7) deja en claro que la dinámica de crecimiento poblacional bajo este modelo es exponencial. Si \(r_c > 0\), es decir \(b > d\) (mayor tasa de nacimientos que de muertes), entonces la población crecerá en forma exponencial. Si en cambio \(r_c < 0\), es decir \(b < d\) (menor tasa de nacimientos que de muertes), entonces como es de esperar la población decrecerá en tamaño y lo hará en forma exponencial.

En resumen, hemos modelado el crecimiento de las poblaciones bacterianas imaginando un ciclo de vida para tiempo discreto, donde los eventos siguen un orden determinado, que suele ser importante para el resultado de la dinámica de la población, así como otro modelo que considera el tiempo como una variable continua y que por lo tanto me permite describir la evolución a partir de una ecuación diferencial. El único parámetro relevante en este modelo es \(r_c=b-d\), por lo que el comportamiento del mismo es poco flexible (la forma solo cambia cuando es positivo respecto a cuando es negativo) para describir situaciones reales.

Ejemplo 7.1

Un/a asistente de laboratorio decide, en un acto de subversión, dejar de lado la productividad y divertirse viendo haciendo “carreras de crecimiento” entre poblaciones microbianas. Para ello genera en paralelo dos colonias bacterianas: una de ellas se encuentra (la de crecimiento más rápido) es fundada con tres células, mientras que la otra la inicia con cuatro para contar con cierta ventaja inicial. ¿Qué tan grande es la diferencia de número de células entre ambas luego de media hora de procrastinación en el laboratorio? Asuma un modelo continuo, con una tasa neta de crecimiento de \(r_c = 3,632 \times 10 ^ {-3} \text{min}^{-1}\) para la primer colonia y de \(r_c = 3,2630 \times 10 ^ {-3} \text{min}^{-1}\) para la segunda. Se asume que no existen limitantes para el crecimiento bacteriano.

Utilizando la relación \(n(t)=n(0) \cdot e^{r_c\ t}\) estimemos la relación entre ambas poblaciones celulares luego de media hora. Dividiremos el número de células en la segunda población por el de la primera, teniendo en cuenta que se espera existan más células en la colonia con mayor tamaño al momento de fundarse. Notemos que la constante \(r_c\) se encuentra en unidades de \(\text{min}^{-1}\), por lo que tendremos en cuenta \(t = 30\text{ min}\):

\[ \frac{n_2(30\text{ min}^{-1})}{n_1(30\text{ min}^{-1})} = \frac{3 \cdot e^{3,632 \cdot 30}}{4 \cdot e^{3,2630 \cdot 30}} \approx 48.161 \]

Vemos que una sutil diferencia en la tasa neta de crecimiento basta para que en media hora la población más veloz consiga ser cuarenta y ocho mil veces mayor que la otra, aún iniciando con una célula menos. Un gran día en el laboratorio, sin lugar a dudas.

El modelo logístico

Claramente, como vimos más arriba, el modelo exponencial de crecimiento nos lleva a resultados sorprendentes y que no se ajustan a nuestra experiencia o a nuestras observaciones empíricas (nuestro universo no está dominado por una sola especie de bacteria que sigue creciendo ad infinitum). Esto nos lleva a plantearnos la necesidad de establecer modelos más ajustados a la realidad. Una de las primeras limitaciones que se pueden notar en el modelo exponencial es la imposibilidad de modelar con este los cambios en la tasa de crecimiento de la población a medida que la misma evoluciona en el tiempo. Las implicancias de esto a nivel biológico son claras y difíciles de justificar: a medida de que las poblaciones crecen también crece la demanda de recursos por parte de las mismas, pero el ambiente en el que viven tiene una capacidad limitada, que en algún punto se alcanzará y a partir del cuál no será sustentable. Dicho en otras palabras, el sistema tiene una capacidad de carga determinada, que no se puede sobrepasar.

En términos de nuestros parámetros definidos previamente para el modelo exponencial, el que la tasa de crecimiento de la población dependa del tamaño de la misma, podemos explicitarlo utilizando una función \(R(n)\) y asumiendo que se trata de una función que es decreciente en \(n\) (a medida que aumenta el tamaño de la población, menor va a ser \(R\)). Existen diversas funciones que cumplen con este requisito y que han sido utilizadas para modelar este fenómeno, pero una de las más usadas es la función lineal que nos lleva al modelo logístico de crecimiento. En este modelo se asume que la tasa de individuos que sobreviven por cada “progenitor” decrece en forma lineal a medida de que aumenta el tamaño de la población.

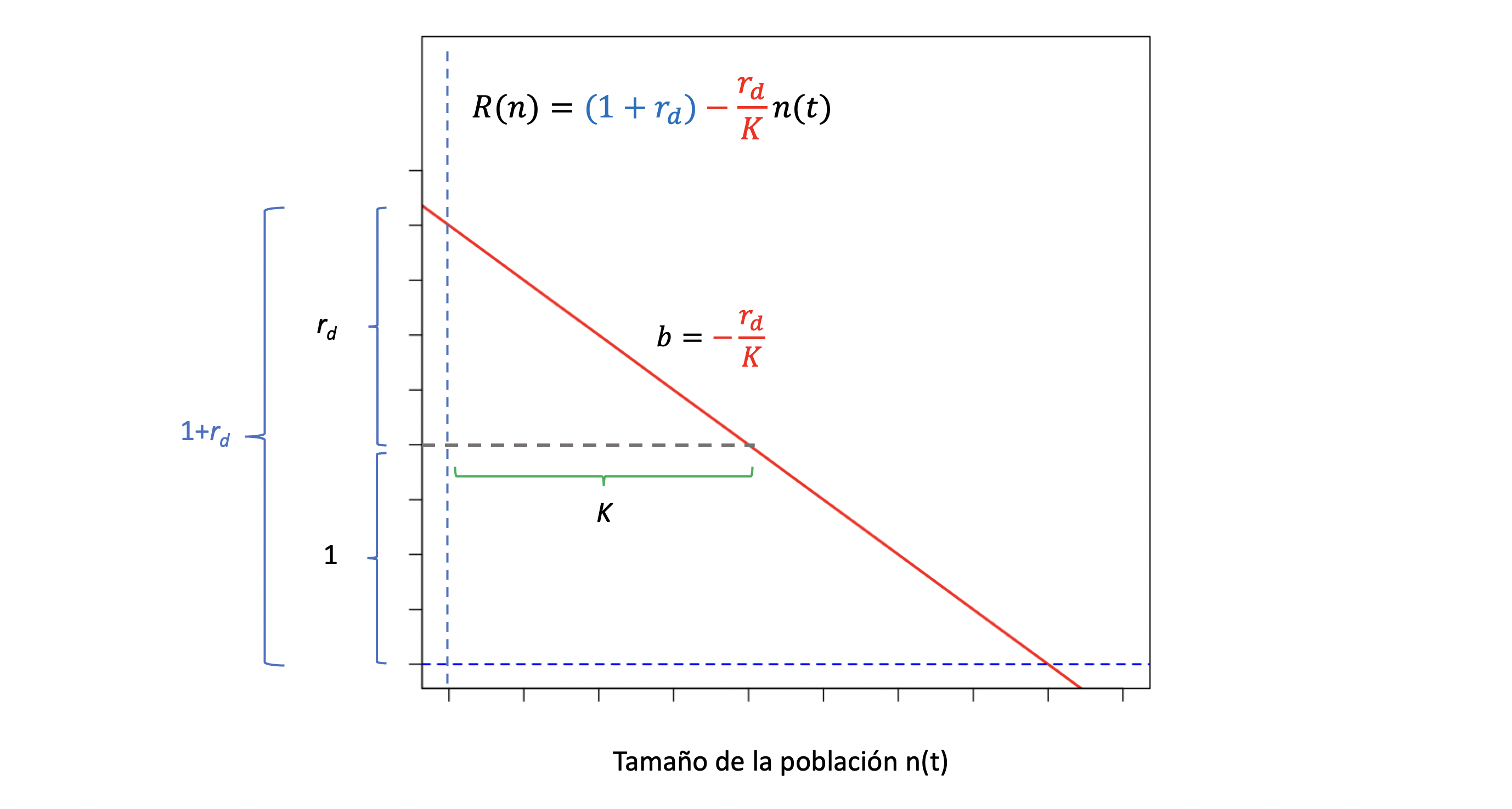
Figura 7.3: El factor reproductivo \(R(n)\) como función lineal del tamaño poblacional. La función lineal \(R(n)=(1+r_d)-\frac{r_d}{K}n(t)\) podemos entenderla como la suma de intercepto igual a \((1+r_d)\), es decir el factor reproductivo cuando no existen limitaciones impuestas por la población (ya que \(n(t)=0\)) y un cambio en función de \(n(t)\) con pendiente \(b=-\frac{r_d}{K}\). Elaboración propia sobre idea de Otto y Day (Otto and Day 2007).

En la Figura 7.3 se puede apreciar el comportamiento del factor reproductivo \(R(t)=(1+r_d)-\frac{r_d}{K}n(t)\) (ordenadas) como función del tamaño poblacional (abscisas). Si llamamos \(K\) a la capacidad de carga del sistema. Cuando el tamaño poblacional es muy bajo en relación a la capacidad de carga (i.e., \(\frac{n(t)}{K} \to 0\)) entonces \(\frac{r_d}{K}n(t) \to 0\) ya que \(r_d\) es una constante y por lo tanto \(R(n \to 0)=(1+r_d)\), el intercepto de la recta. Dado de que \(\frac{n(t)}{K} \to 0\) acontece cuando no existe competencia por los recursos, a \(r_d\) le llamaremos la tasa intrínseca de crecimiento (\(r_d>0\)) o decrecimiento (\(r_d<0\)) de la población. Si expandimos y reordenamos los términos, tenemos que

\[ \begin{split} R(n)=(1+r_d)-\frac{r_d}{K}n(t) \Leftrightarrow R(n)=1+r_d[1-\frac{n(t)}{K}] \end{split} \]

\[ \begin{split} 1+r_d[1-\frac{n(t)}{K}] \end{split} \tag{7.8} \]

y sustituyendo este resultado en la ecuación (7.2) tenemos

\[ \begin{split} n(t+1)=R \cdot n(t)=n(t) \cdot [1+r_d(1-\frac{n(t)}{K})]=n(t)+n(t) \cdot r_d \cdot (1-\frac{n(t)}{K}) \end{split} \tag{7.9} \]

Más aún, el pasaje al cambio de frecuencia entre generaciones para este modelo es inmediato al restarle \(n(t)\) a ambos lados de la ecuación (7.9)

\[ \begin{split} \Delta n=n(t+1)-n(t)=n(t)+n(t)r_d(1-\frac{n(t)}{K})-n(t)=n(t)r_d(1-\frac{n(t)}{K}) \end{split} \tag{7.10} \]

En forma análoga, para el modelo continuo la tasa de cambio en la población queda determinada por

\[ \begin{split} \frac{dn}{dt}=n(t)\ r_c(1-\frac{n(t)}{K}) \end{split} \tag{7.11} \]

En este punto ya nos debe resultar muy claro que la diferencia entre el modelo exponencial de crecimiento y el modelo logístico se encuentra en el factor \((1-\frac{n(t)}{K})\) que aparece multiplicando en el modelo logístico. La interpretación de este factor es muy sencilla analizando los extremos. Cuando la población es muy pequeña \(\frac{n(t)}{K} \to 0\) y por lo tanto \(\lim_{n(t) \to 0} (1-\frac{n(t)}{K}) = 1\), por lo que el modelo queda igual al modelo exponencial y el crecimiento seguirá ese patrón. Por otro lado, a medida de que la población crece, llegará un punto en que su tamaño de acercará a la capacidad de carga del sistema y por lo tanto \(\lim_{n(t) \to K}(1-\frac{n(t)}{K}) = 0\) (ya que \(\lim_{n(t) \to K} \frac{n(t)}{K}=1\)), y por lo tanto el crecimiento será nulo.

Al ser (7.11) una ecuación diferencial de primer orden sencilla, podemos obtener una solución para la misma al integrarla. Para facilitar la visualización llamaremos \(n_0\) a \(n(0)\) (número inicial de individuos a \(t=0\)), y análogamente llamaremos \(n_t=n(t)\) al número de individuos en tiempo \(t\):

\[ \begin{split} \frac{dn}{dt}=n \cdot r_c \cdot(1-\frac{n}{K})\ \therefore\ \int_{n_0}^{n_t} \frac{1}{n(1-\frac{n}{k})} \cdot dn=r_c \int_0^t dt \therefore \\ -K \int_{n_0}^{n_t} \frac{1}{n(n-K)} \cdot dn=r_c\ t \end{split} \tag{7.12} \]

Resolvamos primero la integral indefinida de la izquierda y luego le colocaremos los límites de integración. Sacando el factor común \(n^2\) en el denominador del lado izquierdo de la ecuación (7.12) tenemos que

\[ \begin{split} -K \int \frac{1}{(1-\frac{K}{n})n^2} dn=r_c\ t \end{split} \tag{7.13} \]

Si hacemos el cambio de variables \(u=1-\frac{K}{n}\), entonces

\[ \begin{split} \frac{du}{dn}=\frac{K}{n^2} \Leftrightarrow dn=\frac{n^2}{K} \cdot du \end{split} \tag{7.14} \]

y sustituyendo en la ecuación (7.13), tenemos ahora

\[ \begin{split} \frac{-K}{K} \int \frac{1}{u} \cdot du=r_c\ t \therefore -\ln(u)=r_c\ t \end{split} \tag{7.15} \]

Haciendo el cambio de variable hacia atrás y poniendo los límites de integración tenemos ahora

\[-\ln (1-\frac{K}{n}) \big\rvert_{n_0}^{n_t}=r_c\ t \Leftrightarrow \ln (1-\frac{K}{n_0})-\ln (1-\frac{K}{n_t})=r_c\ t \Leftrightarrow\] \[\ln [ \frac{(1-\frac{K}{n_0})}{(1-\frac{K}{n_t})}] =r_c\ t \Leftrightarrow \ln [ \frac{(n_0-K)n_t}{(n_t-K)n_0} ] =r_c\ t \Leftrightarrow \frac{(n_0-K) \cdot n_t}{(n_t-K) \cdot n_0}= e^{r_c\ t} \Leftrightarrow\] \[n_t=\frac{[(n_t-K) \cdot n_0] \cdot e^{r_c\ t}}{n_0-K} \Leftrightarrow n_t=\frac{n_t \cdot n_0 \cdot e^{r_c\ t}-Kn_0 \cdot e^{r_c\ t}}{n_0-K} \Leftrightarrow n_t [1-\frac{n_0 \cdot e^{r_c\ t}}{n_0-K}]= -\frac{Kn_0 \cdot e^{r_c\ t}}{n_0-K} \Leftrightarrow\] \[ \begin{split} n_t \cdot [n_0-K- n_0 \cdot e^{r_c\ t}]=-Kn_0 \cdot e^{r_c\ t} \Leftrightarrow n_t=\frac{-Kn_0 \cdot e^{r_c\ t}}{n_0-K-n_0 \cdot e^{r_c\ t}} \end{split} \tag{7.16} \]

y finalmente, multiplicando y dividiendo por \(-1\), tenemos la forma final

\[ \begin{split} n(t)=\frac{K \cdot n_0 \cdot e^{r_c\ t}}{K+n_0 \cdot (e^{r_c\ t}-1)} \end{split} \tag{7.17} \]

Ejemplo 7.2

Calcular el tamaño poblacional para una colonia bacteriana que arranca con 5 individuos al cabo de un tiempo \(t=1\) hora y con una tasa neta de crecimiento para el modelo continuo de \(r_c=4,1667\times 10^{-3}s^{-1}\) en el caso de que la capacidad de carga del sistema (\(K\)) sea de 5 millones de individuos.

Como \(t=1\) hora, expresado en segundos (ya que las unidades de \(r_c\) están en \(s^{-1}\)) sería \(t=3600s\). Usando el resultado de la ecuación (7.17), tenemos que \(n(t)=\frac{K\ n_0\ e^{r_c\ t}}{K+n_0\ (e^{r_c\ t}-1)}\) por lo que sustituyendo por los valores del problema, llegamos a \(n(3600)=\frac{5\times 10^{6} \times 5 \times e^{4,1667\times 10^{-3} \times 3.600}}{5\times 10^{6}+5\times (e^{4,1667\times 10^{-3} \times 3.600}-1)}=3.828.879\). Es decir, aproximadamente \(3,8\) millones de bacterias, aún relativamente lejos de la capacidad de carga del sistema.

---

En la Figura 7.4 podemos apreciar el crecimiento de una población que arranca con un individuo y posee una capacidad de carga del sistema de \(K=10.000\) individuos, de acuerdo al modelo logístico.

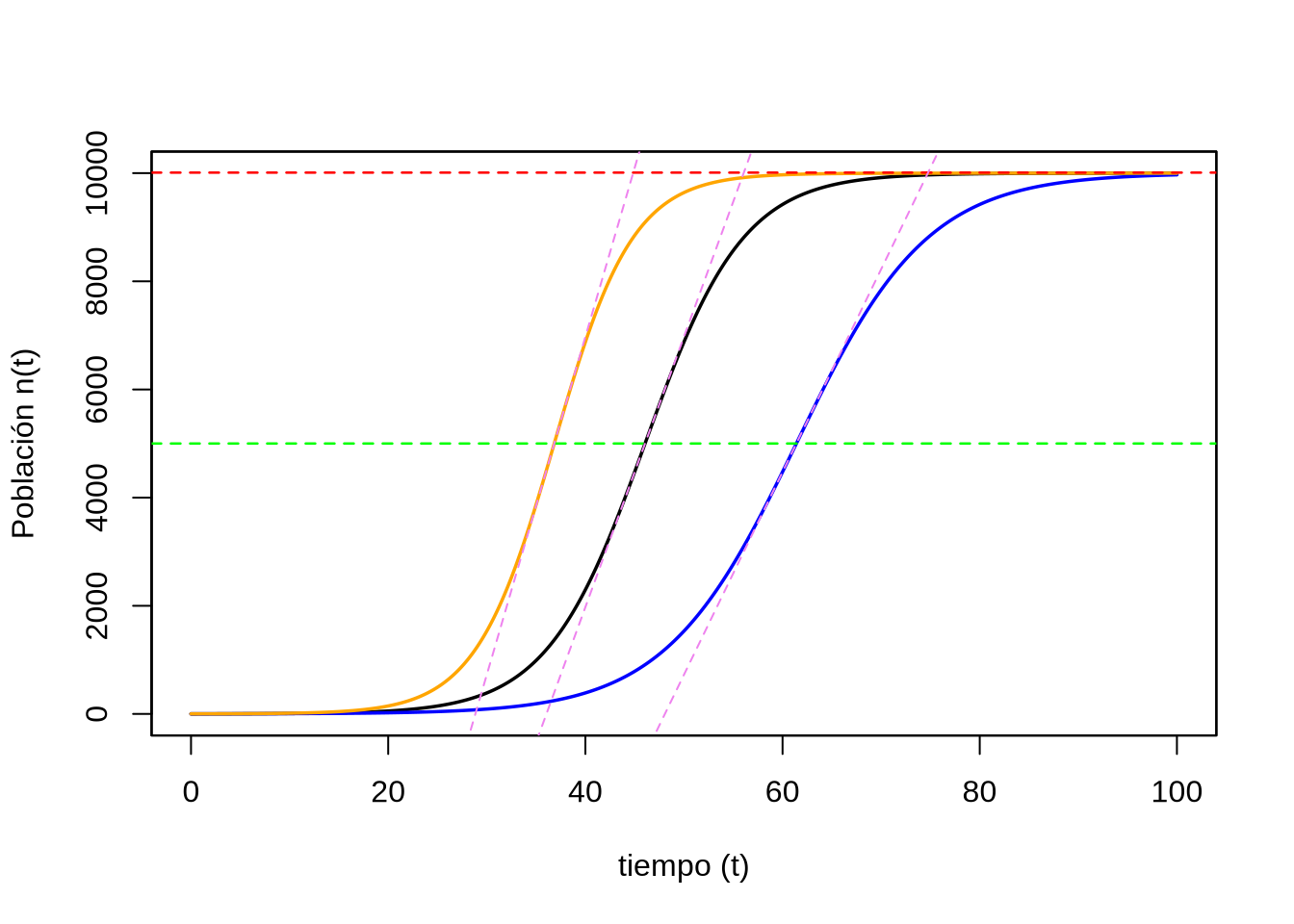
Figura 7.4: Evolución de la población de acuerdo al modelo logístico, con parámetros \(n(0)=1\), \(K=10.000\) individuos y \(r_c=0,25\) (curva anaranjada), \(r_c=0,20\) (curva negra), \(r_c=0,15\) (curva azul) . La línea roja indica la capacidad de carga del sistema, mientras que la línea verde se encuentra en \(K/2\). Las líneas violetas segmentadas representan las pendientes en los correspondientes puntos de inflexión para las 3 curvas.

La tasa intrínseca de crecimiento es de \(r_c=0,25\) en la curva anaranjada, de \(r_c=0,20\) en la curva negra, mientras que es de \(r_c=0,15\) en la curva azul. Claramente, se aprecia en las tres curvas que al comienzo el comportamiento es aproximadamente exponencial, seguido por una fase casi-lineal, en el medio de la cual cambia la concavidad, para finalmente acercarse a una fase asintótica donde se aproxima lentamente a la capacidad de carga. A medida de que la tasa intrínseca de crecimiento es mayor (azul, negra, anaranjada) el crecimiento es más explosivo en la fase exponencial, marcado a su vez por una pendiente mucho mayor en la fase casi-lineal y una entrada más abrupta en la fase asintótica. El modelo logístico es también conocido como modelo de Verhulst en honor del matemático belga que lo reportó por primera vez⁷⁰.

Para determinar el tiempo que nos llevará llegar hasta la mitad de la capacidad de carga del sistema basta con sustituir \(n_t=\frac{K}{2}\) en la ecuación (7.17) y despejar \(t\),

\[ \begin{split} n(t)=\frac{K}{2}=\frac{K \cdot n_0\ e^{r_c\ t}}{K+n_0 \cdot (e^{r_c\ t}-1)} \Leftrightarrow 2n_0\ e^{r_c\ t}=K+n_0 \cdot (e^{r_c\ t}-1) \Leftrightarrow \\ 2 \cdot n_0 \cdot e^{r_c\ t}-n_0 \cdot e^{r_c\ t}=K-n_0 \Leftrightarrow e^{r_c\ t}=\frac{K-n_0}{n_0} \Leftrightarrow \\ r_c \cdot t=\ln (\frac{K-n_0}{n_0}) \Leftrightarrow \\ t=\frac{\ln (\frac{K-n_0}{n_0})}{r_c} \end{split} \tag{7.18} \]

Aplicando el resultado de la ecuación (7.18) a los datos de las tres curvas de la Figura 7.4, llegamos a que \(t=\frac{\ln((10.000-1)/1)}{0,25}=\frac{9,21024}{0,25}=36,84\) unidades de tiempo para la curva anaranjada, \(t=\frac{9,21024}{0,20}=46,05\) unidades para la curva negra, mientras que para la curva azula harán falta \(t=\frac{9,21024}{0,15}=61,40\) unidades de tiempo para alcanzar la mitad de la capacidad de carga del sistema.

Las curvas de la Figura 7.4 muestran que en algún punto de la fase casi-lineal tiene que existir un cambio en la convexidad-concavidad de la curva, es decir pasar de una tasa de crecimiento poblacional creciente en el tiempo a una fase en que la tasa es decreciente. Como recordarás de los cursos de cálculo, ese cambio (de existir) ocurre en uno de los ceros de la derivada segunda de la curva respecto al tiempo. Si bien la ecuación (7.11) ya nos da la derivada primera, debemos sustituir en la misma \(n(t)\) por el resultado de la ecuación (7.17) y volver a derivar respecto al tiempo, lo cual no es difícil pero sí requiere cierto número de operaciones, lo cual vuelve al proceso tedioso.

Sin embargo, podemos llegar a este resultado de una manera más sencilla. En lugar de derivar dos veces la ecuación (7.17), podemos recurrir a la ecuación (7.11), donde ya está presente la derivada primera respecto al tiempo (i.e., la tasa de crecimiento de la población respecto al tiempo). En la Figura 7.5 se observa que la tasa de crecimiento aumenta con el tamaño poblacional hasta determinado punto donde empieza a bajar, lo cual implica que existe un máximo de la derivada de \(dn/dt\) respecto a \(n\) (i.e., un máximo de \(\frac{\partial^2n}{\partial n \partial t}\)); idealmente, este sería el punto de inflexión la gráfica de \(n(t)\).

En función de esto, si volvemos a derivar la ecuación (7.11), pero ahora respecto a \(n\), obtenemos

\[ \begin{split} \frac{\partial^2n}{\partial n \partial t}=\frac{\partial[r_c \cdot n \cdot (1-\frac{n}{K})]}{\partial n}= \frac{\partial[r_c \cdot (n-\frac{n^2}{K})]}{\partial n} = r_c-\frac{2r_c}{K}n \end{split} \tag{7.19} \]

Por lo tanto, igualando a cero, tenemos ahora

\[ \begin{split} \frac{\partial^2n}{\partial n \partial t}=r_c-\frac{2r_c}{K}n=0 \Leftrightarrow n=\frac{Kr_c}{2r_c}=\frac{K}{2} \end{split} \tag{7.20} \]

Es decir, el punto de inflexión en la curva de crecimiento poblacional se alcanzará cuando el tamaño poblacional sea igual a la mitad de la capacidad de carga del sistema, y por lo tanto el tiempo hasta ese punto estará dado por la ecuación (7.18). Si sustituimos ese valor en la ecuación (7.11) que define la derivada primera, es decir la tasa de crecimiento en el punto de inflexión, tendremos que la misma es igual a

\[ \begin{split} \frac{dn}{dt}\big\rvert_{n=K/2}=r_c \cdot (\frac{K}{2}) \cdot (1-\frac{K}{2K})=\frac{Kr_c}{4} \end{split} \tag{7.21} \]

Por ejemplo, con los números de la Figura 7.4, para la curva anaranjada la máxima tasa de crecimiento de la población será \(\frac{dn}{dt}\big\rvert_{n=K/2}=\frac{Kr_c}{4}=\frac{10.000 \times 0,25}{4}=625\) individuos por unidad de tiempo (la unidad en la que se expresa \(r_c\)). Para la curva negra tenemos \(\frac{dn}{dt}\big\rvert_{n=K/2}=\frac{Kr_c}{4}=\frac{10.000 \times 0,20}{4}=500\) invididuos por unidad de tiempo. Finalmente, para la curva azul en cambio \(\frac{dn}{dt}\big\rvert_{n=K/2}=\frac{Kr_c}{4}=\frac{10.000 \times 0,15}{4}=375\) individuos por unidad de tiempo. Estas tres pendientes se pueden apreciar en color violeta en la Figura 7.4.

El modelo logístico no es el único que presenta características razonables para describir el comportamiento de las poblaciones. De hecho, diversas funciones que comparten la característica de ser sigmoidales (con forma de S), son capaces de describir el comportamiento deseado. Por ejemplo, Zwietering y colaboradores comparan diversos modelos usados frecuentemente para describir la dinámica poblacional, incluyendo el logístico, la función de Gompertz, así como los modelos de Richards, Stannard y Schnute (todos estos de 4 parámetros), llegando a la conclusión de que en general el modelo logístico, con 3 parámetros (\(n(0)\), \(r_c\) y \(K\)), es suficiente para describir adecuadamente las poblaciones (Zwietering et al. 1990).

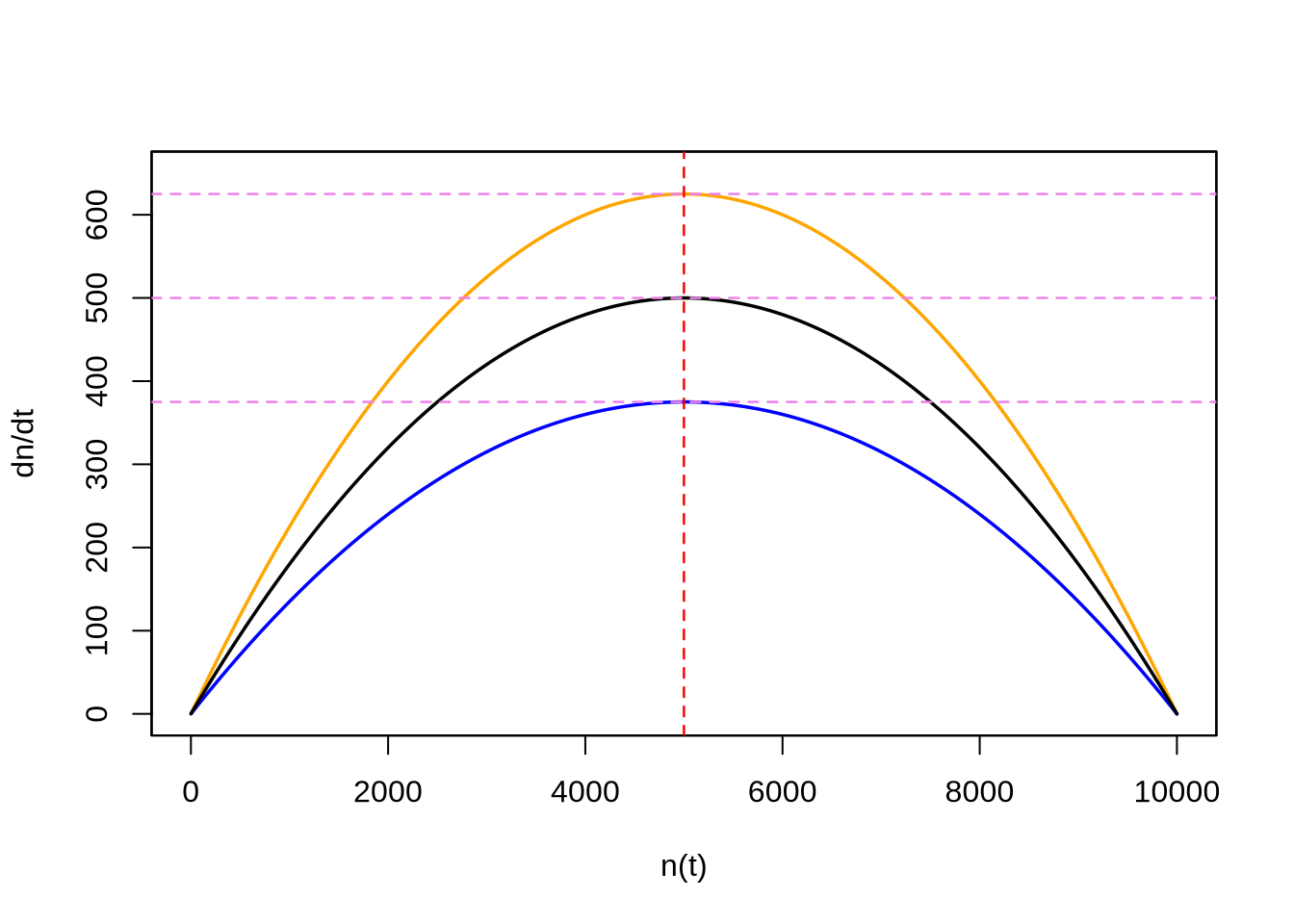
Figura 7.5: Tasas de crecimiento en función del tamaño de la población para las tres poblaciones de la Figura 7.4. Se observa claramente que se trata de una curva parabólica con un máximo en el centro. En violeta los valores máximos, que coinciden con las respectivas pendientes en el punto de inflexión en la Figura 7.4.

PARA RECORDAR

• En el caso del modelo exponencial de crecimiento poblacional \(n(t+1)=(1-d)(1+b)\ n(t)\).

• Si definimos \(R=(1-d)(1+b)\) como el factor reproductivo (el número de individuos sobreviviente por padre), entonces la ecuación de recursión se simplifica a \(n(t+1)=R\ n(t)\).

• Normalmente, para la mejor interpretación de la dinámica de la población nos interesa ver el cambio del número de individuos entre dos generaciones, es decir \(\Delta n\), que es \(\Delta n=n(t+1)\ -\ n(t)=R\ n(t)\ -\ n(t)=n(t)\ (R-1)\) Además, \(r=(R-1)=b-d-bd\) es el cambio per cápita en el número de individuos de una generación a la siguiente.

• En el caso del modelo exponencial en tiempo continuo, tenemos que \(\frac{dn}{dt}=(b-d)\ n = r_c\ n\), con \(r_c=b-d\) la tasa neta de crecimiento para el modelo continuo.

• La solución de la ecuación diferencial que representa la tasa de cambio en la población nos da el tamaño poblacional en función del tiempo \(t\), la tasa de crecimiento \(r_c\) y el número inicial de individuos y tiene la forma \(n(t)=n(0) \cdot e^{r_c\ t}\).

• El modelo exponencial no da cuenta adecuadamente de las condiciones de restricción a las que normalmente están sujetas las poblaciones. Una alternativa es el modelo logístico, donde \(R(n)\) es una función lineal de la densidad de población \(R(n)=1+r_d[1-\frac{n(t)}{K}]\). Al parámetro \(K\) le llamamos capacidad de carga del sistema y representa el número máximo de individuos que puede acomodar el sistema.

• En forma análoga, para el modelo continuo la tasa de cambio en la población queda determinada por \(\frac{dn}{dt}=n(t)\ r_c(1-\frac{n(t)}{K})\).

• La solución a la ecuación diferencial anterior nos da el número de individuos en el tiempo \(t\) a partir del número inicial de individuos \(n_0\), la capacidad de carga del sistema \(K\) y la tasa de crecimiento \(r_c\) y tiene la siguiente forma \(n(t)=\frac{K\ n_0\ e^{r_c\ t}}{K+n_0\ (e^{r_c\ t}-1)}\).

7.3 Modelos haploides de selección natural

En el capítulo sobre Selección natural estudiamos el efecto de las diferencias en fitness entre los genotipos para un locus diploide con dos alelos. En el caso de los procariotas y algunos eucariotas unicelulares los genomas son haploides, o basculan entre fases haploides y diploides (o aún poliploides). Es momento entonces de analizar la dinámica del cambio en las frecuencias alélicas en un locus haploide. El libro de Otto y Day (Otto and Day 2007) presenta un tratamiento simple y claro del problema, y es una excelente referencia para entender mejor los distintos modelos de dinámica de poblaciones y selección, así como sus derivaciones, por lo que seguiremos de cerca su razonamiento.

Selección haploide: modelo discreto

Supongamos, por ejemplo, una población bacteriana en crecimiento. Supongamos además que tenemos un locus con dos alelos, que llamaremos \(A_1\) y \(A_2\), como es nuestra costumbre. Si en una generación \(t\) determinada el número de células bacterianas que tienen el alelo \(A_1\) es \(n_1(t)\) y el número de las que tienen el alelo \(A_2\) es \(n_2(t)\), de acuerdo al modelo exponencial en la siguiente generación (\(t+1\)) el número de células de cada uno estará determinado por

\[ \begin{split} n_1(t+1)=W_1 \cdot n_1(t)\\ n_2(t+1)=W_2 \cdot n_2(t) \end{split} \tag{7.22} \]

siendo

\[ \begin{split} W_1 = (1 − d_1) (1 + b_1) \\ W_2 = (1 − d_2) (1 + b_2) \end{split} \tag{7.23} \]

los factores reproductivos para cada uno de los dos alelos. En este caso \(d_1\) y \(d_2\) representan la tasa de muerte de las células bacterianas por generación, mientras que \(b_1\) y \(b_2\) representan los nacimientos, por duplicaciones normalmente (las letras \(b\) y \(d\) vienen del inglés, “births” y “deaths”, nacimientos y muertes respectivamente). La lógica es clara: en cada generación muere una proporción \(d\) (sobrevive \(1-d\)), y de esos que sobreviven por cada célula habrá \(b\) nuevas células, que junto a las presentes constituyen \(1+b\). Poniendo juntos los términos de muertes y nacimientos tenemos \(W=(1-d)(1+b)\), como aparece en la ecuación (7.23) para cada uno de los dos alelos o genotipos.

Como ya hemos visto antes, para pasar a la frecuencia de cada uno de los alelos alcanza con dividir el número de células de cada genotipo (que es el de portadores del alelo correspondiente, ya que son haploides) entre el número total de células, que es la suma de las de los dos genotipos en (nuestro caso, \(n_1+n_2\)). Por lo tanto, si llamamos \(p\) a la frecuencia de \(A_1\) y \(q\) a la de \(A_2\), entonces

\[ \begin{split} p=\frac{n_1}{n_1\ +\ n_2}\\ q=\frac{n_2}{n_1\ +\ n_2} \end{split} \tag{7.24} \]

con \(p+q=\frac{n_1}{n_1\ +\ n_2}+\frac{n_2}{n_1\ +\ n_2}=\frac{n_1\ +\ n_2}{n_1\ +\ n_2}=1\).

Para analizar la dinámica en el tiempo de las frecuencias debemos tener claro a qué generación nos referimos en cada momento, es decir, debe quedar claro en nuestra notación que \(p\) y \(q\) son funciones del tiempo (en generaciones), por lo que los notaremos \(p(t)\) y \(q(t)\). Puede parecer obvio, pero por si acaso: esto no quiere decir que se multiplique \(p\) por \(t\), sino que como usual en la notación de funciones solo es una forma de expresar que \(p\) cambia en función del valor de \(t\).

De acuerdo a la ecuación (7.24), para la generación \((t+1)\) las frecuencias de los genotipos estarán dadas por

\[ \begin{split} p(t+1)=\frac{n_1(t+1)}{n_1(t+1)\ +\ n_2(t+1)}\\ q(t+1)=\frac{n_2(t+1)}{n_1(t+1)\ +\ n_2(t+1)} \end{split} \tag{7.25} \]

pero, usando la ecuación (7.22), que relaciona el número de individuos en dos generaciones sucesivas, en la ecuación (7.25), tenemos que

\[ \begin{split} p(t+1)=\frac{W_1 \cdot n_1}{W_1 \cdot n_1+W_2 \cdot n_2} \end{split} \tag{7.26} \]

Notar que si bien \(n_1\) y \(n_2\) son funciones de \(t\) y por lo tanto deberíamos escribirlas como \(n_1(t)\) y \(n_2(t)\), para evitar que la ecuación (7.26) sea más difícil de leer sacamos el \((t)\) de la misma. La ecuación (7.26) nos expresa la frecuencia del alelo \(A_1\) en la generación \((t+1)\) en función del número de individuos y sus fitness en la generación previa. Para llegar a una expresión que sea función de la frecuencia en la generación anterior, una alternativa sencilla consiste en multiplicar y dividir por \(n_1+n_2\), es decir

\[ \begin{split} p(t+1)=\frac{(\frac{1}{n_1\ +\ n_2})}{(\frac{1}{n_1\ +\ n_2})}\cdot\frac{W_1 \cdot n_1}{W_1 \cdot n_1\ +\ W_2 \cdot n_2}=\frac{W_1 \cdot (\frac{n_1}{n_1\ +\ n_2})}{W_1 \cdot (\frac{n_1}{n_1\ +\ n_2}) + W_2 \cdot (\frac{n_2}{n_1\ +\ n_2})} \end{split} \tag{7.27} \]

Pero \(\frac{n_1}{n_1\ +\ n_2}=p(t)\) y \(\frac{n_2}{n_1\ +\ n_2}=q(t)\), por lo que la ecuación (7.27) se transforma en

\[ \begin{split} p(t+1)=\frac{W_1\ p(t)}{W_1 \cdot p(t)\ +\ W_2 \cdot q(t)}=\frac{W_1 \cdot p(t)}{W_1 \cdot p(t)\ +\ W_2 \cdot (1-p(t))} \end{split} \tag{7.28} \]

La ecuación (7.28) depende de dos parámetros (\(W_1\) y \(W_2\)) para definir las frecuencias alélicas en la próxima generación. Si recordamos de más arriba, \(W_1\) y \(W_2\) eran los factores reproductivos de cada uno de los dos alelos, es decir la tasa neta de crecimiento de cada uno de los dos alelos, que no es otra cosa que el fitness absoluto de cada uno de ellos (de ahí la notación \(W\)), del que habíamos hablado al comienzo del capítulo Selección natural. Como vimos también en ese capítulo, al dividir el fitness absoluto de los distintos genotipos entre el de alguno de ellos se obtiene el fitness relativo de los mismos, que nuevamente notaremos \(w\).

Con esta lógica, si se define \(w_1 = W_1/W_2\) como el fitness relativo del alelo \(A_1\) respecto del \(A_2\) (con \(W_1=w_1 \cdot W_2\)), sustituyendo en la ecuación (7.28) se llega a

\[ \begin{split} p(t+1)=\frac{w_1 \cdot W_2 \cdot p(t)}{w_1 \cdot W_2 \cdot p(t)\ +\ W_2 \cdot (1-p(t))}=\frac{w_1 \cdot p(t)}{w_1 \cdot p(t)\ +\ (1-p(t))} \end{split} \tag{7.29} \]

La importancia de la ecuación (7.29) radica en que ahora se cuenta con una expresión de la frecuencia del alelo \(A_1\) (y por lo tanto del \(A_2\), ya que \(p+q=1\) en cualquier generación) que solo depende de un parámetro: el fitness relativo de los dos alelos. Dicho de otra manera, ahora las frecuencias en la siguiente generación no dependen de los factores reproductivos en términos absolutos, sino de la relación entre ellos. Este resultado a la vez intuitivo y muy importante, ya que deja en claro que el cambio en frecuencias estará dado por el éxito de un genotipo sobre el otro, aún en condiciones muy diferentes.

Para entender esto basta con imaginarse una situación donde el ambiente cambia en el tiempo, afectando el éxito reproductivo de ambos genotipos de manera similar. Ejemplos de esto pueden ser el cambio de temperatura, la abundancia o escasez de nutrientes, la existencia de un patógeno, entre otros escenarios de relevancia biológica. Supongamos que llamamos a esta función del ambiente \(\sigma(t)\), para dejar claro que se trata de una función que varía con el tiempo. Ahora, asumiendo que \(\sigma(t)\) afecta de la misma manera a ambos genotipos (esto es fundamental), el nuevo número de descendientes por ancestro será para cada uno de los genotipos \(W'_1=\sigma(t)\ W_1\) y \(W'_2=\sigma(t)\ W_2\). Usando la misma notación para el fitness relativo al incluir este efecto ambiental

\[ \begin{split} w'_1 = \frac{W'_1}{W'_2}=\frac{\sigma(t) \cdot W_1}{\sigma(t) \cdot W_2}=\frac{W_1}{W_2}=w_1 \end{split} \]

Este resultado es fundamental ya que, en la medida de los factores ambientales afecten de la misma manera a ambos genotipo, desacopla los factores ambientales o ecológicos del estudio de la dinámica de los genéticos.

El objetivo que nos habíamos planteado es entender la dinámica del cambio en las frecuencias alélicas, y para eso debemos entender como cambia de generación a generación y obtener una expresión que represente el cambio entre dos generaciones sucesivas. El cambio de la frecuencia del alelo \(A_1\) entre dos generaciones será la diferencia entre \(p(t+1)\) y \(p(t)\) para un \(t\) dado, por lo que haciendo uso de la ecuación (7.28) y restándole \(p(t)\) se llega a la siguiente relación

\[ \begin{split} \Delta_sp=p(t+1)-p(t)=\frac{W_1 \cdot p(t)}{W_1 \cdot p(t)\ +\ W_2 \cdot q(t)}-p(t)\ \therefore\ \\ \Delta_sp=\frac{W_1 \cdot p(t)-p(t) \cdot [W_1 \cdot p(t)\ +\ W_2 \cdot q(t)]}{W_1 \cdot p(t)\ +\ W_2 \cdot q(t)} \end{split} \tag{7.30} \]

Notar que volvimos a usar la misma notación que en el capítulo Selección natural, \(\Delta_sp\), con el subscrito \(_s\) para marcar que se trata del cambio debido a la selección (aunque ahora se trata del caso de un locus haploide). Expandiendo los términos de la derecha, tenemos

\[ \begin{split} \Delta_sp=\frac{W_1 \cdot p(t)-W_1 \cdot p^2(t)-W_2 \cdot p(t) \cdot q(t)}{W_1 \cdot p(t)\ +\ W_2 \cdot q(t)} =\frac{W_1 \cdot [p(t)-p^2(t)]-W_2 \cdot p(t) \cdot q(t)}{W_1 \cdot p(t) + W_2 \cdot q(t)} \end{split} \tag{7.31} \]

Pero \(p(t)-p^2(t)=p(t) \cdot [1-p(t)]=p(t) \cdot q(t)\), por lo que sustituyendo en la ecuación (7.31) llegamos finalmente a la siguiente expresión para el cambio de la frecuencia de \(A_1\) en una generación:

\[ \begin{split} \Delta_sp=\frac{W_1 \cdot p(t) \cdot q(t) - W_2 \cdot p(t) \cdot q(t)}{W_1 \cdot p(t) + W_2 \cdot q(t)}=\frac{(W_1-W_2) \cdot p(t) \cdot q(t)}{W_1 \cdot p(t)+W_2 \cdot q(t)} \end{split} \tag{7.32} \]

Si, siguiendo la notación de Otto y Day (Otto and Day 2007), definimos el coeficiente de selección en favor del alelo \(A_1\) como \(s_d=(W_1-W_2)/W_2\) (el subscrito \(_d\) denota que se trata de una derivación a partir de tiempo discreto), entonces \((W_1-W_2)=s_d \cdot W_2\) y \(W_1=W_2\ +\ s_d \cdot W_2 \Leftrightarrow W_1=W_2 \cdot (1+s_d)\). Sustituyendo estas dos últimas expresiones en (7.32), tenemos

\[ \begin{split} \Delta_sp=\frac{s_d \cdot W_2 \cdot p(t) \cdot q(t)}{W_2 \cdot (1+s_d) \cdot p(t)\ +\ W_2 \cdot q(t)} \therefore \\ \Delta_sp=\frac{s_d \cdot W_2 \cdot p(t) \cdot q(t)}{W_2 \cdot [(1+s_d) \cdot p(t)\ +\ q(t)]} \therefore \\ \Delta_sp=\frac{s_d \cdot p(t) \cdot q(t)}{(1+s_d) \cdot p(t)\ +\ q(t)} \end{split} \tag{7.33} \]

Finalmente, expandiendo los términos en el denominador de (7.33) y recordando que \(p(t)+q(t)=1\), se tiene

\[ \begin{split} \Delta_sp=\frac{s_d \cdot p(t) \cdot q(t)}{p(t)+s_d \cdot p(t)\ +\ q(t)}=\frac{s_d \cdot p(t) \cdot q(t)}{1+s_d \cdot p(t)} \end{split} \tag{7.34} \]

o, retirando la notación de la generación \(t\), que a esta altura es evidente, el cambio en la frecuencia del alelo \(A_1\) será

\[ \begin{split} \Delta_sp=\frac{s_d \cdot pq}{1+s_d \cdot p} \end{split} \tag{7.35} \]

La forma del cambio de frecuencia entre generaciones, dependiendo de la frecuencia del alelo \(A_1\) y del coeficiente de selección \(s_d\), se puede apreciar en la Figura 7.6.

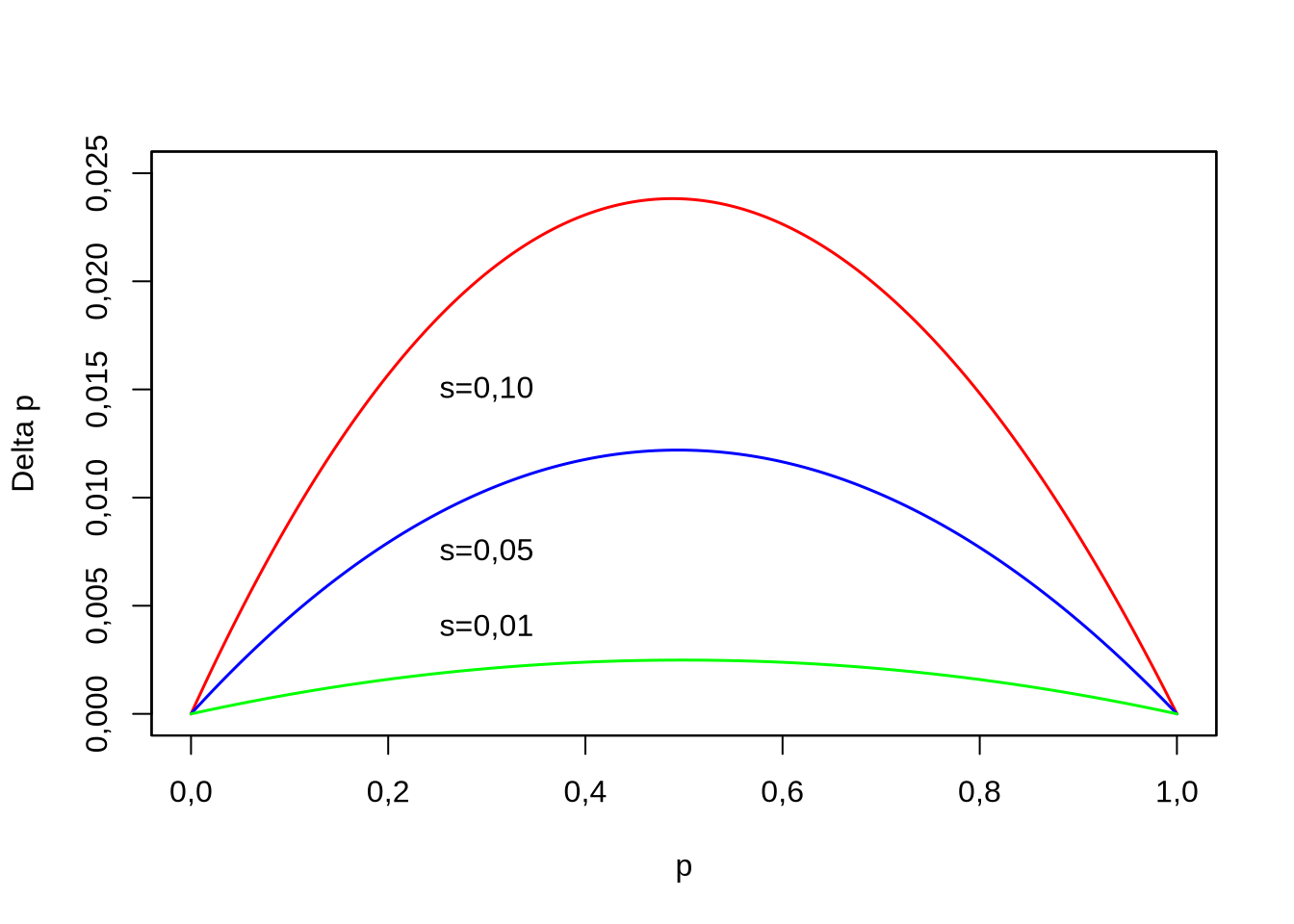
Figura 7.6: Cambio en la frecuencia del alelo \(A_1\) (\(\Delta_sp\)) en función de la frecuencia del mismo (\(p\)) y del coeficiente de selección \(s_d=(W_1-W_2)/W_2\). En rojo \(s_d=0,10\), azul \(s_d=0,05\) y verde \(s_d=0,01\).

La forma luce como aparentemente parabólica aunque no lo sea, ya que el denominador aumenta a medida de aumenta \(p\) (pero a valores muy bajos de \(s_d\), \(1+s_d \approx 1\)). Esto nos hace recordar las formas de la selección estabilizadora. Sin embargo, esto se debe a que en la Figura 7.6 solo manejamos valores de \(s_d\) positivos y relativamente bajos. Por ejemplo, si \(s_d=0,10=(W_1-W_2)/W_2 \Leftrightarrow W_1=W_2 \cdot (1+0,10) \Leftrightarrow W_1=1,1 \cdot W_2\); es decir, el genotipo \(W_1\) crecerá a una tasa un \(10\%\) mayor que el \(W_2\).

Sin embargo, para interpretar correctamente esta ecuación es importante notar la asimetría del coeficiente \(s_d\) respecto a los valores de \(W_1\) y \(W_2\). Un ejemplo claro consiste en intercambiar los valores de \(W_1\) y \(W_2\) y ver el resultado. Un caso extremo es cuando la ventaja de un genotipo respecto al otro es enorme, por ejemplo \(W_2=1\) y \(W_1=0,01\). En esta situación, \(s_d=(W_1-W_2)/W_2=(0,01-1)/1=-0,99\), pero si invertimos los valores se obtiene \(W_1=1\) y \(W_2=0,01\), por lo que \(s_d=(W_1-W_2)/W_2=(1-0,01)/0,01=99\).

Una alternativa para la interpretación de \(\Delta_sp\) es hacerlo a partir de la ecuación (7.33). El denominador es \(W_1 \cdot p(t)\ +\ W_2 \cdot q(t)=\bar{W}(t)\), es decir el fitness medio absoluto, mientras que el numerador es \((W_1-W_2) \cdot p(t) \cdot q(t)\), que se trata de la diferencia en los fitness absolutos de los dos genotipos, modulados por la mitad de la varianza genética: a frecuencias intermedias de \(p\) y \(q\) mayor será el efecto de la diferencia \((W_1-W_2)\).

Ejemplo 7.3

En una especie bacteriana, un locus con dos alelos, \(A_1\) y \(A_2\) produce que los individuos que poseen los mismos presentan un fitness absoluto de \(W_1=1,7\) y \(W_2=1,2\). Si la frecuencia del alelo \(A_1\) es \(p=0,45\), asumiendo que la división de las bacterias opera en tiempo discreto, determinar la frecuencia en la siguiente generación.

Una alternativa es usar la ecuación (7.30), es decir

\[ \begin{split} \Delta_sp = p(t+1)-p(t) = \frac{W_1 p(t)}{W_1 p(t) + W_2 q(t)}-p(t) \end{split} \]

por lo que, sustituyendo los valores tenemos

\[ \begin{split} \Delta_sp=\frac{1,7 \times 0,45}{1,7 \times 0,45+1,2 \times (1-0,45}-0,45=0,08684 \end{split} \]

Por otro lado, si calculamos \(s_d=(W_1-W_2)/W_2=(1,7-1,2)/1,2=0,41667\), entonces aplicando la ecuación @(eq:haplosel13) y sustituyendo los valores correspondientes tenemos

\[ \begin{split} \Delta_sp=\frac{s_d\ pq}{1+s_d\ p}=\frac{0,41667 \times 0,45 \times 0,55}{1+0,41667 \times 0,45}=0,08684 \end{split} \]

que es el mismo resultado obtenido previamente. En función de este resultado, la frecuencia \(p(t+1)>p(t)\) y por lo tanto incrementará la frecuencia del alelo \(A_1\), que tiene una ventaja en fitness respecto al \(A_2\). Notar que esta diferencia de fitness provoca un salto muy grande en las frecuencias alélicas en una sola generación (casi un \(9\%\)).

Selección haploide: modelo continuo

Una forma alternativa de estudiar el cambio de frecuencias alélicas en un modelo de locus haploide con dos alelos es a partir del modelo de crecimiento continuo de la población. Como vimos antes, en este modelo las tasas de crecimiento instantáneo tienen la forma \(r=b-d\), es decir la tasa de nacimientos menos la tasa de muertes. Supongamos entonces que los dos alelos (genotipos) \(A_1\) y \(A_2\) tienen tasas diferentes, las cuales expresaremos como

\[ \begin{split} r_1=(b_1-d_1) \\ r_2=(b_2-d_2) \end{split} \tag{7.36} \]

Si, como antes, \(n_1\) y \(n_2\) representan los número de células (individuos) de cada uno de los dos genotipos, entonces el modelo de crecimiento exponencial nos permite describir el cambio en el número de células como las ecuaciones diferenciales

\[ \begin{split} \frac{dn_1}{dt}=r_1 \cdot n_1(t) \\ \frac{dn_2}{dt}=r_2 \cdot n_2(t) \end{split} \tag{7.37} \]

Pero, de acuerdo a la ecuación (7.24), las frecuencias \(p\) y \(q\) (ambas funciones de \(t\)), son

\[ \begin{split} p=\frac{n_1}{n_1\ +\ n_2}\\ q=\frac{n_2}{n_1\ +\ n_2} \end{split} \]

por lo que sustituyendo en la ecuación (7.37), tenemos que el cambio en la frecuencia del alelo \(A_1\) será

\[ \begin{split} \frac{dp}{dt}=\frac{d(\frac{n_1}{n_1\ +\ n_2})}{dt} \end{split} \tag{7.38} \]

Ahora, aplicando la regla del cociente para las derivadas (ver [APENDICE A: Conceptos Matemáticos Básicos]), tenemos que

\[ \begin{split} \frac{dp}{dt}=\frac{\frac{dn_1}{dt} \cdot (n_1\ +\ n_2) -\ n_1 \cdot \frac{d(n_1\ +\ n_2)}{dt}} {(n_1\ +\ n_2)^2} \end{split} \tag{7.39} \]

Pero la derivada de una suma (o resta) es la suma (o resta) de las derivadas, por lo que, expandiendo la ecuación (7.39), tenemos ahora

\[ \begin{split} \frac{dp}{dt}=\frac{n_1 \cdot \frac{dn_1}{dt}\ +\ n_2 \cdot \frac{dn_1}{dt} -\ n_1 \cdot \frac{dn_1}{dt}\ -\ n_1 \cdot \frac{dn_2}{dt}} {(n_1\ +\ n_2)^2} \therefore \\ \frac{dp}{dt}=\frac{\ n_2 \cdot \frac{dn_1}{dt} -\ n_1 \cdot \frac{dn_2}{dt}} {(n_1\ +\ n_2)^2} \end{split} \tag{7.39} \]

Pero como vimos antes, de acuerdo a la ecuación (7.37), \(\frac{dn_1}{dt}=r_1 \cdot n_1\), mientras que \(\frac{dn_2}{dt}=r_2 \cdot n_1\) (notando \(n_1\) por \(n_1(t)\) y \(n_2\) por \(n_2(t)\)), por lo que sustituyendo en la ecuación (7.39), tenemos

\[ \begin{split} \frac{dp}{dt}=\frac{n_2 \cdot (r_1 \cdot n_1) -\ n_1 \cdot (r_2 \cdot n_2)} {(n_1\ +\ n_2)^2}=(r_1\ -\ r_2) \cdot \frac{n_1 \cdot n_2}{(n_1\ +\ n_2)^2} \end{split} \tag{7.40} \]

Pero \(\frac{n_1\ n_2}{(n_1\ +\ n_2)^2}=\frac{n_1}{(n_1\ +\ n_2)} \cdot \frac{n_2}{(n_1\ +\ n_2)}=pq\), por lo que sustituyendo en la ecuación (7.40), obtenemos finalmente

\[ \begin{split} \frac{dp}{dt}=(r_1\ -\ r_2) \cdot p \cdot q \end{split} \tag{7.41} \]

Considerando que la diferencia entre las tasas netas de crecimiento \(r_1\) y \(r_2\) representa el coeficiente de selección para el modelo continuo, es decir \(s_c=(r_1-r_2)\) (el equivalente de \(s_d\) en el modelo discreto), entonces la ecuación (7.41) la podemos escribir como

\[ \begin{split} \frac{dp}{dt}=s_c \cdot p \cdot q \end{split} \tag{7.42} \]

Es decir, la tasa de cambio en la frecuencia del alelo \(A_1\) es igual al producto de la diferencia entre tasas de crecimiento entre los dos genotipos, multiplicado por \(pq\), que como vimos en el capítulo Variación y equilibrio de Hardy-Weinberg es una función de la variabilidad genética existente (con máximo en \(p=q=\frac{1}{2}\)). Si bien las ecuaciones que describen el cambio de frecuencias en el modelo discreto ((7.35)) y en el modelo continuo ((7.42)) son diferentes, como discutimos antes, cuando \(s_d \ll 1 \Rightarrow 1+s_d \cdot p \approx 1\) y por lo tanto

\[ \begin{split} \Delta_sp=\frac{s_d \cdot p \cdot q}{1+s_d \cdot p} \approx s_d \cdot p \cdot q \sim s_c \cdot p \cdot q = \frac{dp}{dt} \end{split} \tag{7.43} \]

por lo que bajo esas condiciones las soluciones para ambos modelos tienen formas funcionales similares (no son iguales, ya que \(s_c \ne s_d\)).

Ejemplo 7.4

Considerando que las tasas de crecimiento instantáneo que corresponden a los dos alelos, \(A_1\) y \(A_2\) en un locus bacteriano son \(r_1=0,7\) y \(r_2=0,2\) calcular la tasa de cambio en frecuencia, cuando la frecuencia del alelo \(A_1\) es \(p=0,45\).

Utilizando la ecuación (7.42) y recordando que \(s_c=r_1-r_2=0,7-0,2=0,5\), entonces

\[ \begin{split} \frac{dp}{dt}=s_c\ pq=0,5 \times 0,45 \times (1-0,45)=0,12375 \end{split} \]

es decir, que la tasa de cambio instantáneo de frecuencias hará que aumente la frecuencia de \(p\).

PARA RECORDAR

• En el modelo discreto de selección haploide con dos alelos, los fitness absolutos están dados por

\[ \begin{split} W_1=(1-d_1)(1+b_1)\\ W_2=(1-d_2)(1+b_2) \end{split} \]

con \(b_1\), \(b_2\) las tasas netas de nacimientos para los individuos de ambos alelos y \(d_1\), \(d_2\), las tasas de muertes de ambos.

• En el modelo discreto de selección, el cambio esperado en la frecuencia del alelo \(A_1\) estará dado por

\[ \begin{split} \Delta_sp=p(t+1)-p(t)=\frac{W_1\ p(t)}{W_1\ p(t)\ +\ W_2\ q(t)}-p(t) \end{split} \]

• Si los factores ambientales varían en el tiempo de acuerdo a una función \(\sigma(t)\), pero afectan en la misma proporción a los dos genotipos, es decir, si \(W'_1=\sigma(t)\ W_1\), entonces

\[ \begin{split} w'_1 = \frac{W'_1}{W'_2}=\frac{\sigma(t)\ W_1}{\sigma(t)\ W_2}=\frac{W_1}{W_2}=w_1 \end{split} \]

y por lo tanto el fitness relativo del genotipo 1 respecto al 2 es independiente de la forma de \(\sigma(t)\).

• Por otro lado, si \(s_d=(W_1-W_2)/W_2\), entonces una forma alternativa de calcular el cambio de frecuencia del alelo \(A_1\) en una generación estará dado por

\[ \begin{split} \Delta_sp=\frac{s_d \cdot p \cdot q}{1+ s_d \cdot p} \end{split} \]

• En el caso del modelo continuo, si \(r_1=b_1-d_1\), \(r_2=b_2-d_2\) son las tasas de crecimiento instantáneo para los individuos de los dos alelos y \(s_c=r_1-r_2\) es la diferencia entre ambas, entonces la tasa de cambio de frecuencia del alelo \(A_1\) estará dada por

\[ \begin{split} \frac{dp}{dt}=s_c \cdot p \cdot q \end{split} \]

7.4 Los modelos de Moran y de fisión vs el de Wright-Fisher

En el capítulo sobre Deriva Genética vimos por primera vez un modelo que daba cuenta de los procesos estocásticos que ocurren en la elección de los gametos que formarán la siguiente generación de individuos, es decir un modelo reproductivo. Ese modelo que vimos era el modelo Wright-Fisher, y consistía en el muestreo con reemplazo de los \(2N\) gametos necesarios para formar una nueva población de \(N\) individuos diploides. Si bien se trata de un modelo sumamente útil y fácil de conceptualizar, no se trata del único modelo imaginable que represente el proceso de muestreo gamético. De hecho, existe un modelo también ampliamente utilizado que se conoce como el modelo de Moran en honor a Patrick Moran⁷¹, quien lo propuso por primera vez. Estrictamente el modelo de Moran se aplica a poblaciones de especies haploides, aunque con algunas modificaciones funciona para modelar especies diploides. En nuestro caso vamos a trabajar con una población de tamaño constante con \(N\) individuos de una especie haploide.

El algoritmo del modelo de Moran es muy sencillo: a cada instante en el tiempo un individuo es elegido para reproducirse y va a dejar una copia, mientras que un individuo es elegido para morir (puede ser el mismo individuo que acaba de dejar una copia, pero no la copia). Por lo tanto, la posible descendencia de un individuo (considerándose a si mismo como descendencia) en cada instante es 0, 1 o 2 descendientes: 0 si es elegido exclusivamente para morir, 2 si es elegido exclusivamente para copiarse o 1 en el resto de los casos. Como en la población hay \(N\) individuos, la probabilidad de elegir un individuo para copiarse es \(\frac{1}{N}\), mientras que la probabilidad de ser elegido para morir es también \(\frac{1}{N}\). La probabilidad de dejar 0 descendientes es la que resulta de NO ser elegido para copiarse, es decir \((N-1)/N\), y luego ser elegido para morir \(1/N\), por lo que multiplicando ambas tenemos la probabilidad \((\frac{(N-1)}{N}) \cdot (\frac{1}{N})=\frac{(N-1)}{N^2}\). De igual manera, la probabilidad de que un individuo deje 2 descendientes es la probabilidad de ser elegido para copiarse (\(1/N\)), multiplicada por la probabilidad de NO ser elegido para morir (\((N-1)/N\)), por lo que también es \((\frac{1}{N}) \cdot (\frac{(N-1)}{N})=\frac{(N-1)}{N^2}\). Como \(p_1=1-p_0-p_2\), entonces

\[ \begin{split} p_1=1-\frac{(N-1)}{N^2}-\frac{(N-1)}{N^2}=\frac{N^2-2(N-1)}{N^2}=\frac{(N-1)^2+1}{N^2} \end{split} \tag{7.44} \]

En resumen, para el modelo de Moran tenemos entonces

\[\begin{equation} \begin{cases} p_0 = \frac{(N-1)}{N^2} \\ p_1= \frac{(N-1)^2+1}{N^2} \\ p_2 = \frac{(N-1)}{N^2} \end{cases} \end{equation}\]

por lo que cuando \(N \to \infty\), \(p_1 \to 1\) y \(p_0=p_2 \to 0\), es decir la mayor parte de los individuos solo dejarán un descendiente en este modelo.

Veamos que ocurre a nivel de la población. Supongamos que tenemos \(i\) individuos haploides que portan el alelo \(A_1\), y que por lo tanto \(N-i\) llevan el alelo \(A_2\). Para pasar de pasar de \(i\) individuos en el instante de tiempo \(t\) a \(i-1\) en el siguiente instante lo que debería ocurrir es que un individuo con alelo \(A_2\) sea elegido para reproducirse y que uno con alelo \(A_1\) sea elegido para morir. Es decir, en términos de probabilidades, tenemos

\[ \begin{split} p_{i,i-1}=(\frac{(N-i)}{N}) \cdot (\frac{i}{N})=\frac{(N-i) \cdot i}{N^2} \end{split} \tag{7.45} \]

donde el término \(\frac{(N-i)}{N}\) es la probabilidad de elegir un \(A_2\) (para que se copie) y el término \(\frac{i}{N}\) es la probabilidad de elegir un \(A_1\) (para que se muera); como ambos son eventos independientes la probabilidad conjunta es el producto de sus probabilidades. De la misma manera, para pasar en el instante \(t\) de \(i\) copias del alelo \(A_1\) a \(i+1\) copias en el siguiente, debemos elegir un alelol \(A_1\) para que se copie y un alelo \(A_2\) para que muera. Esto ocurrirá con probabilidad

\[ \begin{split} p_{i,i+1}=(\frac{i}{N}) \cdot (\frac{(N-i)}{N}) =\frac{i \cdot (N-i)}{N^2} \end{split} \tag{7.46} \]

donde, nuevamente, \(\frac{i}{N}\) es la probabilidad de elegir un alelo \(A_1\) (esta vez para que se copie) y \(\frac{(N-i)}{N}\) es la probabilidad de elegir un alelo \(A_2\) (para que se muera, ahora). Claramente, \(p_{i,i-1}=p_{i,i+1}\). Por otro lado, la probabilidad de mantener el mismo número de copias de \(A_1\) (y por lo tanto de \(A_2\), ya que la población es de tamaño constante) en el siguiente instante está dada por \(1-p_{i,i-1}-p_{i,i+1}\), o lo que es equivalente

\[ \begin{split} p_{i,i}=\frac{i^2}{N^2}+\frac{(N-i)^2}{N^2}=\frac{i^2+(N-i)^2}{N^2} \end{split} \tag{7.47} \]

La explicación de la ecuación (7.47) es muy sencilla; para mantener el mismo número de copias hay dos posibilidades: a) copiar un alelo \(A_1\) y que muera un alelo \(A_1\), o b) copiar un alelo \(A_2\) y que muera un alelo \(A_2\). El primer escenario ocurre con probabilidad \((\frac{i}{N}) \cdot (\frac{i}{N})=\frac{i^2}{N^2}\), mientras que el segundo ocurre con probabilidad \((\frac{(N-i)}{N}) \cdot (\frac{(N-i)}{N})=\frac{(N-i)^2}{N^2}\). Como ambos son eventos mutuamente excluyentes debemos sumar sus probabilidades, lo que nos da el resultado de la ecuación (7.47).

En resumen, tenemos entonces que las probabilidades de transición en el modelo de Moran están dadas por

\[\begin{equation} \begin{cases} p_{i,i-1}= \frac{(N-i) \cdot i}{N^2} \\ p_{i,i}=\frac{i^2+(N-i)^2}{N^2} \\ p_{i,i+1} =\frac{i \cdot (N-i)}{N^2} \end{cases} \end{equation}\]

A diferencia del modelo de Wright-Fisher en donde excepto desde los estados absorbentes siempre existía una probabilidad de pasar a cualquiera de los estados (ver la sección Cadenas de Markov), en este caso nuestra matriz de transición será tridiagonal, una matriz cuyos elementos son solo distintos de cero en la diagonal principal y las diagonales adyacentes por encima y por debajo de esta. Ambos modelos, en su forma básica, dependen de una serie de supuestos que simplifican el tratamiento, esencialmente que se trata de un locus selectivamente neutro, con todos los alelos de idéntico fitness y que no existe estructura demográfica (i.e., el apareamiento es al azar).

Si recuerdas de la sección El modelo coalescente, a partir de la distribución del número de alelos en una muestra podíamos deducir varias cosas utilizando este modelo. En particular, la probabilidad de que ninguno de los \(k\) alelos converja en las pasadas \(t\) generaciones es igual a

\[ \begin{split} P(T_k^N>t)=(1-\frac{k(k-1)}{2N})^t \end{split} \tag{7.48} \]

Notar que a diferencia de la sección El modelo coalescente en la que trabajamos con individuos diploides, ahora estamos trabajando con especies haploides y por eso el factor \(2N\) en el denominador en lugar del \(4N\) que habíamos visto antes.

De hecho, vimos que era posible escalar el modelo para que no dependiese del tamaño poblacional. Si aplicamos la transformación \(T_k=T_k^N/N\), entonces la siguiente aproximación es válida

\[ \begin{split} P(T_k > v) \approx e^{-\frac{k(k-1)}{2} v} \end{split} \tag{7.49} \]

Claramente, el cambio en el número de alelos en una generación es muy diferente entre el modelo de Wright-Fisher y el de Moran, y eso afectará el número de generaciones necesarias para cada nuevo evento de coalescencia. En una aproximación muy cruda podemos ver el modelo de Wright-Fisher como requiriendo \(N\) generaciones del modelo de Moran y por lo tanto, para poder comparar las expectativas bajos diferentes modelos reproductivos debemos escalar los procesos de manera consistente. Kingman muestra que es posible usar un escalado tal que permita que los tiempos de coalescencia sigan una distribución exponencial con tasa \(k(k-1)/2\) (Kingman 1982a). Ese factor de escala es nuestro conocido tamaño efectivo poblacional (\(N_e\)), pero ahora partiendo de la definición que se refiere a la varianza en el número de descendientes por progenitor. Para tamaños poblacionales grandes \(N_e^{*{WF}}=N\), mientras que para el modelo de Moran \(N_e^{*{M}}=N^2/2\).

Un modelo alternativo es el modelo de fisión, en el cual, en el instante \(t\) cada individuo deja 0, 1 o 2 descendientes con probabilidades \(p_0\), \(p_1\) y \(p_2\). En principio este modelo no asume tamaño constante, pero para que se cumpla la restricción de tamaño constante (y que sea comparable con lo que hemos asumido en otros modelos) es necesario que \(p_0=p_2 \leqslant \frac{1}{2}\). Claramente este modelo es intuitivo para modelar la dinámica de poblaciones bacterianas ya que representa el proceso de fisión por el cual se reproducen: a cada instante la bacteria puede morir (0 “descendientes”, incluyéndose), puede no dividirse (1 “descendiente”, ella misma) o puede dividirise y por lo tanto dejar 2 bacterias para el siguiente instante del tiempo. Para este modelo el factor de escala es \(N_e^{*{F}}=N/(2p_2)\). En el caso de \(p_2=1/N\), como sería en el modelo de Moran, entonces \(N_e^{*{F}}=N/(2p_2)=N/[2(1/N)]=N^2/2=N_e^{*{M}}\) que es el mismo factor de escala que habíamos visto para Moran. En el caso de que \(p_2=\frac{1}{2}\), entonces \(N_e^{*{F}}=N/(2p_2)=N/[2(1/2)]=N=N_e^{_{WF}}\), que es el factor de escalado para el modelo de Wright-Fisher. Un tratamiento más exhaustivo y claro de este tema, así como las implicancias para la inferencia demográfica a partir de las frecuencias alélicas puede encontrarse en Robinson, Falush, and Feil (2010).

PARA RECORDAR

• El algoritmo del modelo de Moran es muy sencillo: a cada instante en el tiempo un individuo es elegido para reproducirse y va a dejar una copia, mientras que un individuo es elegido para morir (puede ser el mismo individuo que acaba de dejar una copia, pero no la copia). Por lo tanto, la posible descendencia de un individuo (considerándose a si mismo como descendencia) en cada instante es 0, 1 o 2 descendientes.
• La probabilidad de dejar 0, 1 o 2 descendientes (\(p_0,\ p_1,\ p_2\)) bajo el modelo de Moran es

\[\begin{equation} \begin{cases} p_0 = \frac{(N-1)}{N^2} \\ p_1= \frac{(N-1)^2+1}{N^2} \\ p_2 = \frac{(N-1)}{N^2} \end{cases} \end{equation}\]

por lo que cuando \(N \to \infty\), \(p_1 \to 1\) y \(p_0=p_2 \to 0\); es decir la mayor parte de los individuos solo dejarán un descendiente según este modelo.

• En general, las probabilidades de transición en el modelo de Moran están dadas por

\[\begin{equation} \begin{cases} p_{i,i-1}= \frac{(N-i) \cdot i}{N^2} \\ p_{i,i}=\frac{i^2+(N-i)^2}{N^2} \\ p_{i,i+1} =\frac{i \cdot (N-i)}{N^2} \end{cases} \end{equation}\]

• Vimos que es posible escalar el modelo coalescente para que no dependa del tamaño poblacional. Si aplicamos la transformación \(T_k=T_k^N/N\), entonces la siguiente aproximación es valida

\[ \begin{split} P(T_k>v) \approx e^{-\frac{k(k-1)}{2} v} \end{split} \tag{7.49} \]

• El factor de escalado que permite que los tiempos de coalescencia sigan una distribución exponencial con tasa \(k(k-1)/2\) es el tamaño efectivo poblacional correspondiente a cada uno de los modelos. Para tamaños poblacionales grandes \(N_e^{*{WF}}=N\), mientras que para el modelo de Moran \(N_e^{*{M}}=N^2/2\).
• Un modelo alternativo es el modelo de fisión, en el cual en el instante \(t\) cada individuo deja 0, 1 o 2 descendientes con probabilidades \(p_0\), \(p_1\) y \(p_2\). En principio este modelo no asume tamaño constante, pero para que se cumpla la restricción de tamaño constante (y que sea comparable con lo que hemos asumido en otros modelos) es necesario que \(p_0=p_2 \leqslant \frac{1}{2}\).
• Para el modelo de fisión el factor de escala es \(N_e^{*{F}}=N/(2p_2)\). En el caso de \(p_2=1/N\), como sería en el modelo de Moran, entonces \(N_e^{*{F}}=N/(2p_2)=N/[2(1/N)]=N^2/2=N_e^{*{M}}\) que es el mismo factor de escala que vimos para Moran, mientras que en el caso de que \(p_2=\frac{1}{2}\), entonces \(N_e^{*{F}}=N/(2p_2)=N/[2(1/2)]=N=N_e^{_{WF}}\), que es el factor de escalado para el modelo de Wright-Fisher.

7.5 El rol de la transferencia horizontal

La forma general de herencia del material genético es que los ancestros traspasen el mismo a sus descendientes. Es decir, el pasaje del material genético es de una generación a la siguiente (por lo tanto entre individuos de diferentes generaciones) y por eso se conoce a esta forma de herencia como transferencia vertical de genes. Este es el mecanismo clásico y el que asegura que los descendientes sean, ignorando la mutación, una mezcla del material genético de sus progenitores. Como vimos anteriormente, pese a que en los procariotas no existen los mecanismos de recombinación clásicos de los eucariotas, existen diferentes formas alternativas que permiten el intercambio de material genético entre los mismos. Vimos así que es usual que bacterias y arqueas intercambien material genético con otros individuos de su especie y aún con individuos de otras especies. Cuando la recombinación es homóloga, en particular con otros individuos de la especie, podemos (abusando de la terminología) considerar a la misma como una forma de recombinación, ya que básicamente existe una conservación del orden y de las secuencias (más allá de las pequeñas diferencias existentes). Sin embargo, cuando se trata de un evento de intercambio no homólogo, o aún con individuos de otras especies, entonces ya no podemos seguir considerando esto como un evento de recombinación y debemos buscar una nueva forma de denominar al fenómeno y de comprender sus consecuencias.

Dado que la transferencia de material genético entre especies no es la forma vertical de transmitirlo, podemos llamar a esta forma horizontal o lateral, y por lo tanto al proceso Transferencia Horizontal de Genes (HGT, por sus siglas en inglés) o Transferencia Lateral de Genes (LGT, ídem). Para comprender mejor alguna de sus consecuencias definamos antes algunos términos evolutivos. En la Figura 7.7 podemos observar la evolución de un gen, la histona H1, en el ser humano y en el chimpancé.

Figura 7.7: Distinción entre diferentes formas de homología entre secuencias. Un evento de duplicación de una histona en el genoma de una especie ancestral al humano y el chimpacé provoca que en la actualidad cada una de las especies también posean un par copias génicas codificantes para histonas. Desde su duplicación inicial las dos copias han evolucionado en forma diferente, y por lo tanto la histona H1.1 es diferentes de la histona H1.2. Más aún, desde el evento de especiación que llevó a que seamos una especie diferente al chimpancé cada una de las histonas ha continuado evolucionando, y por lo tanto ya no serán idénticas las histonas H1.1 de estas especies, y tampoco las copias codificantes para histona H1.2. Se denomina ortólogos a los genes que se relacionan entre sí por un evento de especiación, mientras que se define parálogos a los que se relacionan a través de un evento de duplicación ancestral. Figura de Wikipedia, autor: Thomas Shafee, (CC BY 4.0).

En algún ancestro de ambas especies, mucho tiempo atrás, se produjo un evento que duplicó el gen de la histona H1 produciendo dos copias del mismo, las cuales llamaremos H1.1 y H1.2. Es fundamental entender que a partir de dicho punto existirán dos copias del mismo gen en el genoma haploide de la especie, ubicadas en diferentes lugares del genoma y no necesariamente en el mismo cromosoma (aunque suele ocurrir que sí)⁷². Cada una de estas copias del gen ancestral de la histona H1 seguirá un camino evolutivo relativamente independiente de la otra, y a lo largo del tiempo irá acumulando diferentes mutaciones y cambios. Por lo tanto, a medida que el tiempo transcurre las secuencias de las copias génicas H1.1 y H1.2 ya no serán idénticas. Lo que es más, cuando se produce un evento de especiación los caminos evolutivos pueden diverger también en este nivel. Este concepto se ve también ilustrado en el ejemplo de la Figura 7.7. En los primates un evento de especiación dió lugar a dos ramas que divergieron evolutivamente: una de estas ramas lleva a los humanos, mientras que la otra lleva al chimpancé (Pan troglodytes, la especie viva más cercana al humano). ¿Cómo afecta esto a la divergencia evolutiva entre copias génicas de histona? Una vez se establece el proceso de especiación, las copias de H1.1 en cada una de las ramas seguirá un camino evolutivo independiente; lo mismo ocurrirá para las copias de H1.2. Esto establece diferentes relaciones evolutivas entre las 4 copias (en los genomas haploides) que encontramos en chimpancé y humano. Por ejemplo, en el caso de H1.1 de chimpancé y H1.1 de humanos las copias eran idénticas en el último ancestro de ambas especies, una relación que se define como ortología. Decimos por lo tanto que los genes H1.1 de chimpancé y humano son genes ortólogos. Si en cambio analizamos la situación existente entre copias génicas codificadas en humano, notaremos que las dos copias se relacionan entre sí por el evento de duplicación ancestral mencionado anteriormente. Este tipo de relación se define como paralogía. Decimos por lo tanto que los genes codificantes para histona H1.1 y H1.2 de humano son parálogos.

Hasta este momento se analizaron las relaciones existentes entre genes que son el producto de eventos de duplicación intra-genómica y de especiación. Sin embargo, cuando ocurren eventos de transferencia horizontal de material entre dos especies diferentes puede ocurrir que en el genoma receptor ya estén codificados genes homólogos a parte (o todo) el material transferido. Esto lleva a la duplicación del número de “copias” del material genético en el genoma receptor. Pero el material duplicado es homólogo, y si bien puede ser de alguna manera similar, no es para nada necesario que se trate de copias idénticas. Esto lleva a definir una nueva forma de relación evolutiva entre genes, a los cuales llamaremos genes xenólogos. En la Figura 7.8 podemos apreciar, en forma esquemática, el surgimiento de un par de genes xenólogos producto de un evento de transferencia horizontal.

Figura 7.8: Aparición de una nueva copia de una secuencia proveniente de un homólogo en otra especie a partir de un evento de transferencia horizontal de genes. Los genes \(A_1\) y \(A_2\) son homólogos entre sí en diferentes especies, pero cuando el \(A_2\) se transfiere de la especie 2 a la especie 1, entonces en la especie 1 hay ahora dos copias, que son xenólogas entre sí. Figura de Wikipedia, autor: Thomas Shafee (CC BY 4.0).

Los genes \(A_1\) y \(A_2\) son genes homólogos (i.e., comparten alguna relación de similaridad evolutiva), el primero en la especie 1 y el segundo en la especie 2. Cuando ocurre un evento de transferencia horizontal de la especie 2 a la especie 1, llevando una copia de \(A_2\) hacia el genoma de la especie 1, entonces todos los descendientes de ese individuo de la especie 1 pasarán a tener dos “copias” (diferentes entre sí) del gen \(A\). Estas dos copias serán xenólogas, ya que la relación de homología entre ellas proviene de un evento de transferencia horizontal entre especies diferentes.

Una de las consecuencias de los eventos de transferencia horizontal, posiblemente la menos relevante, es la dificultad para entender las relaciones evolutivas entre especies a partir de unas pocas secuencias nucleotídicas, ya que los árboles filogenéticos (una de las vías usuales de reconstrucción de las relaciones) asumen que la homología y la proporción de similitud entre secuencias es un fiel reflejo de las relaciones evolutivas existentes entre especies, una asunción que es razonable, hasta cierto punto, si se asume la transferencia vertical de información genética durante el proceso evolutivo. A partir de secuencias que han experimentado eventos de transferencia horizontal esto último deja de ser cierto, ya que en dicho caso las trayectorias evolutivas de secuencias y especies serán diferentes. Alcanza con ver nuevamente la Figura 7.8 para comprender este fenómeno. Si analizamos las secuencias codificantes para \(A_2\) en la especie 1 y en la especie 2 inmediatamente después del evento de HGT, las mismas serán idénticas, o lo que es lo mismo coincidirán \(100\%\) en sus secuencias nucleotídicas. Supongamos ahora que en la rama que lleva desde el ancestro común de la especie 1 y 2 a la especie 2 hubiese aparecido una tercera especie, por ejemplo a nivel relativamente basal, la cual llamaremos especie 3. La copias de \(A_2\) en la especie 3 acumularían diferencias con la copia de \(A_2\) codificada en la especie 2. Al reconstruir un árbol filogenético basado en las secuencias de \(A_2\), al ser idénticas las secuencias de \(A_2\) en la especie 1 y la especie 2 (dada la existencia de un evento de HGT), las mismas quedarían agrupadas muy juntas, mientras que la especie 3 quedaría por afuera de estas dos, más lejana, pese a que en realidad la especie 2 y la especie 3 deberían estar más estrechamente emparentadas respecto a la especie 1 (que se separó previamente de ellas) en un árbol filogenético que refleje el proceso evolutivo que dió lugar a estas especies. Si bien esto es una dificultad que ocurre a menudo, existen diferentes alternativas para modelar este fenómeno e incorporlo a la reconstrucción filogenética, o al menos para identficar que las secuencias analizadas son xenólogas y no basar en ellas nuestras conclusiones evolutivas respecto al proceso evolutivo entre especies.

Una forma usual de identificar islas de transferencia horizontal (regiones relativamente largas del genoma que provienen de otra especie) es basarse en la composición de las mismas. Como hemos visto antes (capítulo Introducción a la Genómica), las diferentes especies poseen diferentes estilos de vida y de funcionamiento de la maquinaria celular, con diferentes sesgos mutacionales, tasas de mutación, de aceptación de material externo, así como de requerimientos. Todos estos factores usualmente afectan la composición de los genomas, tanto a nivel de los aminoácidos que constituyen las proteínas, como de los nucleótidos, ya sea en el caso que estos correspondan a secuencias codificantes como no-codificantes para proteínas u ARNs funcionales. En procariotas, donde la uniformidad composicional a nivel nucleotídico es importante, un primer indicador de material procedente del exterior de la especie son las regiones de un genoma que poseen un contenido GC marcadamente diferente al del resto del genoma. Un segundo nivel, algo más complejo pero que puede llegar a tener una mayor capacidad de discriminación respecto del origen de material genético, es el uso de codones de estas regiones (cuando se consideran secuencias codificantes para proteínas, obviamente). En el caso de procariotas, muchas especies suelen tener una preferencia marcada por el uso de algunos codones, en particular dentro de cada aminoácido (para aquellos aminoácidos que tienen codones sinónimos), por lo que aquellas regiones con una composición inusual de codones para la especie pueden ser candidatas interesantes a provenir de eventos de HGT relativamente recientes. Es importante remarcar que la evolución continúa luego de los eventos de HGT, por lo que aún las secuencias que provienen de ellos perderán sus características propias con el paso del tiempo y se irán pareciendo en los aspectos composicionales a las secuencias del genoma receptor donde se instalaron.

Los eventos de transferencia horizontal tienen y han tenido una relevancia extrema en la evolución de la vida en nuestro planeta. Por un lado, tanto las mitocondrias como los plástidos (los cloroplastos, por ejemplo) provienen de eventos de transferencia horizontal desde procariotas a eucariotas. En ambos casos se trataría no solo del material genético sino de la célula en su conjunto, pero desde el punto de vista genético se trata de eventos de HGT (que afortudanamente podemos identificar fácilmente porque no se han integrado totalmente al genoma nuclear, además). Por otra parte, la transferencia de plásmidos entre bacterias constituye también un tipo particular de eventos de transferencia horizontal, eventos mucho más plásticos en términos evolutivos ya que pueden ser fácilmente revertibles: tanto como una “especie” puede ganar un plásmido en un contexto determinado, lo puede perder cuando este no representa una ventaja evolutiva si las presiones selectivas cambian. Por ejemplo, este mecanismo de HGT es usual para adquirir genes de resistencia a compuestos antimicrobianos, que muchas veces se encuentran en los plásmidos por esta razón. Otros eventos de transferencia horizontal en procariotas pueden conferir resistencia a condiciones ambientales desafiantes como la existencia de metales tóxicos, la hipersalinidad o temperaturas extremas, entre otros. Por lo tanto, su importancia va más allá de los fenómenos evolutivos, ya que suelen afectar las dinámicas de las diferentes poblaciones microbianas. Este es sin duda un mecanismo importante de compartir novedades evolutivas dentro y entre especies.

PARA RECORDAR

• Los eventos de transferencia horizontal de genes involucran el pasaje de material genético entre individuos (generalmente) de diferentes especies.
• En el caso de que en el genoma receptor existan secuencias homólogas a las transferidas, se genera una nueva relación evolutiva entre las mismas que se llama xenología (porque su origen es de diferentes especies).
• En procariotas es relativamente sencillo identificar eventos recientes de HGT en los casos en que las diferencias composicionales (nucleotídicas, uso de codones, etc.) entre las dos especies sean relativamente importantes.
• Los eventos de HGT son de gran importancia en la evolución pero también en la genética de poblaciones, por ejemplo a través de la transferencia de genes de resistencia a antimicrobianos, o de tolerancia a concentraciones elevadas de cito-tóxicos.

7.6 Seleccionismo vs neutralismo: los procariotas en el debate

Uno de los puntos de fuerte controversia entre las teorías neutralista y seleccionista de la evolución molecular se encuentra en la explicación de las importantes diferencias observadas en el contenido GC de los genomas, tanto de eucariotas como de procariotas, ya sea entre genomas o dentro de ellos. En vertebrados homeotermos, Bernardi y colaboradores descubrieron hace mucho tiempo que el genoma se encuentra estructurado en largas regiones (\(> 200\text{ Kb}\)) de contenido GC relativamente homogéneo en comparación a las diferencias observadas entre regiones (Bernardi et al. 1985). A lo largo de los años se han encontrado diversas asociaciones entre estas estructuras y propiedades genómicas de distinta importancia: diferencias en el tiempo de replicación (Eyre-Walker 1992), longitud de los genes (Duret, Mouchiroud, and Gautier 1995), bandeo cromosómico (Saccone et al. 1993), islas CpG⁷³ (Aïssani and Bernardi 1991), patrones de metilación (Kazanskaya et al. 1997), así como importantes diferencias en la estructura entre vertebrados homeotermos y poiquilotermos (Belle, Smith, and Eyre-Walker 2002). Existe aún un fuerte debate respecto al origen y evolución de esta estructura en mosaico (Eyre-Walker and Hurst 2001), aunque la disponibilidad de gran cantidad de nuevos genomas ha disminuído el margen de controversia considerablemente (Costantini, Cammarano, and Bernardi 2009).

En procariotas el debate acerca del papel de la selección natural en la evolución del contenido GC ha sido considerablemente más fuerte, en parte debido a la estructura mucho más simple de sus genomas, a los importantes tamaños poblacionales y a las enormes diferencias de GC entre organismos (ya en la década de los ’60 se observaron valores en el rango del 25% al 75%) (Sueoka 1962). Esto fue tomado en un principio como soporte a la teoría neutral de la evolución, propuesta por Motoo Kimura⁷⁴. En razón de que a esta altura resulta muy claro que el sesgo mutacional en procariotas es hacia los pares de base \(A=T\), por lo que la existencia de organismos con un contenido GC muy alto (o lo que es igual, bajo contenido AT) no son esperables, es necesario recurrir a otras explicaciones.

Una opción natural en esta búsqueda de explicaciones alternativas a la teoría neutral es la teoría de la selección natural, que ya hemos visto, operando a nivel molecular. Para que la selección sea operativa es necesario encontrar no solo la característica seleccionada, sino intentar determinar cuál es la ventaja selectiva (evolutiva) que confiere. En nuestro caso se trata del incremento en el contenido GC la característica que estaría siendo seleccionada en forma favorable, aunque nos faltaría encontrar una explicación consistente de la razón para esta ventaja. Entre los diferentes factores eco-fisiológicos propuestos para la ventaja de un contenido GC más elevado se encuentran la temperatura óptima de crecimiento (Kagawa et al. 1984; Musto et al. 2004), la fijación de nitrógeno (McEwan, Gatherer, and McEwan 1998), oxígeno (Hugo Naya et al. 2002; Romero et al. 2009) y parasitismo (Eduardo P. C. Rocha and Danchin 2002), entre otras tantas. Mientras que algunas de estas explicaciones no han soportado demasiado bien el paso del tiempo, viéndose restringidas a casos particulares, otras aún parecen plausibles a la luz de nueva evidencia y explican mejor los datos que las hipótesis neutralistas (excelentes revisiones recientes se encuentran en (Eduardo P. C. Rocha and Feil 2010; E. P. C. Rocha 2018)). Alternativamente, el mecanismo de biased gene conversion, un mecanismo de recombinación homóloga, ha sido propuesto como otra posible explicación del incremento del contenido GC. Como el mismo es dependiente de la recombinación, mientras que la selección se ve favorecida por la recombinación (como vimos en el capítulo Dinámica de 2 loci), es bastante difícil conseguir resolver cuál de estas dos explicaciones alternativas es más verosímil (E. P. C. Rocha 2018).

En resumen, mientras que el debate acerca de las causas subyacentes continúa, resulta claro que existe un papel fundamental del par GC en la evolución a nivel molecular.

PARA RECORDAR

• El debate entre las teorías neutralista y seleccionista de la evolución molecular persiste aún hoy en día, aunque la teoría Neutral en su forma original no es capaz de explicar la distribución de la variabilidad en la mayor parte de los casos conocidos.
• Una arena interesante donde batirse ha resultado ser el contenido GC de los procariotas ya que el mismo muestra una enorme variabilidad entre especies y porque en procariotas la mayor parte de los sitios está posiblemente sujeta a selección, directamente o por ligamiento con regiones bajo selección.
• En procariotas parece bastante claro que el sesgo mutacional-sustitucional es hacia los nucléotidos AT, por lo que para explicar la distribución, con muchos genomas hacia GC alto, requiere de otras explicaciones que el sesgo mutacional.
• La teoría neutral de la evolución no alcanza a explicar esta enorme variabilidad en contenido GC pero el biased gene conversion, un mecanismo de recombinación homóloga independiente de la selección, ha sido propuesto como otra posible explicación del incremento del contenido GC.
• Diferentes factores ambientales y evolutivos han sido propuestos para explicar la distribución de contenido GC en procariotas, entre ellos la temperatura óptima de crecimiento, la fijación de nitrógeno, el parasitismo y la aerobiosis. Algunos han soportado bien el paso del tiempo y son bastante generales, mientras que otros apenas pueden explicar algo en un entorno filogenético muy restringido o han sido descartados por evidencia más reciente.
• Como el mecanismo de biased gene conversion es dependiente de la recombinación, mientras que la selección se ve favorecida por la recombinación, es bastante difícil conseguir resolver cuál de estas dos explicaciones alternativas funciona mejor.

7.7 Genómica poblacional

El primer genoma procariota completamente secuenciado fue el de la bacteria Haemophilus influenzae Rd (Fleischmann et al. 1995) y fue el debut en organismos vivientes del método de secuenciación conocido como shotgun sequencing, en el que la secueciación de fragmentos es aleatoria y por lo tanto el ensamblado (reconstrucción) del genoma depende de secuenciar muchas veces cada base, en general en fragmentos solapantes. El genoma de H. influenzae Rd en el ensamblado original fue de 1.830.137 pares de bases (un genoma relativamente pequeño para una bacteria), pero significó un salto enorme en comparación con los logros previos como la secuenciación del bacteriófago \(\Phi\)X174 (5.386 pb), el bacteriófago \(\lambda\) (48.502 pb), o aún el genoma mitocondrial (187 kb) y del cloroplasto (121 kb) de la planta Marchantia polymorpha. Todos estas secuencias completas fueron obtenidas mediante el método de Sanger⁷⁵, que originalmente implicaba un enorme trabajo manual para cada secuencia. Con el correr de los años el método se fue automatizando, permitiendo su uso masivo e inclusive llegando a ser utilizado en los proyectos originales para secuenciar el genoma humano.

En los años que siguieron a la secuenciación completa de H. influenzae Rd se resolvieron las secuencias de decenas de otros procariotas, y en el año 2001 se finalizó el primer borrador del genoma humano, un evento histórico si se tiene en cuenta que su genoma haploide es de \(\approx 3,3 \text{ Gb}\) (es decir, el equivalente a 711 genomas de la bacteria Escherichia coli K-12 o 1803 genomas de la bacteria H. influenzae Rd). La forma de resolver el genoma humano fue una combinación de dos grandes projectos, uno público y otro privado, dos estrategias de secuenciación (una de ellas shotgun), cientos de centros que colaboraron en la generación de secuencias y un esfuerzo computacional masivo para la época. Una de las consecuencias de la “finalización” de este proyecto fue la disponibilidad de un gran número de secuenciadores, en algunos casos dispuestos en factories (fábricas) a efectos de paralelizar al máximo los procesos de secuenciado. Esta disponibilidad de capacidad ociosa permitió que ideas relativamente nuevas tuvieran lugar para desarrollarse y así surgió la posibilidad de pasar de una visión de la genómica basada en individuos a una centrada en poblaciones. Un artículo histórico, en este sentido, es el de Stein y colaboradores que plantea la secuenciación de un fragmento de genoma de \(40\) Kb de una arquea planctónica marina (Stein et al. 1996), es decir, la secuencia de un organismo no-cultivable con los estándares de aquel momento. La relevancia de esto es extrema, aunque pueda no parecernos, ya que nos permitió pasar del estudio únicamente de organismos cultivables a todos los organismos que podamos de alguna manera muestrear. Si bien en dicho artículo no se menciona el término metagenómica, que recién fue acuñado en el artículo de Handelsman y colaboradores (Handelsman et al. 1998), se trata de alguna manera del inicio de una era en la forma de comprender la diversidad microbiana, así como las dinámicas a las que se encuentran sujetas las poblaciones bajo diferentes condiciones y presiones selectivas.

En la metagenómica el objetivo suele ser comprender la diversidad de organismos presentes, así como sus proporciones en diferentes muestras, a partir de la identificación y cuantificación de ácidos nucléicos, ADN o ARN. A partir de los trabajos de Woese⁷⁶, es conocido que el ARN ribosomal 16S es un excelente marcador filogenético cuando consideramos la profundidad de los dos dominios procariotas (i.e., Archaea y Bacteria), en gran parte debido al alto nivel de conservación de esta molécula. Tener una mólecula o, mejor aún, una región de la misma altamente conservada, abre las puertas no solo al estudio de las relaciones evolutivas entre organismos, sino también al estudio de la distribución y variabilidad de organismos en diferentes muestras y ambientes (ver el trabajo de Lane y colaboradores para usos filogenéticos (Lane et al. 1985)). En una de las formas clásicas, los estudios metagenómicos se realizan secuenciando en cada muestra todo el ARNr 16S detectable, usualmente a través de protocolos que permiten amplificar el material original y luego realizar una transcripción reversa para convertirlo en ADN, que es mucho más estable. Posteriormente, se identifica cada fragmento secuenciado para finalmente cuantificar el número de fragmentos secuenciados (reads) como un proxy de la abundancia de los distintos organismos.

Si bien la metagenómica nació dentro de la era de los secuenciadores “Sanger” (por el método de secuenciación usado), su alcance fue bastante reducido debido a la poca capacidad de generar secuencias de este método. Un cambio fundamental se produjo a comienzos de la primera década del 2000, cuando rápidamente aparecieron varios métodos nuevos de secuenciación que fueron conocidos como Next Generation Sequencing o secuenciadores de segunda generación. De todas la ideas originales, tres métodos en particular terminaron en secuenciadores de gran capacidad que influyeron enormemente en los años siguientes: el 454 de Roche (pirosecuenciado), el secuenciador de Illumina (secuenciación por síntesis) y el SOLiD (secuenciación por ligación). Si bien los tres tenían en común una enorme capacidad de generar secuencias a bajo costo, cada uno tenía una “performance” distinta, así como diferentes debilidades. El 454 producía secuencias relativamente largas (del orden de los 600 pb, cercano al largo obtenible por Sanger), pero el número de fragmentos producidos era mucho menor al de las otras tecnologías y era muy sensible (poseía una mayor tasa de error) a las secuencias de homopolímeros (i.e., cuando se repetía una base). El secuenciador SOLiD, por otra parte, producía una enorme cantidad de fragmentos (órdenes de magnitud superior al 454), pero los mismos eran extremadamente cortos (del orden de las 50 pb), y el resultado primario que se obtenía no era la secuencia de bases sino una secuencia en espacio color que luego debía ser traducida al espacio de bases. Finalmente, el secuenciador de Illumina, basado en secuenciación por síntesis, es el único de los tres que sobrevivió al paso del tiempo y hoy en día convive con los secuenciadores de tercera generación. El mismo produce fragmentos de largo fijo, y si bien en los comienzos estos eran cortos en la actualidad son de 150 o de 300 pb, pudiendose complementar con otras técnicas (por ejemplo, secuenciación paired-end) que permite cubrir grandes regiones con precisión. Más aún, es de las pocas tecnologías que ha sido escalada en los equipos, con algunos como el MiniSeq con una producción de \(1,65-7,5 \text{ Gb}\) por corrida (i.e., entre \(7-25\) millones de fragmentos cada vez), hasta equipos como el HiSeq X con la capacidad de secuenciar hasta 18 mil genomas humanos por año, siendo el primer secuenciador que logró quebrar la barrera de obtener un genoma humano a la profundidad de 30x (cada base cubierta en promedio por 30 fragmentos) por menos de U$S 1000. En la Figura 7.9 se observa el resultado de la secuenciación de una región del exoma humano usando el equipo HiSeq X. En la misma se aprecia claramente que el inicio y fin de los fragmentos no coincide (cada fragmento es una barra gris horizontal), algo esperable ya que se trata de una fragmentación al azar y posterior secuenciación (técnica de shotgun). Además, en la región que se muestra en la figura no se observan posiciones heterocigotas, ya que los pocos puntos de no coincidencia con el genoma de referencia (segmentos de color en las barras grises) no se acercan a la frecuencia esperada para un organismo diploide (\(50\%\) o \(100\%\)) y se trata por lo tanto de errores de secuenciación.

Figura 7.9: Solapamiento de fragmentos para reconstrucción de una secuencias en el método de shotgun. En este caso los fragmentos, luego de secuenciados se alinean contra un genoma de referencia (el del organismo de donde provienen) que fue resuelto previamente (Homo sapiens, en este caso). Se aprecia claramente que al ser fragmentos producido en forma aleatoria (cada barra horizontal de color gris) su inicio y fin difieren, aunque pueden coincidir en caso de que la profundidad de secuenciación sea muy alta. En la parte inferior de la figura se observa la secuencia de nucleótidos y de aminoácidos en el genoma de referencia. Los segmentos cortos de color sobre las barras grises representan nucleótidos diferentes del correspondiente en el genoma de referencia, debido a variantes o a errores de secuenciación. Gentileza de Lucía Spangenberg, Unidad de Bioinformática, Institut Pasteur de Montevideo.

Estos secuenciadores permitieron la explosión de estudios metagenómicos al reducir los costos de manera sustantiva, así como los tiempos requeridos para procesar las muestras. El resultado típico de estos estudios es una tabla con varias muestras por condición en las filas, las diferentes OTUs (Operational Taxonomic Unit, en general un equivalente a especie) identificadas en las muestras y el número de OTUs observado en cada celda. Es decir, se trata de una tabla de abundancias en la escala de lo observado. Como en general no es posible estandarizar las condiciones para secuenciar exactamente el mismos número de fragmentos en cada muestra, usualmente se realiza algún tipo de transformación de estos datos que posibilite comparar en forma “justa” las diferentes muestras y condiciones. Más aún, como el número de OTUs detectadas en cada muestra es una función del número de fragmentos secuenciados, cuando la cantidad de fragmentos obtenidos por muestra no es enorme, es usual realizar algún tipo de procedimiento para comprobar que el esfuerzo de muestreo es suficiente para no perder una parte importante de la diversidad a medida de que el número de fragmentos en las muestras disminuye (rarefactions analysis, en inglés); una alternativa para equilibrar las muestras es realizar un sub-muestreo aleatorio de todas las muestras al tamaño de la más pequeña. Luego de obtenida una tabla de abundancias estandarizada de alguna manera, el procedimiento suele involucrar algún tipo de análisis exploratorio multidimensional, como el análisis de componentes principales (PCA) o escalado multidimensional (MDS) que nos permita reducir la dimensionalidad del espacio original a espacios donde la variabilidad se concentra en pocas dimensiones y que por lo tanto pueden ser graficadas para su interpretación. Como se vió en el capítulo Introducción a la Genómica, en estas gráficas suele ser deseable observar un patrón de agrupamiento espacial por condición de la muestra (e.g., por ambientes de donde fueron extraídas), lo que indicaría que la variabilidad entre muestras se corresponde mayormente a las condiciones biológicas consideradas en el experimento. Finalmente, se suele realizar algún tipo de comparación estadística entre la abundancia de los OTUs más discriminantes, a fin de ayudar a identificar las fuentes más importantes de variación y poder generar hipótesis razonables que expliquen esta variabilidad.

En la actualidad los secuenciadores de tercera generación vienen reemplazando a los de segunda (excepto Illumina) ya que poseen algunas ventajas importantes. El secuenciador de Ion Torrent se basa un chip que posee microscópicos medidores de pH en unos pocillos creados en la superficie; los fragmentos de ADN se amplifican en microesferas que se instalarán en esos pocillos. A intervalos regulares se hace pasar una solución de cada uno de los nucleótidos (A, C, G, T) que se incorporarán solamente en aquellos en que la siguiente base del fragmento sea la complementaria. Cuando se incorpora un nucleótido se libera el ión \(H^+\), lo que indicará el correspondiente pHímetro como la secuencia de esa base. La simplicidad de concepción hace de este instrumento una alternativa económica a los secuenciadores de segunda generación, pese a que comparte problemas con el 454 (problema con los homopolímeros y largo de fragmentos algo reducidos para los estándares actuales). Sin embargo, tanto en la tecnología de Oxford Nanopore, como en la de Pacific Biosciences, ambos instrumentos de tercera generación, el largo de los fragmentos no está limitado a priori y por lo tanto se obtienen fragmentos de miles de pares de bases de longitud. Esto permite otros abordajes al problema de la diversidad microbiana, además de ayudar a la comprensión de la base molecular de la ecología de los distintos ambientes. La tecnología de Oxford Nanopore (ONT) se basa en la creación de unos poros biológicos en una superficie a cuyos lados se aplica un campo eléctrico y que poseen sensores de corriente (cada poro). Cada moléculas que atraviesa un poro, por ejemplo una molécula de ADN, al hacerlo irá variando la corriente a través del poro ya que variará la superficie disponible para que los iones lo atraviesen. En principio, cada nucleótido tiene su “firma” al pasar, por lo que leyendo la secuencia de cambios en la corriente es posible reconstruir la secuencia de bases correspondiente (en realidad cada secuencia corta de nucleótidos tiene una firma ya que los nucleótidos que acaban de pasar y los que van a pasar también obstruyen parte del poro). Lo fantástico de esta tecnología es la posibilidad de escalar los equipamientos, desde grandes equipos que permiten la secuenciación de centenares de muestras al mismo tiempo hasta equipos del tamaño de un estuche de lentes, como el MinION, que conecta en un puerto USB de la computadora, Figura 7.10. En estos equipos las secuencias comienzan a verse en tiempo real, a medida de que son generadas y permiten una enorme flexibilidad, ya que puede interrumpirse la corrida, lavar la celda y cambiar de muestras a procesar cuando se alcance algún objetivo con las secuencias (en teoría permiten un par de lavados y un tiempo máximo de corrida de 48 horas).

Figura 7.10: Secuenciador MinION de Oxford Nanopore Technologies, a la izquierda y secuenciador MinION Mkc1, a la derecha, ambos con sus tapas abiertas, al lado de un lápiz mecánico para referencia de su tamaño. El equipo de la izquierda no es autónomo y debe conectarse al puerto USB de una computadora para funcionar, mientras que el equipo de la derecha posee capacidad propia de almacenamiento y procesamiento de los datos. Foto del autor.

El extremo opuesto de la tecnología de ONT lo representa la tecnología de Pacific Biosciences, con su equipo PacBio Sequel IIe, con hasta 8 millones de pocillos (\(\approx 5\) millones de fragmentos) capaz de secuenciar 150 Gb por celda. Se trata de una tecnología basada en unos pocillos trabajados en una superficie y donde se encuentra una polimerasa que irá procesando el ADN. Los 4 nucleótidos son marcados con colores diferentes y están mezclados en una solución que contiene a los 4, los que por difusión se moverán en forma aleatoria. Cada pocillo es iluminado desde abajo con un láser y cuando un nucléotido es incorporado se mantiene por más tiempo en la región en que puede generar una señal luminosa, lo que será registrado por una cámara que detecta esa señal y la traduce a la base corresponiente al color retenido. Con esta tecnología es posible obtener fragmentos de decenas de miles de pares de bases de largo y con gran fidelidad, lo que permite además de la identificación de la secuencia de nucleótidos entender las variaciones estructurales en las secuencias, cosa que usualmente escapa a las tecnologías de fragmentos cortos.

A partir de las tecnologías de segunda y tercera generación los estudios posibles de genética y dinámica de poblaciones microbianas se han ampliado notablemente. Por un lado, es posible realizar estudios poblacionales no basados en el estudio de amplicones (como era el de 16S), lo que elimina el sesgo de amplificación asociado a esas estrategias (las distintas secuencias pueden amplificar diferente por PCR, distorsionando los datos originales). En estos estudios se secuencia todo el ADN o el ARN (en el caso de metatranscriptómica) que existe en una muestra, para luego ensamblar los fragmentos y recién después identificar los organismos que produjeron esas secuencias. Entre otras cosas, este enfoque permite reconstruir vías metabólicas más comunes en unas condiciones que en otras, una identificación más precisa de organismos y en algunos casos determinar la variabilidad entre individuos de la misma especie. En el área agraria son abundantes los estudios de suelos y aguas a través de la metagenómica, estudios en la rizósfera, así como los estudios de funcionamiento y composición del rumen, la metagenómica de glándula mamaria y en cualquier situación donde la composición y dinámica de las poblaciones microbianas pueden jugar un papel relevante.

PARA RECORDAR

• En la metagenómica el objetivo suele ser comprender la diversidad de organismos presentes, así como sus proporciones en diferentes muestras, a partir de la identificación y cuantificación de ácidos nucléicos, ADN o ARN. En los estudios clásicos de filogenética se emplea el ARNr 16S ya que se trata de una molécula altamente conservada durante la evolución, lo que nos permite apreciar diferencias en grandes tiempos evolutivos.
• Las tecnologías de secuenciación masiva (o Next Generation Sequencing, NGS) permitieron extender los estudios metagenómicos a un amplio rango de problemas, incluyendo aquellos de composición y dinámica poblacional microbiana.
• Las tecnologías NGS de segunda generación aumentaron enormemente la capacidad de secuenciado, pero mientras que dos de ellas (Illumina y SOLiD) eran de fragmentos cortos o muy cortos, la tercera presentaba problemas con los homopolímeros (454) y los fragmentos apenas alcanzaban el largo de los obtenidos por el método de Sanger.
• Las tecnologías NGS de tercera generación abarataron aún más el costo de secuenciación, universalizando el acceso a estas tecnologías. Mientras que una de ellas (IonTorrent) aún presenta problemas con los homopolímeros, las otras dos (Oxford Nanopore y PacBio) permiten obtener fragmentos de largos considerables, aún de decenas de miles de pares de bases, con relativamente alta precisión. Esto no solo permite identificar variaciones a nivel de las bases individuales, sino que también permite identificar variabilidad estructural.
• La cantidad de datos generados a bajo costo por las tecnologías de tercera generación y el largo de los fragmentos permiten acceder a otras técnicas, como la genómica funcional o la metatranscriptómica, que además de los aspectos composicionales y de dinámica de poblaciones permite identificar vías metabólicas expresadas en forma diferencial, lo que ayuda a comprender los cambios a nivel molecular entre condiciones (por ejemplo, entre ambientes).

7.8 Genes de resistencia

Los antimicrobianos han sido utilizados en forma masiva desde el descubrimiento de la penicilina por Alexander Fleming⁷⁷ y han ido incrementando sus aplicaciones, así como el uso de los mismos hasta nuestros días. Hoy en día es frecuente no solo encontrar el uso de antibióticos en seres humanos para curar y prevenir enfermedades, sino que también su uso es frecuente en la producción animal para el tratamiento de patologías, en forma preventiva y rutinaria y hasta como aditivo de crecimiento y producción alterando la microbiota ruminal (por ejemplo, el antibiótico ionóforo monensina, derivado de la bacteria Streptomyces cinnamonensis y usado ampliamente en la producción bovina). Pero como suele ocurrir con la vida en nuestro planeta, a medida de que aumentamos la presión para eliminar determinados organismos, en las poblaciones que estos conforman comienzan a fijarse variantes que permiten a los individuos sobrevivir. A cada nuevo desarrollo humano en esta lucha por eliminar lo que para nosotros son organismos patógenos (ya sean nocivos para humanos, animales, plantas, etc.) los organismos se han ido adaptando de diferentes maneras y desarrollando sus propios mecanismos de resistencia a nuestros embates tecnológicos. Más aún, a medida que se aumenta la presión sobre las poblaciones de patógenos, mayor será la necesidad de estos organismos de buscar alternativas para su supervivencia. Por esta razón, más allá del éxito enorme que han tenido los antibióticos para reducir el impacto de enfermedades de origen bacteriano, el mismo comienza a volverse peligrosamente inestable y gradualmente empezamos a perder el control en esta batalla. Nuestra victorias previas son solo el aliciente para una respuesta aún más dura por parte de los patógenos.

Como vimos previamente, los procariotas poseen varias ventajas en lo que hace al desarrollo de resistencia a los antimicrobianos. Por un lado, su dinámica poblacional sumamente flexible, con capacidad de multiplicarse en forma veloz y de alcanzar tamaños poblacionales enormes a partir de uno o pocos individuos. Esta habilidad les confiere la capacidad de soportar tasas de letalidad enormes y aún así poder reconstruir su tamaños poblacional previo apenas disminuye la presión selectiva o se encuentre una forma de evadirla. Por otro lado, existe una gran plasticidad a nivel genómico, así como la capacidad de intercambiar novedades evolutivas con gran facilidad (e.g. a través del intercambio de plásmidos). A la vez, su gran tamaño poblacional y sus breves intervalos de duplicación (en relación al de eucariotas macroscópicos) los hace candidatos a recibir un gran número de mutaciones por intervalo de tiempo en cada población, por lo que es de esperar la aparición de varios individuos por generación con alguna clase de ventaja selectiva (en un medio en que el cambio de factores de selección ha sido reciente). Además, ciertas bacterias poseen la capacidad de pasar de un modo de vida libre a una forma en que desarrollan un estado de protección mayor (a costo de la actividad), por ejemplo a través de la formación de esporas o la organización en biofilms, lo que hace que los ataques contra ellas estén destinados al fracaso. Finalmente, el hecho de que un individuo esté constituido por una sola célula, algo que podría verse como algo ya que la muerte de esa célula significa la muerte del organismo en su totalidad, constituye en realidad una gran ventaja en lo que refiere a la transmisión de las nuevas capacidades adquiridas. Por todas estas razones, como era de esperar, las bacterias han ido desarrollando distintos mecanismos para bloquear cada intento que la humanidad ha realizado para eliminarlas.

La resistencia a los antimicrobianos, conocida como RAM (AMR, por sus siglas en inglés) es la capacidad que desarrollan determinados microbios para resistir la acción de tratamientos que antes eran eficaces para su eliminación. La resistencia a antibióticos es un caso especial de RAM, referido a la resistencia adquirida por bacterias. Existen cinco diferentes mecanismos que han ido evolucionando para este fenómeno de resistencia:

1. Inactivación o modificación de la droga mediante la acción enzimática en la bacteria.
2. Alteración del “target” o del sitio de unión de la droga.
3. Alteración de la vía metabólica en la bacteria, evitando por ejemplo el uso de la vía blanco de la droga.
4. Reducción de la concentración de la droga, ya sea por reducción de la permeabilidad a la misma o por aumento de la tasa de eflujo de la misma.
5. Desbloqueo y liberación de los ribosomas en bloqueos inducidos por antibióticos.

 

En el primer caso, un ejemplo conocido es el de la inactivación es la que corresponde a la expresión de \(\beta\)-lactamasas que son capaces de neutralizar los antibióticos \(\beta\)-lactámicos como las penicilinas, las cefalosporinas, monobactamicos y carbapenémicos (carbapenemasas). El elemento común a todos estas moléculas es un anillo químico conocido como anillo \(\beta\)-lactámico, el cual es fundamental para su acción antimicrobiana. Las \(\beta\)-lactamasas son enzimas que tienen la capacidad de hidrolizar dicho anillo. Un ejemplo del segundo mecanismo propuesto son las proteínas de unión a la penicilina, un conjunto de moléculas cuyo rol fundamental es la síntesis de péptidoglicanos para constituir la pared celular de bacterias; ante la presencia de penicilina estas proteínas se unen a la misma por su similitud con los péptidoglicanos, formando un enlace covalente y desactivando la droga. Para el tercer mecanismo, un ejemplo posible sería el de algunas bacterias resistentes a las sulfonamidas, que en lugar de usar el ácido para-aminobenzoico en la síntesis de ácido fólico (blanco terapéutico de la droga) y de nucleótido pueden cambiar a usar el ácido fólico disponible. En el caso del cuarto mecanismo, algunas bacterias poseen bombas en la membrana que permiten extraer antibióticos como las quinolonas antes de que alcanzen una concentración dañina. Por último, a modo de ejemplo para el caso del quinto mecanismo, en la bacteria Listeria monocytogenes la secuencia lmo0762 es un homólogo del gen hflX, que codifica para una HSP (heat shock protein) que permite rescatar a los ribosomas bloqueados, separando sus dos subunidades; este mecanismo permite generar resistencia a los antibióticos lincomicina y eritromicina ((Duval et al. 2018)).

El proceso para la generación de resistencia y su expansión a nivel poblacional es sencillo. Frente a una infección de algún tipo, o simplemente producto de la aplicación rutinaria, los antibióticos generan una presión que tiende a eliminar a todos los organismos susceptibles. En general, las bacterias que poseen alguna clase de resistencia a antibióticos poseen una cierta desventaja selectiva frente al resto de los individuos de su especie ya que los mecanismos de resistencia suelen implicar un costo, la pérdida de una vía o modificaciones no-óptimas, por lo que en ausencia de la presión selectiva en general no predominan. Sin embargo, cuando aparece una fuerte presión selectiva las relaciones de fitness cambian en forma sustantiva, y aquellas células que no predominaban pasan ahora a dominar la escena, en particular por la ausencia de competidores, lo que implica que todos los recursos están a disposición de las mismas. El fenómeno puede acontecer aún en ausencia de bacterias de dicha especie con resistencia ya adquirida en la población, ya sea gracias a su aparición por mutación aleatoria, como por existencia de eventos de intercambio de material genético con bacterias resistentes de otras especies (algunas que pueden ser no-patógenas, por ejemplo). Esto permitirá, en muchos casos, que aparezcan individuos resistentes en la especie y que además rápidamente aumenten su representación en la población. Más aún, frente al uso poco racional de antibióticos de diferentes clases, y a veces luego de una sucesión de fracasos por resistencia, puede generarse resistencia a múltiples drogas en bacterias, lo que se conoce como cepas MDR (mutidrug resistance).

La pregunta que nos surge es ¿cómo podemos enfrentar el problema de la generación de resistencia a los antibióticos? La mejor forma de enfrentar este problema es estratégica y está al alcance de la mano. Conociendo el organismo que vamos a atacar, así como los mecanismos de resistencia que posee, la mejor forma consiste en elegir un antibiótico en forma efectiva y disminuyendo el riesgo de generar resistencia. Antes se trataba de cultivar el organismo patógeno para luego poder hacer las pruebas bioquímicas que permitiesen identificarlo. Afortunadamente, hoy en día poseemos la tecnología como para resolver este problema en apenas unas horas. Algunos de los secuenciadores de segunda y tercera generación son capaces de generar secuencias en pocas horas y alguno en tiempo real (como el MinION) a un costo razonable y con poca necesidad de equipamiento muy costoso, por lo que el problema de diagnóstico puede quedar resuelto y solo sería importante agregar un monitoreo a nivel de toda la población para poder comprender las tendencias a nivel de variantes a dicha escala. Más aún, existen en la actualidad herramientas de proteómica masiva, usando equipos de MALDI-TOF⁷⁸, que permiten obtener estos resultados en forma estandarizada y en tiempos mucho menores, lo que refuerza la tendencia en esta área. Por otra parte, en lo que hace a la producción animal, es necesario prohibir el uso sistemático de antibióticos y monitorear también estrechamente la aplicación clínica de los mismos, ya que además de la posibilidad de generar resistencia en patógenos humanos, las excretas suelen estar contaminadas con antibióticos generando resistencia en bacterias ambientales. Sin duda, este es un tema que es motivo de preocupación y responsabilidad de todos, estrechamente vinculado al concepto de una sola salud (el cual contempla que todos los organismos estamos conectados al momento de elaborar el concepto de salud).

PARA RECORDAR

• La resistencia a los antimicrobianos (AMR) es un fenómeno extendido en el que los microbios desarrollan resistencia frente a tratamientos con drogas que anteriormente resultaban eficaces para su control y eliminación.
• La base genética del desarrollo de esta resistencia está en los elevados tamaños poblacionales de los microbios en general y de los procariotas en particular, así como en la flexibilidad de los genomas procariotas y los distintos mecanismos para compartir novedades evolutivas.
• Existen cinco diferentes mecanismos descritos que han ido evolucionando para este fenómeno de resistencia.
• En algunos casos, debido en parte al mal uso de los antibióticos, por ejemplo a través de una secuencia de drogas todas con resultados fallidos, se genera en las poblaciones bacterianas individuos con resistencia a múltiples drogas de familias diferentes, a los que se les conoce como MDR (MultiDrug Resistant). Estos organismos se constituyen en una enorme amenaza para los sistemas de salud ya que la posibilidad de diseminación de esta resistencia múltiple aumenta con el mal manejo de las terapias antibióticas.
• Las tecnologías de secuenciación masiva de segunda y especialmente de tercera generación son una excelente herramienta la el diagnóstico rápido de los patógenos causantes de infecciones, así como de las estrategias de resistencia que tienen desarrolladas, por lo que debería ser la alternativa inmediata para un uso racional de los antibióticos. Las tecnologías de proteómica masiva, con equipos MALDI-TOF son otra alternativa barata y ya estandarizada para este manejo racional.

7.9 Introducción a la epidemiología: modelos compartimentales

El estudio de las epidemias es fundamental para conocer la forma de acción y las estrategias de los patógenos, así como para entender la forma de combatirlas. Existen infinidad de modelos matemáticos desarrollados para comprender su evolución, así como métodos para determinar parámetros críticos de dichos modelos. Una clase de modelos frecuentemente usados son los modelos compartimentales, que permiten modelar diferentes estrategias y ciclos de una epidemia. En la Figura 7.11 vemos un ejemplo de un modelo compartimental sencillo, que se conoce como SIR con dinámica vital y tamaño poblacional constante. Este modelo posee compartimentos para las categorías susceptible (\(S\)), infectados (\(I\)) y recuperados (\(R\)), y de ahí proviene su nombre. En el modelo SIR más simple, capaz de modelar epidemias como la de la gripe donde la dinámica de infección es tan rápida que no afecta la dinámica de nacimientos y muertes en la población, se suelen omitir estos términos, lo cual simplifica en gran medida las ecuaciones del modelo, pudiendose describir soluciones explícitas a las ecuaciones diferenciales del mismo. Sin embargo, el modelo representado en la Figura 7.11 es algo más complejo, porque además de los 3 compartimentos descritos anteriormente, se permite la muerte de los individuos a una tasa \(\mu\) independiente del compartimento (i.e., el patógeno no afecta la tasa de mortalidad), por lo cual para mantener el tamaño poblacional constante debemos permitir que los nacimientos equilibren las muertes, o lo que es lo mismo establecer la igualdad \(\Lambda=bN=\mu S+\mu I+\mu R=\mu(S+I+R)=\mu N\), donde \(b\) es la tasa de nacimientos por individuo en la población.

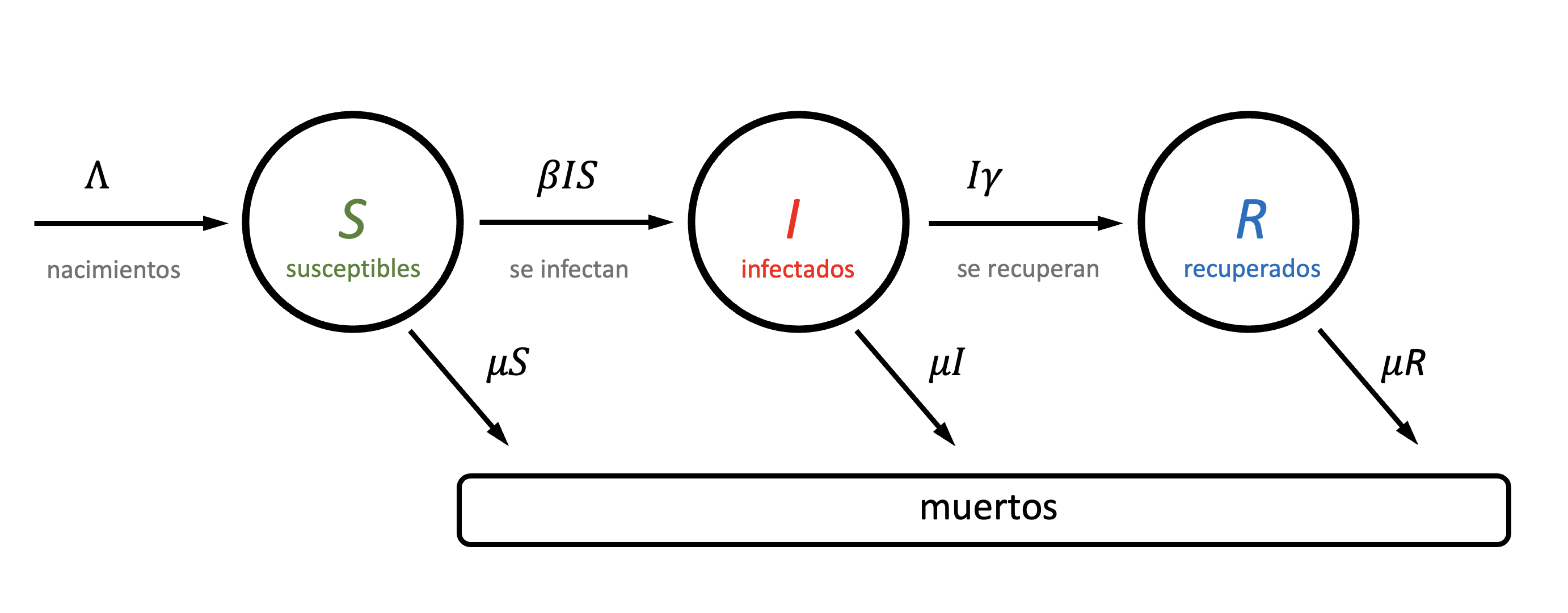
Figura 7.11: Modelo compartimental SIR con dinámica de vida. El modelo tiene 3 compartimentos que se corresponden con los del modelo SIR, más un compartimento que recibe a los muertos con tasa \(\mu\) en todas las categorías y una tasa de nacimientos \(\Lambda\)..

La dinámica de este sistema es fácil de describir a partir de un conjunto de tres ecuaciones diferenciales ordinarias acopladas unas con otras, cada una describiendo la dinámica de un compartimento. Es decir, la forma de cada una de las ecuaciones diferenciales debe describir la tasa de cambio del compartimento correspondiente, que es la diferencia entre los individuos que entran al compartimento en una unidad infinitesimal de tiempo, menos los individuos que abandonan el compartimento en ese instante. Claramente, si observamos nuevamente la Figura 7.11, se trata de las cantidades en las flechas que entran, menos las cantidades en las flechas que salen. Por ejemplo, para el primer compartimento (\(S\), el de los susceptibles, los individuos que aún no se han contagiado), tenemos que a este compartimento entrarán los nacimientos con número \(\Lambda\) (suponemos que los individuos nacen no-contagiados), al mismo tiempo que abandonan el compartimento de dos formas: por muerte el compartimiento decrece un número \(\mu S\) (la tasa de muerte por la cantidad de individuos en el compartimento) y por infección un número \(\beta IS\), siendo \(\beta\) la tasa de transmisión (o contacto) entre individuos. Poniendo todo junto, tenemos que la tasa de cambio en este compartimento es igual a

\[ \begin{split} \frac{dS}{dt}=\Lambda-\mu S-\frac{\beta IS}{N} \end{split} \tag{7.50} \]

Antes de seguir con el siguiente compartimento vamos a intentar explicar por qué el número de individuos contagiados es \(\beta IS\), y por qué a esta forma se le conoce como ley de acción de masas. Si suponemos que los contagios se dan de persona contagiada a persona susceptible, y que por lo son proporcionales a las proporciones en ambas categorías, entonces el número de contagiados será proporcional a \(N \cdot (\frac{S}{N}) \cdot (\frac{I}{N})=S \frac{I}{N}\). Pero no todos los contactos producen enfermedad, y por lo tanto precisamos de un parámetro \(\beta\) que nos permita variar la contagiosidad de las distintas enfermedades. Entonces, el número que abandona el compartimento de susceptibles será \(\frac{\beta SI}{N}\).

De manera análoga, al compartimento de los infectados (\(I\)) entran los \(\frac{\beta SI}{N}\) que abandonan el de susceptibles (\(S\)) y lo abandonan los que mueren en número \(\mu I\), más los que pasan al compartimento de recuperados (\(R\)). Estos últimos lo hacen en número \(\gamma I\), siendo \(\gamma\) la tasa a la que se recuperan los infectados. Poniendo todo junto, la ecuación que describe este compartimento es

\[ \begin{split} \frac{dI}{dt}=\frac{\beta IS}{N}-\gamma I-\mu S \end{split} \tag{7.51} \]

Finalmente el caso del último compartimento, el de los recuperados (\(R\)), es fácil de describir. En el mismo entran \(\gamma I\) individuos que vienen del compartimento de infectados (\(I\)) y lo abandonan \(\mu R\) individuos que mueren, por lo que su correspondiente ecuación diferencial será

\[ \begin{split} \frac{dR}{dt}=\gamma I-\mu S \end{split} \tag{7.52} \]

El tiempo promedio de una infección estará dado por \(\frac{1}{(\mu+\gamma)}\), y el número reproductivo básico por

\[ \begin{split} R_0=\frac{\beta }{(\mu+\gamma)} \end{split} \tag{7.53} \]

El parámetro \(R_0\) es fundamental para determinar la dinámica del sistema, ya que marca el nuevo número de individuos infectados que esperamos por cada infectado en un instante de tiempo.

El modelo que estamos analizando se trata de un sistema de ecuaciones diferenciales ordinarias no-lineal para el cual igualando a cero las ecuaciones anteriores y resolviendo obtenemos dos soluciones. La primera es la correspondiente al equilibrio libre de enfermedad (DFE, por sus siglas en inglés), que se alcanza cuando \(R_0 \leqslant 1\) y es en este sistema igual a

\[ \begin{split} e_1=(S^*,I^*,R^*)=(N,0,0) \end{split} \tag{7.54} \]

es decir, sin individuos en los compartimentos de infectados y recuperados. La segunda solución estará dada por \(\lim_{t \to \infty}(S(t),I(t),R(t))\) y es igual a

\[ \begin{split} e_2=(S^*,I^*,R^*)=(\frac{N}{R_0},Nc_1(R_0−1),Nc_2(R_0−1)) \end{split} \tag{7.55} \]

con \(c_1=\mu/\beta\) y \(c_2=\gamma/\beta\). El equilibrio de la ecuación (7.55) se corresponde al equilibrio endémico de la enfermedad, es decir cuando la misma alcanza un estado de equilibrio en el cual no es posible la erradicación, pero tampoco existe avance; este escenario acontece cuando se cumple \(R_0>1\).

Claramente, el modelo que hemos manejado apenas representa en forma razonable algunos tipos de infección. Por ejemplo, en muchas casos los infectados tienen una tasa de mortalidad muy diferente a la de las otras categorías, por lo que deberíamos agregar un parámetro al modelo. En otros casos, los recuperados vuelven a ser susceptibles al cabo de un tiempo, es decir, la inmunidad dura determinado tiempo, por lo que debemos introducir una flecha que vaya desde el compartimento R al compartimento S, así como un parámetro para indicar la tasa correspondiente. Además, no hemos modelado en ningún momento la estructura de edades de las poblaciones, y en muchos casos todas las tasas son específicas para cada grupo de edades, lo que claramente agrega muchos parámetros al sistema. Por estas razones al aumentar el realismo del modelo también aumentamos la complejidad del mismos y es necesario recurrir a herramientas computacionales para resolver los modelos. Por otra parte, modelos complejos con malos datos es una combinación catastrófica, ya que la sobre-parametrización suele llevarnos a conclusiones completamente inestables e irreproducibles a medida de que llegan nuevos datos.

PARA RECORDAR

• Los modelos epidemiológicos compartimentales son una clase de modelos que nos permite entender la dinámica de una epidemia.
• Los modelos SIR poseen tres compartimentos: susceptibles (S), infectados (I) y recuperados (R).
• En el caso del modelo SIR con dinámica de vida y tamaño poblacional constante, las ecuaciones diferenciales que lo describen son

\[ \begin{split} \frac{dS}{dt}=\Lambda-\mu S-\frac{\beta IS}{N} \frac{dI}{dt}=\frac{\beta IS}{N}-\gamma I-\mu S \frac{dR}{dt}=\gamma I-\mu S \end{split} \]

con \(\Lambda=bN=\mu(S+I+R)=\mu N\), ya que al ser el tamaño poblacional constante \(N\) los nacimientos deben igualar las muertes.

• En el modelo SIR con dinámica de vida y tamaño poblacional constante el tiempo promedio de una infección estará dado por \(\frac{1}{(\mu+\gamma)}\) y el número reproductivo básico por

\[ \begin{split} R_0=\frac{\beta }{(\mu+\gamma)} \end{split} \tag{7.53} \]

• Existen dos equilibrios estables para este modelo, uno correspondientes al estado libre de enfermedad (DFE) cuya solución es

\[ \begin{split} e_1=(S^**,I^**,R^*)=(N,0,0) \end{split} \]

y otro correspondiente al estado endémico, cuya solución es

\[ \begin{split} e_2=(S^**,I^**,R^*)=(\frac{N}{R_0},Nc_1(R_0−1),Nc_2(R_0−1)) \end{split} \]

con \(c_1=\mu/\beta\) y \(c_2=\gamma/\beta\).

7.10 Conclusión

A lo largo de los capítulos anteriores, hemos establecido las bases conceptuales y matemáticas necesarias para abordar el estudio de la genética de poblaciones. Para cerrar esta sección del libro, nos hemos detenido en ciertos aspectos particulares que son de gran relevancia al investigar a los procariotas, los cuales constituyen la mayoría de los seres que habitan nuestro planeta y se agrupan en dos de los tres dominios de la vida (Bacteria y Archaea). Dentro de estas particularidades podemos resaltar su predominante estado haploide a nivel genómica, su reproducción asexual a través del mecanismo de fisión y sus métodos de intercambio genético, como la transferencia horizontal. Estas particularidades nos obligan a adaptar nuestros enfoques en comparación con los que solemos utilizar en el estudio de los eucariotas, tanto a nivel matemático (con modelos como los que vimos en este capítulo) como conceptual (al pensar en cómo las dinámicas poblacionales pueden generar fenómenos tales como la aparición de resistencia a antimicrobianos). La llegada de tecnologías de secuenciación ha revolucionado notablemente la investigación sobre los organismos procariotas. Dado que la mayoría de los procariotas no pueden ser cultivados en laboratorio, disciplinas como la metagenómica representan un avance significativo en la comprensión de la diversidad microbiana. Mientras que el microscopio nos permitió descubrir la existencia del mundo microbiano, la secuenciación ha permitido, en primer lugar, identificar su gran diversidad, que se manifiesta en dos dominios distintos y una variedad considerable de especies. En la actualidad, la secuenciación nos permite ensamblar miles de genomas y transcriptomas de organismos no cultivables con los cuales interactuamos a diario. En resumen, el estudio de estos organismos es esencial para comprender nuestro entorno cotidiano, y la genética de poblaciones proporciona una lente conceptual potente a través de la cual estudiar la diversidad microbiana y sus complejas dinámicas.

7.11 Actividades

7.11.1 Control de lectura

1. Describa las diferencias entre el modelo exponencial y logístico del crecimiento de poblaciones microbianas. ¿Qué fases existen en el crecimiento del último, y cómo se relacionan con los parámetros empleados en el modelo?
2. ¿Qué es el modelo de Moran? Desarrolle los puntos de similitud y discrepancia con el modelo de Wright-Fisher presentados en el capítulo Deriva Genética.
3. Se denomina a dos o más genes como homólogos si existe algún grado de similitud atribuíble a la existencia de un ancestro común entre estos. Distintos fenómenos biológicos pueden llevar a la existencia de homología entre genes. Explique las características que definen a un conjunto de genes como ortólogos, parálogos o xenólogos, distinguiendo los escenarios que llevan a estos tipos de homología.
4. Los eucariotas también generan resistencia frente a compuestos químicos que impongan un régimen selectivo (e.g. uso de plaguicidas en cultivos). ¿En términos generales, qué diferencias existen entre el desarrollo de resistencia a nivel poblacional en eucariotas y procariotas? Nombre algunas características biológicas de procariotas relevantes para analizar el fenómeno.
5. ¿Qué es la metagenómica? Nombre al menos un área de estudio de los organismos microbianos en los cuales los avances tecnológicos en esta área jueguen un rol importante.

7.11.2 ¿Verdadero o falso?

1. La replicación de células procariotas acontece por fisión. Un modelo matemático que no tenga en cuenta esto no es realista, en tanto predice un crecimiento exponencial para la población. El modelo logístico tiene en cuenta esto, siendo una aproximación matemática más realista.
2. A diferencia de modelo de Wright-Fisher, en el modelo de Moran la población se reproduce en poblaciones solapantes.
3. La expectativa de tiempos de coalescencia de un conjunto de alelos varía según el modelo matemático para modelar el proceso evolutivo, debido a que los mismos contemplan distintas escalas temporales. No obstante, es posible hacer escalados a nivel temporal para ajustar por este factor.
4. El proceso evolutivo de un conjunto de genes es siempre un fiel reflejo de la evolución de las especies involucradas.
5. Cuando aparece un agente antimicrobiano, la célula bacteriana responde generando una variante que le permite la evasión del mismo por distintos métodos, logrando así su supervivencia. Esto explica fenómenos como la resistencia a antibióticos, donde una población microbiana responde creando variantes que logran evadir la acción y generando así resistencia a la droga.

Solución

1. Verdadero. Bajo el modelo de crecimiento logístico la población crecerá de forma sigmoidal, pasando por una fase de crecimiento exponencial, una de crecimiento cuasi-lineal y finalmente disminuyendo su capacidad de crecimiento a medida que se aproxima a la capacidad de carga del sistema (parámetro que conceptualmente puede vincularse a la existencia de recursos limitados para la población). La constante intrínseca de crecimiento es en este contexto un parámetro que permite modelar la dinámica de crecimiento en cada caso específico (i.e. tasa de crecimiento en las distintas fases).
2. Verdadero. El modelo de Moran se basa en la elección de un organismo de la población por vez, por lo que el recambio de los \(N\) individuos de una población no se realiza en un único paso (como si sucede en la construcción del modelo de Wright-Fisher). En efecto, a grosso modo se esperan resultados similares para el modelo de Moran luego de renovar \(N\) individuos y las predicciones del modelo de Wright-Fisher. El hecho de que el modelo de Moran no requiera de la asunción de generaciones no-solapantes lo hace un modelo atractivo para el desarrollo de otros modelos teóricos en genética de poblaciones.
3. Verdadero. Este factor de escalado temporal de hecho está relacionado al tamaño poblacional efectivo, y varía según los modelos: parapoblaciones grandes equivale a \(N_e\) en el caso del modelo de Wright-Fisher y el de fisión, mientras que en el caso del modelo de Moran equivale a \(N_e^2/2\).
4. Falso. Esto acontece sólo si el modo de herencia de la información genética es la transferencia vertical, y si no acontecen eventos de pérdida o ganancia de copias génicas. Un caso claro en el que esto no se cumple es cuando acontece la transferencia horizontal de genes, un proceso común en procariotas: los árboles filogenéticos obtenidos del análisis de estos genes reflejarán el proceso evolutivo de los genes, estimándose un mayor grado de similitud entre copias génicas que son producto de un evento de transferencia horizontal y no necesariamente reflejando la cercanía evolutiva entre las especies involucradas.
5. Falso. La aparición de resistencia a un agente microbiano en una población bacteriana es un fenómeno poblacional, y no se basa por lo tanto en un sistema explícito de sensado de la droga y generación de una respuesta por parte de la célula bacteriana. Ésta es una visión común y que parece dar ciertas características humanas al comportamiento microbiano. La pre-existencia o la aparición de individuos portadores variantes que son menos susceptibles a la droga por mutación aleatoria es un fenómeno independiente de la presencia del antimicrobiano. Una vez aparece dicho agente, se establece un régimen selectivo donde las variantes menos susceptibles poseen mayor fitness, aumentando progresivamente el número de individuos portadores en la población. Variantes más eficientes se pueden fijar en la población, en tiempos que se ven favorecidos por la alta tasa de replicación bacteriana y su plasticidad genómica (existencia de mecanismos de transferencia genética).

Ejercicios

Ejercicio 7.1

En un laboratorio de microbiología se intenta caracterizar la dinámica de crecimiento de una cepa bacteriana. En el medio usado como referencia, la cepa posee una capacidad de carga de \(K = 1 \times 10^5\) individuos. Las curvas de caracterización inician siempre con un célula microbiana.

a. Si el tiempo estimado para llegar a la mitad de la capacidad de carga es de \(2,5\ h\), ¿cuál es la constante de crecimiento intrínseca de la cepa en estas condiciones?

b. ¿Cuánto tiempo estima se alcanzar por lo menos el \(99,9\ \%\) de \(K\)?

Solución

a. Notemos que

\[ \begin{split} t_{1/2} = \frac{\ln(\frac{K - N_0}{N_0})}{r_c} \Rightarrow \\ r_c = \frac{\ln(\frac{K - N_0}{N_0})}{t_{1/2}} \end{split} \]

Reemplazando con los valores dados, tenemos

\[ \begin{split} r_c = \frac{\ln(\frac{10^5 - 1}{1})}{50} \\ r_c \approx 0,23 \end{split} \]

b. Para calcular la cantidad de horas para alcanzar el valor \(0,999 \cdot K\), utilizaremos la ecuación

\[ n(t)=\frac{K\ n_0\ e^{r_c\ t}}{K+n_0\ (e^{r_c\ t}-1)} \]

Sustituyendo con los valores dados, tenemos

\[0,999 \cdot K = \frac{K\ n_0\ e^{r_c\ t}}{K+n_0\ (e^{r_c\ t}-1)}\] \[0,999 \cdot 10^5 = \frac{10^5 \cdot 1 \cdot e^{0,23 \cdot t}}{10^5+ 1\cdot \ (e^{0,23 \cdot\ t}-1)}\] \[0,999 \cdot 10^5 = \frac{10^5 \cdot e^{0,23 \cdot t}}{10^5+e^{0,23 \cdot\ t}-1}\] \[(0,999 \cdot 10^5) \cdot (10^5+e^{0,23 \cdot\ t}-1) = 10^5 \cdot e^{0,23 \cdot t}\] \[0,999 \cdot (10^5+e^{0,23 \cdot\ t}-1) = e^{0,23 \cdot\ t}\] \[0,999 \cdot 10^5 + 0,999 \cdot e^{0,23 \cdot\ t}- 0,999 = e^{0,23 \cdot\ t}\] \[0,999 \cdot 10^5 - 0,999 = e^{0,23 \cdot\ t} - 0,999 \cdot e^{0,23 \cdot\ t}\] \[0,999 \cdot 10^5 - 0,999 = 0,001 \cdot e^{0,23 \cdot\ t}\] \[\frac{0,999 \cdot 10^5 - 0,999} {0,001} = e^{0,23 \cdot\ t}\] \[ln(\frac{0,999 \cdot 10^5 - 0,999} {0,001}) = ln(e^{0,23 \cdot\ t})\] \[ln(\frac{0,999 \cdot 10^5 - 0,999} {0,001}) = 0,23 \cdot\ t \Rightarrow\] \[t = \frac{ln(\frac{0,999 \cdot 10^5 - 0,999} {0,001})}{0,23}\] \[t \approx 80,1\ h\]

El valor obtenido refleja la no-linearidad del proceso de crecimiento: en cerca de cincuenta horas alcanzamos la mitad de la capacidad de carga, pero se requiere bastante menos del doble de tiempo para encontrarse extremadamente cerca de la misma (coherente con los gráficos tipo sigmoide del modelo logístico de crecimiento).

Ejercicio 7.2

(Inspirado en Hartl 2020)

Demuestre que bajo el modelo de Moran la heterocigosidad esperada para un un locus bialélico segregando en una población de tamaño \(N\) decae el doble de rápido que en una población que lo predicho según el modelo de Wright-Fisher aplicado a una población haploide de igual tamaño.

Solución

Para ver cómo evoluciona la heterocigosidad esperada según el modelo de Moran podemos tomar un enfoque similar al utilizamos cuando detallamos el modelo de Wright-Fisher. Veremos primero cuál es la heterocigosidad esperada luego de un paso en el modelo, y a partir de allí veremos qué predice el modelo para la heterocigosidad luego de un número arbitrario de pasos (en el caso del modelo de Wright-Fisher, esto eran \(t\) generaciones arbitrarias). Según el modelo de Moran, si se tienen \(i\) copias de un alelo las probabilidades de pasar \(i+1\), mantenerse en \(i\) copias o pasar a \(i+1\) copias son

\[\begin{equation} \begin{cases} p_{i,i-1}= \frac{(N-i) \cdot i}{N^2} \\ p_{i,i}=\frac{i^2+(N-i)^2}{N^2} \\ p_{i,i+1} =\frac{i \cdot (N-i)}{N^2} \end{cases} \end{equation}\]

¿Qué implica esto a nivel de las frecuencias alélicas? Notemos que si el número de copias es \(i\) para un alelo, su frecuencia en la población a tiempo \(t\) es \(p = \frac{i}{N}\), siendo la frecuencia del alelo alternativo \(q = \frac{N-i}{N}\) (contamos con \(N\) alelos por tratarse de una población haploide). Notemos que las probabilidades anteriores pasan a expresarse en función de las frecuencias alélicas como

\[\begin{equation} \begin{cases} p_{i,i-1}= \frac{(N-i) \cdot i}{N^2} = (\frac{N-i}{N}) \cdot (\frac{i}{N}) = (1-p) \cdot p = qp \\ p_{i,i}=\frac{i^2+(N-i)^2}{N^2} = \frac{i^2}{N^2} + frac{(N-i)^2}{N^2} = (\frac{i}{N})^2 + ( frac{(N-i)}{N})^2 = p^2 + (1-p)^2 = p^2 + q^2 \\ p_{i,i+1} =\frac{i \cdot (N-i)}{N^2} = (\frac{i}{N}) \cdot (\frac{N-i}{N}) = p \cdot (1-p) = pq \end{cases} \end{equation}\]

Luego de una ronda del proceso propuesto por el modelo, la heterocigosidad esperada será

\[ H_{t + \delta t} = 2(p + \frac{1}{N})(1 - p - \frac{1}{N})[pq] + 2pq[p^2 + q^2] + 2(p - \frac{1}{N})(1 - p + \frac{1}{N})[qp] \]

donde, como en todo calculo de esperanza, a los valores posibles los multiplicamos por su probabilidad (entre paréntesis rectos en la ecuación anterior). Es importante notar que por cómo se propone el modelo se abarcó en este cálculo a todos los valores de heterocigosidad posibles luego de un paso de replicación y muerte de una célula haploide.

Si desarrollamos el cálculo, llegamos a que

\[ H_{t + \delta t} = 2pq(1 - \frac{2}{N^2}) \]

Pero en el punto de partida \(t\) la heterocigosidad es justamente \(H_t = 2pq\), por lo que la ecuación anterior implica

\[ H_{t + \delta t} = H_t \cdot (1 - \frac{2}{N^2}) \]

Llegado este punto llegamos a una recursión similar a la que obtuvimos cuando desarrollamos el modelo de Wright-Fisher. Tenemos

\[ H_{t + 2\delta t} = H_t \cdot (1 - \frac{2}{N^2})^2 \]

Y si repetimos el proceso hasta reemplazar a un número \(N\) individuos (la idea detrás del modelo de Wright-Fisher, generar una nueva generación de individuos), obtendremos

\[ \begin{split} H_{t + N\delta t} = H_t \cdot (1 - \frac{2}{N^2})^N \approx H_t \cdot (1 - \frac{2N}{N^2}) \\ H_{t + N\delta t} \approx H_t \cdot (1 - \frac{2}{N}) \end{split} \]

El modelo de Wright-Fisher para una población haploide de tamaño \(N\) imṕlica un cambio de heterocigosidad de una generación a la siguiente de

\[ H_{t + 1} \approx H_t \cdot (1 - \frac{1}{N}) \]

donde queda claro que el modelo de Moran predice una pérdida de heterocigosidad el doble de rápido.

Ejercicio 7.3

Un grupo de investigación detectó la existencia de una cepa de Saccharomyces cerevisiae que posee un alto potencial industrial para la elaboración de bebidas alcohólicas. Debido a que la cepa no logra aislarse en forma pura al momento, se decide investigar para buscar condiciones que favorezcan su crecimiento en el medio utilizado para la fermentaci[on. Afortunadamente se identificó un gen marcador (al cual llamaremos \(A\)) para el cual existen dos alelos que separan claramente a la variante de interés (portador del alelo \(A_1\), de frecuencia \(p\)) y otras cepas.

Se realiza un experimento de secuenciación masiva con el objetivo de analizar la proliferación bajo una condición dada, secuenciando a dos tiempos (se estima que a una generación de la población) con tres réplicas cada uno. Se asume que la profundidad de secuenciado (número de bases) en ambos experimentos es la misma.

Variante	\(T1_1\)	\(T1_2\)	\(T1_3\)	\(T2_1\)	\(T2_2\)	\(T2_3\)
\(A_1\)	6555	6520	6590	6980	6915	7030
\(A_2\)	3460	3510	3435	3135	3180	3055

donde en las columnas A y B denotan a las condiciones experimentales estudiadas.

¿En cual de las condiciones experimentales posee mayor fitness relativo la cepa de interés, y en qué magnitud?

Solución

a. Para determinar en qué condición experimental la cepa de interés tiene un mayor fitness relativo y en qué magnitud, utilizamos la ecuación:

\[ \Delta_sp = \frac{s_d \cdot p \cdot q}{1 + s_d \cdot p} \]

Primero, calcularemos las frecuencias \(p\) y \(q\) en cada tiempo. Para ello vamos a calcular las frecuencias en cada réplica de cada tiempo, y luego promediar esos valores para obtener una estimación más precisa las frecuencias de interés.

Para el Tiempo 1 entonces tenemos:

\[\begin{equation} \begin{cases} p_{\text{T1\_1}} = \frac{6555}{6555 + 3460} \approx 0.654 \\ p_{\text{T1\_2}} = \frac{6520}{6520 + 3510} \approx 0.650 \\ p_{\text{T1\_3}} = = \frac{6590}{6590 + 3435} \approx 0.657 \end{cases} \end{equation}\]

de lo cual tenemos \(\bar{p}_{T1} = \frac{p_{T1\_1} + p_{T1\_2} + p_{T1\_3}}{3} \approx 0.6537 \Rightarrow \bar{q}_{T1} \approx 1 - 0,6537 = 0,3463\).

De forma análoga se llega a \(\bar{p}_{T2} \approx 0.6903 \Rightarrow \bar{q}_{T2} \approx 1 - 0,6903 = 0,3097\).

A partir de estos valores podemos calcular \(\Delta_s p\), que representa el cambio en la frecuencia de \(A_1\) entre tiempos, el cual atribuímos a la selección. Tenemos

\[ \Delta_sp = \bar{p}_{T2} - \bar{p}_{T1} = 0,6903 - 0,6537 = 0,0366 \]

Finalmente, despejamos \(s_d\) utilizando la ecuación mencionada al comienzo.

\[\Delta_sp = \frac{s_d \cdot p \cdot q}{1 + s_d \cdot p}\] \[\Delta_sp \cdot (1 + s_d \cdot p) = s_d \cdot p \cdot q \] \[\Delta_s p + \Delta_sp \cdot p \cdot s_d = s_d \cdot p \cdot q\] \[\Delta_sp = s_d \cdot p \cdot q - s_d \cdot \Delta_sp \cdot p\] \[\Delta_s p = s_d \cdot (p\cdot q- p \cdot \Delta_s p) \Rightarrow\] \[s_d = \frac{\Delta_sp}{(p\cdot q- p \cdot \Delta_s p)}\] \[s_d \approx \frac{0,0366}{0,6537 \cdot 0,3463 - 0,6537 \cdot 0.0366}\] \[s_d \approx 0,18\]

En efecto la condición probada parece dar ventaja a la cepa de interés, la cual posee una diferencia en fitness relativo de aproximadamente 0,18.

Ejercicio 7.4

En una población microbiana se encuentra segregando un locus bialélico (al cual nos referiremos como \(A\)). La población tiene un tamaño efectivo aproximado de \(N_e = 10.000\), siendo las frecuencias alélicas \(p = 0,54\) y \(q = 0,46\) para los alelos \(A_1\) y \(A_2\), respectivamente.

a. Compare el valor de heterocigosidad (virtual) esperado según el modelo de Moran respecto al de Wright-Fisher luego de 100, 1000 y 10.000 generaciones.

b. Tomando como punto de partida la situación descrita en la letra, ¿cuál es la probabilidad de que dos alelos no coalezcan luegoe haberse reemplazados 100 individuos de la población (\(1\%\) de la misma)?

Solución

a. El valor de heterocigosidad virtual esperado según el modelo de Moran luego de una generación es de

\[ H_{t+1} = H_{t} \cdot (1- \frac{2}{N}) \]

por lo que luego de \(t\) generaciones esperamos según este modelo un valor de

\[ H_t = H_0 \cdot (1 - \frac{2}{N})^t \]

donde \(H_0\) es la heterocigosidad virtual en la primera generación.

Si aplicamos el modelo de Wright-Fisher a una población haploide, tenemos que la caída de heterocigosidad esperada en una generación es

\[ H_{t+1} = H_t \cdot (1 - \frac{1}{N}) \]

Por razonamiento análogo, tenemos luego de \(t\) generaciones

\[ H_t = H_0 \cdot (1 - \frac{1}{N})^t \]

Como ya se vió en otro ejercicio, el modelo de Moran predice una caída de la heterocigosidad dos veces mayor que el modelo de Wright-Fisher cuando se lo aplica a una población haploide. A efectos de realizar las comparaciones pedidas, se verá el cociente entre los valores esperados, el cual corresponde a

\[ \begin{split} \frac{H_t^{\text{W-F}}}{H_t^{\text{Moran}}} = \frac{H_0 \cdot (1 - \frac{1}{N})^t}{H_0 \cdot (1 - \frac{2}{N})^t} \\ \frac{H_t^{\text{W-F}}}{H_t^{\text{Moran}}} = \frac{(1 - \frac{1}{N})^t}{(1 - \frac{2}{N})^t} \end{split} \]

Reemplazando con el valor de tamaño poblacional dado y los tiempos requeridos se obtiene

\[\begin{equation} \begin{cases} H_{100}^{\text{W-F}}/H_{100}^{\text{Moran}} \approx 1,01 \\ H_{1000}^{\text{W-F}}/H_{1000}^{\text{Moran}} \approx 1,11 \\ H_{10000}^{\text{W-F}}/H_{10000}^{\text{Moran}} \approx 2,71\\ \end{cases} \end{equation}\]

Vemos por lo tanto que a medida que se empiezan a considerar una mayor cantidad de generaciones la estimación de heterocigosidad virtual comienza a discrepar entre los modelos, llegando a ser la heterocigosidad esperada según el modelo de Wright-Fisher casi tres veces mayor luego de 10.000 generaciones.

b. Recordemos que haciendo un escalado temporal la probabilidad de no coalescencia a tiempo \(v\) está dada aproximadamente por la siguiente ecuación

\[ P(T_k > v) \approx e^{-\frac{k(k-1)}{2} v}  \]

El factor de escalado temporal a usar en cada modelo varía y está relacionado con el tamaño poblacional; en el caso del modelo de Moran el escalado factor de escalado es de \(N^2/2\). Deshaciendo el escalado temporal, tenemos la probabilidad de no coalescencia según el modelo de Moran teniendo en cuenta el tamaño de la población, \(P(T_k^N > t)\), la cual estará dada por

\[ \begin{split} P(T_k^N > t) \approx e^{-\frac{k(k-1)}{2} \cdot \frac{2}{N^2} \cdot t } \\ P(T_k^N > t) \approx e^{-\frac{k(k-1)}{N^2} \cdot t } \end{split} \]

donde se deshizo el el escalado temporal teniendo en cuenta que \(-\frac{k(k-1)}{2} \cdot t = - x \cdot \frac{N^2}{2} \cdot t \Rightarrow x = \frac{k(k-1)}{2} \cdot \frac{N^2}{2}\).

Recordemos que \(k\) equivale al número de alelos; dado que la población consta de \(10.000\) individuos haploides, el número de alelos será \(k = 10000\). Teniendo esto en cuenta, podremos realizar el cálculo en la escala temporal del modelo de Moran. La probabilidad de no-coalescencia luego de mil reemplazos estará dada por

\[ \begin{split} P(T_k^N > 100) \approx e^{-\frac{10000 \cdot (10000-1)}{10000^2} \cdot 100} \\ P(T_k^N > 100) \approx 3,76 \times 10^{-44} \end{split} \]

Ejercicio 7.5

En una población de aproximadamente 54 millones de personas ingresa un patógeno. Luego de un tiempo, un grupo interdisciplinario se dispone a estudiar la dinámica de transmisión en la población, logrando determinar una tasa de transmisión de \(\beta = 0,12\text{ contagios \textit{per capita}/dia}\) , una tasa de recuperación de \(\gamma = 0,1\text{ recuperados \textit{per capita}/dia}\) y una tasa de mortalidad de \(\mu = 0,001 \text{ muertes \textit{per capita}/dia}\) .

1. ¿Qué dinámica de transmisión espera en la población con estos datos?
2. Determine la cantidad de individuos sanos, cursando enfermedad y recuperados en el largo plazo, una vez se alcance el equilibrio. Se asume que las condiciones generales de la situación epidemiológica se ven inalteradas.
3. ¿A qué tasa de transmisión máxima se debe llegar si se quiere que la población pueda erradicar la enfermedad? Asuma que no es posible aumentar la tasa de recuperados, y que no es deseable aumentar la tasa de mortalidad.

Solución

a. Para determinar la dinámica de transmisión en la población, primero calcularemos el número básico de reproducción (\(R_0\)) utilizando la fórmula:

\[ R_0 = \frac{\beta}{\gamma + \mu} \]

Sustituyendo estos valores en la ecuación tenemos:

\[ R_0 = \frac{0.1199}{0.1 + 0.001} = \frac{0.1199}{0.101} \approx 1.186 \]

Valores \(R_0 < 1\) indicarían que la enfermedad no puede sostenerse en la población y eventualmente desaparecería. Los valores de \(R_0 \ge 1\) sugieren que la enfermedad puede propagarse en la población. En este caso, con un valor cercano a 1 la propagación sería relativamente lenta, pudiendo mantenerse a largo plazo el patǵeno circulando en la población.

b. Para determinar la cantidad de individuos sanos, cursando la enfermedad y recuperados a largo plazo (cuando se alcance el equilibrio), utilizaremos la ecuación de equilibrio proporcionada para el caso \(R_0 \ge 1\):

\(e_2 = (S^*, I^*, R^*) = (\frac{N}{R_0}, N \cdot c_1 \cdot (R_0 - 1), N \cdot c_2 \cdot (R_0 - 1))\)

donde \(N\) es la población total (54 millones de personas) y las constantes \(c_1\) y \(c_2\) están dadas por \(c_1 = \mu \cdot \beta\) y \(c_2 = \gamma \cdot \beta\).

Sustituyendo los valores, obtenemos

\[\begin{equation} \begin{cases} S^* = \frac{N}{R_0} = \frac{54.000.000}{1,1861} \approx 45.556.246 \\ I^* = N \cdot c_1 \cdot (R_0 - 1) = 54.000.000 \cdot (0,001 \cdot 0,1199) \cdot (1,1861 - 1) \approx 6.276 \\ R^* = N \cdot c_2 \cdot (R_0 - 1) = 54.000.000 \cdot (0,1 \cdot 0,1199) \cdot (1,1861 - 1) \approx 67.116 \end{cases} \end{equation}\]

siendo estos los valores estimados para \(S^*\), \(I^*\) y \(R^*\), la cantidad estimada de personas sanas, cursando la infección y recuperadas en el estado de equilibrio, respectivamente.

c. Para que la población pueda erradicar la enfermedad, es necesario que el número básico de reproducción \(R_0 < 1\). Recordemos que \(R_0 = \frac{\beta}{\mu + \gamma}\). Por lo tanto, tenemos

\[ \begin{split} R_0 < 1 \\ \frac{\beta}{\mu + \gamma} < 1\\ \beta < \mu + \gamma \beta < 0,001 + 0,1 = 0,101 \end{split} \]

Por lo tanto, si se logra disminuir la tasa de transmisión a menos de \(0,101 \text{ contagios/día}\) aproximadamente, se espera a largo plazo la erradicación de la enfermedad (si no existe un cambio en las condiciones dadas)

---

Bibliografía

Achtman, M. 1975. “Mating aggregates in Escherichia coli conjugation.” J Bacteriol 123 (2): 505–15.

Aïssani, B, and G Bernardi. 1991. “CpG Islands, Genes and Isochores in the Genomes of Vertebrates.” Gene 106 (2): 185–95. http://www.ncbi.nlm.nih.gov/pubmed/1937049.

Aminov, R. I. 2011. “Horizontal gene exchange in environmental microbiota.” Front Microbiol 2: 158.

Belle, Elise M S, Nick Smith, and Adam Eyre-Walker. 2002. “Analysis of the Phylogenetic Distribution of Isochores in Vertebrates and a Test of the Thermal Stability Hypothesis.” Journal of Molecular Evolution 55 (3): 356–63. http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?cmd=Retrieve&db=PubMed&dopt=Citation&list_uids=12187388.

Bernardi, G, B Olofsson, J Filipski, M Zerial, J Salinas, G Cuny, M Meunier-Rotival, and F Rodier. 1985. “The Mosaic Genome of Warm-Blooded Vertebrates.” Science 228 (4702): 953–58. http://www.ncbi.nlm.nih.gov/pubmed/4001930.

Chan, K. M., Y. T. Liu, C. H. Ma, M. Jayaram, and S. Sau. 2013. “The 2 micron plasmid of Saccharomyces cerevisiae: a miniaturized selfish genome with optimized functional competence.” Plasmid 70 (1): 2–17.

Costantini, Maria, Rosalia Cammarano, and Giorgio Bernardi. 2009. “The Evolution of Isochore Patterns in Vertebrate Genomes.” BMC Genomics 10 (i): 146. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2678159&tool=pmcentrez&rendertype=abstract.

Duret, L, D Mouchiroud, and C Gautier. 1995. “Statistical Analysis of Vertebrate Sequences Reveals That Long Genes Are Scarce in GC-Rich Isochores.” Journal of Molecular Evolution 40 (3): 308–17. http://www.springerlink.com/index/10.1007/BF00163235.

Duval, M., D. Dar, F. Carvalho, E. P. C. Rocha, R. Sorek, and P. Cossart. 2018. “HflXr, a homolog of a ribosome-splitting factor, mediates antibiotic resistance.” Proc Natl Acad Sci U S A 115 (52): 13359–64.

Eyre-Walker, A. 1992. “Evidence That Both g + c Rich and g + c Poor Isochores Are Replicated Early and Late in the Cell Cycle.” Nucleic Acids Research 20 (7): 1497–1501. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=312229&tool=pmcentrez&rendertype=abstract.

Eyre-Walker, A, and L D Hurst. 2001. “The Evolution of Isochores.” Nature Reviews Genetics 2 (7): 549–55. http://opus.bath.ac.uk/4362/.

Fleischmann, R. D., M. D. Adams, O. White, R. A. Clayton, E. F. Kirkness, A. R. Kerlavage, C. J. Bult, J. F. Tomb, B. A. Dougherty, and J. M. Merrick. 1995. “Whole-genome random sequencing and assembly of Haemophilus influenzae Rd.” Science 269 (5223): 496–512.

Handelsman, J., M. R. Rondon, S. F. Brady, J. Clardy, and R. M. Goodman. 1998. “Molecular biological access to the chemistry of unknown soil microbes: a new frontier for natural products.” Chem Biol 5 (10): R245–249.

Hartl, Daniel L. 2020. A Primer of Population Genetics and Genomics. 4th ed. London, England: Oxford University Press.

Kagawa, Y, H Nojima, N Nukiwa, M Ishizuka, T Nakajima, T Yasuhara, T Tanaka, and T Oshima. 1984. “High Guanine Plus Cytosine Content in the Third Letter of Codons of an Extreme Thermophile. DNA Sequence of the Isopropylmalate Dehydrogenase of Thermus Thermophilus.” The Journal of Biological Chemistry 259 (5): 2956–60.

Kazanskaya, O V, E A Severtzova, K A Barth, G V Ermakova, S A Lukyanov, A O Benyumov, M Pannese, E Boncinelli, S W Wilson, and A G Zaraisky. 1997. “Methylation Patterns in the Isochores of Vertebrate Genomes.” Gene 205 (1-2): 25–34. http://www.ncbi.nlm.nih.gov/pubmed/9461385.

Kingman, JFC. 1982a. “On the Genealogy of Large Populations.” Journal of Applied Probability 19A: 27–43.

Lane, D. J., B. Pace, G. J. Olsen, D. A. Stahl, M. L. Sogin, and N. R. Pace. 1985. “Rapid determination of 16S ribosomal RNA sequences for phylogenetic analyses.” Proc Natl Acad Sci U S A 82 (20): 6955–59.

McEwan, C E, D Gatherer, and N R McEwan. 1998. “Nitrogen-Fixing Aerobic Bacteria Have Higher Genomic GC Content Than Non-Fixing Species Within the Same Genus.” Hereditas 128 (2): 173–78. http://www.ncbi.nlm.nih.gov/pubmed/9687237.

Moldovan, M. A. 2019. “[Prokaryotic and Mitochondrial Linear Genomes: Their Genesis, Evolutionary Significance, and the Problem of Replicating Chromosome Ends].” Mol Biol (Mosk) 53 (2): 218–24.

Musto, Héctor, Hugo Naya, Alejandro Zavala, Héctor Romero, Fernando Alvarez-Valín, and Giorgio Bernardi. 2004. “Correlations Between Genomic GC Levels and Optimal Growth Temperatures in Prokaryotes.” FEBS Letters 573 (1-3): 73–77. http://www.ncbi.nlm.nih.gov/pubmed/15327978.

Naya, Hugo, Héctor Romero, Alejandro Zavala, Beatriz Alvarez, and Héctor Musto. 2002. “Aerobiosis Increases the Genomic Guanine Plus Cytosine Content (GC%) in Prokaryotes.” Journal of Molecular Evolution 55 (3): 260–64. http://www.ncbi.nlm.nih.gov/pubmed/12187379.

Otto, Sarah P., and Troy Day. 2007. A Biologist’s Guide to Mathematical Modeling in Ecology and Evolution. Princeton University Press.

Robinson, D. Ashley, Daniel Falush, and Edward J Feil. 2010. Bacterial Population Genetics in Infectious Disease. Wiley-Blackwell.

Rocha, E. P. C. 2018. “Neutral Theory, Microbial Practice: Challenges in Bacterial Population Genetics.” Mol Biol Evol 35 (6): 1338–47.

Rocha, Eduardo P C, and Antoine Danchin. 2002. “Base Composition Bias Might Result from Competition for Metabolic Resources.” Trends in Genetics 18 (6): 291–94. http://www.ncbi.nlm.nih.gov/pubmed/12044357.

Rocha, Eduardo P C, and Edward J Feil. 2010. “Mutational Patterns Cannot Explain Genome Composition: Are There Any Neutral Sites in the Genomes of Bacteria?” Edited by Michael WEditor Nachman. PLoS Genetics 6 (9): 4. http://dx.doi.org/10.1371/journal.pgen.1001104.

Romero, Héctor, Emiliano Pereira, Hugo Naya, and Héctor Musto. 2009. “Oxygen and Guanine-Cytosine Profiles in Marine Environments.” Journal of Molecular Evolution 69 (2): 203–6.

Saccone, S, A De Sario, J Wiegant, A K Raap, G Della Valle, and G Bernardi. 1993. “Correlations Between Isochores and Chromosomal Bands in the Human Genome.” Proceedings of the National Academy of Sciences of the United States of America 90 (24): 11929–33. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=48098&tool=pmcentrez&rendertype=abstract.

Soppa, J. 2014. “Polyploidy in archaea and bacteria: about desiccation resistance, giant cell size, long-term survival, enforcement by a eukaryotic host and additional aspects.” J Mol Microbiol Biotechnol 24 (5-6): 409–19.

Stein, J. L., T. L. Marsh, K. Y. Wu, H. Shizuya, and E. F. DeLong. 1996. “Characterization of uncultivated prokaryotes: isolation and analysis of a 40-kilobase-pair genome fragment from a planktonic marine archaeon.” J Bacteriol 178 (3): 591–99.

Sueoka, Noboru. 1962. “ON THE GENETIC BASIS OF VARIATION AND HETEROGENEITY OF DNA BASE COMPOSITION.” Proceedings of the National Academy of Sciences of the United States of America 48 (4): 582–92. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC220819/.

Zwietering, M. H., I. Jongenburger, F. M. Rombouts, and K. van ’t Riet. 1990. “Modeling of the bacterial growth curve.” Appl Environ Microbiol 56 (6): 1875–81.

---

64. Louis Pasteur (27 de diciembre 1822 - 28 de septiembre 1895) fue un físico-químico francés que contribuyó al establecimiento de la microbiología como rama de la ciencia. Además de notables contribuciones a la físico-química, por ejemplo en la formación de cristales, realizá trabajos claves para refutar la teoría de la generación espontánea. Es además el fundador del Institut Pasteur, que surgió como instituto anti-rábico y que ha realizado notables contribuciones a la biología y medicina, incluyendo desde 1908 10 premios Nobel en esa categoría.↩︎

65. Carl Richard Woese (15 de july 1928 – 30 de diciembre 2012) fue un microbiólogo y biofísico conocido por sus trabajos en la filogenética de la vida y por haber definido en dominio archaea a partir del análisis del ARNr 16S. Originalmente formado en matemáticas y física, su interés en descifrar en código genético lo fue llevando a trabajar en diferentes preguntas centrales de la biología, algunas relacionadas con el origen de la vida en nuestro planeta.↩︎

66. Se denomina bacteriófagos, o simplemente fagos, a un grupo de virus que infectan bacterias.↩︎

67. Un pilus -plural, pili- es una estructura similar a un pelo existente en las superficie de bacterias, a través del cual la célula ejerce la conjugación.↩︎

68. Se denomina “exon shuffling” (”barajado de exones”, en inglés) al proceso mediante el cual se generan nuevos genes mediante el reordenamiento de la estructura intrón-exón de un gen. Otro mecanismo notable en lo referente a generación de diversidad molecular en eucariotas que tiene su base en la existencia de la estructura exón-intrón es el splicing alternativo (”empalme” alternativo), donde a partir de un mismo gen se generan diferentes copias de ARN mensajero (y por tanto, posibles productos proteicos) mediante la selección de diferentes combinaciones de exones para la conformación del ARN mensajero que será exportado al citosol.↩︎

69. Los números exponenciales crecen de forma extremadamente rápida, y la intuición del cerebro humano suele ser especialmente mala en anticipar esta forma de crecimiento. Existen varios ejemplos referentes a esta subestimación del crecimiento exponencial (el ejemplo del crecimiento bacteriano mostrado en esta sección, sin ir más lejos). La persona interesada puede buscar la célebre “Leyenda de Sissa”, referente al supuesto origen del ajedrez, que ilustra esta enseñanza.↩︎

70. Pierre François Verhulst (28 de octubre 1804 - 15 de febrero 1849) fue un matemático belga, conocido como el primer proponente del modelo logístico para el crecimiento de las poblaciones como alternativa al modelo exponencial de Malthus.↩︎

71. Patrick Alfred Pierce Moran F(14 de julio de 1917 - 19 de septiembre de 1988), fue un estadístico australiano que realizó importantes contribuciones a la teoría de la probabilidad y a su aplicación a la genética poblacional y evolutiva. En particular, fue el que propuso el modelo de muestreo de gametos como un proceso de nacimiento-muerte, un tipo de modelos con amplia aplicación en otras ramas de la ciencia.↩︎

72. El mecanismo específico mediante el cual se produce la duplicación génica será el que determinará si las copias génicas se encuentran o no ubicadas en un mismo cromosoma.↩︎

73. Las “islas CpG” son regiones en el genoma que se caracterizan por la repetición de dinucleótidos de citosina (C) seguidos de guanina (G). La “p” en este término hace referencia al enlace fosfodiéster entre los nucleótidos. Es relevante destacar que en la hebra complementaria también se encuentra el mismo dinucleótido, lo que lleva a la analogía con una ‘isla’.↩︎

74. Motoo Kimura (13 de noviembre 1924 – 13 de noviembre 1994) fue un biólogo evolutivo japonés y uno de los genetistas de poblaciones más importantes del siglo XX. Originalmente formado como botánico, pero con gran interés en las matemáticas, después de la segunda guerra mundial comenzó a publicar en genética teórica. Propuso la teoría neutral de la evolución que pese a no ajustarse al conocimiento actual y a los datos moleculares disponibles, aún hoy en día sigue cosntituyendo el patrón de comparación para otras teorías alternativas.↩︎

75. Frederick Sanger (13 de agosto de 1918 - 19 de noviembre de 2013) fue un bioquímico británico, que obstuvo dos veces el Premio Nobel de Química, una de las dos únicas personas en haberlo obtenido dos veces en la misma categoría (John Bardeen es el otro, en Física) y la cuarta persona del mundo en recibir dos premios Nobel. En 1958 obtuvo su primer Premio Nobel por los trabajos que llevaron a la comprensión de la estructura de la proteínas, de la insulina en particular, mientras que el segundo lo obtuvo en forma compartida con Walter Gilbert en el año 1980 por sus contribuciones a la determinación de la secuencia de bases del ADN.↩︎

76. Carl Richard Woese (15 de july 1928 – 30 de diciembre 2012) fue un microbiólogo y biofísico conocido por sus trabajos en la filogenética de la vida y por haber definido en dominio archaea a partir del análisis del ARNr 16S. Originalmente formado en matemáticas y física, su interés en descifrar en código genético lo fue llevando a trabajar en diferentes preguntas centrales de la biología, algunas relacionadas con el origen de la vida en nuestro planeta.↩︎

77. Sir Alexander Fleming (6 de agosto 1881 – 11 marzo 1955) fue un médico u microbiólogo escoces. Descubridor en 1928 de un compuesto que llamó penicilina y que luego se llamaría bencilpenicilina (o penicilina G), obtenido a partir del hongo Penicillium rubens. Fue ganador del premio Nobel de Medicina y Fisiología en 1945, junto a Howard Florey y Ernst Boris Chain.↩︎

78. La tecnología MALDI-TOF (matrix-assisted laser desorption/ionization time-of-flight) es una técnica de espectrometría de masas que se utiliza para identificar y analizar moléculas como proteínas, péptidos y otros compuestos químicos. Funciona mediante la ionización de muestras y la medición del tiempo que tardan las partículas cargadas en moverse a través de un campo eléctrico.↩︎