Capítulo 12 Correlaciones y respuesta correlacionada

Hasta ahora, en la mayor parte de nuestro recorrido nos hemos limitado a examinar un solo fenotipo cada vez. Hemos construido modelos sobre el genotipo, descomponiendo su expresión en la suma de los aportes genéticos y ambientales y en algunos casos su interacción. Más aún, en el capítulo [selartifI] estudiamos cómo sería la respuesta a nuestro esfuerzo de selección direccional en función de la presión de selección que ejercemos y de los parámetros genéticos asociados a la característica. Sin embargo, por lo general estamos interesados en mejorar más de un fenotipo en los individuos. En ovinos deseamos aumentar el peso del vellón, pero al mismo tiempo deseamos reducir el diámetro de las fibras. En producción lechera (en nuestro país) deseamos aumentar la producción de grasa y de proteína (en kg), pero al mismo tiempo deseamos reducir los litros de leche (ya que la industria castiga el volumen), reducir el recuento de células somáticas (al premiado por la industria) y al menos mantener el nivel de fertilidad del rodeo. En el capítulo Selección Artificial II veremos diferentes estrategias para alcanzar estos objetivos múltiples, pero para llegar a eso primero debemos entender la base causal de las relaciones entre diferentes características fenotípicas.

En el presente capítulo definiremos los tipos de correlaciones fenotípica (observable), genética (aditiva) y ambiental, en un modelo genético simplificado, donde el ambiente extendido contendrá además de los efectos ambientales propiamente dichos, todos los efectos genéticos no-aditivos. Esto nos permitirá simplificar los análisis mediante la comprensión de las correlaciones genéticas y ambientales.

OBJETIVOS DEL CAPÍTULO

\(\square\) Definir tipos de correlaciones y utilizarlas para analizar las correlaciones genéticas y ambientales.

\(\square\) Explorar las causas subyacentes de estas correlaciones, incluyendo pleiotropía y ligamiento.

\(\square\) Analizar la respuesta correlacionada en la selección de características.

\(\square\) Introducir el análisis de coeficientes de paso (path analysis).

\(\square\) Describir la relación entre correlaciones fenotípicas, genéticas y ambientales.

\(\square\) Discutir métodos para estimar correlaciones genéticas y ambientales.

\(\square\) Organizar la información genética, ambiental y fenotípica mediante matrices de varianza-covarianza y calcular parámetros genéticos a partir de estas.

\(\square\) Generalizar la ecuación del criador a varias características (ecuación de Lande).

\(\square\) Analizar la información proporcionada por la matriz de varianza-covarianza genética en la selección y las restricciones que la misma impone a la evolución de características.

12.1 Causas genéticas y ambientales de las correlaciones

El fenotipo, de acuerdo a nuestro modelo genético básico, lo hemos descompuesto en los aportes genéticos y los aportes ambientales, más (en algunos casos) los aportes de la interacción entre el genotipo y el ambiente. Por lo tanto, cuando hablamos de correlaciones fenotípicas entre características que observamos en los individuos, no es de extrañar que la base de estas correlaciones se puedan descomponer también en los aportes de la genética, es decir las correlaciones genéticas y los aportes ambientales y sus correspondientes correlaciones. En la presente sección vamos a discutir las bases biológicas y causales de estas correlaciones, mientras que en las siguientes secciones de este capítulo desarrollaremos la teoría para interpretarlas y cuantificarlas.

Correlación fenotípica entre dos características, medidas ambas en los mismos individuos es la correlación entre los valores fenotípicos (observables) de cada individuo en ambas características.

Causas de las correlaciones genéticas

Claramente, podemos calcular correlaciones entre cualquier par de mediciones que tengamos en los mismos individuos y por lo tanto podemos luego buscar las causas, genética y ambientales de los resultados obtenidos. Sin embargo, en algunos casos las características que pretendemos medir como dos características diferentes son apenas distinguibles entre sí, por lo que no es sorprendente que en esos casos la correlación genética se explique por sí sola. Por ejemplo, si pesamos a los individuos en una balanza que usa el Sistema Internacional de Unidades (SI, kg) y luego las pesamos en otra balanza que utiliza las unidades del sistema imperial Británico (libras), la correlación entre las dos características debería ser muy alta, particularmente si las balanzas funcionan bien y el intervalo entre las dos medidas realizadas es corto. Técnicamente son dos características distintas, peso en la primer balanza y peso en la segunda balanza, pero más allá de factores que podemos asociar al error (calibración y variaciones temporales mínimas, por ejemplo una vaca que orinó entre medidas), la variable biológica de interés es exactamente la misma. Por lo tanto, la genética que controla el peso de los individuos es la misma y no hace falta buscar causas misteriosas. De hecho, si las estimaciones de la correlación genética entre ambas características nos dieran un valor bajo, deberíamos sospechar fuertemente de problemas serios en el estudio. Sin duda se trata de un caso extremo, pero en general resulta útil reflexionar sobre el origen posible de cualquier correlación entre características para las que obtengamos estimaciones de correlaciones fenotípicas, genéticas y ambientales.

Correlación genética (aditiva) entre dos características, medidas ambas en los mismos individuos es la correlación entre los valores de cría de cada individuo en ambas características.

Desde el punto de vista genético hay dos causas que claramente pueden estar por detrás de la correlación entre dos mediciones realizadas en individuos (muestreados al azar) de la población: pleiotropía y ligamiento. En el capítulo Dinámica de 2 loci discutimos lo que acontecía cuando la proximidad física de los loci disminuía la probabilidad de recombinación entre los mismos. En ese caso, determinadas combinaciones de alelos (haplotipos) tienden a aparecer con mayor frecuencia de lo que sería esperable por azar si no estuviesen “ligados” (que sería el producto de las frecuencias de cada alelo). Si, por ejemplo, dos loci se encuentran fuertemente “ligados” y cada uno de ellos controla (genes de efecto mayor) una característica diferente, entonces valores específicos en una característica estarán asociados a valores específicos en otra característica, lo que genera correlación. Supongamos un caso sencillo, dos loci \(A\) y \(B\), cada uno gobernando una característica diferente, con dos alelos cada uno: \(A=5\), \(a=1\) para la primera característica, \(B=4\), \(b=2\) para la segunda característica. Si los dos loci no se encuentran ligados, la segregación distribuirá los gametos en forma independiente para los dos loci y por lo tanto no existirá correlación de valores entre las dos características. Sin embargo, en el caso de que se encuentren totalmente “ligados”, supongamos que \(A\) va siempre con \(B\) y que \(a\) va siempre con \(b\). En ese caso, solo tendremos dos haplotipos posibles: \(AB\) y \(ab\). Sin pérdida de generalidad, supongamos que las frecuencias de \(A\) y \(B\) son iguales a \(\frac{1}{2}\), por lo que los haplotipos \(AB\) y \(ab\) tendrán también frecuencias de \(\frac{1}{2}\). Ahora, los posibles genotipos y sus valores para las dos características serán

Genotipo	Frecuencia	Caract..1	Caract..2	Dif.1	Dif.2	Prod.1.2
\(AB/AB\)	\(\frac{1}{4}\)	\(5+5=10\)	\(4+4=8\)	\(4\)	\(2\)	\(8\)
\(AB/ab\)	\(\frac{1}{2}\)	\(5+1=6\)	\(4+2=6\)	\(0\)	\(0\)	\(0\)
\(ab/ab\)	\(\frac{1}{4}\)	\(1+1=2\)	\(2+2=4\)	\(-4\)	\(-2\)	\(8\)
		\(\mu_1=6\)	\(\mu_2=6\)	\(\sigma^2_1=8\)	\(\sigma^2_2=2\)	\(\sigma_{12}=4\)

Arriba, Dif. 1 y Dif.2 representan las diferencias de los valores de cada genotipo respecto a las medias correspondientes de cada característica (que están en la última línea de la tabla, en la columna respectiva), mientras que Prod.1,2 se refiere al producto cruzado de esas diferencias.

Las varianzas de las características 1 y 2 y la covarianza entre ellas se calculan como de costumbre, es decir

\[{\sigma^2_1=\frac{1}{4}(4)^2+\frac{1}{2}(0)^2+\frac{1}{4}(-4)^2=4+0+4=8}\] \[{\sigma^2_2=\frac{1}{4}(2)^2+\frac{1}{2}(0)^2+\frac{1}{4}(-2)^2=1+0+1=2}\] \[{\sigma_{12}=\frac{1}{4}8+\frac{1}{2}0+\frac{1}{4}8=2+0+2=4}\]

De acuerdo a la definición del coeficiente de correlación, podemos calcularla a partir de los datos de la tabla de arriba como

\[ \begin{split} {r_{12}=\frac{\sigma_{12}}{\sqrt{\sigma^2_1\ \sigma^2_2}}=\frac{4}{\sqrt{8 \times 2}}=\frac{4}{\sqrt{16}}=\frac{4}{4}=1} \end{split} \]

Es decir, en este caso, la correlación genética (aditiva) entre las dos características es igual a 1. Como no hemos invocado ningún otro fenómeno, solo el ligamiento completo entre estos dos loci, pese a que hemos tomado valores arbitrarios para los alelos, la posibilidad de que el ligamiento sea causa de la correlación genética queda asentado.

En el caso de la correlación inducida por el desequilibrio de ligamiento, se trata de un fenómeno de carácter temporal; excepto en las regiones cromosómica que no poseen recombinación, en la medida de que discurra el tiempo, dependiendo de la tasa de recombinación, en algún momento se producirán dichos eventos de recombinación entre los loci y por lo tanto el fenómeno de ligamiento tenderá a desaparecer, como vimos en la sección La evolución en el tiempo del desequilibrio de ligamiento del capítulo Dinámica de 2 loci. De hecho, como vimos en dicha sección, la tasa de decaimiento del ligamiento es aproximadamente exponencial, ya que para una tasa de recombinación \(r\), el desequilibrio en el tiempo \(t\) (medido en generaciones) es igual a

\[ \begin{split} D_t=(1-r)^t D_0 \approx e^{-rt} D_0 \end{split} \]

Este comportamiento exponencial del decaimiento en el desequilibrio de ligamiento, ver Figura 5.4, lleva a que en unas pocas generaciones el efecto del mismo en la correlación genética prácticamente desaparezca.

El segundo fenómeno que puede explicar fácilmente la correlación genética entre dos características es la pleiotropía. Existen muchas definiciones de pleiotropía ya que el concepto ha ido cambiando con el tiempo, pero básicamente es el efecto que un locus produce en más de una característica fenotípica, sea esta entendida en el sentido tradicional o en el extendido que incluye, por ejemplo, la expresión génica (el transcriptoma). En la Figura 12.1 se ilustra el mecanismo básico de la pleiotropía. La línea horizontal a trazos separa lo que sería lo determinado a nivel genómico de lo que observamos a nivel fenotípico (en el sentido tradicional, pesos, alturas, colores, diámetros de características, cantidad de productos, porcentaje de materias, etc.), aunque esta distinción no se aplica a los fenotipos de expresión génica.

La característica fenotípica 1 se encuentra controlada desde el punto de vista genético por un solo gen, que es a su vez regulado por un regulador exclusivo para ese gen. Por lo tanto, desde el punto de vista genético no existe razón para que la pleiotropía induzca una correlación de la característica 1 con cualquiera de las otras. En cambio, mientras que la característica 2 está controlada desde el punto de vista genético por un solo gen, el gen 2 con su propio regulador, la característica 3 está gobernada por dos genes, el gen 2 y el gen 3. Esto hace que la expresión del gen 2 controle, al menos parcialmente, las dos características. Sin duda, es una buena razón para esperar que esta causa en común genere una correlación (de origen genético) en los datos fenotípicos observados. Por último, las características 4 y 5 están cada una de ellas gobernadas por un solo gen, distinto, por que podríamos pensar que no hay razón para que exista pleiotropía. Sin embargo, ambos genes, el gen 4 y el gen 5 comparten un mismo regulador (además de la posibilidad de que tengan otros reguladores), por lo que la expresión de ambos genes será una función del mismo regulador y por lo tanto tendrán expresiones correlacionadas, lo que a su vez, posiblemente induzca una correlación a nivel fenotípico.

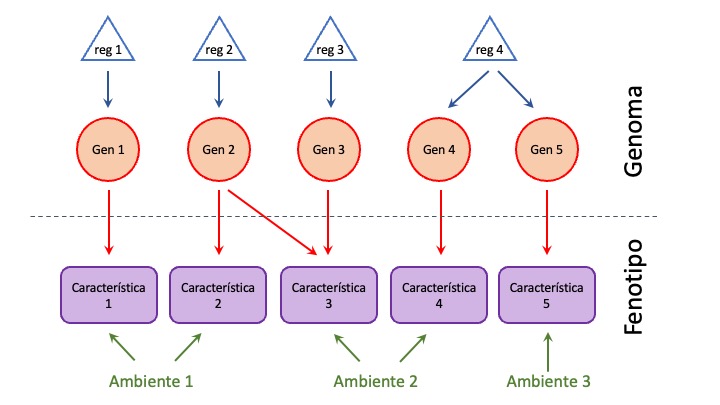
Figura 12.1: Ilustración de algunos mecanismos moleculares que generan pleiotropía. La característica 1 (“rectángulos” violetas) se encuentra controlada a nivel genético por un solo gen (círculos rojos), que es controlado a su vez por un regulador (triángulos azules) que no afecta ningún otro gen, por lo que su correlación genética con el resto de las características en el diagrama es cero. Las características fenotípicas 2 y 3 se encuentran al menos parcialmente controladas por el gen 2 (que tiene un solo regulador), por lo que este gen afecta simultaneamente la expresión de ambas características y es posible que aparezca una correlación genética. Finalmente, las características 4 y 5 se encuentran controladas a nivel genético por diferentes genes, pero ambos genes están regulados (posiblemente en forma parcial) por un solo regulador (el regulador 4), por lo que ambos genes tendrán expresiones correlacionadas y posiblemente se observe correlación entre las características fenotípicas. Los diferentes “ambientes” que influyen a las características pueden incidir en las correlaciones fenotípicas si son compartidos entre características, como por ejemplo el ambiente 1 y el ambiente 2.

Como hemos discutido previamente en otros capítulos, son raras las características de interés cuantitativas gobernadas por un solo gen y no demasiadas las que parecen gobernadas por unos pocos genes de efecto mayor. Esto lleva a una dificultad importante a la hora de identificar el mecanismo preciso a nivel molecular y estimar sus efectos: existen pocas características cuantitativas gobernadas por muy pocos genes, donde se podrían identificar en forma relativamente sencilla los mecanismos de las interacciones. La mayoría están gobernadas por muchos genes, donde por lo tanto resulta casi imposible determinar todas las posibles interacciones entre los mismos (reguladores, inhibidores, etc.) y mucho menos estimar sus efectos. Sin embargo, entre las correlaciones genéticas estudiadas hay muchas que son fuertes o moderadamente fuertes y que persisten a lo largo del tiempo, por lo que debemos suponer que existe un nivel importante de pleiotropía para las mismas.

Existen numerosos ejemplos de pleiotropía en características más cualitativas que cuantitativas (en muchos casos porque las mismas resultan difíciles de cuantificar, como por ejemplo con el grado de padecimiento de una enfermedad). Un ejemplo clásico de pleiotropía a nivel de enfermedades que se ven en humanos es la fenilcetonuria (también conocida como PKU), una alteración congénita del metabolismo causada por reducción o ausencia de la actividad en la enzima fenilalanina hidroxilasa. Esta última enzima es codificada por el gen PAH, localizado en el cromosoma 12 entre las bandas 12q22-q24.2 y tiene como cometido metabolizar el aminoácido fenilalanina (“Phe”), convirtiéndolo en otros metabolitos útiles para el cuerpo, es especial el aminoácido tirosina (“Tyr”). Se conocen más de 400 mutaciones en ese gen que producen una alteración en la capacidad metabólica del mismo, lo que lleva bajo una dieta normal a un incremento patológico en los niveles de fenilalanina. Estos niveles elevados de fenilalanina dañan el cerebro (usualmente en recién nacidos), provocando anormalidades en su funcionamiento, microencefalia, discapacidad intelectual, desórdenes de conducta, pero también otras manifestaciones físicas como decoloración de cabellos y piel, un olor muy particular y eccema. Claramente, el efecto genético de un gen (PAH) se manifiesta en diferentes características fenotípica, lo que es nuestra definición de pleiotropía. Afortunadamente, en nuestro país y en gran parte del mundo se les realiza a los recién nacidos un test que se conoce como despistaje de enfermedades metabólicas (y que en nuestro país incluye Hipotiroidismo congénito, Fenilcetonuria, Hiperplasia suprarrenal congénita y Fibrosis quística) por lo que detectada en forma temprana alcanza con un control estricto de la dieta para eliminar sus consecuencias.

Entre los animales domésticos se debate el rol que pudo (y puede haber tenido la pleiotropía) en los procesos de domesticación. De hecho, pese a que hemos domesticado a diferentes especies, de grupos tan distantes como las aves y los mamíferos, en general determinadas características se repiten cuando comparamos la especie domesticada con la correspondiente salvaje (mansedumbre, tolerancia al humano, menor curiosidad, menor tamaño de las glándulas suprarrenales, etc.). Sin duda que podemos apelar en algunos casos al ligamiento entre características y en algunos casos se han encontrado determinantes genéticos en el mismo entorno genómico, pero parece difícil de generalizar a todas las características. Sin embargo, por las dificultades que hemos mencionado previamente para identificar las bases moleculares de la pleiotropía en características cuantitativas, ha resultado una teoría con poco sustento (D. Wright (2015)).

Un ejemplo de pleiotropía en animales es el de la sordera en gatos blancos de ojos azules, donde el 40% de estos padecen la enfermedad. Una pista acerca de la base genética de esta enfermedad proviene de que los gatos con un ojo amarillo y el otro azul solo son sordos del lado del ojo azul. Se trata de una patología no exclusivamente observable en gatos, ya que por ejemplo, el síndrome de Waardenburg (SW) en humanos es un trastorno que se caracteriza por sordera (en grados variables) y en anomalías en la pigmentación de los ojos, cabello y piel (todas ellas estructuras derivadas de la cresta neural). Otro ejemplo de pleiotropía en animales domésticos es la que produce el gen “frizzle” en aves, por ejemplo la raza Kirin de gallinas. En efecto, mutaciones en este gen provocan un curvado hacia afuera de las plumas, en lugar de su disposición paralela al cuerpo original. Pero además de ese llamativo fenotipo, dicho gen también incrementa la temperatura corporal, aumenta la tasa metabólica y el flujo de sangre, además de incrementar la capacidad digestiva y disminuir la producción de huevos (Lobo (2008)).

Causas de las correlaciones ambientales

Muchas de las características fenotípicas de interés poseen, por varias razones, una base causal muy similar y que a veces subyace a varias características. Por ejemplo, todas aquellas características que aumentan su expresión con el tamaño de los animales tendrán una correlación derivada de esa base común. Resulta lógico que, dentro de la misma población y de la misma raza, ovejas más grandes (más pesadas) tiendan a producir una mayor superficie de cuero y un vellón mayor (más pesado) ya que tienen más superficie. Por lo tanto, para las características de superficie de cuero ovino y peso de vellón limpio esperamos una correlación fenotípica positiva. Pero, ¿cuál es la base causal de esta correlación? Como lo expresamos antes, la causa está en que, a una densidad de fibras determinada, la superficie se vincula directamente con el número de fibras totales. Si nos ponemos más finos en la búsqueda de las causas, podríamos pensar que el tamaño (volumen) de los animales influencia directamente la superficie, ya que las formas de las ovejas son bastante similares (hay pocas ovejas esféricas, mucho menos cúbicas y no conocemos reportes de ovejas cónicas) y por lo tanto, dentro de una misma raza y población las relación superficie/volumen es una función relativamente estable. De hecho, esta relación tiene que ver con el tamaño de los animales y con el clima donde viven, ya que el calor se genera proporcionalmente al volumen, mientras que se disipa en proporción al área. Como dato curioso, algunos osos que habitan en climas muy fríos son, desde este punto de vista casi “esféricos”, ya que la esfera es el cuerpo con menor relación superficie volumen.

Correlación ambiental entre dos características, medidas ambas en los mismos individuos, estrictamente es la correlación entre los desvíos ambientales que forman parte del valor fenotípico de cada individuo en ambas características. Usualmente, en la práctica se considera un ambiente extendido, que incluye además del ambiente propiamente dichos los desvíos genéticos no-aditivos.

Volvamos a nuestras ovejas. Por lo anterior, el tamaño de la oveja está determinando varias características fenotípicas que podemos medir. Lo mismo ocurre en vacas lecheras, donde el peso del animal se correlaciona con la producción de leche, grasa y proteína. Claramente, el tamaño de la vaca (a la misma raza y población) es un componente causal importante de todas estas características. A primera vista podríamos pensar que esta correlación es genética, ya que vacas más grandes y productivas producen crías más grandes y productivas. Sin embargo, un poquito de reflexión nos permite dudar de este argumento: el crecimiento de los animales depende de su alimentación también, es decir, animales mal alimentados no crecerán pese a tener el potencial. La alimentación la consideramos ambiente, por lo tanto el ambiente influencia también el tamaño, que de alguna manera determina las características productivas que nos interesa medir (producción de leche, grasa y proteína, por ejemplo). Desvíos positivos ambientales (producto de mejor alimentación que el promedio) en una característica, también (en este caso) lo serán en la otra, por lo que la correlación ambiental será positiva.

En ovinos, mejor alimentación suele producir vellones con mayor peso, pero al mismo tiempo incrementar el diámetro de la lana. En plantas, mejores suelos mejorarán varias características de rendimiento al mismo tiempo, por lo que si realizamos mediciones de pares de características en plantas obtenidas de un número de sustratos diferentes vamos a tener una correlación de origen ambiental importante. De hecho, esto sugiere un método para estimar dicha correlación en plantas clonales, ya que al ser idéntica la genética, toda la correlación fenotípica observada será producto de las diferencias en el ambiente.

PARA RECORDAR

• Llamaremos correlación fenotípica entre dos características, medidas ambas en los mismos individuos a la correlación entre los valores fenotípicos (observables) de cada individuo en ambas características.

• Llamaremos correlación genética (aditiva) entre dos características, medidas ambas en los mismos individuos a la correlación entre los valores de cría de cada individuo en ambas características.

• Desde el punto de vista genético existen dos causas aparentes para que exista corelación entre carácterísticas, ellas son la pleitropía y el ligamiento.

• En el caso del ligamiento, determinadas combinaciones de alelos (haplotipos) tienden a aparecer con mayor frecuencia de lo que sería esperable por azar si no estuviesen “ligados”. En este caso,si por ejemplo, dos loci se encuentran fuertemente “ligados” y cada uno de ellos controla (genes de efecto mayor) una característica diferente, entonces valores específicos en una característica estarán asociados a valores específicos en otra característica, lo que genera correlación.

• En el caso de la correlación inducida por el desequilibrio de ligamiento, se trata de un fenómeno de carácter temporal; excepto en las regiones cromosómica que no poseen recombinación, en la medida de que discurra el tiempo, dependiendo de la tasa de recombinación, en algún momento se producirán dichos eventos de recombinación entre los loci y por lo tanto el fenómeno de ligamiento tenderá a desaparecer.

• En el caso de la pleitropía, la misma se entiende como el efecto que un locus produce en más de una característica fenotípica, sea esta entendida en el sentido tradicional o en el extendido que incluye, por ejemplo, la expresión génica.

• Llamaremos correlación ambiental entre dos características, medidas ambas en los mismos individuos, a estrictamente la correlacción entre los desvíos ambientales que forman parte del valor fenotípico de cada individuo en ambas características. Usualmente, en la práctica se considera un ambiente extendido, que incluye además del ambiente propiamente dichos los desvíos genéticos no-aditivos.

12.2 Introducción al “path analysis”

En muchos casos podemos observar correlaciones entre variables (que por lo tanto son observables), pero sabemos que dichas correlaciones son producto de relaciones entre otras variables que las explican, pero que no son observables. De hecho, en muchos casos podemos establecer modelos claros con las relaciones entre las distintas variables, tanto las observables como las no-observables. El objetivo pasa a ser entonces entender y estimar los coeficientes del modelo. Con eso en mente, Sewall Wright (S. Wright (1918); Sewall Wright (1934b)) desarrolló el método conocido como de los coeficientes de paso (“path coefficients” en inglés).

La idea es sencilla, como se ilustra en la Figura 12.2. Supongamos que tenemos una serie de variables, representadas con letras mayúsculas en la figura. Tenemos dos tipos básicos de relaciones entre variables: a) las “causales”, que vamos a representar con flechas rectas y con una sola punta, que apuntan desde la variable que explica a la explicada y b) las “no-causales”, que representan asociación de algún tipo entre variables (posiblemente debido a una causa común, no modelada), que vamos a representar con flechas curvas de dos puntas. A las variables que no reciben ninguna flecha recta (es decir, que no son explicadas por otras en el modelo) se las conoce como exógenas, mientras que las que reciben alguna flecha recta se las conoce como endógenas. Las flechas rectas representan, en un modelo lineal, variables que explican la variable a la que apuntan y por lo tanto, cuando trabajamos con correlaciones entre variables (es decir, variables estandarizadas), los coeficientes correspondientes serán los coeficientes de regresión estandarizados. Las coeficientes correspondientes a las flechas curvas de dos puntas serán simplemente los coeficientes de correlación entre las dos variables, marcando una situación de simetría que no tienen las flechas rectas.

De hecho, al observar con atención la Figura 12.2 vemos que hay un “tercer tipo” de flecha, representadas en color verde, que son flechas rectas pero que no salen desde ninguna variable específica. Estas flechas se usan para representar la variación residual, es decir, la no explicada por el modelo. En ciertos casos estas flechas son omitidas de los diagramas, pero deben ser tenidas en cuenta a la hora de entender la varianza explicada por las distintas variables del modelo. En algunos casos, como veremos más adelante, el residuo se modela específicamente (por ejemplo, dentro del ambiente), por lo que este tipo de flechas no aparece en dichos diagramas.

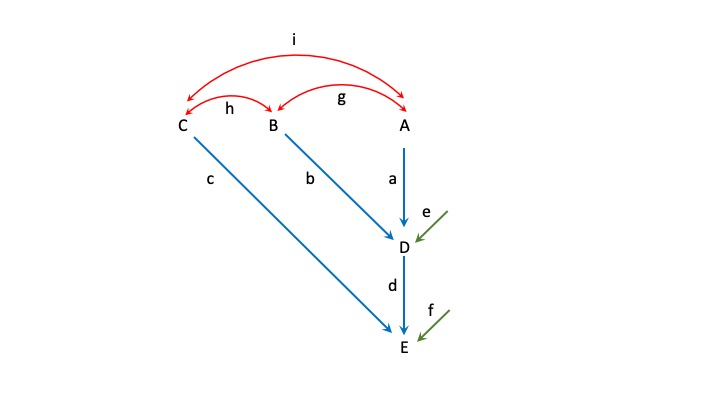
Figura 12.2: Ejemplo de un diagrama de caminos (o de paso), ilustrando las relaciones entre variables. Las líneas rectas con una sola flecha (marcadas en azul aquí para mayor claridad) representan relaciones “causales” entre variables, apuntando desde la que explica a la explicada, mientras que las flechas curvas con dos puntas (en rojo) explican asociaciones de correlación entre variables.

De acuerdo con Wright, si un diagrama de caminos está correctamente representado, entonces la correlación entre dos variables puede representarse como la suma de caminos compuestos, en los que para cada camino se multiplican los coeficientes que lo integran, que siguen tres reglas:

1. No hay bucles (es decir, no se puede pasar dos veces por la misma variable en un camino)

2. No se puede avanzar y luego retroceder (para una correlación solo se utilizan las causas comunes, no los efectos comunes)

3. Solo se admite un máximo de una flecha curva por trayectoria

Veamos algún ejemplo, utilizando la Figura 12.2 antes de pasar a la aplicación en genética que es de nuestro interés. La correlación entre \({A}\) y \({B}\) está determinada por el coeficiente correspondiente al único camino que cumple las tres reglas, es decir \({g}\). Lo mismo, para cualquiera de los pares de variables exógenas (\({A}\), \({B}\) y \({C}\)), con los coeficientes \({h}\) e \({i}\). Si queremos ahora calcular la correlación entre \({A}\) y \({D}\), que denotaremos como \({r_{AD}}\), tenemos un camino directo entre \({A}\) y \({D}\), con coeficiente \({a}\) y otro camino indirecto, desde \({A}\) hacia \({B}\) y luego hacia \({D}\), es decir, con coeficientes \(g\) y \(b\) (que deben multiplicarse). Sumando los dos caminos, tenemos entonces que

\[ \begin{split} {r_{AD}=a+b\cdot g} \end{split} \]

Pongámosle números a los coeficientes y veamos si podemos calcular alguna correlación más compleja. Supongamos que los coeficientes estimados (de alguna forma) son los siguientes: \(a=0,3\);\(b=0,1\);\(c=0,4\);\(d=0,2\);\(e=0,15\);\(f=0,25\);\(g=0,05\);\(h=0,05\);\(i=0,15\). Vamos a calcular la correlación esperada entre \({A}\) y \({E}\). De acuerdo a las tres reglas que vimos más arriba, los caminos posibles son: \({a\cdot d}\), \({g \cdot b \cdot d}\) y \({i\cdot c}\). Por lo tanto, la correlación buscada será

\[ \begin{split} {r_{AE}=a \cdot d + g \cdot b \cdot d + i\cdot c=0,3 \cdot 0,2 + 0,05 \cdot 0,1 \cdot 0,2 + 0,15 \cdot 0,40=0,121} \end{split} \]

La idea es bastante sencilla, aunque la estimación estadística de los coeficientes suele ser relativamente compleja y la especificación de los modelos muy importante. Al mismo tiempo que no deben faltar variables que sean relevantes, ya que sesgarían los estimados de los coeficientes, el agregar flechas innecesarias vuelve inestable las estimación de los coeficientes y por lo tanto representa modelos poco fiables a la hora de extraer conclusiones de los mismos. Existen muchos tratados sobre el tema, pero un excelente tratamiento del método y sus aplicaciones se encuentra en Loehlin and Beaujean (2017).

La relación entre las correlaciones fenotípica, genética y ambiental

La pregunta que se nos viene en mente es cómo se relaciona esto con la genética, y en particular con con la correlaciones fenotípicas, genéticas y ambientales que trataremos en este capítulo. Un excelente y extenso tratamiento del tema se puede ver en el libro Li (1955), que se recomienda como lectura suplementaria. Como vimos previamente en el capítulo El modelo genético básico, por lo general solo observamos los fenotipos de los individuos, no los diferentes efectos genéticos y ambientales. Pero como vimos antes también, la correlación que observamos entre dos características medidas en cada uno de los individuos de una población posee, en general, una base genética y una base ambiental. La tentación inicial sería entonces de suponer (en forma errónea) que la correlación fenotípica es la suma de las correlaciones genética y ambiental. Sin embargo, tenemos una situación un poco más compleja y para modelarla vamos a utilizar el método de los coeficientes de paso desarrollado por Sewall Wright.

Para simplicar nuestro modelo, supongamos que solamente vamos a modelar el fenotipo de cada característica como la suma de los efectos aditivos y el resto de los componentes, que llamaremos “ambiente”, pero que tiene también los componentes genéticos no-aditivos y los errores de medición. Es decir, si llamamos \({E^{*}}\) al ambiente propiamente dicho (más los errores de medición, entonces los fenotipos de las dos características que consideramos los modelamos como

\[ \begin{split} {P_1=A_1+E_1;\ E_1=D_1+I_1+E^{*}_1} \\ {P_2=A_2+E_2;\ E_2=D_2+I_2+E^{*}_2} \end{split} \tag{12.1} \]

En la Figura 12.3 podemos observar una representación del diagrama de paso que representa la relación entre las variables correspondientes a las dos características (por ejemplo, entre Peso de Vellón Limpio y Diámetro de Fibra, entre Peso al Destete y Peso a los 18 meses, etc.). De acuerdo a nuestro modelo especificado en las ecuaciones (12.1), no existe interacción entre genotipo y ambiente, por lo que estas variables (y los caminos que las conectan) serán independientes. La línea horizontal a trazos representa la separación entre lo observable y lo no observable. La flecha curva a trazos NO se especifíca normalmente en los diagramas ya que precisamente dicha correlación es la que el diagrama intenta explicar (con las otras variables); por dicha razón aparece representada a trazos y algo separada.

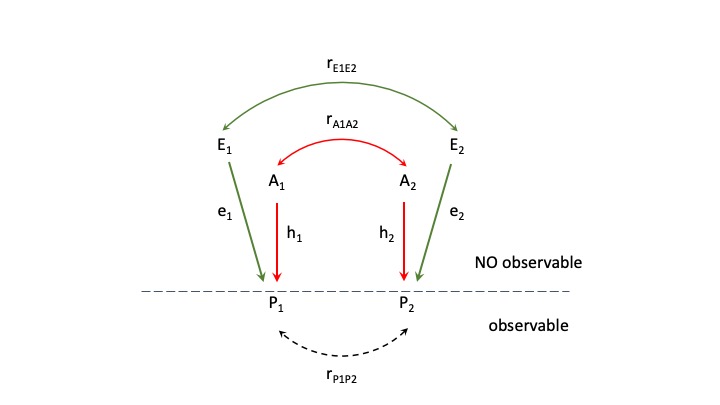
Figura 12.3: Método de los “coeficientes de paso” para determinar las relaciones entre los componentes causales de la correlación fenotípica entre dos características en el mismo individuo. La línea a trazos horizontal representa la separación entre lo observable y y lo no-observable. Formalmente, el diagrama de pasos no incluye la curva a trazos representando \({r_{P_{12}}}\) (la correlación fenotípica entre las variables). En este modelo el “ambiente” \({E}\) incluye todos los efectos excepto los genéticos aditivos, es decir \({E=I+D+E^{*}}\) (con \({E^{*}}\) el “ambiente” propiamente dicho, incluyendo los errores de medición).

Existen entonces dos caminos independientes que debemos sumar, el genético (aditivo) y el ambiental. Para ello necesitamos obtener los coeficientes asociados a cada uno de los pasos. Los coeficientes de las flechas curvas son precisamente las correlaciones genética y ambiental, que dependerán de cada característica y que aún no sabemos cómo estimar (lo veremos más adelante), pero que a los fines de esta sección (relación entre correlaciones) nos alcanza con dejar así. Por otra parte, si recordamos de más arriba que los coeficientes de las líneas rectas eran los coeficientes de regresión estandarizados, debemos entonces determinar su valor.

Primero procederemos con los coeficientes de paso que unen a las variables \({A_1 \rightarrow P_1}\) y \({A_2 \rightarrow P_2}\). De acuerdo a la definición de coeficiente de regresión estandarizado, \({\beta^{*}_{yx}=b_{yx}\frac{\sigma_x}{\sigma_y}}\), si el fenotipo es la variable dependiente y el valor de cría la independiente (es decir, la que explica parcialmente el fenotipo), el correspondiente coeficiente de regresión estandarizado sería

\[ \begin{split} {\beta^{*}_{PA}=b_{PA}\frac{\sigma_A}{\sigma_P}=\frac{Cov(A,P)}{\sigma^2_A}\frac{\sigma_A}{\sigma_P}=\frac{\sigma^2_A}{\sigma^2_A}\frac{\sigma_A}{\sigma_P}=\frac{\sigma_A}{\sigma_P}=h} \end{split} \tag{12.2} \]

Por lo tanto, el coeficiente de paso para \({A_1 \rightarrow P_1}\) será \({h_1}\) y el correspondiente a \({A_2 \rightarrow P_2}\) será \({h_2}\).

Es conocido (de los cursos previos de estadística) que la proporción de la varianza explicada por una variable en la regresión lineal es el coeficiente de regresión estandarizado elevado al cuadrado (conocido como \(R^2\), no confundir esta \(R\) con la respuesta a la selección para la que también usamos \({R}\), o con la repetibilidad, que en algunos textos también utilizan la misma letra), por lo que lo explicado por los efectos genéticos aditivos sería, para la característica 1, \({(h_1)^2=h^2_1}\), es decir la heredabilidad. Como hay solo dos variables independientes para cada fenotipo (lo genético-aditivo y el resto, ambiente más genética no-aditiva, incluyendo el error), entonces el otro componente debe explicar el resto de la varianza, es decir

\[ \begin{split} {(h_1)^2+(e_1)^2=1} \therefore {e^2_1=1-h^2_1 \therefore e_1=\sqrt{1-h^2_1}} \end{split} \tag{12.3} \]

De la misma manera, para la segunda característica

\[ \begin{split} {(h_2)^2+(e_2)^2=1} \therefore {e^2_2=1-h^2_2 \therefore e_2=\sqrt{1-h^2_2}} \end{split} \tag{12.4} \]

Aplicando la reglas de Wright, solo hay dos caminos posibles para explicar la correlación entre \({P_1}\) y \({P_2}\), el camino formado por \({h_1\ r_{A_{12}}\ h_2}\) y el camino formado por \({e_1\ r_{E_{12}}\ e_2}\) y por lo tanto debemos sumarlos. Por lo tanto (reordenando los términos en cada camino), la correlación fenotípica observada es igual a

\[ \begin{split} {r_{P_{12}}=h_1\cdot h_2\cdot r_{A_{12}}+e_1\cdot e_2\cdot r_{E_{12}}} \end{split} \tag{12.5} \]

Ejemplo 12.1

En las ovejas verdes se observa una correlación (fenotípica) entre el Peso al Año de edad (PA) y el Peso de Vellón Sucio (PVS) de \({r_P}=0,70\) (no vamos a usar los subíndices \(_{12}\) en las correlaciones para simplificar la notación). Las heredabilidades de ambas características fueron estimadas en \(h^2_{PA}=0,49\) y \(h^2_{PA}=0,36\). Por otra parte, un estudio reciente determinó que el mejor estimado de la correlación genética (aditiva) entre ambas características es de \({r_A}=0,55\). Estimar la correlación ambiental (en sentido amplio) y discutir los resultados.

De acuerdo a la ecuación (12.5), la relación entre las correlaciones fenotípica, genética (aditiva) y ambiental es

\[ \begin{split} {r_P=h_1\cdot h_2\cdot r_{A}+e_1\cdot e_2\cdot r_{E}} \end{split} \]

Por lo tanto, si despejamos la correlación ambiental, tenemos que

\[ \begin{split} {r_{E_{12}}=\frac{r_{P_{12}}-h_1\cdot h_2\cdot r_{A_{12}}}{e_1\cdot e_2}} \end{split} \]

Los coeficientes de paso genéticos se calculan directamente haciendo la raíz cuadrada de las correspondientes heredabilidades, es decir

\[ \begin{split} {h_{PA}=\sqrt{h^2_{PA}}=\sqrt{0,36}=0,6}\\ {h_{PVS}=\sqrt{h^2_{PVS}}=\sqrt{0,49}=0,7} \end{split} \]

Por otra parte, los coeficientes de paso ambientales se calculan utilizando los resultados de la ecuaciones (12.3) y (12.4)

\[ \begin{split} {e_{PA}=\sqrt{1-h^2_{PA}}=\sqrt{1-0,36}=\sqrt{0,64}=0,80} \\ {e_{PVS}=\sqrt{1-h^2_{PVS}}=\sqrt{1-0,49}=\sqrt{0,51} \approx 0,71} \end{split} \]

Ahora, poniendo estos valores en la ecuación para \({r_{E_{12}}}\), tenemos

\[ \begin{split} {r_{E}=\frac{r_{P}-h_{PA}\cdot h_{PVS}\cdot r_{A}}{e_{PA}\cdot e_{PVS}}=\frac{0,70-0,6 \cdot 0,7 \cdot 0,55}{0,80 \cdot 0,71} \approx 0,83} \end{split} \]

Por lo tanto, observamos que tanto la correlación fenotípica, como la genética (aditiva) y la ambiental son todas positivas y de carácter importante. La razón de la correlación genética entre las dos características consideradas es bastante esperable (dentro de la misma raza y población) ya que animales más pesados suelen ser más grandes y por lo tanto tener mayor superficie para generar lana. Se trata de una relación que estaría fundamentada, de alguna manera, en la pleiotropía, ya que los genes que regulan el crecimiento afectan a ambas características. Al mismo tiempo, la correlación ambiental también parece esperable, por similares razones a las de la correlación genética: animales que crecen más (por factores ambientales), van a producir medidas más altas en las dos características.

PARA RECORDAR

• Haciendo una introducción al “path analysis”, de acuerdo con Wright, si un diagrama de caminos está correctamente representado, entonces la correlación entre dos variables puede representarse como la suma de caminos compuestos, en los que para cada camino se multiplican los coeficientes que lo integran, que siguen tres reglas: 1) No hay bucles (es decir, no se puede pasar dos veces por la misma variable en un camino); 2) No se puede avanzar y luego retroceder (para una correlación solo se utilizan las causas comunes, no los efectos comunes); 3)Solo se admite un máximo de una flecha curva por trayectoria

• En el proceso de entender la relación entre las correlaciones fenotípica, genética y ambiental, supongamos que solamente vamos a modelar el fenotipo de cada característica como la suma de los efectos aditivos y el resto de los componentes (que llamaremos “ambiente”), pero que tiene también los componentes genéticos no-aditivos y los errores de medición. Es decir, si llamamos \(E^*\) al ambiente propiamente dicho (más los errores de medición, entonces los fenotipos de las dos características que consideramos los modelamos como: \({P_1=A_1+E_1;\ E_1=D_1+I_1+E^{*}_1} \\{P_2=A_2+E_2;\ E_2=D_2+I_2+E^{*}_2}\)

• Relacionando todas las variables, podemos decir que la correlación fenotípica observada es: \({r_{P_{12}}=h_1\cdot h_2\cdot r_{A_{12}}+e_1\cdot e_2\cdot r_{E_{12}}}\)

12.3 Métodos para determinar la correlación genética

Hasta acá hemos discutido acerca de los distintos tipos de correlaciones, fenotípica, genética (aditiva) y ambiental, sin preocuparnos demasiado en su determinación. De hecho, la correlación fenotípica se puede calcular directamente de las observaciones. Por otra parte, también vimos la relación entre las tres correlaciones, por lo que si contamos con dos de ellas y las heredabilidades también podemos estimar la faltante. Más aún, veremos más adelante como calcular la correlación genética a partir de la matriz de varianza-covarianza genética \(\mathbf{G}\), pero no discutimos cómo llegamos a la determinación de los elementos de la misma (las varianzas y covarianzas genéticas).

Históricamente, los métodos experimentales que se usaron para estimar la correlación genética fueron los mismos que se usaron para determinar las heredabilidades de las característícas. De hecho, con un mínimo de planificación, el mismo experimento permite obtener todas las estimaciones de interés. En la actualidad, la mayor parte de las estimaciones se realizan a través de modelos mixtos lineales en su forma multivariada, usando métodos iterativos sobre la versión multivariada del BLUP, propuesta inicialmente por C. R. Henderson and Quaas (1976) y que veremos en el capítulo Selección Artificial II.

De cualquier manera, simplemente como forma de comprender las bases de la estimación vamos a ver uno de los diseños experimentales posibles. La idea es obtener estimaciones a través de un diseño del tipo progenitor-progenie. Para eso vamos a medir las dos características en todas las parejas de progenitor-progenie. Vamos a llamar \({X}\) a los progenitores e \({Y}\) a las progenies, mientras que vamos a utilizar los subíndices \(1\) y \(2\) para las dos características.

De acuerdo con la notación anterior, vamos a obtener las siguientes 4 covarianzas:

• \({Cov_{X_{1}Y_{2}}}\) es la covarianza de la característica 1 en progenitor con la característica 2 en la progenie

• \({Cov_{X_{2}Y_{1}}}\) es la covarianza de la característica 1 en progenitor con la característica 2 en la progenie

• \({Cov_{X_{1}Y_{1}}}\) es la covarianza de la característica 1 en progenitor con la misma característica en la progenie

• \({Cov_{X_{1}Y_{1}}}\) es la covarianza de la característica 2 en progenitor con la misma característica en la progenie

La fórmula para las covarianzas observadas, para \(N\) parejas de progenitor progenie es

\[ \begin{split} {Cov_{XY}\frac{\sum XY-\frac{\sum X \sum Y}{N}}{N-1}} \end{split} \tag{12.6} \]

Desde el punto de vista causal, las covarianzas cruzadas (una característica en el progenitor y la otra, diferente, en la progenie) se pueden describir como

\[ \begin{split} {Cov_{X_{1}Y_{2}}=Cov_{X_{2}Y_{1}}=\frac{1}{2}Cov_{A_{12}}+\frac{1}{4}Cov_{AA_{12}}+...} \end{split} \tag{12.7} \]

es decir, un medio de la covarianza aditiva entre las características \(1\) y \(2\), un cuarto de la covarianza epistática del tipo \({A \times A}\), etc.

Por otro lado, como vimos en la sección Semejanza entre parientes, las covarianzas fenotípicas progenitor-progenie estiman un medio de varianza aditiva, por lo que

\[ \begin{split} {Cov_{X_{1}Y_{1}}=\frac{1}{2} V_{A_{1}}} \\ {Cov_{X_{2}Y_{2}}=\frac{1}{2} V_{A_{2}}} \end{split} \tag{12.8} \]

Por lo tanto, si despreciamos en la ecuación (12.7) los términos epistáticos, un estimador razonable de la correlación genética entre las dos características sería

\[ \begin{split} {\hat r_{A_{12}}=\frac{Cov_{X_{1}Y_{2}}+Cov_{X_{2}Y_{1}}}{2 \sqrt{Cov_{X_{1}Y_{1}}\cdot Cov_{X_{2}Y_{2}}}}} \end{split} \tag{12.9} \]

Siempre es importante recordar que se trata de un estimador del “verdadero” valor de un parámetro genético y por lo tanto, la estimación es función de una o más variables aleatorias, es decir, con incertidumbre asociada a la estimación. Aunque la derivación escapa el alcance de la presente sección (Robertson (1959); Tallis (1959)), un estimador aproximado del error estándar (\({EE()}\)) del estimador de la correlación genética es

\[ \begin{split} {EE(r_A) \approx (1-r^2_A)\sqrt{\frac{EE(h^2_1)\ EE(h^2_2)}{2\ h^2_1\ h^2_2}}} \end{split} \tag{12.10} \]

Un diseño alternativo es el de medios hermanos, donde un padre (de \(I\) disponibles) es apareado con varias (\(K\)) madres. Con el cambio de notación de que ahora \(X\) e \(Y\) representan las dos características de interés, de acuerdo al análisis de varianza-covarianza para este diseño, tenemos la siguiente tabla de las esperanzas de cuadrados medios y del producto medio:

Factor	g.l.	\({E[CM_X]}\)	\({E[CM_Y]}\)	\({E[PM_{XY}]}\)
Intergrupos	\(I−1\)	\(\sigma^2_{WX}+K\sigma^2_{BX}\)	\(\sigma^2_{WY}+K\sigma^2_{BY}\)	\(cov_W+Kcov_B\)
Error	\(I(K-1)\)	\(\sigma^2_{WX}\)	\(\sigma^2_{WY}\)	\(cov_W\)

A su vez, desde el punto de vista de los componentes causales, tenemos que

\[ \begin{split} \sigma^2_{BX}= {\frac{V_{A_{X}}}{4}} \\ \sigma^2_{BY}= {\frac{V_{A_{Y}}}{4}} \\ cov_B= {\frac{Cov_{A_{XY}}}{4}} \end{split} \tag{12.11} \]

Por lo tanto, de acuerdo a la definición del coeficiente de correlación genético aditiva, si dividimos la covarianza entre grupos de la ecuación (12.11) entre la raíz cuadrada del producto de las varianzas entre grupos, tenemos

\[ \begin{split} r_{A_{XY}}=\frac{cov_B}{\sigma_{BX}\ \sigma_{BY}}=\frac{\frac{Cov_{A_{XY}}}{4}}{\sqrt{\frac{V_{A_{X}}}{4}\frac{V_{A_{Y}}}{4}}}=\frac{Cov_{A_{XY}}}{\sigma_{A_{X}}\sigma_{A_{Y}}} \end{split} \tag{12.12} \]

que es el estimador de la correlación genética aditiva para este diseño de medio hermanos.

Un tratamiento mucho más detallado, así como diferentes estimados de correlaciones genéticas para diferentes características de interés productivo se encuentra en Cardellino and Rovira (1987). También, en la sección Respuesta correlacionada veremos un procedimiento sencillo para estimar la correlación genética entre dos características, basado en la medición simultanea de la respuesta directa y la respuesta correlacionada.

Ejemplo 12.2

La morfometría craneal en ovinos es un área de investigación en expansión. En un experimento para determinar la correlación genética entre el largo de la sutura frontal (Lsf) y el largo del hueso parietal (Lhp) en ovejas verdes, se midieron ambas variables en un conjunto de 100 cráneos, obtenidos de 50 parejas madre-hija.

Los resultados del experimento se pueden resumir de la siguiente manera

Covarianza	Valor
\(\textbf{Lsf}\text{ en la madre con }\textbf{Lhp}\text{ en hija}\)	\(0,33 \text{ cm}^2\)
\(\textbf{Lhp}\text{ en la madre con }\textbf{Lsf}\text{ en hija}\)	\(0,29 \text{ cm}^2\)
\(\textbf{Lsf}\text{ en la madre con }\textbf{Lsf}\text{ en hija}\)	\(0,36 \text{ cm}^2\)
\(\textbf{Lhp}\text{ en la madre con }\textbf{Lhp}\text{ en hija}\)	\(0,39 \text{ cm}^2\)

Estimar la covarianza genética entre el largo de la sutura frontal (Lsf) y el largo del hueso parietal (Lhp).

Utilizando la ecuación (12.9), tenemos que un estimador de la correlación genética a partir de estos datos esta dado por

\[ \begin{split} \hat r_{A_{12}}=\frac{Cov_{X_{1}Y_{2}}+Cov_{X_{2}Y_{1}}}{2 \sqrt{Cov_{X_{1}Y_{1}}\cdot Cov_{X_{2}Y_{2}}}} \end{split} \]

Sustituyendo los valores, tenemos que

\[ \begin{split} {\hat r_{A_{12}}=\frac{0,33 \text{ cm}^2 +0,29 \text{ cm}^2 }{2 \sqrt{0,36 \text{ cm}^2 \times 0,39 \text{ cm}^2}}}=0,8273 \end{split} \]

Es decir, una correlación positiva e importante entre ambas medidas craneales.

PARA RECORDAR

• Mediante un diseño de progenitor-progenie donde llamaremos \(X\) a los progenitores e \(Y\) a las progenies y utilizando los subíndices \(1\) y \(2\) para las dos características, un estimador razonable de la correlación genética entre ambas sería: \({\hat r_{A_{12}}=\frac{Cov_{X_{1}Y_{2}}+Cov_{X_{2}Y_{1}}}{2 \sqrt{Cov_{X_{1}Y_{1}}\cdot Cov_{X_{2}Y_{2}}}}}\)

• Al mismo tiempo, un estimador aproximado del error estándar del estimador de la correlación genética sería: \({EE(r_A) \approx (1-r^2_A)\sqrt{\frac{EE(h^2_1)\ EE(h^2_2)}{2\ h^2_1\ h^2_2}}}\)

• Si por otra parte utilizaramos un diseño de medios hermanos, el estimador de la correlación genética aditiva para ese diseño sería: \(r_{A_{XY}}=\frac{Cov_{A_{XY}}}{\sigma_{A_{X}}\sigma_{A_{Y}}}\)

12.4 La correlación fenotípica y su relación con otras correlaciones

Más arriba, en la sección [Introducción al “path analysis”], dedujimos la relación entre las correlaciones fenotípica, genética y ambiental usando esa herramienta poderosa. Ahora vamos a arribar al mismo resultado partiendo desde otra perspectiva y discutiremos algunas restricciones asociadas a la relación entre las tres correlaciones y las heredabilidades de las dos características.

Nuevamente, como hicimos antes, usaremos una versión simplificada de nuestro modelo genético básico, \({P=A+E}\), con \({E=D+I+E^{*}}\) y \({E^{*}}\) representando el ambiente propiamente dicho, más los errores de medición. La simplificación anterior significa que nuestro fenotipo ahora solo lo dividimos en el componente genético aditivo y el resto, que notamos como \({E}\) en este contexto, pero que comprende tanto lo ambiental como lo genético no-aditivo. De acuerdo con esto, a partir de las reglas que ya conocemos para las covarianzas y asumiendo que no existe co-variación entre el componente aditivo de un individuo y el ambiente (extendido) en el otro,

\[ \begin{split} {P=A+E}\\ {Cov(P_1,P_2)=Cov(A_1+E_1,A_2+E_2)=Cov(A_1,A_2)+Cov(E_1,E_2)} \end{split} \tag{12.13} \]

A su vez, a partir de la definición de coeficiente de correlación,

\[{r_{P_{12}}=\frac{Cov(P_1,P_2)} {\hat \sigma_{P_{1}}\ \hat \sigma_{P_{2}}} \iff Cov(P_1,P_2)= r_{P_{12}}\ \hat \sigma_{P_{1}}\ \hat \sigma_{P_{2}}}\] \[{r_{A_{12}}=\frac{Cov(A_1,A_2)} {\hat \sigma_{A_{1}}\ \hat \sigma_{A_{2}}} \iff Cov(A_1,A_2)= r_{A_{12}}\ \hat \sigma_{A_{1}}\ \hat \sigma_{A_{2}}}\] \[ \begin{split} {r_{E_{12}}=\frac{Cov(E_1,E_2)} {\hat \sigma_{E_{1}}\ \hat \sigma_{E_{2}}}} \iff {Cov(E_1,E_2)= r_{E_{12}}\ \hat \sigma_{E_{1}}\ \hat \sigma_{E_{2}}} \end{split} \tag{12.14} \]

Si asumimos que la heredabilidad representa la partición de la información que corresponde a los efectos aditivos, podemos definir un coeficiente de “ambientalidad” (que claramente no representa el ambiente, sino todo lo que no es heredable), que sumado a la heredabilidad debe dar 1 (el todo):

\[{h^2_1+e^2_1=1 \iff e^2_1=1-h^2_1 \iff e_1=\sqrt{1-h^2_1}}\] \[{h^2_2+e^2_2=1 \iff e^2_2=1-h^2_2 \iff e_2=\sqrt{1-h^2_2}}\] \[{h_1=\sqrt{h^2_1}=\sqrt{\frac{\sigma^{2}_{A_1}}{\sigma^{2}_{P_1}}}= \frac{\sigma_{A_1}}{\sigma_{P_1}}}\] \[{h_2=\sqrt{h^2_2}=\sqrt{\frac{\sigma^{2}_{A_2}}{\sigma^{2}_{P_2}}}= \frac{\sigma_{A_2}}{\sigma_{P_2}}}\] \[ \begin{split} {r_{P_{12}}=r_{A_{12}}\ h_1\ h_2\ + r_{E_{12}}\ e_1\ e_2} \end{split} \tag{12.15} \]

Ahora, sustituyendo las covarianzas en la parte de más arriba por su correspondiente producto del coeficiente de correlación multiplicado por los devíos estándar, tenemos

\[{Cov(P_1,P_2)=Cov(A_1,A_2)+Cov(E_1,E_2) \iff}\] \[{r_{P_{12}}\ \hat \sigma_{P_{1}}\ \hat \sigma_{P_{2}}= r_{A_{12}}\ \hat \sigma_{A_{1}}\ \hat \sigma_{A_{2}} + r_{E_{12}}\ \hat \sigma_{E_{1}}\ \hat \sigma_{E_{2}}}\] \[{r_{P_{12}}=\frac{r_{A_{12}}\ \hat \sigma_{A_{1}}\ \hat \sigma_{A_{2}} + r_{E_{12}}\ \hat \sigma_{E_{1}}\ \hat \sigma_{E_{2}}}{\hat \sigma_{P_{1}}\ \hat \sigma_{P_{2}}} =\frac{r_{A_{12}}\ \hat \sigma_{A_{1}}\ \hat \sigma_{A_{2}}}{\hat \sigma_{P_{1}}\ \hat \sigma_{P_{2}}} +\frac{r_{E_{12}}\ \hat \sigma_{E_{1}}\ \hat \sigma_{E_{2}}}{\hat \sigma_{P_{1}}\ \hat \sigma_{P_{2}}}}\] \[ \begin{split} {r_{P_{12}}=r_{A_{12}}\ \frac{\hat \sigma_{A_{1}}}{\hat \sigma_{P_{1}}}\ \frac{\hat \sigma_{A_{2}}}{\hat \sigma_{P_{2}}}\ + r_{E_{12}}\ \frac{\hat \sigma_{E_{1}}}{\hat \sigma_{P_{1}}}\ \frac{\hat \sigma_{E_{2}}}{\hat \sigma_{P_{2}}}} \end{split} \tag{12.16} \]

Lo que nos lleva, finalmente a la relación

\[ \begin{split} {r_{P_{12}}=r_{A_{12}}\ h_1\ h_2+ r_{E_{12}}\ e_1\ e_2} \end{split} \tag{12.17} \]

Claramente, la correlación fenotípica no solo depende de las correlaciones genética (aditiva) y ambiental (extendida), sino que también depende de las exactitudes de las dos características (o de sus heredabilidades). Cuanto mayores sean las heredabilidades, mayor será la influencia relativa de la correlación genética y viceversa para la ambiental.

Una perspectiva interesante de la correlación fenotípica es analizar el comportamiento de la respuesta en la ecuación (12.17) al variar alguno de los parámetros. Un problema mayor es que el número de parámetros a variar no es pequeño; tenemos dos correlaciones, más dos heredabilidades (o sus raíces cuadradas). Notar que tanto \(e_1\) como \(e_2\) no son parámetros independientes (se pueden calcular directamente a partir de \(h_1\) y \(h_2\). Sin embargo, a los efectos de analizar el impacto en la respuesta correlacionada, basta observar que más que el efecto individual de \(h_1\) y \(h_2\), lo que es importante observar es el producto de las mismas para el aporte de la correlación genética aditiva, mientras que para la correlación fenotípica, a partir de las heredabilidades, tenemos

\[ \begin{split} e_1=\sqrt{1-h^2_1}\ \text{y}\ e_2=\sqrt{1-h^2_2}\ \therefore \\ e_1 \cdot e_2 = \sqrt{1-h^2_1} \cdot \sqrt{1-h^2_2} = \sqrt{(1-h^2_1) \cdot (1-h^2_2)} \\ {e_1 \cdot e_2 = \sqrt{1-h^2_1-h^2_2+h^2_1 \cdot h^2_2}} \end{split} \tag{12.18} \]

Ahora, claramente no alcanza con una función que tome el producto de las heredabilidades para caracterizar el aporte de la correlación fenotípica. De hecho, para el mismo resultado del producto \({h^2_1 \cdot h^2_2}\), \({e_1 \cdot e_2}\) será menor cuanto mayor la diferencia entre \({h^2_1}\) y \({h^2_2}\). Sin pérdida de generalidad, solo para ilustrar el comportamiento de la correlación fenotípica respecto a la genética y la ambiental, asumiendo para simplificar que \({h^2_1 = h^2_2 = h^2}\), tenemos

\[ \begin{split} {\sqrt{(1-h^2_1) \cdot (1-h^2_2)} = \sqrt{1-2 \cdot h^2 + (h^2)^2}} \end{split} \tag{12.19} \]

Es decir, bajo el supuesto anterior, a partir del producto de las heredabilidades es posible analizar la correlación fenotípica como función de las correlaciones genética y ambiental. Los resultados de este análisis, para distintos valores del producto de heredabilidades se pueden observar en la Figura 12.4. Si llamamos

\[ \begin{split} {a = \sqrt{(h^2)^2} = h^2\ \text{y}\ b = \sqrt{1-2 \cdot h^2 + (h^2)^2}} \end{split} \tag{12.20} \]

entonces

\[ \begin{split} {r_{P_{12}} = a \cdot r_{A_{12}}\ + b \cdot r_{E_{12}}} \end{split} \tag{12.21} \]

O sea, dado el producto de las heredabilidades (bajo el supuesto de que provengan de iguales heredabilidades), la correlación fenotípica es una combinación lineal de las correlaciones genética y ambiental. Más aún, se trata de una combinación lineal aunque no se cumpla la igualdad de heredabilidades, solo que ahora

\[ \begin{split} {b=\sqrt{1-h^2_1-h^2_2+h^2_1 \cdot h^2_2}} \end{split} \tag{12.22} \]

y por lo tanto será en general menor que cuando son idénticas las heredabilidades. Para demostrar esto último, basta que se cumpla

\[ \begin{split} {\sqrt{1-h^2_1-h^2_2+h^2_1 \cdot h^2_2} \leq \sqrt{1-2 \cdot h^2 + (h^2)^2}} \end{split} \tag{12.23} \]

para lo que alcanza con que

\[{h^2_1+h^2_2 \geq 2 \cdot h^2\ \text{ya que}\ (h^2)^2 = h^2_1 \cdot h^2_2\ \therefore}\] \[{h^2_1+h^2_2 \geq 2 \cdot \sqrt{h^2_1 \cdot h^2_2} \iff (h^2_1+h^2_2)^2 \geq 4 \cdot h^2_1 \cdot h^2_2}\] \[{(h^2_1)^2 + 2 \cdot h^2_1 \cdot h^2_2 + (h^2_2)^2 \geq 4 \cdot h^2_1 \cdot h^2_2 \iff (h^2_1)^2 - 2 \cdot h^2_1 \cdot h^2_2 + (h^2_2)^2 \geq 0}\] \[ \begin{split} {\iff (h^2_1 - h^2_2)^2 \geq 0} \end{split} \tag{12.24} \]

El único caso donde el lado izquierdo de la última expresión se anula es cuando \({h^2_1=h^2_2}\), mientras que en el resto de los casos \({h^2_1+h^2_2 > 2 \cdot h^2}\). Por lo tanto, en el caso de que las heredabilidades no sean idénticas el aporte de la correlación ambiental será menor respecto a la genética (a un mismo valor del producto de las heredabilidades).

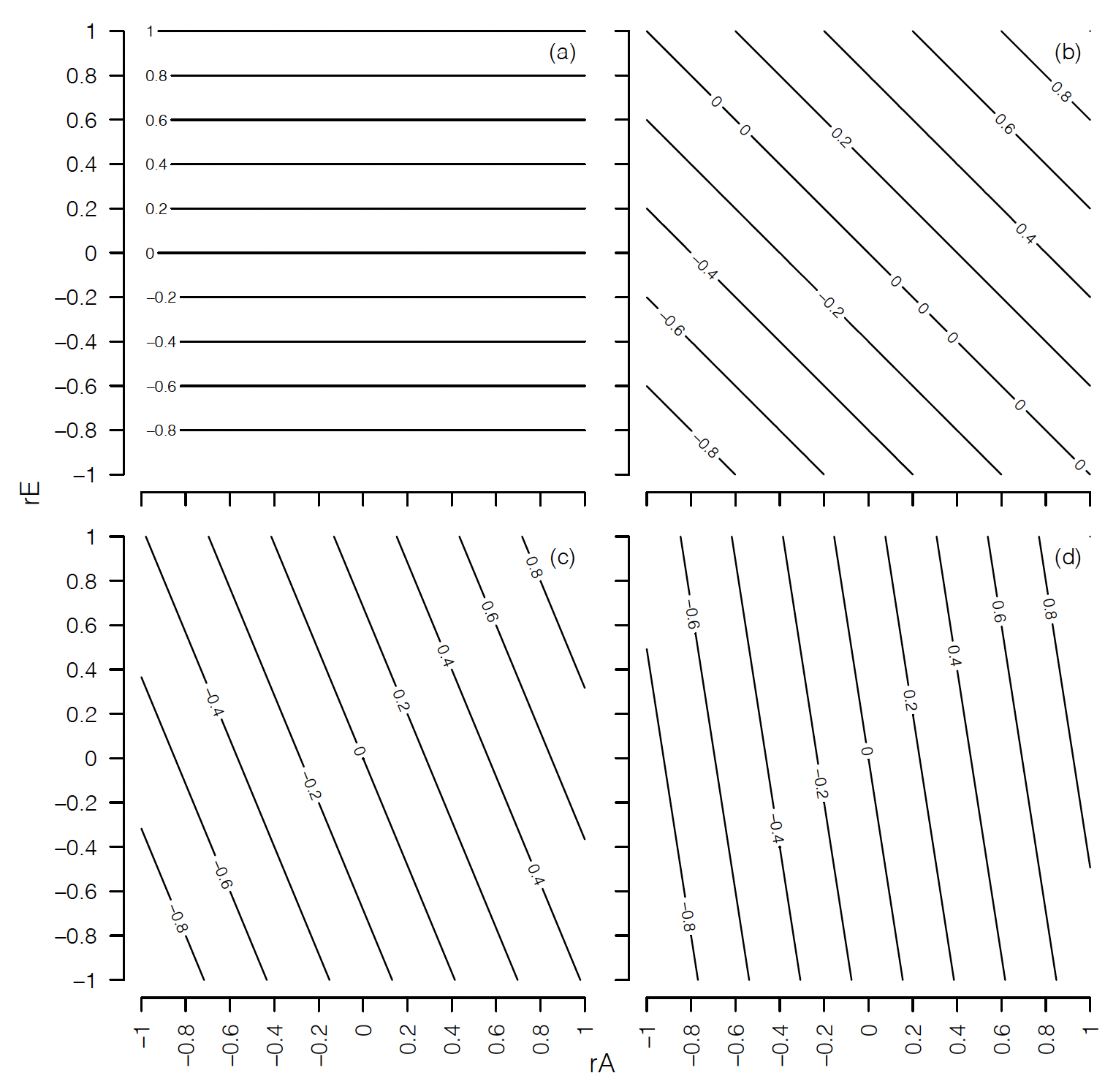
Figura 12.4: Correlaciones fenotípicas para distintas combinaciones de correlaciones genéticas (aditivas) y ambientales (a) \(h^2_1 * h^2_2 = 0\) , (b) \(h^2_1 * h^2_2 = 0.25\), (c) \(h^2_1 * h^2_2 = 0.50\), (d) \(h^2_1 * h^2_2 = 0.75\).

El comportamiento de la relación entre las correlaciones genética aditiva y ambiental con la correlación fenotípica se puede ver en la Figura 12.4, para distintos valores del producto de las heredabilidades (considerándolas iguales). En la misma, se aprecia claramente cómo al aumentar el producto de las heredabilidades (la varianza aditiva explica una mayor parte de la fenotípica), las curvas de nivel de correlación fenotípica pasan de la horizontalidad (\({r_{P_{12}}=r_{E_{12}}}\)) a gradualmente irse hacia la vertical (donde \({r_{P_{12}}=r_{A_{12}}}\)). Además, en la figura se observa claramente la relación lineal entre las tres correlaciones ya que cualquier curva de nivel (correlación fenotípica) se puede construir como combinación lineal de las otras dos correlaciones. Una discusión interesante de este tema se puede encontrar en Searle (1961).

Ejemplo 12.3

Dos características fenotípicas se encuentran correlacionadas a través de una correlación genética \(r_A\) y una correlación ambiental \(r_E\). Si las heredabilidades de las dos características son \(h^2_1=0,25\) y \(h^2_2=0,75\), ¿cuál es la relación entre el aporte de la correlación genética y la ambiental a la correlación fenotípica? ¿Cuáles son las ponderaciones de la correlación genética y de la correlación ambiental?

Si las heredabilidades fuesen \(h^2_1=0,40\) y \(h^2_2=0,60\), ¿cuál sería la relación? ¿Cuáles son ahora las ponderaciones de la correlación genética y de la correlación ambiental?

De acuerdo a la ecuación (12.17), el aporte de la correlación genética estará ponderado por \(h_1h_2=\sqrt{h^2_1h^2_2}\), mientras que el aporte de la correlación ambiental estará ponderado por \(\sqrt{1-h^2_1}\sqrt{1-h^2_2}\). La relación se aportes será entonces

\[ \begin{split} \mathrm{rel_{A/E}}=\frac{\sqrt{h^2_1h^2_2}}{\sqrt{1-h^2_1}\sqrt{1-h^2_2}}=\sqrt{\frac{h^2_1h^2_2}{(1-h^2_1)(1-h^2_2)}} \end{split} \]

En el caso de que \(h^2_1=0,25\) y \(h^2_2=0,75\), entonces lo anterior se transforma en

\[ \begin{split} \mathrm{rel_{A/E}}=\sqrt{\frac{0,25 \times 0,75}{(1-0,25)(1-0,75)}}=\sqrt{\frac{0,25 \times 0,75}{0,75 \times 0,25}}=\sqrt{1}=1 \end{split} \]

En este caso el peso de la correlación genética aditiva y de la correlación ambiental será igual en su contribución a la correlación fenotípica. La ponderación para la correlación genética será \(\sqrt{h^2_1h^2_2}=\sqrt{0,25 \times 0,75}=0,433\), mientras que la ponderación para la correlación ambiental será de \(\sqrt{1-h^2_1}\sqrt{1-h^2_2}=\sqrt{0,75}\sqrt{0,25}=\sqrt{0,25 \times 0,75}=0,433\) (obviamente, ya que \(\mathrm{rel_{A/E}}=1\)).

En el segundo caso, sustituyendo \(h^2_1=0,40\) y \(h^2_2=0,60\), tenemos

\[ \begin{split} \mathrm{rel_{A/E}}=\sqrt{\frac{0,40 \times 0,60}{(1-0,40)(1-0,60)}}=\sqrt{\frac{0,40 \times 0,60}{0,60 \times 0,40}}=\sqrt{1}=1 \end{split} \]

mientras que las ponderaciones de la contribución genética y ambiental serán \(\sqrt{h^2_1h^2_2}=\sqrt{0,40 \times 0,60}=0,49\) (ambas son iguales porque \(\mathrm{rel_{A/E}}=1\)).

En general, para que las ponderaciones de lo genético y lo ambiental sean iguales alcanza con que

\[\mathrm{rel_{A/E}}=\sqrt{\frac{h^2_1h^2_2}{(1-h^2_1)(1-h^2_2)}}=1 \Leftrightarrow h^2_1h^2_2=(1-h^2_1)(1-h^2_2)\Leftrightarrow\] \[\Leftrightarrow h^2_1h^2_2=1-h^2_1-h^2_2+h^2_1h^2_2 \Leftrightarrow 1-h^2_1-h^2_2=0 \Leftrightarrow h^2_1+h^2_2=1 \Leftrightarrow\] \[\Leftrightarrow h^2_1=1-h^2_2\]

es decir, siempre que la suma de heredabilidades sea igual a 1.

PARA RECORDAR

• Retomando la relación entre las correlaciones fenotípica, genética aditiva y ambiental a través de la sigueiente expresión: \({r_{P_{12}}=r_{A_{12}}\ h_1\ h_2+ r_{E_{12}}\ e_1\ e_2}\), podemos notar que la correlación fenotípica no solo depende de las correlaciones genética (aditiva) y ambiental (extendida), sino que también depende de las exactitudes de las dos características (o de sus heredabilidades). Es decir, cuanto mayores sean las heredabilidades, mayor será la influencia relativa de la correlación genética y viceversa para la ambiental.

• A su vez, a un mismo valor del producto \({h^2_1 \cdot h^2_2}\), \({e_1 \cdot e_2}\) será menor cuanto mayor la diferencia entre \({h^2_1}\) y \({h^2_2}\).

12.5 Respuesta correlacionada

Hasta ahora hemos venido trabajando las correlaciones entre características desde el punto de vista de la observación de sus efectos y de las relaciones entre ellas (fenotípica, genética y ambiental). Sin embargo, desde el punto de vista del mejoramiento genético es fundamental entender lo que sucede con las características que están correlacionadas desde el punto de vista genético con las características por las que realizamos la selección. Es decir, si dos características se encuentran correlacionadas genéticamente, al realizar selección en una de ellas, también estaremos desplazando la media de la otra característica, a pesar de no haber realizado ninguna selección en forma explícita en ella.

Para analizar cómo la selección en una característica afecta a las características correlacionadas genéticamente vamos a suponer que tenemos dos características, una que llamaremos \({X}\) y sobre la que realizaremos la selección y una segunda característica \({Y}\), que se encuentra correlacionada con la primera (notar el cambio de notación que hicimos, ya que en lugar de llamarlas \(1\) y \(2\) vamos a usar las tradicionales \({X}\) e \({Y}\)).

Como vimos antes, la respuesta en la característica bajo selección, \({X}\) en nuestro caso, es equivalente al valor reproductivo medio de los individuos seleccionados (porque es lo que se transmite completamente). Al mismo tiempo, el cambio que ocurrirá en \({Y}\), es decir la respuesta, lo podemos plantear entonces como la regresión de los valores reproductivos de \({Y}\) en \({X}\). El coeficiente de esta regresión sería por lo tanto

\[ \begin{split} { b_{A_{YX}}=\frac{Cov_{A}(X,Y)}{\sigma^2_{A_{X}}}} \end{split} \tag{12.25} \]

Pero de la ecuación (12.14) sabemos que la relación entre la covarianza genética (aditiva) y su correspondientes coeficiente de correlación nos permite escribirla como

\[ \begin{split} {r_{A_{XY}}=\frac{Cov_{A}(X,Y)}{\sigma_{A_{X}}\sigma_{A_{Y}}} \therefore Cov_{A}(X,Y)=r_{A_{XY}} \sigma_{A_{X}}\sigma_{A_{Y}}} \end{split} \tag{12.26} \]

por lo que, sustituyendo este último resultado en la ecuación (12.25), tenemos que el coeficiente de regresión es igual a

\[ \begin{split} {b_{A_{YX}}=\frac{r_{A_{XY}} \sigma_{A_{X}}\sigma_{A_{Y}}}{\sigma^2_{A_{X}}}=r_{A_{XY}}\frac{\sigma_{A_{Y}}}{\sigma_{A_{X}}}} \end{split} \tag{12.27} \]

Como vimos en el capítulo Selección Artificial I, la respuesta a la selección (en una generación realizando selección individual) para la característica \({X}\) la podemos escribir como

\[ \begin{split} {R_X=i_X\ h_X\ \sigma_{A_{X}}} \end{split} \tag{12.28} \]

Por lo tanto, la respuesta correlacionada en la característíca \({Y}\) es

\[ \begin{split} {RC_Y=b_{A_{YX}}\ R_X=b_{A_{YX}}\ i_X\ h_x\ \sigma_{A_{X}}=}\\ {=r_{A_{XY}}\frac{\sigma_{A_{Y}}}{\sigma_{A_{X}}} \ i_X\ h_X\ \sigma_{A_{X}} \therefore}\\ {RC_Y=i_X\ h_X\ r_{A_{XY}}\ \sigma_{A_{Y}}} \end{split} \tag{12.29} \]

El resultado de la ecuación anterior es intuitivo y fácil de interpretar. El cambio que vamos a esperar en la característica \({Y}\) cuando se realiza selección en la característica \({X}\) es igual a la intensidad de selección (en \({X}\)) multiplicada por el desvío estándar aditivo de la característica \({Y}\) (que es la que estamos observando y que, además, debe tener las unidades de la respuesta) y por un “coeficiente de paso” formado por \({h_X\ r_{A_{XY}}}\). Si observamos nuevamente la Figura 12.3, vemos que \({A_2}\) (que actúa con efecto \({h_2}\) sobre \({P_2}\)) podría ser sustituida por \({h_1\ r_{A_{12}}}\) (la correlación entre \({A_2}\) y \({P_1}\)). Cambiando \(1\) por \({X}\) y \(2\) por \({Y}\), se entiende perfectamente el rol que juega el producto \({h_X\ r_{A_{XY}}}\) en lugar de \({h_Y}\).

Finalmente, si tenemos en cuenta que \({h_Y=\frac{\sigma_{A_{Y}}}{\sigma_{P_{Y}}}}\) y que por lo tanto \({\sigma_{A_{Y}}=h_Y\ \sigma_{P_{Y}}}\), una forma alternativa de escribir la ecuación (12.29) es

\[ \begin{split} RC_Y=i_X\ h_X\ r_{A_{XY}}\ \sigma_{A_{Y}}=i_X\ h_X\ r_{A_{XY}}\ h_Y\ \sigma_{P_{Y}} \end{split} \tag{12.30} \]

que en lugar de depender del desvío aditivo de la característica, depende ahora del desvío fenotípico de la misma.

De hecho, estas últimas ecuaciones sugieren un método para estimar la correlación genética entre las dos características. La idea es sencilla: separamos la población en dos grupos, uno sobre el que vamos a realizar selección directa en la característica \({X}\) y el otro sobre el que vamos a realizar selección directa sobre la característica \({Y}\). En ambos grupos realizamos la misma presión de selección, por lo que \({i_X=i_Y=i}\) y en ambos vamos a medir la respuesta a la selección en ambas características, la seleccionada directamente y la correlacionada. El cociente entre selección directa e indirecta para la característica \({X}\) es igual a

\[ \begin{split} {\frac{RC_X}{R_X}=\frac{i_Y\ h_Y\ r_{A_{XY}}\ \sigma_{A_{X}}}{i_X\ h_X\ \sigma_{A_{X}}}=\frac{h_Y}{h_X}\ r_{A_{XY}}} \end{split} \tag{12.31} \]

mientras que para la característica \({Y}\) es igual a

\[ \begin{split} {\frac{RC_Y}{R_Y}=\frac{i_X\ h_X\ r_{A_{XY}}\ \sigma_{A_{Y}}}{i_Y\ h_Y\ \sigma_{A_{Y}}}=\frac{h_X}{h_Y}\ r_{A_{XY}}} \end{split} \tag{12.32} \]

Ahora, si multiplicamos los resultados de las ecuaciones (12.31) y (12.32), tenemos que

\[ \begin{split} {\frac{RC_X}{R_X}\frac{RC_Y}{R_Y}=\frac{h_Y}{h_X}\ r_{A_{XY}} \frac{h_X}{h_Y}\ r_{A_{XY}}=\frac{h_Y}{h_X} \frac{h_X}{h_Y}\ (r_{A_{XY}})^2 \therefore}\\ {r^2_{A_{XY}}=\frac{RC_X}{R_X}\frac{RC_Y}{R_Y}} \end{split} \tag{12.33} \]

que es un buen estimador de la correlación genética (aditiva) entre las dos características, siempre y cuando las respuestas recíprocas coincidan, de acuerdo a lo esperado por la teoría.

Ejemplo 12.4

La oveja galesa de montaña Balwen (Balwen Welsh Mountain), Figura 12.5, es una raza que se cría especialmente para carne. A fin de definir estrategias para mejorar su producción de lana, para estimar la correlación genética entre peso de vellón sucio (PVS) y peso de vellón limpio (PVL) se realizó un experimento de selección directa y selección indirecta para ambas características, donde se obtuvieron las siguiente respuestas en una generación:

Característica.Seleccionada	Característica..de.Interés	Tipo	Valor
\(\text{PVL}\)	\(\textbf{PVL}\)	\(\text{Directa}\)	\(0,113 \text{ kg}\)
\(\text{PVS}\)	\(\textbf{PVS}\)	\(\text{Directa}\)	\(0,101 \text{ kg}\)
\(\text{PVS}\)	\(\textbf{PVL}\)	\(\text{Indirecta}\)	\(0,084 \text{ kg}\)
\(\text{PVL}\)	\(\textbf{PVS}\)	\(\text{Indirecta}\)	\(0,082 \text{ kg}\)

Estimar la correlación genética (aditiva) entre ambas características.

Figura 12.5: La oveja galesa de montaña Balwen (Balwen Welsh Mountain) es originaria del valle de Tywi, en Gales y es una de las variedades criadas esencialmente para la producción de carne. Tiene un patrón de color característico, con el cuerpo negro y las extremidades blancas. (By Mick Lobb, CC BY-SA 2.0, https://commons.wikimedia.org/w/index.php?curid=14555593).

Utilizando la ecuación (12.33), tenemos que un estimador de la correlación genética (aditiva) a partir de experimentos de este tipo está dada por

\[ \begin{split} r^2_{A_{XY}}=\frac{RC_X}{R_X}\frac{RC_Y}{R_Y} \end{split} \]

Sustituyendo los valores que tenemos en la tabla, si llamamos \(X\) a PVL e \(Y\) a PVS, tenemos entonces que

\[ \begin{split} r^2_{A_{XY}}=\frac{0,084\text{ kg}}{0,113\text{ kg}}\frac{0,082\text{ kg}}{0,101\text{ kg}}=0,6035\\ r_{A_{XY}}=\sqrt{r^2_{A_{XY}}}=\sqrt{0,6035}=0,7769 \end{split} \]

que es una correlación genética positiva y mediana

PARA RECORDAR

• Para analizar cómo la selección en una característica afecta a las características correlacionadas genéticamente vamos a suponer que tenemos dos características, una que llamaremos \(X\) y sobre la que realizaremos la selección y una segunda característica \(Y\), que se encuentra correlacionada con la primera.

• Podemos plantear el cambio que ocurrirá en \(Y\), es decir la respuesta, como la regresión de los valores reproductivos de \(Y\) en \(X\). El coeficiente de esta regresión sería: \({b_{A_{YX}}=\frac{Cov_{A}(X,Y)}{\sigma^2_{A_{X}}}}=r_{A_{XY}}\frac{\sigma_{A_{Y}}}{\sigma_{A_{X}}}\)

• La respuesta correlacionada en la característica \(Y\) es: \({RC_Y=i_X\ h_X\ r_{A_{XY}}\ \sigma_{A_{Y}}}\). Según esto, el cambio que vamos a esperar en la característica \(Y\) cuando se realiza selección en la característica \({X}\) es igual a la intensidad de selección (en \({X}\)) multiplicada por el desvío estándar aditivo de la característica \({Y}\) (que es la que estamos observando y que, además, debe tener las unidades de la respuesta) y por un “coeficiente de paso” formado por \({h_X\ r_{A_{XY}}}\). Alternativamente podemos escribir esta expresión como \({RC_Y=i_X\ h_X\ r_{A_{XY}}\ h_Y\ \sigma_{P_{Y}}}\) que en lugar de depender del desvío aditivo de la característica, depende ahora del desvío fenotípico de la misma.

Eficiencia en relación a la selección directa

Los resultados obtenidos respecto al cambio de la media (respuesta, progreso genético generacional) en una característica cuando se selecciona por otra sugiere la posibilidad de hacer selección indirecta, es decir usar criterios de una característica (su fenotipo, intensidad de selección, etc.) para mejorar otra, la de nuestro interés.

Supongamos que queremos mejorar la característica \({Y}\) y estamos analizando la posibilidad de hacerlo directamente, o como alternativa, utilizar la información de la característica \({X}\) y realizar selección indirecta. Como vimos en la ecuación (12.32), el cociente entre los dos tipos de selección, indirecta en el numerador, directa en el denominador, es igual a

\[ \begin{split} {\frac{RC_Y}{R_Y}=\frac{i_X\ h_X\ r_{A_{XY}}\ \sigma_{A_{Y}}}{i_Y\ h_Y\ \sigma_{A_{Y}}}=\frac{i_X}{i_Y} \frac{h_X}{h_Y}\ r_{A_{XY}}} \end{split} \tag{12.34} \]

En general, cuando por razones de manejo de la población (rodeo, majada, piara, etc.) debemos retener una determinada proporción de animales como reproductores, la misma proporción será retenida más allá del criterio o característica por la que realicemos la selección. Más aún, si las dos características \({X}\) e \({Y}\) poseen distribución normal, como vimos previamente en la sección Intensidad de selección y proporción seleccionada, la intensidad de selección es una función de la proporción \({p}\) seleccionada (\({i=\frac{z}{p}}\)) y por lo tanto, \({i_X=i_Y}\). En ese caso, la ecuación (12.34) se transforma en

\[ \begin{split} {\frac{RC_Y}{R_Y}=\frac{h_X}{h_Y}\ r_{A_{XY}}} \end{split} \tag{12.35} \]

lo que es una expresión muy sencilla de evaluar. Para que nos convenga el método de selección indirecta, el cociente \({\frac{RC_Y}{R_Y}}\) debe ser mayor a \(1\). Por lo tanto, aplicando este criterio en la ecuación (12.35) tenemos que la condición puede expresarse como

\[ \begin{split} {\frac{h_X}{h_Y}\ r_{A_{XY}} > 1 \Leftrightarrow r_{A_{XY}} > \frac{h_Y}{h_X}} \end{split} \tag{12.36} \]

Dicho de otra forma, para que nos convenga utilizar selección indirecta (usando información de \({X}\) para seleccionar en \({Y}\)), la correlación aditiva entre las características debe ser mayor que la relación entre las precisiones \({\frac{h_Y}{h_X}}\). Cuanto mayor sea la precisión para selección fenotípica individual en la característica indirecta (\({h_X}\)), menor será el cociente \({\frac{h_Y}{h_X}}\) y mayor la probabilidad de que \({r_{A_{XY}}}\) lo supere. Entendido todo esto, igualmente es necesario comprender que los principales motivos para realizar selección indirecta no se basan en estos conceptos, sino que la facilicidad y el bajo costo de medición de la característica correlacionada respecto a la de interés son lo que usualmente motiva la aplicación de este tipo de selección.

La ecuación (12.36) también puede arreglarse de forma tal que la condición quede expresada como \({h_X\ r_{A_{XY}} >h_Y}\), es decir, que el producto de la precisión en la característica indirecta por la correlación genética sea mayor que la precisión directa. Es decir, en términos cualitativos, se debe cumplir que la precisión de la indirecta sea alta respecto a la directa, así como la correlación genética también sea relativamente alta. En general esto se aplica a condiciones donde la heredabilidad de la característica de interés es muy baja y que al mismo tiempo sea posible encontrar una característica fuertemente correlacionada a nivel genético con la de interés y que posea una heredabilidad razonable. Las características difíciles de medir poseen en general una baja heredabilidad, producto de que el error de medición constituye una parte importante de la varianza fenotípica, por lo que la heredabilidad (la fracción de varianza aditiva) resulta reducida.

Un problema en el que la selección indirecta (a través de la respuesta correlacionada) es de gran utilidad, es el de aquellas características que se expresan solamente en un sexo, pero que tienen alguna característica fuertemente correlacionada desde el punto de vista genético. Eso permitiría utilizar la selección por la característica directa en el sexo donde la característica de interés se expresa (a menos que la indirecta sea también más eficiente) y utilizar la selección indirecta en el otro sexo, mejorando de esta forma la intensidad de selección.

Finalmente, otro uso de las correlaciones genéticas tiene que ver con la interacción entre genotipo y ambiente. Como vimos antes, el valor de cría de los individuos es una función de la heredabilidad de la característica y la misma se refiere a una determinada población en determinadas condiciones. Más aún, la existencia de interacción entre genotipo y ambiente hace que las diferencias esperadas entre individuos sea una función del ambiente. Por ejemplo, no podemos pretender que las diferencias en producción de leche de vacas Holando de alta producción sea la misma en sistemas estabulados en climas templados que en la producción pastoril en los trópicos. Por lo tanto, si bien la producción de leche parece ser la misma característica, es dudoso que las mismas combinaciones de expresión génica estén actuando en los dos ambientes, por lo que no suena insensato considerarlas (en términos operativos) como dos características diferentes. En este sentido, las producciones en los dos ambientes serían consideradas como dos características diferentes y que por lo tanto, se les pueden calcular las correlaciones fenotípica, aditiva y ambiental. A partir de esto, será posible predecir el comportamiento esperado de un animal con información en un ambiente en el otro ambiente.

Ejemplo 12.5

En una población de ganado de la raza Braunvieh el peso al destete (PD) tiene una heredabilidad de \(h^2_{PD}= 0,36\), mientras el peso a los 18 meses (P18) tiene una heredabilidad de \(h^2_P18=0,25\). Suponiendo que los animales se aparean por primera vez a los 2 años y que la característica que nos interesa mejorar es P18, teniendo en cuenta que la correlación genética (aditiva) entre PD y P18 es de \(r_A=0,5\), ¿seleccionaríamos en forma directa por peso a los 18 meses o indirectamente por peso al destete para mejorar P18?

Si la intensidad de selección es la misma en las dos características (como sería el caso), de acuerdo a la ecuación (12.35), utilizando \(RC\) para la respuesta correlacionada en \(Y\) al seleccionar por \(X\) y \(RD\) para la respuesta a la selección directa,tenemos que

\[ \begin{split} {\frac{RC}{RD}=\frac{h_X}{h_Y}\ r_{A_{XY}}} \end{split} \]

En nuestro caso \(Y\) es el peso a los 18 meses, mientras que \(X\) es PD, por lo que poniéndole números

\[ \begin{split} RC/RD = \frac{0,5 \times\sqrt{0,36}}{\sqrt{0,25}}=\frac{0,5 \times 0,6}{0,5}=0,6 \end{split} \]

Por lo tanto, es preferible seleccionar directamente para mejorar P18. La razón de esto es que las heredabilidades no son muy distintas (por lo que la raíz de su relación no es mucho mayor a uno), sumado a que la correlación genética aditiva es intermedia.

PARA RECORDAR

• Cuando por razones de manejo de la población debemos retener una determinada proporción de animales como reproductores, la misma proporción será retenida más allá del criterio o característica por la que realicemos la selección. Más aún, si las dos características \({X}\) e \({Y}\) poseen distribución normal, la intensidad de selección será \(i_X=i_Y\). En ese caso, podemos determinar que \({\frac{RC_Y}{R_Y}=\frac{h_X}{h_Y}\ r_{A_{XY}}}\)

• Dicho esto, para evaluar que método de selección nos conviene aplicar, basta una simple observación de los resultados: si el cociente \(\frac{RC_Y}{R_Y}\) es mayor a 1, nos será más conveniente realizar selección indirecta. Dicho de otra forma, la correlación aditiva entre las características debe ser mayor que la relación entre las precisiones \(\frac{h_X}{h_Y}\).

• Como norma general, las características difíciles de medir poseen en general una baja heredabilidad, producto de que el error de medición constituye una parte importante de la varianza fenotípica, por lo que la heredabilidad (la fracción de varianza aditiva) resulta reducida.

• Más allá de estas relaciones matemáticas, la selcción indirecta es funamental en los casos en los que las carácterísticas se expresan sólo en un sexo, son costosas o muy difíciles de medir.

El signo de la correlación y el beneficio-demérito de la misma

Un detalle a considerar en nuestras disquisiciones anteriores sobre el mérito relativo de la selección indirecta es el del signo de la correlación genética. Si la correlación es fuertemente negativa, pongamos por ejemplo \({r_{A_{XY}}=-1}\), sustituyendo ese valor en la ecuación (12.36) tendríamos que \({-1 > \frac{h_Y}{h_X} \Leftrightarrow \frac{h_Y}{h_X}< -1}\), lo que claramente es imposible para cualquier valor de \({h_Y}\) y \({h_X}\) ya que los mismos deben ser positivos (son las raíces cuadradas de heredabilidades).

Dicho de otra forma, pese a que existe una asociación perfecta entre variables, como el signo de la misma es negativo no podríamos usarla para realizar selección indirecta. Claramente, debe existir una inconsistencia en nuestro razonamiento que lleva a este absurdo. La inconsistencia proviene del supuesto que \({i_X=i_y=i}\) que nos permitía simplificar la relación de la ecuación (12.34) a la de la ecuación (12.35), de donde derivamos la ecuación (12.36). De hecho, en términos generales \({i=\frac{S}{\sigma_P}}\). Como el diferencial de selección tiene signo y el desvío estándar fenotípico es siempre positivo (raíz cuadrada de una varianza), entonces la intensidad de selección tendrá signo también. Asumiendo que seleccionamos la misma proporción de individuos para cualquiera de los dos métodos (directo e indirecto), como los sentidos son opuestos (signo negativo de la correlación aditiva), entonces su cociente será igual a \(-1\) y por lo tanto la ecuación equivalente a la ecuación (12.36) \({-r_{A_{XY}} > \frac{h_Y}{h_X}}\).

Por otra parte, es importante entender que el signo de una correlación, por ejemplo la genética, no habla de por sí de si la misma es favorable o desfavorable. Pongamos un ejemplo sencillo de entender. En la producción lanera, en las condiciones actuales, el ingreso por venta de lana que tienen los productores es función directa de la cantidad (Kg) de lana producida e inversa al diámetro de las fibras. Esto se debe, entre otras cosas, a que la lana fina produce una mejor sensación al tacto y por lo tanto se usa preferentemente para vestimenta de alta calidad. En ausencia de otros grandes defectos en la lana (color, fibras pigmentadas, largo de mecha), los objetivos de mejora del productor lanero deberían ser aumentar el peso de vellón (limpio, por ejemplo) y disminuir el diámetro de las fibras. Desafortundamente para el productor lanero, la naturaleza tenía otra cosa en mente al desarrollar el “pelaje” de los mamíferos. En una oveja de un tamaño determinado, por ejemplo, hay tres formas en las que la naturaleza podría incrementar el peso del vellón limpio anual, a saber: a) aumentar el número de folículos por unidad de superficie, b) aumentar la velocidad de crecimiento (largo) de las fibras, c) aumentar el diámetro de las mismas (es decir, el área de la sección transversal). Sin descartar la importancia de las dos primeras, la tercera sin duda juega un papel importante: fibras de mayor diámetro tienen mayor superficie en la sección transversal (aún siendo relativamente huecas), que se transforman en mayor volumen (al mismo largo) y si no disminuye la densidad del material, mayor peso. Esto explica la correlación positiva entre peso de vellón y diámetro, que desafortunadamente va en contra de los criterios de pago del mercado actual. Por lo tanto, esta correlación genética es desfavorable, positiva y desfavorable. Si por alguna extraña razón, por ejemplo, si no existiese más interés en elaborar prendas finas de lana y el la gente deseara sentir un fuerte escozor al usar prendas de lana, posiblemente el mercado pagaría más por las lanas gruesas, por lo que ahora la misma correlación genética positiva pasaría a ser favorable.

En general, es difícil de que en corto tiempo cambie el signo de una correlación genética, aunque como veremos en la sección La forma generalizada de la ecuación del criador, las correlaciones genéticas también evolucionan en el tiempo (usualmente, el tiempo en términos evolutivos). Si embargo, las tendencias del mercado, que es de última lo que refleja las preferencias de los clientes, usualmente cambian en el tiempo en forma mucho más acelerada. Por ejemplo, la importancia en la ecuación de ingresos del productor lechero de la grasa ha cambiado sustancialmente en los últimos 50 años y en los diferentes mercados: desde ignorar completamente su valor, asignarle un valor importante, reducir su valor relativo (favoreciendo las proteínas), hasta volver a incrementar su valor relativo. Más aún, actualmente existen mercados que pagan muy bien por ella, otros que pagan poco y algunos nada. Sin embargo, su correlación genética con la producción de leche, con la producción de proteínas, etc. sigue siendo aproximadamente la misma en cada población de vacas Holando. Por ejemplo, mientras que la correlación genética (aditiva) entre producción de leche (litros o kilogramos) y la producción de grasa o proteína es positiva, mientras que en los mercados de leche fluida (aquellos en los que el destino principal es el consumo de leche) se trata de una relación neutra o aún favorable, en los mercados de leche destinada a la producción mayoritaria de sólidos (manteca, queso, leche en polvo), la misma es totalmente desfavorable.

PARA RECORDAR

• Es muy importante no confundir correlaciones positivas o negativas con favorables y desfavorables. Es decir, el signo de la correlación no representa si esta nos es favorable productivamente.

• Como ejemplo podemos pensar en el micraje de la lana y el peso del vellón, esta correlación es positiva, debido a que en general un mayor peso de vellón implica un mayor grosor de la fibra, sin embargo nos es desfavorable debido a que lo deseado es aumentar el peso de vellón pero manteniendo o disminuyendo el grosor de la fibra.

12.6 Matrices de varianza-covarianza

Como vimos antes, para cada par de características de interés es posible, en principio, estimar las covarianzas correspondientes a nuestro modelo simplificado. En particular, las covarianzas genético-aditivas, las covarianzas ambientales y las covarianzas fenotípicas. Si tenemos dos características, existirá una sola covarianza de cada tipo (genético-aditiva, ambiental, fenotípica), pero cuando consideramos más características debemos considerar todos los pares de variables posibles para cada tipo de covarianza. Por ejemplo, si tenemos tres características de interés, las covarianzas genético-aditivas serán \({Cov(A_1,A_2)}\), \({Cov(A_1,A_3)}\) y \({Cov(A_2,A_3)}\), o usando una notación más sintética \(\sigma_{A_{1,2}}\), \(\sigma_{A_{1,3}}\) y \(\sigma_{A_{2,3}}\). Claramente, cuando tenemos \(k\) características en consideración, habrá \(k(k-1)/2\) pares posibles de características (asumiendo que el orden no es relevante, es decir \(\sigma_{A_{i,j}}=\sigma_{A_{j,i}}\)).

Por otro lado, la covarianza de una variable consigo misma es igual a la varianza de dicha variable, ya que

\[ \begin{split} {Cov(x,x)=\frac{1}{n-1} \sum (x-\bar x) (x-\bar x)=\frac{1}{n-1} \sum (x-\bar x)^2=Var(x)} \end{split} \]

Puesto en la notación anterior, \(\sigma_{A_{i,i}}=\sigma^2_{A_i}\). De estas varianzas, habrá \(k\) para \(k\) características, es decir, una por característica. Esto nos lleva a que el número de parámetros para cada uno de los tipos de covarianza (genético-aditiva, ambiental, fenotípica) será igual a

\[ \begin{split} \frac{k(k-1)}{2}+k=\frac{k(k-1)+2k}{2}=\frac{k[(k-1)+2]}{2}=\frac{k(k+1)}{2} \end{split} \]

Una forma sencilla de acomodar todos los parámetros es ubicarlos en una matriz, como se ilustra en la Figura 12.6 para las varianzas-covarianzas genético-aditivas (matriz que llamaremos \(\mathbf{G}\)) de tres características. El arreglo de los elementos en la misma es muy sencillo: la matriz es cuadrada (es decir, tiene el mismo número de filas que de columnas) de orden \(k=3\) en este caso. Los índices de filas y columnas se corresponden con los números de las características; por ejemplo, la fila \(i=2\) y la columna \(j=3\) se corresponde al parámetro de interés (covarianza, genético-aditiva en este caso) entre las características \(2\) y \(3\). Como la diagonal está formada por la restricción en los índices tales que \(i=j\), en la misma aparecen las covarianzas entre la característica \(i\) consigo misma, que como ya vimos se trata de las varianzas (genético-aditivas) de las características. Fuera de la diagonal, los índices son distintos necesariamente, es decir \(i \ne j\) y por lo tanto de trata de covarianzas (genético-aditivas) entre dos características distintas. Además, como \(\sigma_{A_{i,j}}=\sigma_{A_{j,i}}\), la matriz es simétrica, es decir que a cada elemento de la triangular superior le corresponde un elemento en la triangular inferior, producto de intercambiar los índices \(i\) y \(j\). Las matrices de varianza-covarianza son positivas-semidefinidas, es decir que para cualquier vector \(\mathbf{z}\) perteneciente a los reales, el escalar \(\mathbf{z'Gz}\) debe ser mayor o igual a cero, con \(\mathbf{G}\) la matriz de varianza-covarianza (en este caso genético-aditiva).

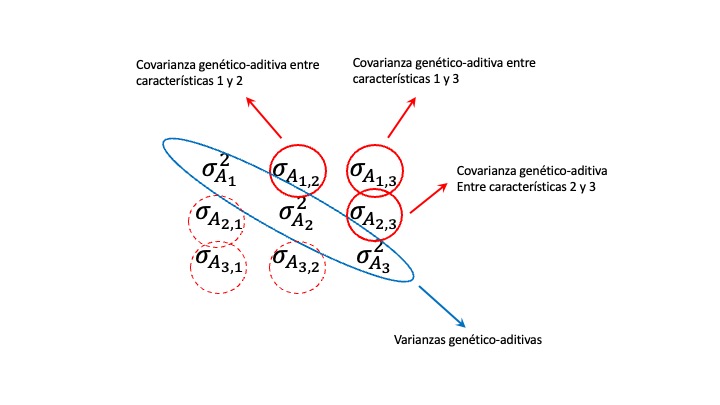
Figura 12.6: La matriz de varianza-covarianza genético-aditiva para 3 características. La diagonal (encerrada en un óvalo azul) representa las covarianzas de cada variable consigo misma, es decir las varianzas genético-aditivas de cada característica. Fuera de la diagonal aparecen las covarianzas genético-aditivas entre las características definidas por la fila y columna correspondiente (encerradas en círculos rojos). Como \(\sigma_{A_{i,j}}=\sigma_{A_{j,i}}\), la matriz es simétrica y a cada círculo rojo en la triangular superior le corresponde un círculo rojo a trazos en la triangular inferior, resultado de intercambiar los índices de filas y columnas.

De la misma forma que definimos la estructura de la matriz \(\mathbf{G}\) para las varianzas-covarianzas genético-aditivas entre característica, podemos hacer lo mismo para el resto de las covarianzas de nuestro interés, por ejemplo fenotípicas o ambientales. En la Figura 12.7 se representa la estructura de la matriz de varianza-covarianza fenotípica, que llamaremos \(\mathbf{P}\), para tres categorías de interés. Se aprecia claramente que la estructura es completamente análoga a la que definimos previamente para \(\mathbf{G}\)

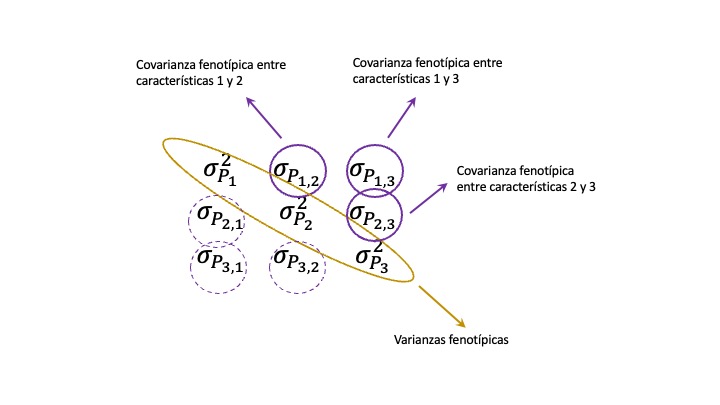
Figura 12.7: La matriz de varianza-covarianza fenotípica para 3 características. La diagonal representa las covarianzas de cada variable consigo misma, es decir las varianzas fenotípica de cada característica. Fuera de la diagonal aparecen las covarianzas fenotípica entre las características definidas por la fila y columna correspondiente. Como \(\sigma_{P_{i,j}}=\sigma_{P_{j,i}}\), la matriz es simétrica.

Como veremos más adelante en este capítulo, organizar todos los parámetros en forma matricial nos premitirá extender la ecuación del criador a varias características en forma simultanea manteniendo la notación muy sencilla, y como veremos en el próximo capítulo, será esencial en el desarrollo de los métodos de predicción de valores de cría. Sin embargo, antes de entrar en esos temas, veamos en forma sencilla cómo podemos obtener correlaciones genéticas (aditivas) y fenotípicas, así como las heredabilidades de las características, a partir de las matrices \(\mathbf{G}\) y \(\mathbf{P}\). Los diferentes programas que se utilizan en mejoramiento genético o en genética cuantitativa para estimar los parámetros genéticos suelen reportarnos ambas matrices y a partir de ellas debemos ser capaces de calcular los parámetros genéticos más relevantes para las decisiones de mejoramiento, usualmente las heredabilidades y las correlaciones genéticas (aditivas) entre características. Supongamos que nos encontramos estudiando \(k\) características diferentes y que obtuvimos las correspondientes matrices \(\mathbf{G}\) y \(\mathbf{P}\), ambas de orden \(k\) (\(k\) filas y \(k\) columnas).

De acuerdo a la definición, la correlación genética entre la característica \(i\) y la característica \(j\) estará dada por

\[ \begin{split} {r_{A_{i,j}}=\frac{Cov(A_i,A_j)}{\sqrt{Var(A_i) Var(A_j)}}=\frac{\sigma_{A_{i,j}}}{\sqrt{\sigma^2_{A_{i}}\sigma^2_{A_{j}}}}=\frac{\sigma_{A_{i,j}}}{\sigma_{A_{i}}\sigma_{A_{j}}}} \end{split} \tag{12.37} \]

Por lo tanto, para calcular la correlación genética (aditiva) entre la característica \(i\) y la característica \(j\) a partir de la matriz \(\mathbf{G}\) el procedimiento es muy sencillo:

1. Ubicar la covarianza genético-aditiva entre las dos características como la entrada \({G_{i,j}}\) en la matriz \(\mathbf{G}\) (o sea, el valor que aparece en la fila \(i\), columna \(j\)).

2. Calcular los desvíos estándar aditivos de ambas características, haciendo la raíz cuadrada a los elementos \(i\) y \(j\) de la diagonal (o sea, a las entradas \({G_{i,i}}\) y \({G_{j,j}}\)).

3. Dividir la covarianza obtenida en el punto 1 entre el producto de los desvíos estándar obtenidos en el punto 2. Ese será el valor de la correlación genética (aditiva) entre las características \(i\) y \(j\).

De la misma manera, las correlaciones fenotípicas quedan definidas por

\[ \begin{split} {r_{P_{i,j}}=\frac{Cov(P_i,P_j)}{\sqrt{Var(P_i) Var(P_j)}}=\frac{\sigma_{P_{i,j}}}{\sqrt{\sigma^2_{P_{i}}\sigma^2_{P_{j}}}}=\frac{\sigma_{P_{i,j}}}{\sigma_{P_{i}}\sigma_{P_{j}}}} \end{split} \tag{12.38} \]

por lo que el procedimiento para obtener las correlaciones fenotípicas será igual al descrito más arriba para las correlaciones genéticas, pero ahora usando la matriz \(\mathbf{P}\) en lugar de la matriz \(\mathbf{G}\).

Para calcular las heredabilidades de las diferentes características a partir de las matrices \(\mathbf{G}\) y \(\mathbf{P}\), el procedimiento es aún más sencillo, ya que solo haremos uso de las diagonales de ambas matrices. De acuerdo a la definición de Heredabilidad que vimos en el capítulo Parámetros Genéticos: Heredabilidad y Repetibilidad, para la característica \(i\) la misma sería

\[ \begin{split} {h^2_i=\frac{Var(A_i)}{Var(P_i)}=\frac{\sigma^2_{A_{i}}}{\sigma^2_{P_{i}}}} \end{split} \tag{12.39} \]

Por lo tanto, el procedimiento para calcular nuestra estimación de la heredabilidad de cada característica es trivial: dividir cada elemento de la diagonal de \(\mathbf{G}\) entre el correspondiente elemento de la diagonal en la matriz \(\mathbf{P}\), es decir

\[ \begin{split} {h^2_i}=\frac{G_{i,i}}{P_{i,i}} \end{split} \tag{12.40} \]

Como vimos previamente, la relación entre las correlaciones fenotípicas, genéticas (aditivas) y ambientales viene dada por

\[ \begin{split} {r_{P_{i,j}}=h_i\cdot h_j\cdot r_{A_{i,j}}+e_i\cdot e_j\cdot r_{E_{i,j}}} \end{split} \]

Por lo que, recordando que \({e_i=\sqrt{1-h_i}}\), \({e_j=\sqrt{1-h_j}}\), podemos obtener también la correlación ambiental (más allá de que a veces tenemos la matriz \(\mathbf{E}\) disponible) a partir de ::::{.equationbox data-latex=““}

\[ \begin{split} {r_{E_{i,j}}=\frac{r_{P_{i,j}}-h_i\cdot h_j\cdot r_{A_{i,j}}}{e_i\cdot e_j}=\frac{r_{P_{i,j}}-h_i\cdot h_j\cdot r_{A_{i,j}}}{\sqrt{1-h^2_i}\sqrt{1-h^2_j}}=\frac{r_{P_{i,j}}-h_i\cdot h_j\cdot r_{A_{i,j}}}{\sqrt{(1-h^2_i)(1-h^2_j)}}} \end{split} \tag{12.41} \]

::::

Ejemplo 12.6

A partir de un experimento donde se midieron en todos los animales el largo de la pata trasera izquierda (en cm) y el peso (en kg) a los dos años en ovejas verdes, mediante un modelo BLUP se pudieron determinar las siguientes matrices de varianza-covarianza:

\[ \begin{split} \mathbf{G}=\left(\begin{matrix}100 & 180\\180 & 800\end{matrix}\right) \end{split} \]

para la matriz de varianza-covarianza genética y

\[ \begin{split} \mathbf{P}=\left(\begin{matrix}250 & 380\\380 & 2400\end{matrix}\right) \end{split} \]

para la matriz de varianza-covarianza fenotípica. Las varianzas se expresan en \(\text{cm}^2\) para el largo, en \(\text{kg}^2\) para el peso, mientras que las covarianzas son en \(\text{cm . kg}\).

A partir de estas matrices estimar las heredabilidades de las dos características, así como las correlaciones genéticas y fenotípicas de las mismas. A partir de los resultados previos estimar la correlación ambiental.

En cada matriz, el elemento \(_{1,1}\) corresponde a la varianza de la característica 1 (largo de la pata), mientras que el el elemento \(_{2,2}\) corresponde a la varianza de la característica 2 (peso). En general, los elementos de la diagonal son las varianzas de las características (en el caso de \(\mathbf{G}\) las aditivas, mientras que en el caso de \(\mathbf{P}\) las fenotípicas).

Por otra parte, los elementos fuera de la diagonal representan covarianzas, obviamente entre las características de los subíndices de la matriz. Por ejemplo, \(\mathbf{G}_{ij}\) es la covarianza genética (aditiva) entre la característica \(i\) y la característica \(j\). Las matrices de varianza-covarianza son simétricas, por lo que \(\mathbf{G}_{ij}=\mathbf{G}_{ji}\). En nuestro caso las matrices son de \(2 \times 2\), por lo que solo existe \(\mathbf{G}_{1,2}=\mathbf{G}_{2,1}\) y \(\mathbf{P}_{1,2}=\mathbf{P}_{2,1}\).

La definición de heredabilidad como cociente de varianzas (\(h^2=\frac{V_A}{V_P}\)) nos lleva a que para la característica 1 (largo de pata trasera izquierda) esta sería

\[ \begin{split} h^2_1=\frac{\mathbf{G}_{1,1}}{\mathbf{P}_{1,1}}=\frac{100 \text{ cm}^2}{250 \text{ cm}^2}=0,400 \end{split} \]

Para la característica 2 (peso), la heredabilidad se estimaría como

\[ \begin{split} h^2_2=\frac{\mathbf{G}_{2,2}}{\mathbf{P}_{2,2}}=\frac{800 \text{ kg}^2}{2400 \text{ kg}^2}=0,333 \end{split} \]

La correlación genética, por definición es igual a \(r_A=\frac{\sigma_{A_{1,2}}}{\sqrt{\sigma^2_{A_1} \sigma^2_{A_2}}}\), que utilizando los datos de la matriz \(\mathbf{G}\) nos deja con

\[ \begin{split} r_A=\frac{180 \text{ cm.kg}}{\sqrt{100 \text{ cm.kg} \times 800 \text{ cm.kg}}}=0,6364 \end{split} \]

Finalmente, la correlación fenotípica es por definición \(r_P=\frac{\sigma_{P_{1,2}}}{\sqrt{\sigma^2_{P_1} \sigma^2_{P_2}}}\) y utilizando los valores de la matriz \(\mathbf{P}\), sería entonces igual a

\[ \begin{split} r_P=\frac{380 \text{ cm.kg}}{\sqrt{250 \text{ cm.kg} \times 2400 \text{ cm.kg}}}=0,4906 \end{split} \]

Utilizando la relación entre las correlaciones fenotípica, genética y ambiental, tenemos que \(r_{P_{12}}=h_1 h_2 r_{A_{12}}+e_1 e_2 r_{E_{12}}\). Por definición, tenemos que

\[ \begin{split} e_1=\sqrt{1-h^2_1}=\sqrt{1-0,4}=\sqrt{0,6}=0,7746\\ e_2=\sqrt{1-h^2_2}=\sqrt{1-0,333}=\sqrt{0,667}=0,8165 \end{split} \]

por lo que despejando y sustituyendo estos valores llegamos a que la correlación ambiental en este caso es igual a

\[ \begin{split} r_{E_{12}}=\frac{r_{P_{12}}-h_1 h_2 r_{A_{12}}}{e_1e_2}=\frac{0,4906-(0,6364 \times \sqrt{0,4 \times 0,333})}{0,7746 \times 0,8165}=\frac{0,2583}{0,6325}=0,4084 \end{split} \]

PARA RECORDAR

• Como vimos previamente, si tenemos dos características, existirá una sola covarianza de cada tipo (genético-aditiva, ambiental, fenotípica), pero cuando consideramos más características debemos considerar todos los pares de variables posibles para cada tipo de covarianza.

• Si tenemos \(k\) característericas, el número de parámetros para cada uno de los tipos de covarianza será \(\frac{k(k+1)}{2}\). Para mayor facilidad, podemos ubicar los mismos en una matriz de varianzas-covarianzas genético- aditivas (matriz que llamaremos \(G\)).

• La matriz \(G\) será cuadrada y simétrica de órden \(k\) dónde los índices de filas (\(i\)) y columnas (\(j\)) se corresponderán con los números de las características. Como la diagonal está formada por la restricción en los índices tales que \(i=j\), en la misma aparecen las covarianzas entre la característica \(i\) consigo misma, que se trata de las varianzas (genético-aditivas) de las características. Fuera de la diagonal, los índices son distintos necesariamente, es decir \(i \ne j\) y por lo tanto de trata de covarianzas (genético-aditivas) entre dos características distintas.

• Llamaremos \(P\) a la matriz de varianza-covarianza fenotípica y la misma poseerá una estructura análoga a la descrita para \(G\).

• Si nos encontramos estudiando \(k\) características diferentes y que obtuvimos las correspondientes matrices \(\mathbf{G}\) y \(\mathbf{P}\), ambas de orden \(k\) (\(k\) filas y \(k\) columnas), la correlación genética entre la característica \(i\) y la característica \(j\) estará dada por: \({r_{A_{i,j}}=\frac{\sigma_{A_{i,j}}}{\sigma_{A_{i}}\sigma_{A_{j}}}}\)

• Por lo tanto, para calcular la correlación genética (aditiva) entre la característica \(i\) y la característica \(j\) a partir de la matriz \(\mathbf{G}\) el procedimiento: 1) Ubicar la covarianza genético-aditiva entre las dos características como la entrada \({G_{i,j}}\) en la matriz \(\mathbf{G}\) (o sea, el valor que aparece en la fila \(i\), columna \(j\)); 2) Calcular los desvíos estándar aditivos de ambas características, haciendo la raíz cuadrada a los elementos \(i\) y \(j\) de la diagonal (o sea, a las entradas \({G_{i,i}}\) y \({G_{j,j}}\)); 3) Dividir la covarianza obtenida en el punto 1 entre el producto de los desvíos estándar obtenidos en el punto 2. Ese será el valor de la correlación genética (aditiva) entre las características \(i\) y \(j\).

• El procedimiento para obtener las correlaciones fenotípicas será igual al descrito más arriba para las correlaciones genéticas, pero ahora usando la matriz \(\mathbf{P}\) en lugar de la matriz \(\mathbf{G}\).

• Para calcualar las heredabilidades sólo haremos uso de las diagonales de ambas matrices, tal que para la característica \(i\) la misma sería \({h^2_i=\frac{Var(A_i)}{Var(P_i)}=\frac{\sigma^2_{A_{i}}}{\sigma^2_{P_{i}}}}\). Por lo tanto, el procedimiento para calcular nuestra estimación de la heredabilidad de cada característica será dividir cada elemento de la diagonal de \(\mathbf{G}\) entre el correspondiente elemento de la diagonal en la matriz \(\mathbf{P}\), es decir \({h^2_i}=\frac{G_{i,i}}{P_{i,i}}\)

• Recordando la relación entre las correlaciones fenotípicas que vimos previamente, podemos obtener también la correlación ambiental (más allá de que a veces tenemos la matriz \(\mathbf{E}\) disponible) a partir de: \({r_{E_{i,j}}=\frac{r_{P_{i,j}}-h_i\cdot h_j\cdot r_{A_{i,j}}}{\sqrt{(1-h^2_i)(1-h^2_j)}}}\)

12.7 La forma generalizada de la ecuación del criador

En el capítulo Parámetros Genéticos: Heredabilidad y Repetibilidad estudiamos diferentes definiciones de la heredabilidad (como relación de varianzas o como regresión), pero siempre nuestro contexto fue univariado, es decir, estudiamos cada característica de nuestro interés como si no tuviera ningún tipo de relación, dependencia o restricción, con otras características. Más aún, vimos el concepto de Heredabilidad lograda, lo que nos permitió una primera conexión entre los conceptos de heredabilidad y progreso genético. Más adelante, en el capítulo [Selección Artifical I] formalizamos la ecuación del criador, \({R=S\ h^2}\), que nos permitía predecir la respuesta (o progreso genético) a la selección direccional en una generación.

A partir de la ecuación del criador, teniendo en cuenta las definiciones de heredabilidad y de intensidad de selección (para características con distribución normal) derivamos la expresión de la ecuación (11.22), \({R=i\ h\ \sigma_A}\) que nos muestra que la respuesta a la selección está directamente relacionada con la varianza aditiva de la característica, algo que reafirmamos en la ecuación (11.42) \(R=\sigma^2_A \frac{s}{2a}\) para el modelo de un locus con dos alelos, o en términos más generales en la identidad de Robertson-Price, ecuación (11.52) \(R=\sigma_A^2 b_{w(z),z}\). En función de esto, no pasó desapercibido el hecho que características que poseían importante varianza aditiva y que se encontraban sujetas a una importante selección direccional no mostrasen casi respuesta a la selección. Dicho de otra manera, todo el marco teórico que venimos desarrollando hasta el momento deja de funcionar en ciertas circunstancias, por lo que es necesario entender las razones y atenderlas en un nuevo marco teórico. Una de las razones posibles a considerar es el hecho de que por lo general nunca la selección actúa en una sola dirección o es posible realizar selección exclusivamente por una característica. Por ejemplo, más allá de nuestro esfuerzo por seleccionar solo una característica de interés, la selección natural actúa de formas muchas veces desconocidas para nosotros y que por lo tanto no podemos evitar. Como vimos antes, existen bases genéticas para la correlación entre muchas características de interés y el éxito reproductivo de los individuos, por lo que muchas veces al seleccionar por determinada característica (es decir, incrementando el fitness de dicho fenotipo) estamos eligiendo individuos con menor fitness y que por lo tanto dejaran menos descendencia. Es por lo tanto fundamental el mayor conjunto de características posibles en nuestro estudio de la respuesta a la selección.

El primero en desarrollar una teoría formal de la selección multivariada fue Lande (1979), quien propuso que la ecuación del criador se podía extender fácilmente a una forma multivariada de acuerdo a la siguiente ecuación matricial

\[ \begin{split} \mathbf{R}=\Delta \bar z=\mathbf{G}\mathbf{P}^{-1}\mathbf{S} \end{split} \tag{12.42} \]

donde ahora \(\mathbf{R}\) es un vector de respuestas a la selección en cada una de las características (si tenemos \(k\) características entonces \(\mathbf{R}\) es un vector de \(k\) elementos), \(\mathbf{S}\) es un vector con los diferenciales de selección direccional en cada una de las características y \(\mathbf{G}\) y \(\mathbf{P}\) son las matrices de varianza-covarianza genética (aditiva) y fenotípica, respectivamente.

La relación de la ecuación (12.42) con la ecuación del criador es evidente. Si recordamos la definición de heredabilidad como coeficiente de varianzas, la misma era \({h^2=\frac{V_A}{V_P}}\). En matrices no existe el concepto de división, pero si el de multiplicación por la inversa, de tal manera que \(\mathbf{PP^{-1}=I}\) (la matriz identidad). Por lo tanto, el producto de \(\mathbf{G}\) por la inversa de \(\mathbf{P}\) (es decir, \(\mathbf{P}^{-1}\)) es una especie de análogo al concepto de “dividir” la matriz de varianza-covarianza genética entre la matriz de varianza-covarianza fenotípica. Una forma de ver la equivalencia con el caso de considerar las \(k\) variables como no correlacionadas a ningún nivel (es decir, como \(k\) análisis univariados) es ver que en ese caso, tanto \(\mathbf{G}\) como \(\mathbf{P}\) serán matrices diagonales (las únicas entradas con valores distintos de cero están en la diagonal). En ese caso, la inversa de \(\mathbf{P}\) será una matriz diagonal, con valores en la diagonal iguales a \(\frac{1}{P_{i,i}}=\frac{1}{\sigma^2_{P_{i}}}\). Al multiplicar \(\mathbf{GP^{-1}}\), el resultado será una matriz diagonal con valores

\[ \begin{split} \frac{G_{i,i}}{P_{i,i}}= {\frac{\sigma^2_{G_{i}}}{\sigma^2_{P_{i}}}=h^2_i} \end{split} \]

que no son otra cosa que las heredabilidades de cada una de las características. Como lo mencionamos antes para el caso univariado, la validez de la versión multivariada de la ecuación del criador, la ecuación (12.42), es dependiente de la distribución conjunta mutivariada normal entre fenotipos y valores de cría.

En el caso univariado, la identidad de Roberston-Price nos indicaba que el diferencial de selección era igual a \(S= {\sigma}[z,w(z)]\), ecuación (11.50), es decir la covarianza entre el fenotipo y el fitness asociado al mismo. La extensión a multivariado nos indica que ahora \(\mathbf{S}\) es un vector de covarianzas, por lo que de acuerdo a la teoría de regresión múltiple, el producto

\[ \mathbf{P}^{-1}\mathbf{S}=\beta \tag{12.43} \]

es el vector de coeficientes de regresión del fitness en los distintos fenotipos de las características bajo consideración. Es decir, el fitness global basado en los distintos fenotipos lo podemos describir como

\[ \begin{split} w=a+\sum_{i=1}^k \beta_i z_i+e_i \end{split} \tag{12.44} \]

donde los \(\beta_i\) son los coeficientes del gradiente de selección direccional. La idea es que los mismos representan el esfuerzo de selección en cada característica luego de haber removido las correlaciones fenotípicas con el resto de las características bajo selección.

Sustituyendo el resultado de la ecuación (12.43) en la ecuación (12.42), tenemos entonces que

\[ \begin{split} \mathbf{R}=\mathbf{G}\mathbf{P}^{-1}\mathbf{S}=\mathbf{G}\beta \end{split} \tag{12.45} \]

que se conoce como la ecuación de Lande. Si los fenotipos son multivariados normales, Lande (1979) muestra que \(\beta\) es el gradiente del logaritmo del fitness medio, es decir

\[ \beta=\mathbf{P^{-1}S}=\nabla ln \bar{\mathbf{W}} \tag{12.46} \]

donde \(\mathbf{\bar W}\) es el vector de fitness medios (para las distintas características) y \(\nabla\) es el operador gradiente, \(\nabla=(\frac{\partial}{\partial \bar z_1},...,\frac{\partial}{\partial \bar z_k})'\). Por lo tanto, al ser \(\beta\) el gradiente del logaritmo del fitness medio, la dirección que maximizará el cambio en el fitness medio de la población es precisamente la dirección del vector \(\beta\).

Sin duda lo anterior es muy interesante, ¿pero cuál es la importancia práctica de lo mismo? Si miramos con más cuidado la ecuación de Lande vemos que más allá del gradiente de selección direccional que nosotros o la naturaleza le impongan a las características relevantes para desplazar las medias en el sentido deseado, la respuesta es una función de la matriz \(\mathbf{G}\) y que por lo tanto tendrá sus propias restricciones. De hecho, de acuerdo a la ecuación de Lande, \(\mathbf{R=G \beta}\), la multiplicación del vector de gradiente \(\beta\) (es decir el “óptimo”) por la matriz \(\mathbf{G}\) producirá un vector de respuesta \(\mathbf{R}\), que en general no coincidirá en dirección con el vector \(\beta\). En general, la multiplicación de un vector por una matriz produce tanto una rotación, como un escalado del vector resultante.

Una forma sencilla de evaluar la concordancia (o diferencia) en la dirección de dos vectores es examinar el ángulo entre ellos. Si el ángulo es de cero grados, entonces las direcciones de los dos vectores coinciden y la respuesta a la selección sigue exactamente la dirección del gradiente de selección (que si solo incluimos las características de interés para nosotros, representaría la dirección deseada en el progreso genético); por el contrario, si el ángulo es de 90 grados, la respuesta a la selección será totalmente ortogonal a nuestros deseos. En nuestro caso, los dos vectores en consideración son \(\mathbf{R}\) y \(\beta\), por lo que aplicando la definición de producto escalar tenemos que

\[\mathbf{R} \cdot \beta= || \mathbf{R} || \ ||\beta|| cos(\theta)\ \therefore\] \[ \begin{split} cos(\theta)=\frac{\mathbf{R} \cdot \beta}{||\mathbf{R}|| \ ||\beta||} \end{split} \tag{12.47} \]

Por lo tanto, para saber el ángulo entre el vector del gradiente de selección y la respuesta a la selección en una generación alcanza aplicar a esta ecuación la función arcocoseno, lo que nos deja con

\[ \begin{split} \theta= {cos^{-1}}({\frac{\mathbf{R} \cdot \beta}{|| \mathbf{R} || \ ||\beta||}}) \end{split} \tag{12.48} \]

Claramente, la matriz \(\mathbf{G}\) es la que impone las restricciones a las direcciones en las que la selección tendrá respuesta, por lo que el análisis de la misma se vuelve esencial. De los cursos de álgebra lineal podemos recordar que llamábamos valores propios (\(c\)) y vectores propios (\(\mathbf{v}\)) (también conocidos como eigenvalues y eigenvectors, respectivamente) de una matriz \(\mathbf{M}\) a aquellos que cumplían

\[ \begin{split} \mathbf{Mv=}c\mathbf{v} \end{split} \tag{12.49} \]

es decir, aquellos vectores \(\mathbf{v}\) que al ser multiplicados por la matriz no cambiaban de dirección. El valor propio es el factor de escalado en la multiplicación. Utilizando esto, las direcciones de vectores que no cambiarán al ser multiplicados por \(\mathbf{G}\) serán las de los vectores propios de la misma. Más aún, entre ellos, los que más responderán serán, en orden, los de mayor valor, por lo que el primer vector propio (el de mayor valor) será la dirección preferida para la evolución de acuerdo a las restricciones de la arquitectura genética de las características. Más aún, en el caso de que la matriz tenga valores propios iguales a cero, aplicando la definición de ecuación (12.49) a la matriz \(\mathbf{G}\) tenemos

\[ \begin{split} \mathbf{Gv=}c\mathbf{v=0}\ \mathbf{v=0} \end{split} \tag{12.50} \]

lo que significa que no habrá respuesta ninguna en dicha dirección. Usualmente, en mejoramiento genético, se realizan estimaciones regulares de las varianzas y covarianzas genéticas, pero no existe una fuerte tradición en la interpretación de la evolución de las mismas a lo largo del tiempo, asumiendo de alguna forma que los cambios se deben a problemas de estimación. En realidad, a medida de que avanzamos en la selección direccional las varianzas aditivas de las características de interés suelen disminuir, pero también se modifican las covarianzas entre las características, por lo que aún existiendo varianza aditiva disponible en ciertos casos no hay respuesta a la selección. Por lo tanto, es fundamental entender que al mismo tiempo que la respuesta está condicionada por la matriz \(\mathbf{G}\), las restricciones también pueden evolucionar, cambiando la matriz \(\mathbf{G}\) en un juego complejo y dinámico. Un tratamiento más profundo y al mismo tiempo ameno se encuentra en Blows and Walsh (2009).

Ejemplo 12.7

Las ovejas verdes tienen una tendencia importante a la esfericidad de sus cuerpos, lo que dificulta enormemente el esquilado, por lo que uno de los objetivos de selección planteados para mejorar la majada experimental es hacerlos más cilíndricos. Para ello se desarrolló un índice que es igual al diámetro de la panza en la zona media divida entre el largo del cuerpo y multiplicado por 100, es decir

\[ \begin{split} I_e=100 \times \frac{D_{panza}}{L_{cuerpo}} \end{split} \]

Al mismo tiempo, se plantea incrementar la producción de lana verde, por lo que debemos mantener los dos objetivos en mente. Un estudio preliminar determinó que la matriz de varianza-covarianza genética estaría dada por

\[ \begin{split} \mathbf{G}=\left(\begin{matrix}100 & 0\\0 & 800\end{matrix}\right) \end{split} \]

con sus correspondientes unidades (la varianza del índice en unidades de índice al cuadrado y la producción de lana en \(g^2\)). Como se trata de una matrix diagonal, no existen en principio restricciones genéticas. Sin embargo, veamos qué pasa si elegimos un gradiente de selección

\[ \begin{split} \beta=\left(\begin{matrix}-0,09\\ 0,03 \end{matrix}\right) \end{split} \]

La respuesta a la selección de acuerdo a la ecuación de Lande será

\[ \begin{split} R=\mathbf{G \beta}=\left(\begin{matrix}100 & 0\\0 & 800\end{matrix}\right) \left(\begin{matrix}-0,09\\ 0,03 \end{matrix}\right)=\left(\begin{matrix}-9\\ 24 \end{matrix}\right) \end{split} \]

Si calculamos ahora el ángulo entre los dos vectores, usando la ecuación (12.48) tenemos que

\[\theta={cos^{-1}}(\frac{ \mathbf{R} \cdot \beta}{|| \mathbf{R} || \ ||\beta||})=\] \[ \begin{split} {cos^{-1}}(\frac{1,53}{2,431666})=51^{\circ} \end{split} \]

lo que pese a la inexistencia de correlación genética entre ambas características nos deja con un desfasaje importante entre la dirección de selección elegida y la favorecida por \(\mathbf{G}\). Esto se debe a que, pese a que no existe correlación genética entre las características la respuesta se encuentra rotada respecto a la dirección óptima para el incremento del fitness medio. La dirección de máxima variación es en peso del vellón, pero en términos relativos estamos haciendo mucha más presión de selección en una dirección (índice de esfericidad) con poca variación, por lo que no debería sorprendernos esta diferencia en las direcciones de gradiente de selección y de respuesta.

Un segundo estudio, sin embargo, con muchos más animales obtuvo un diferente estimado de la matriz de varianzas-covarianzas genéticas, la que fue ahora

\[ \begin{split} \mathbf{G}=\left(\begin{matrix}100 & 282,8\\282,8 & 800\end{matrix}\right) \end{split} \]

Ahora, si utilizamos el mismo gradiente de selección que antes, la respuesta a la selección predicha por la ecuación de Lande será

\[ \begin{split} \mathbf{R}=\mathbf{G \beta}=\left(\begin{matrix}100 & 282,8\\282,8 & 800\end{matrix}\right) \left(\begin{matrix}-0,09\\ 0,03 \end{matrix}\right)=\left(\begin{matrix}-0,5151\\ -1.4547 \end{matrix}\right) \end{split} \]

Claramente, la respuesta a la selección en este caso no parece haber seguido siquiera cerca nuestros objetivos. Si calculamos el ángulo ahora entre los dos vectores, tenemos que el mismo es de

\[\theta={cos^{-1}}(\frac{ \mathbf{R} \cdot \beta}{|| \mathbf{R} || \ ||\beta||})=\] \[ \begin{split} {cos^{-1}}\left(\frac{0,002718}{0,1464012}\right)=88^{\circ}93' \end{split} \]

lo que indica una restricción casi total (cercana a \(\mathbf{\theta=90^{\circ}}\)). La explicación de esto es muy sencilla, la matriz \(\mathbf{G}\) posee uno de los valores propios muy cercanos a cero y cuyo vector propio es

\[ \begin{split} \left(\begin{matrix}-0,9428\\ 0,3333 \end{matrix}\right) \end{split} \]

lo que coincide casi exactamente con la dirección elegida para la selección, por lo que esta no tendrá respuesta. Esto no debería sorprendernos, ya que en este caso, la correlación genética entre ambas características, de acuerdo a la ecuación (12.37) es de

\[ \begin{split} {r_A=\frac{\sigma_{A_{i,j}}}{\sigma_{A_{i}}\sigma_{A_{j}}}=\frac{282,8}{\sqrt{100 \times 800}}=0,9999} \end{split} \]

es decir, queda muy poco espacio disponible para selección de ambas características en sentido opuesto.

PARA RECORDAR

• Podemos extender la ecuación del criador a una forma multivariada de acuerdo a la siguiente ecuación matricial: \(\mathbf{R}=\Delta \bar z=\mathbf{G}\mathbf{P}^{-1}\mathbf{S}\) donde ahora \(\mathbf{R}\) es un vector de respuestas a la selección en cada una de las características (si tenemos \(k\) características entonces \(\mathbf{R}\) es un vector de \(k\) elementos), \(\mathbf{S}\) es un vector con los diferenciales de selección direccional en cada una de las características y \(\mathbf{G}\) y \(\mathbf{P}\) son las matrices de varianza-covarianza genética (aditiva) y fenotípica, respectivamente.

• La ecuación de Lande (\(\mathbf{R}=\mathbf{G}\mathbf{P}^{-1}\mathbf{S}=\mathbf{G}{\beta}\)) nos muestra que más allá del gradiente de selección direccional que nosotros o la naturaleza le impongan a las características relevantes para desplazar las medias en el sentido deseado, la respuesta es una función de la matriz \(\mathbf{G}\) y que por lo tanto tendrá sus propias restricciones. De hecho, de acuerdo a la misma, \(\mathbf{R=G \beta}\), la multiplicación del vector de gradiente \(\beta\) (es decir el “óptimo”) por la matriz \(\mathbf{G}\) producirá un vector de respuesta \(\mathbf{R}\), que en general no coincidirá en dirección con el vector \(\beta\). En general, la multiplicación de un vector por una matriz produce tanto una rotación, como un escalado del vector resultante.

12.8 Conclusión

Como vimos anteriormente, podemos realizar una influencia direccional sobre una característica fenotípica, en un proceso que denominamos selección artificial. La eficiencia de esta selección depende tanto de la intensidad de la misma como de la heredabilidad del caracter fenotípico considerado. No obstante, en nuestro análisis dejamos de lado que la selección de un caracter puede influir en otros, fenómeno que puede ser o no deseado según el caso. ¿A qué se debe esta dependencia entre caracteres? Fenómenos como la pleiotropía o la influencia de factores ambientales comunes pueden subyacer a esta respuesta correlacionada entre caracteres fenotípicos. Incluso fenómenos que analizamos en capítulos anteriores, como el desequilibrio de ligamiento, pueden ser la causa subyacente a estas correlaciones, lo cual hace que el fenómeno pueda estar influido por la historia de cada población particular. Entender las causas y el comportamiento de estas respuestas correlacionadas es fundamental para los propósitos del mejoramiento genético. Para entender el por qué, podemos pensar en los casos extremos: dos caracteres que se encuentran totalmente correlacionados, o dos en los que no existe ningún tipo de correlación. Resulta claro que es necesario contemplar estas restricciones genético-evolutivas tanto si se tiene interés en ambos caracteres, o si uno lo es pero el otro no. En estos casos resulta informativo incluso poseer conocimiento simplemente del signo de la correlación entre estos caracteres fenotípicos. Si bien es difícil (y en algunos casos, imposible), el separar los componentes genéticos y ambientales de las respuestas correlacionadas, los análisis que permiten tal separación son un aporte fundamental, tanto a nivel práctico como conceptual, de la genética cuantiativa.

12.9 Actividades

12.9.1 Control de lectura

1. ¿Qué tipos de correlaciones existen?
2. ¿Cómo se tienen en cuenta los diferentes tipos de correlaciones al momento de analizar la respuesta a selección?
3. ¿Qué fenómenos pueden subyacer a la existencia de correlación entre dos variables fenotípicas? Expláyese para alguno de estos fenómenos
4. En algunos casos es preferible optar por la selección indirecta de una característica (en lugar de seleccionarla directamente). ¿Cuál es el criterio determinante para tomar esta decisión?
5. Parte de la correlación entre dos características fenotípicas es explicable por la existencia de un componente genético aditivo compartido. No obstante, en la práctica solo podemos observar correlaciones fenotípicas. ¿Qué formas conoce para estimar la correlación aditiva entre dos características?

12.9.2 ¿Verdadero o falso?

1. La correlación fenotípica no es la simple suma de la correlación genotípica y ambiental.
2. Utilizando el “path analysis” es posible demostrar que el coeficiente de correlación estandarizado entre dos fenotipos equivale a la heredabilidad.
3. Se puede realizar selección para una característica de interés seleccionando sobre otra si existe correlación fenotípica entre las mismas.
4. En casos donde la correlación genética (aditiva) entre dos características es mayor a la precisión entre ambas, conviene optar por la selección indirecta.
5. A partir de una matriz de varianza-covarianza genética (aditiva) para una característica fenotípica de interés es posible calcular la heredabilidad de la misma.

Soluciones

1. Verdadero. Se puede demostrar que la correlación fenotípica entre dos características involucra a las correlaciones genotípicas y ambientales en forma más compleja que una suma.
2. Falso. Recordemos que este coeficiente equivale a \(h\) (\(\sqrt{h^2}\)), no a la heredabilidad (\(h^2\)).
3. Falso. La existencia de correlación fenotípica no implica necesariamente que ambos caracteres fenotípicos aumenten en la misma dirección; es necesario tener en cuenta el signo de dicha correlación. Resulta claro que si la misma es negativa será imposible seleccionar la característica de interés a partir de la selección de la característica correlacionada (de hecho se logrará lo contrario a lo deseado).
4. Verdadero.
5. Falso. Recordemos que la heredabilidad equivale a \(h^2 = \frac{\sigma_A}{\sigma_P}\), por lo que para estimar la misma para una característica se requiere también de la matriz de varianza-covarianza fenotípica.

12.9.3 Ejercicios

Ejercicio 12.1

Un grupo de laboratorio se encuentra estudiando una enfermedad rara (i.e., de baja incidencia en poblaciones celulares comunes). La selección de células que presentan el fenotipo resulta engorrosa, por lo que se plantean la posibilidad de realizar un proceso de selección indirecta, a efectos de enriquecer los cultivos celulares en dichas células. La idea es seleccionar células según su capacidad de metabolización de diferentes medios de cultivo (algo que es fácil de manipular a nivel experimental).

Un estudio previo estimó la matriz de varianza-covarianza genético aditiva para tres fenotipos: \(F_E\) (fenotipo de la enfermedad), \(F_\text{M1}\) (alta capacidad de metabolización de un compuesto) y \(F_\text{M2}\) (alta capacidad de metabolización de otro compuesto). La misma se muestra a continuación

	\(F_E\)	\(F_{\text{M1}}\)	\(F_{\text{M2}}\)
\(F_E\)	\(0,23\)	\(0,76\)	\(0,15\)
\(F_{\text{M1}}\)	\(0,76\)	\(0,12\)	\(0,21\)
\(F_{\text{M2}}\)	\(0,15\)	\(0,21\)	\(0,1\)

A su vez, el mismo estudio estima que las heredabilidades de estos tres fenotipos son \(h^2_E = 0,69\), \(h^2_{\text{M1}} = 0,82\) y \(h^2_{\text{M2}} = 0,55\)

¿Conviene al grupo realizar selección indirecta para este fenotipo? ¿Empleando cuál de los metabolitos?

Solución

Recordemos que para que sea preferible utilizar el método de selección indirecta (\(X\)) sobre una característica seleccionando directamente a otra (\(Y\)) se debe cumplir

\[r_{A_{XY}} > \frac{h_X}{h_Y}\]

En este caso puntual, debemos tener en cuenta dos comparaciones (las que contemplan a \(F_E\))

Tenemos que

\[h_{E} = \sqrt{h^2_E} = \sqrt{0,69}\] \[h_{M1} = \sqrt{h^2_{M1}} = \sqrt{0,82}\] \[h_{M2} = \sqrt{h^2_{M2}} = \sqrt{0,55}\]

A su vez los coeficientes de correlación genético aditivas pueden calcularse a partir de la matriz de varianza-covarianza, recordando que

\[r_{A_{XY}} = \frac{\text{Cov}(X,Y)}{\sqrt{\sigma^2_{AX}} \cdot \sqrt{\sigma^2_{AY}}}\]

De esto tenemos

\[ \begin{cases} r_{A_{E-M1}} = \frac{0,76}{\sqrt{0,23} \cdot \sqrt{0,12}} \approx 4,58 \\ r_{A_{E-M2}} = \frac{0,15}{\sqrt{0,23} \cdot \sqrt{0,1}} \approx 0,989 \end{cases} \]

Notemos que para la primera comparación se da \(r_{A_{E-M1}} > \frac{h_E}{h_{M1}} = \frac{\sqrt{0,69}}{\sqrt{0,82}} \approx 0,917\), mientras que en el segundo caso tenemos \(r_{A_{E-M1}} < \frac{h_E}{h_{M2}} = \frac{\sqrt{0,69}}{\sqrt{0,55}} \approx 1,12\). De esto se deduce que el grupo de investigación sí puede optar por una técnica de selección indirecta, siempre y cuando opte por emplear como régimen selectivo la capacidad de metabolización del compuesto \(M1\).

Ejercicio 12.2

(Adaptado de Blows and Walsh 2009)

Un productor se encuentra intentando mejorar un caracter fenotípico \(A\) mediante selección artificial. Otro caracter fenotípico, \(B\), también es registrado en las mediciones.

a. Las varianzas aditivas estimadas para los caracteres son \(\sigma_A^2 10\) y \(\sigma^2_B = 40\). Además, se asume que el régimen selectivo afecta a estos dos caracteres de forma que el cambio en dos unidades en el caracter \(A\) lleva a la disminución en una unidad del caracter \(B\). ¿Cuál es la respuesta esperada para cada caracter, si asumimos que no existe covarianza aditiva entre ambos?

b. Un estudio revela que la asunción de inexistencia en la covarianza genética aditiva entre los dos caracteres es demasiado ingenua. Los mismos sí están correlacionados, siendo la matriz de varianza-covarianza genético aditiva

\[ \textbf{G} = \begin{pmatrix} 10 & 20 \\ 20 & 40 \end{pmatrix} \]

¿Cuál es la respuesta esperada entonces? ¿Cómo explica conceptualmente el resultado obtenido?

Solución

a. Se pide calcular la respuesta a la selección en más de un caracter fenotípico. En estos casos se puede aplicar la ecuación de Robertson-Price generalizada:

\[\textbf{R} = \textbf{G} \beta\]

donde \(\textbf{G}\) es la matriz de varianza-covarianza genético aditiva y \(\beta\) es la respuesta a selección de los caracteres (i.e. \(\beta = \textbf{P}^{-1} \textbf{S}\))

En nuestro caso se plantea que

\[ \textbf{G} = \begin{pmatrix} 10 & 0 \\ 0 & 40 \end{pmatrix} \]

y

\[ \beta = \begin{pmatrix} 2 \\ -1 \end{pmatrix} \]

Tenemos entonces una respuesta esperada \(\textbf{R}\) de

\[\textbf{R} = \begin{pmatrix} 10 & 0 \\ 0 & 40 \end{pmatrix} \begin{pmatrix} 2 \\ -1 \end{pmatrix}\] \[\textbf{R} = \begin{pmatrix} 20 \\ -40 \end{pmatrix}\]

Notemos que, si bien la respuesta a selección no es la más eficiente (ya que debería ser un vector alineado a \(\beta\), es decir algún múltiplo de este), sí se esperaría un cambio en los valores fenotípicos de estas características.

b. Notemos que la existencia de covarianza genético aditiva cambia la situación planteada: ahora el cambio en un caracter influye necesariamente en la respuesta a selección del otro [hay que revisar esta parte.]. Tenemos ahora que

\[\textbf{R} = \begin{pmatrix} 10 & 20 \\ 20 & 40 \end{pmatrix} \begin{pmatrix} 2 \\ -1 \end{pmatrix}\] \[\textbf{R} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\]

¡Es decir que en este caso no tenemos respuesta a la selección! ¿Cómo es esto posible? Este resultado deja en evidencia un aspecto importante de la respuesta a la selección: los organismos están constituídos por múltiples caracteres fenotípicos, por lo que un régimen selectivo operará afectando varios de los mismos; lo que es más, la existencia de correlación genética aditiva y fenotípica entre estos caracteres hace que la respuesta de una variable afecte a la respuesta de otra. En un caso extremo, como el presente, dos caracteres pueden estar siendo seleccionados pero influyendo a la respuesta del otro de tal forma que no exista una respuesta final a la selección.

Ejercicio 12.3

En una majada comercial, existe interés en mejorar el peso de los borregos al año de edad (PB; \(h^2=0,32\); \(\sigma_A=8 kg^2\)). Sin embargo, debido a que se quiere realizar una selección más temprana de los animales se ha decidido seleccionar a través del peso al destete (PD; \(h^2=0,47; \sigma_A=6 kg^2\)) de estos animales. A la vez, la correlación genético aditiva entre las características es de 0,7 y la intensidad de selección posible es de 2,4209 para los machos y 0,6439 para las hembras.

¿Cuánto será el progreso genético por generación en PB si selecciona por PD?

Solución

Para poder estimar el progreso genético que es posible lograr en PB seleccionando por PD usaremos:

\[{RC_Y=i_X\ h_X\ r_{A_{XY}}\ \sigma_{A_{Y}}}\]

Dónde \(Y\) corresponde a la característica de nuestro interes (PB) y \(X\) a la caraterística mediante la cual seleccionamos (PD).

Aplicando entonces la fórmula:

\[RC_{PB}=\frac{2,4209+0,6439}{2} * \sqrt{0,47} * 0,7 * \sqrt{8} \approx 2,08 \text{ kg}\]

Es decir, por generación, al seleccionar por peso al destete, es posible mejorar algo más de \(2\) kg el peso del borrego al año.

Ejercicio 12.4

El búfalo de agua (Bubalus bubalis) es un gran bóvido de origen asiático pero que actualmente se ha diseminado virtualmente por todo el mundo. Este animal se puede encontrar en estado salvaje o doméstico, dónde la presencia de astas presenta dificultades a la hora del manejo especialmente dado el gran tamaño de estos animales. Se ha observado que la correlación fenotípica entre el tamaño de cuerpo (\(TC\)) y el tamaño de astas (\(TA\)) es de \(r_P=0,68\) mientras que las heredabilidades de las características son \(h^2_{TC}=0,48\) y \(h^2_{TA}=0,56\). Por otra parte, se ha determinado que el mejor estimado de la correlación genética (aditiva) entre ambas características es de \(r_A = 0,47\).

¿Cuál es la correlación ambiental entre las características?

Solución

Recordemos que podemos expresar la relación entre las correlaciones fenotípica, genética y ambiental como \(r_P=h_1 h_2 r_A+e_1 e_2 r_E\) donde podremos despejar la correlación ambiental tal que \(r_E=\frac{r_P-h_1 h_2 r_A}{e_1e_2}\).

Procederemos entonces a calcular los parámetros \(e\):

\[e_1=\sqrt{1-h^2_1}=\sqrt{1-0,48}=\sqrt{0,52}= 0,7211\] \[e_1=\sqrt{1-h^2_2}=\sqrt{1-0,56}=\sqrt{0,44}= 0,6633\]

Entonces, la correlación ambiental entre las características será:

\[r_E=\frac{0,68-\sqrt{0,48} * \sqrt{0,56}* 0,47}{0,7211 * 0,6633} = 0,913\]

Ejercicio 12.5

(Modificado de D. S. Falconer and MacKay 1996; trabajo original de Reeve and Robertson 1953)

En un antiguo estudio (Reeve and Robertson 1953) Reeve y Robertson se dedicaron a estudiar la correlación genética aditiva en dos caracteres fenotípicos de la mosca D. melanogaster vinculados al tamaño corporal: largo de ala y largo de tórax. Para ello realizaron experimentos con dos líneas de moscas. Al seleccionar individuos a efectos de generar una línea con mayor largo de ala (con un diferencial de selección de \(S_{\text{ala}} = 0,2 \text{ cm}\)), los investigadores observan un aumento del largo de tórax. La covarianza entre ambos caracteres fenotípicos fue de \(\text{Cov}_{\text{ala}-\text{tórax}} = 0,726\), con una varianza para largo de alas de \(\sigma^2_\text{ala} = 1\) y de \(\sigma^2_\text{tórax} = 2\) para largo de tórax. Por otro lado, la selección de individuos con el fin de aumentar el largo de tórax (con un diferencial de selección de \(S_{\text{tórax}} = 1,3 \text{ cm}\)) también resultó en un aumento del largo de alas, esta vez con covarianza \(\text{Cov}_{\text{tórax}-\text{ala}} = 0,679\), siendo las varianzas fenotípicas \(\sigma^2_\text{ala} = 1,2\) y \(\sigma^2_\text{tórax} = 1,8\).

Si un estudio previo arroja que la heredabilidad del largo de ala y tórax es de \(h^2_{\text{ala}} = 0,74\) y \(h^2_{\text{tórax}} = 0,69\) , respectivamente, ¿cuál es la correlación genético aditiva entre ambas características?

Nota: A efectos de simplificar los cálculos se asume que no existe varianza genética de dominancia, y que la varianza ambiental es despreciable.

Solución

Recordemos que la correlación aditiva entre dos caracteres fenotípicos se puede calcular según

\[r^2_a = \frac{\text{CR}_{T2}}{R_{T1}} \cdot \frac{\text{CR}_{T1}}{R_{T2}}\]

donde la respuesta correlacionada del caracter \(T2\) al cambiar el caracter \(T1\) está dada por \(\text{CR}_{T2} = i h_{T1} h_{T2} r_a \sigma_{P,T2}\) (y vice versa si se intercambian los roles), \(r_a = \frac{\text{Cov}_a (T1,T2)}{\sigma_{a, T1} \cdot \sigma_{a, T2}}\) y siendo la respuesta de selección directa dada por \(R{.} = i h_{.} \sigma_{A.}\).

Pasemos por lo tanto a calcular cada una de estas cantidades, a efectos de poder calcular la correlación genética aditiva entre largo de ala y largo de tórax.

Empecemos por la precisión de cada uno de los caracteres. Tenemos

\[ \begin{cases} h_{\text{ala}} = \sqrt{h^2_\text{ala}} \Rightarrow h_{\text{ala}} = \sqrt{0,74} \\ h_{\text{tórax}} = \sqrt{h^2_\text{tórax}} \Rightarrow h_{\text{tórax}} = \sqrt{0,69} \end{cases} \]

Luego tenemos la respuesta a la selección directa de cada característica, dadas por

\[ \begin{cases} R_{\text{ala}} = 0,2 \cdot \sqrt{0,74} \cdot \sqrt{1} \Rightarrow R_{\text{ala}} = 0,2 \cdot \sqrt{0,74} \\ R_{\text{tórax}} = (\frac{0,15}{\sqrt{1,8}}) \cdot \sqrt{0,69} \cdot \sqrt{1,8} \end{cases} \]

donde las intensidades de selección fueron calculadas según \(i_{\text{ala}} = \frac{S_{\text{ala}}}{\sigma_{P, \text{ala}}} = \frac{0,2}{\sqrt{1}} = 0,2\) e \(i_{\text{tórax}} = \frac{S_{\text{tórax}}}{\sigma_{P, \text{tórax}}} = \frac{0,15}{\sqrt{1,8}}\)

Podemos ahora calcular las respuestas correlacionadas para cada caracter

\[ \begin{cases} \text{CR}_{\text{ala}} = i h_{\text{ala}} h_{\text{tórax}} r_a \sigma_{P,\text{ala}} = (\frac{1,3}{\sqrt{1,8}}) \cdot \sqrt{0,84} \cdot \sqrt{0,79} \cdot \frac{0,879}{\sqrt{1,2} \cdot \sqrt{1,8}} \cdot \sqrt{1,2} \Rightarrow \text{CR}_{\text{ala}} \approx 0,517146 \\ \text{CR}_{\text{tórax}} = i h_{\text{ala}} h_{\text{tórax}} r_a \sigma_{P,\text{tórax}} = (1,2) \cdot \sqrt{0,84} \cdot \sqrt{0,79} \cdot \frac{0,726}{\sqrt{1} \cdot \sqrt{2}} \cdot \sqrt{2} \Rightarrow \text{CR}_{\text{tórax}} = 0,709694 \end{cases} \]

donde tenemos en cuenta el efecto de cambio en una característica al haber seleccionado directamente a la otra.

A partir de los datos podemos calcular la correlación genético aditiva entre características

\[r^2_a = \frac{\text{CR}_{\text{ala}}}{R_{\text{tórax}}} \cdot \frac{\text{CR}_{\text{tórax}}}{R_{\text{ala}}}\] \[r^2_a \approx (\frac{0,517146}{(\frac{1,3}{\sqrt{0,8}}) \cdot \sqrt{0,79} \cdot \sqrt{1,8}}) \cdot (\frac{0,709694}{1,2 \cdot \sqrt{0,84}})\] \[r^2_a \approx 0,193\]

---

Bibliografía

Blows, Mark, and Bruce Walsh. 2009. “Spherical Cows Grazing in Flatland: Constraints to Selection and Adaptation.” In Adaptation and Fitness in Animal Populations: Evolutionary and Breeding Perspectives on Genetic Resource Management, edited by Julius van der Werf, Hans-Ulrich Graser, Richard Frankham, and Cedric Gondro, 83–101. Dordrecht: Springer Netherlands. https://doi.org/10.1007/978-1-4020-9005-9_6.

Cardellino, Ricardo, and Jaime Rovira. 1987. Mejoramiento Genético Animal. 1era. ed. Editorial Hemisferio Sur.

Falconer, D S, and Trudy F C MacKay. 1996. Introduction to Quantitative Genetics. 4th ed. London, England: Longman.

Henderson, C. R., and R. L. Quaas. 1976. “Multiple Trait Evaluation Using Relatives’ Records.” Journal of Animal Science 43 (6): 1188–97. https://doi.org/10.2527/jas1976.4361188x.

Lande, R. 1979. “QUANTITATIVE GENETIC ANALYSIS OF MULTIVARIATE EVOLUTION, APPLIED TO BRAIN:BODY SIZE ALLOMETRY.” Evolution 33 (1Part2): 402–16.

Li, Ching Chun. 1955. Population Genetics. First. Chicago Press.

Lobo, Ingrid. 2008. “Pleiotropy: One Gene Can Affect Multiple Traits.” Nature Education 1 (1): 10.

Loehlin, John C, and A. Alexander Beaujean. 2017. Latent Variable Models: An Introduction to Factor, Path, and Structural Equation Analysis. Fifth. Routledge (Taylor; Francis group).

Reeve, E. C. R., and Forbes W. Robertson. 1953. “Studies in Quantitative Inheritance: II. Analysis of a Strain ofDrosophila Melanogaster Selected for Long Wings.” Journal of Genetics 51 (2): 276–316. https://doi.org/10.1007/bf03023299.

Robertson, Alan. 1959. “The Sampling Variance of the Genetic Correlation Coefficient.” Biometrics 15 (3): 469–85.

Searle, Shayle R. 1961. “Phenotypic, Genetic and Environmental Correlations.” Biometrics 17 (3): 474–80.

Tallis, George Michael. 1959. “SAMPLING ERRORS OF GENETIC CORRELATION COEFFICIENTS CALCULATED FROM ANALYSES o f VARIANCE AND COVARIANCE.” Australian Journal of Statistics 1 (2): 35–43.

Wright, D. 2015. “The Genetic Architecture of Domestication in Animals.” Bioinform Biol Insights 9 (Suppl 4): 11–20.

Wright, S. 1918. “On the Nature of Size Factors.” Genetics 3 (4): 367–74.

———. 1934b. “The Method of Path Coefficients.” Ann. Math. Statist. 5 (3): 161–215.