Capítulo 7 Genética de Poblaciones Microbianas

Ejercicio 7.1

En un laboratorio, una colonia bacteriana comienza con 5 individuos. La tasa neta de crecimiento para el modelo continuo es de $r_c=5,1667\times 10^{-3}s^{-1}$. Asumiendo de que no existen limitantes a su crecimiento en el tiempo considerado,

Calcular el tamaño poblacional al cabo de un tiempo $t=1$ hora.
Si usa tasa neta de crecimiento $r_c=4,1667\times 10^{-3}s^{-1}$ produce 16.347.048 bacterias al cabo de una hora, partiendo de los mismos 5 individuos, calcular la relación entre las tasas y entre el número de bacterias al cabo de una hora. ¿Será similar la relación? ¿Cómo se explica lo observado?

Ejercicio 7.2

Calcular el tamaño poblacional para una colonia bacteriana que comienza con 5 individuos, al cabo de un tiempo $t=1$ hora y con una tasa neta de crecimiento para el modelo continuo de $r_c=4,1667\times 10^{-3}s^{-1}$, en el caso de que la capacidad de carga del sistema ($K$) sea de 4 millones de individuos.

Ejercicio 7.3

En una especie bacteriana, un locus con dos alelos, $A_1$ y $A_2$ produce que los individuos que poseen los mismos presentan un fitness absoluto de $W_1=1,7$ y $W_2=1,2$.

Si la frecuencia del alelo $A_1$ es $p=0,45$, asumiendo que la división de las bacterias opera en tiempo discreto, determinar la frecuencia en la siguiente generación.

Ejercicio 7.4

En un locus bacteriano con dos alelos, considerando que las tasas de crecimiento instantáneo que corresponden a los mismos son de $r_1=0,75$ para el alelo $A_1$ y $r_2=0,25$ para el alelo $A_2$,

Calcular la tasa de cambio en frecuencia, cuando la frecuencia del alelo $A_1$ es $p=0,35$.

Ejercicio 7.5

La derivada segunda de la función $n(t)=\frac{K\ n_0\ e^{r_c\ t}}{K+n_0\ (e^{r_c\ t}-1)}$ que describe el tamaño poblacional en función del tiempo para el modelo logístico es

\[\begin{equation} \dfrac{d^2n}{dt^2}=\dfrac{Kn_0\left(n_0-K\right)r_c^2\mathrm{e}^{r_ct}\left(n_0\mathrm{e}^{r_ct}+n_0-K\right)}{\left(n_0\mathrm{e}^{r_ct}-n_0+K\right)^3} \end{equation}\]

Demostrar que el punto de inflexión en la curva $n(t)$ se dará en $t=\dfrac{\ln\left(\frac{K-n_0}{n_0}\right)}{r_c}$, como propusimos antes.

Ejercicio 7.6

Calcular el tamaño poblacional para una colonia bacteriana que comienza con 3 individuos al cabo de los tiempos $t=1$ hora, $t=2$ horas, $t=3$ horas y $t=4$ horas, con una tasa neta de crecimiento para el modelo continuo de $r_c=3,3\times 10^{-3}s^{-1}$ en el caso de que la capacidad de carga del sistema ($K$) sea de 12 millones de individuos.

Ejercicio 7.7

Señala cuáles de las siguiente afirmaciones son verdaderas y cuáles falsas:

En la transformación, luego de entrar en un estado particular conocido como competencia, las células bacterianas son capaces de captar ADN libre de doble cadena e incorporarlo en su genoma.
En la transducción un bacteriófago se adsorbe sobre la superficie bacteriana para inyectar su material genético en la célula.
Dependiendo de si se trata de un fago virulento o moderado, en la transducción, el programa genético puede derivar en un ciclo lítico donde se producirán múltiples copias del mismo y luego se producirá la lisis celular o el fago puede integrar su ADN en el genoma bacteriano, transformándose en un profago.
En procariotas los genes están generalmente organizados en una estructura de exones separados por intrones, además de poseer secuencias reguladoras que pueden encontrarse a miles de pares de bases.
En los eucariotas la arquitectura de los genes es extremadamente sencilla, por lo general solo una secuencia codificantes continua, con regulación en la región inmediata upstream.
En el modelo exponencial de crecimiento las poblaciones bacterianas crecen linealmente en el tiempo.
En el modelo de crecimiento exponencial, el tamaño poblacional en función del tiempo $t$, la tasa de crecimiento $r_c$ y el número inicial de individuos $n(0)$ tiene la forma $n(t)=n(0)e^{r_C\ t}$, lo que nos indica que el número de individuos en un tiempo dado crece linealmente con el número inicial ($n(0)$).
El modelo de crecimiento exponencial tiene en cuenta que las poblaciones bacterianas no pueden crecer indefinidamente.
El modelo de crecimiento logístico tiene en cuenta que las poblaciones bacterianas no pueden crecer indefinidamente e incorpora un parámetro para la capacidad de carga del sistema.
La capacidad de carga del sistema en el modelo de crecimiento logístico representa la máxima tasa de crecimiento de la población.
Los modelos haploides de selección natural se usan en plantas y animales, mientras que los modelos diploides de selección natural son los que se usan en procariotas.
Los eventos de transferencia horizontal de genes involucran el pasaje de material genético entre individuos (generalmente) de diferentes especies.
El debate entre las teorías neutralista y seleccionista de la evolución molecular persiste aún hoy en día, aunque la teoría Neutral en su forma original no es capaz de explicar la distribución de la variabilidad en la mayor parte de los casos conocidos.
Las tecnologías de secuenciación masiva (o Next Generation Sequencing, NGS) permitieron extender los estudios metagenómicos a un amplio rango de problemas, pero no tienen ninguna utilidad en los estudios de composición y dinámica poblacional microbiana.
La resistencia a los antimicrobianos (AMR) es un fenómeno extendido en el que los microbios desarrollan resistencia frente a tratamientos con drogas que anteriormente resultaban eficaces para su control y eliminación.
Una de las bases genéticas del desarrollo de la resistencia a los antimicrobianos (AMR) está en los reducidos tamaños poblacionales de los microbios en general y de los procariotas en particular.
El intercambio de plásmidos de resistencia es un mecanismo muy común en la resistencia a los antimicrobianos (AMR) y es extremadamente flexible ya que las poblaciones bacterianas pueden adquirir los plásmidos frente a un evento de presión selectiva inducido por drogas y luego perderlos cuando la amenaza desaparece.

Ejercicio 7.8

Dada la siguiente gráfica para el factor reproductivo $R(n)$ en función del número de individuos en la población, determinar los parámetros correspondientes del modelo logístico discreto y estimar el cambio esperado entre generaciones ($\Delta n$) cuando $n(t)=95$.

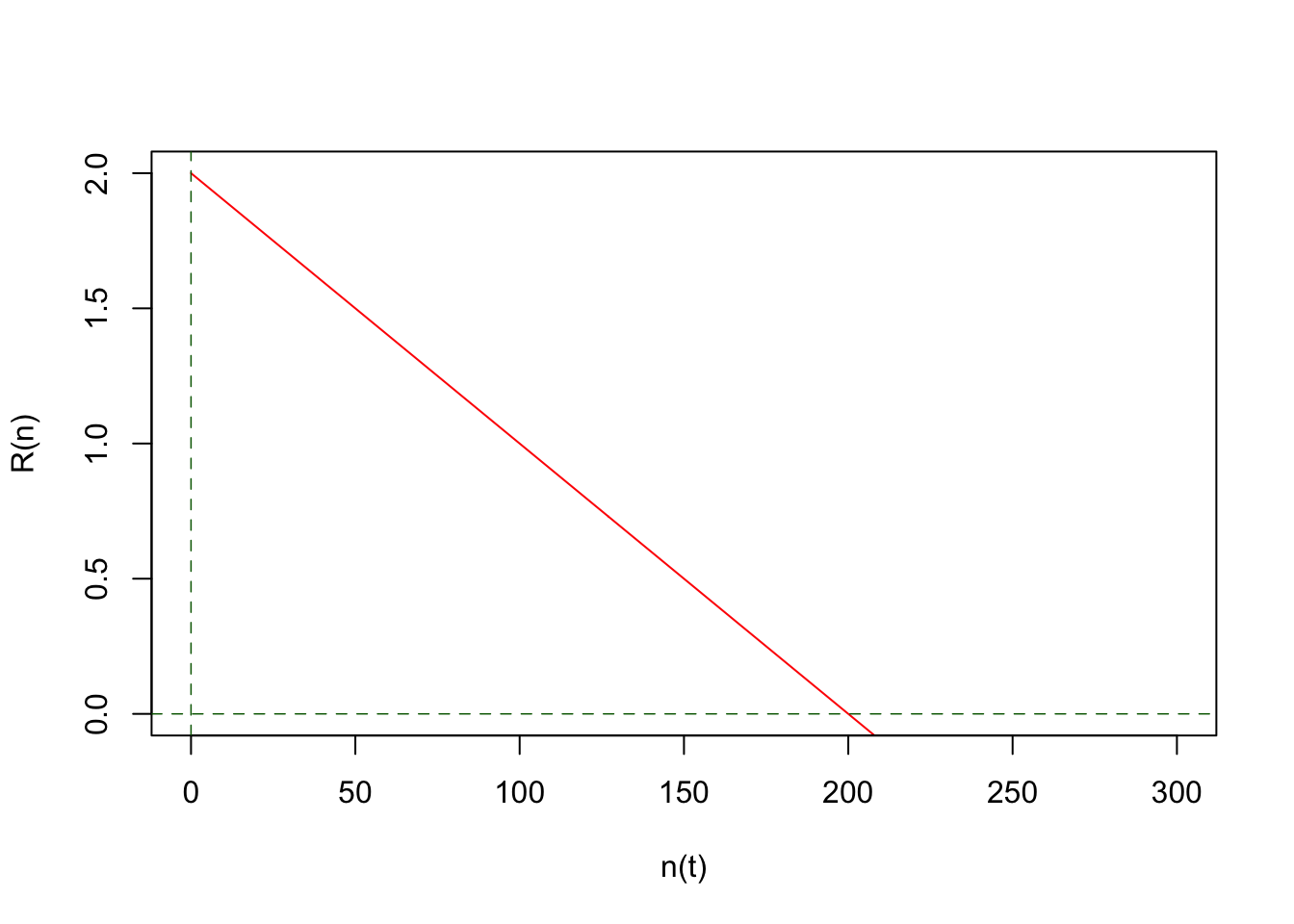
$Factor reproductivo $R(n)$ como función del tamaño poblacional..$

Figure 7.1: Factor reproductivo $R(n)$ como función del tamaño poblacional..

Ejercicio 7.9

Un reactor para la producción comercial de bacterias tiene una capacidad de carga $K=5 \times 10^{12}$ bacterias. La tasa neta de crecimiento del cultivo en tiempo continuo es $r_c=4,1667 \times 10^{-4}s^{-1}$. El funcionamiento del reactor permite cosechar bacterias de forma continua.

Determinar el punto óptimo (tamaño poblacional) en que el reactor permita retirar la mayor cantidad de bacterias por segundo y cuántas bacterias por segundo se retirarían en ese punto.
¿Cuantos gramos de bacterias se producirán por hora, considerando el peso aproximado de cada bacteria en $1 \times 10^{-12} g$?
Si el reactor se arranca a partir de un número inicial de $1 \times 10^{6}$ células ¿cuánto tiempo llevará llegar al punto óptimo si no se realiza cosecha de células hasta ese momento?